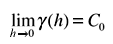Abstracts
The Pantanal of Mato Grosso presents distinct landscape units: permanently, occasionally and periodically flooded areas. In the last ones, sampling is especially difficult due to the high heterogeneity occurring inter and intrastratas. This paper presents a comparison of different methodological approaches showing that they can influence decisively the knowledge of distribution organic matter dynamics. In such an area in order to understand the role of the flood pulse in the distribution dynamics of organic matter in a wetland at the Pantanal, we considered that there is spatial dependence between points. This consideration contradicts the classical statistic principle that focuses on the aleatority, and allowed the obtainment of a larger volume of information from a minor sampling effort, which means better performance, with time and money economy.
geostatistics; sampling; organic matter; Pantanal of Mato Grosso
O Pantanal de Mato Grosso apresenta unidades distintas em sua paisagem: áreas permanentemente alagadas, áreas eventualmente alagáveis e áreas periodicamente alagáveis. Nestas últimas, as amostragens são particularmente difíceis, dada a heterogeneidade não apenas entre os estratos a serem amostrados como também dentro dos mesmos. Este trabalho usa como exemplo a avaliação do papel do pulso de inundação na dinâmica de distribuição de matéria orgânica em um campo inundável pantaneiro para mostrar que diferentes enfoques metodológicos e delineamentos amostrais podem influenciar decisivamente. Partimos do princípio de que há dependência espacial entre os pontos, contrariando a estatística clássica que enfoca a aleatoriedade. Este procedimento permite a obtenção de maior volume de informações a partir de menor esforço amostral, o que significa melhor desempenho, com economia de tempo e recursos.
geoestatística; amostragem; matéria orgânica; Pantanal de Matogrosso
GEOSTATISTICS AS A TOOL TO IMPROVE SAMPLING AND STATISTICAL ANALYSIS IN WETLANDS: A CASE SUDY ON DYNAMICS OF ORGANIC MATTER DISTRIBUTION IN THE PANTANAL OF MATO GROSSO, BRAZIL
NOGUEIRA, F.,1 COUTO, E. G.2 and BERNARDI, C. J.1
1Departamento de Botânica e Ecologia, IB, Universidade Federal de Mato Grosso, CEP 78060-900, Cuiabá, MT, Brazil
2Departamento de Solos e Engenharia Rural, FAMEV, Universidade Federal de Mato Grosso, CEP 78060-900, Cuiabá, MT, Brazil
Correspondence to: Flávia Maria de Barros Nogueira, Instituto de Biociências, Departamento de Botânica e Ecologia, Universidade Federal de Mato Grosso, Av. Fernando Correa s/n, Coxipó, CEP 78060-900, Cuiabá, MT, Brazil, e-mail: fnog@zaz.com.br
Received October 16, 2001 Accepted January 16, 2001 Distributed November 30, 2002
(With 7 figures)
ABSTRACT
The Pantanal of Mato Grosso presents distinct landscape units: permanently, occasionally and periodically flooded areas. In the last ones, sampling is especially difficult due to the high heterogeneity occurring inter and intrastratas. This paper presents a comparison of different methodological approaches showing that they can influence decisively the knowledge of distribution organic matter dynamics. In such an area in order to understand the role of the flood pulse in the distribution dynamics of organic matter in a wetland at the Pantanal, we considered that there is spatial dependence between points. This consideration contradicts the classical statistic principle that focuses on the aleatority, and allowed the obtainment of a larger volume of information from a minor sampling effort, which means better performance, with time and money economy.
Key words: geostatistics, sampling, organic matter, Pantanal of Mato Grosso.
RESUMO
A geoestatística como ferramenta para aprimorar a amostragem e a análise estatística em áreas inundáveis: um estudo de caso sobre a dinâmica da distribuição da matéria orgânica no Pantanal de Mato Grosso, Brasil
O Pantanal de Mato Grosso apresenta unidades distintas em sua paisagem: áreas permanentemente alagadas, áreas eventualmente alagáveis e áreas periodicamente alagáveis. Nestas últimas, as amostragens são particularmente difíceis, dada a heterogeneidade não apenas entre os estratos a serem amostrados como também dentro dos mesmos. Este trabalho usa como exemplo a avaliação do papel do pulso de inundação na dinâmica de distribuição de matéria orgânica em um campo inundável pantaneiro para mostrar que diferentes enfoques metodológicos e delineamentos amostrais podem influenciar decisivamente. Partimos do princípio de que há dependência espacial entre os pontos, contrariando a estatística clássica que enfoca a aleatoriedade. Este procedimento permite a obtenção de maior volume de informações a partir de menor esforço amostral, o que significa melhor desempenho, com economia de tempo e recursos.
Palavras-chave: geoestatística, amostragem, matéria orgânica, Pantanal de Matogrosso.
INTRODUCTION
The Pantanal of Mato Grosso presents distinct landscape units in relation to their flooding status: dry areas, permanently and periodically flooded areas. The dry areas with very small flood occurrence probability are located in higher levels showing vegetation with dominance of typical savanna species. Sampling for specific purposes, as ecological research for instance is complex as in any other environment, being even more complex in periodically flooded areas, because the environmental gradients and vegetation change very much along the year due to flooding. The spatial variability is one of the most important factors causing such complexity. Usually a large number of samples are necessary to decrease the coefficient variation values. Despite efforts and high costs, the results are limited to average values that may hardly show the stratum representability. In this context, a spatial distribution analysis considering the different flooding pulses can improve the results considering that if a large number of samples are necessary, most of the information should be extracted from them (Patil et al., 1997). Following this approach, the spatial variability is not a problem, but an important key towards understanding the system (McBratney & Laslett,1993; Burrough et al., 1994).
Here we show an example that portrays how different methodological focuses can influence decisively in studies with systemic approach. We show the role of the flood pulse in the Northern part of Pantanal of Mato Grosso, comparing the classical statistics and geostatistics.
MATERIAL AND METHODS
Study area and characteristics
Extensive cattle is a traditional economic activity in the Pantanal of Mato Grosso, especially in the Northern region, where the wetlands are used as native pastures. The economical success of the activity depends, mostly on the duration of the flooding during the wet period and on the soil surface moisture during the dry period (Cunha, 1990). The soils are sandy and the flood pulse determines sucessional dynamics that reinvigorate the communities (Junk et al., 1989). In this context, the understanding of the inputs and outputs of organic matter seems to be decisive in unders tanding the system and subsidy proposals for the sustainable use of these wetlands that have undeniable regional economic importance.
Soil sampling
To understand the importance of the flood pulse on the organic matter distribution dynamic, samples were collected in July 1999 and April 2000 respectively during the dry and the wet season. Once the seasonal sampling was defined, it was necessary to define the number of samples in the chosen periodically flooded area at the cattle farms in the municipality of Nossa Senhora do Livramento (Fig. 1).
In order to estimate the sample size, we collected the top layer of sediments surface soils (upper 2 cm) at six random points at each of the four units identified in the study area: a monospecific flooded forest (cambarazal), a flooded grassland with native pasture species (pasture), a permanently flooded area (swamp) and a multispecific flooded forest (located near the borders of a permanent lake) during the dry (September 1999) and wet season (April 2000). The samples were collected in triplicate and were dried (60°C), sieved (mesh of 0.297 mm) and chemically analyzed for organic carbon (Walkley & Black method).
We decided to adopt de geostatistical approach for the same area during the dry and wet season, collecting samples in systematic sampling scheme, in which sampling points were located at regular intervals on a grid of 25 x 25 m (Fig. 2), and each point was identified with a wooden stake.
Statistics and geostatistics
Statistics, such as minimum, maximum, means, range, standard deviation and coefficient of variation summarise the data using the software SPSS (SPSS 10.0, 1999). Considering that geostatistics is a tool that has been successfully used in tropical soil studies (Couto et al., 1997) and has proven useful to sustainability studies, e.g. for characterising and mapping spatial variation of soil properties. Common procedures include characterisation and modelling of spatial variability, estimating values at unvisited locations, spatial simulations of random fields and optimisation spatial sampling (Cahn et al., 1994).
To analyze the spatial variability between observation points use was made of geostatistics methods (Webster & Oliver, 1990).
Each soil variable that is measured is associated with its observation location x. For the ithvariable, denoted as zi(x), the variogram gi(h) is expected squared differences as a function of the distance h or lag between two locations and can be defined by:
where N(h) is the number of pairs of points z(si) and z(si + h), separated by a vector h of which the two points si and si+h fall within the same stratum. Calculation of the variogram thus becomes insensitive to obvious differences in mean z(si) values between different strata. The variogram is characterised by three major properties: the nugget effect (C0), the sill (C) and the range (a). The nugget effect C0 is a discontinuity of the variogram close to the origin:
and expresses both the variability at a scale smaller than the sampling interval and non-spatial variation. The nugget effect cannot be removed by close sampling, but only by repeated measurements (Trangmar et al., 1985). The range is the lag distance where the variance approaches an asymptotic maximum, the sill. It expresses the distance beyond which samples are uncorrelated.
Once the variogram is known, the value of an attribute at any point in a mapping unit can be predicted from the available data points using kriging. Kriging gives the standard deviation of the prediction error as well. This standard deviation depends only on the variogram, the number of data and the spatial configuration with which these are taken (Burrough, 1991) and can hence be used to determine the required number of data.
In this study, variograms were estimated using the software Gamma Design (Robertson, 2000). In this study, kriging was estimated using the software Surfer (Surfer, 1999).
RESULTS AND DISCUSSION
The classical statistical approach
The results obtained from this preliminary sampling procedure are shown in Table 1. The statistical tests applied to verify if there was homogeneity between the three samples of each of the six points of each unit did not indicate significant difference between locations inside the same unit (Oneway Anova, p = 0.01, SPSS version 10.0).
This means that a large number of samples would be necessary to characterize each unit, which would need a huge investment in field and laboratory structure in addition to increasing the costs very much. Moreover the results would give just an average number for each unit and define the similarity or difference between them with regard to organic matter contents.
This problem is a consequence of the high heterogeneity inter and intraunits as corroborated by coefficients of variation higher than 35% (Wilding & Drees, 1983). In this context a different approach was need in order to describe and analyze more efficiently the dynamics of the organic matter distribution in the system.
The geostatistical approach
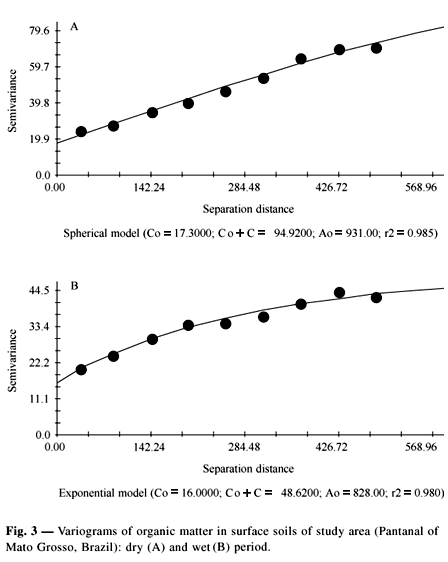
For the same area, a systematic sampling scheme would reduce drastically the number of samples (Table 1) and the obtained results would bring much more information regarding the units, because they can be expressed by maps, showing the spatial distribution of the organic matter. Variograms of organic matter content (OMC) are shown in Fig. 3. The sill value (Co + C) for OMC for wet season is reached at a shorter range than in the dry season, where as the range (Ao) is larger in dry season, showing that the spatial dependence is higher in this period. The same field procedures were repeated for the wet period (April 2000), when the classical sampling of the six points randomly showed the same bias (statistical parameters/wet period, Table 1). The spatial OMC estimated by kriging is shown in Fig. 4, where values range from 3 to more than 23% in the dry season. Moreover, the small values are concentrated in the wet season.
The Fig. 5 shows the differences in the number of samples comparing the four units, which used the classical statistics, if we consider a sample size of 6 samples, as used in this study. These resulted in estimates of organic matter content with more than 50% probable error on both seasons.
Considering the four units and the 10% of probable error, usually considered as an acceptable error (Davis et al., 1995), the sample size ranges from 155 samples for the unit "Swamp" to 381 for the unit "pasture", showing a high variability between the landscape units.
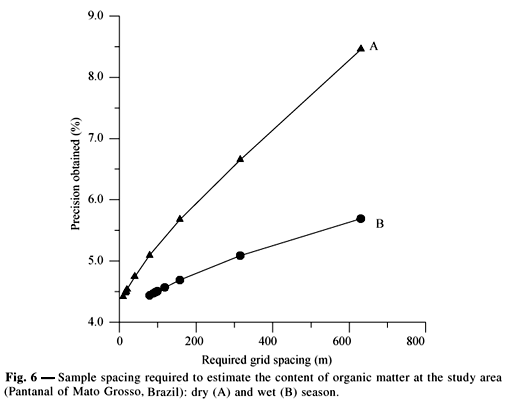
The variograms between current and future observation points can be used to calculate the optimal grid spacing for sampling to achieve a predetermined level of accuracy (PA). The PA, in the same units as the variables, is defined as the highest uncertainty that exists on an interpolated map. It is equal to the kriging standards deviation in the most isolated location of prediction, that is, the center point of a square grid cell with observations in each of the corners of this cell (Winkels & Stein, 1997). In this study, the interactive program OPTIM (Staritsky & Stein, 1993) was used to calculate the optimal grid spacing based on the PA of each variable in a square grid using their specific variograms with fitted models (Fig. 3). The Fig. 6 shows the maximum distance between sampling points to have the highest accuracy in the organic matter estimate values, through interpolation by kriging technique. Analysis of spatial variability through the design of an adequate sampling grid could be helpful in future studies in similar ecosystems. In this study, a grid pattern for adequate measurement of the organic matter content in dry and wet season has to be chosen.
We used OPTIM to determine the grid spacing necessary to achieve a predetermined level of accuracy.
The highest accuracy was estimated at 4.5% for both seasons; however, in the dry season the grid spacing (10 m) is 8 times shorter than in the wet season (80 m).
Maps overlapping dynamics of organic matter distribution
The Fig. 7 shows the resulting map overlapping the organic matter content in the dry season minus the organic matter content in the wet season. The Siarcs software (EMBRAPA, 1998) was used to estimate areas with input or output of organic matter in the final map. The results indicate that in 91.9% of the sampled area organic matter was removed during the flood wile in the 8.1% of the remaining area there was organic deposition. Moreover it indicated that most of the organic matter addition/deposition occurred in the pasture unit. This means that it appears to add little organic matter to the wetlands. We postulate that the water removes organic matter by decomposition of the organic material accumulated at the surface soil during the dry period, in more than 90% of the studied area. These results confirm the cyclic dynamics of the system, and stress the importance of the flood pulse for its maintenance.
CONCLUSIONS
Geostatistics gave a larger volume of information from a minor sampling effort, which means better performance, time and money economy.
The overlapping of maps produced for the different phases of the flood pulse showed the important role these processes play in the dynamics of addition/removal of organic matter in the flood gradient, indicating that geostatistics is a useful tool in studies considering seasonal variations.
Acknowledgments We are grateful to SHIFT Program (CNPq/IBAMA/DLR) (Pantanal Ecology Project-IB UFMT/MPIL Plön), for the financial support and Cristine Carole Muggler, for her review and comments on the manuscript.
- BURROUGH, P. A., 1991, Sampling designs for quantifying map unit composition, pp. 89-126. In: M. J. Mausbach & L. Wilding (eds.), Spatial variabilities of soils and landforms. Special publication, n. 28, Madison, Soil Sci. Soc. of America
- BURROUGH, P. A., BOUMA, J. & YATES, S. R., 1994, The state of the art in pedometrics. Geoderma, 62: 311-326.
- CAHN, M. D., HUMMEL, J. W. & BROUER, B. H., 1994, Spatial analysis of soil fertility for site-specific crop management. Soil. Sci. Soc. Am. J., 58: 1240-1248.
- COUTO, E. G., STEIN, A. & KLAMT, E., 1997, Large area spatial variability of soil chemical properties, in central Brazil. Agriculture Ecosystems and Environment, 66: 139-152.
- CUNHA, C. N., 1990, Estudos florísticos e fitofisionômicos das principais formaçőes arbóreas do Pantanal de Poconé, MT Master Thesis, Universidade Estadual de Campinas, Campinas, 146p.
- DAVIS, J. G., HOSSNER, L. R., WILDING, L. & MANU, A., 1995, Variability of soil chemical properties in two sandy, dunal soils of Niger. Soil Science, 159: 321-330.
- EMBRAPA, 1998, SIARCS 3.0. Manual do usuário EMBRAPA CNPDIA, São Carlos, 30p.
- JUNK, W., BAYLEY, P. B. & SPARKS, R. E., 1989, The flood-pulse concept in river-floodplain systems. In: D. P. Dodge (ed.), Proceedings of the International large Rivers Symposium (LARS). Canadian Special Publication, Fish Aquatic Sciences, 106: 110-127.
- McBRATNEY, A. B. & LASLETT, G. M., 1993, Sampling schemes for contamined soil., pp.435-439. In: H. J. P. Eijsackers (ed.), Integrated soil and sediment research: a basis for proper protection Kluwer Academic Publishers, Dordrecht.
- PATIL, G. P., JOHNSON, G. D., MYERS, W. L. & TAILLIE, C., 1997, Statistical ecology, environmental statistic and ecological assessment. International Journal of Ecology and Environmental Sciences, 23: 119-164.
- ROBERTSON, G. P., 2000, GS+: Geostatistics for the environment sciences GS+ User's Guide Version 5: Plainwell, Gamma design software, 200p.
- SPSS 10.0, 1999, SPPSS Base 10.0 Users Guide SPSS inc., Chicago, 537p.
- STARITSKY, I. G. & STEIN, A., 1993, SPATANAL , SPATIN and OPTIM Software Wageningen Agricultural University, Wageningen, 19p.
- SURFER, 1999, SURFER 7.0 Countouring and 3D surface mapping for scientists and engineers. Users Guide. Golden software, Inc., New York, 619p.
- TRANGMAR, B. B., YOST, R. S. & UEHARA, G., 1985, Applications of geostatistics to spatial studies of soil properties. Advances in Agronomy, 38: 45-94.
- WEBSTER, R. & OLIVER, M. A., 1990, Statistical methods in soil and land resource survey Oxford University Press, Oxford, 316p.
- WILDING, L. & DREES, L. R., 1983, Spatial variability and pedology, pp. 83-116. In: L.Wilding, N. E. Smeck & G. F. Hall (eds.), Pedogenesis and soil taxonomy I Concepts and interactions Elsevier, Amsterdam.
- WINKELS, H. J. & STEIN, A., 1997, Optimal cost-effective sampling for monitoring and dredging of contaminated sediments. J. Environ. Qual., 26: 933-946.
Publication Dates
-
Publication in this collection
17 Feb 2003 -
Date of issue
Nov 2002
History
-
Received
16 Oct 2001 -
Accepted
16 Jan 2001