Abstracts
In this study, patterns of spatial synchrony in population fluctuations (cross-correlation) of an endemic fish assemblage of a Neotropical reservoir (Segredo Reservoir, Iguaçu River, Paraná State, Brazil) were reported. First, the level of population synchrony for 20 species was estimated. Second, population synchrony was correlated, using the Mantel test, with geographical distances among sites (n = 11) and also environmental synchrony (temperature). Nine species presented significant correlations between spatial synchrony and geographic distances (Astyanax sp. b, Astyanax sp. c, Pimelodus sp., Hoplias malabaricus, Crenicichla iguassuensis, Hypostomus derbyi, Hypostomus myersi, Rhamdia branneri, and R. voulezi). Considering the ecology of the species and the significant relationship between population and environmental synchronies, it seems that environmental stochasticity is the most plausible hypothesis in explaining the observed synchrony patterns.
spatial synchrony; fish assemblage; reservoirs
Neste estudo, os padrões de sincronia espacial de uma assembléia de peixes endêmica em um reservatório neotropical (reservatório de Segredo, rio Iguaçu, Paraná, Brasil) foram descritos. Primeiro, foi estimado o nível de sincronia (correlação entre as densidades ao longo do tempo) para 20 espécies. Segundo, a matriz de sincronia populacional foi correlacionada, utilizando o teste de Mantel, com a distância geográfica entre os locais (n = 11) e com a sincronia ambiental (temperatura da água). Nove espécies apresentaram correlações significativas entre sincronia espacial e distância geográfica (Astyanax sp. b, Astyanax sp. c, Pimelodus sp., Hoplias malabaricus, Crenicichla iguassuensis, Hypostomus derbyi, Hypostomus myersi, Rhamdia branneri e R. voulezi). Considerando a ecologia das espécies e a relação significativa entre a sincronia populacional e a sincronia ambiental, é possível inferir que estocasticidade ambiental é a hipótese mais plausível para explicar os padrões de sincronia detectados.
sincronia espacial; assembléia de peixes; reservatórios
Spatial synchrony of a highly endemic fish Assemblage (Segredo Reservoir, Iguaçu River, Paraná State, Brazil)
Sincronia espacial de uma assembléia de peixes endêmica (reservatório de Segredo, rio Iguaçu, Paraná, Brasil)
Domingues, W. M.,I; Bini, L. M.II; Agostinho, A. A.I
INupelia (Bloco H-90), Universidade Estadual de Maringá, Av. Colombo, 5790, CEP 87020-900, Maringá, PR, Brazil
IIDepartamento de Biologia Geral, Instituto de Ciências Biológicas, Universidade Federal de Goiás, C.P. 131, CEP 74001-970, Goiânia, GO, Brazil
Correspondence Correspondence to Wladimir Marques Domingues Nupélia (Bloco H-90) Universidade Estadual de Maringá Av. Colombo, 5790 CEP 87020-900, Maringá, PR, Brazil e-mail: domingueswm@nupelia.uem.br
ABSTRACT
In this study, patterns of spatial synchrony in population fluctuations (cross-correlation) of an endemic fish assemblage of a Neotropical reservoir (Segredo Reservoir, Iguaçu River, Paraná State, Brazil) were reported. First, the level of population synchrony for 20 species was estimated. Second, population synchrony was correlated, using the Mantel test, with geographical distances among sites (n = 11) and also environmental synchrony (temperature). Nine species presented significant correlations between spatial synchrony and geographic distances (Astyanax sp. b, Astyanax sp. c, Pimelodus sp., Hoplias malabaricus, Crenicichla iguassuensis, Hypostomus derbyi, Hypostomus myersi, Rhamdia branneri, and R. voulezi). Considering the ecology of the species and the significant relationship between population and environmental synchronies, it seems that environmental stochasticity is the most plausible hypothesis in explaining the observed synchrony patterns.
Key words: spatial synchrony, fish assemblage, reservoirs.
RESUMO
Neste estudo, os padrões de sincronia espacial de uma assembléia de peixes endêmica em um reservatório neotropical (reservatório de Segredo, rio Iguaçu, Paraná, Brasil) foram descritos. Primeiro, foi estimado o nível de sincronia (correlação entre as densidades ao longo do tempo) para 20 espécies. Segundo, a matriz de sincronia populacional foi correlacionada, utilizando o teste de Mantel, com a distância geográfica entre os locais (n = 11) e com a sincronia ambiental (temperatura da água). Nove espécies apresentaram correlações significativas entre sincronia espacial e distância geográfica (Astyanax sp. b, Astyanax sp. c, Pimelodus sp., Hoplias malabaricus, Crenicichla iguassuensis, Hypostomus derbyi, Hypostomus myersi, Rhamdia branneri e R. voulezi). Considerando a ecologia das espécies e a relação significativa entre a sincronia populacional e a sincronia ambiental, é possível inferir que estocasticidade ambiental é a hipótese mais plausível para explicar os padrões de sincronia detectados.
Palavras-chave: sincronia espacial, assembléia de peixes, reservatórios.
INTRODUCTION
Temporal and spatial fluctuations in number of individuals are marked characteristics of all animal populations (Heino et al., 1997; Lundberg et al., 2000). Inspired by the seminal work of Elton & Nicholson (1942) and Moran (1953), the temporal dynamics in number of individuals from spatially distributed subpopulations are currently one of the main themes investigated by ecologists (Kendal et al., 2000; Ylikarjula et al., 2000; Grenouillet et al., 2001).
The fact that conspecific populations fluctuate in synchrony over large spatial scales has turned a phenomenon known as spatial synchrony (see Koenig, 1999) into what is now considered a common ecological pattern. Several studies have convincingly demonstrated that local populations of different species present synchronized temporal dynamics (Koenig, 1998; Cattadori et al., 1999; Shanker & Sukumar, 1999).
Spatial synchrony has several implications, among them that increasing spatial synchrony decreases the expected persistence of metapopulations (Hanski & Woiwod, 1993, and references therein). This is because if a harmful environmental event occurs over a large geographic area, all those that fluctuate synchronically suffer the same risk of being affected (Sutcliffe et al., 1996). The validity of various metapopulation models and that of answers to many questions arising in population biology, including application issues (see Earn et al., 1998, and Rohani et al., 1999), depends on the degree of spatial synchrony (Hanski & Woiwod, 1993), as does conservation biology.
Dependence on the degree of synchrony between local populations and the distance that separates them is a second factor that should be quantified. Recurrently, the degree of synchrony between pairs of population levels off with increasing distance between them (Ranta et al., 1995). This dependence may help in distinguishing processes that produce spatial synchrony (Hanski & Woiwod, 1993; Ranta et al., 1999). Among the main causal processes possibly producing synchronized population dynamics are migration, regional stochasticity, and the presence of nomadic predators. Basically, identifying one of these processes as the most important is the final objective of this research (Cattadori et al., 1999).
Despite the importance of the theme, studies on spatial synchrony in fish are rare (Myers et al., 1997; Lande et al., 1999; Grenouillet et al., 2001). To the best of our knowledge, they are inexistent for Neotropical freshwater fishes. Lack of familiarity with spatial synchrony patterns for Neotropical fish in general, and species of economic interest in particular, results from a paucity of historical data. However, due to legal requirements, data gathered by monitoring programs in Brazilian dammed rivers already provide enough information for beginning spatial synchrony studies on the dynamics of Neotropical fish populations.
The general objective of the present study was to quantify the spatial synchrony (at a specific level) of a fish assemblage in a recently created Neotropical reservoir. The following questions were addressed: (1) On short time scales and in an unstable environment, can the degree of synchrony be considered high, and (2) is there a relationship between synchrony (estimated for different species) and distance between the populations compared? In light of the results obtained, possible causal mechanisms behind spatial synchrony were discussed.
METHODS
Study area
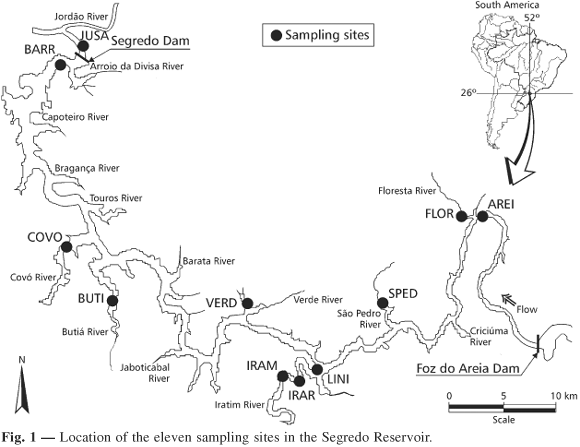
With an 82.5 km2 expanse and a drainage area of approximately 34,100 km2, the Segredo Reservoir (10 years old) was constructed in the Iguaçu River (Paraná State, Southern Brazil, 25º45" and 25º58'S and 51º30" and 52º05'W; Fig. 1). The Segredo Reservoir is the second one in a cascade of five reservoirs constructed in the main channel of the Iguaçu River, and the area it drains lies entirely within a subtropical-humid region with annual precipitation of 1,980 mm and no a dry season. Temperature values vary seasonally, averaging between 12 and 16ºC in winter and 20 and 23ºC in summer.
The Iguaçu River is of special interest for conservation biology because approximately 80% of the fish species are endemic (Agostinho et al., 1997), a probable consequence of geographic isolation produced by Iguaçu Falls, a 72-meter-high barrier, and at least two other falls.
Sampling
This study included three sampling sites within the reservoir, seven others in tributaries, and another located downstream from the dam (Fig. 1). Samples were taken monthly, from March 1993 to February 1995, using gill nets (sizes varying from 3 to 14 cm knot-to-knot) set for 24 hours. Catch per unit of effort (CPUE in number of individuals per 1,000 m2 caught by each gill net per 24 hours) was used as an abundance index. Monthly temperature values were recorded at all sites (ºC, using a thermistor).
Data analysis
Spatial synchrony was estimated following methods described by Pyper & Peterman (1998). Autocorrelation was initially removed from each time series by fitting the first-order autoregressive model Xt = pXt-1 + et, where Xt = log (CPUEt + 1), CPUEt is the abundance index for month t, p is the autoregressive coefficient, and e is the prewhitened series (white noise in the terminology used in temporal series; see Box & Jenkins, 1976). In this study, the first-differencing technique was also used to remove autocorrelation. The series of first differences is given by sXt = Xt-1, where sX denotes the new first-differenced time series. (This is another very simple approach that is generally effective in removing autocorrelation (Pyper & Peterman, 1998).) Prewhitened (e) and first-differenced (sX) time series were then used to estimate the degree of spatial synchrony in the dynamics of conspecific populations. Transformed rather than original time series were used in calculating spatial synchrony in order to avoid spurious correlations due to autocorrelation generated by local dynamics and not by processes related to migration or regional stochasticity (see Hanski & Woiwod, 1993). In addition, these methods are effective to control Type I error rates in tests of correlations (Pyper & Peterman, 1998).
For each species, Pearson product-moment correlation coefficients (cross-correlations with lag zero) were calculated for all pairs of sampling sites (i and j) using transformed time series (Hanski & Woiwod, 1993; Sutcliffe et al., 1996; Bjørnstad et al., 1999). Thus, for each species there are k = 55 correlation coefficients (rij), which is because data from n = 11 sampling sites yield k = [(n ´ n 1)/2] pairwise correlations (for i ¹ j) (Koenig, 1999). Two species-specific measures of spatial synchrony were used. The arithmetic mean of the 55 (rij) values was used as a first species-specific measure of spatial synchrony. A bootstrap confidence interval for these means was estimated by sampling with replacement among the sampling sites (deleting cross-correlations arising from comparing a site with itself). The percentile bootstrap (with 5,000 bootstrap iterations) was used to construct the bootstrap confidence intervals (Bjørnstad et al., 1999). Following the methods used by Hanski & Woiwod (1993), the intercept of the linear regression of rij against the geographic distances between sampling sites (dij) was used as a second species-specific measure of spatial synchrony. This is a preferable measure when there is a significant relationship between rij and dij (Hanski & Woiwod, 1993; Ranta et al., 1995).
The matrix of spatial synchrony for each species was transformed into a matrix of distance (chord) using the formula cij = Ö(2 2rij), where cij is the chord distance between sites i and j. In this case, values of cij equal to zero indicate that the temporal dynamics of local populations are perfectly correlated. Thereafter, the Mantel test was used to test the significance of the correlation between values of cij and dij (Euclidian distance between sampling points i and j) (Shanker & Sukumar, 1999). Both matrices were previously normalized so that the Mantel statistic (m) behaved as a product-moment correlation varying between 1 and +1 (Mantel, 1967; Fortin & Gurevitch, 1993). Due to the transformation of rij in cij, a positive value of m indicates that the degree of population synchrony decreases with increasing distance among the populations compared. In order to evaluate the significance of m, a randomization test was conducted. After each permutation the m statistic was calculated and the resulting values provided an empirical distribution (under the null hypothesis of no relationship between matrices) that was then used for the significance test. For each species, 20,000 random permutations of the data were used to ensure relative stability in the estimated level of significance (Jackson & Somers, 1989).
The same procedures described above were used to analyze geographical synchrony in air temperature. Thus, the chord distance between sampling sites was derived from Pearson's correlation coefficient (cross-correlations with lag zero) between prewhitened time series. The resulting matrix thus reflects the similarity level in the pattern of air temperature variation among sampling sites. Following the application of the procedures previously referred to, Mantel tests were used to evaluate the relative influence of spatially correlated environmental stochasticity on the spatial synchrony level in the dynamics of fish populations.
In this study, the model proposed by Hanski & Woiwod (1993) was used to evaluate the relative roles played by correlated environmental fluctuations (the Moran effect) and migration on the level of population synchrony. According to Hanski & Woiwod (1993), a positive relationship between maximum growth rate (see below) and the degree of spatial synchrony is consistent with the migration hypothesis. This prediction may be tested by assuming that species with high maximum population growth rates present a greater degree of intrinsically generated variability than species with low maximum population growth rates. Therefore, application of this model requires for each species measures of population synchrony, population variability, and growth rate. Following Hanski & Woiwod (1993), a species-specific measure of spatial synchrony was provided by the y-intercept of the linear regression of rij against the geographic distances between sampling sites (dij). For a given species, the arithmetic mean of the standard deviation values estimated for each sampling site (i.e., standard deviation of Xt) was used as a species-specific measure of population variability. There are no data to estimate intrinsic growth rate for every species. As an alternative, the maximum value of log (CPUEt+1/CPUEt ) was calculated for each time series with no zero. A species-specific measure of maximum growth rate was calculated by averaging these values across conspecific populations. Linear multiple regression analysis was used to test the model proposed by Hanski & Woiwod (1993). Thus, the degree of species-specific spatial synchrony was regressed against maximum growth rate and population variability.
RESULTS
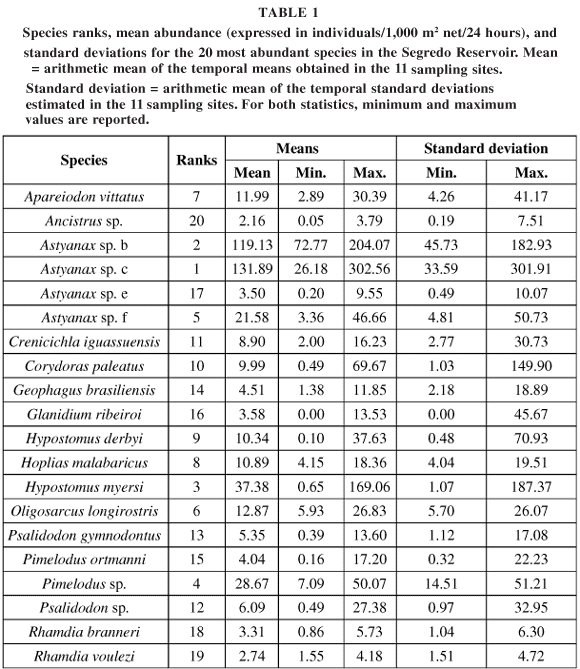
Captured individuals belonged to 7 orders, 13 families, 21 genera, and 40 species. The 20 most abundant species were analyzed in this study (see Table 1). The high number of species designed with epithets is explained by endemism. However, these clearly constitute different morphotypes, which justified their treatment as distinct taxa in this paper.
Species-specific spatial synchronies, as indicated by the y-intercept of the linear regression of rij against dij, estimated by either prewhitening or first-differencing the original time series strongly correlated with each other (r = 0.95; n = 20 species). Thus, only the results obtained with the last method are presented.
Considering the different species, the mean spatial synchrony (cross-correlation) between the 11 sites varied from 0.01 to 0.31. For mean spatial synchrony, the confidence intervals that are positive indicate species with significantly regionalized dynamics (Table 2). C. iguassuensis, Astyanax sp. c, H. myersi, P. gymnodontus, and H. derbyi stand out among them. Judging by the confidence intervals, the species that did not have regionalized dynamics (spatial synchrony) were Ancistrus sp., Astyanax sp. e, Pimelodus ortmanni, R. branneri, and R. voulezi. However, there were significant relationships between synchrony (chord transformed) and distance (see results below). These results indicate that the mean of all correlation coefficients is an unreliable species-specific measure of population synchrony (Hanski & Woiwod, 1993; Ranta et al., 1999), especially for R. branneri and R. voulezi.
For nine species, the degree of synchrony was significantly correlated with distance among the sampling sites (Table 3). However, the negative relationship between synchrony (rij values) and distance (dij) was more evident for those species that presented significant regionalized dynamics (Table 2 and Fig. 2).
Spatial synchrony in air temperature dynamics was significant (CI95% = 0.30, 0.46). The symmetric matrix associated with this variable (previously transformed into a chord distance matrix) was significantly related with the geographic distance matrix (m = 0.73; p = 0.0001). Thus, using the correlation coefficients, a clear decline in environmental synchrony with increasing distance between sampling sites was also observed (Fig. 3; y-intercept = 0.79).
The relationships between population synchrony and environmental synchrony were assessed using data from those species with significantly regionalized dynamics (Table 2) or those with a significant relationship between population synchrony and geographical distance (Table 3). For seven species, the Mantel test indicates a significant relationship between population synchrony and environmental synchrony matrices (Astyanax sp. b, Astyanax sp. c, H. derbyi, H. myersi, Pimelodus sp., R. branneri, R. voulezi; Table 3).
According to multiple regression analysis, regression coefficients for maximum growth rate and population variability were not significant. Thus, population synchrony was uncorrelated with both explanatory variables (Table 4). Multicollinearity problems were not detected in this analysis.
DISCUSSION
Synchrony values for the fish assemblage analyzed in this study were inferior to those obtained in other studies (Sutcliffe et al., 1996; Myers et al., 1997; Lande et al., 1999). As fish dispersal is generally highly constrained over large areas, especially in the Iguaçu River, we could expect fish to show less synchrony than other groups (Grenouillet et al., 2001). In addition to the clear distinction of taxonomic groups as well as the life-histories and ecosystems analyzed, all of which produce intrinsic ecological differences, various other characteristics may explain the variation in the degree of spatial synchrony detected. Among these characteristics, the following two may be considered important: number of local populations (Ylikarjula et al., 2000) and both temporal (Thompson & Page, 1989) and spatial (Hanski & Woiwod, 1993) scales analyzed.
In the present study, the number of locations is comparable, or even greater, than those considered in similar research (e.g., Ranta et al., 1997; Shanker & Sukumar, 1999). The spatial scale also seems adequate in view of the fact that the sampling sites were widely distributed. The influence of the relatively few months analyzed (n = 24), which may have jeopardized detection of correlations was, however, minimized by the first-differencing technique. According to Thompson & Page (1989) and Pyper & Peterman (1998), if high frequency (i.e., rapid changes in CPUE) components of variability are the dominant source of covariation, then first-differencing may be useful because it should increase covariation and the statistical power to detect it by removing low frequency variability that obscures the detection of that covariation. Thus, it may be assumed that the available data was generally adequate for estimating the degree of spatial synchrony.
A decline in population synchrony between sites as the distance between them increases is the main pattern that emerges in the studies of spatially structured populations (Lande et al., 1999; Koenig, 1999; Ranta et al., 1999). This pattern was true for 9 of the 20 species analyzed in this study. Although interesting and with conservation biology implications (Hanski & Woiwod, 1993; Ranta et al., 1999; Kendall et al., 2000), the detection of decline in synchrony with increase in distance between locations is not sufficient to identify the main mechanism that engenders population synchronization. In fact, at least three processes may be discerned as causal agents of this pattern, i.e., (1) the presence of nomadic predators moving between areas containing high densities of prey ("predation" hypothesis); (2) dispersal (migration hypothesis), and (3) spatially correlated environmental stochasticity (Moran effect) (Koenig, 1999; Hudson & Cattadori, 1999; Kendall et al., 2000).
In this study, the first two hypotheses listed above are less probable. For example, the migration hypothesis is doubtful since there are no large migrators in the Iguaçu river basin. Unlike the fish fauna of other rivers of the Paraná river basin, those developing in the Iguaçu River confront several obstacles (Suzuki & Agostinho, 1997; Júlio Jr. et al., 1997).
The only genus registered that includes migratory species, such as those observed in other basins, was Pimelodus (Agostinho et al., in press). However, there is no evidence that species of this genus in the Iguaçu basin present similar behavior. The predation hypothesis is also dubious in view of the fact that characteristic predators in the area of study are generally sedentary (H. malabaricus, Rhamdia, Crenicichla) or whose migrations are short (O. longirostris). In addition, except for Astyanax spp., species with significant relationships between synchrony levels and geographic distance were either not registered in the diet of piscivores or registered at very low frequencies. Even in the juvenile phases these species are not consumed with great frequency (Hahn et al., 1997; Gealh & Hahn, 1998).
We can expect the synchronizing effect of temperature (mainly driven by region-wide climatic factors) to be more important for fish, which are poikilotherms, than they are for homeotherms (Grenouillet et al., 2001). Thus, temporal dynamics of the environment (spatially correlated) are the most probable explanation for the patterns detected in this study.
In addition, a positive relationship between maximum population increase and spatial synchrony, expected according to the migration hypothesis, was not found. In this way, the evaluation of the model proposed by Hanski & Woiwod (1993) also demonstrates that patterns of spatial synchrony for fish assemblages in the Segredo Reservoir are probably caused by environmental stochasticity. It can be concluded from this study that, although estimated degrees of synchrony for the species analyzed are lower in relation to other studies, they may be detected in a relatively short time scale, in a recently-formed environment, and in a comparatively high number of species.
Acknowledgements Permission to collect this material was granted by PORT. N0 182/87 DEFOP/DF (Ministério do Ambiente/Sudepe). I thank Drs. Luiz Carlos Gomes, Alberto Carvalho Peret, Claudio José Von Zuben, and Harumi Irene Suzuki for helpful discussions and for comments on earlier drafts of the manuscript. In addition, I am grateful to the Núcleo de Pesquisa em Limnologia, Ictiologia e Aqüicultura (NUPÉLIA) for support and making available the infrastructure needed to conduct this research.
Received September 8, 2003 Accepted December 15, 2003 Distributed August 31, 2005
- AGOSTINHO, A. A., BINI, L. M. & GOMES, L. C., 1997, Ecologia de comunidades de peixes da área de influência do reservatório de Segredo. In: A. A. Agostinho & L. C. Gomes (eds.), Reservatório de Segredo bases ecológicas para o manejo EDUEM, Maringá, pp. 97-112.
- AGOSTINHO, A. A., GOMES, L. C., SUZUKI, H. I. & JÚLIO Jr., H. F., 2003, Migratory fish from the upper Paraná River basin, Brazil. In: J. Carolsfeld, B. Harvey, A. Baer & C. Ross (eds.), Migratory fishes of South America: biology, social importance and conservation status Occurrence and status of migratory fish biodiversity in South America, with special reference to Brazil World Fisheries Trust, Victory, BC, pp. 19-98.
- BJØRNSTAD, O. N., STENSETH, N. C. & SAITOH, T., 1999, Synchrony and scaling in dynamics of voles and mice in northern Japan. Ecology, 80: 622-637.
- BOX, G. E. P. & JENKINS, G. M., 1976, Time series analysis: forecasting and control 2nd ed. Holden Day, San Francisco.
- CATTADORI, I. M., HUDSON, P. J., MERLER, S. & RIZZOLI, A., 1999, Synchrony, scale and temporal dynamics of rock partridge (Alectoris graeca saxatilis) populations en the Dolomites. J. Anim. Ecol., 68: 540-549.
- EARN, D. J. D., ROHANI, P. & GRENFELL, B. T., 1998, Persistence, chaos and synchrony in ecology and epidemiology. Proc. R. Soc. Lond. B., 265: 7-10.
- ELTON, C. & NICHOLSON, M., 1942, The ten-year cycle in numbers of the lynx in Canada. J. Anim. Ecol., 11: 215-244.
- FORTIN, M. J. & GUREVITCH, J., 1993, Mantel tests: spatial structure in field experiments. In: S. M. Scheiner, J. Gurevitch (eds.), Design and analysis of ecological experiments Chapman & Hall, New York, pp. 342-359.
- GEALH, A. M. & HAHN, N. S., 1998, Alimentação de Oligosarcus longirostris Menezes & Gèry (Osteichthyes, Acestrorhynchinae) do reservatório de Salto Segredo, Paraná, Brasil. Rev. Bras. Zool., 15: 985-993.
- GRENOUILLET, G., HUGUENY, B., CARRE, G. A., OLIVIER, J. M. & PONT, D., 2001, Large-scale synchrony and inter-annual variability in roach recruitment in the Rhine River: the relative role of climatic factors and density-dependent processes. Freshw. Biol, 46: 11-26.
- HAHN, N. S., FUGI, R., ALAMEIDA, V. L. L., RUSSO, M. R. & LOUREIRO, V. E., 1997, Dieta e atividade alimentar de peixes do reservatório de Segredo. In: A. A. Agostinho & L. C. Gomes (eds.), Reservatório de Segredo bases ecológicas para o manejo EDUEM, Maringá, pp. 141-162.
- HANSKI, I. & WOIWOD, I. P., 1993, Spatial synchrony in the dynamics of moth and aphid populations. J. Anim. Ecol., 62: 656-668.
- HEINO, M., KAITALA, V., RANTA, E. & LINDSTRÖM, J., 1997, Synchronous dynamics and rates of extinction in spatially structured populations. Proc. R. Soc. Lond. B., 264: 481-486.
- HUDSON, P. J. & CATTADORI, I. M., 1999, The Moran effect: a cause of population synchrony. Trends Ecol. Evol., 14: 1-2.
- JACKSON, D. A. & SOMERS, K. M., 1989, Are probability estimates from the permutation model of Mantel's test stable? Can. J. Zool., 67: 766-769.
- JÚLIO, Jr. H. F., BONECKER, C. C. & AGOSTINHO, A. A., 1997, Reservatório de Segredo e sua inserção na bacia do rio Iguaçu. In: A. A. Agostinho & L. C. Gomes (eds.), Reservatório de Segredo bases ecológicas para o manejo EDUEM, Maringá, pp. 1-17.
- KENDALL, B. E., BJØRNSTAD, O. N., BASCOMPTE, J., KEITT, T. H. & FAGAN, W. F., 2000, Dispersal, environmental correlation, and spatial synchrony in population dynamics. Am. Nat., 155: 628-636.
- KOENIG, W. D., 1998, Spatial autocorrelation in California land birds. Conserv. Biol., 12: 612-620.
- KOENIG, W. D., 1999, Spatial autocorrelation of ecological phenomena. Trends Ecol. Evol., 14: 22-26.
- LANDE, R., ENGEN, S. & SAETHER, B. E., 1999, Spatial scale of population synchrony: environmental correlation versus dispersal and density regulation. Am. Nat., 154: 271-281.
- LUNDBERG, P., RANTA, E., RIPA, J. & KAITALA, V., 2000, Population variability in space and time. Trends Ecol. Evol., 15: 460-464.
- MANTEL, N., 1967, Detection of diseases clustering and a generalized regression approach. Cancer Res., 27: 209-220.
- MORAN, P. A. P., 1953, The statistical analysis of the Canadian lynx cycle. Aust. J. Zool., 1: 291-298.
- MYERS, R. A., MERTZ, G. & BRIDSON, J., 1997, Spatial scales of interannual recruitment variations of marine, anadromous and freshwater fish. Can. J. Fish. Aquat. Sci., 54: 1400-1407.
- PYPER, B. & PETERMAN, R. M., 1998, Comparison of methods to account for autocorrelation in correlation analyses of fish data. Can. J. Fish. Aquat. Sci., 55: 2127-2140.
- RANTA, E., KAITALA, V., LINDSTROM, J. & HELLE, E., 1997, The Moran effect and synchrony in population dynamics. Oikos, 78: 136-142.
- RANTA, E., KAITALA, V., LINDSTRÖM, J. & LINDÉN, H., 1995, Synchrony in population dynamics. Proc. R. Soc. Lond. B., 262: 113-118.
- RANTA, E., KAITALA, V., LINDSTRÖM, J. & LINDÉN, H., 1999, Spatially autocorrelated disturbances and patterns in population synchrony. Proc. R. Soc. Lond. B., 266: 1851-1856.
- ROHANI, P., EARN, J. D. & GRENFELL, B. T., 1999, Opposite patterns of synchrony in sympatric disease metapopultions. Science, 286: 968-971.
- SHANKER, K. & SUKUMAR, R., 1999, Synchrony in small mammal populations of montante forest patches in southern India. J. Anim. Ecol., 68: 50-59.
- SUTCLIFFE, O. L., THOMAS, C. D. & MOSS, D., 1996, Spatial synchrony and asynchrony in butterfly population dynamics. J. Anim. Ecol., 65: 85-95.
- SUZUKI, I. H. & AGOSTINHO, A. A., 1997, Reprodução de peixes do reservatório de Segredo. In: A. A. Agostinho, L. C. Gomes (eds.), Reservatório de Segredo bases ecológicas para o manejo EDUEM, Maringá, pp. 163-182.
- THOMPSON, K. R. & PAGE, H., 1989, Detecting synchrony of recruitment using short, auto-correlated time series. Can. J. Fish. Aquat. Sci., 46: 1831-1838
- YLIKARJULA, J., ALAJA, S., LAAKSO, J. & TESAR, D., 2000, Effects of patch and dispersal patterns on population dynamics and synchrony. J. Theor. Biol., 207: 377-387.
Correspondence to
Publication Dates
-
Publication in this collection
13 Dec 2005 -
Date of issue
Aug 2005
History
-
Accepted
15 Dec 2003 -
Received
08 Sept 2003