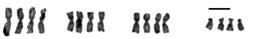Abstract
Chromosome stoichiometry, a form of genetic plasticity, specifically refers to variation in the standard diploid genomic composition of an individual or species. In the present work, freshwater planarians (Girardia schubarti) were analyzed to recognize variations in chromosomal stoichiometry especially of complete ploidal change between specimens, within specimens and between cells within specimens and any relations they might have with selected components of phenotypic plasticity. Homoploid polyploids for the group reached rational scalar multiples (e.g. tetraploids) or irrational scalar multiples (e.g. triploids). Karyotypic mosaics emerged where individual cells presented polyploid multiples in arithmetic and geometric progressions. Ploidal multiplicity, a chromosomal component of stochastic noise, had positive phenotypic effects (increased dimensions) on morphologic criteria of body length, body width and dorsal surface reflecting a significant genotypic plasticity (GP) and robust phenotypic plasticity (PP). Variable but significant association of genotypic plasticity with robust phenotypic variance suggests kinetics of phenotypic homeostasis that is species-specific permitting phenotypic adaptability to environmental variables by means of GP. That association is diminished, deactivated or lost in more advanced and more complex organisms.
Keywords:
haploid (n); genetic plasticity; karyotypic mosaics; kinetic homeostasis; ploidal value
Resumo
A estequiometria cromossômica, uma forma de plasticidade genotípica, representa variações na composição genômica diploide de um indivíduo ou espécie. Planárias límnicas (Girardia schubarti) foram analisadas para verificar a estequiometria cromossômica, especialmente alterações na ploidia entre espécimes, em cada espécime e entre células do mesmo espécime, além de relações dessas alterações com a plasticidade fenotípica. Espécimes poliploides homoploides apresentaram múltiplos escalares racionais ou irracionais, tais como triploides. Mosaicos cariotípicos ocorreram quando células apresentaram poliploides múltiplos em progressões aritméticas e geométricas. Nas planárias estudadas, a multiplicidade ploidal, um componente cromossômico de ruído estocástico, apresentou efeitos fenotípicos positivos, causando aumento das dimensões dos indivíduos, tais como comprimento corporal, largura do corpo e superfície dorsal, indicando plasticidade genotípica (GP) significativa e plasticidade fenotípica (PP) robusta. Associações significativas da plasticidade genotípica com variâncias fenotípicas robustas, embora variáveis, sugerem que a homeostase fenotípica, a qual é espécie-específica, possibilita adaptações a variáveis ambientais através da GP. Tal associação apresenta-se reduzida, desativada ou perdida em organismos mais complexos.
Palavras-chave:
haploides; plasticidade genética; mosaicos cariotípicos; homeostase cinética; valor ploidal
1. Introduction
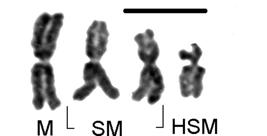
An essential point of biological identity for eukaryotes is the singular presence of chromosomes that constitutes the ploidal genomic base “n-value” (i.e. n-aggregate) for an individual and the species of which it is a part. Distinct morphological forms of chromosomes (Figure 1) allow identification by centricity class and number. This ploidal base however is usually multiplied by a scalar (λ) within individuals thus presenting a copy number. Diploidy (λ=2) (Figure 2) is the common “copy” of haploid (n(i,…,j)) chromosomal complements found in most species, thus defining the diploid genotype or genome (2n or “2 × n”) of a species where the total number of chromosomes is “y” so that (Equation 1): ,
the usual homeostatic ploidal value for most species.
Girardia schubarti: haploid (n=4) morphologic chromosomal aggregate (left to right) of one metacentric (M), two sub-metacentric (SM) and one highly sub-metacentric (HSM) (sub-acrocentric) chromosomes (scale bar=10 μm).
Complications arise when multiples of the ploidal base lead to variations in the homeostatic chromosomal aggregate. These multiples can be entire “2n” (gp::2n+∆2n(i,…,j)) (Equation 2)
or partial “n” haploid (gp∝∆n(i,…,j)) (Equation 3):
Such variations define genetic plasticity (gp) (Benya et al., 2007BENYA, E., LEAL-ZANCHET, A.M., SANTOS, W.H., HAUSER, J. and ERDTMANN, B., 2007. Chromsome polymorphism and complements in populations of Girardia species (Platyhelminths, Tricladida, Paludicola) from southern Brazil. Brazilian Journal of Biology = Revista Brasileira de Biologia, vol. 67, no. 4, suppl., pp. 951-955. PMid:18278365. http://dx.doi.org/10.1590/S1519-69842007000500021.
http://dx.doi.org/10.1590/S1519-69842007...
; Beukeboom et al., 1998BEUKEBOOM, L.W., SHARBEL, T.F. and MICHIELS, N.K., 1998. Reproductive modes of ploidy distribution, and supernumerary chromosome frequencies of the flatworm Polycelis nigra (Platyhelminthes: Tricladida). Hydrobiologia, vol. 383, no. 1/3, pp. 277-285. http://dx.doi.org/10.1023/A:1003460132521.
http://dx.doi.org/10.1023/A:100346013252...
) a measured variation in standard chromosome number for an individual or species, a physical component of genetic variance (). Such multiples at the sub-cellular physical level plus physiological variation can manifest a distinct presence within overall biological identity collectively called “stochastic noise” (Li et al., 2010LI, J., MIN, R., VIZEACOUMAR, F.J., JIN, K., XIN, X. and ZHANG, Z., 2010. Exploiting the determinants of stochastic gene expression in Saccharomyces cerevisiae for genome-side prediction of expression noise. Proceedings of the National Academy of Sciences of the United States of America, vol. 107, no. 23, pp. 10472-10477. PMid:20489180. http://dx.doi.org/10.1073/pnas.0914302107.
http://dx.doi.org/10.1073/pnas.091430210...
).
Chromosome stoichiometry (Pavelka et al., 2010PAVELKA, N., RANCATI, G., ZHU, J., BRADFORD, W.D., SARAF, A., FLORENS, L., SANDERSON, B.W., HATTEM, G.L. and LI, R., 2010. Aneuploidy confers quantitative proteome changes and phenotypic variation in budding yeast. Nature, vol. 468, no. 7321, pp. 321-325. PMid:20962780. http://dx.doi.org/10.1038/nature09529.
http://dx.doi.org/10.1038/nature09529...
), specifically refers to variation in the standard diploid (gp∝∆n(i,…,j)
±∆2n) genomic composition of an individual or species. It is a form of genetic plasticity.
Rational numeric scalar variations can occur in the haploid chromosomal base (n(i,…,j)) in its entirety termed “Whole Genome Duplication” (WGD) (n(i,…,j)
::∆2n) (Bekaert et al., 2011BEKAERT, M., EDGER, P.P., PIRES, J.C. and CONANT, G.C., 2011. Two-phase resolution of polyploidy in the Arabidopsis metabolic network gives rise to relative and absolute dosage constraints. The Plant Cell, vol. 23, no. 5, pp. 1719-1728. PMid:21540436. http://dx.doi.org/10.1105/tpc.110.081281.
http://dx.doi.org/10.1105/tpc.110.081281...
; Comai, 2005COMAI, L., 2005. The advantages and disadvantages of being polyploidy. Nature Reviews. Genetics, vol. 6, no. 11, pp. 836-846. PMid:16304599. http://dx.doi.org/10.1038/nrg1711.
http://dx.doi.org/10.1038/nrg1711...
). These multiples vary from the regular diploid (2n) complement such that polyploidy (2n(i,…,j)) of the 2n set (2n(i,…,j)
::∆2n) is manifest (Hieter and Griffiths, 1999HIETER, P. and GRIFFITHS, T., 1999. Polyploidy: more is more or less. Science, vol. 285, no. 5425, pp. 210-211. PMid:10428719. http://dx.doi.org/10.1126/science.285.5425.210.
http://dx.doi.org/10.1126/science.285.54...
). This ploidal variation can arise between populations within a species, between specimens within a population or between cells, within a specimen (i.e. karyotypic mosaicism). Polyploidy thus refers to complete haploid (n) copy number variability, as multiplicative variation, in the diploid base of a complete chromosomal complement (2n) (Hieter and Griffiths, 1999HIETER, P. and GRIFFITHS, T., 1999. Polyploidy: more is more or less. Science, vol. 285, no. 5425, pp. 210-211. PMid:10428719. http://dx.doi.org/10.1126/science.285.5425.210.
http://dx.doi.org/10.1126/science.285.54...
; Speicher and Carter, 2005SPEICHER, M.R. and CARTER, N.P., 2005. The new cytogenetics: blurring the boundaries with molecular biology. Nature Reviews. Genetics, vol. 6, no. 10, pp. 782-792. PMid:16145555. http://dx.doi.org/10.1038/nrg1692.
http://dx.doi.org/10.1038/nrg1692...
). It is a type of genomic mutation (Pala et al., 1999PALA, M., CASU, S. and STOCCHINO, G., 1999. Karyology and karyotype analysis of diploid freshwater planarian populations of the Dugesia gonocephala group (Platyhelminthes, Tricladida) found in Sardinia. Hydrobiologia, vol. 392, no. 2, pp. 113-119. http://dx.doi.org/10.1023/A:1003534507632.
http://dx.doi.org/10.1023/A:100353450763...
; Rajagopalan et al., 2004RAJAGOPALAN, H., JALLEPALLI, P.V., RAGO, C., VELCULESCU, V.E., KINZLER, K.W., VOGELSTEIN, B. and LENGAUER, C., 2004. Inactivation of hCDC4 can cause chromosomal instability. Nature, vol. 428, no. 6978, pp. 77-81. PMid:14999283. http://dx.doi.org/10.1038/nature02313.
http://dx.doi.org/10.1038/nature02313...
) where the entire ploidal base of “n” chromosomes is affected at meiosis or mitosis, but individual genes almost always remain intact, undergoing only multiplicative changes in their numbers.
In organisms of indeterminate growth (e.g. angiosperms) such multiplication can be beneficial (Sterken et al., 2012STERKEN, R., KIEKENS, R., BORUC, J., ZHANG, F., VERCAUTEREN, A., VERCAUTEREN, I., DE SMET, L., DHONDT, S., INZÉ, D., DE VEYLDER, L., RUSSINOVA, E. and VUYLSTEKE, M., 2012. Combined linkage and association mapping reveals CYCD5;1 as a quantitative trait gene for endoreduplication in Arabidopsis. Proceedings of the National Academy of Sciences of the United States of America, vol. 109, no. 12, pp. 4678-4683. PMid:22392991. http://dx.doi.org/10.1073/pnas.1120811109.
http://dx.doi.org/10.1073/pnas.112081110...
; Pennisi, 2011PENNISI, E., 2011. Green genomes. Science, vol. 332, no. 6036, pp. 1372-1375. PMid:21680823. http://dx.doi.org/10.1126/science.332.6036.1372.
http://dx.doi.org/10.1126/science.332.60...
; Jaio et al., 2011JAIO, Y., WICKETT, N.J., AYYAMPALAYAM, S., CHANDERBALI, A.S., LANDHERR, L., RALPH, P.E., TOMSHO, L.P., HU, Y., LIANG, H., SOLTIS, P.S., SOLTIS, D.E., CLIFTON, S.W., SCHLARBAUM, S.E., MA, H., LEEBENS-MACK, J. and DEPAMPHILIS, C.W., 2011. Ancestral polyploidy in seed plants and angiosperms. Nature, vol. 473, no. 7345, pp. 97-100. PMid:21478875. http://dx.doi.org/10.1038/nature09916.
http://dx.doi.org/10.1038/nature09916...
). However in organisms of determinate growth (e.g. mammals) such change can be deleterious (Leitch and Leitch, 2008LEITCH, A.R. and LEITCH, I.J., 2008. Genome plasticity and the diversity of polyploidy plants. Science, vol. 320, no. 5875, pp. 481-483. PMid:18436776. http://dx.doi.org/10.1126/science.1153585.
http://dx.doi.org/10.1126/science.115358...
). Mechanisms or processes that determine polyploidy are numerous. Endoreduplication, sometimes referred to as endoreplication (Edgar and Orr-Weaver, 2001EDGAR, B.A. and ORR-WEAVER, T.L., 2001. Endoreplication cell cycles: more for less. Cell, vol. 105, no. 3, pp. 297-306. PMid:11348589. http://dx.doi.org/10.1016/S0092-8674(01)00334-8.
http://dx.doi.org/10.1016/S0092-8674(01)...
) is one of the best documented processes giving rise to polyploidy (Hieter and Griffiths, 1999HIETER, P. and GRIFFITHS, T., 1999. Polyploidy: more is more or less. Science, vol. 285, no. 5425, pp. 210-211. PMid:10428719. http://dx.doi.org/10.1126/science.285.5425.210.
http://dx.doi.org/10.1126/science.285.54...
; Sterken et al., 2012STERKEN, R., KIEKENS, R., BORUC, J., ZHANG, F., VERCAUTEREN, A., VERCAUTEREN, I., DE SMET, L., DHONDT, S., INZÉ, D., DE VEYLDER, L., RUSSINOVA, E. and VUYLSTEKE, M., 2012. Combined linkage and association mapping reveals CYCD5;1 as a quantitative trait gene for endoreduplication in Arabidopsis. Proceedings of the National Academy of Sciences of the United States of America, vol. 109, no. 12, pp. 4678-4683. PMid:22392991. http://dx.doi.org/10.1073/pnas.1120811109.
http://dx.doi.org/10.1073/pnas.112081110...
). Individual gene expression can be induced or repressed by variation in ploidal numbers (i.e. n, 2n, 3n, etc.) between individual specimens of a population or species (Galitski et al., 1999GALITSKI, T., SALDANHA, A.J., STYLES, C.A., LANDER, E.S. and FINK, G.F., 1999. Ploidy regulation of gene expression. Science, vol. 285, no. 5425, pp. 251-253. PMid:10398601. http://dx.doi.org/10.1126/science.285.5425.251.
http://dx.doi.org/10.1126/science.285.54...
). Such variation can amplify or contract the physical expanse of a genome.
Results of such mechanisms or processes are especially frequent in triclads (Kawakatsu et al., 1983KAWAKATSU, M., HAUSER, J., FRIEDRICH, S.M.G., OKI, I., TAMURA, S. and YAMAYOSHI, T., 1983. Morphological, karyological and taxonomic studies of freshwater planarians from south Brazil IV. Dugesia anderlani sp. nov. (Turbellaria, Tricladida, Paludicola), a new species from São Leopoldo in Estado de Rio Grande do Sul. Annotationes Zoologicae Japonenses, vol. 56, pp. 196-208., 1984KAWAKATSU, M., OKI, I., TAMURA, S., YAMAYOSHI, T., HAUSER, J. and FRIEDRICH, S.M.G., 1984. Morphological, karyological and taxonomic studies of freshwater planarians from south Brazil VI. Dugesia schubarti (Marcus, 1946) from the vicinity of São Leopoldo, Estado de Rio Grande do Sul (Turbellaria, Tricladida, Paludicola). The Bulletin of Fuji Women's College, vol. 22, pp. 45-62.). However isolation, identification and referential indexing of these processes in individual specimens and populations can present problems of ploidal stability. Specimens of freshwater triclads are known for their robust regenerative capacity after suffering multiple partitions (e.g. amputations) where each segment regenerates a clone of the original specimen (Newmark and Alvarado, 2002NEWMARK, P.A. and ALVARADO, A.L., 2002. Not your father’s planarian: a classic model enters the era of functional genomics. Nature Reviews. Genetics, vol. 3, no. 3, pp. 210-219. PMid:11972158. http://dx.doi.org/10.1038/nrg759.
http://dx.doi.org/10.1038/nrg759...
; Wagner et al., 2011WAGNER, D.E., WANG, I.E. and REDDIEN, P.W., 2011. Clonogenic neoblasts are pluripotent adult stem cells that underlie planarian regeneration. Science, vol. 332, no. 6031, pp. 811-816. PMid:21566185. http://dx.doi.org/10.1126/science.1203983.
http://dx.doi.org/10.1126/science.120398...
).
Goal of this research was to recognize variations in chromosomal stoichiometry especially of complete ploidal change between specimens, within specimens and between cells within specimens of the species Girardia schubarti (Marcus, 1946), any tendencies those variations might present and any relations they might have with selected components of phenotypic plasticity (PP).
2. Material and Methods
Specimens of G. schubarti (Marcus, 1946) analyzed for this study were from the South Brazilian State of Rio Grande do Sul (Table 1), which has a sub-tropical climate, allowing emphasis on ploidal variation. A tissue liquefaction-and-spread method was used, as previously described (Benya et al., 2007BENYA, E., LEAL-ZANCHET, A.M., SANTOS, W.H., HAUSER, J. and ERDTMANN, B., 2007. Chromsome polymorphism and complements in populations of Girardia species (Platyhelminths, Tricladida, Paludicola) from southern Brazil. Brazilian Journal of Biology = Revista Brasileira de Biologia, vol. 67, no. 4, suppl., pp. 951-955. PMid:18278365. http://dx.doi.org/10.1590/S1519-69842007000500021.
http://dx.doi.org/10.1590/S1519-69842007...
), to extract metaphase stage chromosomes from each specimen, then spread, fix, stain, count and classify their morphology within each plate. Specimens were primarily distinguished as having haploid chromosomal morphologic base aggregates of n=4. They were then further distinguished as being diploid (2n) so that (2n=2λx=8, where x=1 and λ=4); the homeostatic standard genomic complement for most organisms, or as being polyploid; a numerical multiple [) (2) =(2 )] of that diploid complement, thus being some putative metastatic genomic complement (i.e. triploid, tetraploid, pentaploid, etc.) (Figures 3-5).
Regions furnishing specimens for this investigation and their altitudes, ploidal constitution and ploidal value (PV).
Girardia schubarti: triploid 3n=12; irrational multiple (λ=1.5) of an original homeostatic 2n=8 complement presenting metastatic 3n sequence of n=4-aggregate of chromosomal morphologic forms (scale bar=10 μm).
Girardia schubarti: pentaploid 5n=20; irrational multiple (λ=2.5) of an original homeostatic 2n=8 complement presenting metastatic 5n sequence of n=4-aggregate of chromosomal morphologic forms (scale bar=10 μm).
Pure polyploid specimens were recognized as were karyotypic mosaics, those with diverse inter-cellular chromosome stoichiometry (i.e. specimens presenting a matrix of cells having differing multiples of the diploid base within the same specimen). Mathematically rational multiples (i.e. 2, 3, 4, etc.) of the diploid complement were documented. Mathematically irrational multiples (e.g. 1.5, 2.5) also termed “off ploidy” (Pavelka et al., 2010PAVELKA, N., RANCATI, G., ZHU, J., BRADFORD, W.D., SARAF, A., FLORENS, L., SANDERSON, B.W., HATTEM, G.L. and LI, R., 2010. Aneuploidy confers quantitative proteome changes and phenotypic variation in budding yeast. Nature, vol. 468, no. 7321, pp. 321-325. PMid:20962780. http://dx.doi.org/10.1038/nature09529.
http://dx.doi.org/10.1038/nature09529...
), presenting triploid and pentaploid, chromosome plates, were also documented. Each specimen was then assigned a “Ploidal Value” (PV) recognized according to karyotype (i.e. 2n, 3n, 4n, mosaic), a genotypic variable. For homoploid specimens for the diploid complement or for any rational numerical multiple of that complement, the PV was simply the multiple (rational or irrational) of the diploid (i.e. 2n, 3n, 4n, etc.).
Specimens presenting mosaic plate proportions varying between 0 and 100% for each diploid multiple received a PV calculated in one of three ways. Where the diploid chromosomal plate count dominates within a specimen (>50% of plates) take the highest irrational polyploidal plate count within that mosaic (i.e. 3n, 5n, etc.). Calculate the percentage contribution of that “off-ploidal” polyploid to the entire mosaic of that specimen. Multiply that percentage by the haploid (i.e. n=4) of the specimen. Add this result to the predominant homeostatic plate count (2n=8). Thus Σ (plate count) =18 where 16 plates=2n and 2 plates=3n, then 2/18=0.11x(n=4)=0.44+(2n=8)=8.44=PV.
Where plate counts, present at irrational scalar multiples of the 2n diploid complement (e.g. 3n), dominate a specimen, thus having an “off ploidy” (Pavelka et al., 2010PAVELKA, N., RANCATI, G., ZHU, J., BRADFORD, W.D., SARAF, A., FLORENS, L., SANDERSON, B.W., HATTEM, G.L. and LI, R., 2010. Aneuploidy confers quantitative proteome changes and phenotypic variation in budding yeast. Nature, vol. 468, no. 7321, pp. 321-325. PMid:20962780. http://dx.doi.org/10.1038/nature09529.
http://dx.doi.org/10.1038/nature09529...
), all chromosomal plates presenting numerically irrational multiples of that “off ploidy” (e.g. 3n, 6n) are combined and analyzed as a homologous entity with the predominant polyploidy being the divisor in total percentage calculations. Thus a specimen presenting 54 total plates where 5 plates=2n, 42 plates=3n, 4 plates=4n and 3 plates=6n, polyploids 3n and 6n are scalar multiples “1x” and “2x” respectively of irrational (2n×1.5=3n) yielding off ploidal polyploid 3n. The number of 3n plates=42 and the number of 6n plates=3 Σ 42+3=45 total “off ploidal” count. Diploids 2n and polyploids 4n are rational scalar multiples “1x” and “2x” of diploid 2n. As the number of 2n plates=5 and the number of 4n plates=4; thus Σ 5+4=9 (homeostatic diploid and polyploidy). Polyploid plates 3n+6n=45 predominate; thus 45/54=0.83x(n=4)=3.33+(2n=8)= 11.33=PV.
Where a specimen is dominated by polyploidy at numerically rational multiples (e.g. 3n, 4n, 8n) total plate count will be the denominator in calculating overall polyploid proportions so that Σ [total plate count]=2n+3n+4n+…), when 7 plates at 2n=8, 15 plates at 3n=12, 41 plates at 4n=16, 9 plates at 8n=32; Σ [total plate count]= 7+15+41+9=72. Any plate count that is a geometric scalar multiple of the polyploid dominant (e.g. 4n=16, 8n=32) is counted with/and as a component of the predominant polyploid count (e.g. 7 plates at 2n=8, 41 plates at 4n=16, 9 plates at 8n=32). The predominant polyploid plate count = 41 at 4n=16 Σ [predominant polyploidy plate count ] = 7+41+9=57. Use this sum to calculate the percentage that is the dominant polyploid component of the specimen (e.g. 57/72=0.792). Multiply that percentage by the haploid (i.e. n=4) of the specimen (e.g. 0.792×n=4=3.17). Add this result to the highest irrationally numerical scalar multiple of 2 n (e.g. 3n plus any of its rational multiples) within that specimen: Σ [predominant polyploidy plate count] = 41 (at 4n=16)+9(at 8n=32)+7 (at 2n=8) =57/72=0.792 x [n=4] =3.17 + [3n=12]= 15.17=PV.
Measurements of body length (BL), body width (BW) and their composite measure as “dorsal body surface” (DS) (i.e.) furnished the phenotypic variables (i.e. body criteria) for this study. Identification of these variables associated with that of ploidal variation allowed statistical analysis (i.e. ANOVA, correlations, regressions, using SPSS) of data with the goal of identifying ploidal tendencies as well as their possible relations with phenotypic plasticity. The investigation then focused on statistical analysis of individual populations. The 40 specimens distributed and associated into 14 clusters of two to 40 specimens per cluster. Association within each cluster was according to rational or irrational scalar multiples of the n-aggregate base (n=4). A specimen could thus belong to more than one cluster.
3. Results
Chromosome plates (n=927) from 40 specimens of the species G. schubarti were examined. A group of three populations from three geographic regions of the state of Rio Grande do Sul, Brazil, presented metaphase chromosome plates, the qualities of which revealed polyploidy at varying scalar multiples of the diploid 2n homeostatic chromosome complement. Physiologic phenotypes are not addressed in this report. Chromosome plates within each individual specimen were classified as diploid (2n=8) (Figure 2), triploid (3n=12) (Figure 3) tetraploid (4n=16) (Figure 4), or stable mosaic at 2n, 3n, 5n, 6n, up to and including 8n and any variation therein (Table 1).
Girardia schubarti: tetraploid 4n=16; rational multiple (λ=2) of and original homeostatic 2n complement presenting metastatic 4n sequence of n=4-aggregate of chromosomal morphologic forms (scale bar=10 μm).
Of the three populations, two were tetraploid and one was sympatric pure diploid, triploid, tetraploid plus mosaic. Karyotypic mosaics presented the 2n, 3n, 4n, 5n, 6n or 8n ploidal multiples in varying proportions. Of the 40 specimens studied, nine were pure homoploid 2n (i.e. 2n=8) and 31 were polyploid homoploid multiples (>2n), or mosaic (heteroploid) combinations, significantly variant from a random 50:50 expectation. This distribution indicates significant variability in ploidal stability (ploidal lability) within the species G. schubarti having a high genotypic plasticity, reflected in notable levels of endoreduplication and/or non-segregation at the haploid level (Sterken et al., 2012STERKEN, R., KIEKENS, R., BORUC, J., ZHANG, F., VERCAUTEREN, A., VERCAUTEREN, I., DE SMET, L., DHONDT, S., INZÉ, D., DE VEYLDER, L., RUSSINOVA, E. and VUYLSTEKE, M., 2012. Combined linkage and association mapping reveals CYCD5;1 as a quantitative trait gene for endoreduplication in Arabidopsis. Proceedings of the National Academy of Sciences of the United States of America, vol. 109, no. 12, pp. 4678-4683. PMid:22392991. http://dx.doi.org/10.1073/pnas.1120811109.
http://dx.doi.org/10.1073/pnas.112081110...
) but also at the diploid and even triploid levels. Complete polyploids at 3n and 4n (y=2n ) (8 specimens, 20%) formed a notable minor cluster (Table 1). Statistical analysis revealed varying levels of difference or relationship between clusters.
This species is distinguished by morphologic forms of chromosomes constituting its total aggregate. At n=4 the species has one metacentric, two sub-metacentric and one highly sub-metacentric chromosome (Figures 1-5) whose form was approaching sub-acrocentric, a key indicator of basic chromosomal aggregation (n) and ploidal level.
These 40 specimens presented body criteria dimensions having positive correlations with PV, those of BW and DS being significant. Regression analysis indicated significant quadratic and cubic effects of PV on BL, BW and DS. A group of specimens at Salvador do Sul (alt. 113 m) showed highly significant positive correlations of body criteria measurements with PV at r=0.464, P=0.004, r=0.563,P<0.001 and r=0.511,P=0.001 for BL, BW and DS. BL reached significant lengths of 25.0 mm and BL measured 4.0 mm as DS reached 100 mm2 at maximum PV of 18.86. However these values significantly regressed (quadradically and cubically) to 2n (wild type) levels as the mean PV diminished to 10.3.
All three body criteria showed significant regression with PV confirming the linear correlations but reflecting a phenotypic tendency toward the body dimensions of the homeostatic 2n specimens after significant growth to variable but predictable dimensions. This tendency was reinforced in a cluster of 11 specimens, homoploid or mosaic, presenting binary step-wise multiples (i.e. 4n, 6n, 8n) of their 2n base. Positive linear correlations and regressions of body criteria with PV were all significant.
Specimens (n=15) presenting strictly rational multiples of the diploid, n=4-aggregate (i.e. 2n=8 and 4n=16) showed significant linear correlation of the body criteria BW and DS with PV at r=0.587, P=0.021 and r=0.529, P=0.043 respectively. Specimens (n=25) at Salvador do Sul presenting irrational multiples, homoploid or mosaic for the diploid n=4-aggregate (e.g. 3n, 5n) showed significant linear correlation of BW and DS with PV (i.e. r=0.504 and 0.437) and significant regression of these criteria with PV.
4. Discussion
Chromosome stoichiometry (Becskei et al., 2005BECSKEI, A., KAUFMANN, B.B. and VAN OUDENAARDEN, A., 2005. Contributions of low molecular number and chromosomal positioning to stochastic gene expression. Nature Genetics, vol. 37, no. 9, pp. 937-944. PMid:16086016. http://dx.doi.org/10.1038/ng1616.
http://dx.doi.org/10.1038/ng1616...
; Pavelka et al., 2010PAVELKA, N., RANCATI, G., ZHU, J., BRADFORD, W.D., SARAF, A., FLORENS, L., SANDERSON, B.W., HATTEM, G.L. and LI, R., 2010. Aneuploidy confers quantitative proteome changes and phenotypic variation in budding yeast. Nature, vol. 468, no. 7321, pp. 321-325. PMid:20962780. http://dx.doi.org/10.1038/nature09529.
http://dx.doi.org/10.1038/nature09529...
; Chester et al., 2012CHESTER, M., GALLAGHER, J.P., VAUGHAN SYMONDS, V., SILVA, A.V.C., MAVRODIEV, E.V., LEITCH, A.R., SOLTIS, P.S. and SOLTIS, D.E., 2012. Extensive chromosomal variation in a recently formed natural allopolploid species, Tragopogon miscellus (Asteraceae). Proceedings of the National Academy of Sciences of the United States of America, vol. 109, no. 4, pp. 1176-1181. PMid:22228301. http://dx.doi.org/10.1073/pnas.1112041109.
http://dx.doi.org/10.1073/pnas.111204110...
) can be used as a gauge of genome amplification which can be measured in numerically complete multiples of n-aggregate ploidal complements within cells (Xi et al., 2011XI, R., HADJIPANAYIS, A.G., LUQUETTE, L.J., KIM, T.-M., LEE, E., ZHANG, J., JOHNSON, M.D., MUZNY, D.M., WHEELER, D.A., GIBBS, R.A., KUCHERLAPATI, R. and PARK, P.J., 2011. Copy number variation detection in whole-genome sequencing data using the Bayesian information criterion. Proceedings of the National Academy of Sciences of the United States of America, vol. 108, no. 46, pp. 1128-1136. PMid:22065754. http://dx.doi.org/10.1073/pnas.1110574108.
http://dx.doi.org/10.1073/pnas.111057410...
). In the present study, that multiplicity was especially obvious (31 of 40 specimens: 77.5%) in populations presenting a basic n=4 chromosomal aggregate. However within specimens studied herein, this multiplicity usually occurred in varying degrees between zero and 100% in multiples of “2” (i.e. 𝜆=2) being arithmetic and even geometric (i.e. mosaics 3n=12, 4n=16, 6n=24, 8n=32) in its sequence resulting in karyotypic mosaic individuals and even homoploid polyploidy individuals.
Consonant with antecedent studies (Comai, 2005COMAI, L., 2005. The advantages and disadvantages of being polyploidy. Nature Reviews. Genetics, vol. 6, no. 11, pp. 836-846. PMid:16304599. http://dx.doi.org/10.1038/nrg1711.
http://dx.doi.org/10.1038/nrg1711...
; Gregory et al., 2000GREGORY, T.R., HEBERT, P.D.N. and KOLASA, J., 2000. Evolutionary implications of the relationship between genome size and body size in flatworms and copepods. Heredity, vol. 84, no. Pt 2, pp. 201-208. PMid:10762390. http://dx.doi.org/10.1046/j.1365-2540.2000.00661.x.
http://dx.doi.org/10.1046/j.1365-2540.20...
), specimens studied here showed significant linear increase in the morphologic body criteria BW and DS in response to overall PV increase (i.e. r=0.400, P=0.01 and r=0.317, P=0.046 respectively). The response was more striking when considering specimens (diploid, polyploidy and mosaic) exclusively from Salvador do Sul (n=11) where scalar values yielded complete hexaploid (λ=3; 6n=24) and octaploid (λ= 4 or [2]5=8n=32) chromosome plates. All three morphologic body criteria BL, BW and DS showed significant linear increases in response to increases in PV. Phenotypic significance diminished for the cluster of specimens (n=25) presenting only irrational multiples of the diploid aggregate. Only the body criteria BW and DS showed significant linear increases with increasing PV at r=0.504, P=0.01 and r=0.438, P=0.029 respectively.
Irrational polyploid multiplicity of the 2n=8-aggregate reached the level of 5n=20 (λ=2.5). A solitary mosaic specimen presented over 70% of its chromosome plates at the pentaploid (5n) level (Figure 5). This is the only such case represented in this data and in fact for hundreds of specimens analyzed in this laboratory from this and other parts of South America (unpublished data).
Such complete ploidal increases, at times geometric in scale, well documented in previous work (Duncan et al., 2010DUNCAN, A.W., TAYLOR, M.H., HICKEY, R.D., HANLON NEWELL, A.E., LENZI, M.L., OLSON, S.B., FINEGOLD, M.J. and GROMPE, M., 2010. The ploidy conveyor of mature hepatocytes as a source of genetic variation. Nature, vol. 467, no. 7316, pp. 707-710. PMid:20861837. http://dx.doi.org/10.1038/nature09414.
http://dx.doi.org/10.1038/nature09414...
), can be accompanied by variable yet significant increases in distinct morphologic phenotypic measurements. This indicates that the kinetics of this type of ploidal increase for this group can be beneficial to the specimen. However they are relatively rare beyond the 4n level. Positive and significant regression of phenotypic measurements in response to increases in PV indicate a homeostasis of kinetics for at least some morphologic phenotypic criteria, a kinetics that can be significantly influenced by genomic labiality. It did not surpass DS = 100 mm2 but usually began regression at about 54 mm2 to a more wild type DS phenotype.
Multiplying diploids of the group, at 2n=8, reached as high as 8n=32 (as mosaics) and showed significant positive linear effects of PV on anatomic criteria. Previous studies for this region, analyzing correlations of anatomic criteria with ploidal multiplicity (Knakievicz et al., 2006KNAKIEVICZ, T., VIEIRA, S.M., ERDTMANN, B. and FERREIRA, H.B., 2006. Reproductive modes and life of freshwater planarians (Platyhelminthes, Tricladida, Paludicula) from southern Brazil. Invertebrate Biology, vol. 125, no. 3, pp. 212-221. http://dx.doi.org/10.1111/j.1744-7410.2006.00054.x.
http://dx.doi.org/10.1111/j.1744-7410.20...
), employed specimens of two species (i.e. G. schubarti and G. tigrina). The positive correlations of body criteria measurements of a group of specimens from Salvador do Sul with PV disagree with results of previous research for G. schubarti also from southern Brazil (Knakievicz et al., 2006KNAKIEVICZ, T., VIEIRA, S.M., ERDTMANN, B. and FERREIRA, H.B., 2006. Reproductive modes and life of freshwater planarians (Platyhelminthes, Tricladida, Paludicula) from southern Brazil. Invertebrate Biology, vol. 125, no. 3, pp. 212-221. http://dx.doi.org/10.1111/j.1744-7410.2006.00054.x.
http://dx.doi.org/10.1111/j.1744-7410.20...
) but are commensurate with research findings in other parts of the Americas (Gregory et al., 2000GREGORY, T.R., HEBERT, P.D.N. and KOLASA, J., 2000. Evolutionary implications of the relationship between genome size and body size in flatworms and copepods. Heredity, vol. 84, no. Pt 2, pp. 201-208. PMid:10762390. http://dx.doi.org/10.1046/j.1365-2540.2000.00661.x.
http://dx.doi.org/10.1046/j.1365-2540.20...
). The 2n chromosomal aggregate for G. schubarti was treated as 2n, 3n and 2n/3n mosaic with no consideration of any possible specific PV values for the mosaics. In this research PV calculations for scalar multiples, rational or irrational in homoploid or mosaic polyploid specimens were essential in recognizing positive linear correlation of PV with selected body criteria. Ploidal increase was accompanied by body size increase but only to a predictable level after which regression to more wild type PV began.
5. Conclusion
Diploid (2n) is the homeostatic chromosome complement of the basic n-aggregate for most species. Genotypic plasticity (i.e. genomic lability) can occur in varying degrees under diverse circumstances. Chromosome stoichiometry is a form of genotypic plasticity. The lambda (λ) scalar multiplier is a measure of ploidal increase. At λ=2 (e.g. 2×n=2n) it measures the diploid chromosomal complement, homeostatic for most eukaryotes. At λ>2 (applied to complete diploids) it is a measure of polyploidy which was significantly associated with certain phenotypic criteria of body dimensions in this study. Measurements of polyploidy herein thus capture something of the chromosomal stochastic “noise”. As such, polyploidy is also a partial measure of the kinetics associated with that “noise” and at least some of the related anatomic phenotypic response.
Robustness of a specimen or species, especially of “wild type” phenotype is the ability to withstand or avoid deleterious phenotypic effects of genotypic plasticity. Platyhelminth genera are especially robust in regenerative capacity after anatomic partition (Newmark and Alvarado, 2002NEWMARK, P.A. and ALVARADO, A.L., 2002. Not your father’s planarian: a classic model enters the era of functional genomics. Nature Reviews. Genetics, vol. 3, no. 3, pp. 210-219. PMid:11972158. http://dx.doi.org/10.1038/nrg759.
http://dx.doi.org/10.1038/nrg759...
; Wagner et al., 2011WAGNER, D.E., WANG, I.E. and REDDIEN, P.W., 2011. Clonogenic neoblasts are pluripotent adult stem cells that underlie planarian regeneration. Science, vol. 332, no. 6031, pp. 811-816. PMid:21566185. http://dx.doi.org/10.1126/science.1203983.
http://dx.doi.org/10.1126/science.120398...
). Polyploidy is the main type of genotypic plasticity documented in this analysis. Endoreduplication at the meiotic and mitotic levels (Sterken et al., 2012STERKEN, R., KIEKENS, R., BORUC, J., ZHANG, F., VERCAUTEREN, A., VERCAUTEREN, I., DE SMET, L., DHONDT, S., INZÉ, D., DE VEYLDER, L., RUSSINOVA, E. and VUYLSTEKE, M., 2012. Combined linkage and association mapping reveals CYCD5;1 as a quantitative trait gene for endoreduplication in Arabidopsis. Proceedings of the National Academy of Sciences of the United States of America, vol. 109, no. 12, pp. 4678-4683. PMid:22392991. http://dx.doi.org/10.1073/pnas.1120811109.
http://dx.doi.org/10.1073/pnas.112081110...
) is a major mechanism giving rise to polyploidy.
The preponderance of stable 2n/3n karyotypic mosaic populations suggests a fairly high level of endoreduplication. G. schubarti presented specimens showing variable yet significant positive morphologic phenotypic response to wholesale chromosome dosage and even wholesale ploidal multiplicity change. “Wholesale chromosome dosage effect” at the physiologic level is documented in yeast (Pavelka et al., 2010PAVELKA, N., RANCATI, G., ZHU, J., BRADFORD, W.D., SARAF, A., FLORENS, L., SANDERSON, B.W., HATTEM, G.L. and LI, R., 2010. Aneuploidy confers quantitative proteome changes and phenotypic variation in budding yeast. Nature, vol. 468, no. 7321, pp. 321-325. PMid:20962780. http://dx.doi.org/10.1038/nature09529.
http://dx.doi.org/10.1038/nature09529...
). Data herein indicate that populations of G. schubarti can receive such genotypic dosage effect at the level of the entire ploidal base; increase leading to significant positive phenotypic (anatomic morphologic) response. This response then maintains a robust fitness of phenotype(s) in response to diverse environmental effects.
Kinetics of positive, robust phenotypic morphologic response to polyploidal scalar variation manifest a significant dynamic as reflected in significant regressions of phenotypic body criteria on ploidal values. A measure of the kinetics involving this dynamic is the scalar multiples of the diploid (2n) chromosomal complement present in this species. Robust regenerative homeostasis is a classic, characteristic of platyhelminths. This research demonstrates that this robust homeostasis is significantly based in similar genomic homeostasis grounded in dynamic kinetics where both genotypic plasticity and resulting phenotypic morphologic plasticity can be significant and beneficial. This robustness is diminished, inactivated or lost in species of higher complexity (e.g. Homo sapiens) where minimal genetic plasticity results in deleterious effects on phenotype up to and including morbidity. Definition of the kinetics documented herein present challenge of continuing refinement.
Acknowledgements
We thank the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) for research grants. L.A. Guterres, and A.F. Centa assisted with laboratory chemical preparations. T.H. Oliveira helped with photographic work. V. Batista and W. Santos assisted with tissue preparation. F. Gil was instrumental in preparation of figures and in extricating the senior author from various computerized dilemmas.
-
(With 5 figures)
-
Erratum
In the article “Polyploidy as a chromosomal component of stochastic noise:variable scalar multiples of the diploid chromosome complement in the invertebrate species Girardia schubarti from Brazil”, DOI https://doi.org/10.1590/1519-6984.20615, published in Brazilian Journal of Biology, Braz. J. Biol. vol.77 no.4, pp, 745-751:Where it reads:Where a specimen is dominated by polyploidy at numerically rational multiples (e.g. 3n, 4n, 8n) total plate count will be the denominator in calculating overall polyploid proportions so that Σ [total plate count]=2n+3n+4n+…), when 7 plates at 2n=8, 15 plates at 3n=12, 41 plates at 4n=16, 9 plates at 8n=32; Σ [total plate count]= 7+15+41+9=72. Any plate count that is a geometric scalar multiple of the polyploid dominant (e.g. 4n=16, 8n=32) is counted with/and as a component of the predominant polyploid count (e.g. 7 plates at 2n=8, 41 plates at 4n=16, 9 plates at 8n=32). The predominant polyploid plate count = 41 at 4n=16 Σ [predominant polyploidy plate count ] = 7+41+9=57. Use this sum to calculate the percentage that is the dominant polyploid component of the specimen (e.g. 57/72=0.792). Multiply that percentage by the haploid (i.e. n=4) of the specimen (e.g. 0.792×n=4=3.17). Add this result to the highest irrationally numerical scalar multiple of 2 n (e.g. 3n plus any of its rational multiples) within that specimen: Σ [predominant polyploidy plate count] = 41 (at 4n=16)+9(at 8n=32)+7 (at 2n=8) =57/72=0.792 x [n=4] =3.17 + [3n=12]= 15.17=PVIt should read:Where a specimen is dominated by polyploidy at numerically rational multiples (e.g. 3n, 4n, 8n) total plate count will be the denominator in calculating overall polyploid proportions so that Σ [total plate count]=2n+3n+4n+…), when 7 plates at 2n=8, 15 plates at 3n=12, 41 plates at 4n=16, 9 plates at 8n=32; Σ [total plate count]= 7+15+41+9=72. Any plate count that is a geometric scalar multiple of the 2n polyploid dominant (e.g. 4n=16, 8n=32) is counted with/and as a component of the predominant polyploid count (e.g. 7 plates at 2n=8, 41 plates at 4n=16, 9 plates at 8n=32). The predominant polyploid plate count = 41 at 4n=16 Σ [predominant polyploidy plate count ] = 7+41+9=57. Use this sum to calculate the percentage that is the dominant polyploid component of the specimen (e.g. 57/72=0.792). Multiply that percentage by the haploid (i.e. n=4) of the specimen (e.g. 0.792×n=4=3.17). Add this result to the highest irrationally numerical scalar multiple of 2 n (e.g. 3n plus any of its rational multiples) within that specimen: Σ [predominant polyploidy plate count] = 41 (at 4n=16)+9(at 8n=32)+7 (at 2n=8) =57/72=0.792 x [n=4] =3.17 + [3n=12]= 15.17=PV. Wherever the dominant (rational multiple) polyploid percentage is ≥90%, the PV becomes that dominant rational polyploid scaler (e.g, 4n plate count = 9, 8n plate count = 1, dominant polyploid percentage is = 90%, PV = 16.00).Where it reads:Table 1 Regions furnishing specimens for this investigation and their altitudes, ploidal constitution and ploidal value (PV).Region Altitude (m) Ploidal Constitution (λ)n-value Number of specimens PV Cachoeirinha 23 Tetraploid 4n=16 3 16.00 Camaquã 39 Tetraploid 4n=16 1 16.00 Salvador do Sul 113 Diploid 2n=8 9 8.00 Triploid 3n=12 2 12.00 Tetraploid 4n=16 2 16.00 SS-1 Mosaic * 8 8.44 8.44 8.80 9.90 11.458 15.112 15.608 15.630 SS – 2 Mosaic * 15 8.485 8.50 8.667 8.769 8.883 9.22 9.22 9.33 9.33 9.50 9.67 10.03 11.20 11.33 18.857 n=40 - *
Karyotypic mosaics (SS-1 and SS-2) presented 2n, 3n, 4n, 5n, 6n or 8n ploidal multiples in varying proportions.It should read:Table 1 Region, distribution, ploidal value (PV), regional altitude of origin for the 40 specimens of Girardia schubarti.Region Altitude (m) Ploidal
Constitution(λ)n-value Number of specimens PV Cachoeirinha 23 Tetraploid 4n=16 3 16.00 Camaquã 39 Tetraploid 4n=16 1 16.00 Salvador do Sul 113 Diploid 2n=8 9 8.00 Triploid 3n=12 2 12.00 Tetraploid 4n=16 2 16.00 SS-1 Mosaic * 8 8.44 8.50 8.67 8.97 11.41 15.28 15.608 15.32 SS – 2 Mosaic * 15 8.485 8.50 8.667 8.769 8.883 9.11 9.22 9.33 9.33 9.50 9.667 9.87 11.20 11.33 18.857 n=40 - *
Karyotypic mosaics (SS-1 and SS-2) presented 2n, 3n, 4n, 5n, 6n or 8n ploidal multiples in varying proportions. - *
References
- BECSKEI, A., KAUFMANN, B.B. and VAN OUDENAARDEN, A., 2005. Contributions of low molecular number and chromosomal positioning to stochastic gene expression. Nature Genetics, vol. 37, no. 9, pp. 937-944. PMid:16086016. http://dx.doi.org/10.1038/ng1616
» http://dx.doi.org/10.1038/ng1616 - BEKAERT, M., EDGER, P.P., PIRES, J.C. and CONANT, G.C., 2011. Two-phase resolution of polyploidy in the Arabidopsis metabolic network gives rise to relative and absolute dosage constraints. The Plant Cell, vol. 23, no. 5, pp. 1719-1728. PMid:21540436. http://dx.doi.org/10.1105/tpc.110.081281
» http://dx.doi.org/10.1105/tpc.110.081281 - BENYA, E., LEAL-ZANCHET, A.M., SANTOS, W.H., HAUSER, J. and ERDTMANN, B., 2007. Chromsome polymorphism and complements in populations of Girardia species (Platyhelminths, Tricladida, Paludicola) from southern Brazil. Brazilian Journal of Biology = Revista Brasileira de Biologia, vol. 67, no. 4, suppl., pp. 951-955. PMid:18278365. http://dx.doi.org/10.1590/S1519-69842007000500021
» http://dx.doi.org/10.1590/S1519-69842007000500021 - BEUKEBOOM, L.W., SHARBEL, T.F. and MICHIELS, N.K., 1998. Reproductive modes of ploidy distribution, and supernumerary chromosome frequencies of the flatworm Polycelis nigra (Platyhelminthes: Tricladida). Hydrobiologia, vol. 383, no. 1/3, pp. 277-285. http://dx.doi.org/10.1023/A:1003460132521
» http://dx.doi.org/10.1023/A:1003460132521 - CHESTER, M., GALLAGHER, J.P., VAUGHAN SYMONDS, V., SILVA, A.V.C., MAVRODIEV, E.V., LEITCH, A.R., SOLTIS, P.S. and SOLTIS, D.E., 2012. Extensive chromosomal variation in a recently formed natural allopolploid species, Tragopogon miscellus (Asteraceae). Proceedings of the National Academy of Sciences of the United States of America, vol. 109, no. 4, pp. 1176-1181. PMid:22228301. http://dx.doi.org/10.1073/pnas.1112041109
» http://dx.doi.org/10.1073/pnas.1112041109 - COMAI, L., 2005. The advantages and disadvantages of being polyploidy. Nature Reviews. Genetics, vol. 6, no. 11, pp. 836-846. PMid:16304599. http://dx.doi.org/10.1038/nrg1711
» http://dx.doi.org/10.1038/nrg1711 - DUNCAN, A.W., TAYLOR, M.H., HICKEY, R.D., HANLON NEWELL, A.E., LENZI, M.L., OLSON, S.B., FINEGOLD, M.J. and GROMPE, M., 2010. The ploidy conveyor of mature hepatocytes as a source of genetic variation. Nature, vol. 467, no. 7316, pp. 707-710. PMid:20861837. http://dx.doi.org/10.1038/nature09414
» http://dx.doi.org/10.1038/nature09414 - EDGAR, B.A. and ORR-WEAVER, T.L., 2001. Endoreplication cell cycles: more for less. Cell, vol. 105, no. 3, pp. 297-306. PMid:11348589. http://dx.doi.org/10.1016/S0092-8674(01)00334-8
» http://dx.doi.org/10.1016/S0092-8674(01)00334-8 - GALITSKI, T., SALDANHA, A.J., STYLES, C.A., LANDER, E.S. and FINK, G.F., 1999. Ploidy regulation of gene expression. Science, vol. 285, no. 5425, pp. 251-253. PMid:10398601. http://dx.doi.org/10.1126/science.285.5425.251
» http://dx.doi.org/10.1126/science.285.5425.251 - GREGORY, T.R., HEBERT, P.D.N. and KOLASA, J., 2000. Evolutionary implications of the relationship between genome size and body size in flatworms and copepods. Heredity, vol. 84, no. Pt 2, pp. 201-208. PMid:10762390. http://dx.doi.org/10.1046/j.1365-2540.2000.00661.x
» http://dx.doi.org/10.1046/j.1365-2540.2000.00661.x - HIETER, P. and GRIFFITHS, T., 1999. Polyploidy: more is more or less. Science, vol. 285, no. 5425, pp. 210-211. PMid:10428719. http://dx.doi.org/10.1126/science.285.5425.210
» http://dx.doi.org/10.1126/science.285.5425.210 - JAIO, Y., WICKETT, N.J., AYYAMPALAYAM, S., CHANDERBALI, A.S., LANDHERR, L., RALPH, P.E., TOMSHO, L.P., HU, Y., LIANG, H., SOLTIS, P.S., SOLTIS, D.E., CLIFTON, S.W., SCHLARBAUM, S.E., MA, H., LEEBENS-MACK, J. and DEPAMPHILIS, C.W., 2011. Ancestral polyploidy in seed plants and angiosperms. Nature, vol. 473, no. 7345, pp. 97-100. PMid:21478875. http://dx.doi.org/10.1038/nature09916
» http://dx.doi.org/10.1038/nature09916 - KAWAKATSU, M., HAUSER, J., FRIEDRICH, S.M.G., OKI, I., TAMURA, S. and YAMAYOSHI, T., 1983. Morphological, karyological and taxonomic studies of freshwater planarians from south Brazil IV. Dugesia anderlani sp. nov. (Turbellaria, Tricladida, Paludicola), a new species from São Leopoldo in Estado de Rio Grande do Sul. Annotationes Zoologicae Japonenses, vol. 56, pp. 196-208.
- KAWAKATSU, M., OKI, I., TAMURA, S., YAMAYOSHI, T., HAUSER, J. and FRIEDRICH, S.M.G., 1984. Morphological, karyological and taxonomic studies of freshwater planarians from south Brazil VI. Dugesia schubarti (Marcus, 1946) from the vicinity of São Leopoldo, Estado de Rio Grande do Sul (Turbellaria, Tricladida, Paludicola). The Bulletin of Fuji Women's College, vol. 22, pp. 45-62.
- KNAKIEVICZ, T., VIEIRA, S.M., ERDTMANN, B. and FERREIRA, H.B., 2006. Reproductive modes and life of freshwater planarians (Platyhelminthes, Tricladida, Paludicula) from southern Brazil. Invertebrate Biology, vol. 125, no. 3, pp. 212-221. http://dx.doi.org/10.1111/j.1744-7410.2006.00054.x
» http://dx.doi.org/10.1111/j.1744-7410.2006.00054.x - LEITCH, A.R. and LEITCH, I.J., 2008. Genome plasticity and the diversity of polyploidy plants. Science, vol. 320, no. 5875, pp. 481-483. PMid:18436776. http://dx.doi.org/10.1126/science.1153585
» http://dx.doi.org/10.1126/science.1153585 - LI, J., MIN, R., VIZEACOUMAR, F.J., JIN, K., XIN, X. and ZHANG, Z., 2010. Exploiting the determinants of stochastic gene expression in Saccharomyces cerevisiae for genome-side prediction of expression noise. Proceedings of the National Academy of Sciences of the United States of America, vol. 107, no. 23, pp. 10472-10477. PMid:20489180. http://dx.doi.org/10.1073/pnas.0914302107
» http://dx.doi.org/10.1073/pnas.0914302107 - NEWMARK, P.A. and ALVARADO, A.L., 2002. Not your father’s planarian: a classic model enters the era of functional genomics. Nature Reviews. Genetics, vol. 3, no. 3, pp. 210-219. PMid:11972158. http://dx.doi.org/10.1038/nrg759
» http://dx.doi.org/10.1038/nrg759 - PALA, M., CASU, S. and STOCCHINO, G., 1999. Karyology and karyotype analysis of diploid freshwater planarian populations of the Dugesia gonocephala group (Platyhelminthes, Tricladida) found in Sardinia. Hydrobiologia, vol. 392, no. 2, pp. 113-119. http://dx.doi.org/10.1023/A:1003534507632
» http://dx.doi.org/10.1023/A:1003534507632 - PAVELKA, N., RANCATI, G., ZHU, J., BRADFORD, W.D., SARAF, A., FLORENS, L., SANDERSON, B.W., HATTEM, G.L. and LI, R., 2010. Aneuploidy confers quantitative proteome changes and phenotypic variation in budding yeast. Nature, vol. 468, no. 7321, pp. 321-325. PMid:20962780. http://dx.doi.org/10.1038/nature09529
» http://dx.doi.org/10.1038/nature09529 - PENNISI, E., 2011. Green genomes. Science, vol. 332, no. 6036, pp. 1372-1375. PMid:21680823. http://dx.doi.org/10.1126/science.332.6036.1372
» http://dx.doi.org/10.1126/science.332.6036.1372 - RAJAGOPALAN, H., JALLEPALLI, P.V., RAGO, C., VELCULESCU, V.E., KINZLER, K.W., VOGELSTEIN, B. and LENGAUER, C., 2004. Inactivation of hCDC4 can cause chromosomal instability. Nature, vol. 428, no. 6978, pp. 77-81. PMid:14999283. http://dx.doi.org/10.1038/nature02313
» http://dx.doi.org/10.1038/nature02313 - SPEICHER, M.R. and CARTER, N.P., 2005. The new cytogenetics: blurring the boundaries with molecular biology. Nature Reviews. Genetics, vol. 6, no. 10, pp. 782-792. PMid:16145555. http://dx.doi.org/10.1038/nrg1692
» http://dx.doi.org/10.1038/nrg1692 - STERKEN, R., KIEKENS, R., BORUC, J., ZHANG, F., VERCAUTEREN, A., VERCAUTEREN, I., DE SMET, L., DHONDT, S., INZÉ, D., DE VEYLDER, L., RUSSINOVA, E. and VUYLSTEKE, M., 2012. Combined linkage and association mapping reveals CYCD5;1 as a quantitative trait gene for endoreduplication in Arabidopsis. Proceedings of the National Academy of Sciences of the United States of America, vol. 109, no. 12, pp. 4678-4683. PMid:22392991. http://dx.doi.org/10.1073/pnas.1120811109
» http://dx.doi.org/10.1073/pnas.1120811109 - WAGNER, D.E., WANG, I.E. and REDDIEN, P.W., 2011. Clonogenic neoblasts are pluripotent adult stem cells that underlie planarian regeneration. Science, vol. 332, no. 6031, pp. 811-816. PMid:21566185. http://dx.doi.org/10.1126/science.1203983
» http://dx.doi.org/10.1126/science.1203983 - XI, R., HADJIPANAYIS, A.G., LUQUETTE, L.J., KIM, T.-M., LEE, E., ZHANG, J., JOHNSON, M.D., MUZNY, D.M., WHEELER, D.A., GIBBS, R.A., KUCHERLAPATI, R. and PARK, P.J., 2011. Copy number variation detection in whole-genome sequencing data using the Bayesian information criterion. Proceedings of the National Academy of Sciences of the United States of America, vol. 108, no. 46, pp. 1128-1136. PMid:22065754. http://dx.doi.org/10.1073/pnas.1110574108
» http://dx.doi.org/10.1073/pnas.1110574108
Publication Dates
-
Publication in this collection
12 June 2017 -
Date of issue
Nov 2017
History
-
Received
10 Dec 2015 -
Accepted
14 July 2016