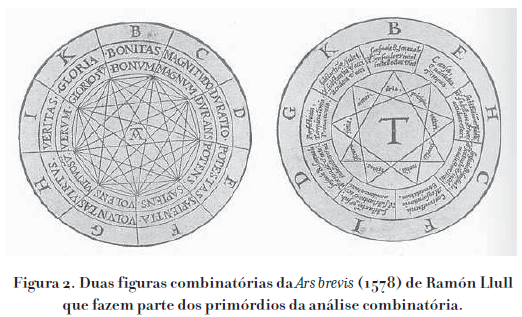
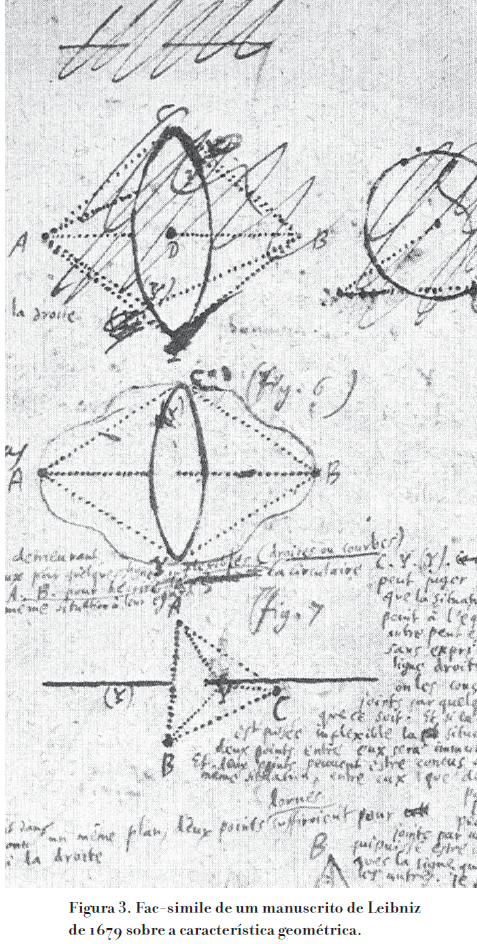
DOCUMENTOS CIENTÍFICOS
Nova ordem para novos conhecimentos: o projeto leibniziano de enciclopédia científica
New order for new knowledges: Leibniz’s project for a scientific encyclopedia
Jorge Alberto MolinaI; Edgar Affonso HoffmannII
IProfessor Doutor do Departamento de Ciências Humanas da Universidade de Santa Cruz do Sul (UNISC), Brasil. molina@unisc.br
IIProfessor Doutor do Departamento de Ciências Humanas da Universidade de Santa Cruz do Sul (UNISC), Brasil. hoffmann@unisc.br
1 O consilium de encyclopaedia nova conscribenda methodo inventoria
Em muitos de seus escritos, Leibniz se referia aos sábios de sua época por meio da seguinte metáfora: eles são como um rico negociante que tem grande quantidade de mercadorias na sua loja, mas que carece de um inventário delas. Leibniz era ciente de que o século xvii tinha acumulado uma grande porção de conhecimentos novos, ultrapassando assim os limites da ciência antiga e medieval, não apenas nas ciências ditas racionais, tais como a matemática e a astronomia, mas também na física, no estudo da composição dos minerais e dos seres vivos. Em um texto de 1686, Leibniz caracteriza nos seguintes termos os avanços de sua época:
Tendo sido restauradas as belas letras e restituído o método do discurso, o que foi principalmente o benefício do século precedente, o destino reservou ao nosso principalmente isto: que de novo brilhasse o que chamei da luz da mathesis, depois de estar tanto tempo eclipsada, uma vez descobertos e ampliados os métodos arquimedianos de invenção mediante indivisíveis e infinitos, [métodos] que poderias chamar metafísica da geometria, e afirmo que foram desconhecidos pela maioria dos antigos com exceção de Arquimedes; e, ao mesmo tempo, foi criada aquela análise do cálculo especioso, que fora em parte ocultada cuidadosamente pelos antigos, e em parte não suficientemente explorada; análise que devemos a Viète, na qual toda a geometria é reduzida a uma aritmética singular.
Mas aconteceu algo mais importante, isto é, os inícios de certa física que deve ser reduzida à geometria, da qual primeiros entre todos Galileu, Kepler e Gilbert deram exemplos e aos quais deve juntar merecidamente Harvey em razão da descoberta da lei mecânica da circulação (Leibniz, 1988, p. 340-1).
Vemos assim que Leibniz considerou como grandes realizações intelectuais do século xvii:
(a) A invenção e o desenvolvimento dos métodos infinitesimais;
(b) a invenção e o desenvolvimento da álgebra (cálculo especioso) por Viète e da geometria analítica por Descartes;
(c) a construção de uma nova ciência da natureza por Galileu, Kepler e Gilbert, baseada na matemática e na concepção mecanicista da natureza.
Essas expressões de Leibniz correspondem ao espírito de uma época desejosa de adquirir novos conhecimentos. Mesmo admirando os prodigiosos avanços de seu tempo, Leibniz pensava faltar uma ordem nesses novos conhecimentos, e o objetivo de sua enciclopédia seria estabelecer essa ordem. Diferentemente das Enciclopédias de hoje que ordenam as matérias pela ordem do alfabeto, Leibniz pensava numa ordenação dos conhecimentos pela ordem de sua descoberta. A função da Enciclopédia seria não apenas a de organizar os conhecimentos já sabidos, mas também a de tornar possível sua ampliação. A enciclopédia deveria assim conter um inventário dos conhecimentos possuídos e indicar a forma de ampliá-los.
Convém lembrar aqui que no século xvii aparece, quiçá por vez primeira, a noção de progresso científico. Teve lugar nessa época uma ruptura importante com as concepções sobre o saber vigente até então. No século anterior, em grande parte do mundo culto, pensava-se que tudo o que podia ser sabido, já tinha sido descoberto na Antigüidade clássica, e que a ordem apropriada para a organização dos conhecimentos devia ser aquela que fosse mais apta para seu ensino. A partir dessa perspectiva didática, duas tarefas se tornaram relevantes: primeiro, distribuir todos os conhecimentos em classes e segundo, lembrar deles. Na Renascença essa distribuição era feita colocando os conhecimentos em lugares chamados loci. Esses lugares eram definidos a partir da tradição antiga e medieval de comentários dos Tópicos de Aristóteles (cf. Curtius, 1996, caps. iv, v). Por outro lado, segundo a visão daquela época, a arte da memória deveria permitir ao aprendiz que perguntasse por um tema, e ao mestre que o ensinava, saber qual era o locus onde esse assunto se encontrava. Dessa forma, os Tópicos que, para Aristóteles (1973), tinham uma função heurística, seja porque permitiam encontrar argumentos para vencer numa discussão, seja porque orientavam a busca dos primeiros princípios de uma ciência, passaram a ter uma função didática (cf. Gaukroger,1989, p. 31-8). Nessa concepção, a silogística aristotélica era considerada principalmente uma ferramenta para o ensino. Em Descartes ecoa essa concepção sobre a lógica, quando ele escreve no Discurso do método "[...] notei que, quanto à lógica, os seus silogismos e a maior parte de seus outros preceitos servem mais para explicar a outrem as coisas que já se sabem [...] do que para aprendê-las" (Descartes, 1973, p. 45).
A progressiva substituição, no século xvii, da filosofia natural aristotélica pela ciência matemática e experimental da natureza, levou os filósofos e cientistas da modernidade a construir um método para o conhecimento da verdade, diferente da silogística aristotélica e da disputatio medieval baseada nos Tópicos de Aristóteles. O que se busca no século xvii é um método de ampliação do conhecimento, um método para a descoberta de novas verdades, uma ars inveniendi e não um método para ensinar o que já se sabia.
Muitos dos filósofos modernos pensaram ter encontrado esse tão buscado e desejado método de descoberta no antigo método de análise e síntese da geometria grega. Existem muitas discussões sobre se a análise dos antigos era um método de descoberta, de prova ou um método para conseguir ambos os fins (cf. Robinson, 1983; Cornford, 1946; Gulley, 1983; Hintikka & Remes, 1983). Essas polêmicas têm a ver com a questão da direção da análise (se ela procede dedutivamente das premissas para conclusão, isto é, se a análise tem uma direção descendente ou se, pelo contrário, ela vai da conclusão para as possíveis premissas, seguindo uma ordem ascendente) e com sua relação com a síntese. O que aqui nos interessa é como o método da análise foi interpretado pela maioria dos filósofos e cientistas modernos, e não qual foi o uso real desse método no seio da Geometria grega. Para a maioria dos filósofos modernos a análise era um método de descoberta, um método de invenção, diziam os modernos, que se combinava com a síntese que era um método de prova, um método de exposição dedutiva das proposições descobertas pela análise. Diz-se na Lógica de Port Royal: "Assim existem dois tipos de métodos: um, que se chama análise, ou método da resolução, para descobrir a verdade e que se pode também chamar método de invenção; e outro, que é chamado de síntese ou método de composição, para fazer entender aos outros quando se tem encontrado aquela, e que se pode também chamar de método de doutrina" (Arnauld & Nicole, 1970, p. 368). Em contraposição à silogística aristotélica, que na visão dos modernos só servia para ensinar aos outros aquilo que já se sabia e não para alcançar novos conhecimentos, a análise parecia realizar o ideal de ser um método de ampliação do saber.
Segundo Duchesneau (1993, p. 18-55), podemos distinguir uma evolução nas sucessivas realizações do projeto leibniziano de construção de uma enciclopédia, de modo que, nas últimas formulações a posição das ciências da natureza ganha autonomia com relação à metafísica e à lógica. Encontramos um primeiro esboço da enciclopédia leibniziana nos Dialogi de rerum arcanis (Diálogos sobre os princípios das coisas) (GP, vol. vii, p. 51-2). Dentro da ordem das disciplinas a tratar, estabelecida nesse texto, vêm, em primeiro lugar, as disciplinas que têm a ver com os métodos de invenção ou de juízo: arte da razão e método para encontrar novas verdades, língua racional, arte característica e combinatória, e álgebra. Essa última tinha sido identificada por Descartes com a análise ou a arte da descoberta das verdades. A característica universal era um projeto leibniziano de construção de uma língua filosófica universal que deveria servir como base para a aplicação do método de descoberta de verdades e para acabar com as infindáveis disputas da filosofia escolástica. Em segundo lugar, Lebiniz, nessa ordem, coloca a metafísica, ciência que se ocupa de Deus, das almas e dos dois labirintos: o labirinto do destino, da fortuna e da liberdade, e o labirinto do contínuo, ou do tempo, do lugar, do movimento, do átomo, do indivisível e do infinito. As ciências da natureza são colocadas, nesse texto, numa terceira posição. Essa terceira parte da Enciclopédia expõe os fundamentos de um sistema da natureza que abrange os seguintes tópicos: (i) geometria do movimento ou phoronomia; (ii) física do movimento ou dinâmica; (iii) artes mecânicas; (iv) hipóteses da física demonstrativa e das artes físicas; (v) causas ocultas das coisas e constituição de uma medicina racional; (vi) segredos da natureza.
Um segundo esboço da enciclopédia, encontra-se no texto Guilielmi pacidii plus ultra (GP, vol. vii, p. 49-53). Nele, Leibniz novamente coloca em primeiro lugar as disciplinas que expressam a arte de julgar ou inventar. Mas desta vez elas aparecem sob uma ciência mais geral: Elementa veritatis aeternae, et de arte demonstrandi in omnibus disciplinis ut in mathesi (Elementos de verdade eterna, e sobre a arte de demonstrar em todas as disciplinas como nas matemáticas). Agora, a ordem das disciplinas é a seguinte: em primeiro lugar, os elementa veritatis aeternae, depois a característica universal e, finalmente, a ars inveniendi. Esta última divide-se em síntese ou arte combinatória, que estuda a qualidade em geral e a distinção entre o semelhante e o dessemelhante, e em análise, que estuda a quantidade em geral. Análise e síntese dão origem à matemática geral que, por sua vez, é o fundamento da dinâmica ou estudo das causas do movimento. A seguir, vem o estudo dos elementos da física, que consistem na explicação causal das qualidades sensíveis e do modo de apreensão dessas qualidades. Seguem-se, na ordem, a astronomia física e os princípios gerais sobre o sistema de mundo. Vemos, assim, como Leibniz coloca a astronomia subordinada à física, em oposição à tradição aristotélica que as considerava como duas ciências diferentes. Aparece também subordinada à física a medicina, sendo o último lugar nessa enciclopédia ocupado pelas ciências políticas e jurídicas e pela teologia revelada.
Um terceiro esboço de construção de uma Enciclopédia é encontrado no Consilium de Encyclopaedia nova conscribenda methodo inventoria (Leibniz, 1988, p. 30-41), escrito em junho de 1679. Esse texto, cuja tradução publicamos a seguir, pode ser considerado não apenas um projeto de construção de uma enciclopédia, mas também um esboço de uma filosofia da ciência. Nele, Leibniz, como já Aristóteles tinha feito nos Segundos analíticos, afirma que toda ciência deve ter uma estrutura demonstrativa, o que nos permitiria separar as proposições científicas em dois grupos, o dos princípios e o das conclusões. Esta estrutura demonstrativa não deve ser considerada, em Leibniz, como um conjunto de cadeias dedutivas, no sentido que tem para nós, hoje, o termo "dedução". Trata-se, com efeito, de inferências ou ilações que podem ser ou dedutivas, ou indutivas, ou heurísticas ou abdutivas. Lembremos, como já o fizemos, que para Leibniz não apenas a análise exerce um papel heurístico, mas também a síntese, identificada com a combinatória, exerce esse papel.
No Consilium, os princípios de uma ciência são caracterizados como definições, axiomas e hipóteses; estas últimas são concebidas como proposições provisórias que ainda não podem ser demonstradas, mas que possuem amplo uso. As definições são consideradas, como já tinha feito Pascal no opúsculo Sobre o espírito da geometria, como definições nominais. No Consilium, não encontramos traços da teoria lebniziana da definição real. Dentro do grupo das conclusões são situadas as observações, os teoremas e os problemas. Como o fizeram os geômetras gregos, Leibniz considera os teoremas como proposições que exigem uma demonstração, ao passo que os problemas exigem a realização de construções ou de experimentos.
Um aspecto interessante do Consilium é a atenção dada ao caráter cooperativo da atividade científica. Mesmo que, segundo as próprias palavras de Leibniz (1988, p. 30-41), o conjunto de conhecimentos científicos forme um oceano cujas partes são difíceis de distinguir, as diferentes ciências podem ser colocadas em uma ordem dada pela seqüência das possíveis descobertas científicas: em primeiro lugar, deve-se colocar nessa ordem as disciplinas que estudam a linguagem, seja a língua filosófica universal, chamada por Leibniz de característica universal, seja as diferentes línguas naturais (gramática universal) . Em segundo lugar, viriam aquelas disciplinas que versam sobre a arte de julgar (lógica), de descobrir verdades (tópica) ou de lembrá-las (arte da mnemônica). Em terceiro lugar, as disciplinas matemáticas, concebidas já nesse texto fora dos limites cartesianos, pois enquanto para Descartes as matemáticas são as ciências da ordem e da medida (Regras para a direção do espírito, Regra iv), para Leibniz elas também se ocupam do estudo da arte das formas, isto é, sobre o diverso, o semelhante e o diferente. Assim, as matemáticas leibnizianas abrangem também aspectos qualitativos. A combinatória e a analysis situs pertencem a esses ramos qualitativos da matemática.
Em quarto lugar, Leibniz coloca as ciências da natureza. A mecânica serve de elo entre as ciências matemáticas e as ciências da natureza. A mecânica não pode ser reduzida, como pensava Descartes, à geometria, ela deve tirar seus fundamentos da metafísica. Dado que para Leibniz as matemáticas estudam tudo aquilo que é um objeto possível da imaginação (cf. Mercer & Sleigh, 1995), e a metafísica estuda o que é objeto do intelecto, adquire sentido a afirmação de Leibniz no Consilium de que os objetos da mecânica não podem ser estudados somente pela imaginação e de que é necessária uma ciência superior (a metafísica). Em último lugar de sua enciclopédia, Leibniz coloca a moral, a política e a teologia, todas elas consideradas como ciências.
O Consilium expressa uma concepção da ciência e da atividade científica diferente daquela dos aristotélicos, dos cartesianos e dos empiristas ingleses. O ideal matematizante presidiu todos os esforços leibnizianos de organização do conhecimento. Por aceitar esse ideal, ele se contrapôs aos empiristas ingleses como Boyle. Leibniz buscava integrar a ciência boyliana através de modelos matemáticos. Numa carta a Oldenburg de 1675, Leibniz afirma:
Os homens filosofarão sempre de modo boyliano, toda vez que persigam nosso fim; a menos que também a própria natureza das coisas, enquanto é conhecida, possa ser submetida aos cálculos, e tendo sido descobertas e reduzidas ao mecanicismo novas qualidades, isso dará aos geômetras novos campos de aplicação (GM, vol. i, p. 86).
Em outra carta, dirigida agora a Huyghens, de 29 de dezembro de 1691, Leibniz se declara surpreso pelo fato de que Boyle, mesmo tendo realizado muitos experimentos, não chegou a desenvolver nenhuma teoria sobre a química, concluindo a partir de seus experimentos o que todos os cientistas já sabiam: que tudo acontece de forma mecânica. O erro de Boyle, segundo Leibniz, reside na sua concepção de que, na ciência, só há lugar para aquelas proposições que julgamos indubitáveis. Para Leibniz, a formulação e proposição de conjecturas, isto é, de hipóteses, também faz parte da atividade científica.
2 A enciclopédia, a arte da invenção e a ciência geral
Leibniz se afasta da visão que a maioria dos filósofos e cientistas modernos tinha da análise e da síntese. Ele pensa que a síntese também pode servir para a descoberta de novas verdades, identificando-a com a combinatória. Segundo Leibniz:
Dois são os métodos, o sintético ou o da arte combinatória, e o analítico. Ambos podem mostrar a origem da invenção, o que, portanto, não é privilégio da análise. A distinção entre eles consiste no fato de que a combinatória <originada a partir das coisas mais simples> mostra a totalidade de alguma ciência, ou exibe ao menos uma série de teoremas e problemas e, entre eles, também aquilo que se busca. Na verdade, a análise reduz o problema proposto a problemas mais simples; e que é realizado por saltos, como na álgebra, ou por meio de problemas intermediários, como na tópica ou na redução. A mesma distinção ocorre também na combinatória, pois começamos ou pelos primeiros princípios ou pelas coisas próximas (Leibniz, 1988, p. 557).
Dessa forma, a ordem da descoberta, para Leibniz, tanto pode ser a ordem estritamente dedutiva dada pela síntese, como aquela heurística dada pela análise. Análise e síntese pertencem àquela parte da lógica que na Idade Moderna passou a estar associada à doutrina do método. Essa doutrina tinha duas partes: a invenção (ars inveniendi) ou a arte de descobrir verdades, e o juízo (ars judicandi) ou a arte de julgar as verdades propostas para consideração. No Consilium, a lógica é considerada como uma ars judicandi (cf. Leibniz, 1988, p. 36). Porém na Introductio ad Encyclopaediam arcanam (Introdução aos princípios da enciclopédia), também do ano 1679, a lógica é incluída na ciência geral "que nada mais é do que a ciência do pensável enquanto tal, que não apenas compreende a lógica tal com o a entendemos ainda hoje, mas também a arte da descoberta, o método ou modo de ordenar os conhecimentos, a síntese e a análise, e a didática ou ciência de ensinar" (cf. Leibniz, 1988, p. 511). Portanto, depois do Consilium, Leibniz apresentou em outros textos uma ampliação do escopo da lógica que passou a ser considerada não apenas como arte de julgar, mas também como arte da invenção e da memória. Às vezes Leibniz , usando a terminologia aristotélica, chama a ars judicandi de analítica, e a ars inveniendi de tópica (cf. Esquisabel, 2004, p. 45). Podemos perceber em Leibniz uma concepção da lógica diferente da concepção aristotélica. Enquanto que para Aristóteles a lógica não é propriamente uma ciência, mas um instrumento para a ciência, em Leibniz, que continua a tradição de Lullio, a lógica aparece como uma Ontologia geral, identificando-se com aquilo que Leibniz chama de ciência geral. A construção da Enciclopédia leibniziana está, portanto, estreitamente ligada ao projeto de construção da ciência geral. Assim, em um fragmento de Leibniz lemos:
O projeto do autor consiste em duas coisas: primeiro, em tratar da ciência geral, na qual usamos, na medida do possível, conhecimentos já dados para a partir dai encontrar outros; e, segundo, em construir um tesouro do conhecimento humano, no qual todas as coisas, que foram já observadas pelos homens ou que estão em livros ou que estão dispersas entre homens de qualquer habilidade ou profissão, sejam ordenadas e inventariadas <para que possamos usá-las com maior facilidade ao escolher experimentos segundo certo projeto> de modo a começar pelas coisas mais gerais e úteis (Leibniz, 1988, p. 218-9).
No seu escrito Initia et specimina scientiae generalis (Inícios e exemplares da ciência geral), Leibniz define a ciência geral como "aquela que ensina o modo de inventar e demonstrar todas as outras ciências a partir de dados suficientes; por conseqüência, todos aqueles pensamentos que puderam ser encontrados fortuitamente não dependem dessa ciência" (GP, vol. vii, p. 60). Aqui é importante destacar a expressão "inventar e demonstrar a partir de dados suficientes". Leibniz foi o primeiro filósofo a estender o conceito de prova para além do conceito de prova geométrica, pois foi o primeiro que formulou um esboço de uma lógica probabilística (cf. Haacking, 1995, caps. 10, 14, 15; Leibniz, 2003, p. 245-301; Leibniz, 1948, Partes ii, ix) e que se interessou pelas provas formais no direito. Essa extensão foi importante para o projeto de construção da ciência geral. Na prova geométrica, a verdade da conclusão (por exemplo, de um teorema) decorre com necessidade das premissas assumidas (as hipóteses do teorema), as quais se deduzem, por sua vez, necessariamente dos axiomas da geometria e das definições. Mas, segundo Leibniz, há âmbitos do conhecimento, fora da geometria, nos quais, mesmo que nós não possamos concluir com necessidade a verdade da conclusão a partir das hipóteses assumidas, podemos, no entanto, estabelecer qual é a probabilidade da conclusão ser verdadeira com base nas hipóteses e dados disponíveis. Dessa forma, Leibniz considerou que o provável é objeto de ciência e que pode ser submetido a uma estimativa numérica. Assim, Leibniz se afastou tanto dos cartesianos como dos aristotélicos. A dúvida metódica cartesiana considerava como falso tudo aquilo que é meramente provável, enquanto os aristotélicos identificavam o provável com as endóxa, aquilo que é opinado pelos mais sábios ou pela maioria dos homens (cf. Aristóteles, Tópicos, I, 1, 100b 20-25). Mas os aristotélicos nunca pensaram que o provável podia ser objeto de uma estimativa quantitativa. Para Leibniz, ao contrário, da mesma forma que podemos estimar, a partir dos dados disponíveis, sejam eles hipóteses ou fatos, a probabilidade de que uma tese seja verdadeira, também podemos, a partir de dados suficientes, estimar qual é a probabilidade de que uma hipótese, que visa explicar esses dados, seja verdadeira. No percurso da evolução das ciências, ou da construção da ciência geral, essas hipóteses serão progressivamente deduzidas com necessidade a partir dos primeiros princípios admitidos por Leibniz para as verdades de razão e as verdades de fato, a saber, o princípio de não-contradição e o princípio de identidade1 1 Ver Mercer & Sleigh (1995) para um estudo detalhado sobre as diversas formas que Leibniz usou para expressar o princípio de identidade. para as primeiras, e o princípio de razão suficiente para as segundas.
Argumenta-se (cf. Esquisabel, 2004) que existem várias fases na concepção leibniziana da arte da invenção (ars inveniendi) e da arte de julgar (ars judicandi). A partir de 1680, a ars judicandi leibniziana se identifica com as doutrinas que Leibniz chamou de "elementos das verdades eternas", "método da certeza" ou "método dos estabelecimentos" (Leibniz, 1988, p. 219).2 2 Leibniz afirma que "a ciência geral consiste no juízo e na invenção, ou na analítica e na tópica, isto é, nos sinais da verdade e no fio da invenção. Por conseqüência, ocupar-nos-emos, antes de tudo, dos elementos da verdade eterna, pois quem não tem os sinais para reconhecer a verdade quando ela ocorrer, buscá-la-á em vão. Deve-se aqui falar sobre a natureza da verdade, e sobre as verdades absolutamente primeiras <ou indemonstráveis pela natureza das coisas>, e de que modo as restantes derivam delas" (Leibniz, 1988, p. 219). Por outro lado, a ars inveniendi identifica-se com a combinatória. Em um manuscrito sem título, Leibniz afirma que:
Encontro duas partes na arte da invenção, a combinatória e a analítica; a combinatória consiste na arte de inventar questões; a analítica consiste na arte de descobrir as soluções das questões. Freqüentemente, contudo, acontece que as soluções de algumas questões têm mais relação com a combinatória do que com a analítica, como acontece quando se procura o modo de fazer alguma coisa no campo natural ou civil, onde os meios a serem buscados estão fora da coisa. Contudo, em poucas palavras, inventar questões é mais próprio da combinatória, enquanto que resolvê-las é mais da analítica.
São, porém, dois os gêneros de questões: um, quando se procura o modo de indagar ou a forma de acontecer algo futuro ou pretérito, outro, quando se procura a verdade e o exame daquelas coisas que foram investigadas ou realizadas por outros. E entre esses dois existe tanta diferença quanto entre a arte de bem redigir ou falar e a arte de bem julgar os textos. O exame, porém, daquilo que foi pesquisado é exclusivamente analítico, enquanto a arte de indagar ou realizar cabe mais propriamente à combinatória. Também isto pode de novo ser distinguido mais adequadamente. Falando claramente, é analítica a investigação quando dividimos com exatidão a própria coisa em tantas partes com a máxima exatidão possível, observadas minuciosamente a posição, a relação, a forma das partes e as partes das partes. A arte sintética ou combinatória ocorre quando, para explicar uma realidade, assumimos outras coisas externas à coisa que deve ser explicada. Assim, explicamos a anatomia dos animais pela analítica; mas sufocar animais na máquina pneumática e posteriormente dissecá-los é próprio da arte combinatória. Examinar líquidos por destilação cabe à analítica; examiná-los, tendo já aplicado outros líquidos ou reagentes que provocam outra fermentação, pertence à combinatória (Leibniz, 1988, p. 167).
No seu escrito De synthesi et analysi universali seu arte inveniendi et judicandi (Das sínteses e análises universais segundo a arte da invenção e a arte de julgar GP, vol. vii, p. 297), Leibniz esclarece a diferença entre a análise e a síntese do seguinte modo: inferimos sinteticamente quando, começando desde os princípios e percorrendo por ordem as verdades, identificamos certas progressões e estabelecemos tabelas ou fórmulas gerais, por meio das quais pode ser encontrado o que foi proposto no início. Assim a tabela
permite gerar os números quadrados por meio da soma de números ímpares. A análise, entretanto, parte de um problema dado e retorna aos princípios como se nós nada tivéssemos anteriormente descoberto. Existem dois tipos de análise: um é o redutivo que consiste na redução de um problema a problemas mais simples (cf. Leibniz, 1988, p. 557), o outro é o por saltos que se usa na álgebra.
Um comentarista de Leibniz, Esquisabel, argumenta que nos escritos de maturidade a ars inveniendi adquire um caráter formal-estrutural (cf. Esquisabel, 2004, p. 49-53). Esquisabel se opõe àqueles autores, tais como Cassirer (cf. 1986, vol. ii, p. 64-103), que caracterizam a concepção leibniziana da ars inveniendi a partir da leitura da dissertação escrita por Leibniz na sua juventude sob o título De arte combinatória. Segundo Cassirer, a ars inveniendi leibniziana consistiria na composição e decomposição de conceitos. É verdade que, na sua juventude, Leibniz acreditou na possibilidade de obter uma decomposição de qualquer conceito em termos de conceitos mais básicos, da mesma forma que podemos decompor um número inteiro em seus fatores primos. Através dessa decomposição poder-sei-a obter a redução de qualquer enunciado verdadeiro a um enunciado da forma AB é A, onde A e B são conceitos irredutíveis. No entanto, a partir de um determinado momento, Leibniz conscientizou-se da impossibilidade de obter uma análise exaustiva dos conceitos. Talvez a descoberta de que p/4 pode ser dado por meio da série infinita 1-1/3+1/5-1/7..... tenha levado Leibniz a essa consideração. Por outro lado, ele percebeu que, para justificar uma verdade, não é preciso ter uma redução exaustiva das noções que ocorrem nela; é suficiente que ela possa ser reduzida à forma AB é A, onde A e B são conceitos quaisquer. Segundo Esquisabel, podemos distinguir em Leibniz dois modelos da arte da invenção. Um modelo combinatório e um modelo formal-subordinante. Este último modelo tem uma parte formal e uma parte material. A parte formal seria identificada com uma teoria das formas abstratas. Enquanto que, no modelo combinatório, a ordem dos conhecimentos seria dada por sua maior ou menor proximidade com os conceitos básicos, no modelo formal, essa ordem seria dada pelas relações dedutivas entre os enunciados.
A formação da Enciclopédia está, para Leibniz, associada ao projeto de construção de uma língua filosófica, a característica universal, definida como a língua universal e racional da enciclopédia (cf. Eco, 2001, Cap. 14). Essa língua teria três funções: primeiro, por si mesma ao mesmo tempo uma ars inveniendi et judicandi; segundo, prover a enciclopédia de uma estrutura formal; terceiro, servir como meio de comunicação universal e científico. Na tentativa de construir essa característica universal, Leibniz edificou várias características regionais. A mais desenvolvida entre elas foi a característica geométrica, construída no intuito de suprir um novo fundamento para a geometria, por meio da derivação dos axiomas e postulados de Euclides a partir de enunciados de identidade, que substituem os conceitos que ocorrem nesses axiomas e postulados por definições desses conceitos (cf. Leibniz, 1995). Em um fragmento sem título, Leibniz vincula a enciclopédia, a característica universal e a combinatória do seguinte modo:
Ela (a arte das combinações) significa para mim tanto a ciência das formas ou das fórmulas como ainda das variações em geral; em uma palavra, ela é a especiosa universal ou a característica. De modo que ela trata do mesmo e do diverso, do semelhante e do dessemelhante; do absoluto e do relativo; assim como a matemática ordinária trata do uno e do múltiplo, do muito e do pouco, do todo e da parte (Leibniz, 1988, p. 531).
Quando os caracteres são letras e essas letras representam grandezas, temos a álgebra; se as letras representam conceitos, temos a silogística; e se elas representam palavras, temos a criptografia. Nesse mesmo fragmento, Leibniz faz uma observação interessante sobre a evolução do conhecimento humano. Como o alfabeto tem 24 letras, Leibniz encontra que o número de palavras (com ou sem sentido) não pode ultrapassar [(2433- 24) / 23] e encontra como limite superior para o número de enunciados possíveis 10 elevado a 7300000000000. Sendo assim, conclui Leibniz, se a humanidade perdurasse um tempo suficiente "não se diria mais nada, que já não tivesse sido dito".
Em outro fragmento que se supõe escrito entre os anos 1685 e 1692, Leibniz define a característica como um olho do espírito ou Organon da ciência geral que permitirá por meio do cálculo superar a arte de disputar (cf. GP, vol. vii, p. 198-203). É interessante destacar que, nesse texto, Leibniz apresenta uma classificação das verdades científicas. Essa classificação é feita segundo critérios epistemológicos e lógicos. O que nós conhecemos, conhecemos ou por meio de demonstrações (verdades de razão) ou por meio de experiências (verdades de fato). Mas, por outro lado, podemos dar um critério lógico para distinguir entre as verdades de razão e as verdades de fato. Em uma verdade de razão, conduzida a análise dos conceitos até um ponto adequado, pode ser demonstrado que o predicado está no sujeito. Predicado e sujeito de uma verdade racional comportam-se de forma análoga àquela dos números comensuráveis entre si. Em uma verdade de fato, tal demonstração não pode ser efetuada. Predicado e sujeito comportam-se como dois números incomensuráveis entre si. No caso das verdades de fato, temos duas possibilidades: ou pelo uso de uma análise infinita dos conceitos, podemos visualizar que o predicado está no sujeito, ou, a partir dos dados disponíveis, podemos determinar qual é a probabilidade de que o enunciado em questão seja verdadeiro.
Apesar de Leibniz ter tratado, como mostramos, do projeto de uma enciclopédia em vários textos, o Consilium, ocupa um lugar central nessa investigação, motivo pelo qual publicamos a seguir a sua tradução.
- Aristóteles. Tópicos Tradução L. Vallandro & G. Bornheim. São Paulo: Abril Cultural, 1973. p. 1-152. (Os pensadores, 4)
- Arnauld, A. & Nicole, P. La logique ou l' art de penser Paris: Flammarion, 1970.
- Cassirer, E. El problema del conocimiento en la filosofía y en la ciencia modernas. México: Fondo de Cultura Económica, 1986. 4 v.
- Boyer, C. História da matemática São Paulo: Edgard Blücher, 1974.
- Cornford, F. Matemática e dialéctica na "República". Mind, 61, p. 43-7, 1946.
- Curtius, E. R. Literatura européia e idade média latina São Paulo: Hucitec, 1996.
- Descartes, R. Discurso do método. Tradução J. Guinsburg & B. Prado Júnior. São Paulo: Abril, 1973. p. 33-79. (Os pensadores, 15)
- _____. Regras para a direção do espírito Lisboa: Edições 70, 1985.
- Duschesneau, F. Leibniz et la méthode de la science Paris: PUF, 1993.
- Duhem, P. Salvar os fenômenos. Cadernos de História e Filosofia da ciência, 3, 1984.
- Eco, H. A busca da língua perfeita na cultura européia. Bauru: EDUSC, 2001.
- Esquisabel, O. Leibniz Erfindungskunst und der Entwurf der Charakteristik. Studia Leibnitiana, 36, 1, p. 43-56, 2004.
- Gaukroger, S. Cartesian logic: an essay on Descartes´s conception of inference Oxford: Clarendon Press, 1989.
- Gerhardt, C. I. (Ed.). Leibniz - Die philosophischen Schriften. Hildesheim: Georg Olms, 1960-1961. 7 v. (GP)
- _____. Leibniz Mathematische Schriften von G. W. Leibniz. Hildesheim: Georg Olms, 1971. 7 v. (GM)
- Gulley, N. A análise na Geometria grega. Cadernos de História e Filosofia da Ciência, 4, p. 16-27, 1983.
- Hacking, I. El surgimiento de la probabilidad: un estudio filosófico de las ideas tempranas acerca de la probabilidad, la inducción y la inferencia estadística. Barcelona: Gedisa, 1995.
- Hintikka, J. & Remes, U. A análise geométrica antiga e a lógica moderna. Cadernos de História e Filosofia da Ciência, 4, p. 28-47, 1983.
- Jolley, N. (Org.). The Cambridge companion to Leibniz Cambridge: Cambridge University Press, 1995.
- Kneale, W & Kneale, M. O desenvolvimento da lógica Lisboa: Fundação Calouste Gulbenkian, 1991
- Leibniz, G. W. Opuscules et fragments inédits Hildesheim: Edição de Louis, 1988.
- _____. La caracteristique géométrique Paris: Vrin, 1995.
- Losee, J. Introdução histórica à filosofia da ciência. Belo Horizonte: Ed. Itatiaia, 1979.
- Mercer, C. & Sleigh, J. Metaphysics: the early period to the "Discourse on metaphysics". In: Jolley, N. (Org.). The Cambridge companion to Leibniz Cambridge: Cambridge University Press, 1995. p. 67-123.
- Reboul, O. Introdução à retórica. São Paulo: Martins Fontes, 1988.
- Robinson, R. A análise na geometria grega. Cadernos de História e Filosofia da Ciência, 4, p. 5-15, 1983.
- Rossi, P. Francis Bacon: de la magia a la ciencia Madrid: Alianza, 1990.
- _____. O nascimento da ciência moderna na Europa Bauru: Edusc, 2001.
- Szabó, A. Les débuts des mathématiques grecques Paris: Vrin, 1977.
Datas de Publicação
-
Publicação nesta coleção
22 Mar 2010 -
Data do Fascículo
Mar 2007