Geometry, dynamics and fractals

TECHNICAL PAPERS

Geometry, dynamics and fractals

Luiz Bevilacqua^I; Marcelo M. Barros^II; Augusto.C.R.N.Galeão^III

^IHonorary Member, ABCM, [e-mail], National Lab. for Scientific Computing - LNCC 25651-075 Petrópolis,RJ, Brazil Universidade Federal do ABC 09210-170 Santo André, SP, Brazil

^[e-mail], National Lab. for Scientific Computing - LNCC 25651-075 Petrópolis,RJ, Brazil

^IIIMember, ABCM, [e-mail], National Lab. for Scientific Computing - LNCC 25651-075 Petrópolis, RJ, Brazil

ABSTRACT

Consider a collection of elastic wires folded according to a given pattern induced by a sequence of fractal plane curves. The folded wires can act as elastic springs. Therefore it is easy to build up a corresponding sequence of simple oscillators composed by the elastic springs clamped at one end and carrying a mass at the opposite end. The oscillation periods of the ordered sequence of these oscillators are related following a power law and therefore display a fractal structure. The periods of each oscillator clearly depend on the mechanical properties of the wire, on the mass at the end and on the boundary conditions. Therefore there are infinitely many possibilities to design a dynamical fractal sequence in opposition to the well defined fractal dimension of the underneath geometric sequence. Nevertheless the geometric fractal dimension of the primordial geometric curve is always related somehow to the dynamical fractal dimension characterizing the oscillation period sequence. It is important to emphasize that the dynamical fractal dimension of a given sequence built up after the geometry of a primordial one is not unique. This peculiarity introduces the possibility to have a broader information spectrum about the geometry which is otherwise impossible to achieve. This effect is clearly demonstrated for random fractals. The present paper deals with a particular family of curves, namely curves belonging to the Koch family. The method is tested for the simple Koch triadic and for random Koch curves. The method has also proved to be useful to identify the fractal dimension of a sequence given just one of its terms. Remarkable is the quality of information obtained with this technique based on very simple and basic concepts. Some of these aspects will be presented in this paper but much more, the authors believe, is still hidden behind the dynamic properties of fractal structures.

Keywords: fractal curves, fractal dimension, random fractals, dynamical dimension, Koch curves

Introduction.

The Hausdorff theory is the main reference to find out the geometric dimension of singular curves, since it is well founded on a rigorous analytical approach. But the determination of the Hausdorff dimension (Falconer, 1990) is usually very difficult since in general it is far from trivial to find the proper cover required by the Hausdorff measure theory (Hausdorff, 1919). ^{Appendix I} introduces a very brief account of the basic elements of the Hausdorff measure and the related fractal dimension as suggested in (Bassingthwaighte et al., 1994). In order to overcome this difficulty several other approximate methods have been proposed to determine what has been recently referred to as fractal dimension of a sequence of self-similar objects. We can point out the box counting method, mass distribution method and packing capacity, just to mention some examples, (Feder, 1988), (Guyet, 1996), (Bevilacqua, 2004). All those approaches are approximate and frequently relying on the observation of the behavior of numerical experiments. The validation is usually experimental by comparison of numerical outcomes with well known analytical results. In principle we can not expect to have the same characterization with two different approaches.

Those methods are very efficient when information is collected under the format of digital data which usually can be obtained directly from patterns displayed on some support. If, however, we are dealing with material objects particularly objects embedded into a 3D space, those techniques may become unsuitable. This paper extends and presents a more rigorous approach of a new method (Bevilacqua and Barros, 2007) that, besides the application as a numerical tool to characterize the fractal geometry of a given sequence, can also be used for this same purpose through direct experiments performed on the object itself.

Outline of the Method

The method introduced here links geometry to physics, particularly the dynamical properties of geometrically self-similar structures properly ordered. Suppose that we are given some geometrically self-similar sequence that we will call the primordial sequence. It is then possible to build up a corresponding one consisting of harmonic oscillators after the geometry of the primordial. We call this new sequence offspring sequence. The periods of those oscillators as function of a set of geometric and physical parameters are related to a power law that may characterize the fractal dimension of the original objects.

Fig.1 displays the two fundamental sequences representing the classical Koch triadic. The offspring sequence consists of very simple harmonic oscillators connecting a concentrated mass at one of the ends of a weightless elastic structure which is clamped at the opposite end. The motion of the mass is determined by the boundary conditions which are, in principle, arbitrary. The offspring sequence translates the geometry into a physical phenomenon. This correlation is, however, not unique because the characterization of the physical phenomenon, the period of oscillation, for a given geometry, depends on material properties and boundary conditions.

A fractal offspring sequence as a matter of fact is richer than the primordial one since it displays not only a geometric fractal dimension but also fractal characteristics of different nature. Consider some primordial self-similar sequence of plane curves with a fractal dimension equal D. We claim that the periods of the oscillators composing the offspring sequence follow the law:

or

where the parameter B depends on D, on the geometric and material properties of the oscillators, on the mass m_k and on the boundary conditions. Additionally:

0 <

G(l_k) < M (finite)

This means that the curve defined by equation (1-b) approaches asymptotically a straight line with slope (1 – B)/2 on the plane log(T_k/T₀)x log(l_k/L). In other words the governing equation (1) tends to a power law when k ® ¥.

We will call B the dynamical dimension of the offspring sequence. It will be shown that even if D¹1, that is, when the primordial sequence displays a fractal structure the dynamical dimension can be made equal 1 by a proper selection of material properties, for instance. That is, physical properties of geometrically self-similar sequences may have different fractal dimensions.

As will be shown in the sequel, equation (1-a) and, consequently, equation (1-b) hold for plane curves provided that some regularity requirements are fulfilled.

Curves of the Class l_k/L₀=q^-k and _Nk=p^k

Let us examine a particular deterministic law of formation. Consider the generator term composed by p elements with length equal to l/q where p and q are integers. The sequence is embedded in a one-dimensional topological space. Suppose that the total number of elements in the term of order k is given by:

N_k = p^k

and the corresponding length of the elements is:

l_k/L₀ = q^-k

The above relations written in another form read:

log N_k = k log p

log = -k log q

Eliminating k we obtain:

where coincides with the Hausdorff dimension for this particular case and also with the cluster dimension and the box dimension as well.

This paper deals with the family of curves, that will be called Koch curves, for which the above relationships prevail, namely N_k = p^k and l_k/L₀ = q^-k.

Direct Problem.

Consider a primordial sequence of fractal objects belonging to the class defined above characterized by a fractal dimension D. Suppose for instance that the classical Koch triadic is selected as the reference geometry or with the present terminology, the primordial sequence. It is possible then to build up an offspring sequence as shown in Fig. 1. A single element of the offspring sequence is shown in Fig. 2.

It is not our aim to discuss the dynamics of the oscillators that otherwise is very simple. It suffices to say that each oscillator is a three-degree-of-freedom system. The mass displacement vector reads w = {u,v,q}^T while the forces exerted by the boundary conditions on the mass can be represented by the force vector f= {H,V,M}^T as shown in Fig. 2._. The classical equations of motion can be written under the form:

Clearly, M is the mass matrix, K is the rigidity matrix. Now the components of f can be chosen in such a way so as to put at least one of the equations (3-a) into a more convenient form. This is equivalent to introducing a corresponding boundary condition, that is, a suitable steering surface controlling the trajectory of the mass m_k. In order to simplify some analytical developments we will introduce steering forces of the form f= Qw. It is not difficult to show that it is always possible to find a feedback matrix Q_I such that the first equation in the system (3-a) is reduced to:

where u_k/ = H

Note that it is not necessary to determine the matrix Q_Iexplicitly. Certainly, this procedure can be equally used for the other two displacements v and q with feedback matrices Q_II and Q_IIIleading to:

and

with v_k/ and q_k/ = M.

Now (j=1,2,3) can be determined from the stored elastic energy corresponding to the respective forces H, V, M as usual. Note that the offspring sequence is composed of material elements, wire-like folded structures. The stored bending energy for the k^th order term is:

where E_k is the Young Modulus of the wire material and I_k the moment of inertia of the wire cross section which can be functions of k. is the bending moment acting on the elementary segment (i-1,i) as shown in Fig. 3 and N_k is the total number of segments in the k^th order term. We are disregarding the contribution of shear and normal forces to the strain energy.

Let us consider first the case represented by (3-b). Now the offspring sequence fits into a box L₀ x h₀ as can be seen in Fig.3. The bending moment along a segment (i-1,i) is:

where 0 < s < 1

Now introducing Eq. (5) into Eq. (4), integrating over all segments l_k and summing up we get:

where = and with z_j= y_j/h₀.

Note that from the definition of h₀ clearly z_j< 1 for all j, and consequently a_i(k) < 1.

The horizontal displacement then reads:

Therefore

Introducing this expression into Eq. (3-b) we obtain:

where the period T_k is given by:

The mass attached at the free end of the oscillator is represented by m_k. Suppose that m_k, E_k and I_k vary according to the power laws:

where v, g and µ are real numbers.

Introducing in Eq.(7) the expression for N_k given by Eq.(2) and after some straightforward calculations we obtain:

where: B = -v + g + µ + D and D = log p/log q is the classical fractal dimension, that coincides with the Hausdorff dimension for this case. is a reference period:

The parameter B is the dynamical fractal dimension. It coincides with the box and the Hausdorff fractal dimensions provided that the mass, the Young modulus and the diameter of the wire cross section are all constant, that is v=g=µ=0.

Now, if the offspring sequence has a fractal characterization, that is, the normalized periods of the corresponding terms are governed by a power law, it is necessary that the equation (8-a) plotted on the plane Y_k x X_k, with Y_k = log (T_k/T₀) and X_k = log (l_k/L₀), approaches a straight line whose angular coefficient is equal to (1-B)/2 as shown in Fig.4. Define the functional relation Y_k Û X_k as a continuous curve with sectionaly continuous first derivative, composed by straight segments connecting the points (X_k, Y_k); (X_k+1, Y_k+1). Let us prove the asymptotic behavior. The following lemma is proved in the ^{Appendix II}.

Lemma.For curves belonging to the Koch family – class of curves defined by N_k = p^k and l_k/L₀ = 1/q^k – the first order differential form of the bilinear term W_k with respect to l_k is finite for increasing values of k, or equivalently decreasing values of l_k. That is(DW_k/Dl_k) = (DW_k/Dl_k) ® finite.

Now, recalling equation (8-a) and with Y_k=log(T_k/T₀) and X_k=log(l_k/L₀), the calculation of the differential ratio DY_k/DX_k after some simple operations gives:

Therefore from the lemma above and since W_k is finite and different from zero we have:

Proposition I. As k ® ¥ the curve given by equation (8-a) approaches asymptotically a straight line with slope equal to (1-B)/2.

Now following the same procedure for the cases corresponding to equations (3-c) and (3-d) relative to the elastic energy produced by a vertical force and to a couple respectively, the periods of the offspring sequence terms are given by:

for the energy generated by the action of a vertical force, and

for the energy generated by the action of a couple.

The behavior of the function Y_k is similar to the behavior of W_k. Therefore we will skip the discussion about this term. The computational experiments will make it clear. Now, a similar term is missing for the case represented by equation (8-c) obtained with the energy induced only by the action of a couple. The reason is that for this case the bending moment is constant along the entire length of the wire. The sum on the left hand side of equation (4) reduces to N_k l_kM².

The respective normalizing periods are:

Note that J₀ is the reference rotational inertia for the equation (3-d).

We will refer in the sequel as case I, II and III the plots representing respectively the curves given by equations (8-a), (8-b) and (8-c). Let us examine now some examples. Consider the first 9 terms of the offspring sequence derived from the Koch triadic as primordial sequence. We will assume here for sake of simplicity v=g=µ=0 which makes B=D. The normalized periods (T_k/T₀) corresponding to cases I, II and III as function of the ratio (l_k/L₀) are depicted in the Fig.5.

We expect the normalized periods versus the relative length to approach asymptotically a straight line with slope (1-D)/2 for cases I and II. For case III, as can be seen from the equation (8-c) the curve is a straight line. The exact fractal dimension of the Koch triadic is found to be log4/log3 or approximately 1.26186 up to the fifth decimal place. The values obtained from the dynamic approach are given in the Table I. It is also clear from Fig. 6 that the curve corresponding to the case I approaches asymptotically the straight line with slope 0.13093. Fig. 6 shows the ratio D_k/D_exact where . The values obtained are in agreement with the exact value up to the fourth decimal digit.

A first approximation to simulate the dynamical behavior under the action of the weight can be obtained by taking the mass proportional to the total length for each term of the sequence. That is m_k = m₀ (N_kl_k / L₀) or equivalently taking v = (1 – D) in the expression for B with E_k and I_k constants. It is easy to find that the term (1-B)/2 appearing in the equations (8-a,b,c) will be multiplied by 2. The results for this variable mass approach are shown in Fig. 7. As can be seen the solutions are equally good.

Inverse Problem

More interesting is the inverse problem. The quest is to find out the topological characteristics of a primordial sequence given a representative term of order n. Let Q_n be such a term of the primordial sequence. Build up the corresponding term 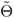_n of the offspring sequence. Let the total length of Q_n and consequently of 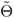_n be L_T and the projection on the horizontal axis be equal to L_n. The question now is to find out whether or not some fractal structure, if any, can be associated to the primordial sequence. Select first one of the uncoupled displacements, u, v, or q corresponding to cases I, II and III respectively. Following a similar procedure as that introduced to obtain the dynamic fractal dimension for the direct problem, obtain first the period T_n of 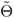_n.

The second step is to cut off successively from

_n a subset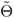 _n/1, 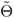_n/2

_n/m to get an offspring sub-sequence with projections L_n, L_n/1, L_n/m on the horizontal axis and find the periods T_n , T_n/1 , T_n/m of these new oscillators subjected to the same boundary conditions. Fig. 8 displays an example derived from the Koch triadic. If the original object belongs to a particular fractal primordial sequence then it is possible to show that the corresponding dynamic fractal dimension can be obtained from the offspring sub-sequence as explained above. Moreover there exists also a self-similar primordial sequence subjacent to the terms L_n, L_n/1, L_n/m. Consider the m^th order term. For case III the vibration period of the m^th term of the offspring sequence is given by:

It is assumed that the rotation inertia J_m can be variable. Note that for this case the length of the elementary segment is l_ncorresponding to the term Q_n. Let us take J_m = s_n/mJ_n where J_n is the rotation inertia for the original term. That is, the rotation inertias corresponding to the samples are proportional to J_n. Equation (9) can be rewritten:

Now L_m is a subset of the original set L_n. The subset L_m is scaled relatively to L_n such that L_m = b_mL_n.

Proposition 2. Let L_m be the horizontal projection of a sample cut off from a fractal curve whose horizontal projection is L_n , if L_m = b_mL_n then N_m = r_m (b_m)^D N_n provided that the curve is a term of a sequence belonging to the class N_k = p^k and l_k/L₀ = (1/q)^k. The correction factor r_m depends strongly on the boundary conditions and varies within the interval 1–e < r_m <1+ e where e is small for sufficiently large b_m.

The factor (b_m)^Dcan be interpreted as the stretching ratio, that is, the total length of the sample 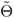_n/m given by l_nN_m divided by the total length of the original curve 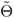_n given by l_nN_n. That is, the ratios of the stretched curves divided by the correction factor r_m constitute a fractal sequence with the same dimension D as the curves 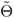_n, 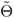_n/m themselves. Of course, this proposition is valid for regular curves and for sufficiently large scales. Fractal theory of plane curves, and in general fractal theory, has to be seen as the geometric counter part of the fuzzy set theory. There are relations that are approximately valid or valid under certain circumstances.

Introducing this correlation in Eq.(9) we obtain after some simple operations:

Consider now three possible cases. Constant inertia, s_n/m = 1, inertia proportional to the total length of the sample, s_n/m = N_m/N_n = and inertia proportional to the projection of the sample on the horizontal axis, s_n/m = L_m/L_n = b_m. For those three cases equation (9) takes the following forms, respectively:

For cases I and II, the solution can be deduced following the steps introduced previously. Equation (7) adjusted for the present case, considering variable mass, reads:

Here the term W_n/m is the truncation of order m of the term W_n defined before, that is:

where the parameters a_i(n) refer to the elements of order n. Note that here the integer m serves only to count the number of segments and has nothing to do with the m^th element of the series. Equation (12) can now be rewritten as:

We introduced now the following proposition having in mind that the terms a_i(n) are quadratic functions of the ordinates of the corners of the n^th order element in the series:

Proposition 3. Let L_m be the horizontal projection of a sample cut off from a fractal curve whose horizontal projection is L_n. The truncation of order m, i.e. W_n/m, of the quadratic form W_n is given by W_n/m = r_n/mW_n

, where b_m = L_m/L_n, and 1 – e < r_n/m < 1 + e , e is small and depends on the boundary conditions, provided that the curve is a term of a sequence belonging to the class N_k = p^k and l_k/L₀ = (1/q)^k.

After propositions 2 and 3, with the mass variation given by , the equation (13) reads:

or:

Now considering, as previously, the cases of constant mass s_n/m = 1, mass proportional to the total length of the sample, s_n/m = N_m/N_n = and mass proportional to the projection of the sample on the horizontal axis, s_n/m = N_m/N_n = b_m, the corresponding three values of are obtained:

= (D + 2), = (D + 1) and = (D + 3)

Case II is similar to case I. Proposition 3 holds for Y_n/m and Y_n in the place of W_n/m and W_n and s_n/m defined as Y_n/m = s_n/mY_n varying within the same limits as r_n/m. Therefore, equation (15) holds for the case II with s_n/m in the place of r_n/m.

Next let us present some numerical experiments. Consider the sequence of cuts of the Koch triadic as shown in Fig.8. The results corresponding to cases I, II and III with constant mass are depicted in Fig.9 and Fig.10.

The reference term corresponds to the 9^th term in the primordial sequence and the cuts are such that two consecutive terms of the offspring sub-sequence scale always with the same ratio, that is L_m+1 = bL_m.

The slopes of the interpolated straight lines S_aver obtained by minimizing the root mean square deviations from the points derived from equations (11-a) and (15) properly adjusted for cases I and II are shown in tables III and IV. Clearly it is seen that the nonlinear term r_n/m and possibly r_m introduce large perturbations for case I causing the more significant deviation – 1.38% – from the expected fractal dimension in comparison with 0.34% for case II and 0.614% for case III with the scale factor equal to 1/1.3 as depicted in Fig. 8. Nevertheless even the largest deviation is quite acceptable. Note that for the scale factor equal 1/2.0 – Fig. 9 – the deviations fall down considerably, 0.669% , 0.019% and 0.264% respectively for cases I,II and III. The reason for this reduction is that for this particular scale the terms of the offspring sub-sequence are cut at very particular positions preserving the integrity of the Koch triadic generator along the length of each term.

Under more general conditions the offspring subsequence may be cut at random, that is, the extremities of a sample may not coincide with any particular convenient points of the preceding one. In any case it is important to observe that very short samples may introduce relatively large errors in the analysis. It is convenient to keep the shortest sample with a projection length L_m>0.4L_n as indicated by numerical experiments since the dynamical fractal characteristics fade out for very short lengths.

The solutions corresponding to variable mass proportional to the total length and to the projection on the horizontal axis of the samples are presented on Figs.11-a, ^b for the scale factor equal to 1.3.

Clearly the most sensitive case corresponds to the horizontal force with deviation of the order of 5%. It is interesting that this disadvantage of the horizontal force for the regular deterministic case turns out to be a great advantage to identify random deviation in the formation process of the Koch curves as will be seen in the next section.

Random Fractals

In this section we will examine a simple case of random fractals using again the Koch triadic as the fundamental reference curve. The random character is very simple, nevertheless very illustrative to show the power of the dynamical dimension. Recall that the Koch triadic sequence can be built up using each preceding term to derive the next one.

Consider the term of order k of the random Koch triadic as a support. Attach to each elementary segment l_k the Koch triadic generator properly down scaled, that is, with a basis length equal to l_k and elementary segments: l_k+1 = l_k/3, call it G_k.

Now the randomness introduced here is simply to allow the orientation of the G_K’s to be taken by chance starting with the first term of the sequence k=1. This formation law contrasts with the well organized deterministic Koch triadic as introduced earlier. So the terms obtained are not strictly self-similar as shown in Fig.12.

The Hausdorff dimension for this fractal sequence is the same as that for the deterministic, well organized, self-similar, Koch triadic sequence, that is D » 1,26186. The reason is that the outer measure of the cover for this sequence is undistinguishable from that used for the deterministic Koch triadic. Therefore the Hausdorff dimension does not detect the randomness of this sequence. Turning now to the dynamical dimensional we have at least two possibilities. Consider first the case III. In that case the strain energy is the same for all elementary segments of a given term k. Therefore the strain energy corresponding to any two different terms, k and k+n scales exactly as determined by the Hausdorff dimension. Consequently the result obtained with the boundary conditions corresponding to the case III should lead to the Hausdorff dimension.

This is clearly apparent from Fig.13. Six random sequences were generated independently. The straight lines representing the logarithm of the normalized periods versus the logarithm l_k/L₀ of coincide for all cases. The straight line slope leads to the value of the Hausdorff dimension within the expected approximation interval. Now if we plot the normalized periods corresponding to the case I the results are not regular as shown in Fig.14. The reason is that the strain energy doesn’t scale as assumed by the Hausdorff theory. In this case even small deviation from the classical deterministic triadic is detected by the perturbation on the energy distribution.

Conclusions

As far as we know, the concept of dynamical fractal dimension has not been explored before. This first attempt has shown to be encouraging. Although this paper deals with Koch curves, numerical experiments have shown that this method applies also for more complex curves (Barros 2007). The dynamical fractal dimension depends on the distribution of the elastic energy, due to bending, along the components of the offspring sequence. If the distribution is uniform the dynamic dimension coincides with the Hausdorff dimension. The reason is that this uniform distribution is the dynamical equivalent of the cover proposed by Hausdorff. For non uniform distributions the dynamical dimension may converge to a different value. If on one hand the diversification of the boundary conditions determines the multiplicity of dynamical dimensions on the other hand it may provide meaningful information for random fractals as shown in the previous section. This is a great advantage over the classical methods that are unable to provide such information. Another interesting outcome is that through the comparison of the results obtained experimentally with real objects – wires – where all the energy components are present – bending, shear forces and normal forces – with computational results taking into account only the bending energy, it is possible to determine the contribution of shear and normal forces for the total elastic energy stored in the wire. Therefore we don’t see the non-uniqueness of the dynamical dimension as a disadvantage of the method; the point is that additional information has to be provided which goes together with the dynamical dimension.

It is important to remark that the theory developed here disregard dissipative effects. The inclusion of damping introduces a correction factor on the frequency equals to where x = c/w and 2c is the damping coefficient. This factor is frequency dependent and therefore will disturb the relation T_k/T₀ = f(l_k/L₀). How this new function would provide information about the fractal characteristics of the sequence under consideration deserves further investigation. Maybe some important information about damping effects could be obtained from the behavior of this new function.

We have shown with simple examples that the fractal dimension of a given primordial sequence may be unrelated to the fractal characteristics of the offspring sequence. This means that physics is not always hooked up by geometry. Nature can take advantage of this property and human design as well. Here we have dealt with dynamical characterization but certainly other physical phenomena could be used. Mandelbrot (1982) discussed several examples where fractal geometry is present in nature. Particularly in biological phenomena (Bassingthwaighte et alli, 1994) the investigation of the fractal aspects of geometry and physics could be explored.

The theory is barely beginning so there are multiple possibilities to explore theoretical developments as multi-fractals and applications as the fractal nature of composite materials and tissue fibers.

Acknowledgements

We would like to thanks the National Research Council – CNPq – and the Rio de Janeiro State Foundation for Research Support – FAPERJ – whose support have been decisive to carry on this research project.

Paper accepted December 2007.

Technical Editor: Domingos A. Rade.

Moreover there exists one and only one number D_H , defined as the Hausdorff dimension of the fractal object such that:

Application for the Koch triadic.

For this case it is easy to see that the minimal cover of a general term of order n consists of balls with diameter equal to ln = (L0 /3)n Therefore:

Now the limit when 2r = (1/3)ⁿ® 0 is equivalent to let n ® ¥. Let D= log4 / log3. If s > D then H ® 0 and if s < D then H ® ¥. The measure jumps from zero to infinity when s is precisely equal to log4/log3. According to the definition of the Hausdorff dimension:

s = D = log4 / log3 is the Hausdorff dimension of the Koch triadic.

We want to show that the first derivative of the bilinear term W_k with respect to l_k is finite for increasing values of k. Recall that:

First let us write a_i(k) under the form:

where:

_i-1,i = (z_i-1 + z_i)/2 and Dz_i-1i = (z_i - z_i-1)/2

Introducing equation (A1) in the expression for W_k we get:

Clearly

_i < 1 and |Dz_i-1,i| < 1.

Consider first the second term on the right hand side of equation (A2). By definition Dy_i-1,i = y_i – y_i-1 as shown in Fig.A1 and therefore it is possible to write:

Dy_i-1,i = g_i-1,il_k with g_i-1,i< 1,

from which follows:

Dz_i-1i = img34 Dy_i-1,i = img34 g_i-1,il_k = b_i-1,il_k

Introducing this expression in equation (A2 ) we get:

Now define the vector functions:

and

Then the equation (A3) in vector notation reads:

Now since:

|z_i-1i| < 1, |b_i-1,i| < 1 and l_k < M

for all k and M is finite we may claim that W_k is finite as k ® ¥. Similarly the term of order k+1 can be written as:

where the components of z_k+1 are proportional to the ordinates of the corners of the curve corresponding to the term of order k+1. In general we may write:

Referring to the preceding term in the sequence as shown in Fig.A2 we have:

Note that

represents respectively the ordinates of the corners of the k^th curve in the sequence and the ordinates of the added corners for the (k+1)^th curve. It is possible then to decompose the vector z_k+1 in the following way:

where U₁and U₂ are Boolean matrices.

Now, with this decomposition it is not difficult to show that the vector

_k+1 can be written as:

nd R is a Boolean matrix.

Now using the definition of W_k+1 and recalling that (Dz_k) = l_kb_k:

where:

Recalling that:

and that R is a Boolean matrix we arrive at:

where R₁(k,k+1) and R₂(k,k+1) are finite for all k, max(R₁ , R₂) < M (finite). Finally we get:

W_k+1 = W_k + l_kR₁ (k,k +1) + R₂(k,k +1).

Now noting that:

Dl_k = l_k+1 - l_k = l_k ,

we may write:

= (R₁ (k, k + 1) + l_kR₂ (k, k + 1))

Lemma.For the family of curves belonging to the class defined by N_k = p^k and l_k/L₀ = 1/q^k, the first differential ratio of the bilinear term W_k with respect to l_k is finite for increasing values of k, that is decreasing values of l_k.

• Barros, M., 2007, Carcaterização de Estruturas Fractais uni-Dimensionais Contidas num Plano, MSc. Dissertation, LNCC, April, 2007.
• Bassingthwaighte, L., Liebovitch, L. S., Bruce, J. W., 1994, "Fractal Physiology", American Physiological Society.
• Bevilacqua, L., Barros M.M., "Dynamical Fractal Dimension: direct and inverse problems.", Proceedings of the IUTAM Symposium on Non-linear Dynamics and Control under Uncertainty pp127-136, Springer Verlag, Berlin, New York, 2007.
• Bevilacqua, L., 2004, "Fractal Balls", Applied Mathematical Modeling, Vol.28, issue 6, pp 547-558.
• Bevilacqua, L., 1999,"Dynamical Characterization of Fractal Surfaces", Proceedings EURODINAME-99, Dynamical Problems in Mechanics and Mechatronics, Univerzität ULM, pp 285-292.
• Falconer, K., 1990, "Fractal Geometry: Mathematical Foundations and Applications", John Wiley&Sons, Chichester and New York.
• Feder, J., 1988, "Fractals", Plenum Press, New York and London.
• Gouyet, J.F., 1996, "Physics and Fractal Structures", Masson, Springer, N.Y.
• Hausdorff, F. 1919, "Dimension und äußeres Maß." Math. Ann. 79, pp157-179.
• Mandelbrott, B., 1982, "The Fractal Geometry of Nature", W.H.Freeman and Co., N.Y.

Appendix I 

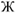. Let B 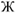that is, 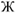belongs to Ç B

Consider a fractal object . Let B_i a countable set of Borel balls B_i with radius r – the largest distance of two points belonging to the ball. Let this set to be a cover of that is, belongs to Ç B_i. The outer measure of the cover is defined to be less or equal to the sum of the diameters of all balls of the cover. The s-dimensional Hausdorff outer measure H(s,r) is the infimum of the all measures raised to the power s of all such covers, that is:

Appendix II 

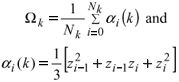
Publication Dates

• Publication in this collection
  25 Apr 2008
• Date of issue
  Mar 2008

History

• Accepted
  Dec 2007
• Received
  0000