Abstract
All over the world traffic injuries and fatality rates are increasing every year. The combination of negligent and imprudent drivers, adverse road and weather conditions produces tragic results with dramatic loss of life. In this scenario, the use of mobile robotics technology onboard vehicles could reduce casualties. Obstacle motion tracking is an essential ability for car-like mobile robots. However, this task is not trivial in urban environments where a great quantity and variety of obstacles may induce the vehicle to take erroneous decisions. Unfortunately, obstacles close to its sensors frequently cause blind zones behind them where other obstacles could be hidden. In this situation, the robot may lose vital information about these obstructed obstacles that can provoke collisions. In order to overcome this problem, an obstacle motion tracking module based only on 2D laser scan data was developed. Its main parts consist of obstacle detection, obstacle classification, and obstacle tracking algorithms. A motion detection module using scan matching was developed aiming to improve the data quality for navigation purposes; a probabilistic grid representation of the environment was also implemented. The research was initially conducted using a MatLab simulator that reproduces a simple 2D urban-like environment. Then the algorithms were validated using data samplings in real urban environments. On average, the results proved the usefulness of considering obstacle paths and velocities while navigating at reasonable computational costs. This, undoubtedly, will allow future controllers to obtain a better performance in highly dynamic environments.
motion tracking; obstacle classification; Kalman Filter; urban-like environment
TECHNICAL PAPERS
2D laser-based probabilistic motion tracking in urban-like environments
Marcelo BeckerI; Richard HallII; Sascha KolskiIII; Kristijan MačekIV; Roland SiegwartV; Björn JensenVI
Ibecker@sc.usp.br, Senior Member, ABCM, University of São Paulo- USP. São Carlos Engineering School EESC, 13560-400 São Carlos, SP, Brazil
II rhall@kth.se
IV kristijan.macek@mavt.ethz.ch
Vrsiegwart@ethz.ch, Swiss Federal Inst. of Technology Zurich - ETHZ. ASLIRIS, CH-8092, Zürich, Switzerland
VIbjoern.jensen@singletontechnology.com, Singleton Technology Sàrl. Parc Scientifique (PSEC), CH-1015 Laussane, Switzerland
ABSTRACT
All over the world traffic injuries and fatality rates are increasing every year. The combination of negligent and imprudent drivers, adverse road and weather conditions produces tragic results with dramatic loss of life. In this scenario, the use of mobile robotics technology onboard vehicles could reduce casualties. Obstacle motion tracking is an essential ability for car-like mobile robots. However, this task is not trivial in urban environments where a great quantity and variety of obstacles may induce the vehicle to take erroneous decisions. Unfortunately, obstacles close to its sensors frequently cause blind zones behind them where other obstacles could be hidden. In this situation, the robot may lose vital information about these obstructed obstacles that can provoke collisions. In order to overcome this problem, an obstacle motion tracking module based only on 2D laser scan data was developed. Its main parts consist of obstacle detection, obstacle classification, and obstacle tracking algorithms. A motion detection module using scan matching was developed aiming to improve the data quality for navigation purposes; a probabilistic grid representation of the environment was also implemented. The research was initially conducted using a MatLab simulator that reproduces a simple 2D urban-like environment. Then the algorithms were validated using data samplings in real urban environments. On average, the results proved the usefulness of considering obstacle paths and velocities while navigating at reasonable computational costs. This, undoubtedly, will allow future controllers to obtain a better performance in highly dynamic environments.
Keywords: motion tracking, obstacle classification, Kalman Filter, urban-like environment
Introduction
As a result of the astonishing advances made over the last decades on several scientific fields, today mobile robots have many real applications. They range from Automatic Guided Vehicles (AGVs) and Autonomous Mobile Robots (AMRs) on factory floors, personal assistants for disabled and elderly people to exploration of hazardous environments such as surface of planets and bottom of oceans. Wherever the robot may be and whatever its purposes are an interface to exchange information is always needed. For many applications, e.g. when the interaction between humans and robots are not close, this interface may be a simple remote control. On the other hand, when robots and humans interact directly or they need to be more autonomous and take decisions based on their perception of their environment, the interface might be much more complex. Autonomous behavior is frequently represented as a perceptionreasoning-action loop. It means that given the specification of a goal, the robot uses perception to identify relevant elements, then it analyses them, plans tasks to attain the goal, and finally executes these tasks. More autonomous systems may even define the goal to be reached based on some criteria.
Recently, several events around the world and research funding agencies have been impelling robotics researchers to focus their works on developing, transferring, and adapting techniques and approaches initially developed for indoor and outdoor mobile robots to car-like autonomous mobile robots. Events such as the DARPA 1st and 2nd Great Challenge (2005, 2007), ELROB (2005), and CELROB (2007) are paving the way for the use of promising technologies in military and civil vehicles (Thrun et al., 2006; Dahlkamp et al., 2006; Lamon et al., 2006; and Stavens et al., 2007). On the other hand, in a near future, an assistance system that helps the driver and acts mostly in peril situations will be implemented more easily when compared to a fully autonomous system and will probably be more attractive for the majority of the drivers (one should take into account that western people tend to be standoffish regarding robots, in severe contrast to the Japanese, who welcome ubiquitous machines).
Systems like the Intelligent Parking Assist (IPS) technology onboard the Toyota Prius are becoming very popular among car buyers. Due to this, many researchers are working on car-like robot autonomous parking problem. This is a perfect example of an assistive system that uses sensors, e.g. ultrasound sensors and cameras, to help the driver during maneuvers. This amounts to saying that a system which is able to provide a full parking maneuver procedure, without any human intervention, is desired and will shortly become a serial item. Another example is the Secure Propulsion using Advanced Redundant Control project - SPARC developed at the Swiss Federal Institutes of Technology (EPFL and ETHZ) in cooperation with a European Consortium of Automotive Companies (Holzmann et al., 2005-a and 2005-b, and Becker et al., 2007-b). Recent developments on sensors, actuators, algorithms, etc. applied on intelligent vehicles can be found in SAE series PT-132 (2006) and PT-133 (2007).
Today it is possible to think of freeways and urban environments interconnected by high-tech networks that will allow the dissemination of fully autonomous vehicles. Traffic jams may be substituted by hundred of vehicles virtually interconnected and moving autonomously in a cooperative way. Onboard computers are likely to work together and control completely the vehicles under any weather and road conditions. Nevertheless, in order to achieve this dream scenario, the entire road network and vehicle fleet need to be adjusted accordingly.
Taking into account that there are hundreds of millions of vehicles and road kilometers in the world, these changes possibly represent a cost of billions of dollars. In a near future, a less expensive solution is an intelligent road network based on road and onboard vehicle sensors and computers. In this case, adapted freeways monitor vehicles, road, and weather conditions act as an assistive system alerting the drivers for peril situations. Today this scenario is becoming a reality in Europe, Asia, and North America. Another option is the use of intelligent assistive systems (e.g.: anticollision systems) onboard vehicles. In case of an imminent collision, the system would alert the driver or assume the vehicle control.
There are several problems to be solved in both cases (fully autonomous and assistive technologies), but recent developments of onboard hardware and sensors are resulting in considerable research progress. However, the best ratio between desired autonomous behavior and costs when selecting the onboard hardware and software necessary for acquiring, extracting, and interpreting the environment features is to be drawn. In the context of autonomous and assistive systems, the importance of cognitive abilities is noticeable. Similarly to persons that need their senses in order to interpret and interact with the environment, an autonomous robot needs sensors that would provide information about his vicinity and state. In practice, the interpretation of the scene (i.e.: environment feature extraction, robot auto-localization, obstacle position detection, obstacle classification, obstacle path prediction, etc.) is essential to provide the robot controllers with information to plan a safe path. Although sensor technology has experienced significant improvements recently, high dynamic changing and unconstrained environments still represent an enormous challenge for the robotics research community. This is the case of urban-like environments where traffic (car, buses, bicycles, etc.) and pedestrian paths are unknown and sometimes difficult to predict. In spite of this, the obstacle motion tracking is an indispensable procedure for improving the robot environment perception. Unfortunately, it is a difficult task when some obstacles close to the robot's sensors may cause blind zones behind them. In this situation, the robot may lose vital information about hidden obstacles that could avoid future collisions.
Some examples of researches developed in the field of autonomous parking are those carried out by Chao et al. (2005), Khoshnejad M. and Demirli (2005), Yamamoto et al. (2005), and Chiu et al. (2005). In this topic, fuzzy logic and artificial neural networks are some of the approaches used by the authors to face the problem. In addition to these researches, the works developed by Wang and Thorpe (2002), Duan et al. (2004), Lee and Chen (2004), Lu and Chuang (2005), Martínez-Marín (2005), Romero-Meléndez et al. (2005), Thompson and Kagami (2005), Kolski et al. (2006), and Maček et al. (2006) addressed a more complex problem: the path-planning task in urban environments for car-like mobile robots. The hidden and visible obstacles tracking problem was addressed in Becker et al. (2007-a). Virtual drivers, drive-assistant systems, and lane detection using artificial vision systems were focused in Maček et al. (2004), Bellino et al. (2005), Holzmann et al. (2005-a and 2005-b), and Lamon et al. (2006).
The present work focuses the 2D laser-based obstacle motion-tracking problem in dynamic unconstrained environments (urbanlike) by applying a Kalman Filter in order to predict the obstacle motions when they are hidden. This would allow the car-like mobile robot controller to take into account hidden and non-hidden obstacles when maneuvering the robot. A probabilistic occupancy-grid representation of the environment was also implemented. It provides a given time horizon prediction view of the robot surrounds based on motion-models of the obstacle classes and obstacle-estimated velocities. Initially, the test platform (Smart Car) is presented. Next, a brief review of the state of art on motion tracking is addressed and the multi-obstacle motion-tracking algorithm (including the Kalman Filter) is shortly described. Then, the results obtained while using real data are shown. Finally, the conclusion and outlook are presented.
Nomenclature
= Mahalanobis distance, m
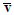
= measurement white noise, m
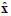
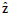
Greek Symbols
= standard deviation, m
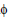
Subscripts
Superscripts
Test Platform - Smart Car and Laser Range Finder
The Smart Car used as test platform is based on an ordinary smart fortwo coupé passenger car (Fig. 1). Obviously some changes and improvements were included in order to allow the vehicle autonomous behavior, e.g.: a steer-by-wire system (Fig. 2). Undoubtedly, the heart of the vehicle is the onboard computer. It is interfaced with several sensors and actuators that control the vehicle through the controller-area network (CAN). For instance, braking, acceleration, and steering controls are made by controlling dedicated motors. A system of cable and pulleys controlled by a motor is used to activate the brake pedal. An electronic system was designed to set the throttle command directly (the voltage, originally provided by the potentiometer in the throttle pedal, is generated by the computer and sent to the CAN).
A set composed by a steering encoder and a motor allows the computer to steer the vehicle front wheels. Summarizing, the vehicle CAN can access the following internal car state data:
1. Vehicle flags: engine on, door closed, brake pedal pressed, etc.;
2. Engine: engine rpm, instantaneous torque, gear shift, temperature, etc.;
3. Odometry: global vehicle speed, individual wheel speeds, ABS activated;
4. Throttle pedal value and steering wheel angle.
A switch enables to select the manual or autonomous vehicle modes. The Smart Car is also equipped with Global Positioning System (GPS) and 6 degree of freedom (DoF) Inertia Measurement Unit (IMU), allowing measuring the vehicle relative movement. The IMU measures lateral acceleration in all three dimensions, angular rates up to 100º/s with a resolution of 0.025º, and lateral acceleration up to 2g with a resolution of 0.01 m/s2. Exteroceptive sensors, such as a monocular camera and a laser range finder (SICK AG Laser Measurement Sensor - LMS 291) both looking forward, have also been installed. The laser sensor was assembled on the front bumper of the Smart Car and it has a 180º field of view with an angular resolution from 1º to 0.25º. Its maximum range is 80 m and it has a statistical error of 10 mm.
In this work we used the data from the laser scanner as the main source of information. This choice was based on the fact that laser sensor prices are gradually decreasing every year, what may make it possible their commercial use in passenger vehicles in a near future.
Sensor Model
Laser scanners are active sensors that emit a laser beam and rely on the time-of-flight principle for measuring distance. A rotating mirror or prism is used in order to cover an angular range. The neighboring points are taken at successive rotations of the revolving unit. Thus, they are taken with a time difference proportional to the rotational frequency (fsensor) of the revolving unit (in our case, fsensor = 75Hz). The sensor data flow can be understood as follows: the laser sensor acquire data over a period of time Δt, which is then sent to the computer via RS422 where a real-time thread reads data at 17Hz. In a first step, the data set is transformed into a coordinate system centered on the vehicle and it is assigned with a time-stamp and the vehicle position at this time. Depending on the desired angular resolution, the acquisition time varies. For 0.5º resolution two rotations are necessary, so the acquisition time amounts to Δt = 2/fsensor. During the first rotation the data points for the angular position 1, 3,... are taken and the second rotation provides the even set of 2, 4,... When running in 0.25º mode even four rotations are necessary and the acquisition time amounts Δt = 4/ fsensor.
In our case, the main objective of modeling the laser scanner is to take into account known sources of uncertainty while tracking the obstacles. The main assumption used is that different sources of error are pair wise independent and can be modeled as Gaussian distributions. Thus, the resulting uncertainty may be represented as its covariance (Jensen, 2004). There are several origins for laser measurements, but the main ones are: the timer counting the timeof-flight, the stability of the rotational frequency of the revolving unity and the frequency with which beams are sent out. Unfortunately, the sensor documentation (SICK AG, 2006) has no data for ranges greater than 20 m and for the angular uncertainty. For the experiments carried out in this research (0.5º angular resolution and 30 m range) we assumed the sensor data specified in the documentation for a 20 m range (the uncertainty on the distance measured to σρ2 = 0.012 m2). Concerning the angular uncertainty, in fact we observed that the angular values provided by the sensor are constant and taken from a table. Due to this, it is difficult to evaluate the angular uncertainty experimentally. So, we used the opening angle of the laser beam (0.5º) and assume the angular uncertainty to be half the beam width ( = 0.252º2). As previously cited, distance and angular uncertainties are assumed to be independent and Gaussian distributed, thus the sensor uncertainty is represented by:
= 0.252º2). As previously cited, distance and angular uncertainties are assumed to be independent and Gaussian distributed, thus the sensor uncertainty is represented by:
Motion Tracking
Applications of motion tracking algorithms range from military (e.g. missile guided systems, air-space surveillance, etc.) to civil ones (e.g. virtual reality systems, human-machine interaction, etc.). All these applications face challenges concerning noise sensor data and data uncertainty. In order to deal with these problems the use of Kalman Filters (KF) was proposed in the early 1960s by Kalman (1960), and Kalman and Bucy (1961). Early studies focused on single and multi-target tracking, and data origin uncertainty applied on environment surveillance also proposed the use of KF (Sittler, 1964; Sea, 1971; and Singer and Stein, 1971). When dealing with the incorporation of uncertainty on the data origin in tracking, one should keep in mind that the robot is dealing with multiple-hypothesis tracking. This means that it has a combinatorial explosion of hypothesis that usually cannot be handled in real-time (Jensen, 2004). There is a large quantity of publications in the literature related to motion tracking using a variety of sensors (vision, laser, etc.). As our test vehicle has an onboard 2D laser sensor used for extracting the environment data, we decided to focus our literature review on the development of systems that use mobile robots with onboard 2D laser sensors. Nevertheless, when it comes to car-like tracking applications in dynamic urban scenarios that use only 2D laser sensor data, literature proved to be scarce up to now. Pradalier et al. (2004) developed an interesting approach using as test vehicle a bi-steerable car called CyCab. However, they did not focus their research on multi-obstacle motion tracking, but on the integration of some essential autonomy abilities into a single application (simultaneous localization and environment modeling, motion planning and motion execution amidst moderately dynamic obstacles).
Considering indoor applications, there are several works that focused the motion-tracking problem based on 2D laser sensor data. Shulz et al. (2001) addressed the application of multi-obstacle motion tracking algorithms onboard mobile robots for tracking moving persons. They applied a sample-based representation of the joint probability density function (SJPDF) of all moving obstacles to avoid the combinatorial explosion of multi-hypothesis tracking. If on the one hand they could combine SJPDF with a local occupancy grid and show the tracking of several persons through temporal occlusions in well structured environments, on the other hand, the use of SJPDF requires the knowledge of the tracked obstacle quantity. It means that they needed to use a Bayesian filter and the time sequence of moving features quantity to estimate the tracked obstacle quantity. At the end, their motion tracking algorithm had to deal with local minima, non-linear relations due to the increased occlusion quantity, local occupancy grids, and the use of probabilistic filters to filter static objects that could become difficult to handle in real-time for non-structured environments. Kluge et al. (2001) presented a strategy for analyzing the robot-human interaction scenario. It was based on a set of prototypical situations in crowded public environments and consists of scene analysis, tracking, action recognition, and intention reasoning procedures. Illmann et al. (2002) extended this analysis by applying local person density and tree-based vector quantization. Bennewitz et al. (2002-a and 2002-b) developed a system to segment tracks of a person in a common household environment. In this work, the trackers were obtained from static laser sensors and the segmentation process was based on Expectation Maximization approach. Their purpose was the detection of the intention of a person based on his or her path. Jensen (2004) addressed the multi-object tracking problem using single Kalman Filters for each individual problem. In order to deal with data association he used validation gates and to solve the measurement-track assignment he utilized linear programming techniques. Our approach is based on (Jensen, 2004) and extends it for urban-like environments focusing on tracking pedestrians and vehicles (e.g.: cars, trucks, and buses).
Figure 3 summarizes the approach developed for urban-like environments. The 2D laser raw data acquired by the SICK laser sensor are used as input data for the obstacle detection algorithm. Initially, the data are segmented in order to extract the environment features and to detect motion. Features that are not moving are considered static and stored in a local map that is also used for detecting motion. After detecting mobile obstacles, a process of data association is applied to start new trackers or update existing trackers. Trackers that are hidden for more than a threshold value (e.g.: one second) are deleted. Put simply, the whole procedure outputs are:
1. Non-hidden obstacle quantity, obstacle positions and estimated velocities (Trackers in Fig. 3);
2. Hidden obstacle quantity, obstacle predicted positions and velocities (Trackers in Fig. 3);
3. Obstacle classification, e.g. pedestrian, car, truck, etc. (Trackers in Fig. 3);
4. Local Occupancy Grid Map;
5. Predicted Occupancy Grid Map for a given time horizon (e.g.: 1 second).
Both procedures, obstacle detection and tracking, are shortly explained as follows.
Obstacle Detection
There are several approaches for detecting objects using a 2D laser scanner in the literature, most of them centered in indoor mobile robotics applications. For a fixed sensor this task is straightforward since it is possible to compare two consecutive scans and immediately determine which points remains in the same spot and which do not. For a mobile sensor like the one onboard a mobile robot or a vehicle such as a car, the task is somewhat more difficult due to the translation and rotation caused by its displacement. Take for example a static obstacle that is seen by only one point in the first scan. In the next scan the sensor has moved a little and the changed viewing angle results in the point being seen at another spot on the same obstacle. This phenomenon can give a false impression that the static obstacle is actually moving. In order to avoid this, it is necessary to take into account, as precisely as possible, the vehicle position. This work focuses on detecting moving obstacles like vehicles and pedestrians. To perform this task, we utilized the Motion Filter approach (Lindstrom and Eklundh, 2001; and Wang and Thorpe, 2002).
It is important to emphasize that this work is not focused on the vehicle position estimation. This topic was previously highlighted in Lamon et al. (2006-a and 2006-b) and Kolski et al. (2007). Basically, in order to accurately localize the vehicle, the GPS, the IMU, and the wheel encoder data were combined using a Kalman Filter to estimate its 6 degrees of freedom, i.e. its position and attitude (Sukkarieh et al., 1999; and Dissanayake et al., 2001). This filter is called Information Filter (IF) and during the experiments it produced excellent results when the vehicle was traveling at low speeds in open areas (far from large structures, tunnels, etc.). The standard deviation of the filtered position was less then 0.025 m for all three position coordinates. Based on this result we decided to neglect the vehicle position uncertainty, while modeling the Kalman Filter used to estimate the obstacle motions when they are hidden (see Kalman Filter item). Following this premise, we could use directly the vehicle position estimated by the IF to produce local maps and detect motion, even when the vehicle was moving.
Segmentation
Grouping measurements that belong to the same object are mandatory, when processing data from a laser scanner. The scans will consist of length measurements at equidistant angles and therefore it is very likely that two points that are close to each other also belong to the same object. Likewise, two consecutive measurements that are far away are likely to imply that a change in the observed object has occurred. Since it is necessary to define a distance threshold, there is always the risk of making errors in the segmentation process, either by creating one single segment out of two or more close objects, or by dividing an object into more than one segment. The segmentation makes it possible to do further processing on the different segments or point clusters. This normally consists of classification by size, dynamic status, or geometrical features (MacLachlan, 2004).
Motion Based Approach
Basically, the idea is to compare two scans apart by some time interval, Δt, trying to match them in order to determine which points are static and which are dynamic. By using this approach one can suppress spurious readings from the static environment, giving a better input to the tracker. The scan matching is made by storing the previous scan and comparing it to the new one. For each point in the new scan, distances to points in the old scan are calculated and compared to a threshold value (in our case, ± 10 cm). If a match is found, the point is likely to be static. One exception is when points are matched to a different area on a moving obstacle, for instance along the side of a passing vehicle. This problem was later solved by checking the dynamic classification in the first scan. If a point was labeled dynamic at that time, it is likely to be dynamic in the next scan. However, if no match is found, one cannot say for sure that the point is moving without further processing. The point could have been occluded in the first scan or out of range due to vehicle motion between scans. Therefore, we make use of the free area that is the space between the robot and the obstacles or scan range. If a point seen in the second scan is not found but within this area in the first scan, thereby observable, it is labeled as moving. A segment containing a certain amount of points labeled as moving can be sent to the tracker, after its center point is calculated.
During the simulation phase, we observed that the simple use of scan matching was not sufficient to deal with spurious readings. One reason for this behavior was the translation and rotation movements of the sensor. Aiming to increase the detection of static points, a local map was created. At first, the map was implemented as a position vector, storing in each scan the coordinates of all points labeled as static ones. New scans were then checked against the map and when a match was found, the weight for that map point was increased. In order to keep down the size of the map, each point kept track of its own age. When a terminal age was reached, e.g. after 10 seconds, the point would be deleted from the map. The static map helped to improve the motion detection, but some disadvantages were noticed. The representation of the map using points was one of them. Measurements are never exact, and therefore, it is difficult to determine how many map points are needed to represent an obstacle. If we add all new static points, we get a very large map which slows down the matching process. But if we only add points that were not matched to the map before, we will certainly miss useful information. A method that turned out to be a better approach to the local mapping was the Time Stamp Method (Fiorini and Shiller, 1998). Basically this method is an Occupancy Grid Representation (Elfes, 1989) that does not consider the uncertain cells. Due to this, only free and occupied cells are considered and the computational time necessary for each environment scan is reduced.
Thanks to the use of the Fiorini and Shiller's occupancy representation, we could improve and simplify the scan matching process. Latter, the occupancy grid was used not only to represent the static environment, but also to represent present and future predictions of the tracker output. This was carried out by adding a probabilistic grid to the occupancy representation (see Predicted Occupancy Grid Map item). Due to this, it was necessary to classify and model the obstacles that were being tracked.
Obstacle Classification
By classification, we refer to the process of determining if a moving segment belongs to vehicles or pedestrians. While working with the MatLab Simulator (Becker et al., 2007-a), pedestrians were rarely detected by more than two or three scan data. Since the sensor is placed about 50 cm from the ground, it usually detects one point on each leg. If the pedestrian stands close to the sensor it is easier to distinguish a contour, but this was rarely the case. An obvious difference between vehicles and pedestrians is their size, so we decided to base the classification on it. We used the standard deviation of each segment to represent its size:
where X and Y are stochastic variables, x and y are measured points on a segment, n is the data quantity, and µ and σ are expected values and standard deviations respectively.
Checking the norm of standard deviations against a predefined threshold yields the classification into vehicle or pedestrian:
Obstacle Tracking
A robot navigating in an environment with other moving obstacles needs some kind of information concerning its environment in order to avoid collisions. Some systems just prohibit movement in directions which will bring the robot too close to an obstacle, regardless of how the obstacle moves (Siegwart and Nourbakhsh, 2004). For efficient path planning it is, however, much better to know more about the dynamic state of the obstacles. The way to achieve this goal is by tracking them and estimating their future positions (states). Tracking makes it possible to measure the dynamic state of an obstacle, i.e. its position and velocity, and with this information predictions can be made on the obstacles future positions (Bar-Shalom and Fortmann, 1998; and Blanc et al., 2005).
In an urban environment, laser measurements are subject to noise, which we have to suppress by filtering. It is also usual to expect obstacles being hidden by other obstacles. However, it is possible to continue to track these obstacles until they are seen again and thereby minimize the risk of a collision. Each obstacle in this setup is characterized by its center of gravity, or at least the center of gravity for the part that is being seen. Since the scanner provides a 2D output, this point is described by (x, y) coordinates. The x and y velocities were also introduced in the state of the dynamic object for tracking the motion of each obstacle and predicting its continued path. The state vector then becomes:
However, from now on we will simply denote it as x. The measurements, containing only the x and y values, are labeled z.
Kalman Filter
The Kalman Filter (KF) is a wide spread technique for estimating the state of a dynamic system observed through noisy measurements. The filter is a recursive state estimator, which means that in every step it uses the output of the previous step to make a new prediction. It consists basically of two steps, the prediction step when estimation is made based on the old state, and an update step when that estimation is updated with a new measurement. The state and measurement predictions are denoted by 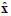 and
and 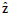 . In order to predict a dynamic system response, a dynamic model is used. In this study the linear constant-velocity model (Jensen, 2004) was applied. Due to its linearity, it is simple to implement. It can be described by its discrete-time transition and noise covariance matrices, respectively Eqs. (6) and (7):
. In order to predict a dynamic system response, a dynamic model is used. In this study the linear constant-velocity model (Jensen, 2004) was applied. Due to its linearity, it is simple to implement. It can be described by its discrete-time transition and noise covariance matrices, respectively Eqs. (6) and (7):
Other models were considered and, especially for vehicles, the constant angular velocity model could improve the tracking for vehicles making turns. However, such implementation would require a more complex filter, Extended Kalman Filter, EKF (Thrun et al., 2005). It is also beneficial to keep a simple, not too specialized, model since the tracker is dealing with obstacles with different dynamic properties (e.g.: pedestrian and vehicles). The evolution of the dynamic system can now be described as:
where υ and w are respectively the white process and measurement noises and H is the measurement matrix, which transforms a state vector into a measurement vector, Eq. (10):
In the prediction step, the latest state estimated at Δt is used to produce a new state prediction at (Δt + t). Predictions are also made on the state and innovation covariances, respectively Eqs. (13) and (14):
where the measurement noise covariance, R, is the variance (σ2) times the identity matrix (I), Eq. (15); in our case the variance is represented by the sensor data uncertainty, Eq. (1). P is the state covariance matrix, and S is the innovation covariance matrix.
The following step is called the update step, because a measurement is used to update the tracker. Now the innovation, υ can be calculated as the difference between the real measurement and the predicted one. The filter gain, W, is calculated after state and covariance updates:
More details concerning the implementation of Kalman Filters and Extended Kalman Filters may be found in: Kalman and Bucy (1961), Bar-Shalom and Fortmann (1998), Jensen (2004), and Thrun et al. (2005).
Data Association
Each tracker must be associated with new measurements when available, if the filter is working properly. There are various approaches for data association that are designed to suit different scenarios. A Joint Probability method (Bar-Shalom and Fortmann, 1998), for instance, is an interesting choice when sampling data in a cluttered environment, because it takes into account the fact that the closest sample is not always the right one in a multi-target scenario. The intuitive approach in this case was the Nearest-Neighbor Standard Filter, NNSF (Bar-Shalom and Fortmann, 1998). The NNSF algorithm iteratively calculates all the distances between trackers and measurements. The distance is represented by the Mahalanobis distance, MD:
MD is the same as the Euclidian distance, if the covariance matrix is the identity matrix, I. Each tracker is then associated with the closest measurement, if it does not exceed a predefined threshold. However, problems may occur if the application deals with unambiguous association. An optimization was carried out by using integer programming: MD was collected in a matrix where one tries to minimize the total sum provided. There may be only one value selected from each column and each row (Jensen, 2004).
Tracking Obstacles
The tracking obstacles task is performed after the data association procedure. In the beginning (the very first scan), all measurements are initialized as new trackers and their initial state vectors, xinitial, represent their positions and null velocities (initially all observed features are considered static ones). Covariance matrices are also initialized to reasonable values, taking into account the sensor documentation (SICK AG, 2006). Each tracker is associated with a variable called hidden that keeps the scan quantity in which the tracker has not been updated with a measurement. At initiation or after a successful update this variable is reset to zero. In every consecutive scan, trackers are updated iteratively in the following sequence:
1: for each TRACKER do 2: Calculate Kalman prediction state; 3: MDall Mahalanobis Distances of all measurement data;
4: MD min(MDall);
5: if MD < threshold1then 6: update Kalman Filter with measurement; 7: hidden = 0; 8: else 9: hidden = hidden + 1;
10: end if 11: if TRACKER is hidden for more than threshold2then 12: Delete TRACKER 13: end if 14: end for 15: for each unmatched measurement do 16: Create a new TRACKER 17: end for
Predicted Occupancy Grid Map
The inclusion of tracked obstacle path predictions in the occupancy grid map of the environment that surrounds the robot improves the map usefulness for navigation. In future, we plan to fuse the procedure presented in this work with the navigation procedures previously presented at Kolski et al. (2006). The predictions are carried out by calculating possible paths for the trackers and adding some uncertainty at some time step in the future. As the trackers are keeping the dynamic state of the tracked obstacles, this information can be used for predicting a future state. For vehicles it is a relatively easy task, taking into account that the vehicle maneuverability model can be expressed in a couple of equations. On the other hand, for pedestrians this task is quite complex. A person is often moving at a speed which allows it to stop abruptly, or entirely change heading. One might, for instance, stop to talk with someone and continue in another direction afterward. Since pedestrians are likely to travel at rather low speeds, the constant-velocity model was considered sufficient for predicting their paths.
Unfortunately, for vehicles this solution was not possible and we decided to use vehicle steering kinematics to model the vehicle behavior. Aiming to keep the model as simple as possible, instead of applying the Ackermann Geometry (Gillespie, 1992), we make use of a simple steering model based on the vehicle instantaneous center of motion - ICM. The vehicle front wheel angles relative to their straight ahead position is called the steering angle, henceforth noted θ. Due to mechanical reasons most vehicles have a maximum steering angle that is by far less than 90º. When maintaining constant steering angle, θ  0, the vehicle is moving on a circular path. A simple car model (LaValle, 2006) gives us Eq. (21):
0, the vehicle is moving on a circular path. A simple car model (LaValle, 2006) gives us Eq. (21):
where L is the distance between the front and rear wheel axles, and R is the radius of the circular path with center in Instantaneous Center of Motion - ICM.
Continuing with deriving the angular velocity in the path we have:
where d is the distance along the circular path, same as v.Δt, and Δ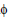 is the change in angular orientation (Δ
is the change in angular orientation (Δ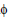 =
=  .Δt,
.Δt,  is the angular velocity). Further simplifications:
is the angular velocity). Further simplifications:
Combining Eqs. (21) and (23) yields:
Equation (24) means that it is possible to calculate the angular velocity of an obstacle knowing its velocity, steering angle and axle distance. Using the velocity and angular velocity, the predicted path can be easily calculated. Obviously, the placement of axles varies between different types of vehicles, but it stays in the same vicinity when the same vehicle class (e.g.: cars) is considered. A future combination of 2D laser sensors and embedded cameras would solve this difficulty by recognizing and classifying the vehicles into more detailed classes (e.g.: buses, cars, trucks, bikes, etc.) based also on visual data. For the moment, this class labeling is possible based only on vehicle speeds and sizes. In order to simplify the model, a maximum steering angle for vehicles was set to 0.42 radians (θmax  24º). Another constraint that was applied to limit the model was the fact that steep steering angle turns are unlikely at high speed. This is related to centripetal acceleration, because if extending it to the extreme, the car would slip taking a steep curve with too high speed. In a city-driving situation it is fairly unlikely that a driver would experience more than 1-g as lateral acceleration. The equation for centripetal acceleration is:
24º). Another constraint that was applied to limit the model was the fact that steep steering angle turns are unlikely at high speed. This is related to centripetal acceleration, because if extending it to the extreme, the car would slip taking a steep curve with too high speed. In a city-driving situation it is fairly unlikely that a driver would experience more than 1-g as lateral acceleration. The equation for centripetal acceleration is:
Combining Eqs. (24) and (25):
The maximum angular velocity is now given as the least value from Eqs. (24) and (26). One limitation in the procedure is that it does not provide angular velocity for the trackers. In order to do that accurately, an EKF is needed. Due to this and keeping in mind that we wanted to maintain the approach as simple as possible, we decided to use predicted velocity changes of each tracked obstacle to estimate the obstacle angular velocities. In addition to this, choosing a number of values in the interval [-
max,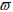 max] and then calculating predicted paths for each one give us a set of tracker possible positions for a given time horizon. Assuming that the predicted tracker is centered on the estimated turning rate,
max] and then calculating predicted paths for each one give us a set of tracker possible positions for a given time horizon. Assuming that the predicted tracker is centered on the estimated turning rate, 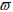 estimated (Fig 4), the highest probability value is assigned to the widest path, obtained from
estimated (Fig 4), the highest probability value is assigned to the widest path, obtained from 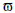 estimated. Therefore, the probability decreases as the distance between the predicted paths and the widest one increase.
estimated. Therefore, the probability decreases as the distance between the predicted paths and the widest one increase.
Now, based on obstacle class path models, it is possible to implement the predicted occupancy grid map for a given time horizon. Since we decided to represent the robot as a point mass, the occupancy grid had to be enlarged to compensate for the robot sizes (we use the robot circumscribed circumference radius as the occupancy grid growth rate). The predicted occupancy grid map is obtained iteratively for each map update in two steps. In the first step, only the environment static features are considered. They have their occupied cells enlarged by the growth rate, forming a new occupancy grid map with expanded occupied cells (EOC). These cells are considered as having the highest probability of being occupied (probability density equals to 1). Then, from the EOC borders to cell borders that are distant up to the growth rate, the probability densities are linearly decreased reaching zero at the borders. Next, in the final step, the obstacle predicted paths are considered. A number of possible path predictions had been calculated for each tracker and for each path a number of equidistant points are selected along that path. The point selection process takes into account the obstacle class parameters (
max,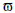 min, and maximum acceleration and deceleration) and the desired time horizon. In the sequence, each point is associated with a grid cell and the process described before for environment static features is applied for all trackers. In the end we obtain an occupancy grid that contains obstacles at present time and their estimated positions at a given time horizon. It is important to emphasize that the predicted occupancy grid map is stored in a separate data structure. It means that the original occupancy grid map is not changed.
min, and maximum acceleration and deceleration) and the desired time horizon. In the sequence, each point is associated with a grid cell and the process described before for environment static features is applied for all trackers. In the end we obtain an occupancy grid that contains obstacles at present time and their estimated positions at a given time horizon. It is important to emphasize that the predicted occupancy grid map is stored in a separate data structure. It means that the original occupancy grid map is not changed.
One may observe that the predicted occupancy grid map building process may be time and memory consuming depending on the characteristics of the environment. Due to this, we adopted two simplification strategies:
1. We reduced the update frequency for the static part of the occupancy grid map;
2. Obstacles whose distances to the robot are increasing above a threshold value were neglected.
The first strategy is justified because static features usually do not change their positions. But if, for instance, a parked car or a person starts to move unexpectedly, there is always an acceleration period that can be noticed by the obstacle tracking procedure (it immediately reclassifies this obstacle as a mobile one). In spite of this, the new mobile obstacle has its update frequency increased for building the predicted occupancy grid map. Concerning the second strategy, obstacles that are not considered dangerous because they are moving away from the robot are obviously negligible. If they change their path and start to represent a risk, they are not neglected anymore. These two strategies allowed us to keep the time and memory consumptions at an acceptable level during the experiments.
Smart Car Simulator
In the beginning, we developed the algorithms using a MatLab Simulator (Becker et al., 2007-a). It reproduces a simple 2D urban-like environment (approximately 800 m by 800 m) with parked and moving cars, buses, trucks, people, buildings, walls, streets, and trees. When using the simulator, one may reproduce the 2D kinematical behavior of the modified Smart Car. The Smart Car vehicle was kinematically modeled by applying the Ackerman steering geometry (Gillespie, 1992) and the real vehicle dimensions. While modeling the sensors, their real characteristics were taken into account. Lines and/or arcs represent all environment static and dynamic features. The sensor data are extracted from the environment based on its geometrical description and used as input data for testing the algorithms. It is important to emphasize that the simulator also allowed testing the algorithms while the simulated Smart Car was in movement.
Basically, the simulator uses the global position of the Smart Car in the environment for selecting a feature-window that contains all lines and/or arcs close to the vehicle. Then it simulates the laser sensor data by verifying the intersections between the simulated laser beam and the environment features. Afterwards, a noise signal is added to the sensor raw data vector (based on SICK AG, 2006 data). As the simulator was designed for testing different approaches before installing the codes in the real car, it allows the user to select and set different strategies, set points, and threshold values.
Results
Firstly, as cited previously in the text, the research was developed using the Smart Car Simulator. During this phase it was possible to test different techniques for tracking the obstacles. Aiming to facilitate the results comprehension, we present simulations and experimental samples with the vehicle parked in the following figures. Due to this choice, it becomes easier for the reader to compare the features, trackers, etc. at different time spots.
Figure 5 shows some simulation results. The trackers inside the range and the matched ones are represented by yellow circles and the hidden or out of range trackers, by pink circles. The black lines represent the obstacle predicted positions for 1 second. All occluded tracks were kept for 1 second. Meanwhile, if they were observed again, their states were updated and they were reclassified as non-hidden tracks. On the other hand, if they were not observed anymore after 1 second, they would be deleted. Regarding the algorithm performance, we compared the moving obstacles estimated speeds with their actual speeds, and the errors observed were less than 5%.
Aiming to test and refine our approach, real sample data were acquired on streets at EPFL. After these tests, it was possible to improve the tracking algorithms. The sites for sampling data were chosen near the parking lots at EPFL for catching as many cars and persons as possible. The sampling took approximately 10 minutes and it was also drawn in the late afternoon when there were people heading home by car. The vehicle was parked in a corner of an intersection where the exit of a parking lot could be seen (Fig. 6-a). We could not use the moving obstacle speeds to verify the algorithm performance because the data sampling took place in a real environment, where we could not control them. However, each tracker had its center point subsequent positions compared with the estimated ones. Again, the errors were less than 5% (5 Hz data acquisition).
Table 1 presents some experiment set-up details and the quantity of moving obstacles observed during the data acquisition. We experienced traffic and the obstacles were often passing by close to the sensor. Because of the intersection we were also lucky to capture a few cases when one obstacle occluded another. An interesting condition in this case was that we had many passing bikes. They were sometimes classified as cars, sometimes as pedestrians depending on the viewing angle. Their tire spokes also produced an interesting problem: some of the laser readings acquired by the sensor were behind the bike (the sensor laser beam passed trough the spokes and detected other environment feature that was behind the bike). Due to this, the segmentation algorithm produced erroneous input data for the feature extraction and motion detection algorithms. This problem was solved latter by refining the segmentation algorithm. In the beginning, the segmentation process was based only on consecutive measurements and from then on we decided to also consider the data that are close together, as if belonging to the same object.
When it comes to computer processing power performance, we used a 5 Hz sensor data acquisition frequency. Undoubtedly, the use of a dedicated computer for processing the obstacle tracking task will increase the frequency up to sensor limits (500 KBd data transmission rate for a serial RS422 data interface). We also decided to use a 0.5º angular resolution to detect pedestrians at large distances. The development framework introduced by Fleury et al. (1997) was also used. It allows us to execute the algorithms as modules on a single laptop running Linux (Dell D505 - Centrino 1.5 GHz). The tasks, coded in GenoM, follow the same approach that is used in embedded systems like typical automotive platforms.
Figures 7 and 8 present more results, now based on real data sampling. In both cases the scanner was placed in the origin (0,0), looking along the positive x-axis and plotted frames which are not consecutive, they were chosen by their contents. On top of each plot, one may observe the time stamp (Time) and the elapsed time between two consecutive scans (dt), both in seconds. The elapsed time is almost constant, but sometimes, if the sensor detects any error while reading or sending the data, it can take longer because the data is excluded and a new scan data is acquired and sent (compare Fig. 7-g and h). Aiming to facilitate the results comprehension, we present in Fig. 7 only the trackers and in Fig. 8 the predicted occupancy grid.
In Fig. 7 one may observe the trackers (represented by circles), the estimated velocities (represented by line segments), and the static environment features laser sensor readings (represented by dots). The line segments length and direction represent respectively their estimated modulus and direction. In the scenario presented in Fig. 7, two pedestrians were moving towards each other, one from the right and one from the bottom of the scene. A bike was also traversing, coming from the upper right corner. The trackers continued from (a) to (b) until the moment when the bike went out of range in (c), although the tracker is kept for one second after disappearance. People continued approaching until they were almost perceived as a single segment, (e). In (f), they could be separated again and both trackers were updated. In addition, Fig. 8 shows the trackers, the estimated velocities, the static environment features laser sensor readings, and the predicted occupancy grid map (represented by gray scale cells - as darker the gray cell is as higher is the probability of an cell being occupied). In Fig. 8, the predicted occupancy grid is shown. It is updated at the same scan acquisition frequency (5 Hz). The static environment features were already detected and enlarged by the growth rate, forming the occupancy grid map with EOCs. In (a), a car was coming from the upper right corner and a bike from the bottom. Then the cyclist started to reduce its speed (b) as it approached the intersection. The car kept moving and crossing the intersection until it hid the cyclist (c), but the bike tracker was kept. In (d) the car continued moving and the bike tracker was seen again. The car is not seen anymore in (e) and finally the cyclist turns left in (f).
Conclusions
The successful implementation of car-like mobile robots that are able to move autonomously on streets and roads depends on the vehicle ability of dealing with highly complex environments. Due to this, many researches initially developed for indoor applications are being extended and adapted for outdoor environments. Recently, some algorithms that fuse path planning and obstacle avoidance tasks into a single navigator structure were presented. However, few researches of obstacle path prediction on urban-like environments are being carried out (most of them are centered on vision systems).
Our work presented results on obstacle tracking task in dynamic urban-like environments. It focused on 2D laser-based obstacle motion-tracking problem. A Kalman Filter was applied in order to predict the obstacle motions even when they were hidden. First of all, we introduced a short review on the motion tracking techniques found in literature and highlighted the scarcity of publications when it comes to car-like tracking applications in dynamic urban scenarios using laser data. Then, our approach and the test platform used, a modified smart fortwo coupé passenger car named Smart Car, were briefly described. Our approach focused on detection, classification, and tracking tasks of vehicles (e.g.: cars, buses, etc.) and pedestrians. This technique allows the controller to take into account hidden and non-hidden obstacles when maneuvering the vehicle. A probabilistic occupancy-grid representation of the environment, named predicted occupancy grid map, was also implemented. It provided a given time horizon prediction view of the vehicle surroundings based on motion-models of the obstacle classes and obstacle estimated velocities. Real data samples were used to refine the algorithms earlier developed and tested using a MatLab simulator. Finally, the results were presented.
The results using real data samples indicated that obstacle detection, classification, and tracking tasks only with a 2D laser scanner are laborious. It happened because we decided to focus our research on the use of a single sensor in order to obtain a cheaper commercial solution that could be used on passenger cars. Due to this, it was necessary to take into account several environment feature details to turn them into diverse algorithm parameters. For instance, the presence of bushes and leaves can produce spurious readings and induce the algorithm to consider them as moving obstacles. In order to overcome these difficulties, we suggest the use of road and chart maps of the urban area and GPS, or its differential version (DGPS), combined with embedded cameras. This would increase the system overall performance by promoting data fusion that would allow false mobile obstacles removal and the recognition and classification of obstacles into more detailed classes, e.g.: walls, trees, buses, cars, trucks, bikes, pedestrians, etc. Obviously, as the use of vision systems is computer time expensive and very dependent on scene illumination, it is necessary to work on scene lighting and find a balance between computer processing consumption and adequate data acquisition. Of course, if more computers are used onboard the vehicle, this drawback can be overcome easily. For the moment, this class labeling is carried based only on obstacle speeds and observed sizes. The pedestrian class uses the constant-velocity model and the vehicle class makes use of a simple steering model based on the vehicle ICM for predicting their paths. When it comes to the predicted occupancy grid map building, we adopted two strategies that allowed us to keep the time and memory consumptions at an acceptable level during the experiments: we reduced the update frequency for the static part of the occupancy grid map and we decided to neglect obstacles whose behaviors were not considered dangerous (e.g.: obstacles whose distances to the Smart Car were increasing above a threshold value). Concluding, our results can be considered a valuable step towards promoting the future interface between the motion tracking and dynamic path planning algorithms found in literature. This procedure allows the controller to obtain a better performance in urban-like environments.
Acknowledgments
The first author thanks CAPES for the financial support during his stay at EPFL - ASL (Grant # 0269-05-0), Switzerland. The staffs of EPFL and ETHZ are also due to gratitude for their priceless assistance and remarkable kindness.
Paper accepted January, 2009.
Technical Editor: Glauco A. de P. Caurin
- Bar-Shalom, Y. and Fortmann, T.E., 1998, "Tracking and data association", Academic Press Inc., London, UK.
- Becker, M., Hall, R., Jensen, B., Kolski, S., Maček, K. and Siegwart, R., 2007-a, "The use of obstacle motion tracking for car-like mobile robots collision avoidance in dynamic urban environments", Proc. of XII International Symposium on Dynamic Problems of Mechanics - DINAME 2007.
- Becker, M., Kolski, S., Jensen, B., Maček, K., Weingarten, J., Lamon, P. and Siegwart, R., 2007-b, "Car-like mobile robots: soon or latter a reality on our streets", Proc. of 6th Brazilian Conf. on Dynamics, Control, and their Applications - DINCON 2007.
- Bellino, M., Lopez de Meneses, Y. and Kolski, S., 2005, "Calibration of an embedded camera for driver-assistant systems", Proc. of Intelligent Transport Systems Conference.
- Bennewity, M., Burgard, W. and Thrun, S., 2002-a, "Learning motion patterns of persons for mobile service robots", Proc. of IEEE Int. Conf. Robotics and Automation - ICRA 2002, Vol. 4, pp. 3601-3606.
- Bennewity, M., Burgard, W. and Thrun, S., 2002-b, "Using EM to learn motion behaviors of person with mobile robots", Proc. of IEEE/RSJ Int. Conf. on Intelligent Robots and Systems - IROS 2002, vol. 1, pp. 502-507.
- Blanc, C., Trassoudaine, L. and Gallice, J., 2005, "EKF and particle filter track to track fusion: a quantitative comparison from radar/lidar obstacle tracks", Proc. of 8th Int. Conf. on Information Fusion, Vol. 2, pp. 25-28.
- Chao, C.H., Ho, C.H., Lin, S.H. and Li, T.H.S., 2005, "Omni-directional vision based parallel-parking control design for car-like mobile robot", Proc. of the 2005 IEEE Int. Conference on Mechatronics, pp. 562-67.
- Chiu, C.S., Lian, K.Y. and Liu, P., 2005, "Fuzzy gain scheduling for parallel parking a car-like robot", IEEE Transactions on Control Systems Tech, Vol. 13, No. 6, November 2005, pp. 1084-1092.
- Dahlkamp, H., Kaehler, A., Stavens, D., Thrun, S. and Bradski, G., 2006, "Self-supervised monocular road detection in desert terrain", Proceedings of the Robotics Science and Systems Conference, Philadelphia, PA, U.S.A., 2006.
- Dissanayake, E.N.G., Sukkarieh, S. and Durrant-Whyte, H., 2001, "The aiding of a low-cost strapdown inertial measurement unit using vehicle model constraints for land vehicle applications", IEEE Transactions on Robotics and Automation, 2001.
- Duan, Q.J., Wang, R.X, Feng, H.S. and Wang, L.G., 2004, "An immunity algorithm for path planning of the autonomous mobile robot", Proc. of INMIC 2004, pp. 346-350.
- Elfes, A., 1989, "Using occupancy grids for mobile robot perception and navigation", Computer, Vol. 22, No. 6, IEEE Computer Society Press, pp. 46-57.
- Fiorini, P. and Schiller, Z., 1998, "Motion planning in dynamic environments using velocity obstacles", International Journal of Robotics Research, Vol. 17, pp. 760-772.
- Fleury, S., Herrb, M. and Chatila, R., 1997, "Genom: a tool for the specification and the implementation of operating modules in a distributed robot architecture", International Conference on Intelligent Robots and Systems, Vol. 2, pp. 842-848.
- Gillespie, T.D., 1992, "Fundamentals of vehicle dynamics", SAE International, ISBN: 1-56091-199-9.
- Holzmann, F., Kolski, S., Sulzmann, A., Spiegelberg, G., Siegwart, R. and Bubb, H., 2005-a, "Improvement of the driving safety using a virtual driver", Proc. of Intelligent Transport Systems Conference.
- Holzmann, F., Bellino, M., Kolski, S., Spiegelberg, G. and Siegwart, R., 2005-b, "Robots go automotive - the SPARC approach", Proc. of IEEE Intelligent Vehicles Symposium, Las Vegas, Nevada, U.S.A. June 6-8, 2005.
- Illmann, J., Kluge, B. and Prassler, E., 2002, "Statistical recognition of motion patterns", Proc. of IEEE/RSJ Int. Conf. on Intelligent Robots and Systems - IROS 2002, Vol. 2, pp. 1259-1264.
- Jensen, B., 2004, "Motion tracking for human-robot interaction", PhD. Thesis No. 3156 (2004), EPFL, Lausanne, Switzerland, 167 p.
- Kalman, R.E., 1960, "A new approach to linear filtering and prediction problems", Transactions of ASME, J. Basic Engineering, Vol. 82, pp. 34-45.
- Kalman, R.E. and Bucy, R., 1961, "New results in linear filtering and prediction theory", Transactions of ASME, J. Basic Engineering, Vol. 83, pp. 95-108.
- Khoshnejad, M. and Demirli, K., 2005, "Autonomous parallel parking of a car-like mobile robot by a neuro-fuzzy behavior-based controller", Proc. of NAFIPS 2005 - 2005 Annual Meeting of the North American Fuzzy Information Processing Society, pp. 814-819.
- Kluge, B., Illmann, J. and Prassler, E., 2001, "Situation assessment in crowded public environments", Proc. of Int. Conf. on Field and Service Robotics.
- Kolski, S., Ferguson, D., Bellino, M. and Siegwart, R., 2006, "Autonomous driving in structured and unstructured environments", Proc. of IEEE Intelligent Vehicles Symposium.
- Kolski, S., Macek, K., Spinello, L and Siegwart, R., 2007, "Secure autonomous driving in dynamic environments: from object detection to safe driving", Proc. of the Workshop on Safe Navigation in Open and Dynamic Environments: Applications to Autonomous Vehicles - IROS 2007.
- Lamon, P., Kolski, S., Triebel, R., Siegwart, R. and Burgard, W., 2006a, "The SmartTer for ELROB 2006 - a vehicle for fully autonomous navigation and mapping in outdoor environments", Technical Report.
- Lamon, P., Kolski, S. and Siegwart, R., 2006-b, "The SmartTer -a vehicle for fully autonomous navigation and mapping in outdoor environments", Proc. of CLAWAR 2006, Brussels, Belgium.
- LaValle, S.M., 2006, "Planning algorithms", Cambridge University Press, Available online at: http://planning.cs.uiuc.edu/
- Lee, Z. and Chen, X., 2004, "Path planning approach based on probabilistic roadmap for sensor based car-like robot in unknown environments", Proceedings of 2004 IEEE International Conference on Systems, Man and Cybernetics, pp. 2907-2912.
- Lindstrom, M. and Eklundh, J.O., 2001, "Detecting and tracking moving objects from mobile platform using a laser range scanner", Proc. of the IEEE/RSJ Int. Conf. on Intelligent Robots and Systems - IROS 2001, Vol. 3, pp. 1364-1369.
- Lu, H.C. and Chuang, C.Y., 2005, "The implementation of fuzzy-based path planning for car-like mobile robot", Proc. of the 2005 International Conference on MEMS, NANO and Smart Systems - ICMENS'05, pp. 467-472.
- Maček, K., Williams, B., Kolski, S. and Siegwart, R., 2004, "A lane detection vision module for driver assistance", Proc. of the IEEE/APS Conference on Mechatronics and Robotics, Aachen, Germany.
- Maček, K., Becker, M. and Siegwart, R., 2006, "Motion planning for car-like vehicles in dynamic urban scenarios", Proc. of IROS 2006 - IEEE/RSJ International Conference on Intelligent Robots and Systems, October 2006, Beijing, China.
- MacLachlan, R., 2004, "Tracking moving objects from a moving vehicle using a laser scanner", Report, Carnegie Mellon University, available online at: http://www.cs.cmu.edu/~ram/resume/datmo_report.pdf
- Martínez-Marín, T., 2005, "Learning optimal motion planning for car-like vehicles", Proc. of the 2005 International Conference on Computational Intelligence for Modeling, Control and Automation, and International Conference on Intelligent Agents, Web Technologies and Internet Commerce - CIMCA-IAWTIC'05, pp. 601-612.
- Pradalier, C., Hermosillo, J., Koike, C., Braillon, C., Bessiere, P. and Laugier, C., 2004, "An autonomous car-like robot navigating safely among pedestrians", Proc. of 2004 IEEE Int. Conf. on Robotics and Automation - ICRA 2004 , Vol. 2, pp. 1945-1950.
- Romero-Meléndez, C., Monroy-Pérez, F. and Vázquez-González, B., 2005, "Complexity and path planning for a car-like robot" Proc. of 2nd International Conference on Electrical and Electronics Engineering - ICEEE and XI Conference on Electrical Engineering - CIE 2005, pp. 463-466.
- SAE Series PT-132, 2006, "Adaptative cruiser control", Edited by Ronald K. Jungen, Published by SAE International, 474 p.
- SAE Series PT-133, 2007, "Object detection, collision warning and avoidance systems - Volume 2", Edited by Ronald K. Jungen, Published by SAE International, 419 p.
- Schulz, D., Burgard, W., Fox, D. and Cremers, A.B., 2001, "Tracking multiple moving targets with a mobile robot using particle filters and statistical data association", Proc. of the 2001 IEEE Int. Conf. on Robotics and Automation (ICRA 2001), Vol. 2, pp. 1665-1670.
- Sea, R.G., 1971, "An efficient suboptimal decision procedure for associating sensor data with stored tracks in real-time surveillance systems", Proc. of 10th IEEE Conf. on Decision and Control, pp. 33-37.
- SICK AG, 2006, "Technical description LMS200/211/221/291 laser measurement systems", 48 p.
- Siegwart R. and Nourbakhsh, I., 2004, "Introduction to autonomous mobile robots", The MIT Press, Cambridge, Massachusetts, USA.
- Singer, R.A. and Stein, J.J., 1971, "An optimal tracking filter for processing sensor data of imprecisely determined origin in surveillance systems", Proc. of 10th IEEE Conf. on Decision and Control, pp. 171-175.
- Sittler, R.W., 1964, "An optimal data association problem in surveillance theory", IEEE Transactions on Military Electronics, MIL-8, pp. 125-139.
- Stavens, D., Hoffmann, G. and Thrun, S., 2007, "Online speed adaptation using supervised learning for high-speed, off-road autonomous driving", Proc. of the International Joint Conference on Artificial Intelligence - IJCAI, Hyderabad, India.
- Sukkarieh, E.N.S. and Durrant-Whyte, H., 1999, "A high integrity IMU/GPS navigation loop for autonomous land vehicle applications", IEEE Transactions on Robotics and Automation
- Thompson, S. and Kagami, S., 2005, "Continuous curvature trajectory generation with obstacle avoidance for car-like robots", Proc. of the 2005 International Conference on Computational Intelligence for Modeling, Control and Automation, and International Conference on Intelligent Agents, Web Technologies and Internet Commerce - CIMCA-IAWTIC'05, pp. 863-870.
- Thrun, S., Burgard, W. and Fox, D., 2005, "Probabilistic robotics", MIT Press, USA, ISBN 0-262-20162-3.
- Thrun, S., Montemerlo, M. and Aron, A., 2006, "Probabilistic terrain analysis for high-speed desert driving", in: G. Sukhatme, S. Schaal, W. Burgard, and D. Fox, editors, Proceedings of the Robotics Science and Systems Conference, Philadelphia, PA, U.S.A., 2006.
- Wang, C.C. and Thorpe, C., 2002, "Simultaneous localization and mapping with detection and tracking of moving objects", Proc. of the IEEE Int. Conf. on Robotics and Automation - ICRA 2002, Vol. 3, pp. 2918-2924.
- Yamamoto, M., Hayashi, Y. and Mohri, A., 2005, "Garage parking planning and control of car-like robot using a real time optimization method", Proc. of the 6th IEEE International Symposium on Assembly and Task Planning: from Nano to Macro Assembly and Manufacturing - (ISATP 2005), pp. 248-253.
Publication Dates
-
Publication in this collection
25 Aug 2009 -
Date of issue
June 2009
History
-
Received
Jan 2009




































