Abstract
A detailed numerical study is presented of the order of accuracy of some proposed cell centered, finite volume schemes used for the solution of the 2-D gasdynamic equations on triangular unstructured grids. The schemes studied are based on a MUSCL-type linear reconstruction of interface properties, which seeks to achieve 2nd-order accuracy in space. They are also nominally flux-vector splitting-type schemes, and the results here presented use Liou's AUSM+ algorithm. The basic aspects effecting the scheme's order of accuracy are the form in which the reconstruction process is designed and the form in which the limiting process is performed. Two basic concepts are tested with regard to the reconstruction process, namely the use of 1-D-type and gradient-based reconstruction. The limiter can also be constructed as a 1-D-type limiter or as a truly multi-dimensional limiter. The schemes are tested on a linear convection-like model equation and the numerical solutions are compared to the analytical solution, for different mesh sizes, in order to assess the scheme's order of accuracy. For comparison purposes, the results obtained with a centered scheme are also presented. Second-order accuracy is shown to be only obtained for the centered scheme. The nominally 2nd-order upwind algorithms lead to actual orders of accuracy, which vary from 0.9 to 1.5.
CFD; unstructured grid methods; finite volume; upwind schemes; order of accuracy
TECHNICAL PAPERS
Order of accuracy study of unstructured grid finite volume upwind schemes
João Luiz F. AzevedoI; Luís F. Figueira da SilvaII; Daniel StraussIII
Ijoaoluiz.azevedo@gmail.com Comando-Geral de Tecnologia Aeroespacial Instituto de Aeronáutica e Espaço - IAE 12228-903 São José dos Campos, SP, Brazil
IIluisfer@esp.puc-rio.br Pont. Univ. Católica do Rio de Janeiro - PUC-Rio 22453-900 Rio de Janeiro, RJ, Brazil
IIIdaniel@tecsis.com.br Universidade de São Paulo - USP Escola Politécnica 05424-970 São Paulo, SP, Brazil
ABSTRACT
A detailed numerical study is presented of the order of accuracy of some proposed cell centered, finite volume schemes used for the solution of the 2-D gasdynamic equations on triangular unstructured grids. The schemes studied are based on a MUSCL-type linear reconstruction of interface properties, which seeks to achieve 2nd-order accuracy in space. They are also nominally flux-vector splitting-type schemes, and the results here presented use Liou's AUSM+ algorithm. The basic aspects effecting the scheme's order of accuracy are the form in which the reconstruction process is designed and the form in which the limiting process is performed. Two basic concepts are tested with regard to the reconstruction process, namely the use of 1-D-type and gradient-based reconstruction. The limiter can also be constructed as a 1-D-type limiter or as a truly multi-dimensional limiter. The schemes are tested on a linear convection-like model equation and the numerical solutions are compared to the analytical solution, for different mesh sizes, in order to assess the scheme's order of accuracy. For comparison purposes, the results obtained with a centered scheme are also presented. Second-order accuracy is shown to be only obtained for the centered scheme. The nominally 2nd-order upwind algorithms lead to actual orders of accuracy, which vary from 0.9 to 1.5.
Keywords: CFD, unstructured grid methods, finite volume, upwind schemes, order of accuracy.
Introduction
1Since the pioneering work of Barth and Jespersen (1989), various upwind, nominally second order accurate, finite volume schemes have been proposed in the literature (see, for instance, Durlofsky, Engquist and Osher, 1992; Lin, Wu and Chin, 1993; Venkatakrishnan, 1995; Aftosmis, Gaitonde and Tavares, 1995; Sleigh et al., 1998; Figueira da Silva, Azevedo and Korzenowski, 1999). In these papers, spatial second order accuracy is sought by some form of gradient evaluation within the control volume, followed by extrapolation of the cell centered properties up to the cell interfaces. Upwinding is achieved via flux vector splitting or flux difference splitting techniques. Limiting procedures are, then, used in order to guarantee solution monotonicity.
Assessment of the effective order of accuracy for unstructured finite volume methods is not a straightforward task, when compared to classical structured finite difference/volume techniques. In these latter cases, an order of accuracy study may be performed via Taylor series expansions of the difference scheme (Hirsch, 1988). Such a study is not applicable when the mesh point connectivity is variable, as it is the case for finite volume unstructured grid methods. Therefore, numerical computations of model problems seem to be the only avenue to pursue, if one seeks to determine the order of accuracy of such methods. For instance, Aftosmis, Gaitonde and Tavares (1995) studied the convergence and accuracy of different cell vertex, unstructured mesh, and finite volume algorithms by comparison with a steady analytical solution of the Euler equations. Another model problem that can be used for these purposes is the two-dimensional linear advection problem (Durlofsky, Engquist and Osher, 1992), which also allows the assessment of the unsteady behavior of the solution.
The present work presents a detailed numerical study of the order of accuracy of some proposed cell centered, finite volume schemes typically used for the solution of the 2-D gasdynamic equations on triangular unstructured grids (Barth and Jespersen, 1989; Figueira da Silva, Azevedo and Korzenowski, 1999). The schemes studied are nominally second order accurate, based on a MUSCL-type linear reconstruction of interface properties, and they are also nominally flux-vector splitting schemes. The basic aspects effecting the scheme's order of accuracy are the form in which the reconstruction process is designed and the form in which the limiting process is performed. Most of the results here presented consider the minmod limiter, although the superbee limiter is also used (Hirsch, 1990).
Two basic concepts are tested with regard to the reconstruction process. The first concept essentially attempts to create a one-dimensional stencil normal to the control volume edge of interest and, then, it uses this 1-D stencil in a very straightforward fashion in order to reconstruct interface properties. The other approach is based on computing cell averaged property gradients and using these in order to obtain linear reconstructed interface properties. The limiter can also be constructed as a 1-D-type limiter or as a truly multi-dimensional limiter. The schemes are tested on the linear convection-like model equation (Durlofsky, Engquist and Osher, 1992) and the numerical solutions are compared to the analytical solution, for different mesh sizes, in order to assess the scheme's order of accuracy. The results obtained with the upwind schemes are also compared to those computed with a centered scheme (Jameson and Baker, 1983; Jameson and Mavriplis, 1986).
Nomenclature
a
=
constant advection velocity for model problem
a x , a y
=
cartesian components of constant advection velocity
C
=
convection operator
CFL
=
Courant number
d
=
vector position
D
=
artificial dissipation operator
e
=
specific internal energy
ε
=
total energy per unit of volume
E, F
=
flux vector for the Euler equations
i, j
=
unit vectors in Cartesian coordinates
l
=
length of control volume edge
n
=
unit vector normal to control volume edge
p
=
pressure
Q
=
vector of conserved properties for the Euler equations
r
=
ratio of consecutive gradients
S
=
boundary of control volume
t
=
time
u
=
conserved property for model problem
u, v
=
V
=
area of control volume
x, y
=
Cartesian coordinates
Greek Symbols
α1...α5
=
coefficients in Runge-Kutta time marching scheme
γ
=
time step value
Δt
=
time step value
Δr
=
vector position with respect to the cell centroid
=
gradient operator
ρ
=
density
ψ
=
limiter
ξ
=
1-D type gradient of conserved variable
Subscripts
i
current control volume
ik
interface between control volumes i and k
k
neighbor f i-th control volume
L
R
right state
Ω
control volume for gradient calculation
Superscripts
l
Runge-Kutta stage counter
n
current time level
n 1 , n 2
end points of ik-th edge
+
right state
-
The Model Problem
In order to be able to analyze the order of accuracy of unstructured finite volume methods, one needs to numerically solve a model problem, the choice of which is dictated by several constraints. Obviously, the model problem must have a known analytical solution at all times. Another desirable feature is that this solution should be continuous, so that the order of accuracy can be measured by comparison with the computed result via successive refinements of the computational mesh. Moreover, it is essential that the numerical results are not influenced by the conditions arising at the boundaries of the computational domain. With these restrictions in mind, and following the work of Durlofsky, Engquist and Osher (1992), the authors have chosen as model problem the two-dimensional, periodic, linear advection problem, using as initial conditions for the scalar quantity a sine curve in both directions. The computational domain is a square with unity side and the mesh is composed of regular triangles. A sketch of the computational domain and of the analytical solution to the model problem at the initial condition and, thus, also at the end of a full period of integration is shown in Fig. 1.
The procedure starts with a coarse mesh, in which the computations are run through one advection period and the L1 norm of the error is calculated. The mesh is halved successively, and the computations rerun. The slope of the best line fit, in a least squares sense, through a plot of the logarithm of the L1 norm as a function of the logarithm of the characteristic size of the mesh, gives a measure of the actual order of accuracy of the method.
Mathematical Formulation
For the classes of problems of interest to the authors, the appropriate theoretical formulation for the fluid dynamic problems would be based on the 2-D Euler equations. For the present paper, however, a two-dimensional linear advection problem is considered. The authors emphasize that the paper maintains a parallel between the problem actually being solved in the present case and the 2-D Euler equations as an attempt to facilitate the interpretation of the procedures developed. Clearly, the motivation for the development here discussed is the solution of the Euler equations for aerospace applications. The authors, however, are applying the methodology to a model advection equation as a form of performing a deeper analysis of order of accuracy of the proposed approaches. Therefore, the governing differential equation for the present case can be written as
Here, u(x, y, t) is the dependent variable, 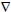 · ( ) is the divergent operator and the constant advection velocity, a, can be written as
· ( ) is the divergent operator and the constant advection velocity, a, can be written as
where i and j represent the unit vectors in the Cartesian directions. As previously discussed, the scalar problem is subjected to an initial condition of the form
and the boundary conditions are periodic on all four sides of the square computational domain.
For the sake of completeness, the Euler equations are presented, since the same general nomenclature is used when dealing with the model problem. The 2-D Euler equations for an ideal gas can be written in integral form for a 2-D Cartesian coordinate system as:
Here, V represents the area of the control volume and S is its boundary. For a stationary mesh, the vector of conserved quantities Q and the convective flux vectors are given by
The nomenclature used here is the standard one, such that ρ is the density, u and v are Cartesian velocity components, p is the pressure and ε is the total energy per unit of volume. Equation (4) must be supplemented by the equation of state for ideal gases, which can be written as
where γ is the ratio of specific heats and e is the specific internal energy, which can be obtained from the total energy by the expression
The governing equations are discretized in a cell centered context, in which the discrete vector of conserved variables for the i-th cell is defined as
where Vi is the volume of the i-th cell. The Euler equations can, then, be rewritten for each i-th control volume as
It should be observed that, for a cell centered approach, the control volume used for the integration of the governing equations is formed by each triangular cell itself (Batina, 1991). The role of the spatial discretization algorithm is to approximate the surface integral in Eq. (9). This aspect is discussed in detail in the forthcoming paragraphs. For now, it is sufficient to define the convective operator, C(Qi), which is responsible for this spatial discretization. Hence, the Euler equations, fully discretized in space and assuming a stationary mesh, can be written as
Here, D(Qi) represents the artificial dissipation operator which is required when a centered scheme is used, and it is identically zero, if an upwind spatial discretization is employed. In order to use the formulation developed for the Euler equations in the analysis of the scalar problem, one must identify the vector of conserved variables and the flux vectors with their appropriate definitions for the present case. Hence, the definition of these "vectors" in the scalar case becomes
It is, probably, important to further emphasize that the test case, which is actually being solved in the present work, is linear and smooth. However, the numerical methods that are implemented rely on limiters in order to achieve the desired behavior for real life problems. These limiters, on the other hand, are typically non-smooth and non-differentiable nonlinear functions. Therefore, it would be correct to state that the present study is actually assessing how such nonlinearities affect the order of accuracy of the resulting schemes. As the work in the paper demonstrates, they clearly have a detrimental effect. However, one cannot do away with such nonlinearities, because they are precisely the ingredients, which allow the resulting schemes to perform adequately for the gasdynamic problems of interest in aerospace engineering.
Time Discretization Algorithm
The present work uses a well-tested, fully explicit, 2nd-order accurate, 5-stage Runge-Kutta time-stepping scheme (Mavriplis, 1988) to advance the governing equations in time. The time integration scheme can be written as
where the superscripts n and n+1 indicate that these are property values at the beginning and at the end of the n-th time step. The values used for the αl coefficients are (Mavriplis, 1988)
Spatial Discretization Schemes
The primary interest in the present work is to discuss order of accuracy issues associated with unstructured upwind schemes. In particular, the emphasis is on triangular grids and flux-vector splitting schemes. Hence, a scalar version of Liou's AUSM+ scheme (Liou, 1996) is presented both as a nominally 1st-order scheme and as a nominally 2nd-order scheme. The 2nd-order version uses a MUSCL reconstruction (van Leer, 1979), and the reconstruction process options implemented are discussed in detail in the forthcoming sections. For comparison purposes, a centered scheme is also implemented and its details are presented in the next section. Note that all schemes presented are implemented using an edge based data structure (Azevedo and Mitchell, 1995; Azevedo and Korzenowski, 1996).
Centered Scheme
The spatial discretization procedure used is equivalent to a central difference scheme. The convective operator, C(Qi), which approximates the surface integral in Eq. (9), is defined as
In this expression, Qik is the arithmetic average of the conserved properties in the cells, which share the ik interface (Jameson and Mavriplis, 1986), i.e.,
Moreover, in the previous expression (xiki, yiki) and (xik2, yik2) are, as shown in Fig. 2, the coordinates of the vertices, which define the interface between cells i and k. These points are always ordered in the counterclockwise direction for each i-th control volume. Note that, in the case of the Euler equations, artificial dissipation terms must be added in order to control nonlinear instabilities (Mavriplis, 1990). In the present linear scalar case, artificial dissipation terms are not required and they were not used in the simulations here reported.
AUSM+ Scheme
The convective operator for the AUSM+ scheme, in the present unstructured grid context (Azevedo and Korzenowski, 1998), and for the scalar advection problem, can be written as
where
and  denotes the length of the ik interface. The current nomenclature considers that i is the triangle "to the left" of the ik interface (see Fig. 2), since all interface segments are assumed oriented as previously indicated. Therefore, for a 1st-order scheme, the left state, L, is identified with the properties of the i-th triangle whereas the right state, R, is identified with those of the k-th triangle.
denotes the length of the ik interface. The current nomenclature considers that i is the triangle "to the left" of the ik interface (see Fig. 2), since all interface segments are assumed oriented as previously indicated. Therefore, for a 1st-order scheme, the left state, L, is identified with the properties of the i-th triangle whereas the right state, R, is identified with those of the k-th triangle.
The AUSM+ scheme performs a splitting of the u ± a eigenvalues of the Euler equations using the M ± 1 base functions. Using the nomenclature previously introduced, one can write the convective velocity in the direction normal to the edge under consideration as
The above equation clearly uses the fact that, in the present case, a is a constant. Actually, if one follows the usual nomenclature of using subscripts L and R to denote left and right states, respectively, at a given interface, it is also possible to write that, in the present case,
Hence, the split convective speeds at the ik interface can be defined as
In order to obtain second order accuracy, and keeping with a MUSCL approach, the left and right states at the interface must be somehow linearly reconstructed at the interface. As previously mentioned, the extension to 2nd-order accuracy is obtained in the present work with the application of the MUSCL approach (van Leer, 1979; Anderson, Thomas and van Leer, 1986). Therefore, the second order scheme follows exactly the same formulation, except that the left and right states are obtained by a MUSCL extrapolation described in the following section.
Reconstruction Methods
Two basic reconstruction procedures are tested in the present work. The first one defines a one-dimensional stencil normal to the control volume edge of interest and, then, it uses this 1-D stencil in a very straightforward fashion in order to reconstruct interface properties. The other approach is based on computing cell averaged property gradients, and using these in order to obtain linear reconstructed interface properties. It is still important to note that the latter approach is also implemented in two quite different forms in the present work. This difference is associated with the gradient calculation, which is computed in the standard finite volume fashion in which the derivatives are transformed into integrals along the boundaries of the control volume. Hence, in one approach, the control volumes used for the cell averaged gradient calculations are the triangles themselves, while the other approach uses an extended control volume (Barth and Jespersen, 1989).
One-Dimensional Reconstruction
This procedure is based on building a 1-D calculation stencil normal to a particular edge under consideration. Once this stencil is defined, linear reconstruction is performed in the most straightforward way as if one were dealing with a 1-D problem. This approach is inspired in the work of Lyra (1994), which is based on a finite element technique. The major difference between the present construction and the one used in Lyra (1994) lies in the direction in which the one-dimensional stencil is constructed. In the cited reference (Lyra, 1994), the stencil for extrapolation is constructed along the direction of the edge. Here, since a cell centered finite volume method is of interest, the extrapolation stencil is constructed in a direction normal to the edge.
In an attempt to reinterpret the 1-D ideas in the present unstructured grid context, a line is drawn normal to the edge passing through the center of the inscribed circle to that triangle. As illustrated by the sketch shown in Fig. 2, a third point is located over this line, and away from the edge under consideration, at a distance from the center of the inscribed circle equal to the diameter of the circle. The control volume within which this 3rd point lies is identified, and the properties of this triangle used in the linear reconstruction.
In order to make the nomenclature clear, the two triangles, which are adjacent to the edge under consideration, are denoted as i and k. The second triangle identified by the previously described process and associated with triangle i is denoted as l. The corresponding one associated with k is denoted as triangle m. This is also illustrated in Fig. 2. Once triangles l and m are identified, the reconstruction of left, L, and right, R, states at the ik interface can be performed as a limited extrapolation of u in the form
In these expressions, ψ± represent the limiter, which is discussed in the next section. Note that the search of l and m triangles constitutes a pre-processing operation. Therefore, although this can be a costly operation, it is performed only once during a given run, provided that the grid topology remains fixed. Clearly, if grid adaptation is performed, the operation would have to be repeated. The additional information regarding the l and m triangles, on the other hand, must be added to the edge-based data structure, which implies in the need for extra storage.
Gradient Reconstruction
The approach followed in this case consists on attributing cell averaged properties and gradients to the control volume centroid, which allows the linear reconstruction of properties at any point within the cell. The basic expression can be written as
where (x, y) denotes the coordinates of a generic point within the control volume, (xi, yi) is the position of the i-th cell centroid, 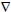 u is the gradient of the u property and Δr is the vector position of the (x, y) point with respect to the cell centroid. Therefore, there are two aspects that need to be discussed. The first one concerns the fact that it is necessary to include a limiter in order to avoid the creation of new extrema. The limiter construction is discussed in the next section. The other aspect concerns the calculation of the gradient itself.
u is the gradient of the u property and Δr is the vector position of the (x, y) point with respect to the cell centroid. Therefore, there are two aspects that need to be discussed. The first one concerns the fact that it is necessary to include a limiter in order to avoid the creation of new extrema. The limiter construction is discussed in the next section. The other aspect concerns the calculation of the gradient itself.
Gradients are computed in the present work using Green's theorem (Swanson and Radespiel, 1991) and, therefore, transforming derivative calculations into line integrals around appropriate control volumes (in the 2-D case). In this context, the cell averaged derivatives for the i-th control volume can be written as
The basic question that remains is: which control volume, VΩ, is used for this integration? The present work uses two different forms of defining this control volume. The first approach consists in defining VΩ = Vi, i.e., the triangles themselves are used as the control volumes for the gradient calculation. This is the simplest approach possible, but it is usually criticized in the literature (Barth and Jespersen, 1989) because it cannot recover the correct gradient of a linear function.
The second option consists in defining the control volume for the gradient calculation as the polygon formed by connecting the centroids of all triangles which have an edge or a vertex in common with the i-th triangle. This is the approach recommended by Barth and Jespersen (1989), since it satisfies the criteria enforced by these authors for gradient calculations:
1. One must obtain the exact solution for the gradient of the function when the function has a linear variation;
2. The gradient must be defined for arbitrary meshes.
However, this approach requires more memory usage to store the new extended control volume areas and it also requires additional computational time, because more complicated control volume yields additional operations in order to form the gradients.
Once the cell averaged gradients have been computed, the ik interface properties can be linearly reconstructed in the standard fashion as
Here,
ui and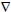 uk are the gradients computed for triangles i and k, respectively, ψ± are the limiters, and Δri and Δrk are the vector positions of the interface midpoint with respect to the centroid of each of the two triangles which share the interface.
uk are the gradients computed for triangles i and k, respectively, ψ± are the limiters, and Δri and Δrk are the vector positions of the interface midpoint with respect to the centroid of each of the two triangles which share the interface.
Limiting Procedures
In order to avoid oscillations, the extrapolated states must be limited (Hirsch, 1990). The majority of the results discussed here uses the minmod limiter. Another aspect concerns the fact that the limiter construction is clearly connected to the approach used for the linear reconstruction. Hence, the form used to define the limiter associated with the one-dimensional approach for property reconstruction is different from the one used when the gradient reconstruction is adopted.
For the 1-D reconstruction case, the limiter is also constructed as a one-dimensional limiter, since the stencil for the calculation is already set up. Hence, the ψ± functions that appear in Eqs. (21) can be written as
where the ratios of consecutive gradients are given by
For the minmod limiter, the ψ(r) function can be written as
Corresponding expressions could be written for the other limiters, e.g., the superbee limiter, and these expressions can be easily found in the literature (Hirsch, 1990).
For the cases in which the reconstruction process uses gradients, two limiter designs are used. The first one attempts to build a limiter which is also sort of one-dimensional, whereas the other approach follows the work of Barth and Jespersen (1989) and considers a truly multidimensional limiter. In order to make the nomenclature clear for the discussion of the 1-D-type limiter with gradient reconstruction, the centroids of the i and k triangles are assumed to have coordinates (x, y)i and (x, y)k, respectively, and the ik interface midpoint has coordinates (x, y)h. The following vector positions can be defined
and it is also convenient to define
With these definitions, the following one-dimensional-type gradients can be computed:
The r± ratios are, then, defined as
and the limiters can be written as in Eq. (25). In this case, instead of using equations (24) for the actual reconstruction, it would be more appropriate to use
since the various terms are available due to the limiter calculation.
This form of limiter has both theoretical and practical drawbacks, although it is very straightforward to implement and quite inexpensive from a computational cost point of view. The theoretical concern is associated with the fact that the property gradients are computed using information from all neighbors of a given triangle whereas the limiter only uses information along a pseudo-one-dimensional stencil normal to the particular edge. In other words, the reconstruction process uses information, which is multi-dimensional, whereas the limiter is one dimensional. Nevertheless, for the model problem, this limiter construction does not cause any difficulties and the results obtained, in terms of order of spatial accuracy for the scheme, are the best the authors were able to achieve throughout this investigation. Unfortunately, and this is the practical drawback, when the authors attempted to use this limiter for inviscid flow simulations at high Mach numbers, the numerical solutions invariably diverged for all cases tested. Numerical solutions could actually be obtained for the Euler equations at low supersonic Mach numbers, of the order of 2 or 3, for flows over a wedge. However, the computations would fail if one attempted the higher Mach numbers of interest to the authors (Figueira da Silva, Azevedo and Korzenowski, 1999). Since the same high Mach number cases could be computed with the other combinations of limiter and type of reconstruction, which are discussed here, the authors concluded that this 1-D-type limiter is not the most adequate for the sake of simulating compressible flows. The results with this limiter for the model problem are, however, presented here for completeness.
The problems observed with the 1-D-type limiter together with the gradient reconstruction prompted the use of a truly multi-dimensional limiter. This procedure closely follows the work of Barth and Jespersen (1989). The limiter definition starts by attributing the cell averaged value of the conserved variable, ui, to the i-th triangle centroid. In other words, it assumes that the property at the centroid has a value ui = u(xi, yi). Then, the values  and
and  are defined such that
are defined such that
where uk, k = 1, 2, 3, denote the neighbors of the i-th triangle. For each j-th vertex of the i-th triangle, the procedure computes uij = u(xj,yj) , j = 1, 2, 3, using Eq. (22), i.e.,
where Δrij = (xj - xi) i + (yj - yi) j. For each node of the i-th control volume, a preliminary limiter value is defined as
Finally, the value of the limiter, which will be used for the reconstruction using properties of the i-th triangle, is
This limiter construction is essentially equivalent to a multi-dimensional version of the minmod limiter. In principle, one could design multi-dimensional limiter constructions, which would mimic the van Leer, superbee or other limiters. However, this is not attempted in the present work and the only version of a multi-dimensional limiter tested is the one indicated in the previous equations. Furthermore, when defining the uij node values, the authors use the gradients already calculated for the control volumes. However, one could also think of defining such node values simply by a weighted averaged of the centroid values of all triangles, which share that particular node. The authors, however, have not experimented with this form of defining property node values.
Mesh Generation and Boundary Treatment
The model problem considered involves an extremely simple geometry and, therefore, one would think that triangular mesh generation in this case would be a trivial task. This would indeed be true, but some additional information, beyond the usual unstructured grid information, is necessary in order to implement the periodic boundary conditions. Furthermore, there is interest in having control over the orientation of the triangles, because the work also investigates the grid orientation effect on the order of accuracy of the schemes tested. One should observe that, since the computational domain is a square with unit side length, it is natural to divide the domain into squared control volumes based on the number of subdivisions in each side of the domain. Hence, the triangular grid could be obtained by dividing each quadrilateral volume by one of its diagonals, yielding two triangles. The implementation adopted allows the user to select the division with diagonals oriented with +45 deg. and -45 deg. with respect to the x axis or a "truly" unstructured grid (Lo, 1985), in which the orientation of the diagonals is somewhat random. Examples of the possible grid types are shown in Fig. 3.
The grids shown in Fig. 3 have the coarsest resolution used in the present work, namely with 10 subdivisions along each side of the squared domain or a characteristic length of 0.1. This yields a grid with 200 triangular control volumes, regardless of the mesh topology adopted. The investigation also considers grids with 20 × 20, 40 × 40 and 80 × 80 divisions. These yield, respectively, a total of 800, 3200 and 12800 control volumes and characteristic lengths of 0.05, 0.025 and 0.0125 in dimensionless units.
Regardless of the grid topology adopted, enough information is stored in order to allow an exact implementation of periodic boundary conditions. For each segment along the boundary, the identification of the corresponding segment along the boundary "on the other side" of the computational domain is stored. Boundary conditions are implemented through the use of ghost volumes in the present code, and the procedure adopted consists in forcing the ghost volume associated with a given triangle at the boundary to receive the property values of the other previously identified internal triangle of the pair.
Results and Discussion
Test Cases and General Information
The work considers a simple 2-D, linear, scalar advection problem, as previously described. Even in such a simple situation, there are quite a few parameters, which can influence the results. Clearly, the main objective of the work is to identify how the error in the computed solution decreases as the mesh is refined. Hence, all simulations compute the model problem for one period of the solution and, then, compare the numerical solution with the exact solution for the problem. The global error is measured in terms of the L1 norm of the difference between exact and numerical results. This can be expressed as where the point with coordinates (xi, yi) indicates the centroid of the i-th control volume. One should observe that this is the natural definition of the error for a cell centered finite volume scheme. However, one might obtain somewhat different results, in terms of order of accuracy, if some form of averaging of the computational results is performed prior to computing the error (Durlofsky, Engquist and Osher, 1992).
Hence, a calculation of the L1 norm of this averaged error is also performed. In the present case, this averaging is performed by obtaining (averaged) numerical results at the nodes of the control volumes. Therefore, the L1 norm of this averaged solution at the nodes is computed using an expression similar to Eq. (37), but with exact and numerical values of u evaluated at the nodal point locations. The averaged numerical values of the function at the nodes are obtained simply by an arithmetic average of the discrete properties of all control volumes, which share a given node. This is sufficient for the present case, since all control volumes have the same area.
The procedure used here to verify the order of accuracy of the proposed schemes consists in running the problem for the four meshes previously defined, with increasing refinement, and plotting the logarithm of the L1 norm of the error as a function of the logarithm of the mesh spacing. A best fit straight line, in the least square sense, is passed through these points and the line slope determines the order of accuracy of the method. Thus, theoretically, a 1st-order method should yield a line with unit slope, whereas a 2nd-order method should yield a line with slope equal to 2.
Four major cases for the nominally 2nd-order upwind scheme are considered. These could be classified as (a) one-dimensional reconstruction with a 1-D-type limiter, (b) gradient reconstruction with a simplified integration control volume and a 1-D-type limiter, (c) gradient reconstruction with a simplified integration control volume and a multi-dimensional limiter, and (d) gradient reconstruction with an extended integration control volume and a multidimensional limiter. These results are compared to the nominally 1st-order upwind scheme, described in the section that discusses the AUSM+ scheme, and to the standard 2nd-order centered scheme, also previously discussed. It should be emphasized that the four cases listed above test the most relevant aspects discussed in the paper, which are the form in which reconstruction is performed, the process used to define the limiter and, for the case of gradient reconstruction, the control volume used for property gradient evaluation.
All tests are performed for a constant CFL of 0.1, except for a single test for which the CFL is 0.01 in order to make sure the order of time accuracy of the scheme has no effect in the results. It should be emphasized that such small CFL numbers are used in order to guarantee that the time integration method has no effect in the subject matter of the present study, which is to assess the spatial accuracy of the schemes under investigation. Both the cases with linear advection in the x-direction as well as advection along a 45 deg. direction with the x-axis are considered, which correspond to the advection velocity a = (ax,ay) = (1, 0) and (1, 1), respectively. The importance of testing these two cases is associated with an evaluation of the effect of the mesh orientation on the final order of accuracy for the schemes. For some of the triangular grids considered in this investigation, an advection velocity a = (1, 1) is either aligned with or perpendicular to a large number of grid edges.
One-Dimensional Reconstruction Results
The initial tests use the one-dimensional-type of property reconstruction at interfaces for the nominally 2nd-order scheme. The first test case considers a "truly" unstructured mesh and the convection velocity a = (1, 0). The results are shown in Fig. 4 for the nominally 1st-order scheme and the 2nd-order scheme with the minmod and superbee limiters. The actual orders of accuracy obtained numerically in each case are 0.82, 0.94 and 0.65, respectively. The L1 norm of the error for these results is calculated without any averaging procedure, i.e., the error is calculated for properties evaluated at the actual control volume centroid. It is clear from these results that none of nominally 2nd-order case is even close to true 2nd-order accuracy. Actually, calculations with the superbee limiter yield results with an order of accuracy smaller than that of the 1st-order scheme. Moreover, the 1st-order scheme is also somewhat worse than true 1st order, and the 2nd-order scheme with the minmod limiter gives a slightly better order of accuracy than the 1st-order scheme. It is also intriguing that calculations with the minmod limiter give better order of accuracy than those with the superbee limiter, since the former is supposed to be much more dissipative. Note that all 1st-order results presented hereafter do not achieve actual 1st-order accuracy. This is also observed by Aftosmis, Gaitonde and Tavares (1995), who attributed such a discrepancy to the non-ortogonality of the cell interfaces with respect to the computed fluxes.
A similar analysis for a grid with diagonals oriented -45 deg. with respect to the x-axis, and still considering a = (1, 0), is presented in Fig. 5. The 2nd-order scheme uses the minmod limiter. Moreover, both cases in which the error is calculated with and without averaging of numerical property values are presented in this figure. The slopes of the least square fits for these cases are indicated in Table 1. One can see that the grid orientation has essentially no effect on the 1st-order scheme in this case, and it has a small effect on the 2nd-order scheme. Moreover, the solution averaging prior to the error calculation improves the measured order of accuracy for the 2nd-order scheme, which is consistent with the results reported in Durlofsky, Engquist and Osher (1992). However, it has a small detrimental effect in the measured order of accuracy for the 1st-order scheme. In any event, it is clear from these results that the nominally 2nd-order scheme is quite far from yielding true 2nd-order accuracy.
Although these results are discouraging and the authors did not analyze any other cases using the one-dimensional reconstruction procedure, it is interesting to try to understand what caused such poor performance. The first idea that comes to mind is the fact that there are reasons to attribute cell averaged values of the properties to the cell centroid. However, the same is not true for attributing cell averaged values to the center of the inscribed circle, which is essentially what the present procedure does. Moreover, the order of accuracy of the scheme could probably be improved if an interpolation is performed in order to obtain the properties at the second points used for the reconstruction, i.e., the points that lie in triangles  and m, as indicated in Fig. 2. The current procedure simply attributes to these points the cell averaged values of the properties. It seemed, at the time, that it was more effective to invest in the reconstruction process using gradients and, hence, no other tests with the one-dimensional reconstruction were performed. As an a posteriori thought, however, the one-dimensional reconstruction technique probably deserves further investigation.
and m, as indicated in Fig. 2. The current procedure simply attributes to these points the cell averaged values of the properties. It seemed, at the time, that it was more effective to invest in the reconstruction process using gradients and, hence, no other tests with the one-dimensional reconstruction were performed. As an a posteriori thought, however, the one-dimensional reconstruction technique probably deserves further investigation.
Results for Simplified Gradient Calculation with 1-D Limiter
The results discussed in this section use property gradient-based reconstruction, but the limiter is still constructed using 1-D-type ideas. Moreover, property gradients are calculated using the triangular cells themselves as control volumes for integration. The plots for the L1 norm of the error for a test case with advection velocity given by ax = 1 and ay = 0, and using the grid with diagonals oriented with -45 deg., are presented in Fig. 6 both for the cases in which no averaging of the results is performed before computing the error and for the cases in which averaging of the numerical results is made prior to the error calculation. This figure shows results for the 1st-order upwind scheme and for the 2nd-order upwind scheme with the minmod limiter and without any limiter at all. Moreover, for comparison purposes, the figures also show the L1 norm of the error for the calculations with a 2nd-order centered scheme. The orders of accuracy actually obtained in each case are summarized in Table 2. Obviously, the 1st-order upwind scheme results are the same reported in the previous section, since the form of reconstruction does not affect the 1st-order scheme.
The actual order of accuracy obtained with the nominally 2nd-order upwind scheme should be compared, for instance, with the results in Table 1. It is clear from this comparison that the use of gradient reconstruction yields better orders of accuracy than the 1-D reconstruction process. However, there are some strange features in the results shown in Table 2. For instance, it is not clear why the calculation without any limiter at all yields an actual order of accuracy which is smaller than that obtained when the calculations are performed with the minmod limiter. The model problem has a smooth solution, which means that a limiter should, in the worst case, be clipping the smooth peaks and valleys of the smooth model function, if it perceives the gradients as too high. But, in any case, there is no apparent reason to obtain better results with the minmod limiter than without any limiter. Moreover, the actual values of the L1 norm of the error for the calculations with the minmod limiter are smaller than those for the unlimited extrapolation case. Furthermore, attempts to run this case with the superbee limiter resulted in numerical instability for the finer grids, although a solution could be obtained with the coarsest grid considered.
The calculations summarized in Table 2 also indicate that even the best results obtained with the 2nd-order upwind scheme were still quite far from true 2nd-order accuracy as displayed by the centered scheme. It is also interesting to observe that the averaging of the solution prior to the error calculation consistently improves the numerical order of accuracy of the 2nd-order upwind scheme. However, this is not true either for the 1st-order upwind scheme or for the 2nd-order centered scheme. These results are in contrast with those reported in Durlofsky, Engquist and Osher (1992), where the averaging always improves the computed order of accuracy. It should be emphasized, however, that the averaging is performed in a different fashion in the present work, when compared to the cited reference. Here, the averaged value of the solution is computed at the nodes of the mesh from the discrete cell-averaged values calculated at the cells by the present cell-centered scheme. In Durlofsky, Engquist and Osher (1992), this "averaged value" is computed at the center of the squared cells formed by two adjacent triangles.
A study is also performed to investigate the effect of the CFL number on the present results. For that, a grid with diagonals oriented with +45 deg. is used, together with an advection velocity given by ax = 1 and ay = 0. The AUSM+ scheme with gradient reconstruction and the 1-D-type limiter, with the minmod limiter, is used and the test case is run with CFL = 0.1 and 0.01. The order of accuracy obtained in the various cases analyzed is presented in Table 3. For comparison purposes, the orders of accuracy indicated in Table 3 are calculated using only the results for the three coarsest meshes. This is done because the initial results already indicated that there was no CFL number influence in the order of accuracy of the methods and the cost of running the finest grid with CFL = 0.01 was very high, of the order of 10 CPU hours in the equipment being used by the authors at the time, namely HP-9000/720 workstations. Moreover, for the cases in which values of the L1 norm of the error are available for the four grids, i.e., for the cases with CFL = 0.1, the order of accuracy obtained using the results for the four grids is indicated within parentheses in Table 3.
The effect of grid orientation is investigated by considering grids with a +45 deg. and a -45 deg. orientation for the quadrilateral diagonals used to construct the triangular meshes. The AUSM+ scheme is used for these tests, with 2nd-order reconstruction using gradients computed on the triangular cell itself and with the 1-D-type of limiter construction. The minmod limiter is also used in these cases. In order to make any grid effects more evident, the linear advection problem with ax = ay = 1 is selected for this test case. Moreover, a CFL number of 0.1 is used in the tests. The plots for the L1 norm of the error are presented in Fig. 7 both for the cases in which no averaging of the results is performed before computing the error and for the cases with averaging of the numerical solution prior to the error calculation. This figure shows results for both the 1st-order and 2nd-order schemes. The orders of accuracy actually obtained in each case are summarized in Table 4.
Figure 7 and Table 4 are indicating that, at least for the 2nd-order scheme, this test case shows very little effect of the grid orientation on the scheme order of accuracy. Moreover, for the advection velocity with ax = ay = 1, there is also very little difference between the orders of accuracy obtained with and without averaging the solution before the error calculation for the nominally 2nd-order scheme. This situation is in direct contrast with what one sees for the 1st-order scheme. For the 1st-order scheme, there is clearly a mesh orientation effect on the results. One can observe that, for the mesh with +45 deg. orientation, the order of accuracy obtained is independent of averaging and its value is somewhat the average between those obtained with and without averaging for the grid with -45 deg. orientation.
The overall conclusion one can draw from the results with gradient reconstruction with the simplified gradient calculation and with 1-D-type limiting procedures is that the orders of accuracy achieved are quite a lot better than those obtained with the one-dimensional-type reconstruction discussed in the previous section. Moreover, even though the orders of accuracy achieved for the present cases are still far from true 2nd order, they are much higher than that delivered by the corresponding 1st-order scheme calculations. In particular, for the cases with advection along a 45 deg. direction with the x-axis, the 2nd-order results are about three times better than those with the 1st-order scheme in terms of the actual order of accuracy one can actually obtain in the numerical calculations. However, as discussed in connection with the results in Table 2, some aspects of the solution behavior with the procedure emphasized in this section are, at least, strange.
The worst problem, however, with the use of gradient reconstruction and a 1-D limiting procedure occurred when the authors attempted to extend the capability in order to perform simulations of inviscid flows at high Mach numbers. The code extended to run cases for the Euler equations is able to obtain solutions for low supersonic Mach numbers as, for instance, for the flow over a wedge with freestream Mach number 2. However, the same test case results in numerical instability if the freestream Mach number is increased to, for instance, 8. These results lead to authors to conclude that this 1-D-type limiter is not the most adequate for these applications. Apparently, these problems arise from the fact that, when gradients are used, the reconstruction process is truly multi-dimensional, using information from all neighbors of the triangle under consideration. On the other hand, the 1-D-type limiting procedure does not use information from all neighbors and, hence, it actually does not provide an adequate limiting at all and leads to numerical instability. Therefore, with a gradient-type reconstruction, a truly multi-dimensional limiting procedure seems to be required in order to avoid numerical problems.
Simplified Gradient Calculation with Multi-Dimensional Limiter
The multi-dimensional limiter is built as previously described and its formulation is based on the work of Barth and Jespersen (1989). Results for the L1 norm of the error for a test case with advection velocity given by ax = 1 and ay = 0 are presented in Fig. 8 for the error calculated both without and with averaging. The curves in Fig. 8 include calculations with the nominally 2nd-order AUSM+ scheme with the multi-dimensional limiter for two different grid types, namely a completely unstructured grid and a grid with -45 deg. orientation of the diagonals, and with the 1-D limiter for the grid with diagonals oriented with -45 deg. For all upwind cases, the 2nd-order reconstruction uses gradients which are calculated using the triangular cell itself as the integration control volume. Moreover, the limiters are always the equivalent of a minmod limiter regardless of whether a 1-D or multi-dimensional construction is used. For comparison purposes, the error for the 2nd-order centered scheme, calculated on a mesh with -45 deg. orientation, is also shown.
One can see in Fig. 8 that the mesh orientation has essentially no effect on the order of accuracy of the upwind scheme with the multi-dimensional limiter. The orders of accuracy for both calculations with the multi-dimensional limiter are smaller than those obtained for the results with the 1-D-type limiter for the case shown in Fig. 8. Clearly, the order of accuracy of the centered scheme is much higher than that displayed by the upwind schemes, regardless of the mesh or the type of limiter construction. The comments that can be made with regard to the results with averaging are essentially the same, except that now one can observe a slight influence of the grid orientation on the multi-dimensional limiter results. In other words, the results with a truly unstructured grid indicate a slightly higher order of accuracy than those obtained for the grid with diagonals at -45 deg.
It is also interesting to observe that the cases with the upwind scheme not only yield a lower order of accuracy than those with the centered scheme, but also the actual value of the error with the nominally 2nd-order upwind schemes is much larger than that observed for the centered scheme for the same mesh spacing. Although not much emphasis is being placed on the actual value of the L1 norm of the error in the present paper, this can also be a very important parameter to be considered. All the results discussed so far have consistently indicated that the nominally 1st-order schemes yield error norms larger than those of the nominally 2nd-order upwind schemes which, on their turn, yield error norms larger than those of the 2nd-order centered scheme.
Calculations with the advection velocity in the direction of the computational domain diagonal, i.e., ax = ay = 1, are shown in Fig. 9. In these cases, both the effect of the mesh orientation and the effect of using a limiter are investigated. Hence, Fig. 9 shows results for the L1 norm of the error both without and with averaging, with gradient reconstruction, simplified gradient calculation and a multi-dimensional minmod limiter, for the three different mesh topologies considered in this work. Moreover, for the case of a truly unstructured grid, the error for the calculations with the use of no limiter at all is also shown in Fig. 9.
One can observe in Fig. 9 that the effect of the grid orientation is not dramatic, but the grids with -45 deg. diagonal orientation clearly yield a lower order of accuracy. For the present case, these grids have a large number of control volume edges exactly normal to the direction of property advection, and this seems to have a detrimental effect on the resulting scheme order of accuracy. Figure 9 also shows that the orders of accuracy for the solutions with the truly unstructured grids and with the grids with +45 deg. diagonal orientation are completely identical, although the magnitudes of the L1 norms of the error are slightly higher for the former grid topology. The results in Fig. 9 indicate that the truly unstructured grids yield a slightly smaller order of accuracy, when compared to the solutions with the +45 deg. grids, if the error with averaging of the numerical solution is used.
The calculations with no limiter yield L1 norms of the error, which are substantially lower than those obtained with the multi-dimensional minmod limiter, as one can observe from the comparison of the results for the truly unstructured grids shown in Fig. 9. Moreover, the actual scheme order of accuracy is better for the results without the limiter. This is the result that should be expected for a problem with a smooth solution such as the present model problem, and it is in accordance with those obtained by Aftosmis, Gaitonde and Tavares (1995). Furthermore, this result is in direct contrast to the one obtained in the previous section for the calculations with the 1-D limiter. As previously discussed, since the model problem has a smooth solution, the limiter should either play no role at all or, in the worst case, clip the smooth peaks and valleys of the smooth model function, if it perceives the gradients as too high. In this latter case, the solution without any limiter should yield a better comparison with the analytical solution than the limited calculation and, hence, a higher actual order of accuracy for the scheme. This is precisely what is being observed in the present calculations with the simplified gradient reconstruction and the multi-dimensional limiter. Moreover, this provides confidence that the multi-dimensional limiter is actually doing a much better job than the previous 1-D-type limiter, and it solves the apparent anomaly observed with the 1-D limiter.
The resulting orders of accuracy obtained in the several tests performed with the nominally 2nd-order AUSM+ scheme using gradient reconstruction and the simplified control volume for gradient calculation and with the multi-dimensional limiter are summarized in Table 5. For comparison purposes, some results already reported in previous tables are repeated here as, for example, the results for the centered scheme and for the upwind scheme with 1-D-type limiter, which appear in Fig. 8. The first important conclusion that can be drawn from these results is that the use of the multi-dimensional limiter has brought the scheme order of accuracy down when compared to the values which are obtained using the 1-D-type limiter. However, considering the discussions in the previous paragraph, the results obtained with the multidimensional limiter are more consistent than those obtained with the 1-D limiter. Moreover, a comparison of the results in Table 5 with those in Tables 2 and 4 indicates that the nominally 2nd-order scheme with the multi-dimensional limiter still consistently yields a higher actual order of accuracy than the nominally 1st-order scheme for the corresponding cases. Furthermore, flow simulations with the Euler equations did not present instability problems, even for very high Mach numbers, when the multi-dimensional limiter is used (Figueira da Silva, Azevedo and Korzenowski, 2000). Hence, despite the decrease in order of accuracy caused by the multidimensional limiter, its use would certainly be recommended as opposed to that of the 1-D-type limiter.
Results for Extended-Volume Gradient Calculation
The last aspect analyzed in the present work considers the use of gradient reconstruction with property gradients computed using an extended integration control volume, as suggested by Barth and Jespersen (1989). An analytical study would indicate that the choice of Barth and Jespersen's integration control volume would allow capturing the exact gradient of a linear function, whereas the use of the triangular control volumes themselves for gradient calculation would not yield the exact result in this case. Hence, one would expect that the adoption of this more costly gradient calculation could improve the actual order of accuracy of the nominally 2nd-order AUSM+ scheme for the present model problem calculations. It should be noted that, considering the results of the previous section, only the multi-dimensional limiter is used in the present tests.
The results presented in Fig. 10 consider the case of advection velocity along the x-axis, i.e., ax = 1 and ay = 0, and 2nd-order gradient reconstruction with the extended control volume for gradient calculation. Figure 10 indicates the evolution of the L1 norm of the error with the grid spacing both without and with averaging of the numerical results performed prior to error calculation. This figure shows both the curves for the truly unstructured grid orientation as well as for the grid with diagonals oriented with +45 deg. with the x-axis. The results for the grid oriented with -45 deg. with respect to the x-axis are not shown in the figure because they are exactly identical to those for the grid with +45 deg., as one would expect in this case. As previously discussed, the multi-dimensional version of the minmod limiter is used and, for comparison purposes, the calculations without any limiting of the extrapolated properties are presented for both cases.
The curves in Fig. 10 are indicating that there is very little effect of the mesh topology for this case, as far as the limited results are considered. On the other hand, the magnitude of the L1 norm of the error is substantially lower when the truly unstructured grid is used with the calculations without a limiter. Moreover, the actual order of accuracy is larger in this case. The calculated order of accuracy for the results without limiting is also larger than that for the calculations with the multi-dimensional minmod limiter, as should be expected. Furthermore, the averaging procedure of the numerical solution prior to error evaluation consistently improves the order of accuracy of the solution for all cases presented in Fig. 10.
The L1 norms of the error for the case of advection velocity along the domain main diagonal, i.e., ax = ay = 1, and 2nd-order gradient reconstruction with the extended control volume for gradient calculation, are shown in Fig. 11. In the present cases, there are grid orientation effects between the +45 and -45 deg. grids. This is to be expected, since the grids with +45 deg. diagonal orientation have a large number of triangle diagonals oriented along the advection direction, whereas the grids with -45 deg. diagonal orientation have a large number of triangle diagonals oriented normal to the advection direction. Moreover, one can also observe that there is not much difference between the results with the truly unstructured grids and the grids with +45 deg. orientation, when the limited calculations are considered, as it was also observed for the case of advection along the x-axis. On the other hand, the same is not true, if the calculations without limiting are considered. Actually, the order of accuracy for the calculations with the truly unstructured grid and no limiting is substantially larger than that obtained for the other cases, especially if measured in terms of the L1 norm without averaging of the numerical results.
The orders of accuracy obtained for all these test cases are summarized in Table 6. The orders of accuracy obtained for the corresponding cases with the 1st-order version of the AUSM+ scheme are also shown in Table 6 for comparison purposes. It is clear that, even with gradients computed using an extended, and presumably better control volume, the nominally 2nd-order versions of the AUSM+ scheme do not yield true 2nd-order accuracy. For the case of the truly unstructured grid, and without any limiting and without averaging the solution, one actually obtains an order of accuracy very close to 2nd order for the case of advection transversal to the computational domain. However, for some of the other cases, the order of accuracy numerically determined is even lower than 1st order for the nominally 2nd-order scheme. Moreover, a comparison of the results in Tables 5 and 6 also indicates that, for some cases, reconstruction using gradients computed on the triangle itself yield a higher order of accuracy than when it uses gradients computed on the extended control volume. It can be stated, though, that the nominally 2nd-order schemes always achieve an order of accuracy larger than that obtained with the nominally 1st-order scheme for the same case, when gradient reconstruction with a multidimensional limiter is used, regardless of the control volume used to compute the gradients.
A final comparison is presented in Fig. 12. For this comparison, a mesh with -45 deg. for the diagonal orientations was selected and the advection velocity along the x-axis was chosen. Figure 12 has the results both without and with averaging the numerical solution prior to error calculation. All calculations used the minmod limiter, either in its 1-D or multi-dimensional versions. Probably the most important conclusions one can draw from these comparisons are that both the order of accuracy of the limited schemes and the actual values of the L1 norms of the error are essentially the same for all three forms of reconstruction here studied, which have yielded relevant results when extended for high speed, supersonic, Euler calculations. The use of a 1-D-type limiter construction together with a gradient reconstruction, as already discussed, clearly has conceptual and practical problems. Therefore, the fact that the corresponding curves in Fig. 12 yield the best order of accuracy amongst the upwind schemes tested is, unfortunately, of no help.
Concluding Remarks
The present paper describes a detailed study of order of accuracy for upwind, MUSCL-type, flux-vector splitting, finite volume schemes on unstructured triangular grids. All the upwind calculations use Liou's AUSM+ scheme. The major emphasis of the work clearly is on the effects of the reconstruction procedure adopted to obtain 2nd-order accuracy together with the limiter construction. The study considers four major cases for the nominally 2nd-order upwind scheme. These can be classified as (a) one-dimensional reconstruction with a 1-D-type limiter, (b) gradient reconstruction with a simplified integration control volume and a 1-D-type limiter, (c) gradient reconstruction with a simplified integration control volume and a multi-dimensional limiter, and (d) gradient reconstruction with an extended integration control volume and a multi-dimensional limiter. The various forms of linearly reconstructing interface properties are tested using a scalar, linear advection problem with periodic boundary conditions and the effects of triangular mesh orientation and direction of the advection velocity are considered in the study.
The results indicate that the nominally 2nd-order upwind schemes do not yield true 2nd-order accuracy. Actually, with a few exceptions, the orders of accuracy achieved are quite far from 2nd order. Only the 2nd-order centered scheme was able to produce results with true 2nd-order accuracy. However, even if the higher order upwind schemes do not achieve 2nd-order accuracy, their orders of accuracy are higher than those obtained with the nominally 1st-order schemes. For some cases, the actual order of accuracy of the 2nd-order schemes is almost twice the order of its corresponding 1st-order version. Moreover, the results also indicate that the actual value of the error, measured in terms of its L1 norm, is much smaller for the 2nd-order schemes than for the corresponding 1st-order schemes. In some cases, the L1 norm of the error can be one order of magnitude smaller for the 2nd-order scheme.
The calculations show that the use of gradient reconstruction with a 1-D-type limiter does not yield reliable results. Although the orders of accuracy achieved are among the best that were obtained in the present investigation, some aspects of the error behavior are not reasonable. It seems that the reconstruction using property gradients is a truly multi-dimensional process and, hence, it does not make sense to use a limiter whose construction is based on 1-D ideas. On the other hand, all the other reconstruction strategies tested in the present work yield results which are essentially equivalent. This means that, if one thinks in terms of gradient reconstruction, the present results did not show any marked advantage of using the extended control volume for gradient calculations. Actually, based on the current results, the recommendation would be to compute the gradients using the triangles themselves as integration control volumes. This is more computationally efficient than the use of the extended control volumes and it yields essentially the same order of accuracy for the nominally 2nd-order scheme. It should be observed, however, that the present conclusion is based on the consideration of a simple advection, or convection, problem. Clearly, it would be interesting to revisit this question of simple versus extended control volume for gradient calculation, when considering the viscous gradients that are necessary for Navier-Stokes computations.
Acknowledgements
The authors gratefully acknowledge the partial support of CNPq under the Integrated Project Research Grants No. 501200/2003-7 and 312064/2006-3. Partial support was also provided by FAPESP under the Process No. 2004/16064-9. The authors are indebted to Dr. Regina C. Almeida from Laboratório Nacional de Computação Científica, LNCC, Brazil, for her comments on a previous version of the manuscript.
Paper accepted August, 2009.
Technical Editor: Aristeu Silveira
- Aftosmis, M., Gaitonde, D., and Tavares, T.S., 1995, "Behavior of linear reconstruction techniques on unstructured meshes", AIAA Journal, Vol. 33, No. 11, pp. 2038-2049.
- Anderson, W.K., Thomas, J.L., and van Leer, B., 1986, "A comparison of finite volume flux vector splittings for the Euler equations", AIAA Journal, Vol. 24, No. 9, pp. 1453-1460.
- Azevedo, J.L.F., and Korzenowski, H., 1996, "Analysis of hypersonic flows using unstructured meshes", Proceedings of the 6th Brazilian Congress of Engineering and Thermal Sciences and 6th Latin American Congress of Heat and Mass Transfer - ENCIT/LATCYM 96, Florianópolis, SC, Vol. I, pp. 547-552 (in Portuguese).
- Azevedo, J.L.F., and Korzenowski, H., 1998, "Comparison of unstructured grid finite volume methods for cold gas hypersonic flow simulations", AIAA Paper No. 98-2629, Proceedings of the 16th AIAA Applied Aerodynamics Conference, Albuquerque, NM, USA, pp. 447-463.
- Azevedo, J.L.F., and Mitchell, V.C.G., 1995, "A comparison of spatial discretization schemes for unstructured grid finite volume calculations", Proceedings of the 16th Iberian Latin American Congress on Computational Methods for Engineering - CILAMCE 95, Curitiba, PR, Vol. 1, pp. 518-526.
- Barth, T.J., and Jespersen, D.C., 1989, "The design and application of upwind schemes on unstructured meshes", AIAA Paper No. 89-0366, 27th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA.
- Batina, J.T., 1991, "Unstructured-grid methods development - lessons learned", Proceedings of the 4th International Symposium on Computational Fluid Dynamics, Davis, CA, Vol. I, pp. 91-96.
- Durlofsky, L.J., Engquist, B., and Osher, S., 1992, "Triangle based adaptive stencils for the solution of hyperbolic conservation laws", Journal of Computational Physics, Vol. 98, No. 1, pp. 64-73.
- Figueira da Silva, L.F., Azevedo, J.L.F., and Korzenowski, H., 1999, "On the development of an unstructured grid solver for inert and reactive high speed flow simulations", Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol. 21, No. 4, pp. 564-579.
- Figueira da Silva, L.F., Azevedo, J.L.F., and Korzenowski, H., 2000, "Unstructured adaptive grid flow simulations of inert and reactive gas mixtures", Journal of Computational Physics, Vol. 160, No. 2, pp. 522-540.
- Hirsch, C., 1988, "Numerical Computation of Internal and External Flows. 1. Fundamentals of Numerical Discretization", Vol. 1, Wiley, New York.
- Hirsch, C., 1990, "Numerical Computation of Internal and External Flows. 2. Computational Methods for Inviscid and Viscous Flows", Vol. 2, Wiley, New York.
- Jameson, A., and Baker, T.J., 1983, "Solution of the Euler equations for complex configurations", AIAA Paper No. 83-1929, Proceedings of 6th AIAA Computational Fluid Dynamics Conference, Vol. 1, pp. 293-302.
- Jameson, A., and Mavriplis, D., 1986, "Finite volume solution of the two-dimensional Euler equations on a regular triangular mesh", AIAA Journal, Vol. 24, No. 4, pp. 611-618.
- Lin, S.-Y., Wu, T.-M., and Chin, Y.-S., 1993, "Upwind finite-volume method with a triangular mesh for conservation laws", Journal of Computational Physics, Vol. 107, No. 2, pp. 324-337.
- Liou, M.-S., 1996, "A sequel to AUSM: AUSM+", Journal of Computational Physics, Vol. 129, No. 2, pp. 364-382.
- Lo, S.H., 1985, "A new mesh generation scheme for arbitrary planar domains", International Journal for Numerical Methods in Engineering, Vol. 21, pp. 1403-1426.
- Lyra, P.R.M., 1994, "Unstructured Grid Adaptive Algorithms for Fluid Dynamics and Heat Conduction", Ph.D. Thesis, Department of Civil Engineering, University of Wales Swansea, Swansea, Wales, U.K.
- Mavriplis, D.J., 1988, "Multigrid solution of the two-dimensional Euler equations on unstructured triangular meshes", AIAA Journal, Vol. 26, No. 7, pp. 824-831.
- Mavriplis, D.J., 1990, "Accurate multigrid solution of the Euler equations on unstructured and adaptive meshes", AIAA Journal, Vol. 28, No. 2, pp. 213-221.
- Sleigh, P.A., Gaskell, P.H., Berzins, M., and Wright, N.G., 1998, "An unstructured finite-volume algorithm for predicting flow in rivers and estuaries", Computers & Fluids, Vol. 27, No. 4, pp. 479-508.
- Swanson, R.C., and Radespiel, R., 1991, "Cell centered and cell vertex multigrid schemes for the Navier-Stokes equations", AIAA Journal, Vol. 29, No. 5, pp. 697-703.
- van Leer, B., 1979, "Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov's method", Journal of Computational Physics, Vol. 32, No. 1, pp. 101-136.
- Venkatakrishnan, V., 1995, "Convergence to steady state solutions of the Euler equations on unstructured grids with limiters", Journal of Computational Physics, Vol. 118, No. 1, pp. 120-130.
Publication Dates
-
Publication in this collection
12 July 2010 -
Date of issue
Mar 2010























































