Abstract
The characteristics associated with the delivery of the fuel to be used as the energy source in any industrial combustion equipment are of extreme importance, as for example, in improving the performance of the combustion process and in the preservation of the equipment. A clean and efficient combustion may be achieved by carefully selecting the fuel and oxidant, as well as the operational conditions of the delivery system for both. In the present work, numerical simulations were carried out using the commercial code FLUENT for analyzing some of the relevant operational conditions inside an aluminum reverb furnace employing liquid fuel and air as the oxidant. Different fuel droplets sizes as well as inlet droplet stream configurations were examined. These characteristics, associated with the burner geometry and the fuel dispersion and delivery system may affect the flame shape, and consequently the temperature and the heat flux distribution within the furnace. Among the results obtained in the simulations, it was shown the possible damages to the equipment, which may occur as a result of the combustion process, if the flame is too long or too intense and concentrated.
combustion; industrial furnaces; liquid fuel
TECHNICAL PAPERS
Combustion performance of an aluminum melting furnace operating with liquid fuel
Angela Ourivio NieckeleI; Mônica Feijó NaccacheII; Marcos Sebastião de P. GomesIII
IPUC-Rio, Department of Mechanical Engineering, 22453-900 Rio de Janeiro, RJ, Brazil. nieckele@puc-rio.br
IIPUC-Rio, Department of Mechanical Engineering, 22453-900 Rio de Janeiro, RJ, Brazil. naccache@puc-rio.br
IIIPUC-Rio, Department of Mechanical Engineering, 22453-900 Rio de Janeiro, RJ, Brazil. mspgomes@puc-rio.br
ABSTRACT
The characteristics associated with the delivery of the fuel to be used as the energy source in any industrial combustion equipment are of extreme importance, as for example, in improving the performance of the combustion process and in the preservation of the equipment. A clean and efficient combustion may be achieved by carefully selecting the fuel and oxidant, as well as the operational conditions of the delivery system for both. In the present work, numerical simulations were carried out using the commercial code FLUENT for analyzing some of the relevant operational conditions inside an aluminum reverb furnace employing liquid fuel and air as the oxidant. Different fuel droplets sizes as well as inlet droplet stream configurations were examined. These characteristics, associated with the burner geometry and the fuel dispersion and delivery system may affect the flame shape, and consequently the temperature and the heat flux distribution within the furnace. Among the results obtained in the simulations, it was shown the possible damages to the equipment, which may occur as a result of the combustion process, if the flame is too long or too intense and concentrated.
Keywords: combustion, industrial furnaces, liquid fuel
Introduction
Numerical modeling has become an important tool in the design and optimization of industrial combustion equipment, including the prediction of the emission of pollutants such as CO (carbon monoxide), SOx (sulfur oxides), and NOx (nitrogen oxides). With the world-wide increase in the utilization of fossil fuels, the control of pollutant emissions has become an issue of global concern. Additionally, with increasing oil prices, the use of lower quality fuels will tend to worsen the problem. Advances in computational modeling have resulted in an extensive application of numerical simulations to industrial furnaces, providing insights and improving the understanding of the combustion operation. Detailed analyses of the effects in the combustion process when using different fuels and oxidants, as well as different operational conditions, provide the means for achieving a cleaner and more efficient combustion.
There are several numerical studies which were developed to analyze the combustion process with different fuels, using pure air, oxygen or a mixture of both as the oxidizer. These studies provided detailed descriptions for the temperature, velocity and species concentration fields within various geometries of interest regarding industrial combustion equipments.
Brewster et al. (2001) carried numerical and experimental investigation in an industrial aluminum melting furnace with oxygen enriched combustion. The temperature distribution on the refractory walls was verified. The model over estimated the turbulent mixture and, on the other hand, the CO (carbon monoxide) concentrations were under estimated near the burner region, probably because the kinetic effects were neglected. Nieckele et al. (2004) described a numerical simulation of the 100% oxy-firing combustion process inside an industrial aluminum re-melting reverb furnace. Three different configurations were analyzed including the comparison between the staged versus non-staged combustion processes. The flow field inside aluminum furnaces with different types of burners and operating conditions was also analyzed by Nieckele et al. (2005, 2006). Golchert et al. (2006) performed a computational fluid dynamics study inside an aluminum melting furnace, using FLUENT software. Fuels with different levels of oxygen enrichment and nitrogen content were used in the simulations, and their effects on the overall operation of an aluminum furnace were investigated. As expected, the results showed that NOx emissions increase with temperature and/or nitrogen concentration in fuel. The authors suggested that it is not useful to employ oxygen enrichment to adjust for variations in the nitrogen content since these variations do not affect NO emission levels for furnaces that are oxidized mostly by air.
The work of Yang and Blasiak (2005) described the CFD modeling of the combustion of liquefied propane gas (LPG) with highly preheated air in a regenerative burner system. Results for various parameters, including the furnace-wall temperature and the concentration of gaseous species, were obtained for a semi-industrial furnace. The results indicated that the flame spread could be well predicted by using the numerical model. Wang et al. (2005) developed a comprehensive CFD model by integrating procedures for detailed chemistry, soot formation and oxidation, and thermal radiation into a three-dimensional unstructured CFD code. The model was applied to an oxygen-enriched, turbulent, non-premixed propane flame. The results showed that soot radiation decreased flame temperature and NOx emissions, substantially, especially in the flame-tip region. They also investigated the importance of modeling the radiation effects accurately for predicting the soot and NOx formation adequately.
With respect to the numerical modeling of the spray flow of liquid fuels, a single model that predicts the source terms for the mean mixture fraction and its variance was proposed by Reveillon and Vervisch (2000). The source term for the mean mixture fraction due to the droplet vaporization is normally provided by an Eulerian-Lagrangian formulation which, according to the authors, was not satisfactory when applied to the calculation of the source terms associated to the fluctuations of the mixture fraction. Demoulin and Borghi (2002) investigated the turbulent combustion of a diesel spray, utilizing probability density functions for each fluctuating variable in the liquid and gas phases. It was shown that a proper description of the temperature fluctuations caused by the presence of the droplets is crucial for a better estimation of the reaction rates. Pera et al. (2006) performed simulations for a dilute spray evaporating in spatially decaying homogeneous turbulence. The flow was modeled by using an Eulerian description while the discrete liquid phase was simulated by using a Lagrangian model. Direct Numerical Simulation was used for obtaining a database of spray carrier phase (CP-DNS). These results were then used for testing sub-grid scale closures (SGS) with the purpose of approximating the level of SGS mixture fraction variance in the Large Eddy Simulation of the fuel spray. The result was a procedure for coupling the evaporation of the spray with the modeling of the SGS turbulent combustion.
Kermes et al. (2008) presented an overview of fuels and burners, as well as an outline of the utilization of statistical analysis methods and modeling by computational fluid dynamics (CFDs) including the formation of pollutants, aiming testing gas and liquid fuel burners. Recently, Collazo et al. (2009) performed an experimental and numerical simulation of a methanol burner. Predictions of droplet diameters, droplet trajectories, temperatures and gas concentrations are presented and compared with an experimental database.
In the present work, numerical simulations are performed using the commercial package FLUENT to determine the flow field, species and temperature distribution inside an aluminum industrial furnace, employing air as the oxidant in the combustion of liquid fuel.
Nomenclature
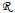
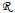 = 8314.47 kJ/(kmolK)
= 8314.47 kJ/(kmolK)Greek Symbols
Subscripts
Problem Set-up
Figure 1 illustrates a typical furnace, with the fuel/oxidant injectors and chimney exit positioned at the frontal plane. The lower horizontal plane represents the aluminum bath surface, with a small layer of 0.5 mm of aluminum oxide above it. The aluminum oxide layer was considered to describe the oxidization of the aluminum surface by the water that results from the combustion, which can act as an isolator and can compromise the quality of the product.
A vertical symmetry plane passes through the center of the chimney exit between the two pairs of oxidant and fuel injectors. Due to symmetry considerations, only half of the furnace needs to be considered. The furnace geometry was represented as a rectangular prism with length L = 4.0 m, width W = 1.5 m and height H = 2.0 m. Figure 1(b) illustrates details of the frontal plane, and Fig. 1(c) different views of the inlet configuration. The chimney exit has a rectangular cross section with dimensions w = 0.50 m and h = 0.60 m, and it is positioned at hc = 0.25 m. The center of the burner is located at hfuel = 0.65 m above the aluminum oxide layer and wox = 0.80 m away from the symmetry plane. Fuel is injected in the center of the burner and the oxidant in its surrounding annulus. The second oxidant injector (oxidant lance) is located 0.20 m above the burner (hox = 0.85 m). In the generation of the computational mesh, both burner and oxidant lance are formed by a central opening and a set of small orifices surrounding the central opening, which represents the annular opening. The jets are directed away from the refractory walls and towards the aluminum bath surface, and angles of θ = 15º in the vertical plane and of Φ = 10º in the horizontal plane were set.
The combustion of the liquid fuel C19H30 with air as oxidants was analyzed. The liquid fuel burner has a central opening area of 2.89 × 10-4 m2. Due to the large air mass flow rate needed, different fuel and oxidant openings were employed in order to provide for the same order of magnitude for both velocities. The oxidant lance was defined with a larger central opening with an area equal to 2.13 × 10-3 m2. The same annular opening area for air was designed for both the burner and the oxidant lance, being equal to 3.53 × 10-3 m2.
Physical and Mathematical Modeling
In order to obtain the flow field, temperature and species distribution for the combustion process, it was necessary to solve the conservation equations of mass, linear momentum, energy and chemical species. The following hypotheses were considered: steady flow; Newtonian fluids; the combustion takes place only after the liquid fuel has vaporized; molecular viscosity µ, thermal conductivity k and molecular diffusion coefficient D were considered constants; the mixture specific heat at constant pressure  p depends on cpℓ, the specific heat of each species ℓ weighted by its mass fraction mℓ; the density of the gaseous mixture ρ was estimated by the ideal gas law, ρ = pop / [
p depends on cpℓ, the specific heat of each species ℓ weighted by its mass fraction mℓ; the density of the gaseous mixture ρ was estimated by the ideal gas law, ρ = pop / [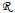 T Σℓ (mℓ/Mℓ)], where pop is the average operation pressure inside the furnace,
T Σℓ (mℓ/Mℓ)], where pop is the average operation pressure inside the furnace, 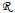 is the universal gas constant, Mℓ is the molecular weight of each species and T is the temperature; the effect of the soot concentration was considered on the radiation absorption coefficient; and since NOx concentration is low, its evaluation was decoupled from the flow, temperature and species conservation equations.
is the universal gas constant, Mℓ is the molecular weight of each species and T is the temperature; the effect of the soot concentration was considered on the radiation absorption coefficient; and since NOx concentration is low, its evaluation was decoupled from the flow, temperature and species conservation equations.
The time average conservation equations of mass, linear momentum, energy and species are given by.
where P = {p - (2/3)[(µ+µt)div v + ρκ] + ρ g y} is the modified pressure, v is the velocity vector, µt is the turbulent viscosity, Prt = 0.5 and Sct = 0.5 are the empirical turbulent Prandtl and Schmidt numbers. The total enthalpy h is defined by h = Σℓ mℓ hℓ. Srad and Sreac are enthalpy sources due to radiation heat transfer and chemical reactions occurring in the combustion process, respectively. The species enthalpy and the source Sreac are defined as
where  is the formation enthalpy at the reference temperature Tref,ℓ, Rℓ is the volumetric rate of creation. The DTRM (Discrete Transfer Radiation Model, Carvalho et al., 1991) was employed to calculate the source Srad, and the Weighted Sum of Gray Gases Model (WSGGM) was used for the calculation of the absorption coefficient (Smith et al., 1982), which is dependent on the concentration of absorbing species.
is the formation enthalpy at the reference temperature Tref,ℓ, Rℓ is the volumetric rate of creation. The DTRM (Discrete Transfer Radiation Model, Carvalho et al., 1991) was employed to calculate the source Srad, and the Weighted Sum of Gray Gases Model (WSGGM) was used for the calculation of the absorption coefficient (Smith et al., 1982), which is dependent on the concentration of absorbing species.
Equation (4) represents the transport in the gas phase and it was solved for a set of n - 1 conservation equations for the chemical species, where n represents the total number of species, since Σℓ mℓ; = 1; Σℓ Rℓ, = 0 and Σℓ Sℓ, = 0. The terms Rℓ and Sℓ represent the sources associated with the transformations due to chemical reactions, and due to addition from the dispersed phase, respectively. The term Rℓ is expressed by the sum of the reaction rates (generation or consumption) for species l in every reaction k, as denoted by Rℓ,k, according to Rℓ = Σk R ℓ,k. The Magnussen model (Magnussen and Hjertager, 1976; ANSYS Fluent 12 User's Guide, 2009) was employed to calculate the combustion reaction rates. The stoichiometric coefficients for the reaction of C19H30 with O2 were specified in accordance to
To close the set of equations (1)-(4) several auxiliary models are necessary. To describe the turbulent flow, the turbulence κ-ε model (Launder and Spalding, 1974) was selected, with the turbulent viscosity defined as µt = cµ ρ κ2 / ε, where cµ = 0.09 is an empirical constant. κ is the turbulent kinetic energy and ε its dissipation rate, and both are obtained by the solution of their conservation equations.
To predict soot formation, the single-step model of Khan and Greeves (1974) was selected. This is a simple empirical model, and should be viewed as providing only qualitative information on the soot formation process, unless an experimental procedure is developed in parallel for adjustment of the model. This model assumes that the combustion of soot is governed by the Magnussen combustion rate (Magnussen and Hjertager, 1976; ANSYS Fluent 12 User's Guide, 2009), and the soot mass fraction ms is obtained from its transport equation. The influence of the soot concentration in the temperature field is manifested through its interaction with the radiation absorption coefficient.
The flow of the fuel droplets (liquid C19H30) was defined by taking into consideration initial conditions associated to the locations for the fuel injection (discrete phase) into the gaseous mixture. These conditions were used as the starting point for calculating the trajectories of the droplets, by integrating their equation of motion (force balance at the droplet). The heat and mass transfer processes occurring in the droplets were modeled separately, by a sequence of physical laws. There are two mechanisms that control the droplets evaporation, depending on its temperature level. At the present formulation, the surface combustion of the particle is not being modeled; therefore, the fuel droplets must vaporize before reacting with the gaseous phase. Once it starts, vaporization proceeds until a boiling temperature is reached (equal to 598 K, in the case of C19H30). Before the particle temperature has reached the boiling point, the vaporization is controlled by the fuel vapor pressure (defined as 1329 Pa) and by the diffusion coefficient for the fuel in the surrounding gas (3.79 × 10-6 m2/s), both assumed constants. Heat transfer to the droplet is evaluated by an energy balance relating the sensible heat change in the droplet to the convective and latent heat transfer between the droplet and the continuous phase, where the latent heat of volatiles in the fuel droplet is equal to 124 kJ/kg. The convective heat transfer coefficient was evaluated by the correlation of Ranz and Marshall (1952). When the boiling temperature is reached, the boiling process becomes convective. The momentum, mass and thermal energy exchanged between the continuous and discrete phases are computed by examining the change in these quantities that a particle experiences as it passes through a control volume. The two-way coupling between continuous and discrete phases is accomplished by alternately solving the continuous and discrete phase equations, until convergence is achieved for both.
Since low concentrations of NOx are expected, they have little impact on density, temperature and on the concentration of other chemical species. Therefore, NOx emissions are predicted by solving a transport equation for nitric oxide (NO) concentration using a converged solution for the flow field, the temperature distribution and the species concentration. In this work, the thermal and prompt mechanisms were considered for NOx formation. The first one is calculated using the extended Zeldovich mechanism (Tomeczek and Gradón, 1997), while in the last one the procedure developed by De Soete (1975) was employed. Equation (4) can be applied to the NO species, mNO, where the source term is directly proportional to the NO formation rate for each case.
The relationships between NOx formation rates, temperature and species concentration are highly non-linear. Therefore, since the flow under analysis is turbulent, temperature and composition fluctuations should be taken into account, otherwise significant errors will result. This is done by considering the probability density functions (PDF). In FLUENT NOx model, a joint-variable PDF in terms of a combination of a normalized temperature and species mass fractions is used to predict the NOx emission ANSYS Fluent 12 User's Guide, 2009).
More details of the previously discussed models are found in ANSYS Fluent 12 User's Guide, 2009).
Boundary Conditions and Properties
The real situation corresponds to a transient process (loading the solid aluminum at ambient temperature, heating it up to the melting temperature, and melting it completely). To simplify the analysis, the proposed simulation is carried on considering a steady state regime, where the aluminum bath is represented by a flat isothermal surface at the aluminum melting temperature.
At the inlet, velocity components, temperature and species concentration were all specified for both burner and oxidant injectors. The inlet values for the turbulent quantities κ and ε were specified as κ = 3/2 (χ Vin)2 and ε = cµ3/4κ3/2 / lin, where χ is the inlet turbulence intensity, Vin is the average inlet velocity and lin is the inlet characteristic dimension. The inlet turbulent intensity was specified as 1% in all openings. The characteristic length lin was set as 0.02 m for the fuel opening and 0.046 m and 0.0067 m for the central air and both annular openings, respectively.
The average operation pressure pop inside the furnace was set equal to one atmosphere. The air entered the domain at 298 K. The fuel vaporization temperature was defined as 400 K, lower than inlet fuel droplets temperature (495 K), indicating that vaporization starts immediately after they enter the furnace, that is, no inert heating occurs.
At the symmetry plane, the normal velocity component was set equal to zero, as well as the normal gradient for all other variables. At the exit plane, the traditional outlet boundary assumption of neglecting the diffusion flux for all variables was employed.
At the solid surfaces, the non-slip condition was enforced. However, in the region close to the wall, the universal logarithmic wall function was employed, following the procedure described in Launder and Spalding (1974). All walls (aluminum surface and refractory walls) were considered as impermeable. The refractory walls were approximated as adiabatic walls, with a constant emissivity equal to 0.65. Since the inferior surface of the furnace represents the aluminum bath, the aluminum melting temperature of 1013 K was imposed at this surface. An additional 0.5 mm layer of aluminum oxide was considered on top of the aluminum, with a high emissivity value of 0.8, typical of shinning surfaces.
The liquid oil spray was defined by 15 particle streams, forming a hollow cone with angle of 45º, with velocity of 10 m/s. A length scale of 0.01 m was used during the integration of the particle trajectory equation, and the diameter distribution of the droplets was considered uniform. The influence of the oil spray stream in the combustion process was investigated, by changing the droplet diameter size. For simplicity, the collisions of the particles with the walls were considered elastic. When a particle reaches the exit section at the chimney, the trajectory calculation terminates, and it is considered that the particles had escaped from the furnace.
The properties used in the simulations are given in Table 1.
To validate the methodology employed in the present work, the numerical results obtained in the simulation of the flow and combustion processes in a cylindrical furnace were compared with available experimental data (Nieckele et al., 2001), presenting a good agreement. Further on, the same turbulence and combustion models were employed in the simulation of a similar industrial aluminum melting reverb furnace, producing realistic results when compared with field data (Nieckele et al., 2004).
Numerical Method
The flow field inside the furnace was numerically determined with the commercial software Fluent, based on the finite volume method (Patankar, 1980). The "power-law" scheme was selected for evaluating the fluxes at the control volume faces. The velocity-pressure coupling was solved by the SIMPLE algorithm (Patankar, 1980). Since the conservation equations are non-linear, relaxation factors were used. The system of algebraic equations related to all conservation equations were solved by the "Algebraic Multigrid" procedure (Hutchinson and Raithby, 1986). The global convergence criteria adopted was that the sum of the normalized residues all over the grid should be smaller than 10-4. For the energy and species equations, a smaller converging tolerance of 10-9 was imposed.
A slightly non-uniform mesh was defined inside the furnace, since a fine mesh was needed to define properly the inlet region close to the burner and oxidant injector regions, both having relatively small dimensions. At the opposite wall of the furnace, the mesh distribution was approximately uniform.
For the grid test, pollutants formation like soot and NOx were neglected. Three different mesh sizes were tested: Mesh 1 with 72,556 nodes, Mesh 2 with 148,192 and Mesh 3 with 255,316. The maximum wall temperature difference between Mesh 1 and 2 varied from 0.5% (frontal wall) to 1.2% (superior wall), while the maximum temperature difference in the whole domain was inferior to 0.25%. This difference dropped from 0.07% (frontal wall) to 0.68%, from Mesh 2 and Mesh 3, with an even smaller variation of the average wall temperature, being inferior to 0.34% for all refractory walls. The average amount of oxygen at the chimney was equal to 0.0136 for Mesh 1, 2 and 3, while the average water concentration at the aluminum surface was equal to 0.0648 for Mesh 2 and 3, and 0.0651 for Mesh 1. Due to the small differences observed on the selected quantities, Mesh 2 with 148,192 nodes was chosen for the present investigation.
Results
Considering a typical aluminum load of 16 tons (which corresponds to a volume of 6 m3), assuming an approximate process time of 1 hour, and knowing that the aluminum latent heat is 397.4 kJ/kg, a heat transfer rate of 880 kW must be extracted from the aluminum surface, in order to represent the energy necessary to melt the entire load of aluminum. In order to represent both the energy necessary to melt the entire load of aluminum and also the possible heat losses inherent to the process, a nominal thermal power equal to 2 MW per burner was specified. Since the liquid fuel superior heating power is 39.8 MJ/kg, the corresponding fuel mass flow rate was calculated to be 180 kg/h. In accordance with the reaction of Eq. (7), it is necessary 26.5 moles of O2 for 1 mol of C19H30. Further, knowing that the O2 mass fraction in the air is equal to 23%, and employing 5% excess of O2, the air mass flow rate was calculated as 2743 kg/h. The total amount of oxidant was equally injected through three inlets.
The influence of the droplet size was also investigated. For the reference case, the droplet size was defined to be 100 µm. The smaller size droplet diameter was equal to 50 µm, while the larger one was equal to 500 µm.
The temperature distribution, considering an initial fuel droplet diameter of 100 µm, can be appreciated by examining Fig. 2. Inside the 1600 K isosurface (Fig. 2(a)), the temperature is larger than 1600 K, and outside it rapidly decays to 1400 K and lower. Figure 2(b) illustrates the temperature distribution on a plane y-z that passes through the air injector and burner (x = 0.80 m). It can be seen that the flame follows the direction of the inlet jets, away from the refractory walls and downward into the load's surface. By examining Fig. 2(b), it can be seen the cold air jet over the liquid fuel jet, close to the inlet region. Due to the presence of the nitrogen, a very large amount of cold oxidant is injected. The cold jet penetrates into the domain. As a result, the liquid droplet evaporation is delayed, as well as the combustion, and the flame is detached from the inlet (Fig. 2(a)). The 1600 K isosurface is long and higher temperatures are found near the back wall. Due to combustion, a substantial temperature raise can be observed, under the cold jet. The high temperatures due to the combustion can be seen close the aluminum surface, reaching the upper back part of the furnace. The temperature level inside the furnace is approximately equal to 1410 K, while the maximum temperature inside the furnace is 1811 K. It should be mentioned that the formation of soot reduces the maximum temperature, due to its effect increasing the radiation heat transfer rate. The maximum temperature when the soot formation is neglected is equal to 1842 K. Figure 2(c) shows the temperature distribution on the refractory walls, which is approximately uniform. However, since the flame is long, warm spots can be seen near the back wall (1501 K) and upper wall (1498 K). These warm spots can damage the refractory wall, increasing the cost of the project. The average temperatures at the frontal, superior, back and side wall are 1377 K, 1433 K, 1424 K and 1380 K, respectively. The overall average wall temperature is equal to 1404 K.
Temperature profiles along selected lines inside the furnace are shown in Fig. 3. Figure 3(a) shows the lines along the z direction that passes through the center of the burner (x = 0.80 m and y = 0.65 m), and through the center of the oxidant injector (x = 0.80 m and y = 0.85 m). Note that the temperature level inside the furnace is around 1410 K. Close to the entrance, it can be seen that at the burner height (y = 0.65 m), the temperature first decreases abruptly (due to the mixing of the cold oxidant and the warm fuel) and then increases. Also, lower temperatures are observed at this height, in accordance to the flame distribution, described above.
The total and radiation heat fluxes on the aluminum surface are presented at Fig. 4. Due to the high temperature flame, the radiation heat flux is dominant. An efficient combustion inside the furnace must lead to a uniform heat flux distribution over the load. An average heat flux equal to 146.67 kW/m2 has been imposed, but the heat flux is higher under the flame.
Since the fuel reacts with the oxygen to form the products, the analysis of the C19H30 distribution as well as the oxygen distribution gives a good idea of how the fuel is consumed inside the furnace, and how the flame distributes itself. The flame region is understood to be the region where the highest consumption of fuel occurs, followed by a great heat release and temperature raise. Figure 5(a) and 5(b) show the isobands of C19H30 and O2 on a plane y-z that passes through the injectors (x = 0.80 m). The fuel and oxygen distributions can also be analyzed with the aid of Figs. 6(a) and 6(b), where isosurfaces corresponding to 2% of mass fraction of C19H30 and 5% of mass fraction of O2 are presented. The mass concentrations of both species are higher inside the respective isosurfaces. It can be seen that the O2 isosurface is connected with the upper air injector and lower burner. The C19H30 is injected only at the lower burner. Therefore the C19H30 concentration is high below the O2 jet. Due to high amount of nitrogen present in the air, it can be noted a poor contact of the oxygen with the C19H30 at the gas phase. As already mentioned, it can be observed that while the droplets do not evaporate, there is no combustion and the inlet cold temperature is practically not altered.
As shown in Eq. (7), the reaction of C19H30 with oxygen forms water and carbon dioxide. Figure 7(a) shows the CO2 distribution at the plane y-z that passes through the injectors (x = 0.80 m). Its distribution is similar to a negative image to the O2 distribution. It can be seen lower values in the flame region, where the products are still being formed. Outside the flame region, the CO2 concentration is approximately uniform, and at the chimney, it is uniform and equal to 20%. Figure 7(b) shows the water distribution over the aluminum surface. High water concentration is not desirable because an aluminum oxide layer can be formed as water reacts with the surface of the load, which increases the thermal resistance and compromises the quality of the product. It is interesting to observe that the lowest water concentration is under the flame. Note however that the water distribution is almost uniform.
An undesirable pollutant formed during the combustion process is the NOx. Its mass fraction distribution is illustrated in Fig. 8(a) at the plane that passes through the injectors (x = 0.80 m). Note that, as expected, the NOx distribution follows the same trend of all other species at the x = 0.80 m. Further, its concentration is approximately uniform at the chimney, where its average value is low, equal to 1 ppm. Soot formation is also an undesirable sub product of the combustion process. The soot distribution is illustrated in Fig. 8(b) at the plane that passes through the injectors (x = 0.80 m). Although the maximum soot mass fraction in the domain is equal to 5.72 × 103, very low values are found in the domain, and it is negligible at the chimney. However, its presence affects the radiation heat transfer, reducing the furnace temperature.
The effect of the oil spray stream in the combustion process was addressed by investigating the influence of the droplets diameter size and the shape of the stream.
Initially, the same hollow cone spray with an angle of 45º was employed with three additional droplets diameters (50 µm, 200 µm and 500 µm). It was observed that the size of the liquid fuel droplets has a small effect on the performance of the furnace. By reducing the droplet diameter to 50 µm, the maximum temperature inside the furnace increased to 1861 K, an increase of only 2.8% in relation to the reference case (d = 100 µm), while by increasing the diameter to 200 µm and 500 µm, a reduction of 3.7 and 13.3% is observed. The same order of magnitude of the refractory wall temperature was obtained for all four cases, with difference smaller than 2%. Qualitatively, the influence of the droplet size on the temperature and species distribution was small. The major difference is related with droplets parameters, like residence time and maximum particle temperature, which are shown in Table 2. As expected, as the particle increases in size, its residence time also increases.
Figure 9 illustrates the droplets trajectories for d = 50 µm, 100 µm, 200 µm and 500 µm, colored by their diameter size. Note that for the base case (d = 100 µm) the full evaporation only occurs at 1/4 of the furnace length, where the combustion begins. It can be seen that a longer trajectory occurs for the larger droplet. For the larger particle size the average heat flux at the aluminum surface was equal to 771 kW, i.e., 3% inferior to the desirable 880 kW. The maximum particle temperatures, maximum amount of soot formed inside the furnace and the bulk NOx concentration at the chimney as a function of the droplet size are also indicated in Table 2.
Since larger droplets take longer to evaporate, as a consequence, the combustion process is less efficient, reducing the overall temperature inside the furnace. It can be seen that the soot increases with the droplet size from 50 µm to 200 µm. However, when the droplet is too large (500 µm), due to incomplete combustion, only a small amount of soot is formed. Note also that the amount of NOx formed, and discarded in the atmosphere through the chimney, decreases in size due to the smaller temperatures found inside the furnace.
Two inlet stream configurations were tested with droplets with 100 µm diameter. For the reference case, the conical shape of the stream was hollow. By employing a solid cone, it was observed that the overall performance of the furnace was the same, with a slight reduction in the amount of NOx and soot formed.
Conclusions
The numerical simulation of the combustion process inside an industrial equipment proved to be extremely helpful, providing information that can contribute to improve several aspects of the actual operation. As an example of the possible benefits, the results of the numerical modeling may provide information that could contribute: (i) to reduce the maintenance costs for the refractory walls, (ii) for increasing the efficiency of the combustion process, (iii) for the assurance of the quality of the product, (iv) in the reduction of pollutants emissions, (v) for the most efficient positioning of the fuel and oxygen injectors, and so on. This information may lead to an optimized and more energy efficient effect of particle diameter and geometry on temperature and pollutants operation of the industrial combustion equipment. However, the mathematical models employed for obtaining the numerical solution must be carefully chosen to maximize reliability on the results, avoiding unreal physical situations. On the other hand, the physical models should include sufficient simplifications for running on nowadays computers in a reasonable period of time, while being comprehensive enough for representing the reality with all its significant physical processes.
In the present work, a detailed analysis of the combustion process inside an Aluminum melting furnace was performed. The temperature and species distributions were obtained and analyzed, and the influence of the fuel droplets size and stream shape were investigated.
The results showed that hot spots occurred at the upper and back refractory walls, due to the flame shape inside the furnace. NOx was also formed, in a non negligible amount. Moreover, furnace performance and final product quality could be evaluated by analyzing the results for the heat fluxes. It was shown that a non uniform heat flux distribution was obtained at the melted aluminum surface, and a small amount of water was formed in this region. The soot formation did not affect directly the results, but it altered the radiation heat transfer characteristics inside the furnace, reducing the furnace temperature.
Fuel droplets size and the stream shape for the fuel inlet were also analyzed. It was observed that larger droplets caused a slight decrease on the combustion efficiency and, consequently, lower furnace temperatures were obtained. No other major effects were observed. The inlet stream shape also did not affect the results in a significant way. Only minor changes in NOx and soot formation were observed.
Acknowledgement
The authors acknowledge the support awarded by the Brazilian Research Council, CNPq.
Paper accepted April, 2010.
Technical Editor: Demétrio Bastos Neto.
- Brewster, B.S., Webb, B.W., McQuay, M.Q., D'Agostini, M. and Baukal, C.E., 2001, "Combustion Measurements and Modelling in an Oxygen-Enriched Aluminium-Recycling Furnace", J. of the Institute of Energy, Vol. 74, pp. 11-17.
- Carvalho, M.G., Farias, T. and Fontes, P., 1991, "Predicting Radiative Heat Transfer in Absorbing, Emitting, and Scattering Media Using the Discrete Transfer Method", In: Fiveland et al. (eds.), Fundamentals of Radiation Heat Transfer, Vol. 160, pp. 17-26.
- Collazo, J., Porteiro, J., Patiño, D, Miguez, J.L., Granada, E. and Moran , J, 2009, "Simulation and Experimental Validation of a Methanol Burner", Fuel , Vol. 88 ( 2), pp. 326-334.
- Demoulin, F.X. and Borghi, R., 2002, "Modeling of Turbulent Spray Combustion with Application to Diesel Like Experiment", Combustion and Flame, Vol. 129 (3), pp. 281-293.
- De Soete, G.G., 1975, "Overall Reaction Rates of NO and N2 Formation from Fuel Nitrogen", Proc. Combust. Inst., pp. 1093-1102.
- ANSYS Fluent 12.0 User's Guide , 2009, Fluent Inc., New Hampshire.
- Golchert, B., Ridenour, P., Walker, W., Gu, M., Selvarasu, N.K. and Zhou, C., 2006, "Effect of Nitrogen and Oxygen Concentrations on NOx Emissions in an Aluminum Furnace", Proc. of 2006 ASME-IMECE, paper number IMECE-15693.
- Hutchinson, B.R. and Raithby, G.D., 1986, "A Multigrid Method Based on the Additive Correction Strategy", Numerical Heat Transfer, Vol. 9, pp. 511-537.
- Kermes ,V., Belohradsky, P., Oral, J. and Stehlik, P., 2008, " Testing of Gas and Liquid Fuel Burners for Power and Process Industries ", Energy, Vol. 33 (10), pp. 1551-1561.
- Khan, I.M. and Greeves, G.A., 1974, "Method for Calculating the Formation and Combustion of Soot in Diesel Engines", In: Heat Transfer in Flames, Scripta, Washington DC.
- Launder, B.E. and Spalding, D.B., 1974, "The Numerical Computation of Turbulent Flows", Computer Methods in App. Mech. and Engineering, Vol. 3, pp. 269-289.
- Magnussen, B.F. and Hjertager, B.H., 1976, "On Mathematical Models of Turbulent Combustion with Special Emphasis on Soot Formation and Combustion", Proc. 16th Symp. Int. on Combustion, Combustion Institute.
- Nieckele, A.O., Naccache, M.F., Gomes, M.S.P., Carneiro, J.N.E. and Serfaty, R., 2001, "Models Evaluations of Combustion Processes in a Cylindrical Furnace", Proc. of 2001 ASME-IMECE, paper number HTD-24232.
- Nieckele, A.O., Naccache, M.F., Gomes, M.S.P., 2004, "Numerical Simulation of a Three Dimensional Aluminum Melting Furnace", J. of Energy Resources Tech, Vol. 126, pp. 72-81.
- Nieckele, A.O., Naccache, M.F., Gomes, M.S.P., Carneiro, J.N.E and Silva, B.G., 2005, "Performance of the Combustion Process Inside an Aluminum Melting Furnace with Natural Gas and Liquid Fuel", Proc. of 2005 ASME-IMECE, paper number IMECE2005-79042.
- Nieckele, A.O., Naccache, M.F., Gomes, M.S.P., Carneiro, J.N.E and Silva, B.G., 2006, "Influence of the Type of Oxidant in the Combustion of Natural Gas Inside an Aluminum Melting Furnace", Proc. of 2006 ASME-IMECE, paper number IMECE2006-15505.
- Patankar, S.V., 1980, "Numerical Heat Transfer and Fluid Flow", Hemisphere, Washington, DC.
- Pera, C., Reveillon, J., Vervisch, L. and Domingo, P., 2006, "Modeling Subgrid Scale Mixture Fraction Variance in LES of Evaporating Spray", Combustion and Flame, Vol. 146, pp. 635-648.
- Ranz, W.E. and Marshall, W.R. 1952, "Evaporation from drops", Chemical Engineering Progress, Vol. 48, pp. 141-146; pp. 173-180.
- Reveillon, J. and Vervisch, L., 2000, "Spray Vaporization in Non-premixed Turbulent Combustion Modeling: A Single Droplet Model", Combustion and Flame, Vol. 121 (1), pp. 75-90.
- Smith, T.F., Shen, Z.F. and Friedman, J.N., 1982, "Evaluation of Coefficients for the Weighted Sum of Gray Gases Model", J. of Heat Transfer, Vol. 104, pp. 602-608.
- Tomeczek, J. and Gradón, B., 1997, "The Rate of Nitric Oxide Formation in Hydrocarbon Flames", Proc. of Fourth Int. Conf. on Tech. and Combust. for a Clean Environment.
- Wang, L., Haworth, D.C., Turns, S.R. and Modest, M.F., 2005, "Interactions among Soot, Thermal Radiation, and NOx Emissions in Oxygen-Enriched Turbulent Non-Premixed Flames: A Computational Fluid Dynamics Modeling Study", Combustion and Flame, Vol. 141, pp. 170-179.
- Yang, W.H. and Blasiak, W., 2005, "Numerical Simulation of Properties of a LPG Flame with High-Temperature Air", Int. Journal of Thermal Sciences, Vol. 44, pp. 973-985.
Publication Dates
-
Publication in this collection
07 Jan 2011 -
Date of issue
Dec 2010
History
-
Received
Apr 2010




















