Abstract
This work determines the preliminary mass distribution of hybrid rockets using 98% H2O2 and solid paraffin mixed with aluminum as propellants. An iterative process is used tocalculate the rocket performance characteristics and to determine the inert mass fractionfrom given initial conditions. It is considered a mission to place a 20 kg payload into a 300 km circular equatorial orbit by air launched and ground launched hybrid rockets usingthree stages. The results indicate total initial masses of about 7800 kg for a groundlaunched hybrid rocket and 4700 kg for an air launched hybrid rocket.
hybrid rocket; paraffin; H2O2; nanosats; low Earth orbit (LEO)
TECHNICAL PAPERS
Preliminary analysis of hybrid rockets for launching nanosats into LEO
Fernando de Souza CostaI; Ricardo VieiraII
IINPE, LCP, 12630-000 Cachoeira Paulista, SP, Brazil. fernando@lcp.inpe.br
IIINPE, LCP, 12630-000 Cachoeira Paulista, SP, Brazil. rvieira@lcp.inpe.br
ABSTRACT
This work determines the preliminary mass distribution of hybrid rockets using 98% H2O2 and solid paraffin mixed with aluminum as propellants. An iterative process is used tocalculate the rocket performance characteristics and to determine the inert mass fractionfrom given initial conditions. It is considered a mission to place a 20 kg payload into a 300 km circular equatorial orbit by air launched and ground launched hybrid rockets usingthree stages. The results indicate total initial masses of about 7800 kg for a groundlaunched hybrid rocket and 4700 kg for an air launched hybrid rocket.
Keywords: hybrid rocket, paraffin, H2O2, nanosats, low Earth orbit (LEO)
Introduction
Hybrid rocket technology is known for more than 50 years; however, only in the 1960's its safety characteristics motivated a significant research. Nowadays, the need for green propellants (propellants with low toxicity and low pollutant characteristics), the requirements of safe operation and storability, low cost missions, and the interest for launching small payloads and nanosats into LEO made hybrid rockets more attractive.
Hybrid propulsion systems employ propellants in different phases, being the most usual hybrid systems with a solid fuel and a liquid oxidizer. Since they use only one liquid propelllant, they require only one liquid line and a relatively simple injection system, as compared to liquid bipropellant systems which require two separate liquid lines and a complex injection plate in order to collide and mix the fuel and oxidizer jets. The control of the oxidizer flow rate in hybrid systems allows several starts and an accurate control of the thrust level.
The safe operation of hybrid propulsion systems is related to the separation of fuel and oxidizer, differently from solid systems which mix fuel and oxidizer in the grain. Another important safety characteristic is the independence of the regression rate with respect to the chamber pressure, making hybrid systems safer than solid systems if pressure peaks do occur.
The main disadvantage of hybrid rockets is the low thrust level attainable, due to the relatively low regression rates of conventional solid fuels, making necessary the use of a large number of ports, i.e., flow passages through the grain. Some methods to increase the regression rate are known, such as i) insert screens or mechanical devices in the ports to increase the turbulence level; ii) use of metallic additives; iii) use of oxidizers mixed within the solid fuel; iv) increase of the surface rugosity adding small solid particles. However, these solutions have also undesirable characteristics such as increase in weight and complexity, non-stop burning and nozzle erosion by solid particles.
Recently, it was developed in Stanford University and in the Ames-NASA Research Center, both in the USA, a new paraffinbased fuel whose regression rate is approximately three times higher than conventional hybrid fuels (Karabeyoglu et al., 2003a,b, 2004). Promising results were obtained by several researchers (Brown and Lydon, 2005; Karabeyoglu et al., 2004; Santos et al., 2005; McCormick et al., 2005; Authors, 2006; Authors, 2007) using paraffin with different oxidizers - liquid oxygen (LOX), gaseous oxygen (GOX), nitrous oxide (N2O) and hydrogen peroxide (H2O2).
The hydrogen peroxide (H2O2) is a well-known oxidizer and has been used for decades in rockets, gas generators, helicopter rotors and rocket belts (Davis Jr. and Keefe, 1956; Wernimont et al., 1999). It was used, for example, as an oxidizer in the British rocket Black Knight. Heister et al. (1998) cite some advantages of using hydrogen peroxide as oxidizer: high density, easy of handling, nontoxicity and mono-propellant characteristics. Turbo-pumps and pressurization systems can utilize the energy released during peroxide decomposition and its products in order to simplify the tank pressurization systems. Walter (1954) describes the decomposition and detonation characteristics of peroxide and mentions that peroxide at concentrations lower than 82% is not detonable and that pressure does not affect the peroxide decomposition velocity. Williams et al. (2004) state that HTP (High Test Peroxide), a high concentration peroxide, above 84% in water, is similar to nitroglycerin in terms of shock sensitivity and explodes with the same strength as the same quantity of TNT (Trinitrotoluene). Ventura et al. (2007) present supporting evidence, analysis, historical technical data, recent test data, prior and current experience, modern and literature test data which can be used to make informed decisions on peroxide applications. They also report that changes in the propellant manufacturing process may have significantly improved peroxide properties in the last decades.
The objective of this work is to make a preliminary analysis of mass distribution of hybrid propulsion systems and to compare the performance of air launched and ground launched hybrid rockets. The propellants are an aqueous solution of 98% H2O2, in mass, burning with solid paraffin mixed with 10% aluminum, in mass. The effects of mixture ratios, thrust/weight ratios and chamber pressures are analyzed. Three stage rockets are considered for placing a 20 kg nanosat into a low Earth circular equatorial orbit at 300 km.
Nomenclature
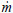
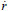
The Mass Distribution of Hybrid Rockets
The optimization of a propulsion system to perform a given mission is a complex task, since there are several coupled variables which depend on time and on rocket trajectory. The mass distribution analysis will also depend on the component level considered, i.e, a more detailed mass distribution analysis would consider the masses of each small part in the rocket, including electronics and control system components, screws, nuts, etc.
To place a satellite into a specified orbit around Earth, the launching vehicle must attain a characteristic velocity, ΔV, to overcome the Earth gravitational field, the air drag, to make maneuvers and to attain a prescribed orbital velocity.
Humble et al. (1995) used historical data of several launching vehicles and presented typical ΔV values between 8800 and 9300 m/s, as required to place satellites into a low Earth orbit. In this work it was adopted a conservative ΔV = 9300 m/s for ground launched rockets and a ΔV = 8700 m/s for air launched vehicles, based on data from the American air launched rocket Pegasus.
Usually, a rocket must have several stages to transport a payload fraction, i.e., the ratio of payload and total initial mass, above 1% into an orbit around Earth. The increase in payload fraction with a larger number of stages is significant up to 3 or 4 stages, but above 4 stages, the propulsion system complexity grows considerably, with consequent reduction in reliability and no significant increase on payload fraction.
In this work, hybrid rockets with three stages are studied, assuming a uniform distribution of characteristic velocities among stages. Sutton (1992) shows that, for simplified cases and disregarding trajectory effects, a uniform distribution of characteristic velocities is an optimum solution.
Initially, in order to determine the rocket mass distribution, it is required to estimate the inert mass fraction of all stages. The inert mass is the total initial mass minus the propellant and the payload masses. The inert mass fraction, finert,j, of the j-stage (j = 1, 2 or 3) is defined by
where mprop,j is the propellant mass and minert,j is the inert mass of the j-stage.
Tables 1 and 2 show data presented by Isakowitz et al. (1999), concerning the mass distribution, in kg, of rocket engines using solid and liquid propellants, respectively. Tables 1 and 2 show the inert fractions of the solid propellant engines, finert,s, and the inert fractions of the liquid propellant engines, finert,l. The complete rocket inert mass, including the engine inert mass, rocket casing, electronics, control, valves, and other components for all stages will be estimated later with aid of Eq. (38).
Humble and Altman (1995) showed that the propellant mass of the j-stage, for constant specific impulse and constant gravity, can be calculated by:
where mpay,j is the payload mass, Ispj is the specific impulse, go is the gravity acceleration at sea level, and ΔVj is the characteristic velocity of the j-stage.
The specific impulse can be related to the exit velocity of combustion products, Ve,j = goIspj, and is obtained from the NASA CEA 2004 code written by McBride and Gordon (1994, 1996), and available in the internet (CEA, 2007). The CEA 2004 code adopts the Gibbs free energy minimization method and solves the mass, energy and atom conservation equations with a generalized Newton method to calculate the equilibrium conditions of the reactive flow in the rocket chamber and along the nozzle. Alternatively, frozen flow conditions can also be considered along the nozzle.
The payload mass of a given stage is the total initial mass of all upper stages, and the payload mass of the last stage is the nanosat mass. The inert mass is calculated in terms of the assumed inert fraction:
and the total initial mass, mT,j, is calculated by
The F/W ratio relates to the thrust, F, and the weight, W, of a rocket, and is generally expressed in g-number. This ratio (acceleration) is limited to a range. It can not be high in order to avoid damages to the equipment, or not to harm an eventual crew. Obviously, it cannot be smaller than unit, but should be small enough to optimize the performance, especially in the first stage, which has to overcome a significant air drag. The thrust to obtain a specified j-stage thrust/weight ratio, (F/W)j, is obtained from
The total mass flow rate of propellants,
prop, j , is related to the thrust and to the specific impulse by
The fuel mass flow rate,
f, j , limits the thrust levels, due to the relatively low regression rates of hybrid fuels. It is related to the total mass consumption rate of propellants and to the OFj (oxidizer/fuel) mass ratio, by the relation:
The oxidizer mass flow rate,
o, j, is calculated by
The burning time, tb,j, is obtained from
The fuel and oxidizer volumes, Vf,j and Vo,j, are calculated, respectively, by
where ρf,j is the fuel density and ρo,j is the hydrogen peroxide density, which varies with temperature, pressure and peroxide concentration. In the next sections the subscript j will be disregarded.
Fuel Chamber and Nozzle
The chamber mass depends on the paraffin grain geometry. The initial port diameter of the fuel grain, Dint,g(0), is calculated by
where Go(0) is the initial mass flow rate of oxidant per unit area in the fuel chamber, assumed as 250 kg/m2/s for peroxide fed by a vortical injector, to avoid blowout. The regression rate of hybrid fuels (Humble and Altman, 1995) is adjusted experimentally by
where t is time and a and n are experimental constants. Equation (13) is derived assuming a turbulent reactive-diffusive boundary layer adjacent to the fuel grain, differently from a solid propellant rocket. For a constant oxidizer mass flow rate, 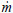 o, the oxidizer flow rate per unit area, Go, and the regression rate,
o, the oxidizer flow rate per unit area, Go, and the regression rate, 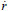 , decrease with time, since the fuel port area increases during the burning period.
, decrease with time, since the fuel port area increases during the burning period.
Assuming a single circular port, integrating Eq. (13) from t = 0 to t = tb, yields the fuel grain external diameter, Dext,g:
and the grain length, Lg, is given by
The fuel chamber internal diameter is Dint,c = Dext,g + 2tins, where tins = 0.003 m is assumed as the insulation thickness, a minimum value for support and molding of the grain. The fuel chamber external diameter is Dext,c = Dint,c + 2tw,c , where tw,c is the chamber wall thickness, given by
where Pc is the chamber pressure, σc is the yielding tensile of the chamber material and fs is a safety factor for the chamber wall stress, assumed as 100%.
The fuel chamber comprises the catalytic bed, injection plate, fuel grain section, pre-combustion section, post-combustion section and nozzle convergent. The catalytic bed decomposes the hydrogen peroxide, by an exothermic reaction which generates H2O and O2 at high temperatures, to ignite and burn the fuel grain. The precombustion, post-combustion and catalytic bed (including injection plate) lengths are assumed as Lpre = 0.5 Dint,c, Lpos = 0.7 Dint,c and Lcat = 0.5 Dint,c, respectively, which are estimated to allow oxidizer atomization, complete burning and full catalytic decomposition. The length of the nozzle convergent section is
where θcon = 45º is the convergence semi-angle. Thus, the fuel chamber length of a stage is
and its mass is, approximately,
where ρc is the fuel chamber wall density and fcat = mcat/mc  0.2 is a mass fraction corresponding to the catalytic bed.
0.2 is a mass fraction corresponding to the catalytic bed.
The throat area is calculated from At = F/(CFPc), where CF is the thrust coefficient, obtained from NASA CEA 2004 code, for a given nozzle expansion rate, ε, and chamber pressure, Pc. Therefore, the nozzle exit area is Ae = εAt and the throat diameter is Dt =(4At π)1/2 .
Considering a conical nozzle, the nozzle divergent length and mass are approximated, respectively, by
where θdiv is the divergence semi-angle, De is the nozzle exit diameter and tw,div =0.5tw,c is the average nozzle wall thickness.
Oxidizer Tank
Spherical oxidizer tanks are used in the second and third stages, with internal diameter, Dint,tko, given by
where Vu  0.05Vo is the initial ullage of the oxidizer tank to allow space for the pressurizer gas and thermal expansion of the liquid oxidizer.
0.05Vo is the initial ullage of the oxidizer tank to allow space for the pressurizer gas and thermal expansion of the liquid oxidizer.
The oxidizer pressure in the tank is Po = Pc + ΔPo, where Pc is the combustion pressure and ΔPo  0.2Pc MPa is the total pressure loss in lines, injection and valves. The pressure loss is mainly due to injection and it is relatively large to avoid flow instabilities. The wall thickness and the mass of the spherical oxidizer tank are, respectively:
0.2Pc MPa is the total pressure loss in lines, injection and valves. The pressure loss is mainly due to injection and it is relatively large to avoid flow instabilities. The wall thickness and the mass of the spherical oxidizer tank are, respectively:
where σtk,o is the yielding tensile of the tank material, ftk = mweld+sup/mtk  0.2 is a tank mass fraction used for welding and support, and Dext,tko = Dint,tko + 2tw,tko is the external diameter of the oxidizer tank.
0.2 is a tank mass fraction used for welding and support, and Dext,tko = Dint,tko + 2tw,tko is the external diameter of the oxidizer tank.
A cylindrical tank with two hemispherical domes is used in the first stage. The total length, Ltko, wall thickness, tw,tko, and mass, mtko, of the cylindrical tank are, respectively:
where Lc,tko = 4(Vo +Vu - (π6)D3int,tko)(πD2int,tko) is the length of the cylindrical section of the oxidizer tank.
Pressurizing System
The oxidizer is pressurized by a gas generator using H2O2 at 70 % in mass decomposed at a catalytic bed. The pressurizer mass is
where fpres  0.05 is a pressurizer mass fraction (pressurizer mass in the lines / pressurizer mass in the tank) for filling the feeding lines and Rpres is the gas constant of the decomposed pressurizer. The liquid pressurizer (70% H2O2) is assumed at constant pressure Ppres = 1.2Po, to overcome pressure losses in the valves and avoid flow instabilities, with density ρpres and volume Vpres = mpres/ρpres.
0.05 is a pressurizer mass fraction (pressurizer mass in the lines / pressurizer mass in the tank) for filling the feeding lines and Rpres is the gas constant of the decomposed pressurizer. The liquid pressurizer (70% H2O2) is assumed at constant pressure Ppres = 1.2Po, to overcome pressure losses in the valves and avoid flow instabilities, with density ρpres and volume Vpres = mpres/ρpres.
The internal diameter, the wall thickness, with fs = 1, and the mass of the spherical pressurizer tank are, respectively:
A small helium tank with a blowdown ratio rp = PHe,i/PHe,f = 5 is used to pressurize the liquid 70% H2O2. The final pressure at the helium tank is assumed PHe,f = 1.2 Ppres, to overcome pressure losses in the valves, and the initial helium volume, assuming an isothermal expansion process, is VHe i , = Vpres/(rp -1) , which is equal to the helium tank volume, VtkHe.
Then, the mass of helium is
and the internal diameter, wall thickness and mass of a spherical helium tank are, respectively,
where Dint,tkHe = Dint,tkHe +2tw,tkHe is the external diameter and ρtkHe is the material density of the helium tank.
Stage Case
The total stage case length is, approximately,
which includes, as a first estimate, depending on available equipments and technology, a 10% increase corresponding to spacing for control system, telemetry, valves, feeding lines, stage coupling and other devices.
In the third stage it is included a fairing, assumed as cylinder with 0.8 m height and 0.6 m diameter, to carry a nanosatellite with a volume of, approximately, 0.4 × 0.4 × 0.4 m3. The internal diameter of the stage case, Dint,case, is assumed equal to the external diameter of the oxidizer tank plus 0.04 m for tank support rings, which are used to increase stiffness, connection with the rocket case and allow electric wiring and cabling passage. The external diameter of the stage case, Dext,case, depends on material compression strength and on the applied compression force due to the rocket acceleration:
where Dint,case is the case internal diameter and σc is the compression strength of the case material. The compression strength of the case was assumed to be equal to its yielding strength. Nevertheless, a minimum thickness of 2 mm was considered for all stages, for manufacturing purposes. The stage case mass is calculated by
Therefore, the total inert mass of a stage is, approximately,
which also includes a 10 % increase corresponding to the masses of the control system, telemetry, valves, feeding lines, stage coupling and other devices. Figure 1 shows a scheme of a typical hybrid rocket configuration.
Results and Comments
Table 3 shows the initial conditions and Table 4 shows the mechanical properties of materials used for the mass distribution analysis. Titanium was used in all tanks, stainless steel was used in the chambers and nozzles, and carbon fiber was used in the cases and fairing. Ground and air-launched hybrid rockets with three stages were compared in order to place a 20 kg payload into a low Earth circular orbit at 300 km height.
Propellants are 98% H2O2 and C20H42 paraffin mixed with 10% aluminum in mass. Aluminum increases the specific impulse and reduces the optimum OF ratio. The paraffin regression rate constants were based on Brown and Lydon (2005) data which obtained a = 0.0344 (mm/s)(m2s/kg)n and n = 0.9593 (nondimensional) for paraffin burning with 84% hydrogen peroxide. The regression rate was multiplied by 0.98/0.84, for the richer peroxide solution used, since the reaction rate in the turbulent reactivediffusive boundary layer is proportional to the oxidizer mass fraction.
Figure 2 shows the theoretical specific impulse and the thrust coefficient obtained with the NASA CEA 2004 code, assuming Pc = 30 atm, equilibrium flow and adapted nozzles. It is verified that chamber pressures have no significant effects on Isp and that the maximum Isp values are obtained with OF  6.5.
6.5.
Assuming Pc = 2.5 MPa, OF = 6.5, F/W = 2.5, CF efficiencies of 93% and initial finert = 0.2 in all stages, the masses and sizes of the main components and stages were calculated. A new inert fraction was calculated for each stage and compared to the previous one. If the difference was less than 0.01% the calculation was stopped, if not a new iteration was made. In general, 6 iterations were enough for convergence. Table 5 shows the final mass distributions and additional data of air and ground launched hybrid rockets to perform the assigned mission, using three stages.
Figures 3 and 4 compare the effects of OF mass ratio on stage mass and on inert fraction, respectively, for ground and air launched rockets. Figures 5 and 6 show the effects of the F/W ratio and chamber pressure, respectively, on mass and inert fraction of air launched rockets. Figures 7 and 8 show the effects of the F/W ratio and chamber pressure, respectively, on length and diameter of air launched rockets.
It can be seen in Table 5 that the masses and sizes of air-launched rockets are significantly smaller, about 60% of the masses and 82% of the sizes of ground launched rockets. The payload fraction and total lengths of ground and air launched rockets are about 0.26% and 18 m, and 0.43% and 14.7 m, respectively. Figures 3 and 4 depict that the minimum total mass is found with OF = 6.5, corresponding to the maximum Isp, whereas the inert fractions are lower with OF = 7. Inert fractions for first stages are below 20%, whereas third stages present inert fractions above 25%. The large inert fractions and low payload ratios obtained using the preliminary mass distribution model can be explained by the conservative parameters adopted. Lower F/W ratios and lower chamber pressures yield smaller sizes and masses for all stages. First stage tanks could have larger diameters in order to reduce the total lengths. Using more advanced materials would also allow to obtain lower masses and sizes.
It is seen that the inert fraction is strongly affected by the oxidant pressures, especially in the first stages, whereas variations on F/W and OF in the ranges considered do not show significant effects on inert fractions and sizes, for all stages.
The 10% mass increase adopted in Eq. (38), considered for control system, telemetry, wiring, etc., may be reduced in a second mass distribution analysis, depending on a deeper knowledge of the available technology. As a consequence the payload fraction could be correspondingly increased.
It should be noted that the mass distribution of existing systems showed in Tables 1 and 2 refer only to the solid and liquid engines and do not include additional masses, such as fairing, rocket casing, connections, rings, control devices, etc., for the entire rocket and stages which were considered to generate the data in Table 5.
Conclusions
A preliminary analysis of the mass distribution of hybrid propulsion systems was described. Paraffin with 10% aluminum and 98% hydrogen peroxide were used as propellants. Three stage air launched hybrid rockets and ground launched hybrid rockets were compared for placing a 20 kg nanosat into a low Earth circular equatorial orbit at 300 km. An iterative process based on the inert mass fraction was used to obtain the mass distributions and the performance characteristics. The results have indicated that the total initial mass is about 7800 kg for a ground launched hybrid rocket and 4700 kg for an air launched hybrid rocket. Such a low mass in the case of air launched rockets would permit the use of relatively light airplanes for placing nanosats into orbit, with great flexibility on launching schedule and launching sites at the equator line. It is verified that the hybrid rockets are comparatively longer than solid propellant rockets for the same payload, and the inert fractions increase up to 50% for upper stages compared to first stages. Future work will provide the rough material required and a cost analysis. The results obtained here can be used as an input for more detailed performance analysis, considering all small components, more efficient materials, less conservative parameters, and the variations on specific impulse, thrust, ambient pressure and drag coefficient along specific trajectories.
Acknowledgements
The authors acknowledge FAPESP (São Paulo State Foundation for Science Support) for financial support to this research through grant 2007/03623-8.
Paper accepted October, 2010.
Technical Editor: Eduardo Belo.
- Brown, T. R., Lydon, M. C., 2005, "Testing of Paraffin-Based Hybrid Rocket Fuel Using Hydrogen Peroxide Oxidizer", AIAA Region 5 Student Conference, Wichita, USA.
- CEA - Chemical Equilibrium with Applications, 2004, Glenn Research Center, NASA, Cleveland, OH, USA, http://www.grc.nasa.gov/WWW/CEAWeb/ceaHome.htm, access in October 2007.
» link - Davis Jr, N. S., Keefe, J. H., 1956, "Concentrated Hydrogen Peroxide as a Propellant", Industrial and Engineering Chemistry, v.48, n.4, pp. 745-748.
- Gouvêa, L. H., Vieira, R., Costa, F. S., 2006, "H2O2/Paraffin Hybrid Rockets for Launching Nanosats into LEO". Proceedings of the 11th Brazilian Congress of Thermal Sciences and Engineering, CD-ROM, Ed. ABCM, Rio de Janeiro, Brazil.
- Gouvêa, L. H., 2007, "Análise de Desempenho de um Motor Híbrido Utilizando Parafina e Peróxido de Hidrogênio como Propelentes", Master Dissertation, INPE, São José dos Campos, SP, Brazil.
- Heister, S. D., Wernimont, E. J., Rusek, J. J., 1998, "High Test Peroxide Hybrid Rocket Research", Hydrogen Peroxide Propulsion Workshop, Surrey, England.
- Humble, R. W., Altman, D., 1995, "Space Propulsion Analysis and Design", Ed. M. A. Hollander, 748 p.
- Isakowitz, S. J., Hopkins Jr, J. P., Hopkins, J. B., 1999, "International Reference Guide to Space Lauch Systems", Washington, D.C., American Institute of Aeronautics and Astronautics, 549 p.
- Karabeyoglu, A., Zilliac, G., Castellucci, P, Urbanczyk, P., Stevens, J., Inalhan, G., Cantwell, B, J., 2003a, "Development of High-Burning-Rate Hybrid-Rocket-Fuel Flight Demonstrators, 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Huntsville, AL, USA.
- Karabeyoglu, A., Zilliac, G., Cantwell, B.J., Dezilwa, S., Castellucci, P., 2003b, "Scale-up Tests of High Regression Rate Liquefying Hybrid Rocket Fuels", American Institute of Aeronautics and Astronautics, Aerospace Sciences Meeting and Exhibit, Nevada, USA.
- Karabeyoglu, A., Zilliac, G., Cantwell, B. J., Dezilwa, S., Castellucci, P., 2004, "Scale-up Tests of High Regression Rate Paraffin-Based Hybrid Rocket Fuels", Journal of Propulsion and Power, v.20, n.6, p. 1037-1045.
- McBride, B.J., Gordon, S., Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications I. Analysis, NASA RP 1311-P1, Cleveland, OH, USA, 1994.
- McBride, B.J., Gordon, S., Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications II. User's Manual and Program Description, NASA RP 1311-P2, Cleveland, OH, USA, 1996.
- Mccormick, A., Hultgren, E., Lichtman, M., Smith, J., Sneed, R., Azimi, S., 2005, "Design, Optimization, and Launch of a 3" Diameter N2O/Aluminized Rocket", AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, 41, Tucson, Arizona.
- Santos, L. M. C., Almeida, L. A. R, Veras, C. A. G., 2005, "Design and Flight Test of a Paraffin Based Hybrid Rocket", Proceedings of the 18th International Congress of Mechanical Engineering, CD-ROM, ABCM, Rio de Janeiro, Brasil.
- Sutton, G. P., 1992, "Rocket Propulsion Elements -An Introduction to the Engineering of Rockets", Wiley, New York, 636 p.
- Ventura, M. C., Wernimont, E., Heister, S., Yuan, S., "Rocket Grade Hydrogen Peroxide (RGHP) for use in Propulsion and Power Devices - Historical Discussion of Hazards", Paper AIAA 2007-5468, 43rd AIAA/ASME/ SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, OH, 8 - 11 July 2007.
- Walter, H., 1954, "Experience With the Application of Hydrogen Peroxide for Production of Power", Jet Propulsion, v.24, pp. 166-171.
- Wernimont, E., Ventura, M., Garboden, G., Mullens, P., 1999, Past and Present Uses Of Rocket Grade Hydrogen Peroxide, International Hydrogen Peroxide Propulsion Conference, West Lafayette, USA.
- Wiliams, G., Macklin, F., Sarigul-Klijn, M., Sarigul-Klijn, N., Benson, J., 2004, "Almost There: Responsive Space", Paper Number RS2-2004-A024, Responsive Space Conference, Los Angeles, CA, USA.
Publication Dates
-
Publication in this collection
07 Jan 2011 -
Date of issue
Dec 2010
History
-
Received
Oct 2010












































