Abstract
The present work implements the spectral finite volume scheme in a cell centered finite volume context for unstructured meshes. The 2-D Euler equations are considered to represent the flows of interest. The spatial discretization scheme is developed to achieve high resolution and computational efficiency for flow problems governed by hyperbolic conservation laws, including flow discontinuities. Such discontinuities are mainly shock waves in the aerodynamic studies of interest in the present paper. The entire reconstruction process is described in detail for the 2nd to 4th order schemes. Roe's flux difference splitting method is used as the numerical Riemann solver. Several applications are performed in order to assess the method capability compared to data available in the literature. The results obtained with the present method are also compared to those of essentially nonoscillatory and weighted essentially non-oscillatory high-order schemes. There is a good agreement with the comparison data and efficiency improvements have been observed.
spectral finite volume; high-order discretization; 2-D euler equations; unstructured meshes
TECHNICAL PAPERS
AEROSPACE ENGINEERING
An unstructured grid implementation of high-order spectral finite volume schemes
Carlos BreviglieriI; João Luiz F. AzevedoII; Edson BassoIII
IInstituto Tecnológico de Aeronáutica CTA/ITA/IEC São José dos Campos 12228-900 SP, Brazil. carbrevi@yahoo.com.br
IIInstituto de Aeronáutica e Espaço CTA/IAE/ALA São José dos Campos 12228-903 SP, Brazil. joaoluiz.azevedo@gmail.com
IIIInstituto de Aeronáutica e Espaço CTA/IAE/ALA São José dos Campos 12228-903 SP, Brazil. edsonbassoeb@iae.cta.br
ABSTRACT
The present work implements the spectral finite volume scheme in a cell centered finite volume context for unstructured meshes. The 2-D Euler equations are considered to represent the flows of interest. The spatial discretization scheme is developed to achieve high resolution and computational efficiency for flow problems governed by hyperbolic conservation laws, including flow discontinuities. Such discontinuities are mainly shock waves in the aerodynamic studies of interest in the present paper. The entire reconstruction process is described in detail for the 2nd to 4th order schemes. Roe's flux difference splitting method is used as the numerical Riemann solver. Several applications are performed in order to assess the method capability compared to data available in the literature. The results obtained with the present method are also compared to those of essentially nonoscillatory and weighted essentially non-oscillatory high-order schemes. There is a good agreement with the comparison data and efficiency improvements have been observed.
Keywords: spectral finite volume, high-order discretization, 2-D euler equations, unstructured meshes
Introduction
Over the past several years, the Computational Aerodynamics Laboratory of Instituto de Aeronáutica e Espaço (IAE) has been developing CFD solvers for two and three dimensional systems (Scalabrin, 2002, Basso, Antunes, and Azevedo, 2003). One research area of the development effort is aimed at the implementation of high-order methods suitable for problems of interest to the Institute, i.e., external high-speed aerodynamics. Some upwind schemes such as the van Leer flux vector splitting scheme (van Leer, 1982), the Liou AUSM+ flux vector splitting scheme (Liou, 1996) and the Roe flux difference splitting scheme (Roe, 1981) were implemented and tested for second-order accuracy with a MUSCL reconstruction (Anderson, Thomas, and van Leer, 1986). However, the nominally second-order schemes presented results with an order of accuracy smaller than the expected in the solutions for unstructured grids. Aside from this fact, it is well known that total variation diminishing (TVD) schemes have their order of accuracy reduced to first order in the presence of shocks due to the effect of limiters.
This observation has motivated the group to study and to implement essentially non-oscillatory (ENO) and weighted essentially non-oscillatory (WENO) schemes in the past (Wolf and Azevedo, 2006).However as the intrinsic reconstruction model of these schemes relies on gathering neighboring cells for polynomial reconstructions for each cell at each time step, both were found to be very demanding on computer resources for resolution orders greater than three, in 2-D, or anything greater than 2nd order, in 3-D. This fact motivated the consideration of the spectral finite volume method, as proposed by Wang and co-workers (Wang, 2002, Wang and Liu, 2002, 2004, Wang, Liu, and Zhang, 2004, Liu, Vinokur, and Wang, 2006, Sun, Wang, and Liu, 2006), as a more efficient alternative. Such method is expected to perform better than ENO and WENO schemes, compared to the overall cost of the simulation, since it differs on the reconstruction model applied and it is currently extended up to 4th-order accuracy in the present work.
The SFV method is a numerical scheme developed recently for hyperbolic conservation laws on unstructured meshes. The method derives from the Godunov finite volume scheme which has become the state of the art for numerical solutions of hyperbolic conservation laws. It was developed as an alternative to k-exact high-order schemes and discontinuous Galerkin methods (Cockburn and Shu, 1989) and its purpose is to allow the implementation of a simpler and more efficient scheme. The discontinuous Galerkin and SFV methods share some similarities in the sense that both use the same piecewise discontinuous polynomials and Riemann solvers at element boundaries to provide solution coupling and numerical dissipation for stability. Both methods are conservative at element level and suitable for problems with discontinuities. The methods differ on how the necessary variables for polynomial reconstruction are chosen and updated. The SFV method has advantages in this reconstruction process. It is compact, extensible and more efficient in terms of memory usage and processing time than k-exact finite volume methods, such as ENO and WENO schemes, since the reconstruction stencil is always known and non-singular. This occurs because each element of the mesh, called a Spectral Volume, or SV, is partitioned in a geometrically similar manner into a subset of cells named Control Volumes (CVs). This allows the use of the same polynomial reconstruction for every SV. Afterwards, an approximate Riemann solver is used to compute the fluxes at the SV boundaries, whereas analytical flux formulas are used for flux computation on the boundaries inside the SV. Moreover, each control volume solution is updated independently of the other CVs. The cell averages in these sub-cells are the degrees-of-freedom (DOFs) used to reconstruct a high-order polynomial distribution inside each SV.
The numerical solver is implemented for the Euler equations in two dimensions in a cell centered finite volume context on triangular meshes, with a three-stage TVD Runge-Kutta scheme for time integration. Initially, the paper presents the theoretical formulation of the SFV method for the Euler equations. The reconstruction process of the high-order polynomial is described and some quality aspects of this process are discussed. Afterwards, the flux limiting formulation is presented, followed by the numerical results and conclusions.
Nomenclature
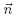
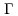
Subscript
Superscript
Theoretical Formulation
Governing Equations
In the present work, the 2-D Euler equations are solved in their integral form as
where
The vector of conserved variables, Q, and the convective flux vectors, E and V, are given by
The system is closed by the equation of state for a perfect gas
where the ratio of specific heats, γ, is set as 1.4 for all computations in this work. The flux Jacobian matrix in the n = (nx; ny) direction can be written as
The B matrix has four real eigenvalues λ1 = λ2 = vn, λ3 = vn + c,λ4 = vn- c, and a complete set of right eigenvectors (r1; r2; r3; r4), where vn = unx + vny and c is the speed of sound. Let R be the matrix composed of these right eigenvectors, then the Jacobian matrix, B, can be diagonalized as
where  is the diagonal matrix containing the eigenvalues:
is the diagonal matrix containing the eigenvalues:
In the finite volume context, Eq. (2) can be rewritten for the i-th control volume as
where Qi is the cell averaged value of Q at time t in the i-th control volume, Vi.
Spatial Discretization
The spatial discretization process determines a k-th order discrete approximation to the integral in the right-hand side of Eq. (8). In order to solve it numerically, the computational domain, Ω, with proper initial and boundary conditions, is discretized into N nonoverlapping triangles, the spectral volumes (SVs) such that
One should observe that the spectral volumes could be composed of any type of polygon, given that it is possible to decompose its bounding edges into a finite number of line segments
K, such that
In the present paper, however, the authors assume that the computational mesh is always composed of triangular elements. Hence, although the theoretical formulation is presented for the general case, the actual SV partition schemes are only implemented for triangular grids.
The boundary integral from Eq. (8) can be further discretized into the convective operator form
where K is the number of faces of Si and Ar represents the r - th face of the SV. Given the fact that 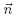 is constant for each line segment, the integration on the right side of Eq. (11) can be performed numerically with a k - th order accurate Gaussian quadrature formula
is constant for each line segment, the integration on the right side of Eq. (11) can be performed numerically with a k - th order accurate Gaussian quadrature formula
where (xrq, yrq) and wrq are, respectively, the Gaussian points and the weights on the r-th face of Si and J = integer((k + 1)/2) is the number of quadrature points required on the r - th face. For the second-order schemes, one Gaussian point is used in the integration. Given the coordinates of the end points of the element face, z1 and z2, one can obtain the Gaussian point as the middle point of the segment connecting the two end points,  . For this case, the weight is w1 = 1. For the third and fourth order schemes, two Gaussian points are necessary along each line segment. Their values are given by
. For this case, the weight is w1 = 1. For the third and fourth order schemes, two Gaussian points are necessary along each line segment. Their values are given by
and the respective weights, w1 and w2, are set as 
Using the method described above, one can compute values of Qi for instant t for each SV. From these averaged values, reconstruct polynomials that represent the conserved variables,  and e; due to the discontinuity of the reconstructed values of the conserved variables over SV boundaries, one must use a numerical flux function to approximate the flux values on the cell boundaries.
and e; due to the discontinuity of the reconstructed values of the conserved variables over SV boundaries, one must use a numerical flux function to approximate the flux values on the cell boundaries.
The above procedures follow exactly the standard finite volume method. For a given order of spatial accuracy, k, for Eq. (11), using the SFV method, each Si element must have at least
degrees of freedom (DOFs). This corresponds to the number of control volumes that Si shall be partitioned into. If one denotes by Ci,j the j-th control volume of Si, the cell-averaged conservative variable, Q, at time t, for Ci,j is computed as
where Vi,j is the volume, or area in the 2-D case, of Ci,j . Once the cell-averaged conservative variables, or DOFs, are available for all CV s within Si, a polynomial, pi(x; y) ∈ Pk-1, with degree k - 1, can be reconstructed to approximate the q(x; y) function inside Si, i.e.,
where h represents the maximum edge length of all CV s within Si. The polynomial reconstruction process is discussed in details in the following section. For now, it is enough to say that this high-order reconstruction is used to update the cell-averaged state variables at the next time step for all the CV s within the computational domain. Note that this polynomial approximation is valid within Si and some numerical flux coupling is necessary across SV boundaries.
Integrating Eq. (8) in Ci,j , one can obtain the integral form for the CV averaged mean state variable
where f represents the E and F fluxes, K is the number of faces of Ci,jand Ar represents the r - th face of the CV. The numerical integration can be performed with a k - th order accurate Gaussian quadrature formulation, similarly to the one for the SV elements in Eq. (12).
As stated previously, the flux integration across SV boundaries involves two discontinuous states, to the left and to the right of the face. This flux computation can be carried out using an exact or approximate Riemann solver, or a flux splitting procedure, which can be written in the form
where  is the conservative variable vector obtained by the pi polynomial applied at the (xrq, yrq) coordinates and qr is the same vector obtained with the pnb polynomial in the same coordinates of the face. Note that the nb subscript represents the element to the right of the face, while the i subscript the CV to its left. As the numerical flux integration in the present paper is based on one of the forms of a Riemann solver, this is the mechanism which introduces the upwind and artificial dissipation effects into the method, making it stable and accurate. In this work, the authors have used the Roe flux difference splitting method (Roe, 1981) to compute the numerical flux, i.e.,
is the conservative variable vector obtained by the pi polynomial applied at the (xrq, yrq) coordinates and qr is the same vector obtained with the pnb polynomial in the same coordinates of the face. Note that the nb subscript represents the element to the right of the face, while the i subscript the CV to its left. As the numerical flux integration in the present paper is based on one of the forms of a Riemann solver, this is the mechanism which introduces the upwind and artificial dissipation effects into the method, making it stable and accurate. In this work, the authors have used the Roe flux difference splitting method (Roe, 1981) to compute the numerical flux, i.e.,
where
Here,
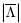 is the diagonal matrix composed of the absolute values of the eigenvalues of the Jacobian matrix, as defined in Eq. (7), evaluated using the Roe averages (Roe, 1981).
is the diagonal matrix composed of the absolute values of the eigenvalues of the Jacobian matrix, as defined in Eq. (7), evaluated using the Roe averages (Roe, 1981).Finally, one ends up with the semi-discrete SFV scheme for updating the DOFs at control volumes, which can be written as
where the right hand side of Eq. (21) is the equivalent convective operator, C(qi,j), for the j-th control volume of Si. It is worth mentioning that some faces of the CVs, resulting from the partition of the SVs, lie inside the SV element in the region where the polynomial is continuous. For such faces, there is no need to compute the numerical flux as described above. Instead, one uses analytical formulas for the flux computation, i.e., without numerical dissipation.
Temporal Discretization
The temporal discretization is concerned with solving a system of ordinary differential equations. In the present work, the authors use a third-order, TVD Runge-Kutta scheme (Shu, 1987). Rewriting Eq. (21) in a concise ODE form, one obtains
where
and
Hence, the time marching scheme can be written as
where the n and n + 1 superscripts denote, respectively, the values of the properties at the beginning and at the end of the n-th time step. The α coefficients are  and
and  .
.
Spectral Finite Volume Reconstruction
General Formulation
The evaluation of the conserved variables at the quadrature points is necessary in order to perform the flux integration over the mesh element faces. These evaluations can be achieved by reconstructing conserved variables in terms of some base functions using the DOFs within a SV. The present work has carried out such reconstructions using polynomial base functions, although one can choose any linearly independent set of functions. Let Pm denote the space of m-th degree polynomials in two dimensions. Then, the minimum dimension of the approximation space that allows Pm to be complete is
In order to reconstruct q in Pm, it is necessary to partition the SV into Nm non-overlapping CVs, such that
The reconstruction problem, for a given continuous function in Si and a suitable partition, can be stated as finding pm ∈ Pm such that
With a complete polynomial basis,  it is possible to satisfy Eq. (27). Hence, pm can be expressed as
it is possible to satisfy Eq. (27). Hence, pm can be expressed as
where e is the base function vector,  and a is the reconstruction α coefficient vector,
and a is the reconstruction α coefficient vector,  . The substitution of Eq. (28) into Eq. (27) yields
. The substitution of Eq. (28) into Eq. (27) yields
If  denotes the
denotes the  column vector, Eq. (29) can be rewritten in matrix form as
column vector, Eq. (29) can be rewritten in matrix form as
where the S reconstruction matrix is given by
and, then, the reconstruction coefficients, a, can be obtained as
provided that S is non-singular. Substituting Eq. (32) into Eq. (27), pm is, then, expressed in terms of shape functions L = [L1; . . . ;LN], defined as L = eS-1, such that one could write
Equation (33) gives the value of the conserved state variable, q, at any point within the SV and its boundaries, including the quadrature points, (xrq; yrq). The above equation can be interpreted as an interpolation of a property at a point using a set of cell averaged values, and the respective weights which are set equal to the corresponding cardinal base value evaluated at that point.
Once the polynomial base functions, el, are chosen, the L shape functions are uniquely defined by the partition of the spectral volume. The shape and partition of the SV can be arbitrary, as long as the S matrix is non-singular. The major advantage of the SFV method is that the reconstruction process does not need to be carried out for every mesh element Si. Once the SV partition is defined, the same partition can be applied to all mesh elements and it results in the same reconstruction matrix. That is, the shape functions at corresponding flux integration points over different SVs have the same values. One can compute these coefficients as a pre-processing step and they do not change along the simulation. This single reconstruction is carried out only once for a standard element, for instance an equilateral triangle, and it can be read by the numerical solver as input. This is a major difference when compared to k-exact methods such as ENO and WENO schemes, for which every mesh element has a different reconstruction process at every time step. Clearly, the SFV is more efficient in this step. Recently, several partitions for both 2-D and 3-D SFV reconstructions were studied and refined (Wang, Liu, and Zhang, 2004, Chen, 2005). For the present work, the partition schemes are presented in the following sections. Moreover, the polynomial base functions for the linear, quadratic and cubic reconstructions are listed in Table 1.
Partition Quality
There are many possible different partition schemes for the SFV method reconstructions. The problem is to find one that produces the smoother interpolation of the conserved variables, so that it improves the method's convergence and stability aspects. Until recently a parameter named Lebesque constant (Chen and Babuska, 1995) was computed for a given partition and its quality or smoothness was determined by its value. The lower this value the better the partition. More detailed description of this parameter can be found in (Wang, 2002,Wang and Liu, 2004,Wang, Liu, and Zhang, 2004).
The linear partition is defined in the following section and it can be easily defined. For the quadratic partition, the authors have first used the one presented by Sun and co-workers (Sun, Wang, and Liu, 2006) as shown in Fig. 1 named SV3W in this work. It was tested with different simulations and yielded good results. To verify its convergence aspect we tried a simple test. A blunt body with zero angle of attack with M∞ = 0.4 was simulated with a mesh of 1014 triangles and C F L = 0.3, as shown in Fig. 2(a). This partition scheme was able to reach machine zero and a solution, but it was noted an instability during the convergence history as shown in Fig. 3. Once the density residual dropped close to -10 it begun to rise and peaked at -7. We were interested to see if this partition scheme would cause the simulation to diverge and so it was simulated up to 1 million iterations and it reached machine zero and produced the result shown in Fig. 2(b) for pressure distribution. This fact brought to our attention the need to investigate other partitions. Indeed this effect was much more noticeable in the cubic reconstruction. The authors first considered the cubic partition scheme proposed by Sun and co-workers (Sun, Wang, and Liu, 2006), named here partition SV4W, shown in Fig. 4. It was unable to produce results for this test case and diverged the simulation as can be seen in the convergence history, Fig. 5.
The quality of the partition is not totally related to a small value of the Lebesgue constant. There are other parameters that can influence its quality as discussed by van Abeele and Lacor (van den Abeele and Lacor, 2007). They showed that the third and fourth order partition schemes shown above can become unstable for a given mesh, C F L number and simulation parameters. Also, they proposed improved partitions for these schemes, and these are present in the following sections.
Linear Reconstruction
For the linear SFV method reconstruction, m = 1, one needs to partition a SV in three sub-elements, as in Eqs. (14) and (25) and use the base vector as defined in Table 1. The partition scheme is given for a standard element, a right triangle for instance, in the sense of the partition nodes that compose the CVs in terms of barycentric coordinates of the SV element nodes. Hence, it is not necessary to perform a mesh element mapping to the standard shape, thus saving memory. The partition for this case is uniquely defined and its coordinates are given in Table 2, according to the nodes orientation of the standard element, as shown in Fig. 6, and the connectivity information in Table 3, relating the nodes that compose the bounding faces of the CVs. The structured aspect of the CVs within the SVs is used to determine neighborhood information and generate the global connectivity data. The original ghost elements necessary for boundary treatment that would be created for the SV simulation are not necessary. Instead, ghost elements must be created for the CV mesh. The reader should observe that the authors implemented the SFV method for a cell-centered data structure. The high-order polynomial distribution is used to obtain the properties at the ghost boundary face where the desired boundary conditions are imposed.
The code has an edge-based data structure such that it computes the convective operator for the faces instead of computing it for the volume. This approach saves a significant amount of time over traditional implementations. For each CV element face, a database is created relating the face start and end node indices, its neighbors (left and right), whether it is an internal or external face, that is, if it lies inside a given SV or on its boundaries, and how many quadrature points it has. This information,  , is obtained once connectivity and neighboring information is available. The linear partition is presented in Fig. 7. It yields a total of 7 points, 9 faces (6 are external faces and 3 internal ones), 9 quadrature points and it has a Lebesgue constant value of 2.866. The linear polynomial for the SFV method depends only on the base functions and the partition shape. The integrals of the reconstruction matrix in Eq. (31) are obtained analytically (Liu and Vinokur, 1998) for fundamental shapes. The shape functions, in the sense of Eq. (33), are calculated and stored in memory for the quadrature points, (xrq, yrq), of the standard element. Such shape functions have the exact same value for the quadratures points of any other SV of the mesh, provided they all have the same partition. There is one quadrature point located at the middle of every CV face.
, is obtained once connectivity and neighboring information is available. The linear partition is presented in Fig. 7. It yields a total of 7 points, 9 faces (6 are external faces and 3 internal ones), 9 quadrature points and it has a Lebesgue constant value of 2.866. The linear polynomial for the SFV method depends only on the base functions and the partition shape. The integrals of the reconstruction matrix in Eq. (31) are obtained analytically (Liu and Vinokur, 1998) for fundamental shapes. The shape functions, in the sense of Eq. (33), are calculated and stored in memory for the quadrature points, (xrq, yrq), of the standard element. Such shape functions have the exact same value for the quadratures points of any other SV of the mesh, provided they all have the same partition. There is one quadrature point located at the middle of every CV face.
Quadratic Reconstruction
For the quadratic reconstruction, m = 2, one needs to partition a SV in six sub-elements and use the base vector as defined in Table 1. The partition scheme is also given in this work for a right triangle. The nodes of the partition are obtained in terms of barycentric coordinates of the SV element nodes in the same manner as the linear partition. The coordinates are given in Table 4, following the node orientation in Fig. 6. Moreover, the connectivity information of the CVs is given in Table 5. The structured aspect of the CVs within the SVs is used to determine neighborhood information and generate the connectivity table. The ghost creation process and edge-based data structure are the same as for the linear reconstruction case. The partition used in this work is the one proposed by van Abeele and Lacor (van den Abeele and Lacor, 2007) named SV3A here, shown in Fig. 8. It has a total of 13 points, 18 faces (9 external faces and 9 internal ones), 36 quadrature points and it has a Lebesgue constant value of 3.075. The shape functions, in the sense of Eq. (33), are obtained as in the linear partition. The reader should note that, in this case, the base functions have six terms that shall be integrated. Again, these terms are exactly obtained (Liu and Vinokur, 1998) and kept in memory.
Cubic Reconstruction
For the cubic reconstruction, m = 3, one needs to partition the SV in ten sub-elements and to use the base vector as defined in Table 1. The barycentric coordinates are given in Table 6 following the node orientation in Fig. 6. The connectivity information of the CVs is given in Table 7. The ghost creation process and edgebased data structure is the same as for the linear and quadratic reconstruction cases. As a matter of fact, the same algorithm utilized to perform these tasks can be applied to higher order reconstructions. The partition used in this work is the improved one cubic partition (van den Abeele and Lacor, 2007) named SV4A, presented in Fig. 9 and has a total of 21 points, 30 faces (12 are external faces and 18 are internal ones) 60 quadrature points and it has a Lebesgue constant value of 4.2446 against 3.4448 of the SV4W partition. Note that for this case, the smaller Lebesgue constant was not favorable to the scheme. The shape functions, in the sense of Eq. (33), are obtained as in the linear partition in a pre-processing step. The simple test case was applied to this partition scheme to check if it indeed was more stable that the SV4W partition. It produced a solution and reached machine zero convergence as can be seen in Fig. 10.
Limiter Formulation
For the Euler equations, it is necessary to limit some reconstructed properties in order to maintain stability and convergence of the simulation if it contains discontinuities. Although the use of the conserved properties would be the natural choice, the literature (van Leer, 1979, Bigarella, 2007) shows that it lacks robustness, since it allows for negative values of pressure in the domain after the limited reconstruction operation. The limiter operator is applied in each component of the primitive variable vector,
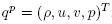 , derived from the conserved variables of the CV averaged mean and its quadrature points. For each CV, the following numerical monotonicity criterion is prescribed:
, derived from the conserved variables of the CV averaged mean and its quadrature points. For each CV, the following numerical monotonicity criterion is prescribed:
where  and
and  are the minimum and maximum cell averaged primitive variables among all neighboring CVs that share a face with Ci;j , defined as
are the minimum and maximum cell averaged primitive variables among all neighboring CVs that share a face with Ci;j , defined as
If Eq. (34) is strictly enforced, the method becomes TVD (Leveque, 2002). However, it would become first order accurate and compromise the general accuracy of the solution. To maintain highorder accuracy away from discontinuities, small oscillations are allowed in the simulation following the idea of TVB methods (Shu, 1987). If one expresses the reconstruction for the quadrature points, in the sense of Eq. (33) converted to primitive variables, as a difference with respect to the cell averaged mean,
then no limiting is necessary if
where Mq is a user chosen parameter. Different Mq values must be used for the different primitive variables which have, in general, very different scales. Then it is scaled according to
where M is the input constant independent of the component,  and
and  are the maximum and minimum of the CVs-averaged primitive variables over the whole computational domain. Note that if M = 0, the method becomes TVD. If Eq. (36) is violated for any quadrature point it is assumed that its CV is close to a discontinuity, and the solution is linearly reconstructed:
are the maximum and minimum of the CVs-averaged primitive variables over the whole computational domain. Note that if M = 0, the method becomes TVD. If Eq. (36) is violated for any quadrature point it is assumed that its CV is close to a discontinuity, and the solution is linearly reconstructed:
The solution is assumed linear also for all CVs inside a SV if any of its CVs are limited. Gradients are computed with the aid of the gradient theorem (Swanson and Radespiel, 1991), in which derivatives are converted into line integrals over the cell faces. This gradient may not satisfy Eq. (34). Therefore, it is limited by multiplying a scalar Φ ∈ [0, 1] such that the limited solution satisfies
The Φ scalar is computed following the general orientation of th literature, such that it satisfies the monotonicity constraint. In this work, the vanAlbada limiter is used (Hirsch, 1990). The limited properties at the quadrature points are then converted to conserved variables before the numerical flux calculation. After this operation, the properties are no longer continuous within the SV if any of its CVs is limited, thus the numerical flux is used on the internal faces, instead of the analytical flux.
Numerical Results
The results presented here attempt to validate the implementation of the data structure, boundary condition treatment, numerical stability and resolution of the SFV method. First, the simulation of the supersonic wedge flow with an oblique shock wave is carried out, for which the analytical solution is known (Anderson, 1982). Second, the transonic external flow over a NACA 0012 airfoil is considered. Next, the simulation of the Ringleb flow is performed followed by the shock tube problem. These test cases were selected to check upon the method capability to deal with discontinuities with the proposed limiter and to measure the effective order of the scheme. For the presented results, density is made dimensionless with respect to the free stream condition and pressure is made dimensionless with respect to the density times the speed of sound squared. For the steady case simulations the CFL number is set as a constant value and the local time step is computed using the local grid spacing and characteristic speeds.
Wedge Flow
The first test case is the computation of the supersonic flow field past a wedge with half-angle θ = 10 deg. The computational mesh has 816 nodes and 1504 volumes. For comparison purposes, the second, third and fourth order SFV methods were utilized along with other schemes. The leading edge of the wedge is located at coordinates x = 0.25 and y = 0.0. The computational domain is bounded along the bottom by the wedge surface and by an outflow section before the leading edge. The inflow boundary is located at the left and top of the domain, while the outflow boundary is located ahead of the wedge and at the right of the domain. The analytical solution gives the change in properties across the oblique shock as a function of the free stream Mach number and shock angle, which is obtained from the θ - β - Mach relation. For this case, a free stream Mach number of M1 = 5.0 was used, and the oblique shock angle β is obtained as ≈ 19.5 deg. For the analytical solution, the pressure ratio is p2=p1≈ 3.083 and the Mach number past the shock wave of M2≈ 3.939. The numerical solutions of the SFV method are in good agreement with the analytical solution. Also, a simulation with the second order WENO (Wolf and Azevedo, 2006) was performed to compare the resolution of the methods, as can be seen in Fig. 11. Note that the SFV scheme is the one that better approximates the jump in pressure on the leading edge. The pressure ratio and Mach number after the shock wave for the fourth order SFV scheme were computed as p2=p1≈ 3.047 and M2 ≈ 3.901. The pressure contours for this solution can be seen in Fig. 12.
For these simulations the use of the limiter was necessary and the M parameter was set to 50, in order to keep the high order reconstruction away from the shock wave. The limited CVs for pressure of the second and fourth order scheme are shown in Figs. 13 and 14.
The same mesh problem was simulated with the WENO 4thorder scheme (Wolf and Azevedo, 2007) to see how it compares to the 4thorder SFV scheme. The residual history for both schemes can be observed in Fig. 15. Both simulations were performed until 5000 iterations with the same flow parameters. The SFV scheme reached the maximum number of iterations in about 20 minutes. The WENO scheme reached the same number of iterations after about 100 minutes. The solution in terms of Cp distribution of both schemes is presented in Fig. 11. This simulation shows the improved efficiency of the SFV method. Both simulations were carried out with an AMD Opteron 246 system running the Linux operational system.
Ringleb Flow
The Ringleb flow simulation consists in an internal subsonic flow which has an analytical solution of the Euler equations derived with the hodograph transformation (Shapiro, 1953). The flow depends on the inverse of the stream function k and the velocity magnitude q. In the present computation, we choose the values k = 0.4 and k = 0.6 to define the boundary walls, and q = 0.35 to define the inlet and outlet boundaries. With this parameters, the Ringleb flow represents a subsonic flow around a symmetric blunt obstacle, and is irrotational and isentropic. This simulation considered four meshes with 128, 512, 2048 and 8192 elements. The analytical and numerical solutions were computed in all of these meshes so we could measure how close the numerical results were from the exact ones. This difference was computed using the L2 error norm of the density. The analytical solution was used as initial condition for all numeric simulations. As the mesh is refined one expects this error to diminish. Analyzing this information on all meshes in a logarithm scale, we can calculate the effective order of the method by computing the slope of the least squares linear fit curve of all meshes errors. This is what is represented in Fig. 16 for the second, third and fourth order simulations. The order of the SFV was computed as 1.956 for second order, 2.337 for the third order and 3.671 for the fourth order case. The mesh with 2048 elements is shown in Fig. 17 along with its analytical and numeric third order density distribution.
A high-order representation of the curved boundaries of the geometry is required to maintain the high resolution of the method (Wang and Liu, 2006, van den Abeele and Lacor, 2007). The highorder boundary representation also reduces the total number of SVs in the mesh. Using standard linear mesh elements one needs so many elements only to represent such curved boundaries. The simulations performed for this case did not consider a curvature approximation of the boundaries and for that reason it is assumed that lower than expected orders were obtained. Note that the measured order of the linear SFV reconstruction is indeed second order accurate, since the representation of the boundary elements as straight lines do not compromise the order of the method, as shown in Fig. 16(a). The values for k and q parameters of the geometry were chosen so that the flow is subsonic everywhere in the domain in an attempt to reduce the errors produced by not using a high-order boundary representation or possible development of a shock wave (Wang and Liu, 2006). Even though, for the fourth order scheme on the finest mesh the simulation actually diverged.
Shock Tube Problem
The third test case analyzed is a shock tube problem with length 10 and height 1, in dimensionless units, discretized with a mesh containing 4697 nodes and 8928 triangular control volumes and is shown in Fig. 18. The results presented here are for a pressure ratio, p1 = p4 = 5.0. Here, p1 denotes the initial static pressure in the driver section (high-pressure side) of the shock tube, whereas p4 denotes the corresponding initial static pressure in the driven section (low-pressure side) of the shock tube. It was assumed that both sides of the shock tube were originally at the same temperature. In this problem, a normal shock wave moves from the driver section of the shock tube to the driven section. As the shock wave propagates to the right, it increases the pressure and induces a mass motion of the gas behind it. The interface between the driver and driven gases is represented by a contact discontinuity. An expansion wave propagates to the left, smoothly and continuously decreasing the pressure in the driver section of the shock tube. All these physical phenomena are well captured by the SFV schemes.
Figures 19 and 20(a) present the density and pressure distribution for the flow in the shock tube for an instant of time equal to 1.0 dimensionless time units after diaphragm rupture. The results presented were obtained along the shock tube centerline. The results are plotted for the second, third and fourth order SFV scheme. One can see in the density distribution that the results of the schemes are in good agreement with the analytical solution. However, it is possible to see that the quadratic and cubic reconstructions were limited to the point that most of their CVs were linearly reconstructed. Nevertheless, the resolution of these methods for the discontinuities is greater than that of the second order scheme, as noted on the pressure distribution at Fig. 20(b).
NACA 0012 Airfoil
For the NACA 0012 airfoil simulation, a mesh with 8414 elements and 4369 nodes was used in the same conditions of the experimental data (McDevitt and Okuno, 1985), that is, freestream Mach number value of M∞ = 0.8 and 0 deg angle-of-attack. The second, third and fourth order schemes were computed with a CFL value of 0.5, 0.3 and 0.2, respectively. Figure 21 shows the results of the simulation using the fourth order SFV method. Its agreement with the experimental data, in terms of shock position and pressure coefficient (Cp) values, is very reasonable and the resolution of the shock wave is really sharp, with only one mesh element to represent it. The same is true for the other schemes. Note that the results presented are those for the SV mesh for all cases. For this simulation the use of limiter is also necessary, and the limiter range parameter is M = 50.
The region where the limiter works in the CVs is shown if Fig. 22 for the second order scheme and in Fig. 23 for the third order scheme for pressure. For the linear reconstruction only the CVs close to the shock wave were limited. For the third order scheme, most SVs on the shock wave region were linearly reconstructed and some limited. The choice of an adequate value for the M parameter can lead to a lower usage of the limiter operator. The fourth order SFV scheme achieved very similar results compared to the 3rd order scheme, given the fact that most CVs on the shock region were limited. The numerical results for the pressure contours are plotted in Fig. 21 for the third-order SFV scheme. Figure 24 indicates that both the second and third order methods capture the shock wave over the airfoil, with a single SV element in it. The Cp distributions in the post-shock region shows that the influence of the limiter operator reduced the third order scheme resolution. It is important to emphasize that the present computations are performed assuming inviscid flow. Nevertheless, the computational results are in good agreement with the available experimental data. One should observe, however, that the pressure rise across the shock wave, in the experimental results, is spread over a larger region due to the presence of the boundary layer and the consequent shock-boundary layer interaction that necessarily occurs in the experiment. For the numerical solution, the shock presents a sharper resolution, as one can expect for an Euler simulation.
Conclusions
The second, third and fourth order spectral finite volume method were successfully implemented and validated for external and internal flow problems, with and without discontinuities. Tests were performed with different partition schemes and it was shown that it can greatly influence the method behavior. The SV partitions in the present work were not the ones with the smallest Lebesgue constant, used until recently to indicate the quality of the polynomial interpolation, but those that produced a smoother interpolation. The effective order of the schemes was measured using the Ringleb flow case and are in the expected values for the current implementation. Further modifications in the code that support curvature boundaries representation is necessary in order to maintain high-order resolution for such simulations. The method behavior for resolution greater than second order showed to be in good agreement with both experimental and analytical data. Furthermore, the results obtained were indicative that the current method can yield solutions with similar quality at a much lower computational resource usage than traditional k-exact schemes, as demonstrated in the supersonic wedge case compared to the WENO fourth order scheme. The method seems suitable for the aerospace applications of interest to IAE in the sense that it is compact, from an implementation point of view, extensible to higher orders, geometry flexible, as it handles unstructured meshes, and computationally efficient.
Acknowledgements
The authors gratefully acknowledge the partial support provided by Conselho Nacional de Desenvolvimento Científico e Tecnológico, CNPq, under the Integrated Project Research Grant No. 312064/2006-3. The authors are also grateful to Fundação de Amparo à Pesquisa do Estado de São Paulo, FAPESP, which also partially supported the present research through the Project No. 2004/16064-9.
Paper accepted August, 2010.
Technical Editor: Eduardo Morgado Belo
- J. D. Anderson. Modern Compressible Flow, with Historical Perspective -2nd Edition McGraw-Hill, Boston, 1982.
- W. K. Anderson, J. L. Thomas, and B. van Leer. Comparison of finite volume flux vector splittings for the Euler equations. AIAA Journal, 24(9):14531460, 1986.
- E. Basso, A. P. Antunes, and J. L. F. Azevedo. Chimera simulations of supersonic flows over a complex satellite launcher configuration. Journal of Spacecraft and Rockets, 40(3):345355, May-June 2003.
- E. D. V. Bigarella. Advanced Turbulence Modelling for Complex Aerospace Applications Ph.D. Thesis, Instituto Tecnológico de Aeronáutica, São José dos Campos, SP, Brazil, 2007.
- Q. Chen and I. Babuska. Approximate optimal points for polynomial interpolation of real functions in an interval and in a triangle. Comput. Methods Appl. Mech. Engrg., 128:405417, 1995.
- Q. Y. Chen. "Partitions for Spectral (Finite) Volume Reconstruction in the Tetrahedron," IMA Preprint Series No. 2035, Minneapolis, MN, April 2005.
- B. Cockburn and C. W. Shu. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws II: General framework. Mathematics of Computation, 52:441 435, 1989.
- C. Hirsch. Numerical Computation of Internal and External Flows Wiley, New York, 1990.
- R. J. Leveque. Finite Volume Methods For Hyperbolic Problems Cambridge University Press, Cambridge, 2002.
- M. S. Liou. A sequel to AUSM: AUSM+ Journal of Computational Physics, 129(2):364382, Dec. 1996.
- Y. Liu and M. Vinokur. Exact integrations of polynomials and symmetric quadrature formulas over arbitrary polyhedral grids. Journal of Computational Physics, 140(1):122147, Feb. 1998.
- Y. Liu, M. Vinokur, and Z. J. Wang. Spectral (finite) volume method for conservation laws on unstructured grids V: Extension to three-dimensional systems. Journal of Computational Physics, 212(2): 454472, March 2006.
- J. McDevitt and A. F. Okuno. Static and dynamic pressure measurements on a NACA 0012 airfoil in the Ames high Reynolds number facility. NASA TP-2485, NASA, Jun. 1985.
- P. L. Roe. Approximate Riemann solvers, parameter vectors, and difference schemes. Journal of Computational Physics, 43(2): 357372, 1981.
- L. C. Scalabrin. Numerical Simulation of Three-Dimensional Flows over Aerospace Configurations Master Thesis, Instituto Tecnológico de Aeronáutica, São José dos Campos, SP, Brazil, 2002.
- A. H. Shapiro. The Dynamics and Thermodynamics of Compressible Fluid Flow Wiley, New York, 1953.
- W. C. Shu. TVB uniformly high-order schemes for conservation laws. Mathematics of Computation, 49:105121, 1987.
- Y. Sun, Z. J. Wang, and Y. Liu. Spectral (finite) volume method for conservation laws on unstructured grids VI: Extension to viscous flow. Journal of Computational Physics, 215(1):4158, Jun. 2006.
- R. C. Swanson and R. Radespiel. Cell centered and cell vertex multigrid schemes for the Navier-Stokes equations. AIAA Journal, 29 (5):697703, 1991.
- K. van den Abeele and C. Lacor. An accuracy and stability study of the 2D spectral volume method. Journal of Computational Physics, 226(1):10071026, Sept. 2007.
- B. van Leer. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov's method. Journal of Computational Physics, 32(1):101136, Jul. 1979.
- B. van Leer. Flux-vector splitting for the Euler equations. Lecture Notes in Physics, 170:507512, 1982.
- Z. J. Wang. Spectral (finite) volume method for conservation laws on unstructured grids: Basic formulation. Journal of Computational Physics, 178(1):210251, May 2002.
- Z. J. Wang and Y. Liu. Spectral (finite) volume method for conservation laws on unstructured grids II: Extension to two-dimensional scalar equation. Journal of Computational Physics, 179(2):665 698, Jul. 2002.
- Z. J. Wang and Y. Liu. Spectral (finite) volume method for conservation laws on unstructured grids III: One-dimensional systems and partition optimization. Journal of Scientific Computing, 20 (1):137157, Feb. 2004.
- Z. J. Wang and Y. Liu. Extension of the spectral volume method to high-order boundary representation. Journal of Computational Physics, 211(1):154178, Jan. 2006.
- Z. J. Wang, Y. Liu, and L. Zhang. Spectral (finite) volume method for conservation laws on unstructured grids IV: Extension to two-dimensional systems. Journal of Computational Physics, 194(2): 716741, March 2004.
- W. R. Wolf and J. L. F. Azevedo. High-order unstructured essentially nonoscillatory and weighted essentially nonoscillatory schemes for aerodynamic flows. AIAA Journal, 44(10):22952310, Oct. 2006.
- W. R. Wolf and J. L. F. Azevedo. High-order ENO and WENO schemes for unstructured grids. Int. J. Numer. Meth. Fluids, 55 (10):917943, Dec. 2007.
Publication Dates
-
Publication in this collection
11 Mar 2011 -
Date of issue
Dec 2010
History
-
Received
Aug 2010 -
Accepted
Aug 2010


 The application of the divergence theorem to Eq. (1) yields
The application of the divergence theorem to Eq. (1) yields

















 is Roe's dissipation matrix computed from
is Roe's dissipation matrix computed from






















































