Abstract
The behavior of inclined slender elastic rods subjected to axial forces and distributed load is discussed in this paper. Mathematical models and numerical solutions are developed for small and large displacements. A double-hinged boundary condition is assumed and the analysis is carried out for different values of non-dimensional weight (distributed load) and angle of inclination. The mathematical formulation results from considering geometrical compatibility, equilibrium of forces and moments and constitutive relations. For large displacements, a set of six first order non-linear ordinary differential equations with boundary conditions prescribed at both ends is obtained. This two-point boundary value problem is numerically integrated using a three-parameter shooting method. When small displacements are assumed the problem simplifies and a power series solution may be conveniently employed. The results for both simulations are presented, compared and discussed.
elastic rods; inclined rods; non-linear analysis
TECHNICAL PAPERS
SOLID MECHANICS
Geometrically non-linear analysis of inclined elastic rods subjected to self-weight
Murilo Augusto VazI; Felipe Sant'Ana CastelpoggiII
IFederal University of Rio de Janeiro, Ocean Engineering Departament. 21941972 Rio de Janeiro, Brazil. murilo@peno.coppe.ufrj.br
IIFederal University of Rio de Janeiro, Ocean Engineering Departament. 21941972 Rio de Janeiro, Brazil. castelpoggi@peno.coppe.ufrj.br
ABSTRACT
The behavior of inclined slender elastic rods subjected to axial forces and distributed load is discussed in this paper. Mathematical models and numerical solutions are developed for small and large displacements. A double-hinged boundary condition is assumed and the analysis is carried out for different values of non-dimensional weight (distributed load) and angle of inclination. The mathematical formulation results from considering geometrical compatibility, equilibrium of forces and moments and constitutive relations. For large displacements, a set of six first order non-linear ordinary differential equations with boundary conditions prescribed at both ends is obtained. This two-point boundary value problem is numerically integrated using a three-parameter shooting method. When small displacements are assumed the problem simplifies and a power series solution may be conveniently employed. The results for both simulations are presented, compared and discussed.
Keywords: elastic rods, inclined rods, non-linear analysis
Introduction
The subject of buckling, post-buckling and large deflection analyses of slender rods has experienced significant evolution since the early classical contributions from Bernoulli, Euler and Lagrange in the 18th century, see Love (1944). This class of problem may exhibit complex phenomena such as limit load, bifurcation, jump and hysteresis, depending on the non-linear nature of geometrical, physical or load assumptions.
The buckling and post-buckling behavior of weightless rods have been addressed, for instance, by Gurfinkel (1965), Wang (1997), Tan and Witz (1995), Lee and Oh (2000) and Vaz and Silva (2002). The use of long submersed columns such as marine risers and drill-strings in the offshore oil&gas industry motivated the study of buckling and initial post-buckling of vertical rods subjected to variable axial forces resulting from self-weight. In Lubinski (1950), Huang and Dareing (1966, 1968 and 1969), Plunkett (1967), Wang (1983), Bernitsas and Kokkinis (1983a-b and 1984a-b), Kokkinis and Bernitsas (1985 and 1987), Vaz and Patel (1995), Patel and Vaz (1996), Jurjo et al. (2001), Vaz and Mascaro (2005) the rod buckling, initial post-buckling and post-buckling solutions are developed.
In some potential applications a heavy slender structure may be supported at its extremities, such as in the areas of drill string mechanics and flexible pipe jumper configuration; for instance, Sampaio Jr and Hundhausen (1998) employed an energy method to derive the governing equations and generalized hypergeometric functions to solve the small displacement problem of inclined beam-columns. In this situation the gravitational field not only imposes a variable axial force (problem is no longer symmetrical), but it also imparts to the rod a lateral distributed load. In this paper a large displacement formulation is developed (hence the geometrical nonlinear nature of the problem is captured), a numerical solution is obtained and results are compared.
Nomenclature
L
= beam length, m
M
= bending moment, N.m
x1
= non-dimensional X1
Greek Symbols
= self-weight per unit length, N/m
Δ
= axial displacement, m
= angle between the tangent and the X-axis, deg
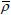
= non-dimensional Δ
Subscripts
0
= relative to top end X-coordinate
max
= relative to maximum
The Mathematical Model
Consider an inextensible slender uniform rod with length L and self-weight (per unit length) ρ supported by two points at an inclination β with respect to the horizontal axis, as shown in Fig. 1(a). When the rod is inclined the self-weight simultaneously modifies the distribution of longitudinal and lateral loads, respectively given by P and H. In addition, a pure bending formulation is assumed and the material is linear elastic so the bending stiffness is given by EI, where E is the Young's Modulus and I is the second moment of cross-sectional area. The problem can be load or displacement controlled, so let Δ be the axial displacement of the upper end as shown in Fig. 1(a).
Geometrical equations
Geometrical restrictions are obtained from trigonometric relations applied to an infinitesimal rod element (see Fig. 1(b)):
Where S is the rod arc-length (0 < S < L), (X,Y) are the Cartesian coordinates of the deflected rod and θ is the angle between the tangent and the X -axis. Furthermore, the curvature Κ may be defined by:
Equilibrium of forces and moments
A schematic of the internal forces and moments in the rod infinitesimal element is shown in Fig. 1(b). The equilibrium of longitudinal and lateral forces and bending moments respectively yields:
where  is the bending moment.
is the bending moment.
Constitutive relations
Assuming linear elastic, homogeneous and isotropic materials, and considering the state of pure (Euler-Bernoulli) bending results in:
Therefore, substituting Eq. (3) into (2c) results:
Boundary conditions
A set of six boundary conditions must be defined and for the double-hinged rod they may be specified as:
where X1 is the top end X-coordinate (X1 = L -Δ). The influence of the boundary conditions on the rod response is obviously significant, but it can be easily approached with the same methodology presented here.
The governing equations
It is clearly advantageous to reduce the set of differential Eqs. (1a)-(1c), (2a)-(2b) and (4) to a non-dimensional form using the following change of variables: S = sL , Y = yL , X = xL , Κ=κ L, 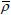 =ρ EI/L3, P = pEI L2 and H = h EI L2 , where 0 <s <1 . Hence:
=ρ EI/L3, P = pEI L2 and H = h EI L2 , where 0 <s <1 . Hence:
where (x, y) constitute the deflected rod non-dimensional Cartesian coordinates, s the non-dimensional arc-length, κ the nondimensional curvature, θ the angle formed by the curve tangent and the longitudinal axis, p and h respectively the non-dimensional longitudinal and lateral loads and 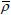 the non-dimensional distributed weight. Furthermore, the boundary conditions are also made non-dimensional:
the non-dimensional distributed weight. Furthermore, the boundary conditions are also made non-dimensional:
where x1 = 1-δ (δ=Δ/L). Equation (7) represents non-movable and movable hinged conditions respectively at the lower (s = 0) and upper (s = 1) ends. Two parameters control the problem, β and 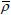 .
.
The Solution for Large Displacements
As the set of six first order non-linear ordinary differential equations and its boundary conditions constitute a two-point boundary value problem, a classical shooting technique may be employed to transform it into an initial value problem, hence allowing a direct integration scheme. Three boundary conditions are given at the end, i.e., x(0) = y(0) = κ(0) = 0 and x(1) - x1= y(1) = κ(1) 0, so the missing initial values h(0), q(0) and p(0) need to be found. The software Mathcad offers a simple procedure to compute the initial missing values. This procedure may be summarized with the following main steps: (a) the set of differential equations is defined (i.e., equations (6a)-(6f)); (b) the initial missing values are guessed (i.e., values for h(0), q(0) and p(0)); (c) the boundary value endpoints are specified (i.e., x(1) - x1 y(1)= κ(1)= 0; (d) a load function which returns the initial condition is defined; (e) a score function to measure the distance between terminal and desired conditions is employed; (f) the equivalent initial conditions are calculated (i.e., the values for h(0), q(0) and p(0)). From this point, a Runge-Kutta high order solution algorithm is applied to solve the set of non-linear ordinary differential equations. Given the highly non-linear nature of the problem adequate convergence may be achieved through successive approximations. If the self-weight is disregarded a closed-form analytical solution via elliptical integrals may be obtained.
The Solution for Small Displacements
When small displacements are assumed, dx  ds, sin(θ)
ds, sin(θ)  θ and cos(θ)
θ and cos(θ)  1, a simplified differential governing equation is obtained:
1, a simplified differential governing equation is obtained:
where p0 and h0 are respectively the longitudinal and lateral loads at x = 0 and β, 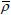 and p0 are known. A solution for Eq. (8) may be obtained via Maclaurin series, yielding:
and p0 are known. A solution for Eq. (8) may be obtained via Maclaurin series, yielding:
where C0,C1,C2,h0 are constants and S(x),T(x),U(x),V(x) are series functions given by:
When the boundary conditions y(0) = d2y/dx2 (0) = y(1) = d2y/dx2 (1) = 0 are applied to Eq. (9), the following linear problem may be written:
where the functions P(x),Q(x),R(x),W(x) are respectively the second differentiation of S(x),T(x),U(x),V(x) . The number of terms required for adequate convergence depends on the values of β and 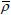 . Once C0, C1, C2, h0 are calculated the angle, curvature and forces distributions may be readily obtained.
. Once C0, C1, C2, h0 are calculated the angle, curvature and forces distributions may be readily obtained.
Analysis of Results
A comparative study is carried out for power series (small displacements) and numerical (large displacements) solutions for several values of inclination (β = 0, 22.5, 45, 67.5, 90 deg) and nondimensional rod self-weight (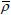 = 35,100). Figures 2 and 3, respectively, show the large displacement configuration for
= 35,100). Figures 2 and 3, respectively, show the large displacement configuration for 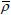 = 35 and 100. In both figures the geometrical configuration is plotted for δ = 0, 0.2, 0.4, 0.6, 0.8, 1.0 . For horizontal rods (β = 0 ) the solution is, as expected, symmetrical. However, when the inclination increases the lateral displacement becomes more asymmetric. The heavier and more inclined rod (i.e.,
= 35 and 100. In both figures the geometrical configuration is plotted for δ = 0, 0.2, 0.4, 0.6, 0.8, 1.0 . For horizontal rods (β = 0 ) the solution is, as expected, symmetrical. However, when the inclination increases the lateral displacement becomes more asymmetric. The heavier and more inclined rod (i.e., 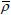 = 100 and β = 90 deg ) exhibits a more pronounced lower bulge as the lower and upper ends are respectively under compression and tension.
= 100 and β = 90 deg ) exhibits a more pronounced lower bulge as the lower and upper ends are respectively under compression and tension.
Figures 4 and 5 show the values of the non-dimensional variables h0, δ , p0 , θ0 and ymax (maximum lateral deflection) when small and large displacements are considered, respectively for 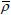 = 35 and 100. The comparison between results for small and large displacement formulations indicates when geometrical non-linear effects take place and must be included for a correct response characterization.
= 35 and 100. The comparison between results for small and large displacement formulations indicates when geometrical non-linear effects take place and must be included for a correct response characterization.
In Figs. 4(a) and 5(a) it is seen that h0 is constant for β = 0 and varies more intensively for β = 90 deg . Observe that negative values for p0 in Figs. 4(b) and 5(b) indicate tensile forces. The change in behavior from a laterally and axially loaded rod to postbuckling phenomenon is evidenced in Figs. 4(c)-(d) and 5(c)-(d) by comparing results for β = 90 deg and β < 90 deg.
Conclusions
This paper presents formulation and solution for inclined elastic rods subjected to terminal forces and a gravitational field. The rod is assumed hinged at both ends. An analytical (power series) solution is obtained when small deflections are considered and the problem is geometrically linear. The large deflection non-linear analysis is obtained from solving a complex two-point boundary value problem governed by a set of six first order non-linear ordinary differential equations. As expected the numerical and analytical solutions are in good agreement when displacements are kept small, once the geometrical non-linearities do not significantly influence the results. In addition, the results evidence a change in the response behavior as the rod becomes vertical and a post-buckling instability phenomenon takes place. The boundary conditions affect the rod response and it can be readily calculated with the methodologies developed here.
Acknowledgement
The authors acknowledge the support of the National Council for Scientific and Technological Development (CNPq) for this work.
References
Bernitsas, M.M., Kokkinis, T., 1983, "Buckling of columns with nonmovable boundaries", J. Struct. Engineering, 109, pp. 2113-2127.
Bernitsas, M.M., Kokkinis, T., 1983, "Buckling of columns with movable boundaries", J. Struct. Mechanics, 11, pp. 351-370.
Bernitsas, M.M., Kokkinis, T., 1984, "Asymptotic behaviour of heavy columns and riser stability boundaries", ASME J. Appl. Mech., 51, pp. 560-565.
Bernitsas, M.M., Kokkinis, T., 1984, "Global static instability of risers", SNAME J. Ship Research, 28, pp. 261-271.
Gurfinkel, G., 1965, "Buckling of elastically restrained columns", ASCE J. Struct. Div., 91, ST 6 159-183.
Huang, T., Dareing, D.W., 1966, "Predicting the stability of long vertical pipe transmitting torque in a viscous medium", J. Engineering for Industry, pp. 191-200.
Huang, T., Dareing, D.W., 1968, "Buckling and lateral vibration of drill pipe", J. Engineering for Industry, pp. 613-619.
Huang, T., Dareing, D.W., 1969, "Buckling and frequencies of long vertical pipes", J. Engineering Mechanics Division, Proceedings of the ASCE, Vol. 95, No. EM1, 167-181.
Jurjo, D.L.B.R., Gonçalves, P.B., Pamplona, D., 2001, "Large deflection behavior and stability of slender bars under self-weight", Proceedings of the 16th Brazilian Congress of Mechanical Engineering, Uberlândia, Brazil, November 2001.
Kokkinis, T., Bernitsas, M.M., 1985, "Post-buckling analysis of heavy columns with application to marine risers", SNAME J. Ship Research, 29, pp. p162-169.
Kokkinis, T., Bernitsas, M.M., 1987, "Effect of fluid static pressure on the immediate postbuckling behavior of heavy tubular columns", Appl. Ocean Research, 9, pp. 141-149.
Lee, B.K., Oh, S.J., 2000, "Elastica and buckling load of simple tapered columns with constant volume", Int. J. Non-Linear Mech., 37, pp. 2507-2518.
Love, A.E.H., 1944, "A treatise on the mathematical theory of elasticity", 4th ed., New York: Dover Publications.
Lubinski, A., 1950, "A study of the buckling of rotary drilling strings", API Drilling and Production Practice, pp. 178-214.
MathCad: Mathcad 2000 Professional for PC, Mathsoft Inc. 2000. Nayfeh, A.H., 2000, "Nonlinear interactions", 1st ed., New York: Wiley Interscience.
Patel, M.H., Vaz, M.A., 1996, "On the mechanics of submerged vertical slender structures subjected to varying axial tension", Proc. the R. Soc. London Ser. A354, pp. 609-648.
Plunkett, R., 1967, "Static bending stresses in catenaries and drill strings", J. Engineering for Industry, pp. 31-36.
Sampaio Jr, J.H.B., Hundhausen, J.R., 1998, "A mathematical model and analytical solution for buckling of inclined beam-columns", Appl. Math. Modeling, 22, pp. 405-421.
Tan, Z., Witz, J.A., 1995, "On the deflected configuration of a slender elastic rod subject to parallel terminal forces and moments", Proc. R. Soc. London Ser. A449, pp. 337-349.
Vaz, M.A., Patel, M.H., 1995, "Analysis of drill strings in vertical and deviated holes using the Galerkin technique", Engineering Structures, 17, pp. 437-442.
Vaz, M.A., Silva, D.F.C., 2002, "Post-buckling analysis of slender elastic rods subjected to terminal force", Int. J. Non-Linear Mech., 34, pp. 483-492.
Vaz, M.A., Mascaro, G.H.W., 2005, "Post-buckling analysis of slender elastic vertical rods subjected to terminal forces and self-weight", Int. J. Non-Linear Mech., 40, pp. 1049-1056.
Wang, C.Y., 1997, "Post-buckling of a clamped-simply supported elastica", Int. J. Non-Linear Mech., 32, pp. 1115-1122.
Wang, C.Y., 1983, "Buckling and postbuckling of a long-hanging elastic column due to a bottom load", ASME J. Appl. Mech., 50, pp. 311-314.
Paper received 16 November 2009.
Paper accepted 3 February 2011.
Technical Editor: Nestor Zouain
- Bernitsas, M.M., Kokkinis, T., 1983, "Buckling of columns with nonmovable boundaries", J. Struct. Engineering, 109, pp. 2113-2127.
- Bernitsas, M.M., Kokkinis, T., 1983, "Buckling of columns with movable boundaries", J. Struct. Mechanics, 11, pp. 351-370.
- Bernitsas, M.M., Kokkinis, T., 1984, "Asymptotic behaviour of heavy columns and riser stability boundaries", ASME J. Appl. Mech., 51, pp. 560-565.
- Bernitsas, M.M., Kokkinis, T., 1984, "Global static instability of risers", SNAME J. Ship Research, 28, pp. 261-271.
- Gurfinkel, G., 1965, "Buckling of elastically restrained columns", ASCE J. Struct. Div., 91, ST 6 159-183.
- Huang, T., Dareing, D.W., 1966, "Predicting the stability of long vertical pipe transmitting torque in a viscous medium", J. Engineering for Industry, pp. 191-200.
- Huang, T., Dareing, D.W., 1968, "Buckling and lateral vibration of drill pipe", J. Engineering for Industry, pp. 613-619.
- Huang, T., Dareing, D.W., 1969, "Buckling and frequencies of long vertical pipes", J. Engineering Mechanics Division, Proceedings of the ASCE, Vol. 95, No. EM1, 167-181.
- Jurjo, D.L.B.R., Gonçalves, P.B., Pamplona, D., 2001, "Large deflection behavior and stability of slender bars under self-weight", Proceedings of the 16th Brazilian Congress of Mechanical Engineering, Uberlândia, Brazil, November 2001.
- Kokkinis, T., Bernitsas, M.M., 1987, "Effect of fluid static pressure on the immediate postbuckling behavior of heavy tubular columns", Appl. Ocean Research, 9, pp. 141-149.
- Lee, B.K., Oh, S.J., 2000, "Elastica and buckling load of simple tapered columns with constant volume", Int. J. Non-Linear Mech., 37, pp. 2507-2518.
- Love, A.E.H., 1944, "A treatise on the mathematical theory of elasticity", 4th ed., New York: Dover Publications.
- Lubinski, A., 1950, "A study of the buckling of rotary drilling strings", API Drilling and Production Practice, pp. 178-214.
- MathCad: Mathcad 2000 Professional for PC, Mathsoft Inc. 2000. Nayfeh, A.H., 2000, "Nonlinear interactions", 1st ed., New York: Wiley Interscience.
- Patel, M.H., Vaz, M.A., 1996, "On the mechanics of submerged vertical slender structures subjected to varying axial tension", Proc. the R. Soc. London Ser. A354, pp. 609-648.
- Plunkett, R., 1967, "Static bending stresses in catenaries and drill strings", J. Engineering for Industry, pp. 31-36.
- Sampaio Jr, J.H.B., Hundhausen, J.R., 1998, "A mathematical model and analytical solution for buckling of inclined beam-columns", Appl. Math. Modeling, 22, pp. 405-421.
- Tan, Z., Witz, J.A., 1995, "On the deflected configuration of a slender elastic rod subject to parallel terminal forces and moments", Proc. R. Soc. London Ser. A449, pp. 337-349.
- Vaz, M.A., Patel, M.H., 1995, "Analysis of drill strings in vertical and deviated holes using the Galerkin technique", Engineering Structures, 17, pp. 437-442.
- Vaz, M.A., Silva, D.F.C., 2002, "Post-buckling analysis of slender elastic rods subjected to terminal force", Int. J. Non-Linear Mech., 34, pp. 483-492.
- Vaz, M.A., Mascaro, G.H.W., 2005, "Post-buckling analysis of slender elastic vertical rods subjected to terminal forces and self-weight", Int. J. Non-Linear Mech., 40, pp. 1049-1056.
- Wang, C.Y., 1997, "Post-buckling of a clamped-simply supported elastica", Int. J. Non-Linear Mech., 32, pp. 1115-1122.
- Wang, C.Y., 1983, "Buckling and postbuckling of a long-hanging elastic column due to a bottom load", ASME J. Appl. Mech., 50, pp. 311-314.
Publication Dates
-
Publication in this collection
10 Apr 2012 -
Date of issue
Mar 2012
History
-
Received
16 Nov 2009 -
Accepted
03 Feb 2011

































