Abstract
The dam-break flow involving non-Newtonian fluids is a type of flow commonly observed in nature as well as in common industrial processes. Experiments of non-Newtonian dam-break flows were conducted in horizontal channels and aqueous solutions of Carbopol 940 were used, which were modeled by the Herschel-Bulkley constitutive equation. Their flows were filmed and the frames were compared with numerical simulations. Two particular results were analyzed: the front wave evolution with time and its stop distance. The CFX software was employed and the simulations were conducted with the VOF method. Both results, numerical and experimental, were compared with shallow water approximation solutions found in literature. The numerical code, which uses complete momentum equations, showed better agreement with the experiments than those using shallow water equations. It seems that the hypotheses used by the shallow water approximated equations are not appropriate for the first instants of the flow, just after the dam-break and errors are introduced. Probably, these errors are propagated producing the differences encountered.
dam-break; Herschel-Bulkley fluids; shallow water; complete solution; VOF
TECHNICAL PAPERS
RHEOLOGY AND NON-NEWTONIAN FLUID MECHANICS
Numerical experimental comparison of dam break flows with non-Newtonian fluids
Roberta Brondani MinussiI; Geraldo de Freitas MacielII
Iroberta@labcet.ufsc.br. UFSC Federal University of Santa Catarina. Department of Mechanical Engineering. 88040-900 Florianóplis, SC, Brazil
IImaciel@dec.feis.unesp.br. UNESP Paulista State University. Department of Civil Engineering. 15385-000 Ilha Solteira, SP, Brazil
ABSTRACT
The dam-break flow involving non-Newtonian fluids is a type of flow commonly observed in nature as well as in common industrial processes. Experiments of non-Newtonian dam-break flows were conducted in horizontal channels and aqueous solutions of Carbopol 940 were used, which were modeled by the Herschel-Bulkley constitutive equation. Their flows were filmed and the frames were compared with numerical simulations. Two particular results were analyzed: the front wave evolution with time and its stop distance. The CFX software was employed and the simulations were conducted with the VOF method. Both results, numerical and experimental, were compared with shallow water approximation solutions found in literature. The numerical code, which uses complete momentum equations, showed better agreement with the experiments than those using shallow water equations. It seems that the hypotheses used by the shallow water approximated equations are not appropriate for the first instants of the flow, just after the dam-break and errors are introduced. Probably, these errors are propagated producing the differences encountered.
Keywords: dam-break, Herschel-Bulkley fluids, shallow water, complete solution, VOF
Introduction
Dam-break flows can be described as the flow caused by the sudden release of a contained portion of fluid. Many environmental flows can be modeled as dam-break flows. It is common to see mud flows generated by clay-water solutions that slumps in mountainous regions after torrential rain or even by the collapse of a barricade. Other examples includes debris flows, lava flows and snow avalanches, which unfortunately, often produces catastrophic effects. But it is not only in nature that dam-break flows occur. Many industrial applications involve the usage of fluids being released suddenly. Food processing, transport of liquid substances in chemical factories, concrete transport in civil constructions and Bostwich consistometers (Balmforth et al., 2007) are just a few examples of industrial related dam-break flows. Therefore, the knowledge of the applicability limits of the existing theories used for the solution of dam-break flows are vital for better engineering projects in industry and also in preventing geological related accidents, like those mentioned above. The main aim of the work presented herein is to show that the most common used theory, the shallow water theory, must be used with care and be reduced, in many cases, only to initial studies.
In free surface problems, like dam-break ones, the surface position introduces difficulties in solving the motion equations. The most common strategy is the usage of shallow water approximation, transforming two phase flows into monophasic problems. Shallow water equations are obtained by the vertical integration of the motion equations. This procedure requires the following considerations:
- Small vertical velocities;
- Hydrostatic pressure field, and
- The independence of the velocity horizontal component with the vertical coordinate, i.e.: u = u(x, t).
It is not unusual the fluids existing in this type of flow to have non-Newtonian rheologies. The inclusion of non-Newtonian constitutive equations into the Cauchy equation of motion introduces another difficulty in dealing with this subject and numerous developments have been made in the last decades.
However, the modern computational tools allow solutions to this issue without the need of shallow water approximation. Therefore, the complete solution of these flows could be used for more detailed analysis leaving more simplified studies for the shallow water approximation developments. The aforementioned considerations of shallow water approximation are generally related to small ratio problems, i.e.:
For dam-break flows this is equivalent to:
where, generally, H0 is the reservoir initial high and L0 is the reservoir length.
In this paper some shallow water solutions found in the literature are compared with numerical simulations that use the complete motion equations (without the shallow water approach). Both kinds of results are also compared with experimental data.
Nomenclature
C = concentration, %
f = function (rheological model) defined by Eq. (3)
H0 = reservoir initial high, mm
k = consistency index, Pa s n
L0 = reservoir length, mm
n = flow index, dimensionless
p = pressure, Pa
pH = hydrogen potential, dimensionless
S = source term, kg/(m 2 s 2 )
t = time, s
T = temperature, ºC
u = vector velocity, mm/(s)
ut = total uncertainty, %
VF = volume fraction, dimensionless
x = horizontal distances, mm
y = vertical distances, mm
Greek Symbols
α = auxiliary variable defined by Eq. (15), 1/(s)
ε = aspect ratio, dimensionless
= strain rate tensor, 1/(s)
II = second invariant of the strain rate tensor, 1/(s 2 )
inf = inferior limit of strain rate, 1/(s)
sup = superior limit of strain rate, 1/(s)
η = apparent viscosity, Pa s
ρ = specific mass, kg/(m 3 )
τ = deviatoric tensor, Pa
τ II = second invariant of the deviatoric tensor, Pa 2
τ c = yield stress, Pa
µ = Newtonian viscosity, Pa s
Subscripts
carb = relative to Carbopol
i = relative to phase
Superscripts
T = symbol for transpose of a matrix
Rheology: Herschel-Bulkley Fluids
The constitutive equation for non-Newtonian fluids can be considered as an expansion of the constitutive equation for Newtonian fluids, replacing the Newtonian viscosity, µ, by an expression for viscosity as function of 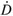 II:
II:
where  =(∇u + ∇uT)/2 is the strain rate tensor, τ is the deviatoric tensor and
=(∇u + ∇uT)/2 is the strain rate tensor, τ is the deviatoric tensor and 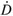 II=[(tr(
II=[(tr( ))2-tr(
))2-tr( 2)]/2 is the second invariant of
2)]/2 is the second invariant of  .
.
For fluids that present yield stress, such equation can be written as follows (Coussot, 1997):
where τcis the yield stress.
The yield stress is a concept used for practical purposes. It was first developed because, in some applications, many fluids appear to behave like solids for stresses below some stress threshold (in fact, it is most probable that the behavior is similar to an elastic solid). Although there have been many discussions on this subject, it is out of the scope of this paper.
In the experiments, aqueous solutions of Carbopol 940 were used. Carbopol is a family of polymers used to produce non-Newtonian fluids, and it was developed by NOVEON™. Many publications use aqueous solutions of Carbopol as test fluid in rheological problems and, in most cases, its rheology is modeled by the Herschel-Bulkley viscosity equation (e.g. in dam-break flows: Ancey and Cochard, 2009; Balmforth et al., 2007; Cochard and Ancey, 2009; Debiane, 2000; Piau and Debiane, 2005; among others), in which:
where n is the flow index and k is the consistency index.
And then, replacing Eq. (5) into Eq. (4) we have:
Although, there is a constant discussion in the scientific community about the validity of using Herschel-Bulkley model for Carbopol solutions, Ancey et al. (2007) affirm that there is much evidence of Carbopol behaving differently than predicted by the equation (6). In fact, it is known that Carbopol presents thixotropy (a time dependent phenomena characterized by differences in the viscosity even when submitted by constant strain rate), viscoelasticy and slip effects. All of these phenomena are macroscopic manifestations of the microstructure of complex material and so have the same origin, which is not contemplated by the Herschel-Bulkley model (see Møller et al., 2006). Roberts and Barnes (2001) comment that although there is the existence of such effects, the usage of Herschel-Bulkley model for Carbopol solutions is reasonable in most engineering applications.
The usage of the yield stress can produce some difficulties in numerical simulations. Rewriting Eq. (4),
where η(-
II) = τc(-II)-1/2+f (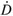 II) is the apparent viscosity, and defining the second invariant of τ as:
II) is the apparent viscosity, and defining the second invariant of τ as:
it is possible to see that, invoking the Von Mises Criterion (Papanastasiou, 1987), for:
the effective viscosity tends to infinity.
A way to avoid this kind of behavior is the usage of the so called regularization methods, which, in this kind of problems, consists in replacing the viscosity at Eq. (7) such that it could be defined for  tending to zero. Friggard and Nouar (2005) revised some existing regularization methods and concluded that they can improve the convergence of simulations, but for |τII| too close to the yield stress, the regularization methods should be avoided.
tending to zero. Friggard and Nouar (2005) revised some existing regularization methods and concluded that they can improve the convergence of simulations, but for |τII| too close to the yield stress, the regularization methods should be avoided.
Dam-Break Flows
As mentioned, dam-break flows correspond to an abrupt release of fluid. At first, the bulk flow is dominated by inertia effects and a rapid transient behavior. Afterwards, the viscous forces become more and more important, until a viscous regime can be characterized.
The study of dam-break problems began a century ago with Ritter, in 1892 (apud Whitham, 1954), who studied the dam-break flow of inviscid fluids in horizontal channels using the shallow water approach. Whitham (1954) introduced the hydraulic resistance effect and, by the Pohlhausen integration of shallow water equations, he produced better results than previous work (Ritter's, 1892, and Dressler (apud Whitham, 1954), who used the Chèzy resistance term).
Over the twentieth century many authors analyzed dam-break flows of inviscid and Newtonian fluids. In the last decades, the study of non-Newtonian fluids and their flow behavior started to be more preeminent and, with that, also dam-break flows of non-Newtonian fluids. The main question is how to solve the front wave position. After the release, when viscous dissipation became dominant (viscous regime), the major part of the flow is nearly steady and uniform, but the front is characterized by a sheared region at the bottom followed by a plug zone near the surface. Unlike dam-break flows of Newtonian fluids, fluids presenting yield stress tends to asymptotically arrest. This arrested state is characterized by two kinds of force balances. For steep slopes, the balance is between gravitational and viscous forces and, for nearly horizontal channels there is a balance between pressure cross flow gradient and viscosity (Ancey and Cochard, 2009).
Huang and García (1998) studied the dam-break flows of Herschel-Bulkley fluids on steep flumes. They used lubrication theory, similar, for this case, to shallow water approach, and analyzed the effect of some rheological parameter variations (varying n and k). Debiane (2000) obtained analytical solutions for Newtonian and non-Newtonian Herschel-Bulkley fluids, in rectangular channels with infinite and finite reservoirs. The flow was divided into three regimes, an inertial regime, followed by two viscous ones. It was found that such regimes have distinct and asymptotic behaviors. An individual equation for the stop distances was also proposed, based on the yield stress. Yabuchi (2004), also working with Newtonian and Herschel-Bulkley fluids, separated the flow in only an inertial regime and one viscous regime, solving the shallow water equations by the Pohlhausen method. Piau and Debiane (2005) applied the analytical results of Debiane (2000) in Bostwick consistometers and Balmforth et al. (2007) analyzed that same device through the shallow water approach and neglecting the inertial forces.
Matson and Hogg (2007) and Ancey and Cochard (2009) used the lubrication theory for Herschel-Bulkley dam-break flows. Matson and Hogg (2007) found asymptotic equations for the arrested state. Ancey and Cochard (2009) found equations for the tip position and surface position. They found good agreement with experimental data for calculating the shape surface and tip position for bigger times, i.e., for the viscous regime. However, in the first instances, the solution presented some errors, owing to the small ratio assumption. Hogg and Matson (2009) studied the approach to the arrested state of Herschel-Bulkley fluids in dam-break flows with steep slopes by approximating the free surfaces as Lambert-W functions. Dubash et al. (2009) used a spline method to construct the interface shape for any aspect ratio. They affirmed that the shallow water results are only reasonable for small yield stress fluids. Cochard and Ancey (2009) introduced a new experimental procedure for the 3-D surface reconstruction of dam-break flows. Finally, concerning other rheological aspects, Chanson et al. (2006) characterized dam-break flows of thixotropic fluids using three categories based on the initial jamming degree.
As can be seen, shallow water equations can predict the final shape of dam-break flows of non-Newtonian fluids, but care is needed for its application in the inertial phase of the flow. Shao and Lo (2003) presented a SPH (Smoothed Particle Hydrodynamics) model to simulate free surface flows. They simulated dam-break flows as test problem and, using the complete motion equations, they founded good agreement between their results and VOF solution. They applied their method to Newtonian and non-Newtonian fluids using the Cross and Bingham constitutive equations. They also mention that shallow water results are only applicable after a certain time from the initial dam-break, mainly, when the dam is high.
Experimental Procedures
All the experiments were conducted at the facilities of the Rheology Laboratory, Paulista State UniversityUNESP, Campus of Ilha Solteira. First of all, many rheological tests were performed to characterize Carbopol 940 aqueous solutions. All the Carbopol solutions were made using deionized water (with electrical conductance 0.4 µS/cm). Carbopol is a very hydrophilic powder and most care was necessary in its mixture with water. In fact, preparing Carbopol for rheological tests still needs a development of an adequate protocol (Ancey et al., 2007), because preparing it for commercial purposes produces many bubbles (NOVEON™, 1993) which is not permissible for rheological tests.
After calculating the necessary masses of Carbopol and deionized water, the powder was gently dispersed on the water surface. After that, its recipient was left at rest until total Carbopol dissolution (which takes between 8 to 24 hours). This procedure diminishes the possibility of Carbopol entrapment and the production of gas bubbles.
Carbopol only exhibits its true rheological properties when it is fully neutralized (pH = 7.0). For the neutralization, a portion of NaOH 3.2 times the mass of Carbopol was necessary. This value was found by a titration procedure of many samples with different concentrations. After the complete dissolution of Carbopol into the water, the NaOH solutions were slowly mixture until reaching complete neutralization.
Rheological tests were performed using a Brookfield Engineering R/S Rheometer (with coaxial cylinders bobs and spindles), with controlled shear stress, varying the Carbopol mass concentration, the pH value and temperature. During these tests no evidence of slip material at the inner cylinder was observed. Furthermore, thixotropy tests were also carried out imposing loading and unloading cycles on samples. For the problem herein, thixotropy found was negligible. For more information about the tests, their observations and the determination of experimental uncertainties, please reference Minussi (2007).
The dam-break tests were made using an acrylic channel. The channel was composed of a barricade, activated by a hydraulic piston, and a reservoir. A guide grid, spaced by 5 mm, was positioned at one of the lateral walls. More details are presented in Fig. 1.
Five different Carbopol 940 mass concentrations, C, were used and its rheometric properties are shown in Table 1. Three samples of each fluid were used to calculate the total uncertainty, ut. The hydrogen potential, pH, and the temperature, T, were also controlled.
Thirteen tests were performed on the channel, varying the initial reservoir high, H0, and the fluid used. In Table 2 the dam-break tests are resumed.
Before each test, the correct amount of fluid was introduced at the reservoir and the channel was verified to make sure it was in the horizontal position. For tests 1 to 8 a ball level was used and for tests 9 to 13 a laser inclinometer was used. With this last instrument, a very small inclination of 0.13º ascendant on the previous tests was noted. The dam wall opening time was about 0.2 s. The fluid was then released and its flow started. The flow was filmed with a JVC (GY DV 500) digital camera. The measures of the channel, the initial height and the concentration of Carbopol were chosen to be of the same order as those used by Debiane (2000).
Numerical Simulations
The numerical simulations were conducted using the VOF (Volume of Fluid Method) in a two dimensional domain through the numerical package ANSYS CFX software.
The different fluids, i.e., the carbopol aqueous solution and the air, were considered to be, respectively, a homogeneous liquid mixture and a pseudo pure substance, both immiscible and separated by an interface. A volume fraction variable was defined as being the ratio of the volume of the heavier phase in a computational cell divided by its total volume. For instance, in the case of two phases, if a cell contains both phases, i.e. the interface passes through such a cell, the volume fraction will be a value between 0 and 1, in the other cells the volume fraction will be equal to 0 (lighter phase: air) or 1 (heavier phase: carbopol solution). The method is divided into two steps, first there is the reconstruction step (algorithm), in which the interface is built, and second the propagation step (algorithm) propagates the interface (Scardovelli and Zaleski, 1999).
The equations solved were the mass conservation equation:
and the momentum conservation equation:
where η is the apparent viscosity; u is the velocity vector; S is the source term and p is the pressure.
However, ρ and η corresponds to average values in the control volumes with volume fraction different from 1 and 0, and are calculated as:
where i represents each phase; N is the total number of phases and VF is the volume fraction.
From Eqs. (3), (5) and (9) the use of the Herschel-Bulkley model sets the liquid viscosity as:
To avoid non physical behavior, ANSYS (2005) recommend, for power-law fluids
the following modification:
where
inf is an imposed inferior limit of the strain rate;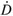 sup is a superior one and α is an auxiliary variable defined as: α = 2(-II)-1/2.
sup is a superior one and α is an auxiliary variable defined as: α = 2(-II)-1/2.
In this work, this model is extended to the yield stress term in the following manner:
Such modification prevents the numerical code from having convergence problems when
II tends to zero.As already mentioned, the beginning of the flow is dominated by inertial effects and as time passes, the viscous dissipation slows it until it stops, when the shear stresses are near the yield stress. Note that this is an idealized model, in which the yield stress exists and there is no surface tension. In the numerical simulations, there is no dam and the flow begins by the pressure difference.
The transient terms were approximated by a totally implicit second order scheme. Weighted Upstream Differencing Scheme (WUDS scheme) was used as the interpolation function. The pressure-velocity coupling was accomplished using a co-located grid and the solution of the linear equations system was made by the ILU MG factorization (Incomplete Lower Upper MultiGrid).
The simulations were made using a rectangular domain which was 1900 mm long, 145 mm high and 5 mm wide. A 5 mm regular grid was used, totalizing 11020 cubic volumes. All the simulations were made using a time step of 0.001 s, total time equal to 1.5 s and convergence criteria with a maximum residuum of 10-4 (based on ANSYS, 2005). Mesh refinement and convergence criteria tests are shown in the end of the next section.
Results and Discussions
The dam-break tests were undertaken using the previously explained methodology. The results were compared with numerical simulations and two literature shallow water solutions.
The flow development was analyzed through the obtainment of the tip distance with time (i.e. front wave position for 0.1 s time intervals). For each test, sixteen frames (0 to 1.5 s) were taken and the front wave positions were obtained with the help of the grid installed at the flume. The data were then compared with the CFX and the results of Debiane (2000) and Yabuchi (2004). The numerical values were defined as the maximum horizontal distances of the wave front for volume fractions equals to 0.5. And, the experimental uncertainty on the front position could be as high as 5 mm.
Kinematic and run out of the wavefront
Figure 2 shows the longitudinal view of Test 1 taken as four shooting frames and, above each one, the corresponding numerical result from CFX software. Figures 3 to 7 contain the front wave position with time for all tests.
Figures 3 and 4 show that Tests 2, 4 and 5 present only one part of the experimental curve. This is due to the wave front having reached the end of the camera focus area earlier than the end of the experiment, i.e., earlier than 1.5 s.
Analyzing Figs. 2 to 7, the numerical results can be observed to have reached bigger horizontal distances than the experimental ones in most of the tests. One of the causes may be the friction on the lateral walls which was not included in the numerical simulations. It is important to notice that a small amount of fluid is retained in the dam and this reduces the total amount of fluid. However, an analysis of the opening law influence on the solution is out of the scope of this work. The non inclusion of the gate influence was intentional as the literature solutions used here do not include it. For the same reason, the surface tension was also not included.
At the beginning of the flow, the difference between the numerical and experimental results is reduced. One of the possible causes is the difficulty that the numerical code has to converge the first times. The dam-break is artificially made through the pressure difference complicating the interface convergence. This fact could balance the previous mentioned effect of the restraint of fluid at the dam wall.
The experimental data is not completely correlated by the theoretical curves. In fact, the division of the flow in distinct phases, similar to that proposed by Debiane (2000) and Yabuchi (2004), is done to enable shallow water equations liable to be analytically solved. The viscous dissipation becomes, after the release, more important in a continuous way, making it difficult to characterize the time when an inertial phase ends and a viscous one begins. For the same reason, Debiane's results were in better agreement than those of Yabuchi's, since Debiane's used two viscous regimes, instead of just one used by Yabuchi (2004), making the transition of inertial to viscous regime more realistic.
However, it is shown that the numerical approach presented in this paper in the majority of the situations is within the uncertainty margin of the experimental data. This reveals that the shallow water solutions presented herein have some difficulties in dealing with this problem. The major cause of these discrepancies is the assumption of small aspect ratio, ε << 1, which is not reasonable in the very beginning of the flow.
It is necessary to notice two things: the overall behavior obtained in the experiments is very similar to those using shallow water, i.e., they achieve the arrested state asymptotically and the experimental values were evaluated at the channel wall and not at the flow centerline. So, front wave position values smaller then the real ones were expected to be obtained, contributing to the difference between shallow water solutions and experimental values. Lateral friction and gate influences also contribute to these differences.
Debiane (2000) obtained a stop distance equation, also called run out equation, which produces results different from those achieved by the evolution developments (shown in Figs. 3 to 7). This equation is not affected by the problems of applying shallow water equations at the beginning and the results are in good agreement with the experimental values. Such results are shown in Table 3.
There are some implications in using the word "stop". First, the arrested state is obtained, theoretically, at t →∞, i.e., asymptotically. But, in the experiments it is difficult to affirm if the flow is completed arrested or is in very slow motion (only detectable over many hours or even days). This difficulty increases in horizontal channels, because the effect of gravity is small.
Wave front velocity
Now, it is important to focus on the beginning of the flow. With the "instantaneous" removal of the barricade the fluid motion is initiated by the pressure gradient. The flow is in the inertial regime, which means that the dynamics are governed by a balance between inertia and pressure gradient force terms. A very big transient behavior happens and the velocity field is almost vertical. This can be seen in Fig. 8.
It can be confirmed that at the beginning of the flow, there is a significant vertical velocity. With time, the horizontal velocity components tend to become increasingly significant and, of course, the local aspect ratio will be smaller. It can be concluded that the application of shallow water equation at the beginning of the flow introduces errors that propagate with time.
Effect of yield stress apparent viscosity
Analyzing the numerical results of Table 2 it is possible to observe that the tests with fluid 3 have reached the arrested state earlier followed by fluids 5, 4, 1 and 2. In a preliminary analysis it is plausible to conclude that such behavior is the result of the yield stress. However, by examining the behavior of the apparent viscosity with the strain rate showed in Fig. 9, we can observe that fluid 3 has the biggest apparent viscosity, followed by fluids 5, 4, 1 and 2.
The Herschel-Bulkley model is nonlinear so, to analyze the conjugate effect of yield stress and the other parameters, more tests would be necessary using hypothetic fluids. Although possible to use the experimental apparatus presented here, such analysis is outside the scope of this work.
Strain rate field
Figure 10 shows the strain rate field of test 5 for some time intervals.
Although there are small viscosities, one can infer that a big amount of fluid stays at rest. It can also be seen that, in the front vicinity, the fluid is almost totally sheared and, with time, a plug zone begins to be more and more significant. This result agrees with Ancey and Cochard (2009). But the asymptotic nature of the flow raises difficulties in the numerical code, when the yield stress is achieved and creates a very big local viscosity. The usage of limiting the strain rates, Eq. (14), prevents the solution from diverging, though for physical times of order of 1 s more computational time spent was observed.
Hydrostatic pressure condition
It is also necessary to verify if the hydrostatic pressure condition has been respected. Figure 11 shows the pressure field at the beginning of Test 5 flow.
The pressure field is not hydrostatic, mainly in the front wave, but the major part of the flow, has an almost hydrostatic pressure field.
Convergence and Mesh Tests
To complete the results analysis convergence and mesh tests were performed. Two tests were performed: test 5, which presented the biggest stop distance, and test 6, with the smallest one. The convergence criteria tests were performed using a maximum residuum of 10-5. The mesh tests were performed using two grids: 1 mm grid and a 2.5 mm one. A smaller time step of 0.0005 s was used. The results are showed next in Figs. 12 and 13.
Concerning the convergence tests, no significant differences were found. However, we can see some differences on the current numerical results and mesh refinement tests showed in Figs. 13, mainly, on the results of test 6. We calculated the position difference between the horizontal wave front of these tests, and the maximum was 18.63% at 1.5 seconds (for the 1 mm grid) and 8.61% at 1.5 seconds (for the 2.5 mm grid), in comparison with the normally used mesh. Although some discrepancies can be seen at the end of the 1 mm mesh simulation at time 1.0 second, this is possibly the result of a difficult local time step convergence at that point in time leading to the difference of 18.63%.
Taking these arguments into consideration, one conclusion that can be drawn is that, although a more refined mesh would have theoretically improved the numerical results, the computational time spent would not be acceptable for the objectives of this work.
Analyzing all the results, the assumption of no vertical velocity, mainly at the flow beginning, seems to be the most critical assumption of shallow water approximation. It also appears that the simplifications used on the numerical experiments were reasonable and for the experimental conditions herein, the shallow water approximation must be reviewed.
Conclusions
The major conclusion of this study is that the complete numerical solutions produced better results than the shallow water theoretical solutions. The necessity of knowledge of the limits of shallow water application and the physical parameters of each problem are emphasized (as also mentioned by Dubash et al., 2009).
The problem with using shallow water approximation is more crucial at the beginning of the flow. The errors inset in the application of shallow water equations in the problem of dam-break, in the early stages, propagate such that the range of distance traveled is considerably higher when compared with the equations of the mathematical model presented in Eqs. (5) to (9) and the experimental results referenced to in this article. One solution could be the usage of another theory in that regime.
However, it is necessary to mention that shallow water approximation has been used for a long time and it is useful in many applications. Shallow water approximation can be used especially in primary studies of complex problems. In all problems in which shallow water conditions are verified, their use should be implemented.
Acknowledgements
The authors would like to thank CNPq for financial support and for the grant awarded to the main author and also FAPESP for its financial support that allowed the authors to equip their laboratory.
Paper received 20 March 2010.
Paper accepted 5 September 2011
Technical Editor: Mônica Naccache
- Ancey, C., Balmforth, N. and Frigaard, I., 2007, "Visco-plastic fluids: from Theory to Application", J. of Non-Newton. Fluid Mech., Vol. 142, pp. 1-3.
- Ancey, C. and Cochard, S., 2009, "The dam-break problem for HerschelBulkley viscoplastic fluids down steep flumes", J. of Non-Newton. Fluid Mech., Vol. 158, pp. 18-35.
- ANSYS Inc. 2005, "ANSYS CFX-Solver, Release 10.0 ANSYS CFX, Release 10.0: Installation and Overview", ANSYS Inc.
- Balmforth, N.J., Craster, R.V., Perona, P., Rust, A.C. and Sassi, R., 2007, "Viscoplastic dam breaks and the Bostwick consistometer", J. of Non-Newton. Fluid Mech., Vol. 142, pp. 63-78.
- Chanson, H., Jarny, S. and Coussot, P., 2006, "Dam break wave of thixotropic fluid", J. of Hydraulic Eng., Vol. 132, No. 3, pp. 280-293.
- Cochard, S., and Ancey, C., 2009, "Experimental investigation of the spreading of viscoplastic fluids on inclined planes", J. of Non-Newton. Fluid Mech., Vol. 158, pp. 73-84.
- Coussot, P., 1997, "Mudflow rheology and dynamics", Ed. A. A. Balkema, Rotterdam, Netherlands, 255 p.
- Debiane, K., 2000, "Hydraulics of laminar free surface flow in channel for viscous or Viscoplastic models: uniform regime, gradually varied flow, and dam break problem" (In French), Ph.D. Thesis, University of Joseph Fourier-Grenoble I, Grenoble, France, 275 p.
- Dubash, N., Balmforth, N.J., Slim, A.C. and Cochard, S., 2009, "What is the final shape of a viscoplastic slump?", J. of Non-Newton. Fluid Mech., Vol. 158, pp. 91-100.
- Friggard, I.A. and Nouar, C., 2005, "On the usage of viscosity regularization methods for viscoplastic fluid flow computation", J. of Non-Newton. Fluid Mech., Vol. 127, pp. 1-26.
- Hogg, A.J. and Matson, G.P., 2009, "Slumps of viscoplastic fluids on slopes", J. of Non-Newton. Fluid Mech., Vol. 158, pp. 101-112.
- Huang, X. and García, M.H., 1998, "A Herschel-Bulkley model for mud flow down a slope", J. of Fluid Mech., Vol. 374, pp. 305-333.
- Matson, G.P. and Hogg, A.J., 2007, "Two-dimensional dam break flows of Herschel-Bulkley fluids: The approach to the arrested state", J. of Non-Newton. Fluid Mech., Vol. 142, pp. 79-94.
- Minussi, R.B., 2007, "Dam break problems experimental and numerical study to preview the front velocities of hiperconcentrated materials" (In Portuguese), Master Dissertation, Department of Mechanical Engineering, São Paulo State University, Ilha Solteira, SP, Brazil, 128 p.
- Møller, P.C.F., Mewis, J. and Bonn, D., 2006, "Yield stress and thixotropy: on the difficulty of measuring yield stresses in practice", Soft Matter, Vol. 2, pp. 274-283.
- NOVEON™ The specialty chemicals innovator©, 1993, "Dispersion techniques for carbopol® resins", Available at: <http://www.noveon.com>
- Papanastasiou, T.C., 1987, "Flows of materials with yield", J. of Rheology, Vol. 31, No. 5, pp. 385-404.
- Piau, J.M. and Debiane, K., 2005, "Consistometers rheometry of power law viscous fluids", J. of Non-Newton. Fluid Mech., Vol. 127, pp. 213-214.
- Roberts, G.P. and Barnes, H.A., 2001, "New measurements of the flowcurves for carbopol dispersions without slip artefacts", Rheological Acta, No. 40, pp. 499-503.
- Shao, S. and Lo, E.Y.M., 2003, "Incompressible SPH method for simulating Newtonian and Non-Newtonian flows with a free surface", Advances in Water Resources, Vol. 26, pp. 787-800.
- Yabuchi, S.T., 2004, "A theoretical-experimental study for the determination the front velocity of mud flowing in channels" (In Portuguese), Master Dissertation, Department of Civil Engineering, São Paulo State University, Ilha Solteira, SP, Brazil, 84 p.
- Scardovelli, R. and Zaleski, S., 1999, "Direct numerical simulation of free-surface and interfacial flow", Annual Rev. of Fluid Mech., Vol. 31, pp. 567-603.
- Whitham, G.B., 1954, "The effects of hydraulic resistance in the dam break problem", Proceedings of the Royal Soc. of London, Vol. A, pp. 399-407.
Publication Dates
-
Publication in this collection
01 Aug 2012 -
Date of issue
June 2012
History
-
Received
20 Mar 2010 -
Accepted
05 Sept 2011

































