Abstract
The use of numerical simulation in the design and evaluation of products performance is ever increasing. To a greater extent, such estimates are needed in a early design stage, when physical prototypes are not available. When dealing with vibro-acoustic models, known to be computationally expensive, a question remains, which is related to the accuracy of such models in view of the well-know variability inherent to the mass manufacturing production techniques. In addition, both academia and industry have recently realized the importance of actually listening to a products sound, either by measurements or by virtual sound synthesis, in order to assess its performance. In this work, the scatter of significant parameter variations on a simplified vehicle vibro-acoustic model is calculated on loudness metrics using Monte Carlo analysis. The mapping from the system parameters to sound quality metric is performed by a fully-coupled vibro-acoustic finite element model. Different loudness metrics are used, including overall sound pressure level expressed in dB and Specific Loudness in Sones. Sound quality equivalent sources are used to excite this model and the sound pressure level at the driver's head position is acquired to be evaluated according to sound quality metrics. No significant variation has been perceived when evaluating the system using regular sound pressure level expressed in in dB and dB(A). This happens because of the third-octave filters that averages the results under some frequency bands. On the other hand, Zwicker Loudness presents important variations, arguably, due to the masking effects.
sound quality; vibro-acoustic model; finite element method; Monte Carlo analysis
TECHNICAL PAPERS
IVDepartment of Mechanical Engineering, São Carlos School of Engineering, University of São Paulo, Av. Trabalhador Sancarlense 400, 13566-590, São Carlos/SP, Brazil mgoncalv@sc.usp.br
ABSTRACT
The use of numerical simulation in the design and evaluation of products performance is ever increasing. To a greater extent, such estimates are needed in a early design stage, when physical prototypes are not available. When dealing with vibro-acoustic models, known to be computationally expensive, a question remains, which is related to the accuracy of such models in view of the well-know variability inherent to the mass manufacturing production techniques. In addition, both academia and industry have recently realized the importance of actually listening to a products sound, either by measurements or by virtual sound synthesis, in order to assess its performance. In this work, the scatter of significant parameter variations on a simplified vehicle vibro-acoustic model is calculated on loudness metrics using Monte Carlo analysis. The mapping from the system parameters to sound quality metric is performed by a fully-coupled vibro-acoustic finite element model. Different loudness metrics are used, including overall sound pressure level expressed in dB and Specific Loudness in Sones. Sound quality equivalent sources are used to excite this model and the sound pressure level at the driver's head position is acquired to be evaluated according to sound quality metrics. No significant variation has been perceived when evaluating the system using regular sound pressure level expressed in in dB and dB(A). This happens because of the third-octave filters that averages the results under some frequency bands. On the other hand, Zwicker Loudness presents important variations, arguably, due to the masking effects.
Keywords: sound quality, vibro-acoustic model, finite element method, Monte Carlo analysis
Introduction
The engine-related interior noise in a vehicle is a key element in the customer's perception of the vehicle's quality, sportiveness, robustness, among others (de Oliveira et al., 2010). Interior cavity structure-induced noise and vibration applications, such as engine noise in a vehicle, can be studied as a vibro-acoustic problem.
The need for a better understanding of vibro-acoustic system performance leads to the necessity of predicting its behavior in an early design stage, usually by means of numerical simulation (Van de Auweraer et al., 2007). However, vibro-acoustic models are known to be computationally expensive, mainly if the frequency range envelope is pushed to higher frequencies, which leads to finer meshes and, consequently, more degrees-of-freedom. A question remains, which is related to the accuracy of such models in view of the well-known variability inherent to the mass manufacturing production techniques.
Products on the scope of this analysis, such as vehicles, may present considerable variations (Gallina et al., 2010; Farkas et al., 2010) which are due to dimensional tolerances, assembly, non-linearities and, even, changes of the environmental conditions which might affect the acoustic properties of the air. More recently, both the academia and industry have realized the importance of actually listening to a products sound, either by measurements or by virtual sound synthesis, in order to assess performance (Vorländer, 2011).
In addition, a car often sounds like a car! One would expect a reasonably small variation on performance parameters of a group of cars of the same brand and model, given that even different vehicles of the same range can present a similar behavior (Brizon & Medeiros 2012). On the other hand, the performance parameters can be designed to be more sensitive to such variations, which is the case of the parameters selected in this paper. It is important to notice that, in contrast with Brizon and Medeiros (2012), the sound quality metrics used in this work are calculated for stationary operating conditions, resulting in a fixed harmonic excitation, which will lead to greater variations when compared to run-ups or any other transient excitation. That has to do with the way humans perceive complex sounds. Although the human ear is a magnificent transducer, capable of distinguishing small shifts in frequency, volume, duration and so on, there are specific mechanisms that play important roles in shaping the way we listen, e.g. the masking and cancellation effects that interfere with the way we perceive sound made up of multiple harmonic components (Zwicker and Fastl, 1999), which is the case of vehicle engine noise. Considering that a particular harmonic component is highly amplified by one of the systems resonance, and considering that physical parameters variations will shift that resonance frequency, it is clear that such dominant component will lose strength, revealing other aspects of the complex sound stimulus that could have been masked before.
Therefore, this paper presents a study that aims at addressing these issues. In order to do so, the scatter of significant parameter variations on vibro-acoustic models is calculated on the sound quality space. This mapping is performed by a finite element (FE) model built in LMS Virtual.Lab and the various simulations are managed by the software Optimus. This fully-coupled vibro-acoustic FE model is described in the section referred to as Vibro-Acoustic Model. The Sound Quality (SQ) metrics used to evaluate the system outputs are briefly introduced in the section referred to as Sound Quality Metrics. Relevant SQ metrics can only be calculated when the system is excited by a signal input that reassembles the real excitation, in order words, a SQ Equivalent source. These input signals are generated by Virtual Car Sound (VCS), a software developed by LMS International to simulate engine sound in real-time operation based on Transfer Path Analysis (TPA) models that can be experimental, numerical or hybrid. According to Fig. 1, the VCS provides the inputs  and
and  to the FE vibro-acoustic model. These force inputs are based on real engine mount forces, therefore resembling a real engine noise composed of multiple harmonic components with relevant amplitude and phase relations.
to the FE vibro-acoustic model. These force inputs are based on real engine mount forces, therefore resembling a real engine noise composed of multiple harmonic components with relevant amplitude and phase relations.
The main structural paths at the vehicle firewall are then excited. The sound pressure level at the driver's head position  (the FE model output in Fig. 1) is acquired and treated to calculate the SQ metrics. The SQ metrics for the nominal model are discussed in the Sound Quality Metrics section. The sound quality scattering due to vibro-acoustic system variability is assessed through the Monte Carlo method in the section referred to as Variability Analysis. Important conclusions on the performance variability considering not only the sound pressure level expressed in dB and dBA, but also Zwicker Loudness, an important SQ metric, are drawn clarifying some of the design trade-offs when developing conceptual models for vibro-acoustic performance analysis.
(the FE model output in Fig. 1) is acquired and treated to calculate the SQ metrics. The SQ metrics for the nominal model are discussed in the Sound Quality Metrics section. The sound quality scattering due to vibro-acoustic system variability is assessed through the Monte Carlo method in the section referred to as Variability Analysis. Important conclusions on the performance variability considering not only the sound pressure level expressed in dB and dBA, but also Zwicker Loudness, an important SQ metric, are drawn clarifying some of the design trade-offs when developing conceptual models for vibro-acoustic performance analysis.
Nomenclature
K = stiffness matrix
D = damping matrix
M = mass matrix
F = load vector
I = identity matrix
p = vector of nodal acoustic pressures
u = vector of structural displacements
q = vector of the modal amplitudes
Greek Symbols
 = frequency
= frequency
 = fluid density
= fluid density
 = eigenvectors
= eigenvectors
 = diagonal matrix of uncoupled natural frequencies
= diagonal matrix of uncoupled natural frequencies
 = modal damping matrix
= modal damping matrix
Subscripts
a = relative to acoustical terms
c = relative to coupling terms
s = relative to structure
n = number of DoFs (degrees-of-freedom)
L = left
R = right
Superscripts
T = transpose
Vibro-Acoustic Model
The system under investigation consists of a scaled simplified car geometry, with rigid acoustic boundary conditions and a flexible bi-partitioned firewall (Fig. 1). The firewall is considered as a 2 mm thick aluminum plate, clamped on its borders and the central pillar that connects both partitions is an aluminum beam of section 25.4 x 25.4 mm. The air is concealed inside the cavity which has no openings and is excited only via the firewall, with no additional acoustic sources. Two structural input points are selected, one on each firewall partition, and an acoustic pressure point, near the driver´s head position, is the system output.
Vibro-acoustic systems can be modeled using Computer Aided Engineering (CAE) tools such as FE and/or boundary element (BE) methods. The present case study requires not only the fluid load on the structure, but also the interaction between the structural vibrations and the pressure field. In other words, the vibro-acoustic model should be fully coupled. To cope with this, a coupled vibro-acoustic FE/FE modeling approach is adopted.
One of the coupled FE/FE formulation is the Eulerian, in which the structural degrees of freedom (DoFs) are displacement vectors, while the acoustic DoFs are expressed as scalar functions. The latter is usually the acoustic pressure, but can also be the fluid velocity potential. If pressure is adopted, the system of equations yields non-symmetrical mass and stiffness matrices, posing a disadvantage to FE solvers. The choice of velocity potential as acoustic DoF also presents a drawback, as the vibro-acoustic coupling terms populate the damping matrix, yielding a symmetric but complex model, which is computationally more expensive than the non-symmetric one (Pan and Bies, 1990; Morand and Ohayon, 1995). Eventually, the modal base resulting from the non-symmetric eigenproblem can easily be handled by the modeling procedure, as will be described in more detail in the next section. Therefore, a displacement/pressure Eulerian formulation is adopted hereafter.
A first step in the FE modelling of vibro-acoustic systems is the definition of appropriate meshes for the acoustic and structural components. Coincident structural and acoustic meshes are adopted over the coupling boundary resulting in a simplified procedure. The frequency range of interest is limited to 0-500 Hz to reduce the computational effort during the modeling procedure. It may not be representative for all interior acoustic problems, but is sufficient to demonstrate the proposed technique and to provide general insights. Moreover, this choice is not a limiting factor, since the methodology employed hereafter is valid as far as FE models can be used.
The size of the structural elements is chosen such that the highest-order mode is represented by at least 6 linear elements. The structural mesh has 512 4-noded shell elements, yielding 3712 DoFs since the borders of the firewall are clamped. The chosen 4-node shell element was an isoparametric quadrilateral element with the evaluation of the forces at the centroid of the element (QUAD4). The element type chosen for the acoustic mesh is the 8-noded brick element. With respect to the element size, this acoustic model exhibits a minimum of 6 linear elements per wavelength up to 500 Hz. The total number of acoustic DoFs is 69272. The structural and acoustic meshes are depicted in Fig. 2.
In a coupled FE/FE approach, the effect of the fluid on the structure dynamics can be considered as a pressure load on the wet surface. For a system with nS structural DoFs and na acoustic DoFs, the structural differential equation takes the following form:
where Ks, Ds and Ms are, respectively, the stiffness, damping and mass matrices of the structural component, KC
are, respectively, the stiffness, damping and mass matrices of the structural component, KC
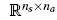 is the coupling matrix,
is the coupling matrix, 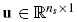 is the vector of structural displacement DoFs,
is the vector of structural displacement DoFs, 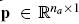 is the vector of nodal acoustic pressures and
is the vector of nodal acoustic pressures and 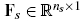 is the structural load vector.
is the structural load vector.
In a similar way, the structural vibrations provide an acoustic velocity input and therefore must be taken into account in the acoustic model as:
where  and
and  are the acoustic stiffness, damping and mass matrices,
are the acoustic stiffness, damping and mass matrices,  is the coupling matrix and
is the coupling matrix and 
 is the acoustic load vector. For the sake of brevity, any frequency dependent function `
is the acoustic load vector. For the sake of brevity, any frequency dependent function ` ' is represented just as
' is represented just as  hereafter.
hereafter.
Using the relation  (de Oliveira et al., 2008), where
(de Oliveira et al., 2008), where  is the fluid density, the combined system of equations, known as the Eulerian FE/FE model, yields:
is the fluid density, the combined system of equations, known as the Eulerian FE/FE model, yields:
Based on Eq. (3) it is clear that the resulting vibro-acoustic system is coupled, though it is no longer symmetric. As a consequence of such non-symmetric nature, the solution of the associated undamped eigenproblem is computationally more demanding and results in different left and right eigenvectors:
where  is the index of the coupled natural frequency
is the index of the coupled natural frequency  and
and  and
and  are, respectively, the left and right coupled modes.
are, respectively, the left and right coupled modes.
Moreover, it has been indicated (Luo and Gea, 1997) that, for the Eulerian formulation, the left and right eigenvectors, can be related as:
where  and the indexes
and the indexes  and
and  represent, respectively, the acoustic and structural DoFs.
represent, respectively, the acoustic and structural DoFs.
A common practice in solving such vibro-acoustic problems is the use of component mode synthesis (CMS). It consists of expanding the structural DoFs in terms of a set of  uncoupled structural modes
uncoupled structural modes  (without any acoustic pressure load along the coupling interface), as well as expanding the acoustic DoFs in terms of a set of
(without any acoustic pressure load along the coupling interface), as well as expanding the acoustic DoFs in terms of a set of  uncoupled acoustic modes
uncoupled acoustic modes  (acoustic boundaries considered rigid at the wet surface). The structural and acoustic expansions become, respectively,
(acoustic boundaries considered rigid at the wet surface). The structural and acoustic expansions become, respectively,
where  is the vector of modal amplitudes related to the structural DoFs,
is the vector of modal amplitudes related to the structural DoFs,  is the vector of modal amplitudes related to the acoustic DoFs,
is the vector of modal amplitudes related to the acoustic DoFs,  is the structural modal matrix,
is the structural modal matrix, 
 is the acoustic modal matrix and r is the index representing the number of the mode.
is the acoustic modal matrix and r is the index representing the number of the mode.
Substituting the component mode expansions in Eqs. (7) and (8) into Eq. (3) and pre-multiplying the structural and acoustic parts of the resulting matrix equation, respectively, with the transpose of the structural and acoustic modal vectors yields the undamped modal representation:
The homogeneous system of equations related to Eq. (9) can be written as:
Since each uncoupled mode is normalized with respect to the uncoupled mass matrices, Eq. (10) yields:
where  and
and  are, respectively, the structural and acoustic diagonal matrices of uncoupled natural frequencies.
are, respectively, the structural and acoustic diagonal matrices of uncoupled natural frequencies.
Equation (11) still results in a non-symmetric eigenproblem and is therefore expensive to solve. The first line of Eq. (11) leads to:
Applying the substitution  in Eq. (12) yields:
in Eq. (12) yields:
Using Eq. (13) it is possible to rewrite Eq. (11) as a symmetric system of equations in  :
:
where
The coupled modal vector  , resulting from the eigenproblem associated with Eq. (14) on
, resulting from the eigenproblem associated with Eq. (14) on  , can be interpreted as the left eigenvector
, can be interpreted as the left eigenvector  of the eigenproblem in Eq. (5) on
of the eigenproblem in Eq. (5) on  . The right eigenvector
. The right eigenvector  can be retrieved using Eq. (6).
can be retrieved using Eq. (6).
Since the uncoupled bases  and
and  result from symmetric eigenproblems, solving Eq. (14) may seem less demanding when compared to the solution of Eqs. (4) and (5). However, the reduction on the computational effort is rather small, as to accurately represent the coupled modes, it is necessary to retain a higher number of uncoupled modes. Nevertheless, the advantage of this method is the possibility of using dedicated software for each component uncoupled modal analysis.
result from symmetric eigenproblems, solving Eq. (14) may seem less demanding when compared to the solution of Eqs. (4) and (5). However, the reduction on the computational effort is rather small, as to accurately represent the coupled modes, it is necessary to retain a higher number of uncoupled modes. Nevertheless, the advantage of this method is the possibility of using dedicated software for each component uncoupled modal analysis.
Eventually, the structural and acoustic DoFs  can be projected using the modal base (
can be projected using the modal base ( and
and  ) and the modal coordinate q using the following expansion:
) and the modal coordinate q using the following expansion:
Moreover, the left and right eigenvectors are normalized such that:
where  and
and  are, respectively, the identity, the squared coupled natural frequencies and the modal damping matrices.
are, respectively, the identity, the squared coupled natural frequencies and the modal damping matrices.
Applying the modal expansion described by Eq. (15) into Eq. (3) and pre-multiplying it by  , Eq. (3) can be re-written as
, Eq. (3) can be re-written as
The frequency response functions can be extracted from Eq. 19 applying Laplace transformation.
For the sake of illustration, the coupled modes at 355 Hz and 482 Hz are depicted in Figs. 3 and 4.
In this work, two simultaneous structural inputs and one acoustic output are considered to calculate the frequency response function. The structural inputs, depicted as two spheres at the structural meshes in Fig. 2, represent the excitation from the motor mounting system. The acoustic output, shown as a sphere at the acoustic mesh in Fig. 2, resembles the driver's ear. The nominal noise transfer function, which is calculated considering a 3.0 mm-thick firewall and speed of sound equal to 340 m/s, is shown in Fig. 5a.
Sound Quality Metrics
Sound quality is the science that studies the human appreciation of a determined auditive stimulus. More than the mathematical interpretation of pressure signals, SQ and psychoacoustics try to correlate acoustic stimuli with hearing sensation (Zwicker and Fastl, 1999). It is also important to define which is the most appropriate set of metrics for each application. Loudness and Roughness have been indicated, among others, as the most important for engine noise (Gonzalez et al., 2003). In summary, Loudness is the term referring to the human perception of sound volume and Roughness is the term that correlates to how noticeable or annoying a sound is heard by the human ear. In this manuscript, the impact of the manufacturing process variability on Loudness is assessed through Monte Carlo analysis. The sound quality metric known as Loudness is properly introduced and discussed in the next subsection. Further information can be found in de Oliveira et al. (2009).
Specific Loudness and Zwicker Loudness
In spite of showing some correlation with actual human perception, and therefore being widely used, dB(A) measurements simply superimpose the effects of different frequency components on complex sound. In this sense, it neglects an important mechanism within the ear transduction of pressure fluctuations into signals to the brain, namely frequency masking (Zwicker and Fastl,1999).
Masking is related to the way hair-cells are positioned in the cochlea, so that a tonal (or narrow band) stimulus excites a specific region in the cochlea with effects on its neighborhood, turning them insensitive to another (lower level) excitation, which rises the concept of critical bands of excitation, measured in Barks. This phenomenon is responsible, for instance, for the way speech intelligibility is affected by background noise. The capability of recognizing a specific sound (test sound) in the presence of another one (masker sound) is very much related to their relations in level and spectral content. Indeed, masking can be interpreted as the variation on the hearing threshold curve to a test sound in the presence of a masker, i.e., if the test sound spectrum lies below the masked threshold it will be inaudible. This concep is illustrated in Fig. 6.
Figure 6(a) shows the magnitude of a periodic signal in the frequency domain. This signal is composed of three sinewave components, one of amplitude 0.10 Pa and two others of 0.05 Pa at 125 Hz, 500 Hz and 1000 Hz, respectively. Figure 6(b) shows the other periodic signal, in all aspects similar to the first one, but for the frequency of the third component that is of 160 Hz instead of 1 kHz. In that way, the energy content of both signals is the same, resulting in 82.4 mPaRMS. Figures 6(c) and (d) show both signals represented in third-octave plots, showing that the signal present on band #20 (1000 Hz) has migrated to band #11, which does not change the overall sound pressure level of 72.3 dB. The difference is, however, clear in Figs. 6(e) and (f), which show the Specific Loudness plots for both signals. While the signal shown in Fig. 6(a) has well spreaded frequency components, each one of them can be seen in the Specific Loudness plot, above each other's masking curves, resulting in 13.7 Sones. However, the second signal presents two frequency components that are close to each other, namely 125 and 160 Hz. As a result, the 160 Hz component with a smaller amplitude will lie under the former masking curve, which means that it will not be audible and will not compute for the overall Loudness, resulting in 9.93 Sones (27% less than the other signal).
From the available techniques, only the method developed by Zwicker and Fastl (1999) is valid to broadband excitation, with or without tonal components in free and diffuse fields. The first step in the numerical procedure consists in filtering the signal with critical band filters, followed by a masking check. In this stage, if the proceeding band level falls under the masking curve of the preceding one, this value is neglected; otherwise the value is kept. Following this procedure, the Specific Loudness graph is obtained with units Sones/Bark. The value for Zwicker Loudness (ZL) is defined as the integral of the Specific Loudness (SL) over Bark, with values expressed in Sones. The advantage of the Sones scale is its linear correlation with the human perception of volume, i.e., an acoustic stimulus of 8 Sones sounds twice as loud as a 4 Sones stimulus.
Figure 7 and Table 1 show the nominal curves (Specific Loudness) and values (Zwicker Loudness) for the six rpms studied in this paper. The harmonic content of the excitation forces used in four of these cases are shown in Fig. 5(b), namely, rpms 1, 2, 5 and 6. The other two are omitted for the sake of clarity. As mentioned before, the amplitude and phase relation of the harmonic excitation have been obtained with the aid of VCS.
Variability Analysis
Variability analysis plays an important role to study uncertainties in dynamical models. For instance, uncertainties related to structures excited by internal flow have been recently investigated by Ritto et al. (2011), uncertainties for hearing protector noise attenuation apparatus by Lima et al. (2010) and electrical uncertainties of passive/active structural vibration control have been numerically and experimentally studied by Santos and Trindade (2011).
In this work, variability analyses are carried out using the Monte Carlo methods. This strategy is the most straightforward sampling method to identify the sensitivity of the design to variations of the variables at any point in the design space. In this method, a number of simulations is performed by generating suitable random numbers and by observing the properties of the results. The parameter generation, model updating and analysis are managed by the software Optimus, which is capable of reading and changing the input files to the FE analysis as well as reading the outputs provided by Virtual.Lab and using the results to calculate the sound quality metrics in Matlab. A probabilistic approach has been used for modeling the variability of two parameters of the model under investigation. In this work, a normal distribution has been selected to describe the uncertainty of the firewall thickness and the speed of sound. The maximum allowed variation of these parameters is 10%. Moreover, a widely used Design of Experiment technique named Latin Hypercube (LH) sampling has been used to improve the efficiency of the sampling distribution. The LH sampling technique divides the design parameter space into n equidistant levels, where n is the number of simulations, guarantying in that way a good coverage of the whole multidimensional deign space. The evaluating points are obtained by selecting for each dimension a permutation of the levels and combining these permutations into a design. Figure 8 shows the selected design points and their distributions.
In this work, Sound Pressure Level (SPL) expressed in dB and dB(A), as well as Zwicker Loudness have been evaluated for variations on the firewall thickness and cavity's fluid speed of sound. The resulting noise transfer functions (between the driver hear position and the input forces) calculated for every design configuration (Fig. 8) are shown in Fig. 9, where the shaded area represents the collective magnitude range and the nominal case is highlighted. As it can be seen, there is a significant variation of the resonance frequencies, mainly due to the 10% variation in both parameters.
The results for the output parameters are summarized in Table 2 . Figure 10 shows the histograms for the four main contrasting results. It is known that the third-octave filters average the results under their frequency band. Because of this fact, small variations on the input parameters have little impact on the output responses. This is the case of dB and dB(A), which range in average 6.5% and 7.5% around the nominal value, respectively. On the other hand, the variation of the Zwicker Loudness is rather high, which is also clear from Fig. 10, ranging up to 37% from its nominal value. The main reason for that is arguably the masking effect, modeled in the Zwicker Loudness algorithm. Whenever there is an important order near to one of the vibro-acoustic system resonances, the parametric variation may change that resonance frequency bringing it closer to that order consideringly amplifying it, which might lead to the masking of neighboring ones; in dB calculations, all the orders will add up to the overall level, while in Zwicker Loudness, the masked orders will not be considered, resulting in high output variations for small input variations. It is important to stress that the present analyses are based on stationary operating conditions, i.e., invariant harmonic excitations, which are more sensitive to such variations than excitations of random or transient nature.
From the statistical point of view, Fig. 11 shows the mean square convergence analysis for the SLP values in dB(A) and dB, and Loudness in Sones. It is possible to observe that for all cases 400 simulations are enough to assure convergence. Despite that, the aforementioned statistical analyses consider all 1200 simulations performed.
Combining information from Figs. 7 and 10, it is possible to conclude that the system is more sensitive to variations in operating conditions where there is a clear dominance of a particular order and/or path, which is the case of 4200 rpm, in contrast with 1800 rpm. While the former has a clear low frequency dominating component, the latter presents a more spreaded combination of different orders that add up to the overall Loudness (as seen in Fig. 7). As a result, small variations on the system parameters result in a wider spread of either dB or Loudness metrics for 4200 rpm while it remains quite narrow for 1800 rpm, as depicted in Table 2.
Conclusions
In this work, the scatter of significant parameter variations on vibro-acoustic models is calculated on the sound quality space using Monte Carlo analysis. The mapping from the system parameters to sound quality metrics is performed by a fully-coupled vibro-acoustic finite element model built in LMS Virtual.Lab. The sound quality equivalent forces used to excite the FE model come from Virtual Car Sound, a software developed to simulate engine sound in real-time operation. Two of the main paths have been selected as inputs for the vibro-acoustic model, and the pressure at the driver's head position as the output. Sound quality metrics have been calculated using this output pressure.
The sound quality scattering due to vibro-acoustic system variability has been assessed by Monte Carlo analysis with the aid of Optimus, a simulation management software with embedded statistics and optimizations tools. A normal distribution has been selected to describe the uncertainty of the firewall thickness and the speed of sound in the vibro-acoustic model. The maximum allowed variation of these parameters, including both structural and acoustic properties, is 10%.
No significant variation has been perceived when evaluating the overall SPL in dB and dB(A), which is due to the fact that third-octave filters average the results under each frequency band. On the other hand, Zwicker Loudness presents important variations, up to 37%, which is related to the masking effects; if a certain order amplitude increases, it may mask the neighboring orders, meaning that those will not be computed for the Loudness calculation, resulting in a significant change in this function value. That could mean engineers have to be carefull when analysing loudness from sharp simulation data, as small uncertainties in important system parameters can lead to big variations on the numerical estimates. It is also true that the present study has considered a rather lowly damped system excited with a harmonic signal, which both combined can be more sensitive to the selected parameter variations as a real vehicle application would do, but in any case it has raised awarness on the subjetc. The study of the influence of damping as well as the inlcusion of other sound quality metrics in this study are considered as future research topics.
Acknowledgements
This research has been supported by FAPESP (grants 10/02198-4 and 10/03556-1) which the authors gratefully acknowledge. The authors would also like to thank Charles Croufer (LMS South-America) and Maximilien Landrain (Noesis Solutions) for providing the software OPTIMUS used in this work.
Paper received 10 April 2012
Paper accepted 6 June 2012.
- Brizon, C.J.S., Medeiros, E.B., 2012, "Combining subjective and objective assessments to improve acoustic comfort evaluation of motor cars,'' Applied Acoustics, Vol. 73, pp. 913-920.
- de Oliveira, L.P.R., da Silva, M.M., Sas, P., Van Brussel, H., Desmet, W., 2008, "Concurrent mechatronic design approach for active control of cavity noise,'' Journal of Sound and Vibration, Vol. 314, No. 3-5, pp. 507-525.
- de Oliveira, L.P.R., Janssens, K., Gajdatsy, P., Van der Auweraer, H., Varoto, P.S., Sas, P., Desmet, W., 2009, "Active sound quality control of engine induced cavity noise,'' Mechanical Systems and Signal Processing, Vol. 23, No. 2, pp. 476-488.
- de Oliveira, L.P.R., Stallaert, B., Janssens, K., Van der Auweraer, H., Sas, P., Desmet, W., 2010, "NEX-LMS: A novel adaptive control scheme for harmonic sound quality control,'' Mechanical Systems and Signal Processing, Vol. 24, No. 6, pp. 1727-1738.
- Farkas, L., Donders, S., Schildermans, D., Moens, D., Vandepitte, D., 2010, "Optimisation study of a vehicle bumper subsystem with fuzzy parameters'', Proceedings of USD2010, Leuven, Belgium, pp. 5015-5026.
- Gallina, A., Lisowski, W., Pichler L., Stachowski, A., Uhl T., 2010, "Analysis of the natural frequency variability of a brake component by combining computer simulations with experimental testing'', Proceedings of USD2010, Leuven, Belgium, pp. 5117-5128.
- Gonzalez, A., Ferrer, M., De Diego, M., Piñero, G., Garcia-Bonito, J.J., 2003, "Sound quality of low-frequency and car engine noises after active noise control,'' Journal of Sound and Vibration, Vol. 265, No. 3, pp. 663-679.
- Lima, F.R., Gerges, S.N.Y., Zmijevski, T.R.L., Bender, D.F., Gerges, R.N.C., " Uncertainty calculation for hearing protector noise attenuation measurements by REAT method,'' Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol. 32, No. 1, pp. 28-36.
- Luo, J., Gea, H.C., 1997, "Modal sensitivity analysis of coupled acoustic - structural systems,'' Journal of Vibration and Acoustics, Vol. 119, pp. 545-550.
- Morand, H.J.-P. and Ohayon, R., 1995, "Fluid Structure Interaction'', J. Wiley & Sons.
- Noesis Solutions, 2011, "Optimus Theoretical Background'', Belgium.
- Pan, G. and Bies, D.A., 1990, "The effect of fluid structure coupling on the sound waves in an enclosure: theoretical part'', J. Acoust. Soc. Am., 2(1987), pp. 691-706.
- Ritto, T.G., Sampaio, R., Rochinha, F., 2011, "A Model uncertainties of flexible structures vibrations induced by internal flows,'' Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol. 33, No. 3, pp. 373-380.
- Santos, H.F.L., Trindade, M. A., 2011, "Structural vibration control using extension and shear active-passive piezoelectric networks including sensitivity to electrical uncertainties,'' Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol. 33, No. 3, pp. 287-301.
- Van der Auweraer, H., Janssens, K., de Oliveira, L., da Silva, M., Desmet, W., 2007, "Virtual prototyping for sound quality design of automobiles,'' Sound and Vibration, Vol. 41, pp. 26-30.
- Vorläander, M., 2011, "Virtual Acoustics'', Proceedings of the 18th International Congress on Sound and Vibration - ICSV18, Rio de Janeiro - Brazil, keynote lecture, 8 p.
- Zwicker, E., Fastl, H., 1999, "Psychoacoustics: Facts and Models,'' Second ed., Springer Series in Information Sciences, Heidelberg.
Loudness scattering due to vibro-acoustic model variability
Publication Dates
-
Publication in this collection
24 July 2013 -
Date of issue
2012
History
-
Received
10 Apr 2012 -
Accepted
06 June 2012



































