Resumos
Este artigo propõe a adoção de um modelo numérico prognóstico para estimar a variável "tempo de execução" para empreendimentos públicos de forma objetiva. O trabalho de campo consistiu na aplicação de métodos estatísticos para analisar dados de obras licitadas e executadas durante o período de 2006 a 2009 na Universidade Federal do Pará (UFPA). A análise de dados envolveu cálculos de regressões lineares e transformadas das funções. Após estratificação e tratamento inicial dos dados, os elementos adotados para construção do modelo final se restringiram a 102 obras de um total de 225 originariamente pesquisadas, resultando nos seguintes parâmetros estatísticos: coeficiente de correlação (R) de 0,899; coeficiente de determinação (R²) de 0,808; coeficiente de determinação ajustado (R² ajustado) de 0,796 e erro padrão (Se) de 0,41. Estes parâmetros indicam forte correlação linear entre as variáveis, indicando que 79,60% da variação do tempo para executar uma obra pública podem ser causadas pela variação, em conjunto, das variáveis área construída, custo orçado, capacidade técnica operacional do contratante, capacidade operacional da empresa, tipologia de serviço e estação do ano.
Modelagem; Tempo de execução; Obras Públicas; Correlação Linearizada; Modelo Numérico
This article proposes the adoption of a numerical prognosis model to estimate the variable "execution time" for public projects in an objective way. The field work consisted of the application of statistical methods for analyzing data from projects that were bid and contracted by the Federal University of Pará (UFPA) between 2006 and 2009.. Data analysis involved linear regression and transformed functions. After the stratification and initial treatment of the data, the evidence adopted for the construction of the final model was limited to 102 out of the 225 projects originally investigated, resulting in the following statistical parameters: correlation coefficient (R) of 0.899, coefficient of determination (R²) of 0.808, adjusted coefficient of determination (adjusted R²) of 0.796, and standard error (Se) of 0.41. These parameters show a strong linear correlation between the variables, indicating that 79.60% of the variability of the execution of a public project is jointly caused by variations in the gross floor area, the estimated cost, the operational technical capacity of the client organization; the operational capacity of the company; the type of service, and the season.
Modeling; Execution time; Public Projects; Linear Correlation; Numerical Model
ARTIGOS
Modelagem do tempo de execução de obras civis: estudo de caso na Universidade Federal do Pará
Modeling the execution time of construction projects: case study at the Federal University of Pará
Lêda Sílvia de Aguiar Lédo CoutinhoI; André Augusto Azevedo Montenegro DuarteII; Renato Martins das NevesIII; Benedito Coutinho NetoIV; Carlos Edilson de Almeida ManeschyV; Ana Maria Guerra Seráfico PinheiroVI
IPrefeitura do Campus Universitário. Universidade Federal do Pará. Rua Augusto Corrêa, n. 1, Guamá, Cidade Universitária Prof. José da Silveira Netto. Belém - PA - Brasil. CEP 66075-110. Tel.: (91) 3201-7517 Ramal 7517. E-mail: ledaledo@ufpa.br
IIFaculdade de Engenharia Civil, Instituto de Tecnologia. Universidade Federal do Pará. Tel.: (91) 3201-8200 Ramal 8200. E-mail: amonte@ufpa.br
IIIFaculdade de Engenharia Civil, Instituto de Tecnologia. Universidade Federal do Pará. Avenida Augusto Corrêa, s/n, São Brás. Caixa-Postal 8612. Belém - PA - Brasil. CEP 66075-970. Tel.: (91) 3201-7917. E-mail: neves@ufpa.br
IVCoordenação da Construção Civil Instituto Federal de Educação, Ciência e Tecnologia do Pará Avenida Almirante Barroso, 1155, Marco, Campus Belém. Belém - PA - Brasil. CEP 66093-020. Tel.: (91) 3201-1700 Ramal 1836. E-mail: benedito.coutinho@ifpa.edu.br
VFaculdade de Engenharia Mecânica, Instituto de Tecnologia. Universidade Federal do Pará. Rua Augusto Correia, n. 1, Guamá Belém - PA - Brasil. CEP 66075-010. Tel.: (91) 3201-7322 E-mail: cemaneschy@ufpa.br
VIUniversidade Federal do Pará, Instituto de Tecnologia. Rua Augusto Correa, Guama. Belém - PA - Brasil. CEP 66075-900. Tel.: (91) 3201-7254. E-mail: serafico@ufpa.br
RESUMO
Este artigo propõe a adoção de um modelo numérico prognóstico para estimar a variável "tempo de execução" para empreendimentos públicos de forma objetiva. O trabalho de campo consistiu na aplicação de métodos estatísticos para analisar dados de obras licitadas e executadas durante o período de 2006 a 2009 na Universidade Federal do Pará (UFPA). A análise de dados envolveu cálculos de regressões lineares e transformadas das funções. Após estratificação e tratamento inicial dos dados, os elementos adotados para construção do modelo final se restringiram a 102 obras de um total de 225 originariamente pesquisadas, resultando nos seguintes parâmetros estatísticos: coeficiente de correlação (R) de 0,899; coeficiente de determinação (R2) de 0,808; coeficiente de determinação ajustado (R2 ajustado) de 0,796 e erro padrão (Se) de 0,41. Estes parâmetros indicam forte correlação linear entre as variáveis, indicando que 79,60% da variação do tempo para executar uma obra pública podem ser causadas pela variação, em conjunto, das variáveis área construída, custo orçado, capacidade técnica operacional do contratante, capacidade operacional da empresa, tipologia de serviço e estação do ano.
Palavras-Chave: Modelagem. Tempo de execução. Obras Públicas. Correlação Linearizada. Modelo Numérico.
ABSTRACT
This article proposes the adoption of a numerical prognosis model to estimate the variable "execution time" for public projects in an objective way. The field work consisted of the application of statistical methods for analyzing data from projects that were bid and contracted by the Federal University of Pará (UFPA) between 2006 and 2009.. Data analysis involved linear regression and transformed functions. After the stratification and initial treatment of the data, the evidence adopted for the construction of the final model was limited to 102 out of the 225 projects originally investigated, resulting in the following statistical parameters: correlation coefficient (R) of 0.899, coefficient of determination (R2) of 0.808, adjusted coefficient of determination (adjusted R2) of 0.796, and standard error (Se) of 0.41. These parameters show a strong linear correlation between the variables, indicating that 79.60% of the variability of the execution of a public project is jointly caused by variations in the gross floor area, the estimated cost, the operational technical capacity of the client organization; the operational capacity of the company; the type of service, and the season.
Keywords: Modeling. Execution time. Public Projects. Linear Correlation. Numerical Model.
Introdução
Atualmente, devido ao momento de expansão da Universidade Federal do Pará (UFPA), inúmeras obras civis são licitadas com tempo insuficiente para execução, pois, no desenvolvimento delas, se mostram inexequíveis no prazo preestabelecido, causando prejuízos à Administração Pública, tais como geração de aditivos de prazos e financeiros. O aditivo de prazo é gerado, em muitos casos, devido à insuficiência do que foi estabelecido no Edital e no contrato para execução do empreendimento. Os percentuais de acréscimos ou aditivos nos prazos foram calculados a partir das informações pesquisadas na Comissão Permanente de Licitação (CPL) e Fundação de Amparo ao Desenvolvimento da Pesquisa (Fadesp) para o período 2006 a 2009, sendo, em cada ano, de 32,57%, 50,67%, 103,27% e 52,74% para as obras licitadas pela CPL, e de 61,63%, 46,34%, 80,28% e 97,30% para as licitadas pela Fadesp. Nesses quatro anos de estudo, as obras licitadas foram acrescidas, em média, em 65,60% do tempo originariamente contratado, com extremos de mais de 100%, o que demonstra, claramente, a necessidade de buscarem-se melhorias nas metodologias de desenvolvimento dos processos de execução dos empreendimentos. Tudo isso impacta em grandes ônus à Administração Pública. Logo, é necessário definir com maior ajuste e correção o tempo que as obras civis da instituição demandam, por meio de modelagem numérica a ser realizada em instante anterior ao processo licitatório.
A literatura internacional relata alguns modelos que foram desenvolvidos com o objetivo de eliminar ou minimizar a subjetividade na estimativa do tempo de execução para uma obra civil. Historicamente, cita-se o pioneiro modelo de Bromilow (1969), BTC (Bromilow Time-Cost), o qual verificou que o tempo é fortemente correlacionado com o tamanho e o custo do empreendimento, adotando a análise de regressão (método dos mínimos quadrados) para encontrar a equação que melhor expressasse essa relação. A equação foi obtida a partir de uma função cúbica invertida, com duas variáveis:
(a) a dependente ou explicada, o tempo da construção (do início até a conclusão); e
(b) a independente ou explicativa, o custo total do empreendimento.
Desde então, diversos trabalhos depuraram, aprofundaram ou mesmo criticaram esse modelo pioneiro. Bromilow e Henderson (1977) consolidaram-no, porém Banki e Esmaeili (2009) consideram-no simples em demasia, embora importante para o segmento da construção civil à época, 1969. Já Walker11 WALKER, D. H. T. An Investigation Into Factors That Determine Building Construction Time Performance. Melbourne, 1994. Thesis (Doctor of Philosophy) - Royal Melbourne Institute of Technology, Melbourne, 1994. (1994 apud NG et al., 2001) criticou-o constatando que não contemplava todos os possíveis fatores que interferem na variabilidade do tempo de construção de uma obra. Ireland22 IRELAND, V. The Role of Managerial Actions in the Cost, Time and Quality Performance of High-Rise Commercial Building Projects. Sydney, 1983. Thesis (Degree of Doctor of Philosophy) - University of Sydney, Sydney, 1983. (1983 apud SKITMORE; NG, 2003) e Ng et al. (2001, p. 4-5) propuseram outro modelo como um "[...] melhor preditor do tempo de construção [...]", desenvolvendo-o através de regressão múltipla, cujas variáveis explicativas eram custo, área e número de pisos, e a variável explicada, o tempo de construção, com o objetivo de melhorar a precisão do modelo pioneiro BTC. Outros estudos, não especificamente de modelagem, mas que tratam da temática de estimar ou calcular o tempo de construção, trabalham distintos fatores que interferem ou podem interferir no prazo das obras.
Para Mulholland e Christian (1999), são os relacionados aos projetos de engenharia, ao gerenciamento dos projetos, ao local de construção e aos termos do contrato. Já Chan e Kumaraswamy (2002) são mais detalhistas, incluindo todos os fatores referentes ao escopo do projeto (custo de construção, área bruta por pavimento, número de pavimentos, tipo de construção, sistema contratual), grau de complexidade do projeto (necessidades dos clientes, condições do local, problemas relacionados com o acesso ao local, qualidade de coordenação de projeto, qualidade de gerenciamento), ambiente de projeto (físico, econômico, sociopolítico, relações de trabalho) e os atributos de gerenciamento (equipe de projeto, equipe de gerenciamento de construção, comunicação gerencial para a tomada de decisão, estrutura organizacional e recursos humanos para gerenciamento e produtividade).
Skomrlj e Radujkovic (2006) externam a importância de determinar certos parâmetros, ainda na fase de planejamento de projeto, tais como custo e duração do projeto, para que ocorra um gerenciamento de construção bem-sucedido.
Mais recentemente, outra vertente de modelagem também tem sido desenvolvida, ainda na tentativa de estimar ou calcular o tempo de construção, porém com uma abordagem diferente, focando, além dos aspectos construtivos, algumas características humanas dos decisores, planejadores, construtores e clientes, considerando variáveis tais como capacidade de negociação e expertise. Sun e Xu (2011) e Yiu e Lee (2011), por exemplo, são trabalhos nessa linha que se fundamentam, geralmente, em algoritmos como Redes Neurais (Inteligência Artificial), os quais simulam ou buscam imitar o pensamento humano.
Este artigo propõe a construção de um modelo que defina o tempo de execução de obras civis, especificamente para o setor público nacional, de forma a minimizar a subjetividade nessa definição, com o intuito de contribuir para que haja menos possibilidades de atrasos e consequentes aditivos de prazos, que causam, via de regra, grandes prejuízos econômico-financeiros, bem como prejudicam as atividades a serem desenvolvidas pela sociedade. O artigo segue a linha de modelagem proposta por Bromilow, pautando-se na inferência estatística (análise de regressão) e adota variáveis inerentes ao processo construtivo que contemplem, além das características físicas ou materiais em si, elementos ou condicionantes institucionais/empresariais como a capacidade operacional.
Obras públicas
Para Meirelles (2011, p. 325), "[...] a obra Pública é um fato administrativo, e, como tal, sujeito às regras específicas da Administração [...]", o que faz o setor público adotar o modelo burocrático e político, fundamentando-se nos princípios constitucionais, e tem como pilares os fundamentos de excelência gerencial, os quais estão disponíveis no Instrumento para Avaliação da Gestão Pública (IAGP) (MINISTÉRIO..., 2011), fundamentado na Constituição Federal, Artigo 37: "A Gestão Pública para ser excelente tem que ser legal, moral, impessoal, pública e eficiente [...]" (BRASIL, 1988).
Para contratação de obra pública, os dispositivos legais que norteiam o processo licitatório não se limitam apenas à Lei nº 8.666/93 (BRASIL, 1993), mas também ao conjunto normativo que estabelece diretrizes relativas a procedimentos, preços e estudos de viabilidade técnica.
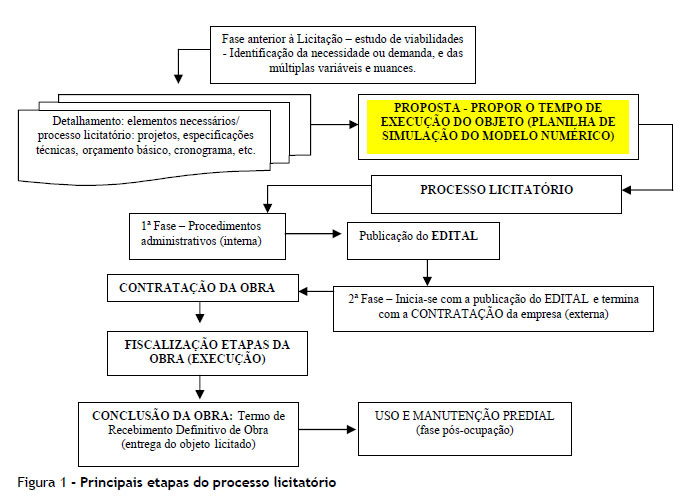
As principais etapas que compõem o processo de licitação, contratação, execução e utilização de um empreendimento público podem ser observadas na Figura 1.
USO E MANUTENÇÃO PREDIAL (fase pós-ocupação)
(c) Fase anterior à licitação: com base na análise das necessidades do usuário-cliente, elabora-se o anteprojeto, que concebe o tipo de fundação, estrutura e instalações em geral, e verifica quais elementos comporão a elaboração do projeto arquitetônico. Conjuntamente, elaboram-se o cronograma físico-financeiro e a especificação técnica;
(d) Processo licitatório: fase interna: inicia-se com a abertura de um processo administrativo, indicando o objeto, a fonte de custeio para a despesa e a autorização da instância superior para que seja procedido o atendimento;
(e) Elementos necessários ao processo licitatório:
- projeto básico: o projeto básico pode ser considerado como o elemento mais importante para a condução do processo licitatório, visto que a legislação estabelece-o como sendo requisito fundamental para licitar. A inexistência ou indefinições na elaboração do projeto básico trarão grandes problemas na condução do gerenciamento da obra, comprometendo, assim, o prazo de execução e, consequentemente, o custo e a qualidade dos serviços;
- elaboração do edital ou convite: caberá à Administração definir os requisitos do edital ou convite, atendendo à Lei nº 8.666/93 (BRASIL, 1993); e
- projeto executivo: representa o conjunto de projetos que auxiliarão nas várias etapas de execução de obras, tais como de instalações prediais, etc., quer sejam terceirizadas ou não, de acordo com as normas da Associação Brasileira deNormas Técnicas (ABNT). É reconhecido pelo alto grau de detalhamento e rigor nas especificações técnicas, possibilitando produzir um nível de trabalho melhor, mais rápido e de maior qualidade, durante a execução das etapas do empreendimento.
(f) Fase externa do processo licitatório: inicia-se com a publicação do edital e finaliza-se com a assinatura do contrato pela firma vencedora da licitação;
(g) Fiscalização das etapas da obra: conforme estabelece o Art. 67 da Lei nº 8.666/93 (BRASIL, 1993), a fiscalização pertencerá ao quadro técnico da Ifes. Todo fato vinculado à execução da obra deverá ser registrado em um livro diário de obra, bem como as indicações para correção de falhas ou defeitos de execução observados;
(h) Conclusão da obra: de acordo com o estabelecido na Lei nº 8.666/93 (BRASIL, 1993), a Ifes emitirá o Termo de Recebimento Definitivo de Obras, devidamente assinado pelas partes envolvidas, fiscalização, unidade usuária e empresa executora, após minuciosa vistoria; e
(i) Uso e manutenção predial: após a conclusão do empreendimento, inicia-se a fase pós-ocupação, sendo prevista durante sua utilização a manutenção predial.
Metodologia
Pautados em Jung (2003), Miguel (2010) e Nahamias (2009), autores da área da pesquisa operacional (operational research), realizaram-se um trabalho de campo com o objetivo de levantar as informações necessárias para montar uma base de dados que representasse de forma genérica situações mais frequentes no âmbito da gestão de obra pública. Optou-se, então, por realizar o estudo com base em dados extraídos dos processos realizados para licitações de obras, reformas e ampliações, cujos certames foram realizados pela Comissão Permanente de Licitação (CPL), pela Fundação de Amparo ao Desenvolvimento da Pesquisa (Fadesp), e nos processos arquivados no Departamento de Finanças (Defin) para o período de 2006 a 2009, totalizando 225 dados. Os processos, embora de fontes distintas e com características não uniformes, apresentavam os elementos quantitativos e qualitativos necessários para alimentar o modelo.
Segundo Lisboa (2011), para desenvolver um estudo de pesquisa operacional é necessário:
(a) definir o problema;
(b) construir um modelo;
(c) encontrar a solução do modelo;
(d) validar o modelo;
(e) implementar a solução; e
(f) realizar a avaliação final.
Na Figura 2 são apresentados os procedimentos adotados e as estratégias desenvolvidas durante cada etapa da pesquisa, detalhados ao longo do artigo.
A escolha da estratégia de pesquisa mais adequada depende de fatores tais como o tipo da questão da pesquisa, o controle do pesquisador sobre o objeto pesquisado e o grau de envolvimento da pesquisa com a investigação de assuntos atuais. Essa escolha é confirmada e/ou corrigida durante a análise de cada etapa, sendo contínua a revisão do processo nas etapas posteriores, conforme delineamento da pesquisa (Figura 2).
A primeira etapa, a partir da definição do problema, sob o fundamento da pesquisa operacional, fundamenta-se em três aspectos principais, a saber:
(a) descrição com exatidão dos objetivos do trabalho;
(b) identificação das variáveis de decisão existentes; e
(c) reconhecimento das limitações, restrições e exigências do sistema.
A descrição dos objetivos é uma das atividades mais importantes do processo de desenvolvimento do trabalho, pois é a partir dela que se dá a concepção do modelo.
O pesquisador deverá captar e refletir acerca da formulação do problema, dos anseios e necessidades dos gestores com relação ao problema de decisão. Na segunda etapa, construção do modelo, observaram-se quais as variáveis que poderiam ser mais expressivas para compor a modelagem numérica, tanto as qualitativas dicotômicas como as quantitativas. Em princípio, com base na literatura e na experiência profissional na área de obras públicas realizadas na UFPA, foram estabelecidas dez que contemplassem as mais diversas nuances do processo construtivo:
X1, estação do ano: (1), se inverno ou (2), se verão;
X2, área construída, em m2;
X3, valor total da obra, em R$;
X4, capital social, em R$;
X5, capacidade operacional da empresa (obtida pela razão entre as variáveis X4 e X3);
X6, prazo inicial previsto, em meses;
X7, destinação: (1), se obra ou (2), se reforma;
X8, finalidade de atendimento: (1) ensino, (2) pesquisa e extensão, e (3) unidades administrativas;
X9, modalidade licitatória: (1) dispensa, (2) convite, (3) tomada de preço, (4) concorrência e (5) pregão; e
Y, a variável dependente ou explicada, que é resposta ao problema de pesquisa (tempo de execução de obras), em meses.
A definição apriorística dessas variáveis explicativas foi realizada tendo as seguintes motivações:
X1: contemplar o ambiente físico do projeto/obra;
no caso específico, consideraram-se as condições climáticas (CHAN; KUMARASWAMY, 2002; MULHOLLAND; CHRISTIAN, 1999);
X2 e X3: considerar o tamanho ou porte, tanto físico (X2) quanto econômico-financeiro (X3) da obra (BROMILOW, 1969; BROMILOW; HENDERSON, 1977; SKITMORE; NG, 2003);
X4 e X5: Estabelecer o porte da empresa (X4) e incorporar a capacidade gerencial ou operacional dela (X5) a partir de uma informação documental disponível e idônea da condição econômicofinanceira (premissa admitida pelos autores, derivada de Chan e Kumaraswamy ( 2002));
X6, X7, X8 e X9: contemplar termos contratuais (no caso, o próprio tempo de execução pactuado - X6 - e a forma de contratação - X9), a tipologia, a complexidade e/ou amplitude da obra (X7), as necessidades demandadas pela contratante a serem atendidas pela contratada (X8) (adaptadas pelos autores a partir de Mulholland e Christian (1999) e Chan e Kumaraswamy (2002), contextualizando-as à realidade e à legislação nacional, assim como às especificidades de uma Ifes).
A terceira etapa é a solução do modelo, solução esta obtida através de algoritmo mais adequado, em nível de rapidez de processamento e precisão na resposta. Foram adotados os fundamentos e os princípios da estatística nessa solução.
Segundo Lapponi (2000), a estatística descritiva objetiva organizar, resumir, analisar e interpretar observações disponíveis; e a inferência estatística visa obter respostas corretas para questões específicas, atendendo a determinado grau de acerto, podendo estabelecer ou conceber um modelo.
Montgomery, Runger Hubele (2001) atentam que modelos empíricos possam ser desenvolvidos ou elaborados através de análise de regressão, que trabalha com um ou mais regressores (as variáveis explicativas ou independentes - Xn) e uma variável dependente ou explicada (Y).
Um modelo de regressão com mais de um regressor é chamado de modelo de regressão múltipla, podendo ser representado da seguinte forma pela Equação 1, a seguir.
Um parâmetro importante, segundo Montgomery, Runger e Hubele (2001) e Lapponi (2000), é o coeficiente de determinação R2, cuja definição é dada pela Equação 2, abaixo.
Sendo:
SQE: a soma dos quadrados do resíduo; e
SQT: a soma dos quadrados totais.
O valor de R2 é uma medida da fração da variabilidade nas observações y, através da equação de regressão pelas variáveis X1, X2, ..., Xk. Um valor grande de R2 não significa obrigatoriamente que o modelo de regressão seja considerado bom. A adição de uma variável ao modelo sempre aumentará o valor de R2, independentemente de a variável adicionada ser ounão, do ponto de vista estatístico, significativa. É importante ressaltar que essa é a medida que expressa o poder de predizer a variação da variável dependente Y, quando se utilizam as variáveis Xs adotadas na construção do modelo.
O coeficiente de determinação pode ainda ser depurado ao ser calculado considerando o número de dados efetivamente utilizados para formação do modelo, sendo então denominado coeficiente de determinação ajustado, R2ajustado, através da equação 3, indicada a seguir.
Sendo:
SQE a soma dos quadrados do resíduo;
SQT a soma dos quadrados totais;
n o número total de eventos ou dados; e
p o grau de liberdade da regressão ou de variáveis explicativas (X).
O valor de R2ajustado melhor expressa a medida da capacidade de explicação do modelo, do que o R2, capacidade esta que pode ter como parâmetro numérico de qualidade o coeficiente de correlação (R), o qual, segundo Pereira33 PEREIRA, R. S. Estatística e Suas Aplicações. São Paulo: Grafosul, 1970. (1970 apud DANTAS, 1998, p. 115), pode ser verificado na é o que, entre as inúmeras rodadas, apresente o Tabela 1.
Os resultados apresentados (Quadro 1) para as análises de regressões lineares foram classificados em seis grupos para o R2ajustado: nula, fraca, média, forte, fortíssima e perfeita, conforme pode ser observado no Quadro 2.
Logo, R2 pode ser o parâmetro adotado para caracterizar a qualidade numérica do modelo, embora só isso não seja suficiente, requerendo ainda a análise de sensibilidade para os dados trabalhados e os resultados obtidos.
A solução do problema da presente pesquisa inicia-se com um modelo denominado histórico, tratando todas as variáveis definidas na etapa anterior na forma linear e adotando como parâmetro numérico fundamental o R2 e a análise de sensibilidade, para verificar a coerência e a lógica nas correlações entre cada uma das variáveis explicativas e a variável explicada tempo de execução de obras.
O processo de melhoria e depuração constitui-se na mudança do modelo histórico em prognóstico, com sucessivas rodadas pelo método dos mínimos quadrados sob a condição Ceteris paribus, na busca do aumento do poder de explicação (o R2), com exclusões e reinclusões das variáveis explicativas, uma de cada vez, assim como transformações nas formas delas (de linear para não linear), sempre com análise da lógica e coerência. O modelo final é o que, entre as inúmeras rodadas, apresente o maior R2.
A quarta etapa, validação do modelo, surge devido ao processo de solução do problema, sendo necessária a validação do modelo mediante simulação e inferência estatística, contribuindo, assim, para a qualidade da decisão a ser tomada. É importante ressaltar que a qualidade da solução do modelo depende da qualidade dos dados de entrada, ou seja, dos dados que fundamentam a elaboração dele.
A quinta etapa, implementação da solução, ocorre após a avaliação dos resultados, sendo convertida em regras operacionais, preferencialmente simples e claras.
Na sexta etapa, avaliação final, o modelo torna-se efetivo na representação simplificada da realidade estudada. Ao aplicá-lo, o gestor ou técnico obtém valores como resultados para o tempo de execução de obras, podendo ser adotados pela Ifes na solução de problemas ou situações reais, sendo, então, compatíveis, adequados e úteis, ainda na fase administrativa da licitação (Figura 1).
Os dados do estudo de caso foram trabalhados no aplicativo Microsoft Excel - ferramenta Análise de Dados (VBA), a fim de inferir resultados qualitativos sobre a variável dependente (Y), que representará o tempo de execução de uma obra civil pública, a partir de estudos quantitativos.
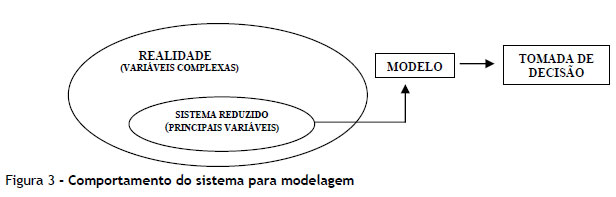
Segundo Miguel (2010), dois processos de abstração são utilizados na construção de um modelo de pesquisa operacional. Primeiramente, o sistema real, um conjunto complexo com grande número de variáveis, de forma não muito definida, sendo separado um modelo conceitual, no qual apenas uma parte das variáveis originais que definem o comportamento do sistema é considerada. Posteriormente, o modelo conceitual é reduzido em um modelo matemático analítico, ou seja, é representado por funções matemáticas que visam igualar, por meio de operações lógicas, o funcionamento do sistema. Então, para formular o modelo matemático, simplificações razoáveis do modelo conceitual (original) devem ser realizadas em vários níveis, objetivando a verificação da validação do modelo proposto em uma solução coerente com os objetivos e restrições do sistema real (Figura 3).
Fica claro, então, que qualquer trabalho de modelagem na pesquisa operacional apresenta limitações, pois é, em síntese, uma simplificação da realidade, uma tentativa de expressar, através de uma fórmula ou mecanismo reducionista ou reduzido, uma resposta que, mesmo não sendo isenta de erros, possa subsidiar ou balizar a tomada de decisão. As limitações da pesquisa devem-se à grande variedade de arranjos possíveis, nas inúmeras variáveis que poderiam ser adotadas na construção do modelo numérico e que não o foram por ser simplesmente impossível contemplar todas as nuances e condicionantes da realidade.
Estudo de caso: obras da UFPA
A UFPA foi criada em 1957 e encontra-se em fase de grande expansão, sendo responsável pelos projetos dos 11 campi, segundo consta no Relatório Social de Gestão (UNIVERSIDADE..., 2009), os quais podem ser observados na Figura 4, a qual representa a distribuição geográfica dos campi da UFPA no Estado do Pará: Abaetetuba, Altamira, Belém, Bragança, Breves, Cametá, Castanhal, Marabá, Soure e os recém-criados campi de Capanema e de Tucuruí, em vermelho. O campus de Santarém atualmente integra a Universidade Federal do Oeste do Pará (Ufopa).
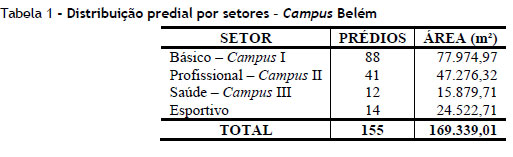
Até 2009, o campus Belém contabilizava 155 edificações, aproximadamente 169.339,01 m2 de área construída, além de 12 prédios fora do campus, que abrigam os cursos de Medicina, Escola de Teatro e Dança, Museu de Artes da UFPA, Casa da Estudante, entre outros. As edificações do campus Belém destinam-se a abrigar funções administrativas, salas de aulas, laboratórios, auditórios, centro de convenções, restaurantes, lanchonetes, biblioteca, hospitais, farmácia, setor recreativo e áreas de convivência, conforme dados pesquisados na Prefeitura (Tabela 1).
Tratamento, análise e discussão dos resultados
Modelo histórico
Os 225 dados pesquisados, que se constituem dos processos licitatórios e de acompanhamento/fiscalização das obras realizadas e concluídas durante quatro anos (2006 a 2009), depois de catalogados, organizados e tabulados, possibilitaram quantificar ou qualificar as dez variáveis citadas na seção 2 deste trabalho (Metodologia).
A opção pela adoção dessas dez variáveis adveio da revisão bibliográfica, sendo algumas delas recorrentes na literatura pesquisada, como área e custo, e outras escolhidas para caracterizar atributos, condições ou componentes recomendados por alguns autores, como termos de contrato (variável modalidade licitatória) e gerenciamento (variável capacidade operacional).
O tratamento desses 225 dados pelo método dos mínimos quadrados formou o que se denominou de modelo histórico, do qual, por análise de sensibilidade, se puderam verificar quais variáveis que mais interferiam ou contribuíam para a variabilidade do tempo de execução real.
Definiu-se o primeiro modelo de regressão (histórico), cujos parâmetros são:
(a) coeficiente de determinação (R2) de 74,69% de poder de explicação e predição dentro do intervalo de 95% de confiança;
(b) significância (R2ajustado) de 73,63%; e
(c) erro padrão (Se) de ±3,23.
Verificou-se, nesse modelo, que a variável X2 (área) mostrou-se a mais significativa ou importante na variabilidade da variável Y (tempo).
Modelo prognóstico
Depurando-se o modelo histórico, excluíram-se as variáveis X4 (capital social) e X6 (prazo previsto), visto que o pretendido é justamente obter ou calcular o prazo (tempo) de execução prognóstico. Inclui-se uma nova variável, a capacidade operacional técnica da Ifes (UFPA), obtida da razão entre o número de engenheiros e o número de obras em execução no período de realização da licitação, obras estas cadastradas na base do Sistema Integrado de Monitoramento do Ministério da Educação (Simec), em http://simec.mec.gov.br.
Para composição do modelo prognóstico foram consideradas nove variáveis (explicativas, endógenas ou independentes):
X1, estação do ano;
X2, área construída;
X3, valor total da obra (orçado);
X4, capacidade operacional da empresa;
X5, capacidade operacional técnica da Ifes;
X6, tipo de serviço;
X7, finalidade de atendimento;
X8, modalidade licitatória; e
Y, variável de resposta (tempo de execução), explicada, exógena ou dependente.
Procedeu-se ao tratamento dos dados, retirando-se as reformas com áreas de até 100 m2, as quais são atendidas pela manutenção predial da Ifes.
O número de dados ficou restrito a 153, contemplando a faixa de área de 102,4 a 1.666,12 m2. Realizou-se a regressão estatística, obtendo-se os valores para o primeiro modelo prognóstico linear múltiplo:
(a) coeficiente correlação (R) de 79,61%;
(b) coeficiente de determinação (R2) de 63,38%;
(c) coeficiente de determinação ajustado (R2ajustado) de 61,17%; e
(d) erro padrão (Se) de ±3,73.
Por análise de sensibilidade, eliminam-se os outliers (dados atípicos), chegando-se a um conjunto com 142 dados representativos para a faixa de 102,4 a 1.079,73 m2. Depurando-se ainda mais, partiu-se, então, para a construção do segundo modelo prognóstico, mais refinado e ajustado, sendo excluídas de sua construção as variáveis:
X7 (finalidade): a qual trata da finalidade de atendimento, considerando a UFPA como um único espaço, ou seja, um todo institucional, não devendo ter restrições no atendimento; e
X8 (modalidade licitatória): visto que as obras são licitadas em uma modalidade "predefinida" por meio do valor orçado.
Nessa busca de construção do modelo mais ajustado, a análise de regressão, trabalhou-se a transformação das variáveis nas formas exponencial, logarítmica, polinomial, inversa, além da linear, com o auxílio de softwares destinados à regressão estatística e do Microsoft Excel. Após as análises numéricas e de sensibilidade, o modelo prognóstico final restringiu-se às variáveis:
X1, estação do ano;
X2, área;
X3, valor da obra;
X4, capacidade operacional da empresa;
X5, capacidade técnica operacional da Ifes; e
X6, tipologia do serviço a 102 dados.
Dos 225 originais efetivamente utilizados, com coeficiente de correlação (R), 89,90%; coeficiente de determinação (R2), 80,80%, indicando que 80,80% da variabilidade do tempo para executar uma obra pública é decorrente da variação, em conjunto, dessas variáveis, tendo coeficiente de determinação ajustado (R2ajustado) de 79,60% e erro padrão (Se) de ±0,41. Tais parâmetros, além do detalhamento do modelo (Equação 4), podem ser verificados por meio das Tabelas 2 a 4, a seguir.
Esse modelo, composto de seis variáveis independentes, apresentou significância e coeficiente de determinação que pode ser classificado como Forte, tendendo a Fortíssimo, ratificado pelo R2ajustado (Quadros 1 e 2), sendo representado pela Equação 4, a seguir:
Validação do modelo (simulação)
Para validar o modelo, procede-se a simulação aleatória com 20 casos, extraídos do conjunto constituído por 102 eventos (dados originais).
Utilizando-se a análise de sensibilidade, verifica-se o resultado obtido pela inferência ou estimativa no modelo de simulação, através do processo de análise dedutiva, se está ou não compatível ou aproximado ao valor real observado. Posteriormente, a análise de sensibilidade consistirá na verificação da coerência da variabilidade, em termos de aumento ou diminuição da variável explicada, de resposta, dependente ou endógena (Y), com relação à variabilidade de cada variável independente, explicativa ou exógena estudada na composição do modelo numérico.
Verifica-se que os valores obtidos das inferências (simulações - coluna II) apresentam variação entre -60% e +5% (coluna IV), em números redondos, dos tempos reais demandados pelas obras (tempo total - coluna III), com variação média de -29%, enquanto os prazos contratuais, estabelecidos de maneira subjetiva, sem a adoção do modelo (coluna VII), em sua grande maioria, apresentam dispersão ou afastamento muito mais intenso dos tempos efetivos, com amplitudes de até -75% (coluna VIII). As grandezas inferidas, dessa forma, mostram-se compatíveis com as efetivas ou reais das obras realizadas, ressaltando ainda que, provavelmente, caso fossem estabelecidos, quando da contratação, prazos mais realísticos, como os da simulação, as obras demandariam menos tempo do que efetivamente demandaram, pois haveria mais força ou credibilidade técnica por parte da contratante (fiscalização) junto à empresa, por terse definido o prazo contratual de maneira racional e objetiva; consequentemente, poder-se-ia cobrar ou exigir com maior rigor o cumprimento do prazo contratado. Os valores obtidos para a variável dependente (Y) podem ser verificados na Tabela 5.
O modelo, portanto, mostra-se válido; responde com coerência e correção ao que é procurado: prever o tempo para execução de uma obra de construção civil pública ou serviço de engenharia, com forte poder explicativo e alto grau de acerto.
Implementação da solução: planilha de cálculo (regras operacionais)
Validado o modelo numérico, inicia-se a implementação da solução na rotina gerencial da Ifes (UFPA). A partir dos resultados obtidos pela modelagem numérica, edita-se uma planilha no Excel que trabalhará com as variáveis consideradas, sendo, portanto, um mecanismo de fácil manuseio e aplicação, com entrada direta de dados e obtenção da resposta com leitura imediata.
Descrição da entrada de dados
Para a entrada de dados, o engenheiro fiscal passa a informar os parâmetros considerados para as variáveis, visando ao cálculo do tempo para a realização de uma obra pública.
X1: informar (1) ou (2) para a estação do ano em que se iniciará a obra: inverno (1) ou verão (2);
X2: informar a área constante no projeto ou orçamento-base, em m2;
X3: informar o valor do orçamento-base, em R$;
X4: informar o valor do capital social, em R$;
X5: informar o número de engenheiros fiscais e o número de obras em execução no período, por base de atendimento (Belém ou interior), constantes na base de dados do Simec; e
X6:informar (1) ou (2) para o tipo de serviço: obra (1) ou reforma (2).
Todos os procedimentos acima indicados poderão ser verificados na Figura 5, que representa a planilha de cálculo, com uma exemplificação para previsão do tempo de execução em uma situação real licitada em 2010. Entretanto, observa-se que no cálculo adota-se o parâmetro de até ±2 Se. Sendo Se o erro padrão, calculado pela regressão estatística, cujo valor é 0,41, considera-se para o tempo máximo (2), de 16 meses, o parâmetro +2 Se, cujo valor +0,82 foi acrescido ao tempo bruto (1), de 15 meses, e para a obtenção do tempo mínimo (3), de 14 meses, deve-se considerar -2Se, cujo valor -0,82 foi deduzido do tempo bruto.
Para o exemplo, ao proceder-se à simulação, o engenheiro fiscal tem parâmetros claros para definir o tempo de obra, ainda na fase anterior à licitação, não estando, entretanto, sua decisão restrita à grandeza calculada pelo modelo, tempo bruto (1), de 15 meses, mas àquela adequada à obra em questão, considerando as peculiaridades da obra em si e outras variáveis não contempladas no modelo.
Pode ainda o fiscal considerar outras nuances, como as necessidades ou, se existir, o caráter de emergência do projeto, além das disponibilidades orçamentárias da instituição, que, em alguns casos, ensejariam alteração no tempo calculado pelo modelo prognóstico.
Ressalta-se que, mesmo com essa flexibilidade e possibilidade de alteração no tempo da obra, o modelo fornece um parâmetro quantitativo consistente e objetivo. Essa flexibilização, se adotada, não deve ser muito significativa, para não retornar uma definição do tempo subjetiva e, consequentemente, frágil e tênue.
No exemplo, que é um caso real, foi adotado pela Ifes para a licitação o valor inferido de 15 meses, estando a obra ainda em curso, na fase de conclusão.
Conclusões
As soluções por modelos numéricos são procedimentos técnico-científicos que visam auxiliar os gestores para a tomada de decisão. O tempo de execução de uma obra civil demandada por uma instituição pública deve ser definido, preferencialmente, de forma precisa, para que sejam minimizadas as possibilidades de atrasos e a consequente necessidade de aditivos de prazo, pois esses aditivos causam grandes problemas e prejuízos à administração pública e à sociedade como um todo.
Este artigo demonstra que é possível a elaboração de um modelo numérico prognóstico pautado no modelo pioneiro BTC, porém adequado e compatível com a realidade nacional, para definir, de forma objetiva, e não subjetiva, o tempo de execução de obras, tendo sido realizado estudo de caso em uma Ifes (UFPA).
O modelo obtido é efetivo, coerente, confiável e numericamente forte, como demonstrado pela análise de sensibilidade, análise gráfica e pelo parâmetro R2ajustado de 79,60%, o que significa que quase 80% da variabilidade do tempo da obra é causada ou produzida pela variação, em conjunto, das seis variáveis explicativas ou independentes utilizadas no modelo, restando cerca de 20% da variação ou variabilidade do tempo da obra (Y) causada por outras variáveis não consideradas.
O modelo apresenta uma variável regional, denominada estação do ano, que, para a região Norte do país, restringe-se a duas estações (inverno, mais chuvoso, e verão, menos chuvoso). Contudo, se modificada e adequada às particularidades de cada região, possibilitará sua aplicação em outras Ifes e órgãos públicos, para prever o tempo de execução de obras, objetivamente.
Entre as seis variáveis explicativas adotadas, foram consideradas duas de caráter técnico/gerencial/administrativo/financeiro, que contemplam a capacidade de fiscalizar da contratante (Ifes) e a capacidade financeira operacional da contratada (empresa), variáveis ainda não contempladas na literatura técnica, mas que se mostraram importantes na formulação do modelo e que podem, em trabalhos futuros, ser mais bem estudadas e aprofundadas.
Outras variáveis, tais como falta de recursos orçamentários/financeiros (fator políticoadministrativo), capacidade técnica da empresa contratada e racionalidade técnica, também podem ser introduzidas na formulação do modelo, o que provavelmente o tornará mais robusto e com maior poder de explicação do que o apresentado neste artigo.
Outros métodos matemático-numéricos, além da regressão estatística, adotada neste trabalho, também podem ser aplicados para a obtenção de modelos que permitam prever o tempo de execução de obras públicas em uma Ifes, tais como Redes Neurais Artificiais ou Lógica Fuzzy, desde que tenham como princípio uma implementação simples e direta nas atividades administrativooperacionais, a fim de que possam ser operacionalizados de forma eficiente e eficaz.
Recebido em 18/01/11
Aceito em 17/02/12
- BANKI, M. T.; ESMAEILI, B. Effects of Variability of the Mathematical Equations and Project Categorizations on Forecasting S-Curves at Construction Industry. International Journal of Civil Engineering, v. 7, n. 4, p. 258-270, dec. 2009.
- BRASIL. Constituição Federal. Constituição da República Federativa do Brasil. Diário Oficial da União, Brasília, 5 de outubro de 1988.
- BRASIL. Lei nº 8.666/93, que regulamenta o Art. 37, inciso XXI da Constituição Federal. Institui normas para licitações e contratos da Administração Pública e dá outras providências. Diário Oficial da República Federativa do Brasil, Brasília, 21 de junho de 1993.
- BROMILOW, F. J. Contract Time Performance Expectations and Reality. Building Forum, v. 1, n. 3, p. 70-80, 1969.
- BROMILOW, F. J; HENDERSON, J. A. Procedures for Reckoning the Performance of Building Contracts 2. ed. Highett, Austrália: CSIRO, Division of Building Research, 1977.
- CHAN, D. W. M.; KUMARASWAMY, M. M. Risk Compressing Construction Durations: lessons learned from Hong Kong building projects. International Journal of Project Management, v. 20, n. 1, p. 23-35, 2002.
- DANTAS, R. A. Engenharia de Avaliações: uma introdução à metodologia científica. São Paulo: Pini, 1998.
- JUNG, C. F. Metodologia Científica: ênfase em pesquisa tecnológica. 3. ed. rev. e ampl. 2003. Disponível em: <http://www.geologia.ufpr.br/graduacao/metodologia/metodologiajung.pdf>. Acesso em: 04 mar. 2012.
- LAPPONI, J. C. Estatística Usando Excel São Paulo: Lapponi Treinamento e Editora, 2000.
- LISBOA, E. Introdução à Pesquisa Operacional Disponível em: <http://www.ericolisboa.eng.br>. Acesso em: 11 set. 2011.
- MEIRELLES, H. L. Direito de Construir, 10. ed. São Paulo: Malheiros Editores, 2011.
- MIGUEL, P. A. C. Metodologia de Pesquisa em Engenharia de Produção e Gestão de Operações Rio de Janeiro: Elsevier, 2010.
- MINISTÉRIO DO PLANEJAMENTO, GESTÃO E ORÇAMENTO. Instrumento para Avaliação da Gestão Pública (IAGP): ciclo 2008/2009. Disponível em: <http://www.pqsp.planejamento.gov.br/publicacoes.aspx?url=pub_opcoes.aspx>. Acesso em: 16 jun. 2011.
- MONTGOMERY, D. C.; RUNGER, G. C.; HUBELE, N. F. Estatística Aplicada à Engenharia 2. ed. Rio de Janeiro: Livros Técnicos e Científicos, 2001.
- MULHOLLAND, B.; CHRISTIAN, J. Assessment in Construction Schedules. Journal of Construction, Engineering and Management, v. 125, n. 1, p. 8-15, 1999.
- NAHAMIAS, S. Production and Operations Analysis Nova York: McGraw-Hill, 2009.
- NG, S. T. et al. The Predictive Ability of Bromilow's Time Cost Model. Construction Management & Economics, v. 19, n. 2, p. 165-173, 2001.
- SKITMORE, R. M.; NG, S. T. Forecast Models For Actual Construction Time Cost. Building and Environment, v. 8, n. 8, p. 1075-1083, 2003.
- SKOMRLJ, N. O.; RADUJKOVIC, M. S-Curve Modelling for Building Construction. 2006. Disponível em: <http://huog.hr/sedma/PROCEEDINGS%20IN%20PDF/Ostojic-skomrlj_radujkovic.pdf>. Acesso em: 19 mar. 2011.
- SUN, C.; XU, J. Estimation of Time for Weunchuan Earthquake Reconstruction in China. Journal of Construction Engineering and Management, v. 137, n. 3, p. 179-187, 2011.
- UNIVERSIDADE FEDERAL DO PARÁ. Mapas 2009. Disponível em: <http://www.portal.ufpa.br//mapas.php>. Acesso em: 10 jun. 2011.
- UNIVERSIDADE FEDERAL DO PARÁ. Relatório Social de Gestão 2009 Disponível em: <http://www.portal.ufpa.br/docsege/UFPA_COMP.pdf>. Acesso em: 10 jun. 2011.
- YIU, T. W.; LEE, H. K. How Do Personality Traits Affect Construction Dispute Negotiation? Study of big five personality model. Journal of Construction Engineering and Management, v. 137, n. 3, p. 169-178, 2011.
Datas de Publicação
-
Publicação nesta coleção
02 Maio 2012 -
Data do Fascículo
Mar 2012
Histórico
-
Recebido
18 Jan 2011 -
Aceito
17 Fev 2012