Resumo
Squeeze flow é uma das principais técnicas para analisar o comportamento reológico de argamassas. Esses materiais podem ser considerados como suspensões concentradas, reativas e heterogêneas com grande extensão granulométrica, nas quais o comportamento reológico é influenciado pelas quantidades e características de seus constituintes. Para avaliar alguns fenômenos de maneira mais detalhada, é interessante reduzir os fatores que influenciam o fluxo. Assim, este trabalho avalia o comportamento reológico de suspensões concentradas de esferas macroscópicas de vidro em fluidos newtonianos de diferentes viscosidades (silicones: 100, 1.000 e 10.000 cSt) e visa analisar a interação entre as fases líquida e sólida e a ocorrência de segregação. As suspensões com 60% e 70% em volume de sólidos foram submetidas a ensaios de squeeze flow com diferentes velocidades. O aumento da quantidade de fluido altera os principais fenômenos relacionados ao fluxo: com baixo volume de líquido o atrito entre as partículas, a capacidade de lubrificação do fluido e a coesão decorrente da formação de meniscos são predominantes na suspensão, enquanto em suspensões com volume de líquido suficiente para afastar as partículas a viscosidade do fluido, a força de arraste e a permeabilidade do sistema granular influenciam no comportamento reológico e na ocorrência de separação de fases.
Palavras-chave:
Squeeze flow; Viscosidade; Teor de sólidos; Sistema bifásico; Separação de fases
Abstract
Squeeze flow is one of the main techniques used to evaluate the rheological behaviour of mortars. This type of material can be considered as a reactive, heterogeneous and concentrated suspension with a wide range of particle sizes, and its rheological behaviour is influenced by the quantity and characteristics of its constituents. In order to evaluate some phenomena in detail, it is interesting to reduce the factors that influence the flow of the material. Thus, this paper assesses the rheological behaviour of concentrated suspensions of macroscopic glass spheres in Newtonian fluids with different viscosities (silicone oils: 100, 1000 e 10000 cSt) aiming to analyse liquid and solid interactions as well as the occurrence of phase separation. Suspensions with 60% and 70%vol of spheres were subjected to squeeze flow tests at different displacement rates (0.01, 0.1 and 1.0 mm/s). The increase in liquid content changed the main phenomena governing the flow: (i) at low liquid volume, friction between particles, liquid lubrication capacity and cohesion generated by meniscus formation have a major effect; while (ii) in suspensions with liquid content enough to separate the particles, the fluid viscosity, drag force and permeability of the granular system determine the rheological behaviour of the suspension and the occurrence of phase separation.
Keywords:
Squeeze flow; Viscosity; Solid content; Biphasic system; Phase separation
Introdução
O teste de squeeze flow consiste na compressão de uma amostra cilíndrica entre duas placas paralelas e é utilizado em diversas classes de materiais (ENGMANN; SERVAIS; BURBIDGE, 2005ENGMANN, J.; SERVAIS, C.; BURBIDGE, A. S. Squeeze Flow Theory and Applications to Rheometry: a review. Journal of Non-Newtonian Fluid Mechanics, v. 132, n. 1/3, p. 1-27, 15 dez. 2005.) devido a sua versatilidade. Esse ensaio pode ser realizado em uma máquina universal, o que permite fácil adaptação para diversos níveis de cargas e geometrias. Sua configuração facilita a análise de materiais que apresentam dificuldades na utilização de outros ensaios reológicos, como enovelamento de fibras na geometria cisalhante em reômetros rotacionais ou entupimento dos capilares em reômetros tubulares. Além disso, a ocorrência de escorregamento ou de atrito na interface entre a amostra e a placa não invalida os resultados. Por essas vantagens, o squeeze flow apresenta uso crescente na caracterização reológica de materiais cimentícios, incluindo argamassas de diferentes tipos: pastas de cimento (MIN; ERWIN; JENNINGS, 1994MIN, B. H.; ERWIN, L.; JENNINGS, H. M. Rheological Behaviour of Fresh Cement Paste as Measured by Squeeze Flow. Journal of Materials Science, v. 29, n. 5, p. 1374-1381, 1994.); argamassas para extrusão (TOUTOU; ROUSSEL; LANOS, 2005TOUTOU, Z.; ROUSSEL, N.; LANOS, C. The Squeezing Test: a tool to identify firm cement-based material's rheological behaviour and evaluate their extrusion ability. Cement and Concrete Research, v. 35, n. 10, p. 1891-1899, 2005.); argamassas de revestimento (CARDOSO, 2009CARDOSO, F. A. Método de Formulação de Argamassas de Revestimento Baseado em Distribuição Granulométrica e Comportamento Reológico. São Paulo, 2009. Tese (Doutorado em Engenharia Civil) - Escola Politécnica, Universidade de São Paulo, São Paulo, 2009.); e argamassas com fibras (CHALENCON et al., 2009CHALENCON, F. et al. Lubricated Compression and X-Ray Microtomography to Analyse the Rheology of a Fibre-Reinforced Mortar. Rheologica Acta, v. 49, n. 3, p. 221-235, 2009.), por exemplo. Com isso, foi inclusive criada a norma NBR 15839 (ABNT, 2010ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 15839: argamassa de assentamento e revestimento de paredes e tetos: CcCaracterização reológica pelo método squeeze-flow. Rio de Janeiro, 2010.) como procedimento padrão de ensaio em argamassas.
As solicitações impostas em argamassas durante o squeeze flow se aproximam das condições da aplicação desses materiais no estado fresco devido ao tipo de fluxo gerado pela redução da altura ao longo do ensaio. O resultado do ensaio é a carga compressiva necessária para impor uma redução controlada da altura da amostra, representado em um gráfico que pode ser dividido em três estágios. No primeiro estágio o material comporta-se como um sólido elástico e apresenta pequenas deformações diretamente relacionadas com sua tensão de escoamento. No segundo estágio há o fluxo viscoso (deformação plástica), em que o material pode sofrer grandes deformações sem aumento expressivo da carga compressiva. No terceiro estágio (enrijecimento por deformação) predominam forças restritivas ao fluxo, que podem ser originadas pela imbricação de partículas ou pela redução da espessura da amostra até próximo à máxima dimensão de partícula que leva à compressão de grãos isolados, o que gera rápido aumento da carga (CARDOSO et al., 2014CARDOSO, F. A. et al. Characterisation of Rendering Mortars by Squeeze-Flow and Rotational Rheometry. Cement and Concrete Research, v. 57, p. 79-87, Mar. 2014.; CARDOSO; JOHN; PILEGGI, 2009CARDOSO, F. A.; JOHN, V. M.; PILEGGI, R. G. Rheological Behavior of Mortars Under Different Squeezing Rates. Cement and Concrete Research, v. 39, n. 9, p. 748-753, 2009.; MIN; ERWIN; JENNINGS, 1994MIN, B. H.; ERWIN, L.; JENNINGS, H. M. Rheological Behaviour of Fresh Cement Paste as Measured by Squeeze Flow. Journal of Materials Science, v. 29, n. 5, p. 1374-1381, 1994.).
A argamassa no estado fresco é uma suspensão multifásica heterogênea com grande extensão granulométrica, em que partículas maiores que 100 µm (agregados) estão imersas em uma matriz aquosa de partículas menores que 100 µm (finos). No caso dos agregados as forças de massa (atrito, impacto, etc.) são predominantes, enquanto nas partículas finas as forças superficiais (van der Waals, atração e repulsão, etc.) têm maior relevância (ROMANO; CARDOSO; PILEGGI, 2011ROMANO, R. C. O.; CARDOSO, F. A.; PILEGGI, R. G. Propriedades do Concreto no Estado Fresco. In: ISAIA, G. C. (Org.). Concreto: ciência e tecnologia. São Paulo: Ibracon, 2011.). Dessa forma, pode-se considerar as argamassas como um sistema complexo, em que atuam forças de diferentes naturezas e que, devido a sua heterogeneidade intrínseca, ainda estão sujeitas à separação de fases. O fluxo diferencial entre as fases (principalmente sólido-líquido) pode ser gerado pelas solicitações impostas durante os diversos momentos do processamento das argamassas no estado fresco, seja em etapas de espera, transporte e aplicação prática do material, ou mesmo durante o ensaio de caracterização reológica. No squeeze flow a separação líquido-sólido pode levar à ocorrência precoce do terceiro estágio e deve ser considerada na análise dos resultados. No entanto, a previsão sobre a manifestação desse evento é complexa, pois depende tanto das características do material - por exemplo, permeabilidade do sistema granular e viscosidade da fase líquida - quanto de parâmetros do teste - configuração, rugosidade das placas e velocidade de deslocamento (CARDOSO et al., 2015CARDOSO, F. A. et al. Parallel-Plate Rotational Rheometry of Cement Paste: influence of the squeeze velocity during gap positioning. Cement and Concrete Research, v. 75, p. 66-74, 2015.).
O comportamento reológico de argamassas é influenciado pelas quantidades e características químicas e físicas das matérias-primas, e também pelas interações entre as partículas. Por isso, para avaliar alguns fenômenos de maneira isolada é interessante reduzir a quantidade de fatores que influenciam o fluxo do material. Dessa forma, diversos pesquisadores utilizaram suspensões formadas por fluidos com comportamento mais simples, como óleo ou silicone, e esferas de vidro para simular macropartículas em estudos com reômetros (FERRARIS et al., 2016FERRARIS, C. F. et al. Calibration of Rheometers for Cementitious Materials. In: INTERNATIONAL CONCRETE SUSTAINABILITY CONFERENCE, Washington, 2016. Proceedings… Washington, 2016.; KOEHLER; FOWLER, 2004KOEHLER, E. P.; FOWLER, D. W. Development of a portable Rheometer for Fresh Portland Cement Concrete. Austin, 2004. Thesis - International Center for Aggregates Research, The University of Texas, Austin, 2004.; SAKANO, 2016SAKANO, V. K. Metodologia Para Aquisição de Sinal Elétrico e Tratamento de Dados em Reômetros Servo Controlados. São Paulo, 2016. Dissertação (Mestrado em Engenharia Civil) - Escola Politécnica, Universidade de São Paulo, São Paulo, 2016.) e squeeze flow (COLLOMB; CHAARI; CHAOUCHE, 2004COLLOMB, J.; CHAARI, F.; CHAOUCHE, M. Squeeze Flow of Concentrated Suspensions of Spheres in Newtonian and shear-Thinning Fluids. Journal of Rheology, v. 48, n. 2, p. 405-416, 2004.; DELHAYE; POITOU; CHAOUCHE, 2000DELHAYE, N.; POITOU, A.; CHAOUCHE, M. Squeeze Flow of Highly Concentrated Suspensions of Spheres. Journal of Non-Newtonian Fluid Mechanics, v. 94, n. 1, p. 67-74, 2000.; NIKKHOO et al., 2013NIKKHOO, M. et al. Normal Stress Distribution in Highly Concentrated Suspensions Undergoing Squeeze Flow. Rheologica Acta, v. 52, n. 2, p. 155-163, 2013.). Com materiais de referência mais homogêneos e com características bem definidas, a influência de alguns parâmetros sobre o comportamento reológico é minimizada ou mesmo evitada (reatividade, efeito de forças superficiais e morfologia de partículas), e, adicionalmente, problemas de amostragem e mistura são reduzidos, o que melhora a repetibilidade dos resultados e possibilita uma resposta mais clara do fenômeno de interesse.
Como parte de uma linha de pesquisa mais ampla para a compreensão do comportamento reológico de argamassas e dos fatores que afetam o fluxo em solicitações de squeeze flow, este trabalho tem como objetivo estudar a influência da viscosidade da fase líquida e sua interação física com as macropartículas em suspensões concentradas formadas por materiais de referência. Silicones e esferas de vidro foram empregados, de forma a simplificar o sistema, mas mantendo algumas características relevantes em relação ao comportamento reológico que remetessem às de uma argamassa. Os silicones utilizados tinham três viscosidades em uma ampla faixa que abrange as encontradas em diferentes pastas de cimento. As esferas possuem uma dimensão semelhante à dos agregados comumente empregados em argamassas, mas com geometria esférica quase perfeita e superfícies lisas. Foram avaliadas suspensões em duas concentrações de sólidos, sendo uma acima e uma abaixo da densidade de empacotamento experimental das esferas, representando condições de diferentes tipos de materiais cimentícios em que fenômenos diferentes predominam no fluxo. Os testes de squeeze flow foram realizados em três taxas de deslocamento. Ainda, para complementar a compreensão dos fenômenos envolvidos, um parâmetro relacionado à permeabilidade do sistema granular foi determinado através de experimentos que utilizam água e os silicones.
Materiais
Fase líquida
Neste trabalho foram utilizados silicones (Dow Corning) com viscosidades cinemáticas de 100, 1.000 e 10.000 cSt como fase líquida das suspensões, todos com densidade próxima de 1 g/cm³. A Tabela 1 apresenta as propriedades dos silicones.
As viscosidades dinâmicas se aproximam da ordem de grandeza encontrada em pastas de cimento com relação a/c entre 0,3 e 0,4, que costumam apresentar valores em torno de 1.000 cP (STRUBLE; SUN, 1995STRUBLE, L.; SUN, G.-K. Viscosity of Portland Cement Paste as a Function of Concentration. Advanced Cement Based Materials, v. 2, n. 2, p. 62-69, 1995.). Quando se utilizam aditivos dispersantes, esse valor diminui para a faixa de 100 cP (FERRARIS, 1999FERRARIS, C. F. Measurement of the Rheological Properties of Cement Paste: a new approach. In: INTERNATIONAL RILEM CONFERENCE ON THE ROLE OF ADMIXTURES IN HIGH PERFORMANCE CONCRETE, Monterrey, 1999. Proceedings… Monterrey: 1999.), enquanto com aditivos celulósicos a viscosidade aumenta para a ordem de 10.000 cP (BETIOLI, 2007BETIOLI, A. M. Influência dos Polímeros MHEC e EVA na Hidratação e Comportamento Reológico de Pastas de Cimento Portland. Florianópolis, 2007. Tese (Doutorado em Engemharia Civil) - Escola de Engenharia, Universidade Federal de Santa Catarina, Florianópolis, 2007.).
Fase sólida
Foram utilizadas esferas de vidro peneiradas entre as malhas de 1 mm e 1,18 mm de abertura, de forma a se obter uma granulometria monomodal. A distribuição de tamanho de partículas obtida por peneiramento é apresentada na Figura 1, em que 100% das partículas encontram-se na faixa selecionada. Adotou-se essa fração granulométrica por se aproximar da dimensão máxima de uma areia média, comumente utilizada em argamassas.
Distribuição granulométrica das esferas de vidro obtida por peneiramento e comparação com a granulometria de matérias-primas comumente utilizadas em argamassas. No gráfico é apresentada uma imagem das esferas por microscopia óptica, com aumento de 50 vezes em um microscópio digital do modelo Hirox KH-7700
Foram utilizadas esferas com relação de aspecto (razão entre as dimensões máxima e mínima da projeção da partícula) média de 97% e esfericidade (relação entre o perímetro de um círculo com a mesma área da projeção da partícula com o perímetro da projeção) média de 95% (determinados por análise dinâmica de imagens, QICPIC, Sympatec). Esses parâmetros indicam partículas com formato bem próximo de esferas ideais. O controle das características físicas das partículas foi feito de forma a minimizar possíveis influências no comportamento reológico das suspensões resultantes de aspectos morfológicos e de rugosidade superficial.
A porosidade de empacotamento das esferas, obtida em um equipamento GeoPyc 1360 (Micromeritics), foi de 64%. Por isso, foram preparadas suspensões com teores de sólidos em volume de 60%, em que o silicone recobre complemente as esferas e as afasta ligeiramente uma da outra, e 70%, nas quais não há silicone suficiente para recobrir completamente as partículas e preencher os vazios entre elas. O sistema com 60% de macropartículas se aproxima de uma argamassa de revestimento com alto teor de agregados (CARDOSO, 2009CARDOSO, F. A. Método de Formulação de Argamassas de Revestimento Baseado em Distribuição Granulométrica e Comportamento Reológico. São Paulo, 2009. Tese (Doutorado em Engenharia Civil) - Escola Politécnica, Universidade de São Paulo, São Paulo, 2009.), enquanto o sistema com teor de 70% se assemelha à de argamassas secas de contrapiso, concretos secos, materiais extrudados ou prensados (SULISTYANA et al., 2014SULISTYANA et al. The Influence of Compression Applied During Production to the Compression Strength of Dry Concrete: an experimental study. Procedia Engineering, v. 95, p. 465-472, 2014.).
Além dos ensaios realizados nas suspensões preparadas, foram também realizados ensaios apenas com esferas com o intuito de observar o comportamento do conjunto de partículas sob compressão, sem a ação da fase líquida, tendo a força de atrito como principal fator atuante.
Métodos
Preparação das amostras
As esferas e o silicone foram misturados manualmente por 5 min mantendo o teor de sólido em 60% ou 70% em volume. Ao término da mistura era possível observar a presença de algumas bolhas, e, por isso, a suspensão foi submetida a vácuo por até 25 min para forçar a saída delas. O procedimento utilizado está ilustrado na Figura 2.
Squeeze flow
A compressão uniaxial das amostras foi realizada em uma máquina universal de ensaios Instron, modelo 5569, com célula de carga de 1 kN. As suspensões foram colocadas dentro de um molde de PVC de 101 mm de diâmetro e 20 mm de altura centralizado sobre um prato metálico. O molde de PVC foi mantido durante todo o teste, atuando como um confinamento lateral, pois as amostras ensaiadas não apresentavam tensão de escoamento suficiente para se sustentar e manter o formato necessário antes do teste. Esse conceito foi proposto por Min, Erwin e Jennings (1994MIN, B. H.; ERWIN, L.; JENNINGS, H. M. Rheological Behaviour of Fresh Cement Paste as Measured by Squeeze Flow. Journal of Materials Science, v. 29, n. 5, p. 1374-1381, 1994.) para possibilitar a análise de pastas de cimento. Por conta das macropartículas, as dimensões do molde e do punção precisam ser maiores e por isso seguem a configuração utilizada por Kudo (2012KUDO, E. K. Caracterização Reológica de Argamassas Colantes. São Paulo: Universidade de São Paulo, 2012.) no estudo de argamassas colantes, conforme ilustrado na Figura 3.
Os ensaios foram realizados com compressão de 8 mm da amostra (40% da altura do molde) utilizando-se um punção de 50,8 mm de diâmetro. Para cada suspensão preparada foram realizados ensaios com velocidades de 0,01 mm/s, 0,1 mm/s e 1,0 mm/s no controle de deslocamento do atuador.
Permeâmetro de carga permanente
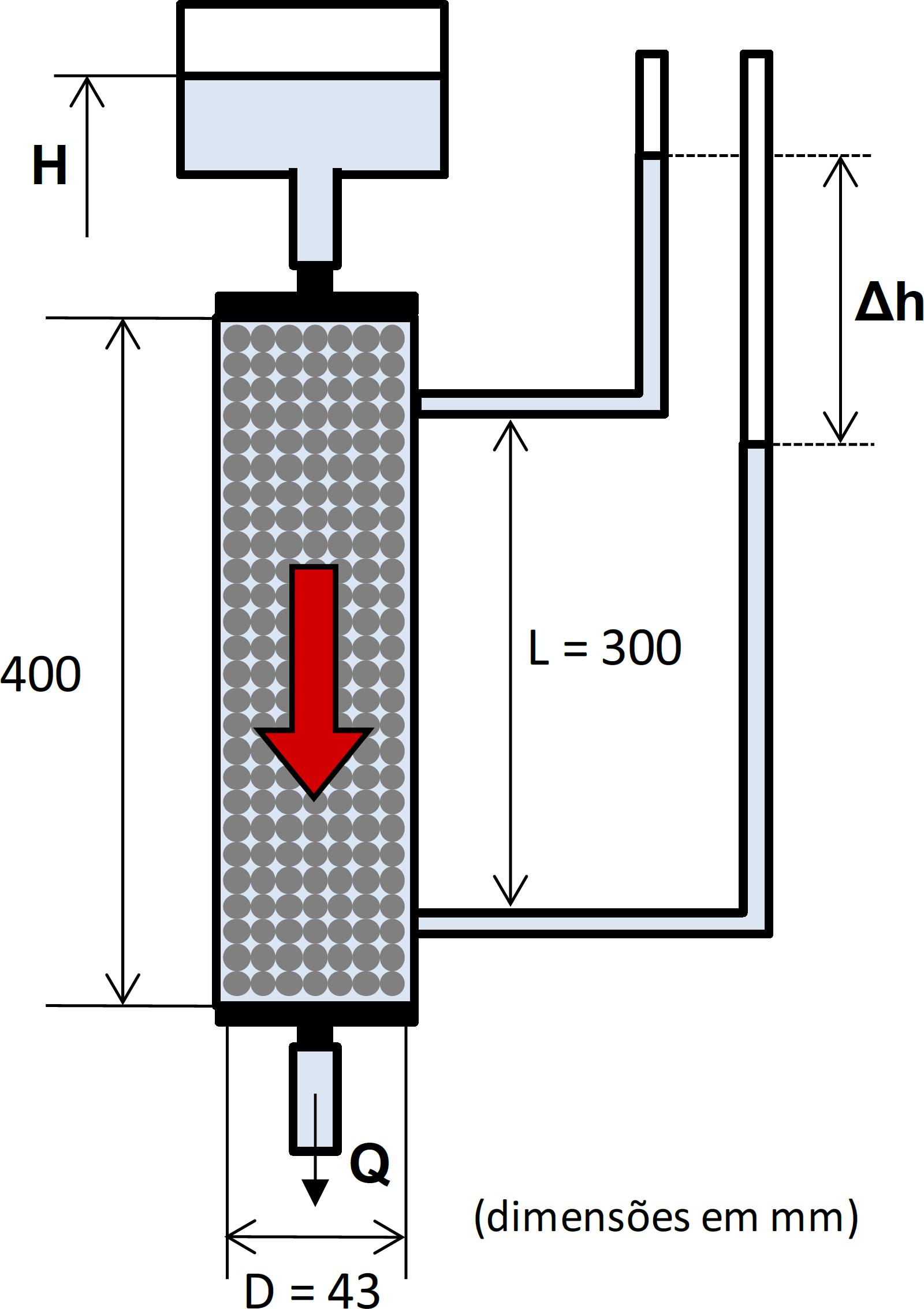
Como durante o squeeze flow pode ocorrer um fluxo diferencial entre as fases (líquida e sólida), é interessante estudar o mecanismo de percolação do fluido pelo meio particulado. Dessa forma, a condutividade hidráulica do sistema granular das esferas de vidro foi avaliada através de um permeâmetro de carga permanente com os silicones utilizados e com água. O equipamento é esquematizado na Figura 4.
A amostra foi posicionada dentro de um tubo e em seguida o fluido foi adicionado até que todos os vazios fossem preenchidos. Com o auxílio de uma bomba peristáltica o líquido foi mantido em circulação pela amostra até a estabilização da carga. Após o atendimento dessas condições, as medidas da vazão de saída (Q), carga total (H) e perda de carga (Δh) são realizadas. A condutividade hidráulica é determinada conforme a Lei de Darcy (Equação 1).
Resultados e discussões
Os resultados são apresentados em três etapas:
-
esferas sem silicone;
-
suspensões com três silicones diferentes com teor de sólidos de 70%vol; e
-
suspensões com três silicones diferentes com teor de sólidos de 60%vol.
Esferas sem silicone
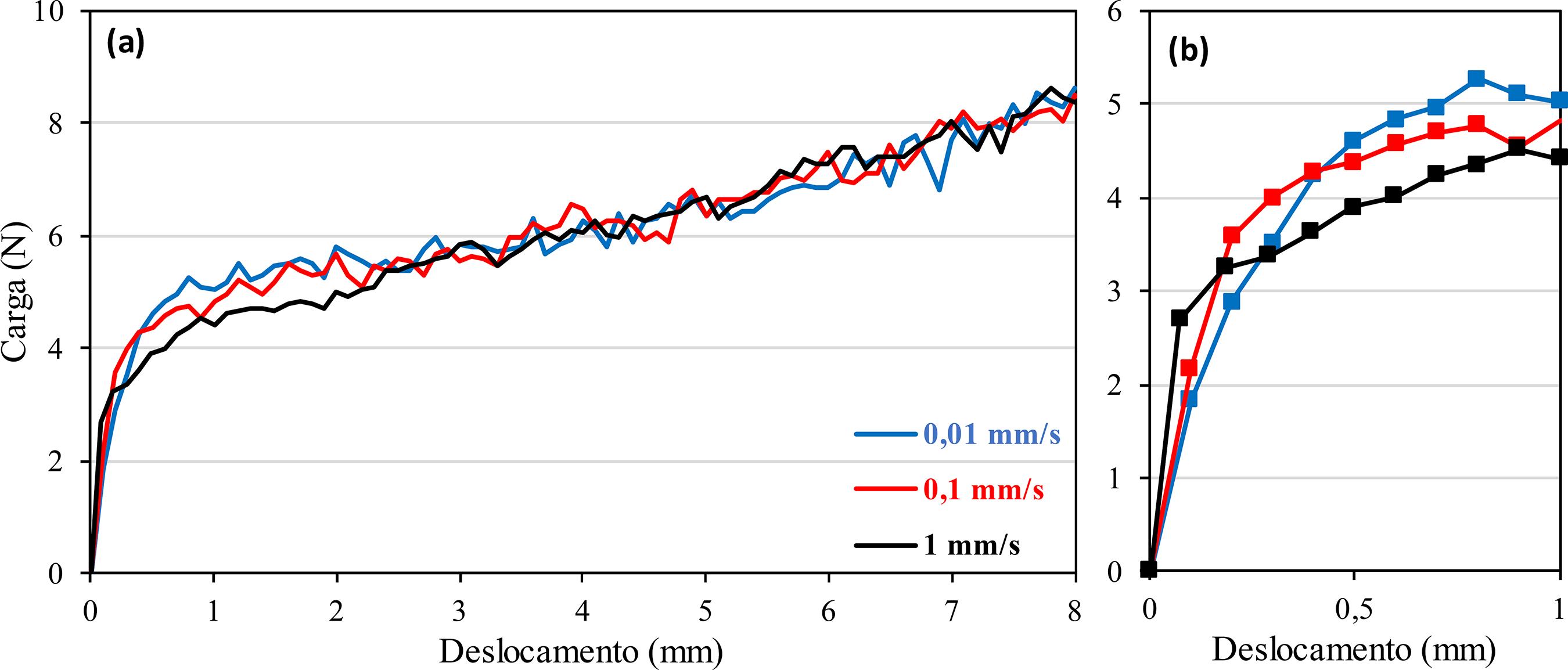
A Figura 5 apresenta o resultado de squeeze flow apenas com as esferas retidas no molde sem fase líquida para as três velocidades de deslocamento.
Observa-se que, independentemente da velocidade de ensaio, os níveis de carga atingidos são semelhantes. Para as três curvas há um crescimento inicial da carga devido ao atrito entre as esferas. Em seguida, esse crescimento segue em uma taxa menor, quando o sistema particulado já está em movimento. Com o decorrer do ensaio, a redução da espessura abaixo do punção dificulta a movimentação das partículas, e, por isso, a carga continua crescendo.
As três curvas apresentadas diferenciam-se apenas no trecho inicial, até 2,5 mm de deslocamento. Logo no início do ensaio (deslocamento de 0,1 mm), para maior velocidade de deslocamento (1,0 mm/s), há uma taxa de crescimento da carga mais acentuada se comparada às demais velocidades. Nesse caso, há pouco tempo para movimentação das esferas, e consequentemente a carga aumenta devido ao atrito gerado entre elas no rápido deslocamento do punção, o que forma uma espécie de estrutura granular instável. Ao atingir a carga de aproximadamente 3 N, há o rompimento dessa estrutura com a liberação de parte das esferas, fazendo com que o crescimento da carga seja atenuado. A partir daí o sistema de esferas apresenta crescimento constante da carga.
Já para os ensaios com velocidades de 0,01 mm/s e 0,1 mm/s, o que se observou foi um crescimento inicial menos acentuado, já que houve mais tempo para que as esferas se deslocassem no sentido radial da amostra. Assim, a formação da estrutura granular se dá mais lentamente, gerando uma condição ligeiramente mais estável e um sistema granular um pouco mais empacotado, que requer maior carga para seu rompimento (aproximadamente 4 N para 0,1 mm/s e 5 N para 0,01 mm/s). Após a quebra da estrutura, o comportamento foi igual nos três ensaios, independentemente da velocidade.
Suspensões com teor de sólidos de 70%
Nesta seção é analisado o comportamento reológico das suspensões com silicones de diferentes viscosidades e teor de sólidos de 70%. Vale destacar que nesse sistema a fase líquida recobre as esferas de vidro, no entanto ainda não é suficiente para preencher completamente os vazios do sistema granular. Dessa forma, as partículas já estão em contato no início do movimento com silicone presente em sua superfície. Nessa condição estão presentes no fluxo alguns fenômenos cujos fundamentos serão explicados a seguir.
O silicone intersticial pode ter ação lubrificante no contato entre as esferas. Em relação ao caso sem fase líquida, em que o atrito entre as partículas resulta em determinado nível de resistência ao movimento, o escorregamento pode ser facilitado pela presença do fluido. Esse efeito é ainda mais evidente no caso de esferas com superfície lisa, pois há apenas um ponto de contato entre duas partículas, enquanto materiais com superfícies irregulares podem apresentar imbricação e travamento entre arestas e faces dos grãos. A lubrificação está diretamente relacionada à viscosidade, e quanto mais viscoso for o fluido, maior será a ação lubrificante (GUO; WONG; GUO, 2017GUO, L.; WONG, P. L.; GUO, F. Effects of Viscosity and Sliding Speed on Boundary Slippage in Thin Film Hydrodynamic Lubrication. Tribology International, v. 107, p. 85-93, 2017.).
Suspensões com baixo teor de líquido tendem a formar meniscos entre as superfícies das partículas sólidas, aumentando a coesão do sistema. A coesão é a forma genérica da resistência ao cisalhamento quando não há nenhuma pressão externa atuando sobre a suspensão, e pode ser originada de duas formas: ligação exercida pelo potencial atrativo de natureza molecular ou efeito das forças associadas ao menisco (KOOS, 2014KOOS, E. Capillary Suspensions: particle networks formed through the capillary force. Current Opinion in Colloid & Interface Science, v. 19, n. 6, p. 575-584, 2014.; MUKHERJEE; MAZUMDAR, 2010MUKHERJEE, S.; MAZUMDAR, A. Study of Effect of the Variation of Inter-Particle Distance on the Erodibility of a Riverbank Under Cohesion With a New Model. Journal of Hydro-environment Research, v. 4, n. 3, p. 235-242, 2010.). Como as partículas utilizadas neste trabalho são inertes e de grande dimensão, o primeiro efeito citado pode ser considerado desprezível. O efeito da tensão superficial que age ao longo da linha de contato entre os grãos e o filme de silicone (menisco) impede o afastamento das partículas, formando uma estrutura granular coesa.
Normalmente, a coesão aparente induz ao aumento da resistência do sistema, que tem um papel importante em processos tecnológicos e em fenômenos naturais (DUAN; BERGGREN, 2010DUAN, H.; BERGGREN, K. K. Directed Self-Assembly at the 10 nm Scale by Using Capillary Force-Induced Nanocohesion. Nano Letters, v. 10, n. 9, p. 3710-3716, 2010.; REIS et al., 2010REIS, P. M. et al. How Cats Lap: water uptake by felis catus. Science, v. 330, n. 6008, p. 1231-1234, 2010.). Este é um efeito temporário, pois os meniscos tenderão a desfazer-se à medida que o movimento entre os grãos aumente e as deformações sejam muito grandes. Os meniscos podem romper, também, por efeito de saturação ou movimentação do líquido intersticial (PINTO, 2001PINTO, C. de S. Curso Básico de Mecânica dos Solos: exercícios resolvidos. [s.l.]: Oficina de Textos, 2001.).
A energia necessária para romper um menisco formado entre duas partículas esféricas em condições perfeitas de recobrimento de sua superfície, denominada energia de ruptura total (W̃total ), é composta da somatória das energias relacionadas à capilaridade e à viscosidade do fluido, conforme a Equação 2 (PITOIS; MOUCHERONT; CHATEAU, 2001PITOIS, O.; MOUCHERONT, P.; CHATEAU, X. Rupture Energy of a Pendular Liquid Bridge. The European Physical Journal B - Condensed Matter and Complex Systems, v. 23, n. 1, p. 79-86, 2001.).
A energia de ruptura referente às forças capilares (W̃cap ) é função de θ, V e R sendo θ o ângulo de contato formado entre o sólido e o líquido, V o volume do menisco e R o raio da esfera, enquanto a energia de ruptura referente às forças viscosas (W̃visco ) é função de V, R, D, η, v e σ, sendo D a distância de separação entre as partículas, η a viscosidade do fluido, v a velocidade da esfera relativa ao fluido, e σ a tensão superficial. Pitois, Moucheront e Chateau (2001)PITOIS, O.; MOUCHERONT, P.; CHATEAU, X. Rupture Energy of a Pendular Liquid Bridge. The European Physical Journal B - Condensed Matter and Complex Systems, v. 23, n. 1, p. 79-86, 2001. observaram ainda que a distância de ruptura do menisco é função da velocidade de deslocamento da esfera e da viscosidade do fluido; quanto maior esses fatores, maior será a energia necessária para romper esses meniscos.
Para todas as suspensões em estudo nesta seção, a força capilar é praticamente a mesma, uma vez que a tensão superficial dos silicones não apresenta grande variação, conforme indicado na Tabela 1. Com isso, a energia de ruptura será governada predominantemente pela magnitude das forças viscosas.
A seguir, os resultados para as suspensões de teor de sólidos de 70% são apresentados em função da viscosidade do fluido e comparados com os da amostra sem silicone nas três velocidades de deslocamento (Figura 6). Em seguida é realizada uma discussão a respeito dos fenômenos envolvidos durante o fluxo. Por fim, para ilustrá-los, os resultados são apresentados novamente, mas em função da velocidade de deslocamento.
Resultado do squeeze flow para as esferas sem silicone e para as suspensões com teor de sólidos de 70% nas velocidades de deslocamento de (a) 0,01 mm/s, (b) 0,1 mm/s e (c) 1,0 mm/s
Observa-se que para o silicone de menor viscosidade (100 cSt) há aumento da carga nos instantes iniciais em comparação à situação sem silicone devido à coesão gerada pelos meniscos capilares, que proveem ao sistema uma espécie de tensão de escoamento. Para o caso das suspensões com silicones de maiores viscosidades (1.000 e 10.000 cSt) a carga nos instantes iniciais do ensaio (até cerca de 1,0 mm) foi mais baixa inclusive do que o caso sem silicone. Isso acontece por conta da lubrificação, que é mais intensa quanto mais viscoso o fluido, reduzindo, assim, o atrito entre as partículas. Há, portanto, uma concorrência entre as ações da coesão e da lubrificação no início do movimento, e a intensidade de cada fator é determinada pelas características do fluido.
Após esse período inicial, no caso da velocidade de 0,01 mm/s (Figura 6a), não há grande diferença no nível das cargas atingidas para as três suspensões. Já para a velocidade de 0,1 mm/s (Figura 6b) há aumento na carga para os silicones de 1.000 cSt e 10.000 cSt, mais elevado para a maior viscosidade, e esse efeito torna-se ainda mais evidente para a velocidade de 1,0 mm/s (Figura 6c). O acréscimo na carga máxima pode ser relacionado à coesão aparente gerada pela formação de meniscos, que é mais intensa em função da viscosidade e da velocidade. Assim, a carga necessária para impor o deslocamento ao sistema está diretamente relacionada à somatória dos esforços necessários para romper os diversos meniscos existentes na suspensão. Após esse momento de máximo a carga se mantém praticamente estável até a parte final do ensaio.
Os resultados das suspensões com 70% de sólidos são novamente apresentados na Figura 7 em função da velocidade para as diferentes viscosidades com o objetivo de demostrar isoladamente o efeito da velocidade para cada suspensão. No caso da suspensão com o silicone de 100 cSt (Figura 7a) praticamente não houve diferença entre os três ensaios. Com o silicone de 1.000 cSt (Figura 7b) a curva da velocidade de 1,0 mm/s já se destaca em relação às demais, e isso é ainda mais acentuado para a suspensão com o silicone de 10.000 cSt (Figura 7c). Esse efeito confirma as observações feitas com relação à Figura 6, o que demonstra a influência das forças viscosas, que, quando foram mais intensas, levaram à maior coesão do sistema e, consequentemente, ao aumento na carga máxima atingida.
Resultado do squeeze flow para as suspensões com teor de sólidos de 70% e silicone com diferentes viscosidades (a) 100 cSt, (b) 1.000 cSt e (c) 10.000 cSt
Além disso, o deslocamento necessário para que a carga máxima seja atingida também aumenta com a viscosidade. Isso pode ter relação com o aumento da distância necessária para a ruptura dos meniscos em função da viscosidade, conforme discutido anteriormente nos fatores da Equação2; no entanto, é necessário também destacar que a carga demora mais para começar a aumentar quando a viscosidade é maior pela ação lubrificante dos silicones. Assim, no início do ensaio há um escorregamento facilitado, e, por isso, a situação crítica para a ruptura dos meniscos acontece em deslocamentos mais avançados.
As conclusões obtidas a partir dos resultados das suspensões com 70%vol de sólidos são aplicáveis para materiais cimentícios com baixo teor de água (argamassas de contrapiso, componentes extrudados ou prensados, etc.), nos quais o atrito entre as partículas, a viscosidade do fluido e a coesão são os parâmetros de maior influência sobre o comportamento reológico. As implicações práticas dessas observações estão relacionadas ao ajuste da viscosidade do fluido (ou da pasta) às solicitações impostas pelo tipo de processamento de cada produto. Por exemplo, em velocidades de solicitação muito baixas a utilização de um fluido (pasta) com viscosidade mais elevada é recomendada, pois sua capacidade de lubrificação das partículas é maior e, nesse caso, facilita o fluxo. Entretanto, para processos em que as taxas de deformação envolvidas são mais elevadas, uma pasta com uma viscosidade muita alta pode não ser a mais adequada, pois o efeito viscoso para ruptura de meniscos causa um aumento significativo na força necessária para o fluxo do material.
Suspensões com teor de sólidos de 60%
Nesta seção são analisadas as suspensões com 60% de concentração de sólidos (40%vol de líquido). Apesar de a diferença no volume do líquido não ser tão grande em relação ao caso anterior (30%vol de líquido), este representa uma condição bem diferente, em que há silicone suficiente para recobrir e preencher completamente os vazios do sistema granular (36%vol de vazios) e separar as partículas. Dessa forma, não há a formação de meniscos como observado nos sistemas com 70% de sólidos, e, assim, outros fenômenos governam o fluxo.
Na primeira parte da análise, os resultados são apresentados em função da viscosidade do fluido e comparados com os da amostra sem silicone nas três velocidades de ensaio (Figura 8). Em seguida, os mesmos resultados são apresentados em função da velocidade de deslocamento. E, por fim, é realizada uma discussão a respeito dos fenômenos de percolação e arraste.
Resultado do squeeze flow para as esferas sem silicone e para as suspensões com teor de sólidos de 60% nas velocidades de deslocamento de (a) 0,01 mm/s, (b) 0,1 mm/s e (c) 1,0 mm/s
Em todos os casos, independentemente da velocidade, a presença da fase líquida atenuou a taxa de crescimento inicial da carga, se comparado com os resultados sem silicone. Assim como observado no item anterior, o silicone lubrifica as partículas, e como a fase sólida é composta por partículas esféricas o escorregamento interparticular é facilitado, fazendo com que as esferas escapem pela lateral do punção mais facilmente. A diferença para o caso de 70% de sólidos é que a suspensão está saturada, não apresentado uma coesão aparente, já que não há formação de meniscos, e, por isso, no início do ensaio o que governa é a ação lubrificante.
Verifica-se que o aumento a viscosidade do fluido facilita o fluxo da suspensão, pois, ao verificarem-se os resultados da velocidade de 0,01 mm/s (Figura 8a) para um mesmo deslocamento, a carga foi inferior quanto maior foi a viscosidade. Isso ocorre por conta da força de arraste do silicone, que é maior em função da viscosidade e possibilita o carregamento das partículas, o que reduz a segregação e cria um fluxo homogêneo na direção radial. Quando o silicone não consegue carregar as esferas, ocorre fluxo diferencial entre as fases, com percolação do líquido pelo meio poroso do sistema granular. Assim, a concentração de partículas aumenta na região abaixo do punção, levando a maiores cargas em razão do contato entre as esferas. Os mesmos efeitos são verificados para a velocidade de 0,1 mm/s (Figura 8b), exceto nos instantes finais do ensaio, com a suspensão de maior viscosidade (10.000 cSt), em que há inversão da curva, com crescimento da carga.
Já na maior velocidade (Figura 8c) o resultado da suspensão de menor viscosidade (100 cSt) indica a ocorrência de segregação. Para as demais viscosidades (1.000 e 10.000 cSt) se observa a resposta do fluido, e, por isso, a carga é maior de acordo com a viscosidade. Nos instantes finais o crescimento da carga se acentua por causa do confinamento, que cria um efeito de crowding, ou seja, um acúmulo de esferas na borda, que acaba atrapalhando a mobilidade da suspensão. Em baixa velocidade (0,01 mm/s) as partículas têm mais tempo para se acomodar e assim conseguem se deslocar para cima com maior facilidade. Em altas velocidades (0,1 mm/s e 1,0 mm/s) não há tempo suficiente para que as esferas escapem, e ocorre um travamento do sistema, o que leva ao acréscimo de carga.
Como a velocidade tem efeito significativo na ocorrência de separação de fases, a avaliação dos resultados em função da velocidade em cada sistema fornece informações relevantes sobre esse fenômeno. Assim, são apresentados na Figura 9 os mesmos resultados ilustrados anteriormente, focando no efeito da velocidade nas suspensões com silicones de diferentes viscosidades.
Resultado do squeeze flow para as suspensões com teor de sólidos de 60% e silicone com diferentes viscosidades: (a) 100 cSt; (b) 1.000 cSt; e (c) 10.000 cSt
No caso do silicone de menor viscosidade (Figura 9a) a estabilidade da suspensão é menor, e verificou-se que, antes mesmo de iniciar o ensaio, houve considerável sedimentação pela gravidade. Com isso, na parte inicial (até 1 mm de deslocamento, aproximadamente) o punção basicamente pressiona o silicone contra o sistema granular até chegar a uma camada de esferas já praticamente em contato. É possível notar diferença entre as três curvas na parte intermediária (1 mm a 4 mm aproximadamente). Para o resultado de 0,01 mm/s verifica-se aumento da carga mais pronunciado, que pode ser atribuído a uma elevada segregação. Já para a velocidade de 0,1 mm/s a taxa de crescimento se mantém e a carga é inferior às demais velocidades, o que indica menor segregação. O ensaio a 1,0 mm/s tem maior facilidade de carregar as partículas, no entanto apresenta maiores cargas no trecho intermediário, o que pode estar relacionado à resposta do fluido, que se torna mais intensa em maiores velocidades (DELHAYE; POITOU; CHAOUCHE, 2000DELHAYE, N.; POITOU, A.; CHAOUCHE, M. Squeeze Flow of Highly Concentrated Suspensions of Spheres. Journal of Non-Newtonian Fluid Mechanics, v. 94, n. 1, p. 67-74, 2000.). Para a parte final (4 mm a 8 mm) observa-se que, independentemente da velocidade, não houve variação relevante de cargas. Nesse caso, a fase líquida não consegue carregar as partículas, permeando pelo meio poroso, e as esferas entram em contato, empurrando umas às outras.
Nas suspensões com os silicones de 1.000 e 10.000 cSt (Figuras 9b e 9c) não ocorreu edimentação antes do ensaio. Além disso, os resultados não demonstram indícios de segregação significativa porque os fluidos mais viscosos têm maior capacidade de carregar as partículas. O aumento das cargas para os casos de maior velocidade e viscosidade devem-se à resposta do silicone ao rápido deslocamento imposto. Ao final dos ensaios, para as maiores velocidades, também se pode observar o efeito de crowding, destacado anteriormente.
A ocorrência de segregação ou o fluxo homogêneo da suspensão depende da intensidade entre os fenômenos de percolação do fluido através do empacotamento das partículas e do arraste das partículas pela movimentação do fluido. A relação com o fluxo mais homogêneo da suspensão está atrelada à facilidade do líquido em carregar as partículas sólidas. Isso é explicado pela força de arraste (Equação 3), que surge quando um objeto se move através do fluido ou quando o fluido passa pelo objeto (BATCHELOR, 2000BATCHELOR, G. K. An Introduction to Fluid Dynamics. Cambridge: Cambridge University Press, 2000.).
Em que:
-
v é a velocidade do objeto relativa ao fluido;
-
μ é a viscosidade dinâmica; e
-
a é um parâmetro relativo ao tamanho do objeto (para uma esfera de raio r, a = 6πr).
Vale ressaltar que a equação só é válida para fluxo laminar e sem interação entre partículas, no entanto indica a influência desses fatores na força de arraste. Observa-se que todos os fatores possuem relação linear, ou seja, quanto maior a viscosidade do fluido ou a velocidade, maior será sua força de arraste.
Analogamente à força de arraste, a capacidade de permear também depende da viscosidade do fluido. A Equação 4 apresenta a fórmula proposta por Kozeny-Carman para o cálculo da condutividade hidráulica (VARGAS, 1977VARGAS, M. Introdução à Mecânica dos Solos. New York: McGraw-Hill, 1977.).
Em que:
-
Cs é o coeficiente de forma da seção;
-
T0 é a tortuosidade do meio poroso;
-
Ss é a área superficial específica;
-
γ0 é a densidade do fluido;
-
ν é a viscosidade cinemática; e
-
n é a porosidade.
Portanto, pode-se concluir que a permeabilidade depende principalmente do tamanho e do arranjo das partículas, da porosidade intergranular, da densidade e da viscosidade da fase líquida. De maneira geral, para um mesmo material, verifica-se que, quanto maior a viscosidade do fluido, menor será a condutividade hidráulica.
Pelos resultados da Figura 9 e como observado anteriormente, em alguns casos o fluido tem mais condições para carregar as esferas e, em outros, permeia pelos vazios do sistema granular. Por isso, foi realizado um ensaio com um permeâmetro de carga constante para avaliar a condutividade hidráulica das esferas. Conforme indica a Figura 10, as medidas realizadas no permeâmetro mostram relação com a fórmula proposta por Kozeny-Carman, pois, ao aumentar a viscosidade do fluido, ocorreu a redução da condutividade hidráulica.
Determinação da condutividade hidráulica das esferas de vidro em função da viscosidade do fluido através de um permeâmetro de carga permanente e variação da velocidade radial da amostra na borda do punção durante os ensaios de squeeze flow (SF)
O ensaio de permeabilidade indica a facilidade que o fluido tem de percolar pelo meio poroso. Por isso os resultados obtidos foram comparados na Figura 10 com a velocidade radial (vr ), imposta durante cada ensaio de squeeze flow, que pode ser calculada conforme proposto por Laun, Rady e Hassager (1999LAUN, H. M.; RADY, M.; HASSAGER, O. Analytical Solutions for Squeeze Flow With Partial Wall Slip. Journal of Non-Newtonian Fluid Mechanics, v. 81, n. 1/2, p. 1-15, Fev. 1999.). Considerando condição de escorregamento total (interface totalmente lubrificada), é determinada a partir da Equação 5, que leva em consideração a posição radial (r), a altura da amostra (h) e a velocidade do punção (-ḣ). A velocidade radial foi calculada na posição limite (borda do punção) no início e no fim do ensaio.
Vale ressaltar que a condição da amostra tem diferenças nos dois ensaios, considerando que as esferas não se movem no ensaio de permeabilidade. No entanto, os resultados mostram relação. Na Figura 10 verifica-se que em alguns casos a velocidade radial está abaixo da condutividade hidráulica e em outros acima. Quando os valores de solicitação no ensaio de squeeze flow estão distantes da curva de condutividade hidráulica, há a predominância quase total de um dos fenômenos, sendo a percolação para o extremo abaixo (silicone de 100 cSt e velocidade de 0,01 mm/s) e arraste para o extremo acima (10.000 cSt e 1,0 mm/s). Em uma condição intermediária, em que os valores estão próximos, os dois fenômenos ocorrem simultaneamente. Há, portanto, uma zona de transição em que a intensidade dos fenômenos varia de acordo com a relação entre a velocidade de solicitação e a condutividade hidráulica. As diferentes condições apontadas são ilustradas na Figura 11.
Ilustração esquemática do fenômeno de percolação (setas laranjas) e arraste das partículas (setas vermelhas): (a) predominância do carregamento de partículas em que ocorre fluxo mais homogêneo; (b) situação intermediária, com ocorrência de ambos os efeitos; e (c) predominância da percolação, em que ocorre maior separação de fases
Os resultados das suspensões com 60%vol de sólidos podem ser relacionados com situações práticas encontradas em materiais de construção como as argamassas de revestimento, assentamento e colantes. Composições com distribuição granulométrica da areia muito estreitas apresentam baixo empacotamento e, consequentemente, elevada permeabilidade. Assim, para que uma argamassa com esse tipo de areia não seja muito suscetível à separação de fases durante a aplicação (ou em testes de squeeze flow), é preciso que a pasta tenha viscosidade elevada, o que normalmente é obtido através da utilização de cal hidratada ou aditivo retentor de água como os éteres de celulose. Por outro lado, quando há adição de água excessiva em uma argamassa, a viscosidade da pasta é reduzida significativamente, e, mesmo que a distribuição granulométrica da areia seja ampla com bom empacotamento (menor permeabilidade), a tendência à segregação aumenta. Portanto, é importante considerar os fenômenos discutidos nesta seção para compreender as causas da ocorrência da separação de fases em argamassas e como evitá-la, pois o comportamento reológico em solicitações semelhantes às do squeeze flow é consideravelmente afetado pela segregação.
Conclusões
Este trabalho buscou avaliar o comportamento reológico de suspensões em squeeze flow e, ao utilizar um sistema com materiais de referência (silicones e esferas de vidro), foi possível identificar a influência dos principais fatores envolvidos. A seguir são listadas as principais conclusões:
-
no caso das esferas de vidro secas (sem fase líquida) o efeito do atrito é predominante e a influência da velocidade de deslocamento só é perceptível em pequenos deslocamentos. Em menores velocidades há mais tempo para movimentação e empacotamento das partículas, assim a estrutura resultante é mais organizada e estável, necessitando de cargas um pouco maiores para a quebra da estrutura formada;
-
nas suspensões com teor de sólido de 70% não há líquido suficiente para recobrir e preencher os vazios do sistema granular, levando à formação de meniscos capilares entre as partículas. No início do ensaio há competição entre os efeitos de lubrificação e de coesão (gerada pela formação dos meniscos). Para a suspensão com o silicone de menor viscosidade (100 cSt) o efeito do aumento de coesão é predominante, o que causa aumento de carga em relação ao sistema sem silicone, enquanto para os silicones de 1.000 cSt e de 10.000 cSt o efeito da lubrificação é intenso quanto maior a viscosidade, reduzindo o atrito entre as partículas e, consequentemente, causando redução das cargas em pequenos deslocamentos. Quando o sistema já está em movimento contínuo, o fator predominante é a componente viscosa para ruptura dos meniscos, a qual é uma função direta da viscosidade do fluido e da velocidade de solicitação. Assim, quanto maiores esses parâmetros, maiores as cargas necessárias para manter a suspensão em fluxo até o final do teste; e
-
nas suspensões com 60% de sólidos em que o volume de líquido é suficiente para recobrir e afastar as partículas, a viscosidade do fluido, a força de arraste e a permeabilidade do sistema granular influenciam a ocorrência de separação de fases e, também, o comportamento reológico, dependendo da velocidade de solicitação em squeeze flow. Na suspensão com o silicone de baixa viscosidade (100 cSt) a separação de fases é intensa e a velocidade de deslocamento mostrou pouca influência, já que as esferas estão em contato e a força predominante é o atrito entre as partículas. Nas suspensões com silicones de maiores viscosidades (1.000 cSt e 10.000 cSt) o fluxo torna-se mais homogêneo, pois o fluido consegue carregar as partículas, sem a ocorrência significativa de separação de fases mesmo na menor velocidade utilizada. Quanto maiores a viscosidade do silicone e a velocidade de deslocamento, maior é o arraste das partículas e, com isso, menor é a tendência de ocorrência da separação de fases. Isso foi verificado experimentalmente através de resultados que demonstraram que a condutividade hidráulica dos sistemas em questão é reduzida em função da viscosidade do fluido percolante. Portanto, foi possível comprovar que em situações nas quais a velocidade radial em squeeze flow é muito menor ou muito maior do que a condutividade hidráulica do sistema granular, a separação de fases é respectivamente predominante ou inexistente. Já em situações intermediárias há uma zona de transição em que os dois fenômenos ocorrem.
Como os fenômenos básicos discutidos também ocorrem em sistemas de interesse tecnológico, os resultados deste trabalho são relevantes. No caso de produtos cimentícios com baixo teor de água - como argamassas de contrapiso, componentes extrudados ou prensados, ou até mesmo concreto compactado com rolo - as conclusões referentes às suspensões com 70%vol de sólidos são aplicáveis, ou seja, o fluxo (ou deformação) desses materiais é predominantemente influenciado por forças de atrito entre as partículas, capacidade de lubrificação do fluido e coesão gerada pelos meniscos. Já para materiais com teor de água mais elevado - como argamassas de revestimento, assentamento e colantes - os fenômenos atuantes nas suspensões com 60%vol de sólidos (viscosidade do fluido, força de arraste e permeabilidade do sistema granular) têm também influência significativa sobre o comportamento reológico em squeeze flow desses produtos cimentícios.
Agradecimentos
Os autores agradecem à Capes, à FAPESP e à FUSP pelo apoio financeiro a esta pesquisa.
Referências
- ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 15839: argamassa de assentamento e revestimento de paredes e tetos: CcCaracterização reológica pelo método squeeze-flow. Rio de Janeiro, 2010.
- BATCHELOR, G. K. An Introduction to Fluid Dynamics Cambridge: Cambridge University Press, 2000.
- BETIOLI, A. M. Influência dos Polímeros MHEC e EVA na Hidratação e Comportamento Reológico de Pastas de Cimento Portland Florianópolis, 2007. Tese (Doutorado em Engemharia Civil) - Escola de Engenharia, Universidade Federal de Santa Catarina, Florianópolis, 2007.
- CARDOSO, F. A. Método de Formulação de Argamassas de Revestimento Baseado em Distribuição Granulométrica e Comportamento Reológico São Paulo, 2009. Tese (Doutorado em Engenharia Civil) - Escola Politécnica, Universidade de São Paulo, São Paulo, 2009.
- CARDOSO, F. A. et al Characterisation of Rendering Mortars by Squeeze-Flow and Rotational Rheometry. Cement and Concrete Research, v. 57, p. 79-87, Mar. 2014.
- CARDOSO, F. A. et al Parallel-Plate Rotational Rheometry of Cement Paste: influence of the squeeze velocity during gap positioning. Cement and Concrete Research, v. 75, p. 66-74, 2015.
- CARDOSO, F. A.; JOHN, V. M.; PILEGGI, R. G. Rheological Behavior of Mortars Under Different Squeezing Rates. Cement and Concrete Research, v. 39, n. 9, p. 748-753, 2009.
- CHALENCON, F. et al Lubricated Compression and X-Ray Microtomography to Analyse the Rheology of a Fibre-Reinforced Mortar. Rheologica Acta, v. 49, n. 3, p. 221-235, 2009.
- COLLOMB, J.; CHAARI, F.; CHAOUCHE, M. Squeeze Flow of Concentrated Suspensions of Spheres in Newtonian and shear-Thinning Fluids. Journal of Rheology, v. 48, n. 2, p. 405-416, 2004.
- DELHAYE, N.; POITOU, A.; CHAOUCHE, M. Squeeze Flow of Highly Concentrated Suspensions of Spheres. Journal of Non-Newtonian Fluid Mechanics, v. 94, n. 1, p. 67-74, 2000.
- DUAN, H.; BERGGREN, K. K. Directed Self-Assembly at the 10 nm Scale by Using Capillary Force-Induced Nanocohesion. Nano Letters, v. 10, n. 9, p. 3710-3716, 2010.
- ENGMANN, J.; SERVAIS, C.; BURBIDGE, A. S. Squeeze Flow Theory and Applications to Rheometry: a review. Journal of Non-Newtonian Fluid Mechanics, v. 132, n. 1/3, p. 1-27, 15 dez. 2005.
- FERRARIS, C. F. Measurement of the Rheological Properties of Cement Paste: a new approach. In: INTERNATIONAL RILEM CONFERENCE ON THE ROLE OF ADMIXTURES IN HIGH PERFORMANCE CONCRETE, Monterrey, 1999. Proceedings… Monterrey: 1999.
- FERRARIS, C. F. et al Calibration of Rheometers for Cementitious Materials. In: INTERNATIONAL CONCRETE SUSTAINABILITY CONFERENCE, Washington, 2016. Proceedings… Washington, 2016.
- GUO, L.; WONG, P. L.; GUO, F. Effects of Viscosity and Sliding Speed on Boundary Slippage in Thin Film Hydrodynamic Lubrication. Tribology International, v. 107, p. 85-93, 2017.
- KOEHLER, E. P.; FOWLER, D. W. Development of a portable Rheometer for Fresh Portland Cement Concrete Austin, 2004. Thesis - International Center for Aggregates Research, The University of Texas, Austin, 2004.
- KOOS, E. Capillary Suspensions: particle networks formed through the capillary force. Current Opinion in Colloid & Interface Science, v. 19, n. 6, p. 575-584, 2014.
- KUDO, E. K. Caracterização Reológica de Argamassas Colantes São Paulo: Universidade de São Paulo, 2012.
- LAUN, H. M.; RADY, M.; HASSAGER, O. Analytical Solutions for Squeeze Flow With Partial Wall Slip. Journal of Non-Newtonian Fluid Mechanics, v. 81, n. 1/2, p. 1-15, Fev. 1999.
- MIN, B. H.; ERWIN, L.; JENNINGS, H. M. Rheological Behaviour of Fresh Cement Paste as Measured by Squeeze Flow. Journal of Materials Science, v. 29, n. 5, p. 1374-1381, 1994.
- MUKHERJEE, S.; MAZUMDAR, A. Study of Effect of the Variation of Inter-Particle Distance on the Erodibility of a Riverbank Under Cohesion With a New Model. Journal of Hydro-environment Research, v. 4, n. 3, p. 235-242, 2010.
- NIKKHOO, M. et al Normal Stress Distribution in Highly Concentrated Suspensions Undergoing Squeeze Flow. Rheologica Acta, v. 52, n. 2, p. 155-163, 2013.
- PINTO, C. de S. Curso Básico de Mecânica dos Solos: exercícios resolvidos. [s.l.]: Oficina de Textos, 2001.
- PITOIS, O.; MOUCHERONT, P.; CHATEAU, X. Rupture Energy of a Pendular Liquid Bridge. The European Physical Journal B - Condensed Matter and Complex Systems, v. 23, n. 1, p. 79-86, 2001.
- REIS, P. M. et al How Cats Lap: water uptake by felis catus. Science, v. 330, n. 6008, p. 1231-1234, 2010.
- ROMANO, R. C. O.; CARDOSO, F. A.; PILEGGI, R. G. Propriedades do Concreto no Estado Fresco. In: ISAIA, G. C. (Org.). Concreto: ciência e tecnologia. São Paulo: Ibracon, 2011.
- SAKANO, V. K. Metodologia Para Aquisição de Sinal Elétrico e Tratamento de Dados em Reômetros Servo Controlados São Paulo, 2016. Dissertação (Mestrado em Engenharia Civil) - Escola Politécnica, Universidade de São Paulo, São Paulo, 2016.
- STRUBLE, L.; SUN, G.-K. Viscosity of Portland Cement Paste as a Function of Concentration. Advanced Cement Based Materials, v. 2, n. 2, p. 62-69, 1995.
- SULISTYANA et al The Influence of Compression Applied During Production to the Compression Strength of Dry Concrete: an experimental study. Procedia Engineering, v. 95, p. 465-472, 2014.
- TOUTOU, Z.; ROUSSEL, N.; LANOS, C. The Squeezing Test: a tool to identify firm cement-based material's rheological behaviour and evaluate their extrusion ability. Cement and Concrete Research, v. 35, n. 10, p. 1891-1899, 2005.
- VARGAS, M. Introdução à Mecânica dos Solos New York: McGraw-Hill, 1977.
Datas de Publicação
-
Publicação nesta coleção
Jan-Mar 2018
Histórico
-
Recebido
05 Fev 2016 -
Aceito
17 Jun 2017