Resumo
A avaliação de imóveis, que auxilia na definição do valor de mercado, é uma ciência importante e com vasto campo de atuação, seja na cobrança de impostos, transações comerciais, seguros e perícias judiciais, por exemplo. Este trabalho apresenta a construção de um modelo de regressão linear para determinação do valor de mercado (variável dependente) de apartamentos residenciais na cidade de Fortaleza, CE. O banco de dados estudado apresenta 17.493 apartamentos, divididos em 227 tipos de planta em um total de 154 empreendimentos lançados entre os anos de 2011 a 2014. O modelo desenvolvido foi obtido utilizando-se a regressão linear múltipla associada à técnica de ridge regression para solucionar o problema de multicolinearidade existente. Na análise de 30 variáveis (12 quantitativas e 18 variáveis qualitativas do tipo dummy) chegou-se a uma equação com 6 variáveis, que atende aos pressupostos teóricos para a sua existência.
Palavras-chave:
Valor de mercado; Avaliação de imóveis; Regressão linear múltipla
Abstract
The valuation of real estate, which assists in the definition of market value, is an important science with a wide field of action, which includes the collection of taxes, commercial transactions, insurance and judicial expertise. This study presents the construction of a linear regression model to determine the market value (dependent variable) of residential apartments in the city of Fortaleza-CE. The studied database presents 17,493 apartments, divided into 227 plan types in a total of 154 projects launched between the years of 2011 and 2014. The model developed was obtained using Multiple Linear Regression associated with the Ridge Regression technique to solve the existing multicollinearity problem. In the analysis of 30 variables (12 quantitative and 18 dummy type qualitative variables), an equation with 6 variables was reached, which meets the theoretical assumptions for its existence.
Keywords:
Real estate; Market value; Property valuers; Multiple linear regression
Introdução
O mercado imobiliário caracteriza-se por proporcionar o desenvolvimento do espaço urbano.
De maneira ampla, o setor imobiliário se delineia a partir do conjunto de atividades relacionadas às etapas do trabalho, antes, durante e depois da construção do imóvel. O processo como um todo passa pela fabricação e comercialização de insumos, aquisição de terrenos até o processo construtivo. Outras atividades fora do âmbito da construção civil são essenciais: promoção de campanhas de marketing, venda das unidades, serviços de corretagem e financiamentos bancários (podendo acontecer por parte da construtora e/ou do comprador). Após a conclusão do empreendimento, há uma grande quantidade de serviços relacionados ao seu funcionamento, como administração, segurança, limpeza, manutenção de instalações e equipamentos, aluguéis, revenda e reformas, por exemplo (BOTELHO, 2005BOTELHO, A. O Financiamento e a Financeirização do Setor Imobiliário: uma análise da produção do espaço e da segregação sócio-espacial através do estudo do mercado da moradia na cidade de São Paulo. São Paulo, 2005. Tese (Doutorado) - Universidade de São Paulo, São Paulo, 2005.). Dessa forma, o mercado imobiliário provoca uma grande movimentação financeira e promove o desenvolvimento de diversos serviços não exclusivos do setor imobiliário.
Além de insumos da construção civil, o setor imobiliário também consome espaços, existindo limites e diminuição da produção em um contexto espacial. Mas em contrapartida essa limitação proporciona a expansão da construção em novas áreas, ocasionando a ocupação e o desenvolvimento destas. Assim, essa concentração fundiária e os estoques de terrenos podem permitir a especulação imobiliária e gerar lucros a partir do desenvolvimento de novas regiões em desenvolvimento (SILVA, 1997SILVA, H. M. B. Terra e Moradia: que papel para o município. São Paulo, 1997. Tese (Doutorado em Engenharia Civil) - Escola de Engenharia, Universidade de São Paulo, São Paulo, 1997.).
Abramo (2007)ABRAMO, P. A Cidade Caleidoscópica: coordenação espacial e convenção urbana: uma perspectiva heterodoxa para a economia urbana. Rio de Janeiro: Bertrand Brasil, 2007. discorre sobre o ciclo do avanço imobiliário nas regiões das cidades ao informar que, com o deslocamento dos investimentos, as empresas do segmento são induzidas a, além de buscar novas áreas, incluir novos elementos nos seus produtos que os diferenciem dos demais concorrentes. O autor também ressalta a importância desse fluxo no processo de inovação dos produtos.
A alta taxa de retorno das empresas é explicada por Rocha Lima Júnior (2014)ROCHA LIMA JUNIOR, J. Movimentos de Preços de Imóveis Residenciais no Brasil: Crônica da Bolha Anunciada e os Preços Adiante. In: LARES INTERNATIONAL CONFERENCE, 14., Rio de Janeiro, 2014. Anais... Rio de Janeiro, 2014., que defende a exploração de momentos positivos no mercado, mas sem uma grande movimentação no valor de mercado a ponto de invalidar o poder de compra dos consumidores, pois a partir desse ponto os empreendimentos podem ter seus resultados comprometidos.
Quesado (2012)QUESADO, W. Atributos de escolha da casa própria da classe C e sua relação com o ciclo de vida familiar. 2012. Dissertação (Mestrado em Administração) - Pós-Graduação em Administração e Controladoria, Universidade Federal do Ceará, Fortaleza, 2012. defende que os valores dados pelos clientes devem ser estudados para que possam ser explorados nos projetos de desenvolvimento de produtos. Em vasto estudo, Freitas (2000)FREITAS, A. A. F. Segmentação do Mercado Imobiliário Utilizando Dados de Preferência Declarada. Florianópolis, 2000. Tese (Doutorado em Engenharia de Produção) - Programa de Pós-graduação em Engenharia de Produção, Universidade Federal de Santa Catarina, Florianópolis, 2000. analisou as características declaradas mais importantes pelos consumidores, informando quais características um empreendimento deve ter para saciar seus anseios. Mas, para Brandstetter (2014)BRANDSTETTER, M. C. G. O. Pesquisa Para o Marketing Imobiliário Por Meio da Investigação do Ciclo de Vida Familiar. In: ENCONTRO NACIONAL DE ENGENHARIA DE PRODUÇÃO, Curitiba, 2014. Anais... Curitiba, 2014., mesmo com vasta literatura mostrando a importância do conhecimento dos anseios dos clientes, muitas empresas construtoras e incorporadoras ainda realizam seus novos empreendimentos apenas com seus conhecimentos empíricos de mercado.
As formas de avaliação do valor de mercado de um imóvel no Brasil são regulamentadas pela NBR 14653 (ABNT, 2001ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-01: avaliação de bens. Rio de Janeiro, 2001., 2011ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-02: imóveis urbanos. Rio de Janeiro, 2011.), que, diante das metodologias utilizadas internacionalmente, é muito básica e tem muito a evoluir. O tratamento científico é a forma de tratamento de dados mais empregada, e com a utilização de regressões lineares vários autores chegam às suas conclusões dentro da engenharia de avaliações. Utilizando essa técnica é possível, segundo Radegaz (2011)RADEGAZ, N. J. Avaliação de Bens: princípios básicos e aplicações. São Paulo: Liv. e Ed. Universitária de Direito, 2011., encontrar uma fórmula linear para se estimar uma variável a partir de outras.
A engenharia de avaliações se torna uma ciência importante no mercado imobiliário por determinar o valor, custos ou direitos sobre um imóvel (DANTAS, 2005DANTAS, R. A. Engenharia de Avaliações: uma introdução à metodologia científica. São Paulo: Pini, 2005.). O modelo proposto por um cientista deve ser o mais claro e objetivo possível (BRAULIO, 2005BRAULIO, S. N. Proposta de Uma Metodologia Para Avaliação de Imóveis Urbanos Baseado em Métodos Estatísticos Multivariados. Curitiba, 2005. 130 f. Dissertação (Mestrado em Ciências) - Programa de Pós-Graduação em Métodos Numéricos em Engenharia, Universidade Federal do Paraná, Curitiba, 2005.).
Este estudo desenvolveu uma equação, por meio de regressão linear múltipla, para predizer o valor de mercado de apartamentos residenciais de Fortaleza, CE, em função das características do imóvel avaliado, sejam elas quantitativas ou qualitativas. A multicolinearidade encontrada durante a construção do modelo foi corrigida com a utilização de ridge regression, evitando que fossem eliminadas variáveis importantes e garantindo a qualidade do modelo proposto.
Referencial teórico
A engenharia de avaliações é definida por Aguiar (1998)AGUIAR, J. B. Introdução à Engenharia de Avaliações e Perícias. In: INSTITUTO MINEIRO DE AVALIAÇÕES E PERÍCIAS DE ENGENHARIA. Fundamentos de Avaliações Patrimoniais e Perícias de Engenharia: curso básico do IMAPE. São Paulo: Pini, 1998. como um conjunto de processos em busca de definir tecnicamente o valor de determinado bem. Dantas (2003)DANTAS, R. A. Engenharia de Avaliações: uma introdução à metodologia científica. São Paulo: Pini, 2003. complementa ao informar que essa engenharia é uma junção de conhecimentos tanto de engenharia civil, quanto de arquitetura, ciências sociais e da natureza, com a mesma finalidade de determinar, por meio de técnicas, o valor do imóvel. Dessa forma, a engenharia de avaliações não é uma ciência exata, em que profissionais com conhecimento adequado buscam estimar os valores de atributos específicos (MOREIRA, 1997MOREIRA, A. L. Princípios de Engenharia de Avaliações. 4. ed. rev. e ampl. São Paulo: Pini, 1997.).
O crescimento urbano e imobiliário é um problema que deve ser acompanhado de perto, pois não pode ser regulado livremente por especulações e forças de mercado. A importância da engenharia de avaliações está associada a esse crescimento desordenado das cidades aliado à incapacidade de se planejar por meio de políticas públicas e privadas (MARTINE; MCGRANAHAM, 2010MARTINE, G; MCGRANAHAN. A Transição Urbana Brasileira: trajetória, dificuldades e lições aprendidas. In: BAENINGER, R. (Org.). População e Cidades: subsídios para o planejamento e para as políticas sociais. Campinas: Núcleo de Estudos de População/Unicamp, 2010.). Portanto, essa ciência não exata funciona como um agente regulador do preço dos imóveis.
De acordo com Rocha Lima Júnior (2014)ROCHA LIMA JUNIOR, J. Movimentos de Preços de Imóveis Residenciais no Brasil: Crônica da Bolha Anunciada e os Preços Adiante. In: LARES INTERNATIONAL CONFERENCE, 14., Rio de Janeiro, 2014. Anais... Rio de Janeiro, 2014., o preço justo no mercado imobiliário consiste na união dos custos de orçamento relativos ao imóvel, dos custos relativos à variação de índices econômicos, que alteram o preço dos insumos e da margem de lucro, que remunera os investidores. Para o autor, a fuga do preço justo para baixo possui uma pequena margem, pois não se pode alterar drasticamente os custos das construções, e a redução do preço justo afetará o lucro dos investidores, que também não pode ser muito reduzido para mantê-los atraídos.
Nos trabalhos desenvolvidos dentro da avaliação de imóveis procura-se estimar o valor de mercado dos imóveis estudados. O valor de mercado, segundo o American Institute of Real Estate Appraisers (1987)AMERICAN INSTITUTE OF REAL ESTATE APPRAISERS. The Appraisal of Real Estate. 9th ed. Chicago, 1987., é o valor mais próximo do preço em uma transação econômica.
O valor de mercado também é definido pela NBR 14653-1 (ABNT, 2001ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-01: avaliação de bens. Rio de Janeiro, 2001.) como a quantia mais provável pela qual se negocia conscientemente e voluntariamente um determinado bem. Dantas (2005)DANTAS, R. A. Engenharia de Avaliações: uma introdução à metodologia científica. São Paulo: Pini, 2005. destaca a facilidade em se confundir valor de mercado com preço; estabelece o preço como a quantia em dinheiro pago pelo imóvel numa transação comercial, podendo ser abaixo ou acima do valor de mercado. Nessa ciência busca-se um modelo matemático que explique o mercado imobiliário. Por meio de inferências estatísticas aplicadas às amostras, estima-se o valor das características dos imóveis ao formular um modelo que demonstre um valor aproximado do preço de uma possível negociação.
Devido à importância econômica e social do mercado imobiliário, há contínuas pesquisas no intuito de se estimar o valor dos imóveis oferecidos no mercado imobiliário, identificando um modelo mais eficaz de avaliações em massa, que é útil para definir planos diretores, cálculos com fins tributários (IPTU e ITBI), bem como auxiliar no conhecimento da demanda habitacional e em estudos de viabilidade econômica de novos lançamentos imobiliários.
De acordo com os estudos de Moreira (1997)MOREIRA, A. L. Princípios de Engenharia de Avaliações. 4. ed. rev. e ampl. São Paulo: Pini, 1997., Dantas (2005)DANTAS, R. A. Engenharia de Avaliações: uma introdução à metodologia científica. São Paulo: Pini, 2005. e Abunahman (1999)ABUNAHMAN, S. A. Curso Básico de Engenharia Legal e de Avaliações. São Paulo: Pini, 1999., observa-se em quais situações a identificação do valor de mercado do imóvel é necessária:
-
transações de compra e venda;
-
transações de locação;
-
financiamentos e operações de crédito, onde um imóvel é colocado como garantia;
-
investimentos imobiliários;
-
impostos, IPTU e ITBI;
-
seguro de imóveis;
-
perícias judiciais; e
-
desapropriação com pagamento de indenização.
Essa ciência de mensuração de valor prima pela clareza e objetividade; assim, quanto mais clara for, mais precisa a avaliação será. E essa objetividade deve ser construída ao escolher o método de avaliação para o imóvel específico a ser avaliado (BRAULIO, 2005BRAULIO, S. N. Proposta de Uma Metodologia Para Avaliação de Imóveis Urbanos Baseado em Métodos Estatísticos Multivariados. Curitiba, 2005. 130 f. Dissertação (Mestrado em Ciências) - Programa de Pós-Graduação em Métodos Numéricos em Engenharia, Universidade Federal do Paraná, Curitiba, 2005.).
Sirmans, Macpherson e Zietz (2005)SIRMANS, G.S.; MACPHERSON, D. A.; ZIETZ, E. The Composition of Hedonic Pricing Models. Journal of Real Estate Literature, v. 13, n. 1, p. 1-44, 2005. afirmam que o valor dos imóveis residenciais é uma função de características físicas e da localização. A abordagem multicritério para avaliação de propriedades é promissora por exigir pequenas informações, fornecidas por decisores experientes, e por apresentar uma diferença, em média, de 10% entre o valor conhecido e a previsão calculada. A desvantagem na aplicação do método TODIM (tomada de decisão interativa multicritério) é a ausência de uma forma lógica de avaliação, mas pode ser resolvida com ajustes no conjunto de propriedades comparáveis (MOSHKOVICH; GOMES; MECHITOV, 2011MOSHKOVICH, H. M.; GOMES, L. F. A. M.; MECHITOV, A. I. An Integrated Multicriteria Decision-Making Approach to Real Estate Evaluation: case of the TODIM method. Pesquisa Operacional, v. 31, n. 1, p. 3-20, 2011.).
Salgado (2011)SALGADO, V. M. Avaliação de Imóveis: metodologia científica. Goiânia: INEAA, 2011. sugere o tratamento utilizando regressão linear, que permite obter a homogeneização dos dados. O objetivo desse tipo de técnica é encontrar uma função linear que permita a compreensão dos dados e estimar uma variável a partir das outras variáveis (RADEGAZ, 2011RADEGAZ, N. J. Avaliação de Bens: princípios básicos e aplicações. São Paulo: Liv. e Ed. Universitária de Direito, 2011.).
Pelli Neto e Zárate (2003)PELLI NETO, A.; ZáRATE, L. E. Avaliação de Imóveis Urbanos Com a Utilização de Redes Neurais Artificiais. In: IBAPE, 12., Belo Horizonte, 2003. Anais... Belo Horizonte, 2003. realizaram um estudo comparativo dessas técnicas utilizando uma amostra de 172 apartamentos de baixa e média renda no município de Belo Horizonte, MG. Essa associação de técnicas também foi utilizada para analisar 1.600 imóveis disponíveis para venda, com 20 atributos cada um, e 500 imóveis disponíveis para aluguel, com 85 atributos cada um, em Porto Alegre, RS. Ao final do estudo, os modelos que foram propostos por Cechin, Souto e González (1999)CECHIN, A. L.; SOUTO, A.; GONZáLEZ, M. A. Análise de Imóveis Através de Redes Neurais Artificiais na Cidade de Porto Alegre. Scientia, São Leopoldo, v. 10, n. 2, p. 5-32, 1999. levaram em consideração apenas seis variáveis.
Em Campo Mourão, PR, Steiner, Braulio e Alves (2008)STEINER, M. T. A.; BRAULIO, S. N.; ALVES, V. Métodos Estatísticos Multivariados Aplicados à Engenharia de Avaliações. Gestão e Produção, v. 15, p. 23-32, 2008. realizaram um estudo dividindo as amostras em grupos de imóveis com características semelhantes, ao usar análise de agrupamento, e também utilizaram a regressão linear múltipla para estimar preços de imóveis que seriam colocados à venda.
Guntermann, Liu e Nowak (2016)GUNTERMANN, K.; LIU, C.; NOWAK, A. Price Indexes for Short Horizons, Thin Markets or Smaller Cities. Journal of Real Estate Research, Fullerton, v. 38, 2016. analisaram imóveis próximos com um modelo próprio de regressão linear múltipla buscando a diminuição de erros que levava em consideração idade, presença de garagem, quantidade de quartos, presença de piscina e outras variáveis; e concluíram que seus resultados se tornaram mais precisos por analisarem imóveis com localização semelhante.
A regressão linear múltipla pode apresentar falhas decorrentes da forte correlação entre uma ou mais variáveis, o que pode ocasionar a multicolinearidade. O uso de ridge regression, estatisticamente, tem como objetivo melhorar os resultados ao se utilizar regressão linear múltipla quando se encontra o problema da multicolinearidade (EL-DERENY; RASHWAN, 2011EL-DENERY, M.; RASHWAN, N. I. Solving Multicollinearity Problem Using Ridge Regression Models. International Journal of Contemporary Mathematical Sciences, v. 6, p. 585-600, 2011. ). E, para Gazola (2002)GAZOLA, S. Construção de Um Modelo de Regressão Para Avaliação de Imóveis. Florianópolis, 2002. Dissertação (Mestrado em Engenharia de Produção) - Programa de Pós-Graduação em Engenharia de Produção, Universidade Federal de Santa Catarina, Florianópolis, 2002., essa técnica impede a retirada de variáveis importantes na composição do modelo, garantindo a qualidade e rigor da predição.
Método
O levantamento dos dados associados aos apartamentos residenciais abordou empreendimentos lançados no mercado de Fortaleza, CE, entre os anos de 2011 e 2014. Essas informações foram catalogadas por uma imobiliária da cidade estudada ao longo dos anos e apresentam diversas características dos empreendimentos. Os bairros da cidade estão divididos em zonas de valor, definidas pela imobiliária a partir da união de bairros com características de mercado e historicamente semelhantes, no intuito de unificar empreendimentos com características equivalentes e pertencentes a um mesmo público-alvo em dada região. Por se tratar de dados não coletados pelo pesquisador, e sim obtidos a partir de pesquisa documental e sem tratamento científico, esses são considerados dados secundários (MATTAR, 2005MATTAR, F. N. Pesquisa de Marketing: metodologia e planejamento. 6. ed. São Paulo: Atlas, 2005.).
Estudou-se o banco de dados com o objetivo de selecionar as informações pertinentes ao estudo. A característica zona de valor corresponde à união de bairros ou partes deles com características de mercado semelhantes historicamente. A definição foi feita pela imobiliária, e, dessa forma, levou-se em consideração apenas a variável zona de valor por ser mais completa e homogênea que a variável bairro.
O segmento é a divisão econômica dos empreendimentos, podendo ser econômico, médio, alto ou altíssimo. A segmentação é defendida por Freitas (2000)FREITAS, A. A. F. Segmentação do Mercado Imobiliário Utilizando Dados de Preferência Declarada. Florianópolis, 2000. Tese (Doutorado em Engenharia de Produção) - Programa de Pós-graduação em Engenharia de Produção, Universidade Federal de Santa Catarina, Florianópolis, 2000., Brandstetter (2014)BRANDSTETTER, M. C. G. O. Pesquisa Para o Marketing Imobiliário Por Meio da Investigação do Ciclo de Vida Familiar. In: ENCONTRO NACIONAL DE ENGENHARIA DE PRODUÇÃO, Curitiba, 2014. Anais... Curitiba, 2014., Fernandez (2006)FERNANDEZ, J. A. da C. G. Ciclo de Vida Familiar e o Projeto de Empreendimentos Multifamiliares. Florianópolis, 2006. Tese (Doutorado em Engenharia Civil) - Programa de Pós-Graduação em Engenharia Civil, Univesidade Federal de Santa Catarina, Florianópolis, 2006. e Garbi e Monetti (2012)GARBI, J. B.; MONETTI, E. Estratégia de Vendas Para Empreendimentos Imobiliários Para Baixa Renda, Com Foco nos Pontos de Venda. In: CONFERÊNCIA INTERNACIONAL DA LARES, 12., São Paulo, 2012. Anais... São Paulo: Ponto. COMM, 2012. como importante nos estudos de real estate. A Tabela 1, que informa como ocorre a divisão dos empreendimentos segundo a imobiliária que gerou o banco de dados. Vale a pena ressaltar que a inclusão de um empreendimento em determinado segmento leva em conta o valor de lançamento do imóvel e não o valor de mercado em data posterior; e que não há redistribuição posterior com o aumento ou diminuição desse valor.
Isoladamente, as informações de data de lançamento e data prevista para entrega do empreendimento não possuem grande relevância para a pesquisa, mas, ao unir as duas, obtém-se a variável tempo de construção previsto, que é importante para a construtora no planejamento da obra e para o cliente no seu planejamento familiar.
O valor da unidade corresponde ao valor de mercado de cada apartamento registrado na imobiliária atualizado até o fim do mês de dezembro de 2014, assim como o número de unidades vendidas é correspondente até o fim do mesmo ano.
As características das unidades habitacionais foram estudadas em relação a sua quantidade e a sua variedade, considerando-se os tipos diferentes de apartamentos. Já em relação às características de empreendimento definiu-se critérios para viabilizar o estudo:
um empreendimento é o conjunto de apartamentos presente no banco de dados com o mesmo nome;
empreendimentos com dois ou mais tipos de apartamento foram considerados como parte do mesmo empreendimento se possuírem as mesmas características de empreendimento (tempo previsto de construção, número de torres, número de apartamentos por andar e número de andares). Caso pelo menos uma dessas variáveis seja divergente, esse tipo de unidade será considerado outro empreendimento; e
empreendimentos com tipos de apartamento em mais de um segmento econômico tiveram suas características de empreendimento consideradas no segmento com maior número de unidades, exceto se houver uma torre para cada tipo diferente de unidade em cada segmento econômico. Nesse caso foi considerado um empreendimento para cada torre diferente.
Modelo de regressão linear múltipla
O desenvolvimento de um modelo de regressão linear para predizer o valor de mercado de imóveis requer uma série de etapas de procedimentos e testes para que atenda aos conceitos teóricos e aos pressupostos da NBR 14563.
O presente estudo utiliza-se de um banco de dados constituído de 17493 apartamentos da cidade de Fortaleza, CE. Porém, considerou-se para o estudo os 227 tipos de apartamento lançados, a fim de verificar a influência das informações de quantidade de unidades e a quantidade de unidades vendidas.
Identificação das variáveis
A variável dependente é o valor da unidade, que representa o valor de venda de cada unidade de um tipo de apartamento, em reais. Inicialmente foram estudadas as características que, ao serem estudadas por diversos autores, são as mais importantes formadoras de valor e que mais atraem os consumidores.
Os atributos mais mencionados são a área útil, a localização, o padrão construtivo, a quantidade de dormitórios (quartos ou suítes); logo em seguida estão a idade do imóvel, a quantidade de vagas de garagem, a quantidade de banheiros e a presença de equipamentos, sendo outras características pouco mencionadas (CAVALCANTE, 2002CAVALCANTE, M. G. Apartamentos Residenciais: formação de valor em Fortaleza/CE. São Paulo: ANNABLUME Editora, 2002.; COUTO, 2007COUTO, P. M. Avaliação Patrimonial de Imóveis Para Habitação. Porto, 2007. Tese (Doutorado em Engenharia Civil) - Laboratório Nacional de Engenharia Civil, Universidade do Porto, Porto. 2007.; FERNANDEZ, 2001FERNANDEZ, J. A. C. G. Estruturação de Estudos de Viabilidade de Mercado Para Empreendimentos Habitacionais. In: SEMINÁRIO INTERNACIONAL DA LARES - LATIN AMERICAN REAL ESTATE SOCIETY, 2., Florianópolis, 2001. Anais... Florianópolis, 2001.; FREITAS, 2000FREITAS, A. A. F. Segmentação do Mercado Imobiliário Utilizando Dados de Preferência Declarada. Florianópolis, 2000. Tese (Doutorado em Engenharia de Produção) - Programa de Pós-graduação em Engenharia de Produção, Universidade Federal de Santa Catarina, Florianópolis, 2000.; GONZAGA, 2003GONZAGA, L. M. R. Contribuição Para o Aumento do Nível de Precisão das Avaliações Imobiliárias Através da Análise das Preferências do Consumidor. Porto Alegre, 2003. Dissertação (Mestrado em Engenharia Civil) - Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2003., GUTERMANN; LIU; NOWAK, 2016GUNTERMANN, K.; LIU, C.; NOWAK, A. Price Indexes for Short Horizons, Thin Markets or Smaller Cities. Journal of Real Estate Research, Fullerton, v. 38, 2016.; PELLI NETO; ZÁRATE, 2003PELLI NETO, A.; ZáRATE, L. E. Avaliação de Imóveis Urbanos Com a Utilização de Redes Neurais Artificiais. In: IBAPE, 12., Belo Horizonte, 2003. Anais... Belo Horizonte, 2003.; QUESADO, 2012QUESADO, W. Atributos de escolha da casa própria da classe C e sua relação com o ciclo de vida familiar. 2012. Dissertação (Mestrado em Administração) - Pós-Graduação em Administração e Controladoria, Universidade Federal do Ceará, Fortaleza, 2012. ; TRIVELONI; HOCHHEIM, 1998TRIVELLONI, C. A. P.; HOCHHEIM, N. Avaliação de Imóveis com Técnicas de Análise Multivariada. In: CONGRESSO BRASILEIRO DE CADASTRO TéCNICO MULTIFINALITÁRIO, Florianópolis, 1998. Anais... Florianópolis, 1998.). O atributo equipamentos corresponde à menção da presença de um ou mais atrativos no apartamento, como box nos banheiros, instalação de TV a cabo, banheira de hidromassagem e instalação de água quente, por exemplo.
As variáveis estudadas mais mencionadas na literatura fazem parte da pesquisa, no intuito de se trabalhar com as variáveis mais relevantes em estudos anteriores. Diante do banco de dados obtido, os atributos foram comparados com as características importantes na literatura e todos foram escolhidos para serem variáveis independentes do modelo a ser desenvolvido.
As variáveis independentes dos modelos serão descritas no Quadro 1. Estas são as variáveis que correspondem aos atributos presentes no banco de dados, com exceção da variável “Relação de vendas”, criada com o intuito de verificar a relação entre o valor do imóvel e a velocidade de venda do imóvel.
Levantamento dos dados
Primeiramente deve-se escolher onde o estudo deverá ser aplicado e em seguida definir as quantidades de imóveis a serem utilizadas como amostras e quais variáveis serão estudadas. Esse levantamento deverá ser detalhado, pois todo o estudo dependerá da qualidade e veracidade das informações obtidas.
Recomenda-se que seja utilizada a mesma metodologia para a obtenção das características das amostras, a fim de não serem levantadas informações irrelevantes ao estudo e se deixe de pesquisar informações importantes.
A amostra é formada por 227 tipos de apartamentos residenciais, lançados entre os anos de 2011 e 2014. O banco de dados corresponde a todos os apartamentos lançados no município de Fortaleza, CE, e foi disponibilizado por uma imobiliária da cidade.
Transformação das variáveis
Nessa etapa as variáveis são definidas como quantitativas ou qualitativas. Em caso de a variável independente ser qualitativa, ela deverá ser transformada em uma variável do tipo dummy, e, caso apresente uma determinada característica (pertencer a uma região da cidade estudada ou possuir dependência de empregada, por exemplo), é atribuído valor 1 (um) à variável; e em caso de negativa (não pertencer a uma região ou não possuir dependência de empregada, por exemplo), é atribuído valor 0 (zero).
No caso das variáveis quantitativas, muitas vezes elas podem apresentar grande variação nos valores. Desse modo, devem ser feitas transformações para a limitação desses valores por meio de pesos e, assim, ser corrigido o problema de linearidade. Geralmente se faz uso de transformações logarítmicas e exponenciais.
As variáveis estudadas podem ser classificadas em quantitativas e qualitativas, e para o presente estudo foi necessária a transformação dessas variáveis para se testar a relação entre elas.
Apenas duas variáveis são consideradas qualitativas: zona de valor e segmento econômico. As zonas de valor Aldeota, Cambeba, Cidade dos Funcionários, Cocó, Fátima, Guararapes, Maraponga, Meireles, Messejana, Montese, Parangaba, Papicú, Parquelândia e Passaré foram renomeadas em categorias que variam de zv0 a zv13, respectivamente. Os segmentos econômicos foram identificados em categorias seg1, seg2, seg3 e seg4, seguindo a ordem do segmento mais econômico até o mais caro.
Essas variáveis qualitativas foram transformadas em variáveis do tipo dummy para que fossem calculados os coeficientes de correlação linear e se fazer a regressão. As variáveis dummy funcionam como sistemas binários, sendo, portanto, variáveis exclusivas quanto à zona de valor e ao segmento, ou seja, um tipo de apartamento não pode estar presente em duas ou mais zonas de valor, assim como só pode pertencer a um único segmento econômico.
Com a transformação das variáveis qualitativas em dummy, passou-se a ter um total de 30 variáveis, sendo 12 variáveis independentes quantitativas.
Para se obter resultados satisfatórios quanto à assimetria das variáveis independentes quantitativas foi utilizada a transformação logarítmica com base 10 em todas as variáveis, exceto na variável relação de vendas, amenizando o problema da assimetria sem as transformações. Também se transformou a variável dependente em logarítmica para melhoria da análise. A transformação logarítmica foi escolhida por ser sugerida pela norma e por proporcionar uma variância do erro do modelo próxima de zero, permitindo um melhor ajuste do modelo. As variáveis utilizadas são todas positivas e diferente de zero, mas há a possibilidade de existir o lançamento de um apartamento sem vaga de garagem, gerando um logaritmo de zero; portanto na transformação todas as variáveis foram somadas a 1.
Análise exploratória das variáveis
São utilizadas técnicas que verificam a correlação entre as variáveis, podendo-se verificar a existência ou não de relação linear entre as variáveis (neste estudo é utilizado a correlação linear de Spearman para as variáveis quantitativas). Os coeficientes variam entre valores menores que 1 e maiores que -1, em que a proximidade de 0 representa uma baixa correlação.
Para o estudo da correlação da variável dependente com as variáveis qualitativas é feito o teste F da Anova, pois a correlação de Spearman não é adequada para esse tipo de variável.
A multicolinearidade do modelo é estudada nesta etapa por meio da análise das raízes características da matriz dos coeficientes de relação, em que são verificadas as correlações das variáveis independentes entre si, a fim de ver o grau de influência entre elas.
Primeiramente foi realizado o teste de correlação de Spearman (Tabela 2) para verificação da relação entre a variável dependente () com as variáveis quantitativas. De acordo com o teste, foram excluídas da análise as variáveis que apresentaram valores de correlação entre -0,2 e 0,2, o que representa uma fraca correlação com a variável dependente. As variáveis excluídas nessa etapa foram: tempo médio de construção, quantidade de torres, tempo no mercado e relação de vendas.
Correlação linear (Spearman) entre variáveis independentes qualitativas e a variável dependente valor de mercado da unidade
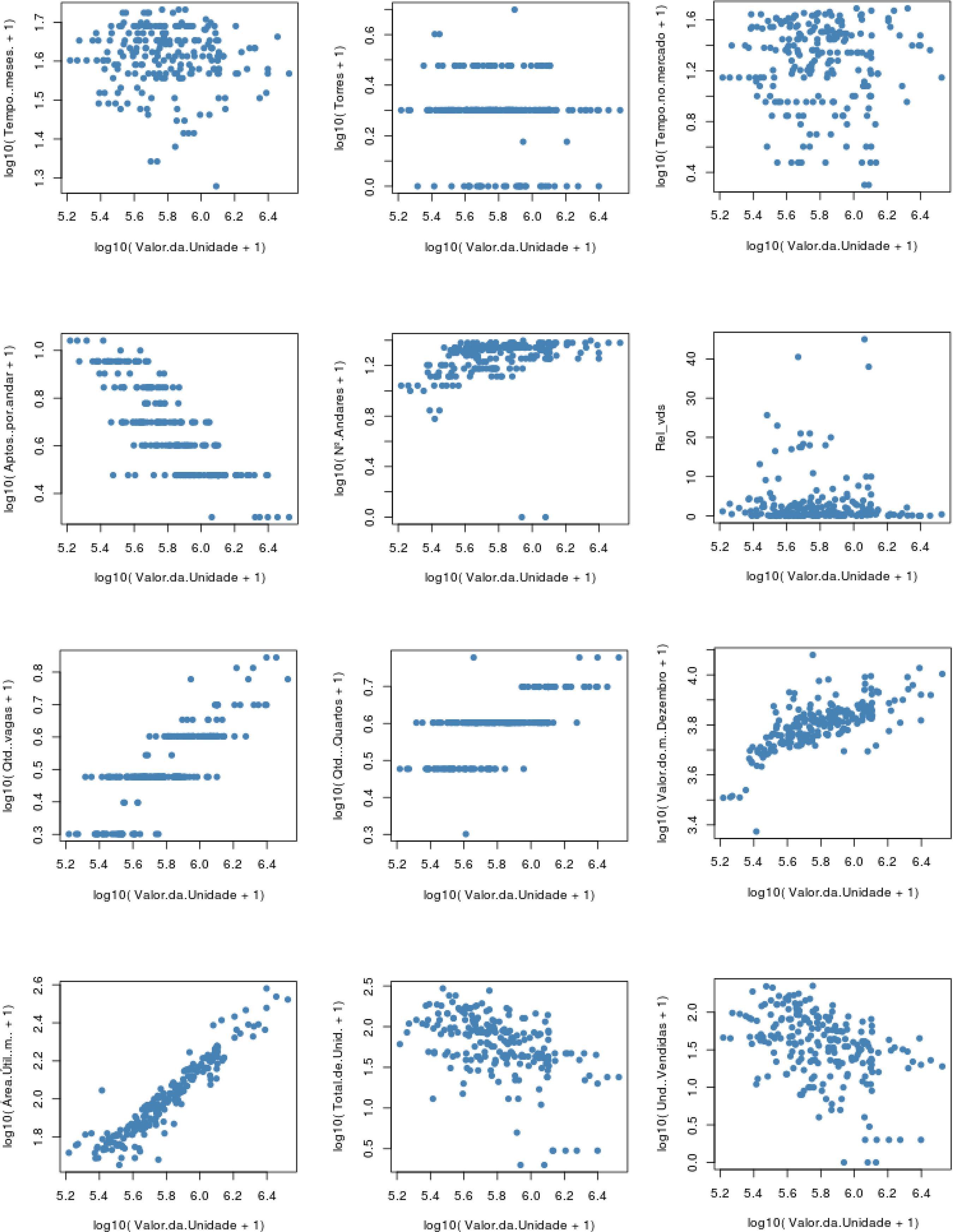
Foi realizado o estudo dos gráficos de dispersão entre a variável dependente e as variáveis quantitativas para melhorar a correlação entre as variáveis, correspondente à Figura 1. A partir desses gráficos puderam ser confirmadas as correlações entre as variáveis com bom resultado no teste da correlação de Spearman e a variável dependente, sendo mantidas, assim, as variáveis transformadas AA, NA, VG, QQ, AU, TU, MQ e TM.
O passo seguinte constitui-se na análise de variância (Anova) por meio do teste F das variáveis qualitativas e assim foi verificado que as duas variáveis, transformadas em dummy, podem fazer parte do modelo, como mostra a Tabela 3.
Dessa forma, o primeiro modelo testado foi composto das 8 variáveis quantitativas e das 16 variáveis dummy qualitativas, mostrando-se inviável.
A correlação entre as variáveis foi calculada utilizando a matriz de correlação. Dentre as variáveis com maior correlação está a quantidade de vagas de garagem com a área útil e o número de apartamentos por andar; o número de unidades vendidas com o total de unidades; e a relação de vendas com o tempo no mercado.
Os altos valores de correlação indicam uma possível multicolinearidade, ou seja, uma correlação entre as variáveis independentes. Esta foi averiguada a partir do uso das raízes características da matriz de correlação, conforme Tabela 4. Observam-se valores muito baixos para as raízes características, indicando a existência de forte multicolinearidade.
Com a existência de forte multicolinearidade, é necessário o uso de métodos mais específicos para a determinação da equação. Para contornar esse problema, foi utilizado o método ridge regression. A função dessa técnica é gerar predições que sejam mais precisas que as predições geradas por meio das regressões geradas a partir do método de mínimo quadrado, pois quando há multicolinearidade entre as variáveis independentes o modelo não segue o mesmo padrão em novas predições (DRAPER; SMITH, 1981DRAPER, N. R.; SMITH, H. Applied Regression Analysis. New York: Jhon Wiley & Sons, 1981.).
Construção do modelo
A construção do modelo se inicia após o estudo da relação linear entre as variáveis. No caso de multicolinearidade forte, como existe na maioria dos casos dos estudos de avaliação imobiliária, uma das soluções adotadas é o uso da técnica ridge regression para que se possa utilizar no modelo as variáveis mais indicadas, evitando problemas futuros na equação. Nessa etapa também é estudado o poder de explicação do modelo com o cálculo do R ajustado 2, que analisa a alteração provocada com a inclusão ou exclusão de variáveis na equação.
Mesmo com a definição das variáveis que entrarão ou não no modelo, ainda se pode fazer uma análise crítica destas e verificar se alguma variável considerada importante pode ser adicionada à equação, desde que não haja prejuízo na sua qualidade.
A análise de regressão foi realizada utilizando as 8 variáveis independentes quantitativas transformadas em logarítmicas e as 16 variáveis independentes qualitativas em dummy. Para a construção do modelo foram efetuadas diversas simulações utilizando o método ridge regression stepwise standard para a verificação do melhor conjunto de variáveis a serem utilizadas no modelo, que são mostradas na Tabela 5.
Após implantar-se um modelo, com as variáveis testadas, em um algoritmo no software R, fez-se uso do teste t para averiguar a significância das variáveis presentes no modelo proposto. Admitindo-se um nível de 1% de significância, algumas variáveis foram retiradas do modelo, tendo como resultado o modelo final proposto.
Apesar de algumas variáveis quantitativas possuírem uma correlação forte com a variável dependente, não se tornaram parte do modelo final devido ao teste de Shapiro-Wilk, que averigua a normalidade dos resíduos. Portanto, ao implementar a função, tiveram que ser retiradas do modelo para que ele atendesse aos requisitos teóricos, restando as variáveis transformadas vagas de garagem, valor do metro quadrado, unidades vendidas, segmento econômico, segmento médio e segmento alto.
O poder de explicação do modelo, previsto no anexo A.4 da norma 14653-2 (ABNT, 2011ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-02: imóveis urbanos. Rio de Janeiro, 2011.), é observado na Tabela 6. Os altos valores de R múltiplo e R ajustado 2 indicam uma grande correlação entre as variáveis independentes e a variável dependente, assim como uma alta explicação da variável dependente em função das variáveis independentes.
Como a função valor de mercado (variável dependente) foi transformada em (Equação 1), é necessário desfazer a transformação para o cálculo do valor de mercado da unidade. A Equação 2 mostra a retirada da função logarítmica, e o seu valor será a diferença de 10 elevado à equação de regressão linear múltipla (ERLM), que é a Equação 3, menos uma unidade.
= equação de regressão linear múltipla
Onde:
VU é o valor de mercado da unidade em dezembro de 2014;
VG é a quantidade de vagas de garagem;
MQ é o valor do metro quadrado em dezembro de 2014;
UV é a quantidade de unidades vendidas;
seg1 é o segmento econômico (deve ser colocado 1 se pertencer a esse segmento e 0 se não pertencer);
seg2 é o segmento médio (deve ser colocado 1 se pertencer a esse segmento e 0 se não pertencer); e
seg3 é o segmento alto (deve ser colocado 1 se pertencer a esse segmento e 0 se não pertencer).
A análise de variância (Tabela 7) demonstra que o modelo proposto acima é significativo.
Análise de resíduos
Os resíduos são analisados graficamente para a verificação da variância, normalidade, adequação do modelo, existência de valores discrepantes e variáveis omitidas. Por se tratar de um modelo para avaliação imobiliária, os resultados devem atender aos pressupostos existentes na NBR 14563-2 (ABNT, 2011ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-02: imóveis urbanos. Rio de Janeiro, 2011.). As suposições do modelo, com a equação de regressão ajustada, serão verificadas a partir da análise gráfica dos resíduos.
A Figura 2 mostra pontos distribuídos aleatoriamente ao redor de uma linha que parte da origem, o que indica uma variância constante razoável e que foi feita a escolha adequada da forma da equação.
A suposição da normalidade é testada por meio da Figura 3, na qual são mostrados os resíduos versus valores esperados pela distribuição normal. Os pontos dispostos sob uma linha reta indicam a normalidade dos erros.
Em relação aos valores discrepantes, não aparecem resíduos padronizados grandes, todos são próximos de zero, o que não caracteriza a existência de pontos discrepantes, como observado na Figura 4.
Resultados e discussões
Após a construção do modelo a equação de regressão linear múltipla é validada com a análise dos resíduos. O valor de mercado da unidade é calculado (Equação 4) a partir da ERLM desenvolvida com variáveis independentes, que são características dos imóveis.
A exclusão de variáveis é feita para melhor adequação do modelo, e verifica-se que estas, como os casos de “quantidade de apartamentos por andar”, “área útil”, “tempo no mercado” e “total de unidades”, são representadas por variáveis formadoras que possuem forte correlação.
A forte multicolinearidade encontrada no trabalho, ou seja, a grande correlação entre as varáveis, foi contornada com a utilização da técnica de ridge regression para não se eliminar variáveis importantes. Mesmo assim, a variável “área útil”, uma das mais importantes formadoras de valor em imóveis, foi eliminada por inviabilizar o modelo e não permitir bons resultados ao se analisar os resíduos, que é uma análise prevista na NBR 14653 como ponto importante de validação dos modelos de regressão linear múltipla.
Um modelo que satisfaz as suposições teóricas não necessariamente é suficiente para garantir a qualidade dos valores preditos. A avaliação prática do modelo confirma o grau de confiança dos resultados obtidos a partir da equação e é a última etapa antes de a equação final ser adotada.
A qualidade do ajuste é verificada com a comparação entre os valores observados na amostra e os valores obtidos a partir da aplicação do modelo; quanto mais próximos forem esses valores, maior será a qualidade da equação construída.
O poder de predição da equação ajustada para novas observações foi realizado utilizando 11 amostras que não tiveram suas características analisadas na construção do modelo, chamadas de amostras teste, e aplicou-se os valores das variáveis à Equação 1, Equação 2 e Equação 3 para se chegar ao valor de cada amostra teste. Foi obtido um erro percentual médio de 21,1% ao serem analisadas as amostras teste (Tabela 8); esse erro encontrado pode ter sofrido a influência da grande variedade de amostras do banco de dados, com apartamentos do baixo ao altíssimo padrão. A NBR 14653-2 (ABNT, 2011ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-02: imóveis urbanos. Rio de Janeiro, 2011.) considera um nível de significância normal o erro percentual médio igual a 20%, portanto pode-se considerar o erro obtido como aceitável.
Ao estudar a Tabela 9, observa-se que 80% dos valores preditos, em relação a todas as amostras, tiveram seu erro de até 20% e apenas 4 valores tiveram um erro maior que 40%.
Portanto, se fossem desconsideradas as amostras com erro maior que 40%, correspondente a 1,77% do total de amostras, do estudo da tabela 7, sobrariam 10 amostras teste para o cálculo do erro médio de predição. Com a exclusão da amostra com erro de 92,03%, obtém-se um erro médio de 14%.
Vale ressaltar que essa exclusão não faz parte dos testes utilizados neste estudo. Foi feita essa análise para demonstrar que uma amostra teste sem grande representatividade percentual dentro do total de amostras pode influenciar no cálculo do erro médio de predição.
Conclusão
Dispondo de um banco de dados com amostras variadas com as características dos imóveis é possível representar o valor de mercado de um imóvel por meio de uma equação de regressão linear. Dentre as características foi possível utilizar as variáveis quantitativas e qualitativas das amostras sem que inviabilizasse a criação do modelo de regressão, sendo apenas possível após as transformações das varáveis.
Apesar de muitas variáveis independentes que apresentaram boa correlação com a variável dependente não terem entrado na equação, não significa que estas não são importantes para a formação do valor do imóvel em outros métodos de avaliação. Elas não entraram na equação final por apresentarem forte correlação com outras varáveis independentes presentes na equação, o que provocaria uma redundância dentro do modelo proposto. Portanto, não se pode afirmar que apenas as variáveis presentes no modelo são formadoras de valor de apartamentos residenciais no município de Fortaleza, CE; estas são importantes para este modelo de avaliação específico.
O modelo de regressão linear proposto permite a avaliação de apartamentos residenciais no município estudado, podendo ser utilizado por empresas imobiliárias nas negociações com clientes, por bancos nas negociações de financiamentos, pelo Poder Judiciário em casos de processos e investigações envolvendo imóveis e também por seguradoras. A administração municipal pode fazer uso da ferramenta como auxílio no cálculo dos tributos referentes a esse tipo de imóvel. As empresas construtoras e incorporadoras também podem utilizar a equação como apoio no momento de definição do preço dos apartamentos a serem lançados e, também, utilizar a equação para definição de alguma característica do seu novo empreendimento ao estipular variáveis.
A utilização da equação obtida restringe-se ao município de Fortaleza, CE, pois um banco de dados com variáveis referentes a esse município inviabiliza a sua utilização em outro local que possui características distintas. Mas nada impede a aplicação da metodologia utilizada para uma nova equação.
Referências
- ABRAMO, P. A Cidade Caleidoscópica: coordenação espacial e convenção urbana: uma perspectiva heterodoxa para a economia urbana. Rio de Janeiro: Bertrand Brasil, 2007.
- ABUNAHMAN, S. A. Curso Básico de Engenharia Legal e de Avaliações São Paulo: Pini, 1999.
- AGUIAR, J. B. Introdução à Engenharia de Avaliações e Perícias. In: INSTITUTO MINEIRO DE AVALIAÇÕES E PERÍCIAS DE ENGENHARIA. Fundamentos de Avaliações Patrimoniais e Perícias de Engenharia: curso básico do IMAPE. São Paulo: Pini, 1998.
- AMERICAN INSTITUTE OF REAL ESTATE APPRAISERS. The Appraisal of Real Estate 9th ed. Chicago, 1987.
- ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-01: avaliação de bens. Rio de Janeiro, 2001.
- ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-02: imóveis urbanos. Rio de Janeiro, 2011.
- BOTELHO, A. O Financiamento e a Financeirização do Setor Imobiliário: uma análise da produção do espaço e da segregação sócio-espacial através do estudo do mercado da moradia na cidade de São Paulo. São Paulo, 2005. Tese (Doutorado) - Universidade de São Paulo, São Paulo, 2005.
- BRANDSTETTER, M. C. G. O. Pesquisa Para o Marketing Imobiliário Por Meio da Investigação do Ciclo de Vida Familiar. In: ENCONTRO NACIONAL DE ENGENHARIA DE PRODUÇÃO, Curitiba, 2014. Anais... Curitiba, 2014.
- BRAULIO, S. N. Proposta de Uma Metodologia Para Avaliação de Imóveis Urbanos Baseado em Métodos Estatísticos Multivariados Curitiba, 2005. 130 f. Dissertação (Mestrado em Ciências) - Programa de Pós-Graduação em Métodos Numéricos em Engenharia, Universidade Federal do Paraná, Curitiba, 2005.
- CAVALCANTE, M. G. Apartamentos Residenciais: formação de valor em Fortaleza/CE. São Paulo: ANNABLUME Editora, 2002.
- CECHIN, A. L.; SOUTO, A.; GONZáLEZ, M. A. Análise de Imóveis Através de Redes Neurais Artificiais na Cidade de Porto Alegre. Scientia, São Leopoldo, v. 10, n. 2, p. 5-32, 1999.
- COUTO, P. M. Avaliação Patrimonial de Imóveis Para Habitação Porto, 2007. Tese (Doutorado em Engenharia Civil) - Laboratório Nacional de Engenharia Civil, Universidade do Porto, Porto. 2007.
- DANTAS, R. A. Engenharia de Avaliações: uma introdução à metodologia científica. São Paulo: Pini, 2003.
- DANTAS, R. A. Engenharia de Avaliações: uma introdução à metodologia científica. São Paulo: Pini, 2005.
- DRAPER, N. R.; SMITH, H. Applied Regression Analysis New York: Jhon Wiley & Sons, 1981.
- DUMM, R.; SIRMANS, G.; SMERSH, G. Price Variation in Waterfront Properties Over the Economic Cycle. Journal of Real Estate Research, Fullerton, v. 38, 2016.
- EL-DENERY, M.; RASHWAN, N. I. Solving Multicollinearity Problem Using Ridge Regression Models. International Journal of Contemporary Mathematical Sciences, v. 6, p. 585-600, 2011.
- FERNANDEZ, J. A. C. G. Estruturação de Estudos de Viabilidade de Mercado Para Empreendimentos Habitacionais. In: SEMINÁRIO INTERNACIONAL DA LARES - LATIN AMERICAN REAL ESTATE SOCIETY, 2., Florianópolis, 2001. Anais... Florianópolis, 2001.
- FERNANDEZ, J. A. da C. G. Ciclo de Vida Familiar e o Projeto de Empreendimentos Multifamiliares Florianópolis, 2006. Tese (Doutorado em Engenharia Civil) - Programa de Pós-Graduação em Engenharia Civil, Univesidade Federal de Santa Catarina, Florianópolis, 2006.
- FREITAS, A. A. F. Segmentação do Mercado Imobiliário Utilizando Dados de Preferência Declarada Florianópolis, 2000. Tese (Doutorado em Engenharia de Produção) - Programa de Pós-graduação em Engenharia de Produção, Universidade Federal de Santa Catarina, Florianópolis, 2000.
- GARBI, J. B.; MONETTI, E. Estratégia de Vendas Para Empreendimentos Imobiliários Para Baixa Renda, Com Foco nos Pontos de Venda. In: CONFERÊNCIA INTERNACIONAL DA LARES, 12., São Paulo, 2012. Anais... São Paulo: Ponto. COMM, 2012.
- GAZOLA, S. Construção de Um Modelo de Regressão Para Avaliação de Imóveis Florianópolis, 2002. Dissertação (Mestrado em Engenharia de Produção) - Programa de Pós-Graduação em Engenharia de Produção, Universidade Federal de Santa Catarina, Florianópolis, 2002.
- GONZAGA, L. M. R. Contribuição Para o Aumento do Nível de Precisão das Avaliações Imobiliárias Através da Análise das Preferências do Consumidor Porto Alegre, 2003. Dissertação (Mestrado em Engenharia Civil) - Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2003.
- GUNTERMANN, K.; LIU, C.; NOWAK, A. Price Indexes for Short Horizons, Thin Markets or Smaller Cities. Journal of Real Estate Research, Fullerton, v. 38, 2016.
- MARTINE, G; MCGRANAHAN. A Transição Urbana Brasileira: trajetória, dificuldades e lições aprendidas. In: BAENINGER, R. (Org.). População e Cidades: subsídios para o planejamento e para as políticas sociais Campinas: Núcleo de Estudos de População/Unicamp, 2010.
- MATTAR, F. N. Pesquisa de Marketing: metodologia e planejamento. 6. ed. São Paulo: Atlas, 2005.
- MOREIRA, A. L. Princípios de Engenharia de Avaliações 4. ed. rev. e ampl. São Paulo: Pini, 1997.
- MOSHKOVICH, H. M.; GOMES, L. F. A. M.; MECHITOV, A. I. An Integrated Multicriteria Decision-Making Approach to Real Estate Evaluation: case of the TODIM method. Pesquisa Operacional, v. 31, n. 1, p. 3-20, 2011.
- PELLI NETO, A.; ZáRATE, L. E. Avaliação de Imóveis Urbanos Com a Utilização de Redes Neurais Artificiais. In: IBAPE, 12., Belo Horizonte, 2003. Anais... Belo Horizonte, 2003.
- QUESADO, W. Atributos de escolha da casa própria da classe C e sua relação com o ciclo de vida familiar 2012. Dissertação (Mestrado em Administração) - Pós-Graduação em Administração e Controladoria, Universidade Federal do Ceará, Fortaleza, 2012.
- RADEGAZ, N. J. Avaliação de Bens: princípios básicos e aplicações. São Paulo: Liv. e Ed. Universitária de Direito, 2011.
- ROCHA LIMA JUNIOR, J. Movimentos de Preços de Imóveis Residenciais no Brasil: Crônica da Bolha Anunciada e os Preços Adiante. In: LARES INTERNATIONAL CONFERENCE, 14., Rio de Janeiro, 2014. Anais... Rio de Janeiro, 2014.
- SALGADO, V. M. Avaliação de Imóveis: metodologia científica. Goiânia: INEAA, 2011.
- SILVA, H. M. B. Terra e Moradia: que papel para o município. São Paulo, 1997. Tese (Doutorado em Engenharia Civil) - Escola de Engenharia, Universidade de São Paulo, São Paulo, 1997.
- SIRMANS, G.S.; MACPHERSON, D. A.; ZIETZ, E. The Composition of Hedonic Pricing Models. Journal of Real Estate Literature, v. 13, n. 1, p. 1-44, 2005.
- STEINER, M. T. A.; BRAULIO, S. N.; ALVES, V. Métodos Estatísticos Multivariados Aplicados à Engenharia de Avaliações. Gestão e Produção, v. 15, p. 23-32, 2008.
- TRIVELLONI, C. A. P.; HOCHHEIM, N. Avaliação de Imóveis com Técnicas de Análise Multivariada. In: CONGRESSO BRASILEIRO DE CADASTRO TéCNICO MULTIFINALITÁRIO, Florianópolis, 1998. Anais... Florianópolis, 1998.
Datas de Publicação
-
Publicação nesta coleção
Jan-Mar 2019
Histórico
-
Recebido
20 Maio 2017 -
Aceito
11 Maio 2018