Abstract
The three-dimensional spectral elasticity problem is studied in an anisotropic and inhomogeneous solid with small defects, i.e., inclusions, voids, and microcracks. Asymptotics of eigenfrequencies and the corresponding elastic eigenmodes are constructed and justified. New technicalities of the asymptotic analysis are related to variable coefficients of differential operators, vectorial setting of the problem, and usage of intrinsic integral characteristics of defects. The asymptotic formulae are developed in a form convenient for application in shape optimization and inverse problems.
singular perturbations; spectral problem; asymptotics of eigenfunctions and eignevalues; elasticity boundary value problem
On asymptotic analysis of spectral problems in elasticity
S.A. NazarovI; J. SokolowskiII,* * Author email: Jan.Sokolowski@iecn.u-nancy.fr
IInstitute of Mechanical Engineering Problems, V.O., Bolshoi pr., 61, 199178, St. Petersburg - Russia
IIUniversité H.Poincaré, Nancy 1, Départ. de Mathematiques, B.P. n. 239, 54506 Vandoeuvre les Nancy Cédex - France
ABSTRACT
The three-dimensional spectral elasticity problem is studied in an anisotropic and inhomogeneous solid with small defects, i.e., inclusions, voids, and microcracks. Asymptotics of eigenfrequencies and the corresponding elastic eigenmodes are constructed and justified. New technicalities of the asymptotic analysis are related to variable coefficients of differential operators, vectorial setting of the problem, and usage of intrinsic integral characteristics of defects. The asymptotic formulae are developed in a form convenient for application in shape optimization and inverse problems.
Keywords: singular perturbations; spectral problem; asymptotics of eigenfunctions and eignevalues; elasticity boundary value problem.
1 INTRODUCTION
1.1 Asymptotic analysis of eigenvalues in singularly perturbed domains
In the paper asymptotic analysis of eigenvalues and eigenfunctions is performed with respect to singular perturbations of geometrical domains (see Fig. 1). By singular perturbations of the boundary it is understood e.g., the creation of the new parts of the boundary due to the nucleation of small voids.
The case of low frequencies is considered for elasticity spectral problems in three spatial dimensions. The results established here can be directly used in some applications, for example in inverse problems of identification of small defects in the body based on the observation of elastic eigenmodes. Compared to the existing results in the literature, the technical difficulties of the present paper mainly concern vectorial setting of boundary value problems, anisotropy of physical properties, and variable coefficients of differential operators, i.e., inhomogeneity of elastic materials. Exisiting results on elasticity problems with singular perturbations of boundaries (see monographs [36,368] and [13]) deal with homogeneous, mainly isotropic elastic bodies. For a system of differential equations, an asymptotic analysis is required to be much more elaborated and direct adopting of the methods proper for scalar equations may lead to an unfortunate mistake (cf. [18] and corrections in [1]).
The known results are given in particular for singular perturbations of isolated points of the boundary (small holes in the domain, see [14], [15], [5], [1], [13], [15] and others), perturbations of straight boundaries including perturbations by changing the type of boundary conditions (cf. [2]-[3]), and the dependence of the obtained results in more general geometrical domains on the curvature is clarified in [8,22,23] in the case of scalar equations. The most of attention is paid in the present paper to derivation of explicit formulae for solutions and extraction of principal characteristics of elastic fields and defects which influence these formulae. To this end, we employ matrix/column notation, use the notion of elastic polarization matrix (tensor), and perform certain additional technical calculations which are not needed in the case of homogeneous, isotropic elastic materials.
Small defects can be regarded as singular perturbations of the interior piece of the boundary of the body. In this way we can consider e.g., the finite number of isolated points which approximate small cavities. More generally, by means of asymptotic analysis we can model the creation of caverns, i.e., some piece of material is taken off from the elastic body. We can also fill the cavern with some other elastic material and model such a phenomenon by formation of one or more inclusions in the body.
Roughly speaking, the influence of a substantial change of local properties of the elastic body cannot be analysed by the classical tools of the shape sensitivity analysis or any other type of sensitivity analysis, but it requires the application of asymptotic methods. Especially, such methods turn out to be of importance for the microcracks, since the microcrack implies the creation of a new portion of internal boundary in the body, which cannot be taken into account in the framework of classical sensitivity analysis based on regular perturbations of the coefficients and of the boundary. The asymptotic methods seem to be the only avalaible tool to perform the efficient analysis of solutions, eigenvalues and eigenfunctions, and of shape functionals, in general setting.
We leave aside an important and still not completed topic related to the so-called concentrated masses. Since the pioneering work [37] of E. Sanchez-Palencia, a lot of attention has been paid to mathematical analysis of vibrations of elastic bodies, with small parts wich are very heavy (e.g., pellets in an aspic or in a meat-jelly); see papers [4,9,12,25,30,33,39], as well as the monographs [34,38] in an incomplete list. Such problems are the best examples of the topping role of the boundary layer effect. Although we analyse the boundary layers in details, the purposes of the present paper is essentially different so that we cannot mutually serve for an analysis of concentrated masses.
1.2 Preliminaries, anisotropic inhomogeneous elastic body
Let us consider in three spatial dimensions the elasticity problem for an elastic body Ω, written in the matrix/column notation, see e.g., [10], [19] for more details,
where (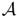 ) is a symmetric positive definite matrix function in
) is a symmetric positive definite matrix function in  of size 6×6, with measurable or smooth elements, consisting of the elastic material moduli (the Hooke's or stiffness matrix) and
of size 6×6, with measurable or smooth elements, consisting of the elastic material moduli (the Hooke's or stiffness matrix) and 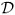 (∇x) is (6×3)-matrix of the first order differential operators,
(∇x) is (6×3)-matrix of the first order differential operators,
u = (u1, u2, u3)T is displacement column, n = (n1,n2,n3)T is the unit outward normal vector on ∂Ω and T stands for transposition. In this notation the strain ε(u;x) and stress σ(u;x)  (x) =
(x) = 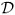 (∇x) u(x) columns are given respectively by
(∇x) u(x) columns are given respectively by
The factors 2-1/2 and  imply that the norms of strain and stress tensors coincide with the norms of columns (4) and (5), respectively. From the latter property in the matrix/column notation, any orthogonal transformation of coordinates in
imply that the norms of strain and stress tensors coincide with the norms of columns (4) and (5), respectively. From the latter property in the matrix/column notation, any orthogonal transformation of coordinates in  3 gives rise to orthogonal transformations of columns (4) and (5) in
3 gives rise to orthogonal transformations of columns (4) and (5) in  6 (cf. [[18];Ch. 2]).
6 (cf. [[18];Ch. 2]).
Remark 1.1The strains and the stresses degenerate on the space of rigid motions,
where
This subspace plays a critical role in many questions in the elasticity theory, it appears also in the so-called polynomial property [26,27] (see also [21]).
The following equalities can be veried by a direct computation,
where
N and N are the unit and null (N × N)-matrices, respectively.
N are the unit and null (N × N)-matrices, respectively.
The boundary load gΩ is supposed to be self equilibrated in order to assure the existence of a solution to the elasticity problem,
2 VIBRATIONS OF ELASTIC BODIES.
Consider inhomogenuous anisotropic elastic bodyΩ ⊂
3 with the Lipschitz boundary ∂Ω. Spectral problems for the body are formulated in a fixed Cartesian coordinate system x = (x1,x2,x3)T, and in the matrix notation. We assume that the matrix  of elastic moduli is a matrix function of the spatial variable x ∈
of elastic moduli is a matrix function of the spatial variable x ∈  3, symmetric and positive definite for x ∈ Ω∪∂Ω. The problem on eigenvibrations of the bodyΩ takes the form
3, symmetric and positive definite for x ∈ Ω∪∂Ω. The problem on eigenvibrations of the bodyΩ takes the form
where γ > 0 is the material density, λ is an eigenvalue, the square of eigenfreguency. The part Γ of the surface ∂Ω is clamped, and the first boundary condition is prescribed on the traction free remaining part Σ = \ ∂Ω\ of the surface. We denote by
of the surface. We denote by  (Ω;Γ)3 the energy space, i.e., the subspace of the Sobolev space H1(Ω)3 with null traces on the subset Γ. The variational formulation of problem (10)-(11) reads:
(Ω;Γ)3 the energy space, i.e., the subspace of the Sobolev space H1(Ω)3 with null traces on the subset Γ. The variational formulation of problem (10)-(11) reads:
Find a non trivial function u ∈  (Ω;Γ)3 and a number λ such that for all test functions v ∈
(Ω;Γ)3 and a number λ such that for all test functions v ∈  (Ω;Γ)3 the following integral identity is verified
(Ω;Γ)3 the following integral identity is verified
where (,)Ω is the scalar product in the Lebesgue space L2(Ω).
If the stiffness matrix  and the density γ are measurable functions of the spatial variables x, and in addition uniformly positive definite and bounded, then the variational problem (12) admits normal positive egenvalues λp, which form the sequence
and the density γ are measurable functions of the spatial variables x, and in addition uniformly positive definite and bounded, then the variational problem (12) admits normal positive egenvalues λp, which form the sequence
taking into account its multiplicities, and the corresponding eigenfunctions u(p), the elastic vibration modes, are subject to the orthogonality and normalization conditions
where δp,q is the Kronecker symbol.
In the sequel it is assumed that elements of the matrix  and the density γ are smooth functions in Ω, continuous up to the boundary. In such the case Ω is called a smooth inhomogenuous body. For such a body the elastic modes u(p) are smooth functions in the interior of Ω, and up to the boundary in the case of the smooth surface ∂Ω. We have also the equivalence between the variational form and the differential form (10)-(11) of the spectral problem. We require only the interior regularity of elastic modes in the sequel, in any case the elastic modes have singularities on the collision line
and the density γ are smooth functions in Ω, continuous up to the boundary. In such the case Ω is called a smooth inhomogenuous body. For such a body the elastic modes u(p) are smooth functions in the interior of Ω, and up to the boundary in the case of the smooth surface ∂Ω. We have also the equivalence between the variational form and the differential form (10)-(11) of the spectral problem. We require only the interior regularity of elastic modes in the sequel, in any case the elastic modes have singularities on the collision line  ∩
∩ and therefore, are excluded from the Sobolev space H2(Ω)3.
and therefore, are excluded from the Sobolev space H2(Ω)3.
Along with the smooth inhomogenuous bodyΩ let us consider a bodyΩh with defects; here h > 0 stands for a small dimensionless geometrical parameter, which describes the relative size of defects. Actually, we select in the interior of Ω the points P1,...,PJ and denote by ω1,...,ωj elastic bodies bounded by the Lipschitz surfaces ∂ω1,...,∂ωj , furthemore, for the sake of simplicity we assume that the origin  belongs to ωj, j = 1,...,J. The body with defects is defined by
belongs to ωj, j = 1,...,J. The body with defects is defined by
where
The stiffness matrix and the density of the composite body take the form
The matrices  and
and  (j) as well as the scalars γ and γ(j) are different from each other, i.e.,
(j) as well as the scalars γ and γ(j) are different from each other, i.e.,  are inhomogenuous inclusions of small diameters. We assume that
are inhomogenuous inclusions of small diameters. We assume that  (j) and γ(j) are measurable, bounded and positive definite uniformly on ωj. In particular, for almost all ξ ∈ ωj the eigenvalues of the matrix
(j) and γ(j) are measurable, bounded and positive definite uniformly on ωj. In particular, for almost all ξ ∈ ωj the eigenvalues of the matrix  (j)ξ are bounded from below by a constant cj > 0. There is no special assumption on the relation between the properties of the inclusions and of the matrix (body without inclusions), we assume only that the densities γ, γ(j), and entries of the matrices
(j)ξ are bounded from below by a constant cj > 0. There is no special assumption on the relation between the properties of the inclusions and of the matrix (body without inclusions), we assume only that the densities γ, γ(j), and entries of the matrices  ,
,  (j) are of similar orders, respectively. We point out that in the framework of our asymptotic analysis, in section there are performed the limit pasages
(j) are of similar orders, respectively. We point out that in the framework of our asymptotic analysis, in section there are performed the limit pasages  (j)→ 0 and γ(j)→ 0 (a hole) as well as
(j)→ 0 and γ(j)→ 0 (a hole) as well as  (j)→ ∞ and γ(j)→ ∞ (an absolutely rigid inclusion). However, the passage γ(j)→ ∞ with the fixed matrix function
(j)→ ∞ and γ(j)→ ∞ (an absolutely rigid inclusion). However, the passage γ(j)→ ∞ with the fixed matrix function  (j) (heavy concentrated masses) can be analysed with some other ansätze, cf. [4,36,39].
(j) (heavy concentrated masses) can be analysed with some other ansätze, cf. [4,36,39].
In the fracture mechanics, the most intereting case is the weakening of elastic material due to the crack formation. The cracks are modelled by two-sided, two dimensional surfaces, with the first boundary conditions from (11) prescribed on the both crack lips, i.e. the surface is traction free from both sides. The case of a microcrack is not formally included in our problem statement, since we assume that the defect ωj is of positive volume and with the Lipschitz boundary ∂ωj. However, the asymptotic procedure works also for the cracks. Small changes which are required in the justification part, are given separately (see the end of section , proof of Proposition and Remark ). The polarization matrices for the cracks can be found in [41], [24].
The exchange of γ and (IMG) by γh and  h from (17), respectively, transforms in the integral identity for the body weakened by the defects
h from (17), respectively, transforms in the integral identity for the body weakened by the defects  ,...,
,..., , this integral identity is further denoted by (12)h. We observe also, that for smooth stiffness matrix (IMG) and the density γ the differential problem for vibrations of a composite body does not consist only of the system of equations, denoted in our notation by (10)h, restricted to the union of domains (15), along with the boundary conditions (11)h, but in addition it contains transmition conditions on the surface
, this integral identity is further denoted by (12)h. We observe also, that for smooth stiffness matrix (IMG) and the density γ the differential problem for vibrations of a composite body does not consist only of the system of equations, denoted in our notation by (10)h, restricted to the union of domains (15), along with the boundary conditions (11)h, but in addition it contains transmition conditions on the surface  where the ideal contact is assumed. Since we use only the variational formulations of the spectral problems, the transmission conditions are not explicitely written. In a similar way as for problem (13), there is the sequence of eigenvalues for the problem (12)h
where the ideal contact is assumed. Since we use only the variational formulations of the spectral problems, the transmission conditions are not explicitely written. In a similar way as for problem (13), there is the sequence of eigenvalues for the problem (12)h
and the corresponding eigenfunctions  meet the orthogonality and normalization conditions
meet the orthogonality and normalization conditions
3 Formal construction of asymptotics
We introduce the following asymptotic ansätze for eigenvalues and eigenfunctions in problem (12)h
where χj ∈  (Ω), j = 1,..., J, are cut-off functions, with non overlaping supports in Ω, and for each j, χj(x) = 1 for x ∈
(Ω), j = 1,..., J, are cut-off functions, with non overlaping supports in Ω, and for each j, χj(x) = 1 for x ∈  and χi(Pj) = δi,j.
and χi(Pj) = δi,j.
First, we assume that the egenvalue λ = λp in problem (12) is simple, and for brevity the subscript p is omitted. The corresponding eigenfunction u = u(p)∈  (Ω; Γ), normalized by condition (14), is smooth in the interior of the domain Ω.
(Ω; Γ), normalized by condition (14), is smooth in the interior of the domain Ω.
Columns of the matrices d(x) and 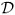 (x)T form a basis in twelve dimensional space of linear vector functions in
(x)T form a basis in twelve dimensional space of linear vector functions in  3. In this way, the Taylor formula takes the form
3. In this way, the Taylor formula takes the form
and, by equalities(4), (5) and (8), the columns
aj = d(∇x)T u(Pj), εj= 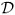 (∇x) u(Pj),
(∇x) u(Pj),
represent the column of rigid motions, and of strains, at the point Pj. Since in the vicinity of the inclusion  we have
we have
ε(u;x) = εj + O(x) = εj + O(h),
the main terms of discrepancies, left by the field u in the problem (12)h for the composite bodyΩh, appear in the system of equations in  and in the transmition conditions on ∂
and in the transmition conditions on ∂ . For the compensation of the discrepancies are used the special solutions of the elasticity problem in a homogenuous space with the inclusion ωj of unit size
. For the compensation of the discrepancies are used the special solutions of the elasticity problem in a homogenuous space with the inclusion ωj of unit size
Here ν is the unit vector of the exterior normal on the boundary ∂ωj of the bodyωj, ek = (δ1,k, ...,δ6,k)T is a orthant in the space  6, W+ and W- are limit values of the function W on the surface ∂ωj evaluated from outside and from inside of the inclusion ∂ωj, respectively.
6, W+ and W- are limit values of the function W on the surface ∂ωj evaluated from outside and from inside of the inclusion ∂ωj, respectively.
We denote by Φ j the fundamental (3×3)-matrix of the operator L0j(∇ξ) in  3. This matrix is infinitely differentiable in
3. This matrix is infinitely differentiable in  3\
3\ and enjoys the following positive homogeneity property
and enjoys the following positive homogeneity property
It is known (see, e.g., [[20], Ch. 6]), that the solutions Wjk of problem (23) admit the expansion
where
p =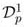 ,
, 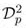 ,
, 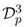 is a line of the matrix
is a line of the matrix 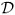 (see (3)), Φj1, Φj2, Φj3 are columns of the matrix Φj, and the radius R of the ball
(see (3)), Φj1, Φj2, Φj3 are columns of the matrix Φj, and the radius R of the ball 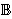 R = { ξ : | ξ | < R} is chosen such that
R = { ξ : | ξ | < R} is chosen such that 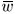 ⊂
⊂ 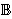 R. The coefficients
R. The coefficients 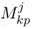 in (25) form the (6×6)-matrix Mj which is called the polarization matrix of the elastic inclusion ωj (see[28,41] and also [[20]; Ch. 6], [5], [21]). Some properties of the polarization matrix, and some comments on the solvability of problem (23) are given in section .
in (25) form the (6×6)-matrix Mj which is called the polarization matrix of the elastic inclusion ωj (see[28,41] and also [[20]; Ch. 6], [5], [21]). Some properties of the polarization matrix, and some comments on the solvability of problem (23) are given in section .
The columnes Wj1,..., Wj6 compose the (3×6)-matrix Wj and we set
In section 5 it is verified, that the right choice of boundary layer is given by formula (26), since it compensates the main terms of discrepancies. From (25) and (26) it follows that
Relation (27) can be differentiated term by term on the set
3\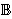 R under the rule ∇ξO(|ξ|-p) = O(|ξ|-p-1) for the remainder.
R under the rule ∇ξO(|ξ|-p) = O(|ξ|-p-1) for the remainder.
In view (24) of the detached asymptotics term equals
It produces discrepancies of order h3 (we point out that there is the factor h on w1j in (21)), which should be taken into account when constructing the regular type term h3u. On the other hand, discrepancies of the same order h3 are left in the problem for u by the subsequent term h2w(h-1(x-Pj)), which solves the transmission problem analoguous to (23)
and with the decay rate O(|ξ|-1) at |ξ|→ ∞, smaller compared to the decay rate of w1j.
Now, we evaluate the right-hand sides of the problems (29),(30) . First, by the representation of the stiffness matrix
and the corresponding splitting of differential operator with the variable coefficients
0(x,∇x) from (10), we find that the right-hand side of system (29) is the main term of the expression
We note that L0j(∇x) w1j(h-1(x-Pj)) = 0 in (32), and the dots... stand for the terms of lower order, which are unimportant for our asymptotic analysis. The following discrepancy appears in the second transmission condition (30):
The second term comes out from the elaborated Taylor formula (31)
and involves the quadratic vector function
Finally, the right-hand side of system (29) takes the form
Besides the term obtained from the quadratic vector function (35) in the Taylor formula (34), the expression (36) contains the discrepancy λγju(Pj) which originates from the inertial term λhγjuh in accordance to the asymptotic ansätze (34) and (35).
In order to establish properties of solutions to the problem (29), (30), we need some complementary results.
Lemm 3.1Assume that Z(ξ) = 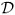 (∇ξ)TY(ξ) and
(∇ξ)TY(ξ) and
where (ρ,θ) are spherical coordinates and  ∈ C∞(
∈ C∞( 2)6,
2)6,  ∈ C∞(
∈ C∞(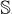 2)3are smooth vector functions on the unit sphere. The model problem
2)3are smooth vector functions on the unit sphere. The model problem
admits a solution X(ξ) = ρ-1 (θ), which is defined up to the term Φj(ξ)c with c ∈
(θ), which is defined up to the term Φj(ξ)c with c ∈  3, and becomes unique under the orthogonality condition
3, and becomes unique under the orthogonality condition
Proof After separating variables and rewriting the operator L0j(∇ξ) = r-2 (θ,∇θ, r∂ / ∂ r) in the spherical coordinates, the system (38) takes the form
(θ,∇θ, r∂ / ∂ r) in the spherical coordinates, the system (38) takes the form
Since  (θ,∇θ, 0 ) is the formally adjoint operator for
(θ,∇θ, 0 ) is the formally adjoint operator for  j(θ,∇θ, -1) (see, for example, [[20]; Lemma 3.5.9]), the compability condition for the system of differential equations (40) implies the equality
j(θ,∇θ, -1) (see, for example, [[20]; Lemma 3.5.9]), the compability condition for the system of differential equations (40) implies the equality
The equality represents the orthogonality condition in the space L2(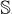 2) of the right-hand side
2) of the right-hand side  of system (40) to the solutions of the system
of system (40) to the solutions of the system
which are nothing but constant columns. Indeed, after transformation to the Cartesian coordinate system ξ equations(42) take the form L0j(∇ξ) V(ξ) = 0, ξ ∈  3\
3\ , and any solution V(ξ) = ρ0
, and any solution V(ξ) = ρ0 (θ) is constant. Let b > a > 0 be some numbers, and let Ξ be the annulus {ξ : a < r < b}. We have
(θ) is constant. Let b > a > 0 be some numbers, and let Ξ be the annulus {ξ : a < r < b}. We have
We have used here the Green formula and the fact that the integrands on the spheres of radii a and b are equal to b-2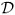 (θ)T
(θ)T and a-2
and a-2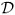 (θ)T
(θ)T , respectively, i.e., the integrals cancel one another.
, respectively, i.e., the integrals cancel one another.
Therefore, the compability condition (41) is verified and the system (40) has a solution  ∈ C∞(
∈ C∞( 2)3. The solution is determined up to a linear combination of traces on
2)3. The solution is determined up to a linear combination of traces on  2 of columns of the fundamental matrix Φ(ξ); recall that the columns of matrix Φ(ξ) are the only homogenuous solutions of degree -1 of the homogenuous model problem (38).
2 of columns of the fundamental matrix Φ(ξ); recall that the columns of matrix Φ(ξ) are the only homogenuous solutions of degree -1 of the homogenuous model problem (38).
According to the definition and utility the columns Φq verify the relations
where ξ is the unit outer normal to the sphere
2 = ∂ 1,
1,  1 = {ξ : ρ < 1}, δ is the Dirac mass, eq = ( δ1 ,q, δ 2,q,δ 3,q)T is the basis vector of the axis xq, and the last integral over
1 = {ξ : ρ < 1}, δ is the Dirac mass, eq = ( δ1 ,q, δ 2,q,δ 3,q)T is the basis vector of the axis xq, and the last integral over 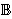 1 is understood in the sense of the theory of distributions. Thus, owing to (43), the orthogonality condition (39) can be satisfied that implies the uniqueness of the solution
1 is understood in the sense of the theory of distributions. Thus, owing to (43), the orthogonality condition (39) can be satisfied that implies the uniqueness of the solution 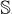 to the problem (38), (39). ■
to the problem (38), (39). ■
In view of (32) and (27), (28), the right-hand side (38) of takes the form
General results of [7] (see also[[20]; §3.5, §6.1, §6.4]) show that there exists a unique decaying solution of problem (29), (30), which admits the expansion
In the same way as in relation (27), the relation (45) can be differentiated term by term under the rule ∇ξO(|ρ|-p(1+|ln ρ|)) = O(|ρ|-p-1(1+|ln ρ|)).
The method [16] is applied in order to evaluate the column Cj.
Lemma 3.2 The equality is valid
where |ωj| is the volume, and  = |ωj|-1∫ωj γj (ξ)dξ the mean scaled density of the inclusion ωj, i.e., its mass is
= |ωj|-1∫ωj γj (ξ)dξ the mean scaled density of the inclusion ωj, i.e., its mass is  |ωj|, and
|ωj|, and
Proof In the ball 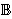 R we apply the Gauss formula and obtain, that for R → ∞,
R we apply the Gauss formula and obtain, that for R → ∞,
We have also taken into accout equalities (39) and (43). On the other hand, in view of formulae (36) and (32) it follows that
We turn back to the decomposition (27), and taking into account the homogeneity degree of the integrand, we see that the integral over the sphere  = ∂
= ∂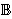 R equals
R equals
The integrals over the surfaces ∂ωj in the right-hand sides of (49) cancel with two integrals, which according (33) to appear in the formula
Finally, by the equality
 ( ∇x)T
( ∇x)T
 ( ∇x)Uj(ξ) +
( ∇x)Uj(ξ) + ( ∇x)T (xT∇x0(Pj))εj = λγ0(Pj)u(Pj) ,
( ∇x)T (xT∇x0(Pj))εj = λγ0(Pj)u(Pj) ,
resulting from equation (33) at the point x = Pj, the sum of the pair of two last integrals in (51) takes the form
∫ωj ( ( ∇ξ)T
( ∇ξ)T
 (∇ξ)Uj(ξ) +
(∇ξ)Uj(ξ) +  ( ∇ξ)T (ξT∇x0(Pj))εj)dξ = λγ0(Pj)|ωj|u(Pj) .
( ∇ξ)T (ξT∇x0(Pj))εj)dξ = λγ0(Pj)|ωj|u(Pj) .
It remains to pass to the limit R→ + ∞. ■
Now, we are in position to determine the terms ν and µ in the ansätze (21) and (20), which are given by solutions of the problem
The weak formulation of (52)-(53) is given below by (59) in the subspace  (Ω;Γ)3 of the Sobolev space H1(Ω). The right-hand side includes the discrepancies, which results from the terms of boundary layer type and of the order h3. By decompositions (27) and (45) we obtain
(Ω;Γ)3 of the Sobolev space H1(Ω). The right-hand side includes the discrepancies, which results from the terms of boundary layer type and of the order h3. By decompositions (27) and (45) we obtain
The terms in the curly braces enjoy the singularities O(|x-Pj|-2) and O(|x-Pj|-1), respectively, therefore, it should be clarified in what sense the differential problem (52), (53) is considered. Equation (52) is posed in the punctured domain Ω , thus the Dirac mass and its derivatives, which are obtained by the action of the operator  on the fundamental matrix, are not taken into account. Beside that, by virtue of the definition of the term Xjimplying a solution to the model problem (38)with the right-hand side (44), and according to the estimates of remainders in the expansions (27), (45), the following relations are valid
on the fundamental matrix, are not taken into account. Beside that, by virtue of the definition of the term Xjimplying a solution to the model problem (38)with the right-hand side (44), and according to the estimates of remainders in the expansions (27), (45), the following relations are valid
which accept the differentation according to the standard rule
∇xO( (1 + | ln rj|))) = O(
(1 + | ln rj|))) = O( (1 + |ln rj|))) .
(1 + |ln rj|))) .
In other words, expression (54) should be written in the combersome way
Here, [A,B] = AB-BA is the commutator of operators A and B, and Sj1, Sj2 = Sj1 +Xj + Φj Cj are expressions in curly braces in (54).
Lemma 3.3Let λ be a simple eigenvalue in the problem (10), (11), and u the corresponding vector eigenfunction normalized by the condition (14). Problem (52), (53) admits a solution ν ∈ H1(Ω)3if and only if
where Ωδ = Ω \ ( ∪ ... ∪
∪ ... ∪  ) and
) and  = {x :rj < δ}.
= {x :rj < δ}.
Proof The variant of the one dimensional Hardy's inequality
provides the estimate
In this way, the last term in the integral identity serving for problem (52), (53)
is a continuous functional over the Sobolev space H1(Ω)3, owing to the inequalities
|(f, V)Ω| < c
< c ∥V ;H1(Ω)∥,
Thus, Lemma follows from the Riesz representation theorem and Fredholm alternative, in addition, formula (57) is valid because the integrand is a smooth function in Ω \ { P1,...,PJ}, with absolutely integrable singularities at the points P1,...,PJ. ■
Remark 3.1If the points Pj are considered as tips of the complete cones 3\Pj, the elliptic theory in domains with conical points (see the fundamental contributions [7,16,17] and also e.g., monograph [20]) provides estimates in weighted norms of the solution v to problem (52), (53). Indeed, owing to relation (55) for any τ > 1/2 the inclusions
3\Pj, the elliptic theory in domains with conical points (see the fundamental contributions [7,16,17] and also e.g., monograph [20]) provides estimates in weighted norms of the solution v to problem (52), (53). Indeed, owing to relation (55) for any τ > 1/2 the inclusions  ∈ L2(
∈ L2( j)3are valid, where
j)3are valid, where  j stands for a neighbourhood of the point Pj, in addition
j stands for a neighbourhood of the point Pj, in addition  j ∩
j ∩  k =
k =  for j ≠k, therefore, the terms
for j ≠k, therefore, the terms  -2u,
-2u,  -1∇xv and
-1∇xv and 
 j. ■
j. ■
We evaluate the limit in the right-hand side of (57) for δ→ + 0. By the Green formula and representation (54), the limit is equal to the sum of the surface integrals
We apply the Taylor formulae (31) and (32) to the matrix  and the vector u, and take into account relations (8) for the matrices d and
and the vector u, and take into account relations (8) for the matrices d and 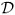 . We also introduce the stretched coordinates ξ = δ-1(x - Pj). As a result, up to an infinitesimal term as δ → +0, integral equals to
. We also introduce the stretched coordinates ξ = δ-1(x - Pj). As a result, up to an infinitesimal term as δ → +0, integral equals to
The integrals I0 and I1 vanish. Indeed, due to the second equality in (8) we have
These equalities are understood in the sense of distributions. By formula (47), we obtain
I2 = -u(Pj)┬Ij.
Relations (39) and (43) yield
I3 = u(Pj)┬Cj.
Finally, in the same way as in (62), we obtain
Now, we could apply the derived formulae. We insert the obtained expressions for Iq into (61) → (60) → (57) and in view of equation (46) for the column Cj, we conclude that
If equality (64) holds, then problem (52), (53) admits a solution υ ∈ H1(Ω)3. The construction of the detached terms in the asymptotic ansätze (20) and (21) is completed.
In the forthcoming sections the formal asymptotic analysis is confirmed and generalized into the following result.
Theorem 3.2Let λp be an eigenvalue in problem (12) with multiplicity 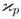 , i.e., in the sequence (13)
, i.e., in the sequence (13)
There exist hp > 0 and cp > 0 such that for h ∈ (0, hp] the eigenvalues  , . . . ,
, . . . ,  of the singularly perturbed problem (12)h, and only the listed eigenvalues, verify the estimates
of the singularly perturbed problem (12)h, and only the listed eigenvalues, verify the estimates
where cp(α) is a multiplier depending on the number p and the exponent α ∈ (0,1/2) but independent of h ∈ (0,hp], while  , . . . ,
, . . . ,  stand for eigenvalues of symmetric (
stand for eigenvalues of symmetric (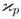 ×
× 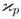 )-matrix
)-matrix 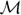 p with the entries
p with the entries
Mj is the polarization matrix of the scaled inclusion (see (25) and (27)), u(p), . . . ,  are vector eigenfunctions in the problem (12) corresponding to the eigenvalue λp and orthonormalized by condition (14), finally the quantities
are vector eigenfunctions in the problem (12) corresponding to the eigenvalue λp and orthonormalized by condition (14), finally the quantities  and |ωj| are defined in Lemma 3.2.
and |ωj| are defined in Lemma 3.2.
We explain which changes are necessary in the asymptotic ansätze (20), (21) and in the asymptotic procedure in order to construct asymptotics in the case of a multiple eigenvalue λp. First, for µp and u(p) in and should be selected unknown number  and the linear combination
and the linear combination
of vector eigenfunctions; the column b(q) = ( , . . . ,
, . . . ,  )T∈
)T∈ 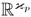 is of the unit norm. After the indicated changes the formulae for the boundary layers w1jq and w2jq remain unchanged. The same applies to problem (52), (53) for the correction term
is of the unit norm. After the indicated changes the formulae for the boundary layers w1jq and w2jq remain unchanged. The same applies to problem (52), (53) for the correction term  of regular type. However, the compability conditions are modified, and turn into the
of regular type. However, the compability conditions are modified, and turn into the 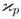 relations
relations
The left-hand side of (69) equals to  by (14) and (68). It can be evaluated by the same method as for formula (57), that (69) becomes the system of algebraic equations
by (14) and (68). It can be evaluated by the same method as for formula (57), that (69) becomes the system of algebraic equations
with coefficients from (67). In this way, the eigenvalues of the matrix
(p) and its eigenvectors b(q)∈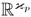 furnish the explicit values for the terms of the asymptotic ansätze (20) and (21). We emphasise that by the orthogonality and normalization conditions (b(q))Tb(k) = δq,k for the eigenvectors of the symmetric matrix
furnish the explicit values for the terms of the asymptotic ansätze (20) and (21). We emphasise that by the orthogonality and normalization conditions (b(q))Tb(k) = δq,k for the eigenvectors of the symmetric matrix 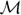 (p), it follows that the vector eigenfunctions u(p) = (
(p), it follows that the vector eigenfunctions u(p) = (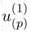 , . . . ,
, . . . , 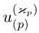 ), p = 1, . . . ,
), p = 1, . . . , 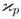 , in problem (12), which are given by formulae (68), are as well orthonormalized by the conditions (14).
, in problem (12), which are given by formulae (68), are as well orthonormalized by the conditions (14).
If we have good luck, and from the beginning the eigenvectors u(p), . . . ,  have the required form (68), then the matrix
have the required form (68), then the matrix 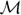 (p) is diagonal and the system of equations (70) is decomposed into a collection of
(p) is diagonal and the system of equations (70) is decomposed into a collection of 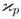 independent relations, fully analoguous to relations (64) in the case of a simple eigenvalue. Such an observation is the key ingredient of the algorithm of defects identification which will be described in a forthcoming paper, and it makes the identification method insensitive to the multiplicity of eigenvalues in the limit problem.
independent relations, fully analoguous to relations (64) in the case of a simple eigenvalue. Such an observation is the key ingredient of the algorithm of defects identification which will be described in a forthcoming paper, and it makes the identification method insensitive to the multiplicity of eigenvalues in the limit problem.
4 REMARKS ON POLARIZATION MATRICES
The results presented in this section are borrowed from [28], and paper [24].
Variational formulation of problem (23) for the special fields Wjk, which define the elements of the polarization matrix Mj in decomposition (25), are of the form
where  (
( 3) is the Kondratiev space [7], which is the completion of the linear space
3) is the Kondratiev space [7], which is the completion of the linear space  (
( 3) (infinitely differentiable functions with compact supports) in the weighted norm
3) (infinitely differentiable functions with compact supports) in the weighted norm
The following result, established in [24,28] can be shown by using transformations analoguous to (62) and (63) operating with the fields Wjk and  jm =
jm = 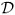 ξTek + Wjm.
ξTek + Wjm.
Pronposition 4.1 The equalities hold true
From the above representation it is clear that the matrix Mj is symmetric, the property follows by the symmetry of the stiffness matrices A0, Aj and of the energy quadratic form Ej. In addition, the representation allows us to deduce if the matrix Mj is negative or positive definite. We write M1 < M2 for the symmetric matrices M1 and M2 provided all eigenvalues of M2- M1 are positive.
Pronposition 4.2 (see [24]) 1° If 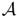 (j)ξ <
(j)ξ < 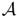 (Pj) for ξ ∈ ωj (the inclusion is softer compared to the matrix material), then Mj is a negative definite matrix.
(Pj) for ξ ∈ ωj (the inclusion is softer compared to the matrix material), then Mj is a negative definite matrix.
2° If the matrix
(j)is constant and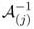 <
< 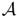 (Pj)-1(the homogenuous inclusion is rigid compared to the matrix), then Mj is a positive definite matrix.
(Pj)-1(the homogenuous inclusion is rigid compared to the matrix), then Mj is a positive definite matrix.
It is also possible to consider the limit cases, either of a cavity with
j = 0, or of an absolutely stiff inclusion with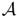 (j) = ∞. For the case of a cavity the diifferential problem takes the form
(j) = ∞. For the case of a cavity the diifferential problem takes the form
For an absolutely rigid inclusion the integral-differential equations occur as follows
where the matrices 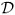 and d are introduced in (3) and (7), respectively.
and d are introduced in (3) and (7), respectively.
The Dirichlet conditions (75) in contains an arbitrary column cjk ∈  6, which permits for rigid motion of ωj and can be determined by the integral conditions which annulate the principal vector and moment of forces applied to the bodyωj. The variational formulation of problems (74) and (75) can be established in the Kondratiev space
6, which permits for rigid motion of ωj and can be determined by the integral conditions which annulate the principal vector and moment of forces applied to the bodyωj. The variational formulation of problems (74) and (75) can be established in the Kondratiev space  (see [7], and e.g., [20]) normed by the weighted norm (72)(cf. the right-hand side of (76)) and in its linear subspace {W ∈
(see [7], and e.g., [20]) normed by the weighted norm (72)(cf. the right-hand side of (76)) and in its linear subspace {W ∈  :W|∂ωj∈
:W|∂ωj∈  }, respectively, where
}, respectively, where  is the linear space of rigid motions (6). The asymptotic procedures of derivation of problems (74) and (75) from problems (23) and (71) can be found in [11,36]. The required estimates can be extracted from these references as well.
is the linear space of rigid motions (6). The asymptotic procedures of derivation of problems (74) and (75) from problems (23) and (71) can be found in [11,36]. The required estimates can be extracted from these references as well.
In accordance with Proposition 4.2 the polarization matrix for a cavity is always negative definite, and that for an absolutely rigid inclusion, it is always positive definite. Theorem 3.2 gives an asymptotic formula, which can be combined with the indicated facts and the information from Proposition 4.2, and it makes possible to deduce the sign of the variation of a given eigenvalue in terms of the defect properties. For example, in the case of a defect-crack, with the null volume and negative polarization matrix, the eigenvalues of the weakened body are smaller compared to the initial body. Such an observation is already employed in the bone China porcelane shops by the qualified personel.
5 JUSTIFICATION OF ASYMPTOTICS
We proceed with the following statements, which are fairly known for the entire body (see [6,32]) but should be verified for a body with small cavities (see (16)). We emphasize that a body with small inclusions is to be regarded in some sense as an intermediate case. In this way, some of given below axiliary results for the intact body are fit for the body with foreign inclusions, however, in some situations it is much simpler to compare the latter with the body with small voids. On the other hand, the whole justification procedure works for any sort of defects.
Proposition 5.1For a vector function u ∈  (Ω; Γ)3the inequality
(Ω; Γ)3the inequality
holds true. The above inequality remains valid with a constant independent of h ∈ (0,h0], if the domain Ω is replaced by the domain Ω(h) with defects.
Proof For analysis of displacement fields in the domain Ω(h) with cavities (in particular, with cracks) we apply the method described in review papier [[31]; §2.3] - in this framework the body with elastic inclusions is considered as intact or entire. Let us consider the restriction û of u to the set  and radius hR of the balls is selected in such a way that
and radius hR of the balls is selected in such a way that  . We construct an extension
. We construct an extension  to Ω of the field û. To this end, we introduce the annulae
to Ω of the field û. To this end, we introduce the annulae  =
=  and perform the stretching of coordinates x
and perform the stretching of coordinates x  ξ j = h-1(x - Pj). The vector functions û and u written in the ξ j-coordinates are denoted by ûj and uj, respectively. It is evident that
ξ j = h-1(x - Pj). The vector functions û and u written in the ξ j-coordinates are denoted by ûj and uj, respectively. It is evident that
where Ξ =  . Let
. Let
where d is the matrix (7), and the column aj ∈ 6 is selected in such a way that
6 is selected in such a way that
where the matrix d is given by (7). By the orthogonality condition (79), the Korn inequality is valid
(see, e.g., [6], [[31]; §2] and [[19]; Thm 2.3.3]), and the last equality follows from the second formula (8) since the rigid motion daj generates null strains (4). Let  denote an extension in the Sobolev class H1 of the vector function
denote an extension in the Sobolev class H1 of the vector function  from Ξ onto
from Ξ onto 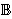 R, such that
R, such that
Now, the required extension of the field u onto the entire domain Ω is given by the formula
In addition, according to (78) and (77), (80), (81) we have
Applying the Korn's inequality in Ω, we obtain
We turn back to the function ûj and find
The other variant of the Korn's inequality
(see e.g., [6], [[31]; §2] or [[19]; §3.1]), after returning to the x-coordinates leads to the relations
By virtue of Ch > rj > ch > 0 for x ∈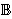 2hR\
2hR\ ⊃
⊃  , the multiplier h-1 can be inserted into the norm, and transformed to rj-1, but the norm || rj-1u; L2(
, the multiplier h-1 can be inserted into the norm, and transformed to rj-1, but the norm || rj-1u; L2( )|| is already estimated in (84), owing to
)|| is already estimated in (84), owing to  = u on
= u on  . Estimates (87), j = 1, . . . , J, modified in the indicated way along with relation (84) imply the Korn inequality in the domain Ω(h). ■
. Estimates (87), j = 1, . . . , J, modified in the indicated way along with relation (84) imply the Korn inequality in the domain Ω(h). ■
Remark 5.1Ifωj is a domain, then in the proof of Proposition 5.1 we do not need to restrict û to Ωh, but operate directly with the sets Ω(h) and 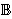 2R\ ωj since there is a bounded extension operator in the class H1over the Lipschitz boundary ∂ωj with the estimate of type (81). The presence of cracks
2R\ ωj since there is a bounded extension operator in the class H1over the Lipschitz boundary ∂ωj with the estimate of type (81). The presence of cracks
The bilinear form
can be taken as a scalar product in the Hilbert space  (Ω; Γ)3. In this way, the integral identity (12)h can be rewritten as the abstract spectral equation
(Ω; Γ)3. In this way, the integral identity (12)h can be rewritten as the abstract spectral equation
where
h = (λh)-1 is the new spectral parameter, and h is a compact, symmetric, and continuous operator, thus selfadjoint,
h is a compact, symmetric, and continuous operator, thus selfadjoint,
Eigenvalues of the operator
h constitute the sequence
with the elements related to the sequence in (18) by the first formula in (90).
The following statement is known as Lemma on almost eigenvalues and eigenvectors (see, e.g., [40]).
Proposition 5.2Let and
and ∈
∈  be such that
be such that
Then there exists an eigenvalue of the operator
of the operator  h, which satisfies the inequality
h, which satisfies the inequality
Moreover, for any δ > δ the following inequality holds
where is a linear combination of eigenfunctions of the operator
is a linear combination of eigenfunctions of the operator  h, associated to the eigenvalues from the segment [
h, associated to the eigenvalues from the segment [ - δ,
- δ,  + δ], and ||
+ δ], and || ||
|| = 1.
= 1.
For the asymptotic approximations  and
and  of solutions to the abstract equation (89) we take
of solutions to the abstract equation (89) we take
where U stands for the sum of terms separated in the asymptotic ansatz (21). Let us evaluate the quantity δ from formula (92). By virtue of λp > 0, for h ∈ (0,hp] and hp > 0 small enough, we have
where  = { V ∈
= { V ∈  : ||V;
: ||V;  || = 1} is the unit sphere in the space
|| = 1} is the unit sphere in the space  . In addition, to estimate the norm ||U;
. In addition, to estimate the norm ||U;  || the following relations are used
|| the following relations are used
where the first relation follows from the continuity at the points Pj of the second order derivatives of the vector function u(p) combined with the integral identity (12) and the normalization condition (19). We transform the expression under the sign sup in (96). Substituting into the expression the sum of terms in ansatz (21), we have
In (98) we used that u(p) and λp verify the integral identity (12). Furthermore, by the Taylor formulae (34) and (31), we obtain
Let explain the derivation of above formulae. The following substitutions are performed
with pointwise estimates for remainders of orders h2, h2, and h, respectively. These gave rise to the following multipliers in the majorants
Note that the factor h3/2 is proportional to (mes3 )1/2, and h-1rj does not exceed a constant on the inclusion
)1/2, and h-1rj does not exceed a constant on the inclusion  . Beside that, the Poincaré inequality
. Beside that, the Poincaré inequality
is employed together with the relation
Here  stands for the mean value of V over
stands for the mean value of V over  . Finally, all the norms of the test function V are estimated by Proposition 5.1.
. Finally, all the norms of the test function V are estimated by Proposition 5.1.
In similar but much simpler way, by virtue of Remark 3.1, the term  from (100) satisfies
from (100) satisfies
where τ > 1/2 is arbitrary. It is clear that h6| | < Ch6. The integral
| < Ch6. The integral  cancels the integral
cancels the integral  in (98) and some parts of the integrals
in (98) and some parts of the integrals  from (99), which we are going to consider.
from (99), which we are going to consider.
In the notation of formula (56) we have
Furthermore, the integrals  and
and  cancel each other according to the integral identities
cancel each other according to the integral identities
The latter formulae are provided by (71), (26) and (29), (30), (32), (33), (36). We point out that the test functionξ  χj (hξ + Pj)
χj (hξ + Pj) (hξ + Pj) in (106) has a compact support, i.e., the function belongs to the Kondratiev space
(hξ + Pj) in (106) has a compact support, i.e., the function belongs to the Kondratiev space  (
( 3), and in the analysed integrals the stretching of coordinates x
3), and in the analysed integrals the stretching of coordinates x  ξ = h-1(x - Pj) has to be performed.
ξ = h-1(x - Pj) has to be performed.
The expressions including asymptotic terms  (h-1(x - Pj)) = h3-i
(h-1(x - Pj)) = h3-i (x - Pj) are detached from the integrals
(x - Pj) are detached from the integrals  and
and  ,
,
and the remainders are estimated by virtue of the decompositions (27) and (45), namely,
Inequalities for the integrals  from (99) are obtained in a similar way and look as follows:
from (99) are obtained in a similar way and look as follows:
According to formula (56) for the right-hand side f of the problem (52), (53) and the associated integral identity (59), the sum of the expressions  from (100) and
from (100) and  from (107), (109) (the latter is summed over j = 1, . . . , J and q = 0,1,2) turns out to vanish. As a result, collecting the obtained estimates, we conclude that the quantity δ from formula (95) (see also (92)) satisfies the estimate
from (107), (109) (the latter is summed over j = 1, . . . , J and q = 0,1,2) turns out to vanish. As a result, collecting the obtained estimates, we conclude that the quantity δ from formula (95) (see also (92)) satisfies the estimate
for any α ∈ (0,1/2).
Now we are in position to prove the main theorem on asymptotics of solutions of singularly perturbed problem.
Proof of Theorem 3.2 From the columns b(1), . . . ,  of matrix
of matrix  (p) with elements (67) can be constructed linear combinations (68) of vector eigenfunctions u(p), . . . ,
(p) with elements (67) can be constructed linear combinations (68) of vector eigenfunctions u(p), . . . ,  as well as the subsequent terms of asymptotic ansatz (21). As a result, for q = p, . . . , p +
as well as the subsequent terms of asymptotic ansatz (21). As a result, for q = p, . . . , p + 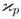 - 1 the approximate solutions {(λp + h3µp)-1,
- 1 the approximate solutions {(λp + h3µp)-1,  } of the abstract equation (89) are obtained, such that the quantity δ from relations (92) verifies the inequality (110). We apply the second part of Proposition 5.2 with
} of the abstract equation (89) are obtained, such that the quantity δ from relations (92) verifies the inequality (110). We apply the second part of Proposition 5.2 with
Let the list
include all eigenvalues of the operator
h, located in the segment
for sufficiently small h > 0, such that (λp + h3µp)-1 with h ∈ (0, h] belongs to segment (113). Our immediate objective becomes to show that
The quantities  for m > n + N - 1 are uniformly bounded in h ∈ (0, h]. By Proposition 5.1, the same assumptions provide the uniform boundedness of the norm ||
for m > n + N - 1 are uniformly bounded in h ∈ (0, h]. By Proposition 5.1, the same assumptions provide the uniform boundedness of the norm || ;
;  (Ω; Γ)|| of the vector functions
(Ω; Γ)|| of the vector functions  ∈
∈  h constructed for the vector eigenfunctions
h constructed for the vector eigenfunctions  in (12)h according to (86). Hence, there exists an infinitesimal sequence {hi}, such that the limit passage hi → +0 leads to the convergences
in (12)h according to (86). Hence, there exists an infinitesimal sequence {hi}, such that the limit passage hi → +0 leads to the convergences
We substitute into the integral identity (12)h the test function v ∈  (
( \(Γ∪{P1, . . ., PJ}))3. According to definition (17) and for sufficiently small h > 0, the stiffness matrix
\(Γ∪{P1, . . ., PJ}))3. According to definition (17) and for sufficiently small h > 0, the stiffness matrix 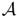 h and the density γh coincide on the support of v with
h and the density γh coincide on the support of v with 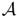 and γ , respectively. Therefore, the limit passage hi → +0 in the integral identity (12)h leads to the equality
and γ , respectively. Therefore, the limit passage hi → +0 in the integral identity (12)h leads to the equality
Since  (
( \(Γ∪{P1, . . ., PJ}))3 is dense in (
\(Γ∪{P1, . . ., PJ}))3 is dense in ( (Ω; Γ)3, the integral identity (116) holds true for all test functions v ∈
(Ω; Γ)3, the integral identity (116) holds true for all test functions v ∈ (Ω; Γ)3. We observe that the weighted norms
(Ω; Γ)3. We observe that the weighted norms  ; L2(Ω)|| are uniformly bounded by virtue of inequality , thus
; L2(Ω)|| are uniformly bounded by virtue of inequality , thus
In this way, taking into account formulae (19) and (115), we find out that
Hence,  is an eigenvalue, and
is an eigenvalue, and  is a normalized vector eigenfunction of the limit problem (12). This implies that p +
is a normalized vector eigenfunction of the limit problem (12). This implies that p + 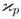 > n + N. Considering consenquently the eigenvalues λp, . . . , λ1, we conclude that
> n + N. Considering consenquently the eigenvalues λp, . . . , λ1, we conclude that
In order to establish the inequalities p < n and 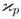 < N we select the factor c in (111) such that for
< N we select the factor c in (111) such that for  the number
the number  is excluded from the segment
is excluded from the segment
Let  be the multiplicity of the eigenvalue
be the multiplicity of the eigenvalue  of matrix M(p). By Proposition 5.1 and estimate (120) there are, not necessarily distinct, eigenvalues
of matrix M(p). By Proposition 5.1 and estimate (120) there are, not necessarily distinct, eigenvalues  ,...,
,...,  of the operator
of the operator  h such that
h such that
In addition, Proposition 5.1 furnishes the normalized columns  , such that
, such that
where  ,...,
,...,  + N-1 are normalized in
+ N-1 are normalized in  vector eigenfunctions of the operator
vector eigenfunctions of the operator  h corresponding to all eigenvalues from segment (119). By formulae (97), and (12), (14),
h corresponding to all eigenvalues from segment (119). By formulae (97), and (12), (14),
| λpδk,l| = o(1) for h → +0 .
λpδk,l| = o(1) for h → +0 .
Furthermore, owing to formula (121), we have
| - λp(
- λp( (k)) T
(k)) T
Thus, for sufficiently small h the number N cannot be smaller than  . Hence, there are eigenvalues
. Hence, there are eigenvalues  ,. . .,
,. . ., which verify inequality (120)with the majorant
which verify inequality (120)with the majorant  (since the exponent α ∈ (0,1/2) is arbitrary, we can choose α < α without loosing of the precision in the final estimate (66)). Selecting all eigenvalues of the matrix M(p), and subsequently the numbers λp-1,...,λ1, it turns out that necesserily the equality in occurs, and also N =
(since the exponent α ∈ (0,1/2) is arbitrary, we can choose α < α without loosing of the precision in the final estimate (66)). Selecting all eigenvalues of the matrix M(p), and subsequently the numbers λp-1,...,λ1, it turns out that necesserily the equality in occurs, and also N =  .
.
The proof of Theorem 3.2 is completed. ■
Remark 5.2Theorem 3 provides inequality (121), which allows for derivation of some asymptotic formulae for vector eigenfunctions  of the problem (12)h. We emphasise that, first, the estimates of remainder are not as good as in the case of eigenvalues, and, second, for multiple eigenvalues of matrix M(p)even the initial approximation for
of the problem (12)h. We emphasise that, first, the estimates of remainder are not as good as in the case of eigenvalues, and, second, for multiple eigenvalues of matrix M(p)even the initial approximation for  is not available. And this is not a lack of the obtained estimates but just the matter of asymptotic procedures; we refer the reader to the chapter 7 of book [19] and to papers [11,29], where is discussed the notion of individual and collective asymptotics of solutions to spectral problems. We present one variant of the estimates proved above.
is not available. And this is not a lack of the obtained estimates but just the matter of asymptotic procedures; we refer the reader to the chapter 7 of book [19] and to papers [11,29], where is discussed the notion of individual and collective asymptotics of solutions to spectral problems. We present one variant of the estimates proved above.
If is a simple eigenvalue of the matrix M(p) (for example, λpis a simple eigenvalue of problem (12)) and b(q)the corresponding normalized eigenvector, then there is an eigenvalue
is a simple eigenvalue of the matrix M(p) (for example, λpis a simple eigenvalue of problem (12)) and b(q)the corresponding normalized eigenvector, then there is an eigenvalue  in problem (12)) (if λpis simple than p = q), which is simple, and together with the corresponding vector eigenfunction verifies the estimates
in problem (12)) (if λpis simple than p = q), which is simple, and together with the corresponding vector eigenfunction verifies the estimates
where α ∈ (0,1/2) is arbitrary, and the factors cp(α), Cp(α) are independent of parameter h ∈ (0,hp].
Acknoledgements The research of S.A.N. was partially supported by the grant Russian Foundation of Basic Research-09-01-00759. The research of J.S. was partially supported by the Projet ANR GAOS Geometrical analysis of optimal shapes.
Received 5 Sep 2010
In revised form 13 Sep 2010
- [1] A. Campbell and S. A. Nazarov. Asymptotics of eigenvalues of a plate with small clamped zone. Positivity, 5(3), 2001.
- [2] R.R. Gadyl'shin. Asymptotic form of the eigenvalue of a singularly perturbed elliptic problem with a small parameter in the boundary condition. Differents Uravneniya, 22:640-652, 1986.
- [3] R.R. Gadyl'shin. Perturbation of the laplacian spectrum when there is a change of the type of boundary condition on a small part of the boundary. Comp. Meths Math. Phys., 36(7):889-898, 1996.
- [4] D. Gomez, S.A. Nazarov, and M.-E. Perez. The formal asymptotics of eigenmodes for oscillating elastic spatial body with concentrated masses. Zap. Nauchn. Sem. St.-Petersburg Otdel. Mat. Inst. Steklov, 342:31-76, 2007. (English translation: J. Math. Sci., 148(5): 650-674, 2008).
- [5] I. V. Kamotski and S. A. Nazarov. Spectral problems in singular perturbed domains and self adjoint extensions of differential operators. Trudy St.-Petersburg Mat. Obshch., 6:151-212, 1998. Engl. transl. in Proceedings of the St. Petersburg Mathematical Society, 6(2000) 127-181, Amer. Math. Soc. Transl. Ser. 2, 199, Amer. Math. Soc., Providence, RI.
- [6] V. A. Kondrat'ev and O. A. Oleinik. Boundary-value problems for the system of elasticity theory in unbounded domains. korn's inequalities. Russian Mathematical Surveys, 43(5):65-119, 1988.
- [7] V.A. Kondratiev. Boundary problems for elliptic equations in domains with conical or angular points. Trudy Moskov. Mat.Obshch., 16:209-292, 1967. Engl. transl. in Trans. Moscow Math. Soc. 16(1967) 227-313.
- [8] A. Laurain, S.A. Nazarov, and J. Sokolowski. Singular perturbations of curved boundaries in dimension three. The spectrum of Neumann Laplacian. Journal for Analysis and its Applications In press.
- [9] C. Leal and J. Sanchez-Hubert. Perturbation of the eigenvalues of a membrane with a concentrated mass. Quart. of Appl. Math., XLVII(1):93-103, 1989.
- [10] S. G. Lekhnitskii. Theory of Elasticity of an Anisotropic Elastic Body Holden-Day, Inc., San Francisco, California, 1963.
- [11] M.H. Lobo, S.A. Nazarov, and M.-E. Pérez. Eigen-oscillations of contrasting non-homogeneous bodies: asymptotic and uniform estimates for eigenvalues. IMA J. of Applied Mathematics, 70:419-458, 2005.
- [12] M.H. Lobo and M.-E. Pérez. Local problems or vibrating systems with concentrated masses: a review. C.R. Mecanique, 331:303-317, 2003.
- [13] V. G. Mazja, S. A. Nasarow, and B. A. Plamenevskii. Asymptotische theorie elliptischer randwertaufgaben in singulär gestörten gebieten. page 432, 1991. English transl.: Maz'ya V., Nazarov S., Plamenevskij B. Asymptotic theory of elliptic boundary value problems in singularly perturbed domains. Vol. 1. Basel: Birkh¨auser Verlag, 2000. 436 p.
- [14] V. G. Mazja, S. A. Nazarov, and B. A. Plamenevskii. On the singularities of solutions of the dirichlet problem in the exterior of a slender cone. Mat. sbornik, 122:435-456, 1983. English transl.: Math. USSR Sbornik. 50(1985) 415-437.
- [15] V. G. Mazja, S. A. Nazarov, and B. A. Plamenevskii. Asymptotic expansions of the eigenvalues of boundary value problems for the laplace operator in domains with small holes. Izv. Akad. Nauk SSSR. Ser. Mat., 48:347-371, 1984. English transl.: Math. USSR Izvestiya. 24(1985) 321-345.
- [16] V. G. Mazja and B. A. Plamenevskii. On coeffcients in asymptotics of solutions of elliptic boundary value problems in a domain with conical points. Math. Nachr., 1977. Bd. 76. S. 29-60. (Engl. transl. in Amer. Math. Soc. Transl. 123, 57-89 (1984)).
- [17] V. G. Mazja and B. A. Plamenevskii. Estimates in Lp and hölder classes and the miranda-agmon maximum principle for solutions of elliptic boundary value problems in domains with singular points on the boundary. Math. Nachr, 1978. Bd. 81. S. 25-82. (Engl. Transl. in: Amer. Math. Soc. Transl. (Ser. 2) 123, 1-56 (1984)).
- [18] N.V. Movchan. Oscilations of elastic bodies with small holes. Vestnik Leningrad University, 1:33-37, 1989.
- [19] S. A. Nazarov. Asymptotic Theory of Thin Plates and Rods, volume 1 of Dimension Reduction and Integral Estimates Nauchnaya Kniga, Novosibirsk, 2001.
- [20] S. A. Nazarov and B. A. Plamenevsky. Elliptic problems in domains with piecewise smooth boundaries. De Gruyter Exposition in Mathematics, 13, 1994. Walter de Gruyter.
- [21] S. A. Nazarov and J. Sokolowski. Asymptotic analysis of shape functionals. Journal de Mathématiques pures et appliquées, 82(2):125-196, 2003.
- [22] S. A. Nazarov and J. Sokolowski. Shape sensitivity analysis of eigenvalues revisited. Control and Cybernetics, 37:999-1012, 2008.
- [23] S. A. Nazarov and J. Sokolowski. Spectral problems in shape optimization. singular boundary perturbations. Asymptot. Anal., 56(3-4):159-204, 2008.
- [24] S. A. Nazarov, J. Sokolowski, and M. Specovius-Neugebauer. Polarization matrices in anisotropic heterogeneous elasticity. Asymptotic Analysis, 68(4):189-249, 2010.
- [25] S.A. Nazarov. Interaction of concentrated masses in a harmonically oscillating spatial body with Neumann boundary conditions. RAIRO Model. Math. Anal. Numer., 27:777-799, 1993.
- [26] S.A. Nazarov. Self-adjoint elliptic boundary-value problems. the polynomial property and formally positive operators. Probl. Mat. Anal., (16):167-192, 1997. St.-Petersburg: St.-Petersburg Univ. English transl.: J. Math. Sci. 92(1998) 4338-4353.
- [27] S.A. Nazarov. The polynomial property of self-adjoint elliptic boundary-value problems and the algebraic description of their attributes. Uspehi mat. nauk., 54:77-142, 1999. English transl.: Russ. Math. Surveys. 54(1999) 947-1014.
- [28] S.A. Nazarov. The damage tensor and measures. 1. Asymptotic analysis of anisotropic media with defects. Mekhanika tverd. tela, 3:113-124, 2000. English transl.: Mechanics of Solids. 35(2000) 96-105.
- [29] S.A. Nazarov. Uniform estimates of remainders in asymptotic expansions of solutions to the problem on eigenoscillations of a piezoelectric plate. Probl. mat. analiz., 25:99-188, 2003. Novosibirsk: Nauchnaya kniga. English transl.: Journal of Math. Sci., 114(2003) 1657-1725.
- [30] S.A. Nazarov. Asymptotic behavior of eigenvalues of the Neumann problem for systems with masses concentrated on a thin toroidal set. Vestnik St.-Petersburg Univ., 3:61-71, 2006. English transl.: Vestnik St.-Petersburg Univ. Math. 39(2006)149-157.
- [31] S.A. Nazarov. Korn's inequalities for elastic junctions of massive bodies and thin plates and rods. Uspehi mat. nauk., 63:37-110, 2008. English transl.: Russ. Math. Surveys 63(2008) 35-107.
- [32] J. Nečas. Les méthodes in théorie des équations elliptiques Masson-Academia, Paris-Prague, 1967.
- [33] O.A. Oleinik. Homogenization problems in elasticity. spectra of singularly perturbed operators. In R. J. Knops and A. A. Lacey, editors, Non-Classical Continuum Mechanics, pages 81-95, New-York, 1987. Cambridge University Press.
- [34] O.A. Oleinik, A.S. Shamaev, and G.A. Yosifian. Mathematical Problems in Elasticity and Homogenization. North-Holland, Amsterdam, 1992.
- [35] Shin Ozawa. An asymptotic formula for the eigenvalues of the laplacian in a three-dimensional domain with a small hole. J. Fac. Sci. Univ. Tokyo Sect. IA Math, 30:243-257, 1983.
- [36] E. Sanchez-Palencia. Nonhomogeneous Media and Vibration Theory. Springer-Verlag, Berlin, 1980.
- [37] E. Sanchez-Palencia. Perturbation of eigenvalues in thermoelasticity and vibration of systems with concentrated masses, volume 195 of Trends in Applications of Pure Mathematics to Mechanics. Lecture Notes in Physics, pages 346-368. Springer-Verlag, Berlin, 1984.
- [38] E. Sanchez-Palencia and J. Sanchez-Hubert. Vibration and coupling of continuous systems. Asymptotic methods Springer, Berlin, 1989.
- [39] E. Sanchez-Palencia and H. Tchatat. Vibration de systèmes élastiques avec des masses concentrées. Rend. Sem. Mat. Univ. Politec. Torino, 42:43-63, 1984.
- [40] M.I. Vishik and L.A. Lyusternik. Regular degeneration and boundary layer for linear differential equations with small parameter. Uspehi matem. nauk, 12:3-122, 1957. English transl.: Amer. Math. Soc. Transl., 20(1962) 239-364.
- [41] I.S. Zorin, A.B. Movchan, and S.A. Nazarov. Application of the elastic polarization tensor in the problems of the crack mechanics. Mekhanika tverd. tela, 6:128-134, 1988. In Russian.
Publication Dates
-
Publication in this collection
04 July 2011 -
Date of issue
2011
History
-
Reviewed
13 Sept 2010 -
Received
05 Sept 2010





























































































































