Abstract
This paper presents the effect of nonlocal scaling parameter on the coupled i.e., axial, flexural, shear and contraction, wave propagation in single-walled carbon nanotubes (SWCNTs). The axial and transverse motion of SWCNT is modeled based on first order shear deformation theory (FSDT) and thickness contraction. The governing equations are derived based on nonlocal constitutive relations and the wave dispersion analysis is also carried out. The studies shows that the nonlocal scale parameter introduces certain band gap region in all wave modes where no wave propagation occurs. This is manifested in the wavenumber plots as the region where the wavenumber tends to infinite or wave speed tends to zero. The frequency at which this phenomenon occurs is called the escape frequency. Explicit expressions are derived for cut-off and escape frequencies of all waves in SWCNT. It is also shown that the cut-off frequencies of shear and contraction mode are independent of the nonlocal scale parameter. The results provided in this article are new and are useful guidance for the study and design of the next generation of nanodevices that make use of the coupled wave propagation properties of single-walled carbon nanotubes.
Carbon Nanotube; Wavenumber; Group Velocity; Nonlocal Elasticity; Escape Frequency; Dispersion
Nonlocal continuum mechanics formulation for axial, flexural, shear and contraction coupled wave propagation in single walled carbon nanotubes
S. NarendarI,* * Author email: snarendar@aero.iisc.ernet.in ; S. GopalakrishnanII,* * Author email: snarendar@aero.iisc.ernet.in
IDefence Research and Development Laboratory, Kanchanbagh, Hyderabad-500 058, India. Tel.: +91 88976 25977 / +91 9949391823
IIComputational Wave Mechanics Laboratory, Department of Aerospace Engineering, Indian Institute of Science, Bangalore-560 058, India
ABSTRACT
This paper presents the effect of nonlocal scaling parameter on the coupled i.e., axial, flexural, shear and contraction, wave propagation in single-walled carbon nanotubes (SWCNTs). The axial and transverse motion of SWCNT is modeled based on first order shear deformation theory (FSDT) and thickness contraction. The governing equations are derived based on nonlocal constitutive relations and the wave dispersion analysis is also carried out. The studies shows that the nonlocal scale parameter introduces certain band gap region in all wave modes where no wave propagation occurs. This is manifested in the wavenumber plots as the region where the wavenumber tends to infinite or wave speed tends to zero. The frequency at which this phenomenon occurs is called the escape frequency. Explicit expressions are derived for cut-off and escape frequencies of all waves in SWCNT. It is also shown that the cut-off frequencies of shear and contraction mode are independent of the nonlocal scale parameter. The results provided in this article are new and are useful guidance for the study and design of the next generation of nanodevices that make use of the coupled wave propagation properties of single-walled carbon nanotubes.
Keywords: Carbon Nanotube, Wavenumber, Group Velocity, Nonlocal Elasticity, Escape Frequency, Dispersion.
1 INTRODUCTION
One interesting nanostructure that has attracted a lot of attention is the carbon nanotube (CNT). The discovery of CNTs in the 1991 [9] is regarded as a revolutionary step in advancement of nanotechnology. CNTs have outstanding mechanical, electronic, and thermal properties that offer great potential for applications in all areas. These properties made CNTs the central element in an array of nanostructured materials, as well as nanosensors and devices. It has also has motivated intense research for potential applications of CNTs as structural materials [24]. For example, direct measurements using atomic force microscopy (AFM) have shown that the Young modulus of multi-walled carbon nanotubes is approximately 1.28 TPa [21], which is about two orders of magnitude larger than that of steel.
Carbon nanotubes can have interesting waveguide properties at very high frequencies in the order of Tera-Hertz (THz). At such high frequencies, continuum model based finite element type methods cannot be adopted due to their limitation of the element size with respect to the wavelength, which is very small at such frequencies. Lattice dynamics for direct observation of phonons [1, 2, 10] and spectral finite element type method are more efficient and consistent to analyze such problem [11]. The nanostructures length scales are often sufficiently small, and hence for the applicability of classical continuum models, we need to consider the small length scales such as lattice spacing between individual atoms, grain size, etc. Although solution through Molecular Dynamics (MD) simulation is a possibility for such problems, its large computational cost prohibits its use for a general analysis. The conventional continuum models cannot handle scale effects. Hence the best alternative is to use those methods which provides the simplicity of continuum models and at the same time incorporate the effects of scale in such chosen continuum models [12, 20, 23, 25, 29].
An important class of modified continuum models are those based on the concept of nonlocal elasticity. These models allow the integration of "small-size" effects into classical continuum models. The theory of nonlocal elasticity introduced by Eringen in the 1970's was originally used to study screw dislocation and surface waves in solids [4-6]. Unlike classical continuum models, the nonlocal elasticity theory assumes that the stress at a reference point in a body depends not only on the strains at that point, but also on strains at all other points of the body. This nonlocal effect becomes significant when the features of a body such as the size of an imperfection or the length of a traveling wave become comparable to the intrinsic length scales of the system such as the inter-atomic distance or the particle spacing of a lattice structure.
The use of nonlocal elasticity to study size-effects in micro and nanoscale structures was pioneered by Pedisson et al. [15]. They studied the bending of micro and nanoscale beams with the concept of nonlocal elasticity and concluded that size-effects could be significant for nano-sized structures and that the magnitude of the size-effects greatly depends on the value of the nonlocal parameter (which has to be determined for each material independently). Since then, the nonlocal elasticity theory has been used by a number of researches to study size-effects on the mechanical response of carbon nanotubes. Zhang et al. used nonlocal elasticity to show the small-scale effects on buckling of MWCNTs under axial compression [28] and radial pressure [27]. Sudak studied the column buckling of MWCNTs using nonlocal continuum mechanics [18]. Other researchers have used nonlocal elasticity to study CNT vibrations [23, 29] and the propagation of waves in CNTs [12, 14, 20, 25, 26]. From these studies, it is clear that most wave propagation studies performed by various researchers using nonlocal continuum models were limited to SWCNT. The previous wave propagation studies using local continuum models [13] and nonlocal continuum models [14] have shown that the wave behavior in a SWCNT is drastically different compared to the behavior of MWCNT. However, there is currently no consensus on the value of the nonlocal parameter that should be used to model CNTs and this could be the subject of further research.
In the present paper, first order shear deformation theory (FSDT) is used, that includes the contribution of stiffness and inertial coupling for studying the characteristic wave propagation in carbon nanotubes. Appearance of higher order Lamb wave modes above certain cut-off frequencies have been studied for metallic beams by Mindlin and Harrmann [22], Doyle [3] and Gopalakrishnan [7] and for laminated composite plates by Karim et al. [11]. In the present paper, contribution of a contractional mode along with shear mode is studied for SWCNTs. Expression of cut-off frequencies and escape frequencies in shear mode and contractional mode are also derived.
The paper is organized as follows. In section 2, Erigen's nonlocal elasticity theory is explained and the coupled wave propagation equations for SWCNT are derived including the nonlocal scale effects. The effect of nonlocal scaling parameter (e0a) on the wave propagation in SWCNTs and also the variation of the escape and cut-off frequencies with nanotube radius and e0a is studied in detail. In section 3, some numerical results are presented on the wave dispersion in SWCNTs. The expressions for the wavenumbers and wave speeds (i.e., phase and group speeds) are also derived. The paper ends with some important observations and conclusions.
2 MATHEMATICAL FORMULATION
2.1 Theory of Nonlocal Elasticity
The length scales associated with nano structures like CNTs are such that to apply any classical continuum techniques, we need to consider the small length scales such as lattice spacing between individual atoms, grain size, etc. This makes the consistent classical continuum model formulation very challenging. The Eringen's nonlocal elasticity theory [4, 6] is useful tool in treating the phenomena whose origins lie in the regimes smaller than the classical continuum models.
This theory assumes that the stress state at a reference point x = (x1, x2, x3) in the body is regarded to be dependent not only on the strain state at x but also on the strain states at all other points x' of the body. This is in accordance with atomic theory of lattice dynamics and experimental observations on phonon dispersion. The most general form of the constitutive relation in the nonlocal elasticity type representation involves an integral over the entire region of interest. The integral contains a nonlocal kernel function, which describes the relative influences of the strains at various locations on the stress at a given location. The constitutive equations of linear, homogeneous, isotropic, non-local elastic solid with zero body forces are given by
Equation (1) is the equilibrium equation, where σkl, ρ, fl and ul are the stress tensor, mass density, body force density and displacement vector at a reference point x in the body, respectively, at time t. Equation (3) is the classical constitutive relation where  (x') is the classical stress tensor at any point x' in the body, which is related to the linear strain tensor ekl(x') at the same point through the lame constants λ and µ. Equation (4) is the classical strain-displacement relationship. The only difference between equations (1)-(4) and the corresponding equations of classical elasticity is the introduction of equation (2), which relates the global (or nonlocal) stress tensor σkl to the classical stress tensor
(x') is the classical stress tensor at any point x' in the body, which is related to the linear strain tensor ekl(x') at the same point through the lame constants λ and µ. Equation (4) is the classical strain-displacement relationship. The only difference between equations (1)-(4) and the corresponding equations of classical elasticity is the introduction of equation (2), which relates the global (or nonlocal) stress tensor σkl to the classical stress tensor  (x') using the modulus of nonlocalness. The modulus of nonlocalness or the nonlocal modulus α(|x - x'|,ξ) is the kernel of the integral equation (2) and contains parameters which correspond to the nonlocalness [16]. A dimensional analysis of equation (2) clearly shows that the nonlocal modulus has dimensions of (length)-3 and so it depends on a characteristic length ratio a/l where a is an internal characteristic length (lattice parameter, size of grain, granular distance) and l is an external characteristic length of the system (wavelength, crack length, size or dimensions of sample) [4]. Therefore the nonlocal modulus can be written in the following form:
(x') using the modulus of nonlocalness. The modulus of nonlocalness or the nonlocal modulus α(|x - x'|,ξ) is the kernel of the integral equation (2) and contains parameters which correspond to the nonlocalness [16]. A dimensional analysis of equation (2) clearly shows that the nonlocal modulus has dimensions of (length)-3 and so it depends on a characteristic length ratio a/l where a is an internal characteristic length (lattice parameter, size of grain, granular distance) and l is an external characteristic length of the system (wavelength, crack length, size or dimensions of sample) [4]. Therefore the nonlocal modulus can be written in the following form:
where e0 is a constant appropriate to the material and has to be determined for each material independently [4].
Making certain assumptions [4], the integro-partial differential equations of nonlocal elasticity can be simplified to partial differential equations. For example, equation (2) takes the following simple form:
where Cijkl is the elastic modulus tensor of classical isotropic elasticity and εij is the strain tensor. where ∇2 denotes the second order spatial gradient applied on the stress tensor σkl,k and ξ = e0a/l. The validity of equation (6) has been justified by comparing the expressions for frequency of waves from the nonlocal model above with those of the Born-Karman model of lattice dynamics [4]. Eringen reports a maximum difference of 6% and a perfect match for nonlocal constant value of e0 = 0.39 [4]. Sudak [18] proposed that e0 = 112.7 for the critical axial strain of a double walled carbon nanotube. To the best of authors knowledge, no experiments have been conducted on CNT to determine the value of e0. Wang and Hu [19] proposed that e0 = 1/  and used this value in the non-local beam model. Zhang et al. [29] estimated that e0≈ 0.82 by matching the theoretical buckling strain obtained by the nonlocal thin shell model obtained by Zhang et al. [28] to those from the molecular mechanics simulations given by Sears and Batra [17]. Wang [20] estimated that e0a < 2.0 nm (which give e0 = 14.08) for a SWCNT wave propagation at frequencies grater than 10 THz. e0, which is a nonlocal scaling parameter, which has been assumed as a constant appropriate to each material in published literature.
and used this value in the non-local beam model. Zhang et al. [29] estimated that e0≈ 0.82 by matching the theoretical buckling strain obtained by the nonlocal thin shell model obtained by Zhang et al. [28] to those from the molecular mechanics simulations given by Sears and Batra [17]. Wang [20] estimated that e0a < 2.0 nm (which give e0 = 14.08) for a SWCNT wave propagation at frequencies grater than 10 THz. e0, which is a nonlocal scaling parameter, which has been assumed as a constant appropriate to each material in published literature.
2.2 Derivation of the Nonlocal Governing Partial Differential Equations The displacement field for axial and transverse motion based on first order shear deformation theory (FSDT) and thickness contraction is given by
where u and w are the axial and transverse displacements, respectively, at a material point. u0 is the beam axial displacement along the reference plane, w0 is the transverse displacement on the reference plane, ϕ is the curvature- independent rotation of the beam cross-section about Y-axis and ψ = εzz is the contraction/elongation parallel to Z-axis (shown in Fig. 1).
The strains are obtained as
Using Hamilton's principle and Eqs. (1) and (2), the governing wave equations can be obtained as The nonlocal constitutive relation for isotropic materials is given as [16]
where, σxx and σzz are the normal stresses in x and z directions respectively and τxz is the in-plane shear stress. For the case of an isotropic plate, the expressions for Cij in terms of Young's modulus E and Poisson's ratio ν are given as C11 = C12 = C22 = E/(1 - ν2) and C66 = E/(2(1 + ν)).
The potential and kinetic energies are given as
assuming constant cross-sectional area of SWCNT,
Using Hamilton's principle,
and Eqs. (9 )-(11 ) and (12 ), and the fundamental lemma of calculus of variations, the nonlocal governing equations of motion are derived as:
where
Here z = r sinθ and p = 0,1,2. One can substitute e0a = 0 in the equations (18 )-(21 ), to recover the local or classical coupled equations for the SWCNTs.
2.3 Wave Dispersion Analysis
2.3.1 Computation of Wavenumbers
Using discrete Fourier transformation (DFT) for the temporal field, the spectral solution for primary displacement field variables can be expressed as
where d = {u0ψ w0ϕ}T is the generic displacement vector as a function of (x,t) and 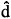 = {
= { 0
0
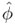 }T represents the the spectral amplitude vector corresponding to generic displacement vector as a function of (x,ω).
}T represents the the spectral amplitude vector corresponding to generic displacement vector as a function of (x,ω). 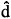 (x,ω) is the frequency domain amplitude vector of the CNTs. k is the wavenumber and ω is the angular frequency of the wave motion and j =
(x,ω) is the frequency domain amplitude vector of the CNTs. k is the wavenumber and ω is the angular frequency of the wave motion and j = 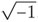 .
.
Substituting Eqs. (24) in the governing equations of motion of SWCNT (see Eqs. (18) -(21 ) yields four homogeneous equations in terms of  ,
,  ,
,  and
and 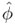 as
as
where [Qab], (a, b = 1, 2, 3, 4) are given in appendix A. The wavenumbers and hence the wave speeds (i.e., phase and group speeds) are solved from Eq. (25 ) by using Polynomial Eigenvalue Problem (PEP) [3, 7, 8, 11, 13, 22]. Equating the determinant of matrix [Qab] to zero (for the non-trivial solution of 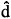 will give the characteristic polynomial in terms of wavenumber k of the order 8, solution of which is quite difficult. PEP converts the characteristic polynomial equation into a matrix of size 4×4, whose eigen values form the solution of the equation. After obtaining the wavenumbers, the wave speeds are extracted. The details of computation of wavenumbers using PEP are as follows.
will give the characteristic polynomial in terms of wavenumber k of the order 8, solution of which is quite difficult. PEP converts the characteristic polynomial equation into a matrix of size 4×4, whose eigen values form the solution of the equation. After obtaining the wavenumbers, the wave speeds are extracted. The details of computation of wavenumbers using PEP are as follows.
where
The elements of matrix [S2] are given in appendix B. This form is amenable to solution of wavenumbers through PEP. From Eq. (26 ), we can clearly see the dependence of nonlocal scale parameter e0a on wavenumber. The plot wavenumber vs frequency is called the Spectrum curve and in this figure, the frequency at which the imaginary part of wavenumber becomes real is called as cut-off frequency. The cut-off frequencies of this SWCNTs are obtained by setting k = 0 in the dispersion relation (Eq. (26 )) i.e., for the present case of PEP one can set Det([S0]) = 0, for the cut-off frequencies as
Fig. 1 shows the spectrum relation plot as a function of nonlocal scale parameter e0a. From the figure, we see that at certain frequencies, the wavenumber is tending to infinity and this frequency value decreases with increase in the scale parameter. Its value can be analytically determined by looking at the wavenumber expression and setting k → ∞. This accounts to setting the Det[S2] = 0, which gives
where X2 =  +
+  ; X1 = I0J2 + I2J0; X0 =
; X1 = I0J2 + I2J0; X0 =  +
+  . Here ωe is called escape frequency or sometimes asymptotic frequency. Differentiating the Eq. (26 ) with respect to the wave frequency (ω), one can obtain the group speeds as
. Here ωe is called escape frequency or sometimes asymptotic frequency. Differentiating the Eq. (26 ) with respect to the wave frequency (ω), one can obtain the group speeds as
Here
where Cg = (∂ω/∂ kω) is the group speed of a wave in SWCNT and the matrices [S2], and [S1] are given in Eqs. (27 ) and (28 ), respectively. This is again a PEP in terms of Cg and one can solve it for group speeds of respective modes (i.e., for axial, flexural, shear and contraction), which is again a function of nonlocal scale parameter.
The phase speed is calculated from the definition as
The detail effect of the nonlocality on wave speeds of single walled carbon nanotubes will be discussed in the next section.
3 RESULTS AND DISCUSSION
In this section, numerical experiments are presented to analyze the wave properties of SWCNTs. First, the wavenumber, phase and group speeds are obtained for SWCNT from local and nonlocal elastic theories. Following Wang [20], the nonlocal parameter e0a should be less than 2.0 nm, so that here in the simulation procedure we choose e0a = 0 nm and 0.5 nm. The spectrum and dispersion curves are plotted for e0a = 0 nm and 0.5 nm.
Fig. (2) shows the real and imaginary parts of the wavenumber of SWCNT obtained from both local and nonlocal models. These wavenumbers are obtained by solving the PEP given in Eq. (26 ). Thick lines represent the real part and the thin lines show the imaginary part of the wavenumbers. From Fig. (2), it can be seen that there are four modes of wave propagation, namely, axial, flexural, shear and contractional. For local/classical elasticity (e0a = 0), the wavenumbers for the axial mode has a linear variation with the frequency which is in the tera hertz (THz) range. The linear variation of the wavenumbers denote that the waves will propagate non-dispersively, i.e., the waves do not change their shapes as they propagate. On the other hand, the flexural wavenumbers have a non-linear variation with the frequency at low frequencies, which indicates that the waves are dispersive in nature. At high frequencies, the flexural waves show a linear variation with frequency. However, the wavenumbers of this flexural wave mode have a substantial real part starting from the zero frequency. This implies that the mode starts propagating at any excitation frequency and does not have a cut-off frequency. The shear and contractional wave modes, however, have certain frequency band within which the corresponding wavenumbers are purely imaginary. Thus, these modes does not propagate at frequencies lying within this band. Both the shear and contraction wavenumbers have a substantial imaginary part along with the real part, thus these waves attenuate as they propagate. In the present study for a 3.5 nm radius SWCNT, we have shear cut-off frequency at 0.8545 THz and contraction cut-off frequency at 1.404 THz. The values of the cut-off frequency are calculated from Eq. (31 ). It can be observed from Eq. (31 ) that these frequencies are independent of the nonlocal scaling parameter, and hence same frequencies are obtained from both local and nonlocal theories.
For e0a = 0, which is the case of local theory of elasticity solution, wavenumbers increase monotonically with the increase in frequency, which is shown in Fig. 2 and correspondingly, the wave speeds, shown in Figs. 3 and 4 increases with increase in wave frequency. However, at higher frequencies, they attain a constant value. However, with the introduction of scale effects (for present analysis e0a = 0.5 nm), the wave behavior is altered drastically. All the wave modes escapes to infinity (as shown in Fig. 2), at a particular frequency called the "escape frequency", beyond this frequency there is no wave propagation i.e, the wavenumber before escape frequency are real and after that are purely imaginary. Thus, scale parameter introduces the escape frequency where the wavenumber k tends to infinite and the corresponding wave speeds (i.e, phase and group speeds) tends to zero as shown in Figs. (3) and (4).
Fig. (5) shows the variation of escape frequencies of flexural and shear wave modes with the nonlocal parameter. The value of escape frequency decreases with increase in the scale parameter e0a, for all the wave modes. The escape frequencies of the axial and flexural waves are same and that of the shear and contraction waves are also same. It shows that as e0a increases, the escape frequency decreases. At higher values of e0a, escape frequencies approach to very small values. as shown in Fig. (5). Equations (32 )-(35 ) gives the expressions for escape frequencies of all waves in SWCNT. From these expressions it is clear that, escape frequency values are independent of SWCNT diameter see Fig.(6), for all wave modes. The detailed variation in escape frequency for SWCNTs as a function of non-local scale parameter is shown in Figs.6(a)-(d) for e0a = 0.5 nm, 1.0 nm, 1.5 nm and 2.0 nm, respectively. It shows the effect of the radius of the nanotube and nonlocal scaling parameter (e0) on the escape frequency of SWCNTs more clearly. The escape frequencies for both axial and flexural modes are same that of the shear and contraction waves is also same and these are constant with respect to the radius of the CNT. These values of escape frequency are decreasing with the nonlocal scale coefficient e0a see Fig.6(a)-(d) and are still constant with radius of CNT.
The variation of the cut-off frequencies of shear contraction wavemodes with radius (R) of SWCNT are shown in Fig. (7). This figure shows that, as the radius of the nanotube increases, the cut-off frequencies decrease and at higher values of R, the cut-off frequencies approach to a very small values. Hence, it can be concluded that for large values of scale parameter, shear deformation on CNT has negligible effect and CNT behaves like more like elementary beam.
Fig. 8 shows the wave modes at 10.067 THz wave frequency of a (30,30) SWCNT of length 244 15.282 nm consisting of 7500 carbon atoms. Fig. 8a is for axial wave mode case, Fig. 8b is for 245 contraction, Fig. 8c is for flexural and Fig. 8d is for shear wave modes of this SWCNT. From 246 these figures one can clearly visualize the type of wave mode and its effect on the CNT.
Finally, wave propagation in CNTs has been a topic of great interest in nanomechanics, where the equivalent continuum models are widely used. In this manuscript, we examined this issue by incorporating the nonlocal theory into the classical model. The influence of the nonlocal effects has been investigated in details. The results are qualitatively different from those obtained based on the local/classical theory and thus, are important for the development of future CNT-based nanodevices.
4 CONCLUSIONS
The effect of nonlocal scaling parameter on the coupled wave propagation in single-walled carbon nanotubes (SWCNTs) is studied.. The axial and transverse motion of SWCNT is modeled based on first order shear deformation theory and thickness contraction. The governing equations are derived based on nonlocal constitutive relations and the wave dispersion analysis is also carried out. The nonlocal elasticity calculation shows that the wavenumber tends to infinite at certain frequencies and the corresponding wave velocity tends to zero at those frequencies indicating localization and stationary behavior. A polynomial eigenvalue problem in wavenumbers is obtained as a function of wave frequency, nonlocal scale parameter and the material properties of the SWCNT. Explicit expressions are derived for cut-off and escape frequencies of all waves in SWCNT. It is also shown that the cut-off frequencies of shear and contraction mode are independent of the nonlocal scale parameter. The results provided in this article are useful guidance for the study and design of the next generation of nanodevices that make use of the wave propagation properties of single-walled carbon nanotubes.
5 APPENDICES:
A. Elements of Matrix [Q]
The elements of the matrix [Q] given in Eq. (25) are
B. Elements of Matrix [S2]
The elements of the matrix [S2] are
Received 17 Apr 2012;
In revised form 30 Apr 2012
- [1] M. Born and K. Huang. Dynamical theory of crystal lattices Clarendon Press, Oxford, 2002.
- [2] A.N. Cleland. Foundation of nanomechanics. Sringer, 2002.
- [3] J.F. Doyle. Wave propagation in structures Springer-Verlag Inc. New York, 1997.
- [4] A.C. Eringen. Linear theory of non-local elasticity and dispersion of plane waves. International Journal of Engineering Sciences, 10:425, 1972.
- [5] A.C. Eringen. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. Journal of Applied Physics, 54:4703, 1983.
- [6] A.C. Eringen and D.G.B. Edelen. On non-local elasticity. International Journal of Engineering Sciences, 10:233, 1972.
- [7] S. Gopalakrishnan. A deep rod finite element for structural dynamics and wave propagation problems. International Journal of Numerical Methods in Engineering, 48:731744, 2000.
- [8] S. Gopalakrishnan, A. Chakraborty, and D. Roy Mahapatra. Spectral finite element method 2008.
- [9] S. Iijima. Helical microtubules of graphitic carbon. Nature, 354:5658, 1991.
- [10] R.A. Jishi, L. Venkataraman, M.S. Dresselhaus, and G. Dresselhaus. Phonon modes in carbon nanotubules. Chemical Physics Letters, 209:7782, 1993.
- [11] M.R. Karim, M.A. Awal, and T. Kundu. Elastic wave scattering by cracks and inclusions in plates: in-plane case. International Journal of Solids and Structures, 29(19):23552367, 1992.
- [12] K.M. Liew and Q. Wang. Analysis of wave propagation in carbon nanotubes via elastic shell theories. International Journal of Engineering Sciences, 45:227241, 2007.
- [13] M. Mitra and S. Gopalakrishnan. Wave charecteristics of multi-walled carbon nanotubes. AIAA, page 1782, 2008.
- [14] S. Narendar and S. Gopalakrishnan. Nonlocal scale effects on wave propagation in multi-walled carbon nanotubes. Computational Materials Science, 47:526538, 2009.
- [15] J. Peddieson, G.R. Buchanan, and R.P. McNitt. Application of nonlocal continuum models to nanotechnology. International Journal of Engineering Science, 41:305312, 2003.
- [16] Y.Z. Povstenko. The nonlocal theory of elasticity and its applications to the description of defects in solid bodies. Journal of Mathematical Sciences, 97(1):38403845, 1999.
- [17] A. Sears and R.C. Batra. Macroscopic properties of carbon nanotubes from molecularmechanics simulations, volume 69. Physical Review B, 2004.
- [18] L.J. Sudak. Column buckling of multiwalled carbon nanotubes using nonlocal continuum mechanics. Journal of Applied Physics, 94:72817287, 2003.
- [19] L.F.Wang and H.Y. Hu. Transverse wave propagation in single-walled carbon nanotubes, volume 71. Physical Review B, 2005.
- [20] Q. Wang. Wave propagation in carbon nanotubes via nonlocal continuum mechanics. Journal of Applied Physics, 98:124301, 2005.
- [21] E.W. Wong, P.E. Sheehan, and C.M. Lieber. Nanobeam mechanics: elasticity, strength, and toughness of nanorods and nanotubes. Science, 277:19711975, 1997.
- [22] M. Xu. A one dimensional theory of compressional waves in an elastic rod. In Proceedings of First US National Congress of Applied Mechanics, pages 187191, 1950.
- [23] M. Xu. Free transverse vibrations of nano-to-micron scale beams. In Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, volume 462, pages 29772995, 2006.
- [24] B.I. Yakobson, C.J. Brabec, and J. Bernholc. Nanomechanics of carbon tubes: Instabilities beyond linear response. Physical Review Letters, 76:25112514, 1996.
- [25] J. Yoon, C.Q. Ru, and A. Mioduchowski. Sound wave propagation in multiwall carbon nanotubes. Journal of Applied Physics, 93:4801, 2003.
- [26] J. Yoon, C.Q. Ru, and A. Mioduchowski. Timoshenko-beam effects on transverse wave propagation in carbn nanotubes. Composites Part B: Eng, 35:8793, 2004.
- [27] Y.Q. Zhang, G.R. Liu, and X. Han. Effect of small length scale on elastic buckling of multi-walled carbon nanotubes under radial pressure. Physics Letters A, 349(5):370376, 2006.
- [28] Y.Q. Zhang, G.R. Liu, and J.S. Wang. Small-scale effects on buckling of multiwalled carbon nanotubes under axial compression. Physical Review Letters, 70:205430, 2004.
- [29] Y.Q. Zhang, G.R. Liua, and X.Y. Xie. Free transverse vibration of double-walled carbon nanotubes using a theory of nonlocal elasticity. Physical Review B, B 71:195404, 2005.
Publication Dates
-
Publication in this collection
21 Jan 2013 -
Date of issue
Aug 2012
History
-
Received
17 Apr 2012 -
Reviewed
30 Apr 2012































