Abstract
Mathematical model describing the development of science (nanotechnology) in Russian Federation is proposed. Results of numerical simulations are presented and discussed in the context of socio-economical interpretation.
Cluster; nanotechnology; model; socio-economic impact
Study of cluster formation in a model of nanotechnology development
Artem BalyakinI; Anna DomnichII; Vladimir ZhulegoIII; Anna IvanovaIV
IArtem Balyakin, Ph.D., Agency of Head Organization Functions implementation, NRC "Kurchatov Institute", 1, ac. Kurchatov sq., 123182, Moscow, Russia, Balyakin_AA@rrcki.ru
IIAnna Domnich, key economist, Agency of Head Organization Functions implementation, NRC "Kurchatov Institute", 1, ac. Kurchatov sq., 123182, Moscow, Russia, anna.domnich@gmail.com
IIIPh.D., head of information and analysis department, Agency of Head Organization Functions implementation, NRC "Kurchatov Institute", 1, ac. Kurchatov sq., 123182, Moscow, Russia, zhulego_VG@rrcki.ru
IVPh.D., Dept. of Mathematical Cybernetics, Saratov State University, 83, Astrakhanskaya str., 410012, Saratov, Russia, anna-ivanova@yandex.ru
ABSTRACT
Mathematical model describing the development of science (nanotechnology) in Russian Federation is proposed. Results of numerical simulations are presented and discussed in the context of socio-economical interpretation.
Keywords: Cluster, nanotechnology, model, socio-economic impact
INTRODUCTION
The development of models that describe the evolution of complex social and economic systems is seen as an important application of nonlinear sciences [1]. On the one hand, a model should be simple enough for numerical simulations, on the other hand, should capture typical features of realistic systems. In addition, an adequate description of these systems requires the understanding of the correspondence of the coefficients used in computer simulations to those in actual systems. Parameters of those systems can be estimated only qualitatively, and their conversion into quantitative values still poses a great challenge (though certain approaches to find their numerical values were discussed in [2]). This problem has been widely studied in sociology and economics, but often is neglected in mathematical modeling and numerical simulations. The solution of this problem will provide us with a deeper understanding of the behavior of complex socio-economic systems, including the insight into the origin of complex dynamics in distributed systems. Some of our previous results were reported at conferences (see, e.g. [3]) and used during foresight studies led by NRC "Kurchatov Institute".
1 PARAMETERS OF THE MODELING
The definition and adjustment of parameters for mathematical/numerical models to realistic systems is always a challenging problem. Our approach is based on a well-known sociological method of the "interference matrix". Firstly, based on experts' opinions, we chose the number of parameters responsible for main characteristics of the studied system. Secondly, using a Delphi method, we find a dependence among different parameters, namely whether one factor reduces or increases others. Numerical simulation was undertaken in the final step of the analysis.
In this paper, we study the development of a research field (nanotechnology) that is assumed to be one of the most prioritized research areas in Russian Federation. A model that has been developed in our work is based on the approach proposed by Kaneko [4]. An individual element of the model (interpreted as a single line of the development of nanotechnology in a region) is able to display complex and chaotic behavior, and the structure of interaction between the elements is fairly simple. The coupling is assumed to be global, each element of the model is a logistic map. Such an approach is traditional in nonlinear dynamics where similar models are used to describe the evolution of competitive scientific fields, the dynamics of the predator-prey system, the dynamics of the brain, etc.
It is commonly accepted that the most important factor in the development of nanotechnology is governmental funding while other factors, such as equipment, the education level of working force, and the judicial system of the country, are usually neglected by experts. We also note that the experts' forecast has the limit of about 5-10 years, and our approach cannot be used for long-term predictions.
In our previous works we used a simpler model (linear coupling between the nearest neighbors, the absence of noise, etc.), focusing primarily on parameters obtained from experts' surveys [5-7]. In this work, we discuss existence of noise in the system that can be treated as "blurring" of funds.
2 RESULTS OF NUMERICAL SIMULATION
Let us consider the case of non-identical sources of noise when each element of added noise has different amplitude and intensity. In this case, the system represents globally coupled maps with two types of communications described as
Here we study the case when a driving factor  can be treated as governmental funding and all other factors (without specifying) are included in
can be treated as governmental funding and all other factors (without specifying) are included in  Figure 1 shows a phase diagram of the system (1-2) in the case of non-identical noise for a dissipative (Fig. 1a) and inertial (Fig. 1b) global coupling. As is seen from the figure, even at fairly low amplitude of noise, the system does not display the phenomenon of clusterization. Therefore, in the case of non-identical noise one cannot identify clusters since the elements do not display the same state. However it is possible to distinguish clusters as groups of elements that match each other with certain accuracy.
Figure 1 shows a phase diagram of the system (1-2) in the case of non-identical noise for a dissipative (Fig. 1a) and inertial (Fig. 1b) global coupling. As is seen from the figure, even at fairly low amplitude of noise, the system does not display the phenomenon of clusterization. Therefore, in the case of non-identical noise one cannot identify clusters since the elements do not display the same state. However it is possible to distinguish clusters as groups of elements that match each other with certain accuracy.
Figure 2a shows a diagram where the accuracy of the clusters is set zero. We see that although all instantaneous states of the elements are distributed over the range from -0.08 to -0.06, the exact match does not occur, and each cluster contains only one element. With a further decrease in the accuracy of "clusters", one observes a decrease in the number of "clusters". This condition corresponds to the "ordered" phase (Fig. 2b,c) in the Kaneko method [4]. Finally, if the accuracy of the "clusters" is comparable with the amplitude of noise, there is a state that is similar to the case of the absence of noise (Fig. 2d). This phenomenon is of great interest and will be the subject of a future study.
We conclude that the presence of non-identical noise leads to the destruction of the phenomenon of clusterization. However we note that the study of "clusters" as groups of elements that have a similar state defined with some accuracy is still possible. For the non-identical noise case, we have also found scaling properties; recalculating factor 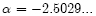 for
for  and
and  for
for  were obtained from a renormalization-group analysis.
were obtained from a renormalization-group analysis.
From the practical standpoint, these results applied to an actual situation can be interpreted as follows. With a sufficient level of external influence (ie, the amount of public funding in the country), an innovative system characterized by a fairly high level of the development of nanotechnology can be formed in certain regions (in the extreme case, in the entire country). In this case, even a loss of funding, for instance, related to bureaucratic hurdles, corruption, etc., as well as additional accidental funding from philanthropists or local authorities cannot affect the formation of clusters, and can only postpone their emergence. The level of noise that allows cluster formation can be quite large, up to 50%. However, such behavior is possible only when the noise in different regions is similar (i.e. additional noise term has the same type, and close quantitative characteristics). Otherwise, there is an uncorrelated development of regions. In our case, the threshold value of noise difference in various regions can be about 10% of the total allocated funds.
3 MODIFICATION OF THE MODEL. CLUSTERIZATION WAVE.
Now let us consider a more complex model in the form of a network consisting of a sequence of layers where an individual element is represented by a quadratic map. The coupling among the elements within each layer is global, and there is a coupling between corresponding elements belonging to adjacent layers (pairwise coupling). The latter can be introduced in two forms: as one way coupling or as mutual coupling. This can be treated as a number of different regions within one country (and the elements in a cell as the number of various scientific fields within nanotechnology as a whole).
The system of equations for a chain with a unidirectional coupling is written in the following form:
And for a mutual coupling:
Here  and
and  is the coupling parameter.
is the coupling parameter.
Let the number of elements belonging to each cell (layer) be  , where
, where  is an integer. We will associate the value of a variable of each element with the color assigned to the appropriate pixel. It will be white if
is an integer. We will associate the value of a variable of each element with the color assigned to the appropriate pixel. It will be white if  , and yellow if
, and yellow if  . Where
. Where  is a stable point of a 1-D quadratic map. The initial conditions were chosen to be in the form of a circle in one layer and random in all others.
is a stable point of a 1-D quadratic map. The initial conditions were chosen to be in the form of a circle in one layer and random in all others.
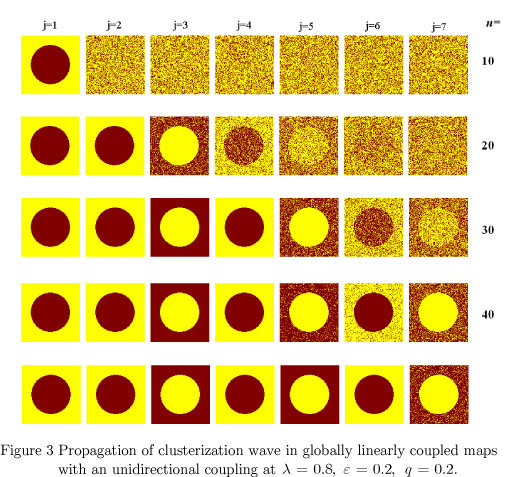
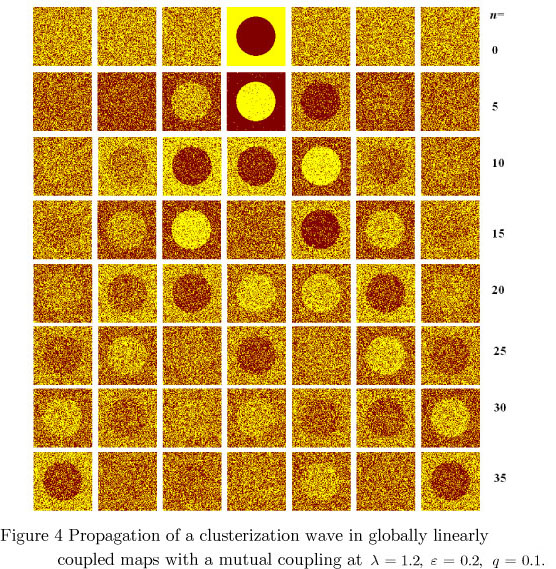
Figure 3 shows a result of numerical simulations for the case of seven layers with an unidirectional coupling. We see that over time, the image recorded in the first cell is formed in the others. In the case of the mutual coupling, the same phenomenon occurred with some blurring (fig. 4). That can be interpreted as follows. If there exists a cluster (an organized form of high-tech) located in one part of the country, it can be transferred to other regions despite 'resistance' from other regions (a new technology may not be accepted and the idea can be rejected/conducted back).
4 MODIFICATION OF THE MODEL. VARIATION OF THE PARAMETERS.
The proposed model can be greatly improved as is described below.
Firstly, we study the case when funding is described not by a logistic map, but can be an arbitrary discrete-time system selected in accordance with current demands. The similar case has been already examined by the example of mobile services providers where advertising spending depend on the strategy of a company. For the case of nanotechnology, we used the known and proposed budgets of Russian Federation for upcoming fiscal years.
We consider the case when, for whatever reasons, there is a reduction of state support. The conclusion was as anticipated: because of strong ties within the system there is a redistribution of funds in favor of Moscow (the capital), and a decrease of funding results in a deeper decay in weak regions, with strong ones being able to survive by attracting additional funds. This reflects a serious imbalance observed now in Russia and also noted by experts.
We also study the case of an abrupt cut in funding. As it turned out, a 10% change of the budget does not affect the system since the proposed links are very rigid. On the one hand, this is a positive outcome because it shows that a short-term financial crisis does not harm the system significantly. On the other hand, it shows that a sudden increase of funding is also not able to drastically change the situation, and the expectation of immediate feedback is groundless.
Secondly, we investigate the proposed system analytically by employing stability analysis. We found that planes of parameters have very narrow regions where stable regimes can exist. For arbitrary chosen variables, the usual behavior of the system is either chaotic or unstable ('running' out/unlimited in numerical simulation). We point out that this fact reflects the socio-economical origin of the studied system.
Thirdly, we consider more complicated links among different factors, such as nonlinear terms of the second and the third order. The main obstacle here is difficulties that are connected with an analytical investigation of the system. Due to a large number of variables, numerical simulations seem to be the only way to study such systems.
Fourthly, we used another approach, presenting our system as a graph with different weighs and links among its elements. Using experts' surveys, we can distinguish between weak and strong links, and, considering only the strong ones, we can reduce the whole system to a number of sub-systems. For each subsystem, we can define a characteristic time, thus obtaining a time-scale for the whole system (the natural frequency of the system). We also introduce simple models particularly suitable for numerical simulations and discuss preliminary results.
CONCLUSIONS
Results obtained in the framework of simple models allow us to deliver a series of new challenges in modeling and forecasting the development of nanotechnology in Russian Federation, as well as broaden our understanding of the nature of the clusterization effects in coupled global discrete-time systems (maps). In addition, we have proposed a method (based on the interference matrix) to find the correspondence between qualitative and quantitative parameters. Our main socio-economical conclusion are: (i) it is possible to start with just one region, transferring a cluster further to other parts of Russia, (ii) there is a great disparity among regions inside one country, and in order to compensate the uneven development of Moscow compared to other regions, there should be stronger governmental support of the regions.
This work was supported by Russian Humanitarian Fund 10-02-00262
- 1. Ott E. Chaos in dynamical systems. Cambridge University Press. 1993.
- 2. Forrester J.W. World Dynamics. Wright-Allen Press 1971.
- 3. Balyakin A., Domnich A., Zhulego V., Ivanova A. Nonlinear dynamics and control. Lodz, December 5-8, 2011, Poland. Book of abstracts. P 221-226
- 4. Kaneko K. Physica D, 1990, vol.41, №2, P. 137-172.
- 5. Balyakin A.A., Domnich A.S., Zhulego V.G., Taranenko S.B. Integral. 2011. № 1 (57), P. 6.
- 6. Balyakin A.A., Zhulego V.G. Proc. III International conference "Mathematical modeling of social and economical dynamics MMSED-2010". P. 39. Lenand. 2010.
- 7. Ivanova A.S. Izvestia vuzov. Applied nonlinear dynamics 2011 (accepted).
Publication Dates
-
Publication in this collection
25 Feb 2013 -
Date of issue
Jan 2013