Large amplitude free vibration of orthotropic shallow shells of complex shapes with variable thickness

Large amplitude free vibration of orthotropic shallow shells of complex shapes with variable thickness

Jan Awrejcewicz^I; Lidiya Kurpa^II; Tatiyana Shmatko^III

^IProfessor: Lodz University of Technology, 1/15 Stefanowski St,90-924 Lodz, POLAND ([e-mail])

^IIProfessor: National Technical University, 21,Frunze str,Kharkov ,61002, UKRAINE ([e-mail]), the author gave a presentation at the conference

^IIIAssociate Professor: National Technical University , 21,Frunze Str,Kharkov, 61002, UKRAINE ([e-mail])

ABSTRACT

The present formulation of the analysed problem is based on Donell's nonlinear shallow shell theory, which adopts Kirchhoff's hypothesis. Transverse shear deformations and rotary inertia of a shell are neglected. According to this theory, the non-linear strain-displacement relations at the shell midsurface has been proposed. The validity and reliability of the proposed approach has been illustrated and discussed, and then a few examples of either linear or non-linear dynamics of shells with variable thickness and complex shapes have been presented and discussed.

Keywords:

1 INTRODUCTION

The problems of nonlinear vibrations of plates and shallow shells are topical for both theory and application in many areas of modern industry. Especially, it concerns the space industry, where the plates and shells are used as members of many structural components. In practice, these elements can have a variable thickness, different form of the middle surface and boundary conditions, as well as different orientation of the anisotropy axes. The studies of linear vibrations of anisotropic shells have attracted the attention of many researchers for a long time [4, 6, 7, 9, 10]. Great progress has been made over the past decades to develop numerical approximate methods as the most effective tools for studying nonlinear vibrations of the composite plates and shallow shells [1-3, 5, 7, 9-11]. This is confirmed by a large number of papers and books. The finite elements method (FEM) is one of the most widely applied approach to non-linear vibration problems of continuous mechanical systems [10, 11]. However, it should be emphasised that even for linear vibrations of shells with variable thickness numerical results are not so widely presented. Furthermore, in the case of non-linear vibrations of anisotropic shells of variable thickness the computational results are rather marginally discussed. This is due to the difficulties that arise while solving this class of problems. First of all, it is difficult to construct the system of eigenfunctions in an analytical form in the case of an arbitrary shape of a shallow shell. However, the latter approach is used mainly to solve nonlinear problems. The second complex question refers to a transition from continuous to discrete models with respect to time. In this paper we propose a method to solve this class of problems using the R-functions theory and variational methods. In the literature devoted to the study of plates/shells statics and dynamics this approach is known as RFM which is an abbreviation for the R-function Method [3, 7, 9]. It should be noted that the use of RFM allows researchers to take into account not only variable thickness of a shell, but also to design eigenfunctions in an analytical form that are then used to solve the problem of geometrically nonlinear vibrations of the shell. Further on in this paper we develop this approach to investigate non-linear free vibrations of orthotropic shallow shells with variable thickness.

2 MATHEMATICAL FORMULATION

The present formulation of the problem is based on Donell's nonlinear shallow shell theory, which adopts Kirchhoff's hypothesis. Transverse shear deformations and rotary inertia of a shell are neglected. According to this theory, the non-linear strain-displacement relations at the shell midsurface can be written as follows

Here u,v,w are the displacements of the shell in directions Ox, Oy and Oz, respectively, whereas -are radii of the shell curvature (Fig.1).

The constitutive relations of the shell can be expressed as follows

where

Here are the stiffness coefficients of the shell depending on x and y, assuming that the shell has a variable thickness.

We introduce the following notation

The equation of equilibrium for free geometrically nonlinear vibration of a shallow shell may be written in the following form

In formulas (12)-(14) differential operators

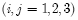are defined as follows

Here are curvatures of the shell in directions Ox, O, respectively.

The obtained system of equations is supplemented by boundary conditions defined by the way of shell fixation.

3 METHOD OF SOLUTION

(i) Solving the linear vibration problem. The linear vibration problem for an orthotropic shallow shell with variable thickness is solved using the Ritz variational method.

The variational statement of the linear problem is reduced to finding the minimum of the following functional

where and are the maximal kinetic and elastic strain energies of the shell, respectively

The R-functions theory is used to find a minimum of the functional including the basic functions satisfying the given boundary conditions. The main advantage of the R-functions method relies on the possibility of constructing these functions in an analytical form. For some kinds of boundary conditions such basic functions have been already presented in references [3, 7, 8, 9, 12]. For example, the system of admissible functions corresponding to a clamped edge, and to in-plane immovable simply supported edges follows

In the above means the equation of the domain border, whereas are the elements of some complete systems.

Observe that the natural modes corresponding to linear vibrations of the shells serve as basic functions to represent the unknown functions.

(ii) Solving the non-linear vibration problem. Let us denote the natural frequency and the corresponding eigenfunctions by and, , respectively. Then displacements of the non-linear problem can be presented as follows

where functions are solutions to a system similar to the Lamè system of the following form

Symbol in equations (27-28) is equal to 1 for shells and and it is equal to 0 for plates. The above mentioned problem is solved by the RFM. Note that the solution to this problem has been already described in references [7, 9]. Substituting expressions (27)- (29) for

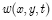into equations (12)-(14) and ignoring inertia terms in equations (12)-(13), one may see that equations (12)-(13) are satisfied identically. Therefore, applying the Bubnov-Galerkin procedure to equation (14) we obtain the following equation

where

Expressions stand as components of the following vectors

which are defined as follows

where

In order to find a backbone curve, let us put and let us apply again the Bubnov-Galerkin procedure [9, 13]. Then, the approximate relation between maximum amplitude A and the ratio of the nonlinear vibration to linear one is as follows:

4 NUMERICAL RESULTS

The so far developed approach is validated on some tested problems and will be applied to solve new problems regarding nonlinear vibrations of shallow shells with variable thickness.

Problem 1. The correctness, validity and reliability of the developed method have been studied by solving the linear vibration problem for an orthotropic clamped spherical shallow shell with square plane-form and variable thickness of the following form

The material properties of the shell are

Coefficient is varied within the interval , stands for the shell thickness corresponding to . The remaining geometric parameters are: , .

A comparison of non-dimensional frequency parameter , where , for a clamped spherical panel versus results reported in reference [4] is given in Table 1. In what follows we study the influence of parameter variation . This problem has been solved in [4], using a spline - approximation to the assumed solution. One may see that the difference between our results and those given in [4] is less than 1.5%. It confirms the validation of the RFM method. Results reported in [4] are in bold.

Below we illustrate how the developed software allows us to investigate the vibration of shallow shells for different values of turn angle of the shell orthotropic axes. For instance, new results regarding the studied panel for various angles are found.

Table 2

Modes of the spherical panel vibration for the following fixed parameters: , ; are presented in Table 3.

Similar results for simply supported spherical shallow shells having square plane-forms are given in Table 4 ( and ).

We are going now to extend our approach by carrying out the nonlinear analysis. Relation versus the values of for clamped spherical panels with square plane-forms are reported in Table 5. Geometric parameters are: , whereas parameter is varied.

The values of non-dimensional frequencies parameter for the clamped orthotropic spherical shallow shell () are given in Table 6.

Backbone curves for simply supported and clamped spherical panels with variable thickness are presented in Figures 2-5.

Problem 2. Now let us study non-linear vibrations of the shell with complicated form shown in Figures 6 and 7. The varying thickness is defined by formula (37). Material properties are the same as these in (38). Parameter is varied in the interval, is the shell thickness corresponding to . The following geometric parameters are taken: ,

The values of non-dimensional frequencies parameter for the clamped orthotropic spherical shallow shell () are given in Table 6.

The so far illustrated and discussed examples regarding nonlinear analysis for the given shells indicate the efficiency of our approach. Influence of curvatures and thickness parameter on backbone curves is shown in Fig. 8 and Fig. 9.

CONCLUSIONS

Analysis of the geometrically nonlinear vibrations of the shallow shells with variable thickness and complex shape has been carried out using the R-functions theory and variational methods. A distinctive feature of the proposed approach is also the original construction of approximate solutions. In a single-mode approximation of the solution, this approach allows to investigate the dynamical behavior of shallow shells with an arbitrary form of their plans and various types of boundary conditions. First, the validity and reliability of the proposed approach has been illustrated and discussed, and then a few examples of either linear or non-linear dynamics of the shells with variable thickness and complex shapes have been presented and discussed.

• 1. Amabili M., Nonlinear vibrations and stability of shells and plates. Cambridge University Press, Cambridge, 2008.
• 2. Amabili M., Non-linear vibration of doubly curved shallow shells. Int. J. Non-Linear Mechanics 40, 2005, 683-710.
• 3. Awrejcewicz J., Kurpa L. and Mazur O., On the parametric vibrations and meshless discretization of orthotropic plates with complex shape. Int. J. of Nonlinear Sciences & Numerical Simulation 1195, 2010, 371-386.
• 4. Budak V.D., Grigorenko A.Ya. and Puzyrev S.V., Free vibrations of rectangular orthotropic shallow shells with varying thickness. Int. J. Applied Mechanics, 43(6), 2007, 670-682.
• 5. Chia C.Y., Nonlinear analysis of doubly curved symmetrically laminated shallow shells with rectangular plane form. Ingenieur-Archiv 58, 1988, 252-264.
• 6. Haldar S., Free vibration of composite skewed cylindrical shell panel by finite element method. J. Sound and Vibr. 311, 2008, 9 - 19.
• 7. Kurpa L., Pilgun G. and Amabili M., Nonlinear vibrations of shallow shells with complex boundary: R-functions method and experiments. J. Sound and Vibr. 306, 2007, 580-600.
• 8. Kurpa L.V., R-functions method for solving linear problems of bending and vibrations of shallow shells. Kharkiv NTU Press, Kharkiv, 2009, in Russian.
• 9. Kurpa L.V., Nonlinear free vibrations of multilayer shallow shells with a symmetric structure and complicated form of the plan. J. Mathem. Sciences, 162(1), 2009, 85-98.
• 10. Qatu M.S., Sullivan R.W. and Wang W., Recent research advances on the dynamic analysis of composite shells: 2000-2009. J. Composite Structures 93, 2010, 14-31.
• 11. Reddy J.N., Arciniega R.A., Shear deformation plate and shell theories: from Stavsky to present. J. Mechanics of Advanced Materials and Structures. 11, 2004, 535-582.
• 12. Rvachev V.L., Theory of R-functions and some of its applications. Nauka Dumka, Kiev, 1982, 552, in Russian.
• 13. Volmir A.S., Nonlinear dynamics of plates and shells. Nauka, Moscow, 1972, in Russian.

Publication Dates

• Publication in this collection
  25 Feb 2013
• Date of issue
  Jan 2013