Abstract
Nowadays, optimization techniques based on the analogy with swarming principles and collective activities of social species in nature have been used in the development of methodologies for solving a variety of real-world optimization problems. In this context, the social behavior of fish colonies has been recently explored to develop a novel algorithm, the so-called Fish Swarm Optimization Algorithm (FSOA), based on the behavior of fish swarm in search for food. In this paper, the FSOA is applied to four engineering systems, involving typical structural design and distillation column design. The results obtained are then compared with those obtained from other classical evolutionary approaches.
Fish Swarm Optimization; Engineering System Design
Fish swarm optimization algorithm applied to engineering system design
Fran Sérgio LobatoI,* * Author email: fslobato@feq.ufu.br ; Valder Steffen Jr.II
ISchool of Chemical Engineering, Federal University of Uberlândia Av. João Naves de Ávila 2121, Campus Santa Mônica, P.O. Box 593, 38408-144, Uberlândia-MG, Brazil
IISchool of Mechanical Engineering Federal University of Uberlândia Av. João Naves de Ávila 2121, Campus Santa Mônica, P.O. Box 593, 38408-144, Uberlândia-MG, Brazil
ABSTRACT
Nowadays, optimization techniques based on the analogy with swarming principles and collective activities of social species in nature have been used in the development of methodologies for solving a variety of real-world optimization problems. In this context, the social behavior of fish colonies has been recently explored to develop a novel algorithm, the so-called Fish Swarm Optimization Algorithm (FSOA), based on the behavior of fish swarm in search for food. In this paper, the FSOA is applied to four engineering systems, involving typical structural design and distillation column design. The results obtained are then compared with those obtained from other classical evolutionary approaches.
Keywords: Fish Swarm Optimization, Engineering System Design.
1 INTRODUCTION
Nowadays, the engineering system design using computational tools has become a major research field. As an example, in the realm of structural engineering, it is very important to determine the external loading under real service conditions, aiming at evaluating the level of security of the structure, to verify the design configurations that were adopted at the design stage, or for redesigning structural elements for new operating conditions (Rojas et al., 2004). Various strategies have been developed for the solution of such problems (Rojas et al., 2004, Cardozo et al., 2011, Gholipour et al., 2013).
The development of optimization techniques based on analogies with swarming principles and collective activities of social species in nature (swarm intelligence) to solve real-world optimization problems characterizes an interesting and encouraging research topic. The corresponding techniques are based on various aspects of the collective activities of social insects, such as foraging of ants, birds flocking and fish schooling, which are self-organizing ones, meaning that complex group behavior emerges from the interactions of individuals who exhibit simple behaviors by themselves (Kennedy et al., 2001, Koide et al., 2013).
Swarm intelligence is inspired in nature, i.e., this characteristic, found among living animals of a given group, contributes to their own experiences as a group, making it stronger in face of other competing groups. The most familiar representatives of swarm intelligence in optimization problems are the following: food-searching behavior of ants (Dorigo and Di Caro, 1999), particle swarm optimization (Shi and Eberhart, 2000), and artificial immune system (Castro and Timmis, 2002).
In this context, an optimization technique known as Fish Swarm Optimization Algorithm (FSOA) based on the fish colonies was recently proposed by Li et al. (2002). The FSOA is an optimization strategy based on the behavior of fish swarm in search for food. From the optimization point of view, this behavior is associated to "learning" capacity that can lead the fish swarm to new directions, i.e., the exploration of new food sources (design space). According to Li et al (2002), this behavior may be summarized as follows: random behavior - in general, fish looks at random for food and other companion; searching behavior - when the fish discovers a region with more food, it will go directly and quickly to that region; swarming behavior - when swimming, fish will swarm naturally in order to avoid danger; chasing behavior - when a fish in the swarm discovers food, the others will find the food dangling after it; and leaping behaviour - when fish stagnates in a region, a leap is required to look for food in other regions.
In the literature, few works using the FSOA can be found. In this context, parameter estimation in engineering systems (Li et al., 2004), feed forward neural networks (Wang et al., 2005), combinatorial optimization problem (Cai, 2010), Augmented Lagrangian fish swarm based method for global optimization (Rocha et al., 2011), forecasting stock indices using radial basis function neural networks (Shen et al. 2011.), hybridization of the FSA with the Particle Swarm Algorithm to solve engineering systems (Tsai and Lin, 2011), determination of cluster number using average information entropy and density function based on fuzzy C-means cluster analysis and FSA (Zhu et al., 2005), combinatorial problems (Zheng and Lin, 2012), parameter estimation in control problems (Lobato et al., 2012), and other applications (Neshat et al. 2012).
In the present contribution, the FSOA is used in engineering system design. This work is organized as follows. Section 2 provides a brief literature overview of the FSOA. The results and discussion are presented in Section 3. Finally, the conclusions and suggestions for future work conclude the paper.
2 FISH SWARM OPTIMIZATION ALGORITHM
The FSOA is based on fish swarm observed in nature: approximately 50% of fish species live in swarm (i. e., present synchronous and coordinated movements) in some moment of their lives, as showed in Figure 1 (Li et al, 2002).
Figure 1 Biological inspiration of the FSOA (Li et al, 2002).
In the development of the FSOA, the following characteristics are considered (Li et al. 2002; Madeiro, 2010): (i) each fish represents a candidate solution of the optimization problem; (ii) food density is related to an objective function to be optimized (in an optimization problem, the amount of food in a region is inversely proportional to value of objective function); and (iii) the aquarium is the design space where the fish can be found.
As noted earlier, the fish weight at the swarm represents the accumulation of food (e.g., the objective function) received during the evolutionary process. In this case, the weight is an indicator of success (Li et al. 2002; Madeiro, 2010). Basically, the FSOA presents four operators that can be classified as "search" and "movement". Details on each of these operators are shown next.
2.1 Individual Movement Operator
This operator contributes to the individual and collective movements of fishes in the swarm. Each fish updates its new position by using the Equation (1):
where xi is the final position of fish i at current generation, rand is a random generator and sind is a weighted parameter.
2.2 Food Operator
The weight of each fish is a metaphor used to measure the success of food search. The higher the weight of a fish, the more likely this fish be in a potentially interesting region in design space.
According to Madeiro (2010), the amount of food that a fish eats depends on the improvement in its objective function in the current generation. The weight is updated according to Equation (2):
where Wit is the fish weight i at generation t and ∆fi is the difference of the objective function between the current position and the new position of fish i. It is important to emphasize that ∆fi=0 for the fishes in same position.
2.3 Instinctive collective movement operator
This operator is important for the individual movement of fishes when ∆fi≠0. Thus, only the fishes whose individual execution of the movement resulted in improvement of their fitness will influence the direction of motion of the school, resulting in instinctive collective movement. In this case, the resulting direction ( ), calculated using the contribution of the directions taken by the fish, and the new position of the ith fish are given by:
), calculated using the contribution of the directions taken by the fish, and the new position of the ith fish are given by:
It is important to emphasize that in the application of this operator, the direction chosen by a fish that located the largest portion of food to exert the greatest influence on the swarm. Therefore, the instinctive collective movement operator tends to guide the swarm in the direction of motion chosen by fish who found the largest portion of food in it individual movement.
2.4 Non-Instinctive collective movement operator
As noted earlier, the fish weight is a good indication of search success for food. In this way, when the swarm weight is increasing it means that the search process is performing successfully. So, the "radius"' of the swarm must decrease so that other regions can be explored. Otherwise, if the swarm weight remains constant, the radius should increase to allow the exploration of new regions.
For the swarm contraction, the centroid concept is used. This is obtained by means of an average position of all fish weighted with the respective fish weights, according to Equation (5):
If the swarm weight remains constant in the current iteration, all fish must update their positions by using the Equation (6):
where d is a function that calculates the Euclidean distance between the centroid and the current position of fish, and svol is the step size used to control fish displacements.
3 RESULTS
In order to evaluate the performance of the FSOA, the following parameters were used: number of fishes (50), weighted parameter value (1), control fish displacements (10-1) and generation number (50). The stopping criterion used was the maximum number of generations. Each case study was computed 20 times before calculating the average values. It should be emphasized 2550 objective function evaluations are required.
3.1 Welded beam design problem
The welded beam design problem is taken from Rao (1996) and He and Wang (2007), in which a welded beam is designed for minimum cost subject to constraints on shear stress (τ), bending stress in the beam, buckling load on the bar (Pc), end deflection of the beam (δ), and side constraints. There are four design variables as shown in Figure 2, i.e., h (x1), l (x2), t (x3), and b (x4).
Mathematically, the problem can be formulated as follows (Rao, 1996):
subject to
where
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
The approaches applied to this problem include genetic algorithm with binary representation and traditional penalty function (Deb, 1991), a GA-based co-evolution model (Coello, 2000), and a co-evolutionary particle swarm optimization (He and Wang, 2007).
The following design space is adopted (He and Wang, 2007): 0.1 in < x1< 2 in, 0.1 in < x2< 10 in, 0.1 in < x3< 10 in, 0.1 in < x4< 2 in. The best solutions obtained by the above mentioned approaches are listed in Table 1. In this table, it can be seen that the best solution found by FSOA is better than the best solutions found by other competing techniques (Deb, 1991; Coello, 2000), but slightly inferior to the result obtained by He and Wang (2007).
Table 1 Comparison of the best solutions for the welded beam design problem using different optimization techniques.
3.2 Tension/compression string design problem
This problem was proposed by Arora (1989), Belegundu (1982) and He and Wang (2007). It is devoted to the minimization of the weight of a tension/compression spring as shown in Figure 3. The design variables are the wire diameter d (x1), the mean coil diameter D (x2) and the number of active coils P (x3).
Figure 3 Tension/compression string design problem.
The mathematical formulation of this problem can be described as follows:
subject to constraints on minimum deflection - Equation (16), shear stress - Equation (17), surge frequency - Equation (18), limits on outside diameter - Equation (19), and on side constraints:
The approaches applied to this problem include eight different numerical optimization techniques (Belegundu, 1982), a numerical optimization technique called constraint correction at constant cost (Arora, 1989), a GA-based co-evolution model (Coello, 2000), and a co-evolutionary particle swarm optimization (He and Wang, 2007).
The following design space is adopted (He and Wang, 2007): 0.05 in < x1< 2 in, 0.25 in < x2< 1.3 in, 2 in < x3< 15 in. Table 2 presents the best solutions obtained by the above mentioned techniques. In this table, it can be seen that the best solution found by FSOA has the same quality of those obtained by others techniques.
Table 2 Comparison of the best solutions for the tension/compression spring design problem using different optimization techniques.
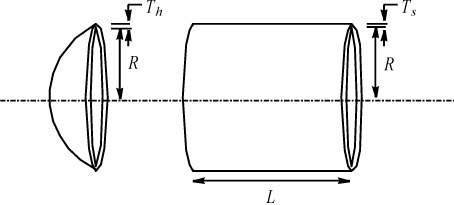
3.3 Pressure vessel design problem
The pressure vessel design problem was proposed by Kannan and Kramer (1994) and is devoted to the minimization of the total cost of the specimen studied, including the cost of the material, forming and welding. A cylindrical vessel is capped at both ends by hemispherical heads as shown in Figure 4. There are four design variables: Ts (x1, thickness of the shell), Th (x2, thickness of the head), R (x3, inner radius) and L (x4, length of the cylindrical section of the vessel, not including the head). Among the four variables, Ts and Th are integer multiples of 0.0625 in that are the available thicknesses of rolled steel plates, and R and L are continuous variables.
The problem can be formulated as follows (Kannan and Kramer, 1994):
subject to
In the literature, this problem has been solved by using an augmented Lagrangian multiplier approach (Kannan and Kramer, 1994), a genetic adaptive search (Deb, 1997), and a co-evolutionary particle swarm optimization (He and Wang, 2007).
In the present work, the following design space is adopted (He and Wang, 2007): 1 in < x1< 99 in, 1 in < x2< 99 in, 10 in < x3< 200 in, 10 in < x4< 200 in. The best solutions obtained by the above mentioned approaches are listed in Table 3. From Table 3, it can be seen that the best solution found by FSOA is better than the best solutions found by other techniques (Kannan and Kramer, 1994; Deb, 1997), and has the same quality as the one obtained by He and Wang (2007).
Table 3 Comparison of the best solutions for the pressure vessel design problem using different methods.
3.4 Binary distillation column design problem
Next case study is a binary distillation system from the MINOPT User's Guide (Schweiger et al., 1997) and Bansal et al. (2003). The column has a fixed number of trays and the objective is to determine the optimal feed location (discrete decision), vapour boil-up, V, and reflux flow rate, R (continuous decisions), in order to minimize the integral square error (ISE) between the bottoms and distillate compositions and their respective set-points. The superstructure of the system is depicted in Figure 5.
The following modeling assumptions were used by Schweiger et al. (1997): (i) constant molar overflow; (ii) constant relative volatility, α, (iii) phase equilibrium; (iv) constant liquid hold-ups, equal to m for each tray and 10m for the reboiler and condenser; (v) no tray hydraulics; (vi) negligible vapour hold-ups; and (vii) no pressure drops. The system is initially at steady-state; at t=0 there is a step change in the feed composition, zf; and the inequality constraints are that the distillate composition must be greater than 0.98, and the bottoms composition must be less than 0.02, at the end of the time horizon of 400 min. The problem can be stated mathematically as:
where
subject to component balances - Equations (27) to (30), overall balances - Equations (31) to (34), vapour-liquid equilibrium - Equations (35) to (36), and step disturbance - Equation (37):
The following design space is adopted (Bansal et al., 2003): 0.05 kmol/min < V < 2 kmol/min, 0.25 kmol/min < R < 1.3 kmol/min, 1 < yf< 30. Model parameters (Bansal et al., 2003): number of trays (N) equal to 30; relative volatility, α equal to 2.5; tray liquid hold-up equal to 0.175 kmol; feed flow rate (F) equal to 1 kmol/min; distillate set-point (xN+1) equal to 0.98 and bottoms set-point (xb) equal to 0.02.
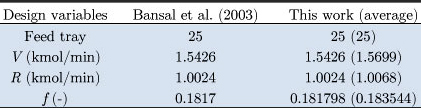
Table 4 presents the results obtained by FSOA and by other techniques. In this table, it can be seen that the best solution found by FSOA has the same quality as compared with the results found by Bansal et al. (2003).
Table 4 Comparison of the best solutions for the binary distillation column design problem.
4 CONCLUSIONS
In this work, Fish Swarm Optimization Algorithm (FSOA) based on the social behavior of fish colonies, was applied to solve different design problems. The simulation results were compared with those obtained from other competing evolutionary algorithms. Besides, the results showed that the methodology is configured as a promising alternative for a number of engineering applications. However, in terms of the number of objective function evaluations, this approach needs yet to be better studied, so that more definitive conclusions can be drawn. This particular characteristic, i.e., the number of objective function evaluations, is inherent to this methodology due to the quantity of loops that is required by the algorithm. Consequently, it is normally expected a high number of objective function evaluations in the present version of the FSOA algorithm.
Further research work will be focused on the influence of the parameter values required by FSOA on the quality of the optimal solutions.
Acknowledgements Dr. Lobato acknowledges the financial support provided by FAPEMIG. Dr. Steffen acknowledges the financial support provided by FAPEMIG and CNPq (INCT-EIE).
Received in 07 Feb 2013
In revised form 19 Mar 2013
- Arora, J. S., (1989). Introduction to Optimum Design. McGraw-Hill, New York.
- Bansal, V., Sakizlis, V., Ross, R., Perkins, J. D., Pistikopoulos, E. N., (2003), New Algorithms for Mixed-integer Dynamic Optimization, Computers and Chemical Engineering 27, 647-668.
- Belegundu, A. D., (1982). A Study of Mathematical Programming Methods for Structural Optimization. Department of Civil and Environmental Engineering, University of Iowa, Iowa City, Iowa.
- Castro, L. N., Timmis, J. I., (2002), Artificial Immune Systems: A New Computational Intelligence Approach, Springer-Verlag, London, UK.
- Cai, Y. (2010), Artificial Fish School Algorithm Applied in a Combinatorial Optimization Problem. Intelligent Systems and Applications 1, 37-43.
- Cardozo, S. D., Gomes, H. M., Awruch, A. M. (2011), Optimization of Laminated Composite Plates and Shells using Genetic Algorithms, Neural Networks and Finite Elements, Latin American Journal of Solids and Structures 8, 413-427.
- Coello, C. A. C., (2000). Use of a Self-adaptive Penalty Approach for Engineering Optimization Problems. Computers in Industry 41, 113-127.
- Deb, K., (1991). Optimal Design of a Welded Beam via Genetic Algorithms. AIAA Journal 29 (11), 2013-2015.
- Deb, K., (1997). GeneAS: A Robust Optimal Design Technique for Mechanical Component Design. In: Dasgupta, D., Michalewicz, Z. (Eds.), Evolutionary Algorithms in Engineering Applications. Springer, Berlin, 497-514.
- Dorigo, M., Di Caro, G., (1999), The Ant Colony Optimization Meta-Heuristic, New Ideas in Optimization, Edited by D. Corne, M. Dorigo, and F. Glover, McGraw-Hill, 11-32.
- Farmer, J. D., Packard, N. H., Perelson, A. S., (1986), The Immune System, Adaptation, and Machine Learning, Physica D 22, 187-204.
- Gholipour, Y., Shahbazi, M. M., Behnia, A. (2013), An Improved Version of Inverse Distance Weighting Metamodel Assisted Harmony Search algorithm for Truss Design Optimization, Latin American Journal of Solids and Structures 10, 283-300.
- He, Q., Wang, L., (2007), An Effective Co-evolutionary Particle Swarm Optimization for Constrained Engineering Design Problems, Engineering Applications of Artificial Intelligence 20, 89-99.
- Kannan, B. K., Kramer, S. N., (1994). An Augmented Lagrange Multiplier based Method for Mixed Integer Discrete Continuous Optimization and its Applications to Mechanical Design. Transactions of the ASME, Journal of Mechanical Design 116, 318-320.
- Kennedy, J. F., Eberhart, R. C., Shi, R. C., (2001), Swarm Intelligence, San Francisco: Morgan Kaufmann Pub.
- Koide, R. M., França, G, von Z., Luersen, M. A., (2013), An Ant Colony Algorithm Applied to Lay-up Optimization of Laminated Composite Plates, Latin American Journal of Solids and Structures 10, 491-504.
- Li, X. L., Shao, Z. J., Qian, J. X. (2002), An Optimizing Method based on Autonomous Animate: Fish Swarm Algorithm, System Engineering Theory and Practice 22 (11), 32-38.
- Li, X. L., Xue, Y. C., Lu, F., Tian, G. H. (2004), Parameter Estimation Method based on Artificial Fish School Algorithm, Journal of Shan Dong University (Engineering Science) 34 (3), 84-87.
- Lobato, F. S., Souza, D. L., Gedraite, R. (2012), A Comparative Study using Bio-Inspired Optimization Methods Applied to Controllers Tuning. Frontiers in Advanced Control Systems, Edited by Ginalber Luiz de Oliveira Serra, ISBN 978-953-51-0677-7, Hard cover, 278 pages.
- Madeiro, S. S. (2010), Modal Search for Swarm based on Density, Dissertation, Universidade de Pernambuco (in portuguese).
- Neshat, M., Sepidnam, G., Sargolzaei, M., Toosi, A. N. (2012), Artificial Fish Swarm Algorithm: A Survey of the State-of-the-art, Hybridization, Combinatorial and Indicative Applications. Artificial Intelligence Review, 1-33, DOI 10.1007/s10462-012-9342-2.
- Rao, S. S., (1996). Engineering Optimization. Wiley, New York.
- Parrich, J., Viscido, S., Grunbaum, D. (2002), Self-organized Fish Schools: An Examination of Emergent Properties. Biological Bulletin 202 (3), 296-305.
- Rocha, A. M. A. C., Martins, T. F. M. C., Fernandes, E. M. G. P. (2011), An Augmented Lagrangian Fish Swarm based Method for Global Optimization. Journal of Computational and Applied Mathematics 235, 4611-4620.
- Rojas, J. E., Viana, F. A. C., Rade, D. A., Steffen Jr, V. (2004), Identification of External Loads in Mechanical Systems Through Heuristic-based Optimization Methods and Dynamic Responses. Latin American Journal of Solids and Structures 10, 297-318.
- Schweiger, C. A., Rojnuckarin, A., Floudas, C. A. (1997), MINOPT: User's Guide. Princeton University. Software Version 2.0.
- Shen, W., Guo, X., Wu, C., Wu, D. (2011), Forecasting Stock Indices using Radial Basis Function Neural Networks Optimized by Artificial Fish Swarm Algorithm. Knowledge-Based Systems 24, 378-385.
- Shi, Y., Eberhart, R. C., (2000), Experimental Study of Particle Swarm Optimization, Proceedings of 4th World Conference on Systems, Cybernetics and Informatics, Orlando, FL, USA.
- Tsai, H. C., Lin, Y. H. (2011), Modification of the Fish Swarm Algorithm with Particle Swarm Optimization Formulation and Communication Behavior, Applied Soft Computing Journal 11, 5367-5374.
- Wang, C. R., Zhou, C. L., Ma, J. W. (2005), An Improved Artificial Fish-Swarm Algorithm and Its Application in Feedforward Neural Networks. Proc. of the Fourth Int. Conf. on Machine Learning and Cybernetics, 2890-2894.
- Zheng, G., Lin, Z. (2012), A Winner Determination Algorithm for Combinatorial Auctions Based on Hybrid Artificial Fish Swarm Algorithm, Physics Procedia 25, 1666-1670.
- Zhu, W., Jiang, J., Song, C., Bao, L. (2011), Clustering Algorithm Based on Fuzzy C-means and Artificial Fish Swarm. Procedia Engineering 29, 3307-3311.
Publication Dates
-
Publication in this collection
25 June 2013 -
Date of issue
Jan 2014
History
-
Received
07 Feb 2013 -
Accepted
19 Mar 2013