Magneto-electro-viscoelastic torsional waves in aeolotropic tube under initial compression stress

Magneto-electro-viscoelastic torsional waves in aeolotropic tube under initial compression stress

Rajneesh Kakar

Principal. DIPS Polytechnic College, India [e-mail]

ABSTRACT

This study examines the effect of electric and magnetic field on torsional waves in hetrogeneous viscoelastic cylindrically aeolotropic tube subjected to initial compression stresses. A new equation of motion and phase velocity of torsional waves propagating in cylindrically aeolotropic tube subjected to initial compression stresses, nonhomogeneity, electric and magnetic field have been derived. The study reveals that the initial stresses, nonhomogeneity, electric and magnetic field present in the aeolotropic tube of viscoelastic solid have a notable effect on the propagation of torsional waves. The results have been discussed graphically. This investigation is very significant for potential application in various fields of science such as detection of mechanical explosions in the interior of the earth.

Keywords: Aeolotropic Material, Viscoelastic Solids, Non-Homogeneous, Bessel Functions.

1 INTRODUCTION

The mutual interactions between an externally applied magnetic field and the elastic deformation in the solid body, give rise to the coupled field of magneto-elasticity. Since electric currents also give rise to magnetic field and vice-versa, the combined effect is also sometimes known as magneto-electro-elasticity. It is evident that since many component fields are interacting, a large number of unknowns are involved and the solution of even the most elementary problems becomes difficult and cumbersome. We therefore almost always have to take certain assumptions to solve the problems. The interaction of elastic and electromagnetic fields has numerous applications in various field of science such as detection of mechanical explosions in the interior of the earth. In spite of the fact that Maxwell equations governing electro-magnetic field have been known for long time, the interest in the coupled field is helpful in the field such as geophysics, optics, acoustics, damping of acoustic waves in magnetic fields, geomagnetics and oil prospecting etc.

Much literature is available on torsional surface wave propagation in homogeneous elastic and viscoelastic media. Pal (2000) presented a note on torsional body forces in a viscoelastic half space. Dey et al.(1996, 2000, 2002, 2003) investigated the effect of torsional surface waves in non-homogeneous anisotropic medium, torsional surface waves in an elastic layer with void pores, torsional surface waves in an elastic layer with void pores over an elastic half space with void pores and effect of gravity and initial stress on torsional surface waves in dry sandy medium. Kaliski (1959) purposed dynamic equations of motion coupled with the field of temperatures and resolving functions for elastic and inelastic bodies in a magnetic field, Narain (1978) discussed magneto-elastic torsional waves in a bar under initial stress, White (1981) studied cylindrical waves in transversely isotropic media. Das et al. (1978) investigated axisymmetric vibrations of orthotropic shells in a magnetic field. The contribution of various researchers on torsional wave propagation such as Suhubi (1965), Abd-alla (1994), Datta (1985) and Selim (2007) cannot be ignored. Kakar and Kakar (2012) discussed torsional waves in fiber reinforced medium subjected to magnetic field. Kakar and Gupta (2013) presented a note on torsional surface waves in a non-homogeneous isotropic layer over viscoelastic half-space. Tang et al. (2010) discussed transient torsional vibration responses of finite, semi-infinite and infinite hollow cylinders. Kakar and Kumar (2013) investigated surface waves in electro-magneto-thermo two layer heterogeneous viscoelastic medium involving time rate of change of strain and recently, Kakar (2013) presented a note on interfacial waves in non-homogeneous electro-magneto-thermoelastic orthotropic granular half space.

In this study an attempt has been made to investigate the torsional wave propagation in non-homogeneous viscoelastic cylindrically aeolotropic material permeated by an electro-magneto field. The graphs have been plotted showing the effect of variation of elastic constants and the presence of electro-magneto field. It is observed that the torsional elastic waves in a viscoelastic solid body propagating under the influence of a superimposed electro-magneto field can be different significantly from that of those propagating in the absence of an electro-magneto field.

2 BASIC EQUATIONS

The problem is dealing with electro-magnetoelasticity. Therefore the basic equations will be electromagnetism and elasticity. The Maxwell equations of the electromagnetic field in a region with no charges (ρ = 0) and no currents (J = 0), such as in a vacuum, are (Thidé, 1997)

where, , , µ₀ and ε₀ are electric field, magnetic field induction, permeability and permittivity of the vacuum. For vacuum, µ₀ = 4π × 10^-7 and ε₀ = 8.85 × 10^-12 in SI units. These equations lead directly to and satisfying the wave equation for which the solutions are linear combinations of plane waves traveling at the speed of light, c = . In addition, and are mutually perpendicular to each other to the direction of wave propagation.

Also, the term Ohm's law is used to refer to various generalizations. The simplest example of this is:

where, is the current density at a given location in a resistive material is the electric field at that location, and σ is a material dependent parameter called the conductivity. If an external magnetic field induction is present and the conductor is not at rest but moving at velocity , then an extra term must be added to account for the current induced by the Lorentz force on the charge carriers (Thidé, 1997).

The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a vacuum. The homogeneous form of the equation, written in terms of either the electric field or the magnetic field induction , takes the form: (Thidé, 1997)

where,

The dynamical equations of motion in cylindrical coordinate (r, θ, z) are (Love, 1944)

where, s_rr, s_rθ, s_rz, s_rr, s_θθ, s_θz, s_zz are the respective stress components, T_R, T_θ, T_Z are the respective body forces and u, v, w are the respective displacement components.

The stress-strain relations are

where, δ_ij = elastic constants (ij = 1, 2......6).

The elastic constants of viscoelastic medium are (Christensen, 1971)

where, and are the first and second order derivatives of δ_ij.

The strain components are

The rotational components are

Equations governing the propagation of small elastic disturbances in a perfectly conducting viscoelastic solid having electromagnetic force (the Lorentz force, is the current density and being magnetic induction vector) as the only body force are (using Eq. (4))

Let us assume the components of magnetic field intensity 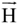are H_r = H_θ = 0 and H_z = H constant. Therefore, the value of magnetic field intensity is (Thidé, 1997).

where,

₀ is the initial magnetic field intensity along z-axis and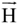 _i is the perturbation in the magnetic field intensity.

The relation between magnetic field intensity 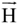and magnetic field induction is

From Eq. (1), Eq. (2), Eq. (3) and Eq. (10), we get

The components of Eq. (12) can be written as (Thidé, 1997).

3 FORMULATION OF THE PROBLEM

Let us consider a semi-infinite hollow cylindrical tube of radii α and β. Let the elastic properties of the shell are symmetrical about z-axis, and the tube is placed in an axial magnetic field surrounded by vacuum. Since, we are investigating the torsional waves in an aeolotropic cylindrical tube therefore the displacement vector has only v component. Hence,

Therefore, from Eq. (14) and Eq. (7), we get,

From Eq. (14) and Eq. (8), we get,

Using Eq. (14), Eq. (15) and Eq. (6), the Eq. (5) becomes

where, and are the first and second order derivatives of δ_ij.

For perfectly conducting medium, (i.e. σ → ∞), it can be seen that Eq. (2) becomes

Eq. (1) and Eq. (18), the Eq. (13) becomes,

From the above discussion, the electric and magnetic components in the problem are related as

Using Eq. (19) and Eq. (1) to get the components of body force in terms of SI system of units as:

Eq. (17) and Eq. (20) satisfy the Eq. (4a) and Eq. (4c), therefore, the remaining Eq. (4b) becomes

where, p is initial compression stress, µ_e and ε_e are the permeability and permittivity of the material.

Let

where, δ_ij, , and ρ₀ are constants, r is the radius vector and l, m are non-homogeneities.

From Eq. (23), we get Eq. (17) as

Using Eq. (23), the Eq. (22) becomes

where, p is initial compression stress, µ_e and ε_e are the permeability and permittivity of the material.

4 SOLUTION OF THE PROBLEM

Let v = ξ(r)e^{i(ςz +ζt)} (Watson, 1944) be the solution of Eq. (25). Hence, Eq. (25) reduces to

where,

Eq. (26) is in complex form, therefore we generalize its solution for l = 0 and l = 2

4.1 Solution for l = 0

For, l = 0 the Eq. (26) becomes,

where,

The solution of Eq. (28) is

From Eq. (24) and Eq. (30)

5 BOUNDARY CONDITIONS AND FREQUENCY EQUATION

The boundary conditions that must be satisfied are

B1. For r = α, (α is the internal radius of the tube)

s_rθ + τ_rθ = τ_(rθ)0

B2. For r = β, (β is the external radius of the tube)

s_rθ + τ_rθ = τ_(rθ)0

where τ_rθ and τ_(rθ)0 are the Maxwell stresses in the body and in the vacuum, respectively. There will be no impact of these Maxwell stresses. Hence,

On simplification, Eq. (18) and Eq. (30) gives

Let,

E₀ = Ψe^{i(ςz + ζt)}

Hence, Eq. (3) becomes

The solution of the Eq. (34) becomes

where J₀ and X₀ are Bessel functions of order zero. R and S are constants.

From Eq. (37) and Eq. (40)

The boundary conditions B1 and B2 with the help of the Eq. (31) and (32) turn into:

Eliminating P and Q from Eq. (38) and Eq. (39)

On solving Eq. (40), we get the obtained frequency equation

On the theory of Bessel functions, if tube under consideration is very thin i.e. β = α + Δα and neglecting Δα², Δα³ ........, the frequency equation can be written as (Watson [18])

where,

Putting the value of Ξ in Eq. (42), the frequency ζ of the wave can be found. Clearly, frequency ζ is dependent on magnetic field, electric field and initial pressure.

Put ,

The phase velocity c₁ = ζ / ς can be written as

where,

The terms H, E and p are negative in Eq. (45) which means that the combine effect of magnetic field, electric field and initial pressure reduces the phase velocity of torsional wave.

Case 1

Since the pipe under consideration is made of an aeolotropic material, then

Hence, from Eq. (42), Eq. (44) and Eq. (47) the frequency equation becomes

Using Eq. (45) and Eq. (46), the phase velocity is

where, = δ₆₆/2ρ₀

The terms h, E and p are negative in Eq. (49) which reduces the phase velocity of torsional wave. This is in complete agreement with the corresponding classical results given by Chandrasekharaiahi (1972).

Case 2

If the pipe under consideration is made of an isotropic material, then

Using Eq. (49) and Eq. (50), the phase velocity is

This is in complete agreement with the corresponding classical results given by Narain (1978).

5.1 Solution for l=2

For, l = 2 the Eq. (26) becomes,

Putting ξ = N(r) in Eq. (53), one get

where,

Solution of Eq. (54) will be (Watson, 1944)

Putting the value of ξ and N in Eq. (55), we get

From the Eq. (24) and Eq. (56)

With the help of Eq. (32), Eq. (56) and boundary conditions B1 and B2, we get

Eliminating R and S from Eq. (58) and Eq. (59)

On solving Eq. (60), we get

If η₁ is the root of the above equation, then

where, F₁ = β/α

On the theory of Bessel functions, if tube under consideration is very thin i.e. β = α + Δα and neglecting Δα², Δα³ ........, the frequency equation can be written as (Watson, 1944)

where,

From the Eq. (62), Eq. (63) and Eq. (64), the phase velocity can be written as (same as above Eq. (45) and Eq. (46))

Case 1

Since the pipe under consideration is made of an aeolotropic material, then

The frequency equation is given by

Using Eq. (65), Eq. (66), Eq. (67) and Eq. (69), we get (calculations are done in the similar manner as for the Eq. (48) to Eq. (50) for l = 0 case)

where, c₀₁² = δ₆₆/2ρ₀

Case 2

If the pipe under consideration is made of an isotropic material, then

The frequency equation (calculations are done as for the l=0 case) is

where

Using Eq. (71) and Eq. (72), the phase velocity for this case is (same as above Eq. (45) and Eq. (46))

where, = χ/2ρ₀

7 NUMERICAL RESULTS

The effect of non-homogeneity, electric field and magnetic field on torsional waves in an aeolotropic material made of viscoelastic solids has been studied. The numerical computation of phase velocity has been made for homogeneous and non-homogeneous pipe. The graphs are plotted for the two cases (l=0 and l=2). Different values of α/λ (diameter/wavelength) for homogeneous in the presence of electro-magneto field and non-homogeneous case in the absence of electro-magneto field are calculated from Eq. (49) and Eq. (65) with the help of MATLAB. The variations elastic constants and presence of electro-magneto field in two curves have been obtained by choosing the following parameters for homogeneous and non-homogeneous aeolotropic pipe (table 1). The curves obtained in fig. 1 clearly show that the phase velocity for homogeneous as well as non-homogeneous case decreases inside the aeolotropic tube. The presence of electro-magneto field also reduces the speed of torsional waves in viscoelastic solids. These curves justify the results obtained in Eq. (50) and Eq. (52) mathematically given by Narain (1978) and Chandrasekharaiahi (1972).

Table 2

We see that for homogeneous case when electro-magneto field is present and for non-homogeneous case when electro-magneto field is not present the variation i.e. shape of the curves is same. For non-homogeneous case, the elastic constants and the density of the tube are varying as the square of the radius vector.

6 CONCLUSIONS

The above problem deals with the interaction of elastic and electromagnetic fields in a viscoelastic media. This study is useful for detections of mechanical explosions inside the earth. In this study an attempt has been made to investigate the torsional wave propagation in non-homogeneous viscoelastic cylindrically aeolotropic material permeated by a electric and magnetic field. It has been observed that the phase velocity decreases as the magnetic field and electric field increases.

ACKNOWLEDGEMENTS

The authors are thankful to the referees for their valuable comments.

• Abd-alla, A.N., (1994). Torsional wave propagation in an orthotropic magnetoelastic hollow circular cylinder, Applied Mathematics and Computation, 63: 281-293.
• Chandrasekharaiahi, D.S., (1972). On the propagation of torsional waves in magneto-viscoelastic solids, Tensor, N.S., 23: 17-20.
• Christensen, R.M., (1971). Theory of Viscoelasticity, Academic Press.
• Dey, S., Gupta, A., Gupta, S. and Prasad, A. (2000). Torsional surface waves in nonhomogeneous anisotropic medium under initial stress, J. Eng. Mech., 126(11):1120-1123.
• Dey, S., Gupta, A., Gupta, S., Karand, K. and De, P.K. (2003). Propagation of torsional surface waves in an elastic layer with void pores over an elastic half space with void pores, Tamkang J. Sci. Eng., 6(4): 241-249.
• Dey, S., Gupta, A. and Gupta, S. (2002), "Effect of gravity and initial stress on torsional surface waves in dry sandy medium", J. Eng. Mech., 128(10), 1115-1118.
• Dey, S., Gupta, A. and Gupta, S. (1996). Torsional surface waves in nonhomogeneous and anisotropic medium, J. Acoust. Soc. Am., 99(5): 2737-2741.
• Kakar, R., Gupta, K.C., (2013). Torsional surface waves in a non-homogeneous isotropic layer over viscoelastic half-space, Interact. Multiscale Mech.,6 (1): 1-14.
• Kakar, R., Kakar, S., (2012). Torsional waves in prestressed fiber reinforced medium subjected to magnetic field, Journal of Solid Mechanics, 4 (4): 402-415.
• Kakar, R., Kumar, A., (2013). A mathematical study of electro-magneto-thermo-Voigt viscoelastic surface wave propagation under gravity involving time rate of change of strain, Theoretical Mathematics & Applications, 3(3): 87-106.
• Kakar, R., (2013). Theoretical and numerical study of interfacial waves in non-homogeneous electro-magneto-thermoelastic orthotropic granular half space, Int. J. of Appl. Math and Mech. 9 (14): 90-115.
• Kaliski, S., Petykiewicz, J., (1959). Dynamic equations of motion coupled with the field of temperatures and resolving functions for elastic and inelastic bodies in a magnetic field, Proceedings Vibration Problems, 1(2):17-35.
• Love, A.E.H., (1944), Mathematical Theory of Elasticity, Dover Publications, Forth Edition.
• Narain, S., (1978). Magneto-elastic torsional waves in a bar under initial stress, Proceedings Indian Academic. Science, 87 (5): 137-45.
• Pal, P.C. (2000). A note on torsional body forces in a viscoelastic half space", Indian J. Pure Ap. Mat., 31(2): 207-213.
• Selim, M., (2007). Torsional waves propagation in an initially stressed dissipative cylinder, Applied Mathematical Sciences, 1(29): 1419 1427.
• Suhubi, E.S., (1965). Small torsional oscillations of a circular cylinder with finite electrical conductivity in a constant axial magnetic field, International Journal of Engineering Science, 2: 441.
• Tang, L., Xu, X. M., (2010). Transient torsional vibration responses of finite, semi-infinite and infinite hollow cylinders, Journal of Sound and Vibration, 329(8): 1089-1100.
• Thidé, B., (1997) Electromagnetic Field Theory, Dover Publications.
• Watson, G.N., (1944). A Treatise on the Theory of Bessel Functions: Cambridge University Press, Second Edition.
• White, J.E., Tongtaow, C., (1981). Cylindrical waves in transversely isotropic media, Journal of Acoustic Society. America, 70(4):1147-1155.

Publication Dates

• Publication in this collection
  30 Jan 2014
• Date of issue
  Aug 2014