Dynamic pull-in instability of geometrically nonlinear actuated micro-beams based on the modified couple stress theory

Dynamic pull-in instability of geometrically nonlinear actuated micro-beams based on the modified couple stress theory

Hamid M.Sedighi^*; Maziar Chan-Gizian; Aminreza Noghreha-Badi

Department of Mechanical Engineering, Shahid Chamran University, Ahvaz, Iran

ABSTRACT

This paper investigates the dynamic pull-in instability of vibrating micro-beams undergoing large deflection under electrosatically actuation. The governing equation of motion is derived based on the modified couple stress theory. Homotopy Perturbation Method is employed to produce the high accuracy approximate solution as well as the second-order frequency- amplitude relationship. The nonlinear governing equation of micro beam vibrations predeformed by an electric field includes both even and odd nonlinearities. The influences of basic non-dimensional parameters on the pull-in instability as well as the natural frequency are studied. It is demonstrated that two terms in series expansions are sufficient to produce high accuracy solution of the micro-structure. The accuracy of proposed asymptotic approach is validated via numerical results. The phase portrait of the system exhibits periodic and homoclinic orbits.

Keywords: Dynamic pull-in instability, Modified couple stress theory, Homotopy Perturbation Method, Frequency - amplitude relationship, Homoclinic orbit.

1 INTRODUCTION

With development of modern technology, micro and nano-electro mechanical systems have shown enormous popularity on engineering and industry. The application of micro-electro-mechanical systems (MEMS) devices especially the electrically actuated MEMS devices which require low actuation voltage levels are continuously growing. Actuated MEMS devices are extensively used in inkjet printers, switches, gyroscopes, chemo-sensors and so on. Recently several numerical and experimental studies have been conducted on the pull-in instability and dynamic behavior of MEMS devices (Ansari et al., 2013; Zhang and Fu, 2012; Rajabi and Ramezani, 2013; Nayfeh et al., 2005; He et al., 2009; Sedighi and Shirazi, 2013; Jia et al., 2011; Younis and Nayfeh, 2003; Mobki et al., 2013; Rahaeifard et al., 2013; Caruntu et al., 2013; Batra et al., 2008; Moghimi Zand and Ahmadian, 2009; Nabian et al., 2013). However, the amplitude dependence of nonlinear frequency and pull-in instability has not been developed, till present.

A distributed size-dependent model based on the modified strain gradient elasticity theory (MSGT) was developed by Ansari et al. (2013) in order to investigate the pull-in instability of circular microplates subjected to the uniform hydrostatic and non-uniform electrostatic actuations. They employed step by step linearization of the equation of motion and utilized the generalized differential quadrature (GDQ) method to solve the problem numerically. A new model for a viscoelastic beam based on the simplified couple stress theory was developed by Zhang and Fu(2012). They investigated the effect of the beam size on the instantaneous pull-in voltage, durable pull-in voltage and pull-in delay time of the system. Rajabi and Ramezani (2013)studied the dynamic behaviour of the micro scale nonlinear beam model based on strain gradient elasticity. They demonstrated that by increasing the beam thickness, the strain gradient effect on increasing the natural frequency decreases and geometric nonlinearity plays the main role on its trend. Nayfeh et al. (2005) reviewed the development of reduced-order models (node and domain methods) for MEMS devices and discussed the advantages and disadvantages of each implementation.

The improved macromodel of the fixed-fixed microbeam-based of MEMS capacitive switch was developed by He et al. (2009) to predict the electromechanical behaviors of electrically actuated MEMS capacitive switch. Their model accounted for moderately large deflections, dynamic loads, axial stress induced by the midplane stretching and the residual stress. Sedighi and Shirazi (2013) presented a new asymptotic procedure to predict the nonlinear vibrational behaviour of classical micro-beams pre-deformed by an electric field using Parameter expansion method. Jia et al. (2011) investigated the pull-in instability of micro-switches under the combined electrostatic and intermo- lecular forces. They accounted for the effect of axial residual stress, the force nonlinearity and geometric nonlinearity in their research and solved the governing equation using the differential quadrature method.

An investigation into the response of a resonant microbeam to an electric actuation was presented by Younis and Nayfeh (2003). They employed the nonlinear model to account for the mid-plane stretching, a DC electrostatic force, and an AC harmonic force and discussed the effect of the design parameters on the dynamic response of the micro-structure. Mobki et al. (2013) studied the mechanical and bifurcation behavior of a capacitive micro-beam suspended between two conductive stationary plates. They used a modified non-linear mass-spring model in order to study the global stability of the fixed points and showed the homoclinic and heteroclinic orbits by plotting phase plane diagrams. Rahaeifard et al. (2013) investigated the dynamic behavior of micro-cantilevers under suddenly applied DC voltage based on the modified couple stress theory. They utilized multiple scales method for analytical analysis and their numerical approach was based on a hybrid finite element/finite difference method. Caruntu et al. (2013) employed the reduced order model (ROM) method to investigate the nonlinearparametric dynamics of electrostatically actuated microelectromechanical systems (MEMS) cantilever resonators under soft alternating current (AC) voltage of frequency near half natural frequency. They found that the fringe effect affects significantly the behavior of the MEMS resonator especially for the narrower micro-cantilevers. Batra et al. (2008) studied the vibrations of narrow microbeams pre-deformed by an electric field with the electromechanical model that estimated the electrostatic fringing field due to both the finite width and the finite thickness of the microbeam. Moghimi Zand et al (2009) studied the dynamic pull-in instability of microbeams subjected to step voltages using homotopy analysis method under the consideration of electrostatic force and midplane stretching. Nabian et al. (2013) examined the stability of a functionally graded clamped-clamped micro-plate subjected to hydrostatic and electrostatic pressures and illustrated that the micro-system undergoes a saddle node and homoclinic bifurcations.

The current work intends to compute the second-order frequency-amplitude relation in a micro clamped-clamped beam due to electrostatic voltage. Recently, considerable progresses had been made in asymptotic approximate solutionsof nonlinear differential equations (Sedighi et al., 2013; Sedighi and Shirazi, 2012; Sedighi et al., 2012). There have been several approaches employed to solve the governing nonlinear differential equations to study the nonlinear vibrations such as Parametrized Perturbation Method (PPM) (Barari et al., 2011), Energy Balance Method (Ghadimi et al., 2012), Variational Iteration Method and Hamiltonian Approach (HA) (Sedighi et al., 2012), Laplace Transform Method (Rafieipour et al., 2012), Max-Min Approach (He, 2008), Homotopy Analysis Method (HAM) (Sedighi et al., 2012), Parameter Expansion Method (Sedighi et al, 2012), Iteration Perturbation Method (IPM) (He, 2001) and Homotopy Perturbation Method (HPM) (He, 1999). It is well known that while the perturbation methods provide the most versatile tools for the nonlinear analysis of engineering problems, they have also some limitations. In order to overcome these drawbacks, combining the standard homotopy and the perturbation method, known as the Homotopy Perturbation Method (HPM), improves the drawbacks of both approaches. He (1999) developed the homotopy perturbation method for solving a variety of problems including the linear and the nonlinear as well as the initial and the boundary value problems by merging two aforementioned techniques. Benefiting from easily computable components and rapid convergence, it has been applied to a wide class of functional equations.

The aim of the present article is to investigate the dynamic pull-in instability of geometrically nonlinear actuated micro-beams by introducing the second-order frequency amplitude relation. The nonlinear equation of motion is derived based on the modified couple stress theory using Hamilton's principle. The effect of vibrational amplitude and system parameters on the pull-in instability and natural frequency is studied via HPM. In this direction, analytical expressions for vibrational response of actuated micro-beams are presented. The proposed analytical method demonstrates that two terms in series expansions is sufficient to obtain a highly accurate solution of micro-beam vibration.

2 MATHEMATICAL MODELING

Consider a double-clamped micro-beam suspended above a rigid plate and under electro-statically actuation voltage as shown in Fig. 1. The actuated micro-beam has length L, cross section area A₀, height h, width b, density r, moment of inertia I and modulus of elasticity E. The air initial gap is d_gap and an attractive electrostatic force which originates from voltage V causes the micro-beam to deflect. Assume that the micro-beam considered here, be the Euler-Bernoulli beam. The strain of a material point located at a distance z from the middle plane for the micro-beam caused by the large rotation and large displacement of the cross-section is represented as (Sedighi et al., 2012):

Taking into account the linear relation between the stress and strain, we have σ = Eε, The strain energy of the micro-beam can be calculated from:

Furthermore, the strain energy of an elastic continuum medium using the modified couple stress theory (MCST) can be mentioned as (Rahaeifard et al., 2013):

where µ represents the shear modulus and l denotes the material length scale parameter, using the descriptions:

The total strain energy of the micro-structure incorporating the MCST micro-beam model can be expressed as:

The virtual work W performed by the axial and electrical forces incorporating the von Karman type nonlinear strain can be written as(Batra et al., 2008):

where N is the axial force and F_es is the electrostatic force per unit length of the micro beam which is described by(Moghimi Zand et al, 2009):

where b = 0.65 for double-clamped micro-beam. The kinetic energy is obtained as follows

Applying the Hamilton's principle leads to:

After some mathematical computations, the nonlinear governing equation of motion for actuated MCST micro-beam model is expressed as follows:

By introducing the dimensionless parameters as:

the non-dimensional nonlinear equation of the micro-beam based on the MCST model can be written as follows:

Using Taylor expansion for electrostatic force in equation (12) results in

Assuming W(ξ, τ) = q (τ)ϕ(ξ), where ϕ(ξ) is the first eigen mode of the clamped-clamped beam and can be expressed as:

where λ_ee = 4.73 is the root of characteristic equation for first eigen mode. Applying the Bubnov-Galerkin decomposition method, the non-dimensional nonlinear governing equation of motion can be written as follows:

where the parameters β₀, ..., β₄ have been described in the ^Appendix.

3 BASIC IDEA OF HOMOTOPY PERTURBATION METHOD

Consider the following nonlinear differential equation (He, 1999):

subjected to the following boundary condition:

where A is a general differential operator, B a boundary operator, f (r) is a known analytical function, Γ is the boundary of the solution domain (Ω), and ∂uf/∂t denotes differentiation along the outwards normal to Γ. Generally, the operator A may be divided into two parts: a linear part L and a nonlinear one N. Therefore, Eq. (16) may be rewritten as follows:

In cases where the nonlinear Eq. (16) includes no small parameter, one may construct the following homotopy equation

In Eq. (19), p ∈ [o,i] is an embedding parameter and u₀ is the first approximation that satisfies the boundary condition. One may assume that solution of Eq. (19) may be written as a power series in p, as the following:

The homotopy parameter p is also used to expand the square of the unknown angular frequency as follows:

where ω₀ is the coefficient of u(r) in Eq. (16) and should be substituted for the right hand side of Eq. (19). Besides, ω₁ (i = 1, 2, 3, ...) are unknown parameters. The best approximations for the solution and the angular frequency ω are

Now we apply the homotopy perturbation method on Eq. (15). We construct a homotopy in the following form:

According to the HPM, we assume that the solution of Eq. (24) can be expressed in a series of p;

the coefficient of q is expanded into a series in p in a similar way (He, 1999):

After substituting Eq. (26) and Eq. (25) into Eq. (24), and rearranging based on powers of p- terms, we have:

Since the solution of Eq. (27-a) is q₀ = Acos(ωτ), the solution of Eq. (27-b) should not contain the so-called secular term cos(ωτ). Substitution of this result into the right-hand side of equation (27-b) yields:

No secular terms in q₁(τ) require eliminating contributions proportional to cos(ωt) on the right-hand side of equation (28), we have:

Solving equation (28) for q₁(τ) gives the following second order approximation for q(τ) as:

equation (26) for two terms approximation of series respect to p and for p = 1 yields:

substitution of this result into the right-hand side of equation (27-c) for q₂(τ) and eliminating the secular terms proportional to cos(ωτ) results in:

solving equation (32) for the fundamental frequency gives the following second-order frequency- amplitude relationship for actuated micro-beam vibrations as:

4 RESULTS AND DISCUSSION

In order to verify the effectiveness of the present modeling and the approximate approach, the obtained results in this work are compared with the results of Rahaeifard et al. (2013) for microcantilever beam vibrations. As can be seen in Fig. 2, the second order approximation for q(t) based on the modified couple stress theory exhibits an excellent agreement with the results obtained by Rahaeifard et al. (2013)using a hybrid finite difference method. It should be noted that in order to achieve the best second-order approximation with zero initial conditions, q₀(τ) = 1 -cos(ωτ) is substituted for the first trial solution.

The effect of normalized parameters on the natural frequency and pull-in instability of actuated clamped-clamped micro-beams have been illustrated in Figs. 3 to ¹⁰. Fig.3 shows the characteristic curves of natural frequency for a micro-beam as a function of under some assigned values of normalized amplitude A. It is demonstrated that this non-dimensional parameter has a significant effect on predicting the pull-in phenomenon. It is obvious from Fig. 3 that by increasing the initial amplitude, the pull-in instability occurs at the lower values of actuation parameter . In addition, it is found that, the fundamental frequency of actuated micro-beam decreases by increasing the applied voltage until the natural frequency vanishes and the micro-beam drops to the rigid plate.

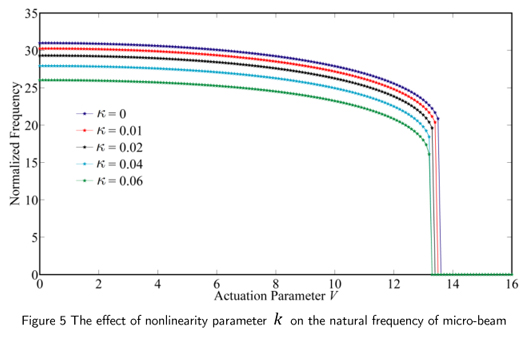
Fig. 4 examines how the nonlinear fundamental frequency of actuated micro-beam is affected by the axial force parameter f_i. As can be observed, the fundamental frequency increases by decreasing initial condition A . Also, it appears from this Fig. that when the normalized amplitude A decreases, pull-in instability occurs at the lower values of parameter f_i. Furthermore, pull-in phenomenon vanishes by increasing the non-dimensional parameter f. The influence of nonlinearity parameter κ on the fundamental frequency is investigated in Fig. 5. According to the illustrated results, it is obvious that the fundamental frequency decreases as the parameter κ increases. Moreover, the pull-in voltage shifts downward by increasing this parameter.

Fig. 6 represents the impact of length scale parameter h/l on the pull-in instability of microsystems. It is clear from the Fig. that,when the beam thickness is in order of the material length scale, the normalized amplitude has no significant effect on the pull-in behavior of the structure. The fundamental frequency decreases by increasing the length scale parameter. In addition, as the initial condition increases, pull-in phenomenon occurs at lower values of non-dimensional parameter h/l. As mentioned earlier, the normalized amplitude and actuation voltage play substantial roles on the pull-in behavior of the system. To this end, the effects of these parameters on the dynamic behavior of micro-beams are studied by plotting the time history and phase portrait diagrams. Figs. 7 and 8 investigate the nonlinear behavior of the system as a function of initial condition A .It is concluded that the time period of oscillation increases by increasing the normalized amplitude. In the vicinity of pull-in point (here A = 0.65 ), a small increase in the amplitude, changes the dynamic behavior of micro-system. In this situation, when the initial amplitude increases, the system loses its stability and drops to the substrate beyond the pull-in point. According to Figs. 9 and ¹⁰, at less values of actuation voltage, the system exhibits periodic motion around the stable center point in the phase plane. Before pull-in point, when the actuation parameter increases, time period of vibration increases. As the actuation parameter approaches to the pull-in voltage (here = 19.35 ), the motion trajectories in the phase plane approach to the unstable saddle node. There exists homo- clinicorbit which starts from the unstable branch and goes back to the saddle node at the stable one. By increasing the applied voltage and above the pull-in voltage, the micro-beam becomes dynamically unstable and collapse onto the rigid plate.

4 CONCLUDING REMARKS

In this research, the Homotopy Perturbation Method was employed to solve governing equation of geometrically nonlinear actuated micro-beams based on the modified couple stress theory. An excellent analytical solution using asymptotic approach was obtained. The integrity of the obtained analytical solutions is verified in comparison with the results in the literature. The presented results showed thatas the normalized amplitude increases, the pull-in phenomenon occurs at lower values of actuation voltage. In addition, the pull-in stability disappears by increasing the axial force parameter. The phase plane portrait of the system illustrated the periodic orbits around the stable center point and homoclinic orbit near the unstable saddle node.

Received in 05 Mar 2013

In revised form 06 Aug 2013

• Ansari, R., Gholami, R., Mohammadi, V., FaghihShojaei, M., (2013). Size-Dependent Pull-In Instability of Hy- drostatically and Electrostatically Actuated Circular Microplates, Journal of Computational and Nonlinear Dynamics, Vol. 8, 021015, doi: 10.1115/1.4007358.
• Barari, A., Kaliji, H.D., Ghadimi, M., Domairry, G., (2011). Non-linear vibration of Euler-Bernoulli beams, Latin American Journal of Solids and Structures, Vol. 8, pp. 139-148.
• Batra, R.C., Porfiri, M., Spinello, D., (2008). Vibrations of narrow microbeams predeformed by an electric field, Journal of Sound and Vibration, Vol. 309, pp. 600-612.
• Caruntu, D.I., Martinez, I., Knecht, M.W., (2013). Reduced Order Model Analysis of Frequency Response of Alternating Current Near Half Natural Frequency Electrostatically Actuated MEMS Cantilevers, Journal of Computational and Nonlinear Dynamics, Vol. 8, 031011, DOI: 10.1115/1.4023164.
• Ghadimi, M., Barari, A., Kaliji, H.D., Domairry, G., (2012).Periodic solutions for highly nonlinear oscillation systems, Archives of Civil and Mechanical Engineering, 12(3), pp. 389-395.
• He, J.H., (2008).Max-Min approach to nonlinear oscillators. International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 9, pp. 207-210.
• He, J.H., (2001).Iteration perturbation method for strongly nonlinear oscillations, J. Vib.Control, Vol. 7, pp. 631642, http://dx.doi.org/10.1177/107754630100700501
• He, J.H. (1999).Homotopy perturbation technique. Computer methods in applied mechanics and engineering, 178(3-4), 257-262.
• He, X.J., Wu, Q., Wang, Y., Song, M.X., Yin, J.H., (2009). Numerical simulation and analysis of electrically actuated microbeam-based MEMS capacitive switch, Microsyst. Technol., Vol. 15, pp. 301-307.
• Jia, X.L., Yang, J., Kitipornchai, S., (2011). Pull-in instability of geometrically nonlinear micro-switches under electrostatic and Casimir forces, ActaMech, Vol. 218, pp. 161-174, DOI: 10.1007/s00707-010-0412-8.
• Mobki, H., Rezazadeh, G., Sadeghi, M., Vakili-Tahami, F., Seyyed-Fakhrabadi, M., (2013). A comprehensive study of stability in an electro-statically actuated micro-beam, International Journal of Non-Linear Mechanics, Vol. 48, pp. 78-85.
• MoghimiZand, M., Ahmadian, M.T. (2009). Application of homotopy analysis method in studying dynamic pull- in instability of microsystems, Mech. Res. Commun., Vol. 36, pp. 851-858.
• Nabian, A., Rezazadeh, G., Almassi, M., Borgheei, A., (2013). On the stability of a functionally graded rectangular micro-plate subjected to hydrostatic and nonlinear electrostatic pressures, Acta Mechanica Solida Sinica, Vol. 26(2), pp. 205-220.
• Nayfeh, A.H., Younis, M.I., Abdel-rahman, E.M., (2005). Reduced-Order Models for MEMS Applications, Nonlinear Dynamics, Vol. 41, pp. 211-236.
• Rafieipour, H., Lotfavar, A., Mansoori, M.H., (2012). New Analytical Approach to Nonlinear Behavior Study of Asymmetrically LCBs on Nonlinear Elastic Foundation under Steady Axial and Thermal Loading, Latin American Journal of Solids and Structures, Vol. 9, pp. 531 - 545.
• Rahaeifard, M., Ahmadian, M.T., Firoozbakhsh, K., (2013). Size-dependent dynamic behaviour of microcantilevers under suddenly applied DC voltage, ProcIMechE Part C: J Mechanical Engineering Science, 10.1177/0954406213490376.
• Rajabi, F., Ramezani, S., (2013).A nonlinear microbeam model based on the strain gradient elasticity theory, Acta Mechanica Solida Sinica, Vol. 26(1), pp. 21-34.
• Sedighi, H. M. and Shirazi, K. H. (2012). A new approach to analytical solution of cantilever beam vibration with nonlinear boundary condition. ASME Journal of Computational and Nonlinear Dynamics, Vol. 7(3), 034502, doi:10.1115/1.4005924.
• Sedighi, H. M., Shirazi, K. H. and Zare, J. (2012). Novel Equivalent Function for Deadzone Nonlinearity: Applied to Analytical Solution of Beam Vibration Using He's Parameter Expanding Method. Latin American Journal of Solids and Structures, Vol. 9, pp. 443-451.
• Sedighi, H.M., Shirazi, K.H., Noghrehabadi, A., (2012). Application of Recent Powerful Analytical Approaches on the Non-Linear Vibration of Cantilever Beams, Application of Recent Powerful Analytical Approaches on the Non-Linear Vibration of Cantilever Beams, DOI 10.1515/ijnsns-2012-0030.
• Sedighi, H. M., Shirazi, K. H. and Zare, J. (2012). An analytic solution of transversal oscillation of quintic nonlinear beam with homotopy analysis method. International Journal of Non-Linear Mechanics, Vol. 47, pp. 777-784.
• Sedighi H. M., Shirazi K. H., Noghrehabadi A. R., Yildirim A. (2012). Asymptotic Investigation of Buckled Beam Nonlinear Vibration. Iranian Journal of Science and Technology, Transaction B. Engineering, in press.
• Sedighi, H. M., Shirazi, K. H., Reza, A. and Zare, J. (2012). Accurate modeling of preload discontinuity in the analytical approach of the nonlinear free vibration of beams. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, doi:10.1177/0954406211435196.
• Sedighi, H.M., Shirazi, K.H., Attarzadeh,M.A., (2013). A study on the quintic nonlinear beam vibrations using asymptotic approximate approaches, Acta Astronautica, Vol. 91, pp. 245-250, doi:10.1016/j.actaastro.2013.06.018.
• Sedighi, H.M., Shirazi, K.H., (2013). Vibrations of micro-beams actuated by an electric field via Parameter Expansion Method, Acta Astronautica, Vol. 85, pp. 19-24. Doi: 10.1016/j.actaastro.2012.11.014.
• Younis, M. I., Nayfeh, A. H., (2003).A Study of the Nonlinear Response of a Resonant Microbeam to an Electric Actuation, Nonlinear Dynamics, Vol. 31, pp. 91-117.
• Zhang, J., Fu, Y., (2012). Pull-in analysis of electrically actuated viscoelastic microbeams based on a modified couple stress theory, Meccanica, Vol. 47, pp. 1649-1658, doi: 10.1007/s11012-012-9545-2.

Appendix

Publication Dates

• Publication in this collection
  03 Feb 2014
• Date of issue
  Oct 2014

History

• Accepted
  06 Aug 2013
• Received
  05 Mar 2013