2.1 Reliability problem

Let X = {X ₁, X ₂, ..., X_m } be a random variable vector describing uncertainties in loads, material strengths, geometry, and models affecting the behavior of a given structure. A limit state equation g(X) is written such as to divide the failure and survival domains (^{Madsen et al., 1986}; ^{Melchers, 1999}):

The failure probability is given by:

where f _x(x) is the probability density function of random vector X. The biggest challenge in solving the simple multi-dimensional integral in equation (2) is that the integration domain is generally not known in closed form, but it is given as the solution of a numerical (e.g., finite element) model. Monte Carlo simulation solves the problem stated in equation (2) by generating samples of random variable vector X, according to distribution function f _x(x), and evaluating weather each sample belongs to the failure or survival domains.

2.2 Crude Monte Carlo Simulation

One straightforward way of performing the integration in equation (2) is by introducing an indicator function I[x], such that I[x] = 1 if x ∈ Ωf and I[x] = 0 if x ∈ Ωs. Hence, the integration can be performed over the whole sample space:

In equation (3), one recognizes that the right-hand term is the expected value (E[.]) of the indicator function. This expected value can be estimated from a sample of size nby:

where n_f is the number of samples which belong to the failure domain and n is the total number of samples. The variance of is given by:

In Crude Monte Carlo simulation, sample vector xj can be generated using the Simple Sampling, Antithetic Variates Sampling or Latin Hypercube Sampling, as detailed in the sequence.

3.1 Simple Sampling

The use of Monte Carlo simulation in solving general problems involving random variables (and/or stochastic processes) requires the generation of samples from random variable vector X. The most straightforward way of generating samples of a vector of random variables is by an inversion of their cumulative distribution function F _X(x):

When components of vector X are correlated, the correlation structure can be imposed by pre-multiplication by the Cholesky-decomposition of the correlation matrix. Details are given in ^{Madsen et al. (1986)} and ^{Melchers (1999)}.

3.2 Antithetic Variate Sampling

In Simple Sampling, a set of random numbers u(n×1) = {u_1j, u_2j , ..., u_nj }t is employed to obtain n samples of random variable Xj. In Antithetic Variate sampling, the idea is to divide the total number of samples by two, and to obtain two vectors u = {u ₁, u ₂, ..., u_n/2 }t and = {1 - u ₁, 1 - u ₂, ..., 1 - u_n/2 }t. Now consider that any random quantity P (including the failure probability, P_j ) can be obtained by combining two unbiased estimators and , such that:

The variance of this estimator is:

Thus, by making = f(u) and = f(), a negative correlation is imposed, Cov[, ] becomes negative, hence the variance of is reduced in comparison to the variances of or . The Antithetic Variates technique, when applied by itself, may not lead to significant improvement; when applied in combination with other techniques, more significant improvements can be achieved.

3.3 Latin Hypercube Sampling

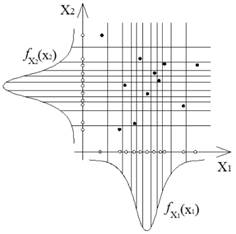
The Latin Hypercube Sampling (LHS) was introduced by ^{McKay et al. (1979)}. The idea of Latin Hypercube Sampling is to divide the random variable domain in stripes, where each stripe is sampled only once (^{McKay et al., 1979}; ^{Olsson et al., 2003}), such as in Figure 1. This procedure guarantees a sparse but homogeneous cover of the sampling space.

Figure 1: Latin Hypercube Sampling. 

To obtain the Latin Hypercube, let m be the number of random variables and n the number of samples. A matrix P(n×m) is created, where each column is a random permutation of 1, ..., n. A matrix R(n×m) is created, whose elements are uniform random numbers between 0 and 1. Then, matrix S is obtained as (^{Olsson et al., 2003}):

The samples are obtained from S such that:

where is the inverse cumulative distribution function of random variable X_j .

In order to reduce memory consumption, equation (8) can be "solved" is scalar fashion. The following algorithm is adopted:

For illustration purposes, Figure 2 shows histograms obtained by Simple Sampling (Figure 2a), Antithetic Variates Sampling (Figure 2b) and Latin Hypercube Sampling (Figure 2c), for a random variable X with normal distribution, with mean equal to 0.0 and standard deviation equal to 0.15. Three thousand samples were used to compute these histograms. One observes the smoother distributions obtained by means of Latin Hypercube Sampling.

Figure 2: Histograms obtained for 3000 samples of a single random variable X~N(0, 0.15). 

4.1 Importance Sampling Monte Carlo

Importance Sampling Monte Carlo centered on design points is a powerful technique to reduce the variance in problems involving small and very small failure probabilities. The drawback is that it needs prior location the design points. Design points can be located using well-known techniques of the First Order Reliability Method, or FORM (^{Madsen et al., 1986}; ^{Melchers, 1999}). However, finding the design point can be a challenge for highly non-linear problems.

Recall the fundamental Monte Carlo simulation equation (equation 3). If numerator and denominator of this expression are multiplied by a conveniently chosen sampling function h _x(x), the result is unaltered:

The expected value, in the right-hand side of equation (10), can be estimated by sampling using:

By properly choosing the sampling function h _x(x), one can increase the number of "successes", or the number of sampled points falling in the failure domain. This is normally accomplished by centering the sampling function h _x(x) in the design point. In other words, the sampling function is usually the joint probability density function f _x(x), but with the mean replaced by the design point coordinates (x*). However, observe that in comparison to equation (4), each sampled point falling in the failure domain (I[xi] = 1) is associated to a sampling weight f _x(xi)/h _x(xi) << 1.

For structures or components with multiple failure modes associated as a series system, the sampling function can be constructed by a weighted sum of functions h_ix (x), centered at the ithdesign point, such that:

where nls is the number of limit states and p_i is the weight related to the limit state i. For a series system, where failure in any mode characterizes system failure, p_i is obtained as:

For parallel system, similar expressions are given in (^{Melchers, 1999}).

The application of Importance Sampling Monte Carlo in combination with Simple Sampling or Antitethic Variates Sampling is straightforward. When applying Importance Sampling in combination with Latin Hypercube Sampling, there is a possibility that most samples be generated on one side of the limit state. This can be avoided by adopting a transformation proposed by ^{Olsson et al. (2003)}. This transformation rotates the Latin Hypercube, on the standard normal space, according the orientation of the design point. This procedure is presented in Figure 3. Further details are given in ^{Olsson et al. (2003)}.

Figure 3: Original and rotated Latin Hypercube, adapted from ^{Olsson et al. (2003)}. 

4.2 Asymptotic Sampling

The Asymptotic Sampling technique (^{Bucher, 2009}; ^{Sichani et al., 2011a}; ^{Sichani et al., 2011b}; ^{Sichani et al., 2014}) was developed based on the asymptotic behavior of failure probabilities as the standard deviation of the random variables tends to zero. One advantage over Importance Sampling is that it does not require previous knowledge of the design point.

Asymptotic Sampling is based on choosing factors f < 1, related to the standard deviations of the random variables as:

where σi is the standard deviation of random variable i and is the modified standard deviation for the same random variable. For small values of f < 1, larger standard deviations, hence also larger failure probabilities are obtained. For each pre-selected value of f a Monte Carlo Simulation is performed, in order to obtain the reliability index β(f). Following ^{Bucher (2009)}, the asymptotic behavior of β with respect to f can be described by a curve:

Where A, B and C are constants to be determined by nonlinear regression (e.g. least squares method), using (f, β/f) as support points. After finding the regression coefficients, the reliability index for the original problem is estimated by making f = 1 in equation (13), such that β = A + B. Finally, the probability of failure is obtained as P_f = Φ (-β), where Φ (.) is the standard normal cumulative distribution function. The Monte Carlo simulations for different values of β (support points) can be obtained by Simple Sampling, Latin Hypercube Sampling or Antithetic Variates Sampling.

The parameters influencing the performance of Asymptotic Sampling are the number of support points and the range of f values considered. In this paper, these parameters are not studied: they are fixed at values providing satisfactory responses: 5 support points are employed with f varying from 0.4 to 0.7 or from 0.5 to 0.8, depending on the problem.

4.3 Enhanced Sampling

The Enhanced Sampling technique was proposed by (^{Naess et al. 2009}, ²⁰¹²) and is based on exploring the regularity of the tails of the PDF's. It aims at estimating small or very small failure probabilities for systems. The original limit state function M = g(x ₁, x ₂, ..., x_m ) is used to construct a set of parametric functions M(λ), with 0 ≤ λ ≤ 1, such that:

where μM is the mean value of M. Thus, it is assumed that the behavior of failure probabilities with respect to λ can be represented as:

Using a set of support points [λ, P_f (λ)], the parameters in equation 15 can be found by nonlinear regression. The probability of failure for the original problem is estimated for λ = 1. One large advantage over Asymptotic Sampling is that, from one single Monte Carlo simulation run, the whole range of parametric functions M(λ) can be evaluated. Hence, a large number of support points can be used, with no penalty in terms of computational cost.

For systems, each limit state or component M_j = gj(x ₁, x ₂, ..., x_m ), with j = 1, ..., nls, must be evaluated. Thus, a parametric set of equations is obtained, such as:

Therefore, for a series system the probability of failure is obtained as:

For a parallel system, the probability of failure is obtained as:

and for a series system with parallel subsystems, the probability of failure is given by:

where C_j is a subset of 1, ..., nls, for j = 1, ..., l.

The parameters of Enhanced Sampling are the number of support points [λ, P_f (λ)] and the values of λ for which failure probabilities are evaluated. Within this paper, these values are kept fixed: 100 support points are used, with λ varying from 0.4 to 0.9.

4.4 Subset Simulation

The Subset Simulation technique was proposed by ^{Au and Beck (2001)}aiming to estimate small and very small probabilities of failure in structural reliability. The basic idea of this technique is to decompose the failure event, with very small probability, into a sequence of conditionals events with larger probabilities of occurrence. For the later, small sample Monte Carlo simulation should be sufficient. Since Simple Sampling is not a good option to generate conditional samples, the Markov Chain Monte Carlo and the modified Metropolis-Hastings algorithms are used.

The estimation of conditional probabilities in Subset Simulation depends on the choice of the intermediates events. Consider the failure event E. The probability of failure associated to it is given by:

Considering a decreasing sequence of events E_i , such as E ₁ ⊃ E ₂ ⊃ ... ⊃ E_m = E, thus:

Hence, the probability of failure is evaluated as:

In equation (22), P[E ₁] can be evaluated by means of Crude Monte Carlo, using Simple Sampling, Latin Hypercube Sampling or Antithetic Variates Sampling. On the other hand, the conditional probabilities P[E_i |E_i-1 ] are estimated by means of Markov Chains using the Modified Metropolis-Hastings algorithm (^{Au and Beck, 2001}; ^{Au, 2005}; ^{Au et al., 2007}).

In Subset Simulation the intermediate events E_i are chosen in an adaptative way. In structural reliability the probability of failure is estimated by:

As the failure event is defined by:

The intermediate failure events are defined by:

with i = 1, ..., m. Hence, the sequence of intermediate events E_i is defined by the set of intermediate limit states.

For convenience, the conditional probabilities are established previously, such that P[E_i|E_i-1 ] = P0. Also, the number of samples n_ss (e.g. n_ss = 500) at each subset is previously established. Hence, sets of samples X_0,k , with k = 1, ..., n_ss are obtained. The limit state functions are evaluated for X_0,k , resulting in vector Y_0,k = g(X_0,k ). Components of vector Y_0,k are arranged in increasing order, resulting in vector . The intermediate limit of failure b1 is established as the sample for which k = P ₀ n_ss , such that P[{ ≤ b ₁}] = P ₀. Thus, there are P ₀ n_ss samples on the "failure" domain defined by intermediate limit b ₁. From each of these samples, by means of Markov Chain simulation, (1 - P ₀)n_ss conditional samples X_(1|0),k are generated, with distribution P(.|E ₁). The limit state function is evaluated for these samples resulting in vector Y_(1|0),k = g(X_(1|0),k ) and in ordered vector , both related to intermediate limit of failure b2, where k = P0nss. Therefore, P[{ ≤ b ₂}] = P ₀. Thus, the next intermediate event E ₂ = {Y ≤ b ₂} is defined. One can notice that P[E ₂|E ₁] = P[Y ≤ b ₂|Y ≤ b ₁] = P ₀. The P ₀ n_ss conditional samples will be the seeds of the conditional samples for the following level. Repeating the process, one generates conditional samples until the final limit b_m is reached, such that b_m = 0. This process is illustrated in Figure 4.

Figure 4: Subset sample generation using Markov Chains. 

The random walk is defined by its probability distribution (e.g. uniform) and by the standard deviation , which is considered as the product of a value α by the standard deviation of the problem, such that = α . σi. Parameters of this algorithm are α, the number of samples for each subset (n_ss ) and the conditional probability P ₀. Different values are used for these parameters for different problems, as detailed in the next Section. In all cases, the random walk is modeled by a uniform probability distribution function.

5.1 Example 1: non-linear limit state function

The first example has a nonlinear limit state function, where the random variables are modeled by non-Gaussian probability distribution functions. The limit state function is (^{Melchers and Ahamed, 2004}):

where X_i , with i = 1, ..., 6, are the random variables. The parameters of the probability distributions are given in Table 1.

The reference probability of failure is obtained using Crude Monte Carlo simulation with Simple Sampling and 2×10⁹ samples. The reference probability of failure is 2.777×10^-5 (β = 4.031). This example aims to evaluate the performance of the intelligent sampling techniques in a problem with nonlinear limit state function involving non-Gaussian distribution functions.

Figures 5, ⁶ and ⁷ show convergence plots for the mean and coefficient of variation (c.o.v) of the P_f , for Simple Sampling, LHS and Asymptotic Sampling, respectively. Convergence results were evaluated for number of samples varying from 1×10³ to 1×10⁶. Results are shown for Crude, Importance, Asymptotic and Enhanced Sampling. For Asymptotic Sampling, the parameter f varies from 0.4 to 0.7, with 5 support points in this range. Subset simulation is not included, because computations are truly expensive for large numbers of samples. On the other hand, only a few samples are required to achieve similar results with Subset simulation, as observed in Table 2.

Figure 5: Convergence of P_f (a) and its c.o.v. (b) using Simple Sampling in Example 1. 

Figure 6: Convergence of P_f (a) and its c.o.v. (b) using Latin Hypercube Sampling in Example 1. 

Figure 7: Convergence of P_f (a) and its c.o.v. (b) using Antithetic Sampling in Example 1. 

Two striking results can be observed in Figures 5 to ⁷ . For all basic sampling techniques, the c.o.v. for Importance Sampling converges very fast to near zero. This is a very positive result. On the other hand, it is observed that the failure probability also converges very fast, but with a bias w.r.t. the reference result. This bias, although small and acceptable, is of some concern, and is introduced by the sampling function. It is also observed, in Figures 5 to ⁷ , that for Asymptotic Sampling the c.o.v. convergence is quite unstable, with results oscillating significantly, and convergence for P_f also shows some bias. Both results are especially true for Simple and Anthytetic Variates Sampling, and less so for LHS. In fact, is observed that LHS improves the results for all sampling techniques illustrated in Figures 5 to ⁷ .

A quantitative comparison of the performance of all sampling techniques, in solution of Problem 1, is presented in Table 2. These results are computed for a much smaller number of samples: 2,300. In Subset Simulation the following parameters are adopted: n_ss = 500, α = 1.5, and P ₀ = 0.1.

One observes in Table 2 that Crude Monte Carlo and Asymptotic Sampling do not lead to any results for such a small number of samples. Importance Sampling leads to the smallest c.o.v.s, but with deviations of around 18 to 30% from the reference result. Enhanced Sampling works, but deviations and c.o.v.s are rather large. For such a small number of samples, Subset Simulation provides the best results, with acceptable c.o.v.s and deviations varying from around 5 to 60%. These deviations could be further reduced by a marginal increase in the number of samples.

5.2 Example 2: Hiper-estatic structural system (truss)

In order to investigate the performance of the intelligent sampling techniques in a structural system problem, an hiper-estatic truss is studied. Service failure is characterized by failure of any component (bar) of the truss, which can be due to buckling (compressed bars) or to yielding (tensile bars). System failure, characterized by failure of a second bar (any), given failure of the hiper-estatic bar (any), is not considered in this study (^{Verzenhassi, 2008}). The truss and its dimensions are shown in Figure 8. The geometrical properties of truss bars are shown in Table 3. Table 4 shows the random variables considered.

Figure 8: Hiper-static truss studied in Example 2. 

Table 4: Random variables of Example 2. 

Six limit state functions are employed to solve the problem: four functions related to elastic buckling of bars 1, 2, 3 and 6:

and two functions related to the yielding of bars 4 and 5:

where E_i is the Young's modulus, I_i is the moment of inertia of the U-shaped steel section, L_i is bar length, A_i is the transversal section area, is the steel yielding stress, V is the vertical load, H is the horizontal load, a_i is the fraction of the vertical load acting at each bar, b_i is the fraction of the horizontal load acting at each bar. The random variables are described in Table 4. A correlation of 0.1 between V and H is considered.

The reference probability of failure is obtained from a Crude Monte Carlo simulation with 2×10⁹ samples using Simple Sampling: P_f = 1.139×10^-4 (β = 3.686).

Figures 9, ¹⁰ and ¹¹ show the convergence plots for the mean and coefficient of variation (c.o.v) of the P_f , for Simple Sampling, LHS and Asymptotic Sampling, respectively. Convergence results were evaluated for number of samples varying from 1×10³ to 1×10⁵. Results are shown for Crude, Asymptotic and Enhanced Sampling. For Asymptotic Sampling, the parameter fvaries from 0.5 to 0.8, with 5 support points. Importance Sampling is not included because the sampling function is composed following equation (12). Hence, the convergence plot could not be obtained. Results for Importance Sampling and for Subset simulation are shown in Table 5, for a fixed (and smaller) number of samples.

Figure 9: Convergence of P_f (a) and its c.o.v. (b) using Simple Sampling in Example 2. 

Figure 10: Convergence of P_f (a) and its c.o.v. (b) using Latin Hypercube Sampling in Example 2. 

Figure 11: Convergence of P_f (a) and its c.o.v. (b) using Antithetic Sampling in Example 2. 

One can notice in Figures 9, ¹⁰ and ¹¹ that Enhanced Sampling performs very well, comparing to Crude Monte Carlo and to Asymptotic Sampling, w.r.t. convergence of the P_f and of its coefficient of variation. The use of LHS (Figure 10) is advantageous for the studied techniques, since faster and smoother convergence is observed.

The comparison of all intelligent sampling techniques is presented in Table 5, computed for a smaller number of samples: 3,700. For Subset Simulation, the following parameters are adopted: n_ss = 1,000; α = 1.5; and P ₀ = 0.1.

In Table 5, one observes that Crude Monte Carlo does not lead to any results for such a small number of samples. Importance Sampling presents a very good performance in comparison with the other techniques, with very small c.o.v.s and small and acceptable deviations from the reference P_f . Subset Simulation also presents an acceptable performance, with small c.o.v.s and larger, but still acceptable deviations from the reference result. The use of Latin Hypercube Sampling is beneficial for all techniques, for this problem.

5.3 Example 3: non-linear steel frame tower

An optimized plane steel frame transmission line tower (Figure 12) is analyzed by finite elements. The problem is based on ^{Gomes and Beck (2013)}, where structural optimization considering expected consequences of failure was addressed. The mechanical problem is modeled by beam elements with three nodes, with three degrees of freedom per node. The frame is composed by L-shaped steel beams. The Finite Element Method with positional formulation (^{Coda and Greco, 2004}; ^{Greco et al., 2006}) is adopted to solve the geometrical non-linear problem. Moreover, the material is assumed elastic perfectly plastic.

Figure 12: FE model of the power line tower addressed in Example 3. 

The limit state function is defined based on the load-displacement curve (Figure 13) for top nodes 11 and 12. Because several configurations had to be tested in the optimization analysis performed in ^{Gomes and Beck (2013)}, a robust limit state function was implemented. The same limit state function is employed herein: g(x,d) = 75º - tan^-1(Δδ/ΔL) , where Δδ is the increment in mean displacement in centimeters, for nodes 11 and 12; ΔLis the increment in the non-dimensional load factor; and 75^o is the critical angle considered.

Figure 13: Load factor × mean displacement diagram for top nodes 11 and 12. 

5.3.2 Results

In ^{Gomes and Beck (2013)}, probability of failure is evaluated by FORM, and values P_f,FORM = 1.088×10-4 (β = 3.6976) are obtained for the tower configuration in Figure 12. In this paper, several Monte Carlo Simulation techniques are adopted for evaluating this failure probability. FORM is very efficient, and efficiency is fundamental for solving the structural optimization problem. However, FORM provides only approximate results for problems with non-linear limit state functions.

The reference probability of failure is evaluated by Crude and by Importance Sampling Monte Carlo simulation, using Simple Sampling, Latin Hypercube Sampling and Antithetic Variates Sampling. 1×10⁵ samples are employed for each solution. Results are given in Table 7, where one observes that Crude Monte Carlo with LHS and Importance Sampling Monte Carlo present probabilities of failure very close to the result obtained by FORM. This shows that, in spite of the non-linearity of the limit state function, FORM provides accurate results. For the remainder of the analysis, the average value of P_f = 1.096×10-4 is used as a reference.

Table 7: Comparison of Crude Monte Carlo and Importance Sampling, using 10⁵samples. 

Estimation Technique			Pf		c.o.v.	Processing Time	Deviation from average (%)
Crude Monte Carlo	Simple Sampling	1.400×10-4	0.2672	11 h e 2 min	27.74
	Latin Hypercube Sampling	1.10×10-4	0.3015	10 h e 17 min	0.36
	Antithetic Variates Sampling	1.50×10-4	0.2582	11 h e 1 min	36.86
Importance Sampling Monte Carlo	Simple Sampling	1.099×10-4	0.0038	13 h e 36 min	0.27
	Latin Hypercube Sampling	1.089×10-4	0.0038	13 h e 41 min	0.64
Antithetic Variates Sampling	1.096×10-4	0.0038	13 h e 43 min	0.00

Figures 14, ¹⁵ and ¹⁶ show the convergence plots for the mean and coefficient of variation (c.o.v) of the Pf, for Simple Sampling, LHS and Asymptotic Sampling, respectively. Convergence results were evaluated for number of samples varying from 1×10³ to 1×10⁵. Results are shown for Crude, Importance, Asymptotic and Enhanced Sampling. In Asymptotic Sampling, parameter f varies from 0.5 to 0.8, with 5 support points.

Figure 14: Convergence of P_f (a) and its c.o.v. (b) using Simple Sampling in Example 3. 

Figure 15: Convergence of P_f (a) and its c.o.v. (b) using Latin Hypercube Sampling in Example 3. 

Figure 16: Convergence of P_f (a) and its c.o.v. (b) using Antithetic Sampling in Example 3. 

In Figs. 14 to ¹⁶ , one observes that convergence of Importance Sampling, for this problem, is very fast and accurate, for all basic sampling techniques. Also, it can be clearly seen that LHS improves the results for all sampling techniques, reducing oscillations during convergence. The convergence behavior of Asymptotic Sampling is very unstable, both for the c.o.v. and the P_f ; hence this technique does not perform very well for this problem. Enhanced Sampling works much better, providing results similar to Crude sampling for this number of samples.

A quantitative comparison of the performance of all sampling techniques, in solution of Problem 3, is presented in Table 8. These results are computed for 14,800 samples. In Subset Simulation the following parameters are adopted: n_ss = 4000, α = 1.5, P ₀ = 0.1.

Table 8: Comparison of results for 14,800 samples in Example 3. 

Estimation Technique				Pf	c.o.v.	Deviation (%)
Simple Sampling	Crude Monte Carlo	2.703×10-4	0.4999	146.62
	Importance Sampling	1.090×10-4	0.0099	0.55
	Asymptotic Sampling	2.697×10-4	8.0852	146.08
	Enhanced Sampling	1.327×10-4	0.4103	21.08
	Subset Simulation	1.960×10-4	0.1970	78.83
Latin Hypercube Sampling	Crude Monte Carlo	6.757×10-5	--	38.35
	Importance Sampling	1.091×10-4	0.0100	0.46
	Asymptotic Sampling	8.300×10-5	1.5114	24.27
	Enhanced Sampling	1.659×10-4	0.3106	51.37
	Subset Simulation	1.110×10-4	0.2046	1.28
Antithetic Variates Sampling	Crude Monte Carlo	2.703×10-4	0.4999	146.62
	Importance Sampling	1.086×10-4	0.0100	0.91
	Asymptotic Sampling	1.393×10-4	4.7499	27.10
	Enhanced Sampling	1.650×10-4	0.3941	50.55
Subset Simulation	1.623×10-4	0.1963	48.08

One observes in Table 8 that Importance Sampling and Subset simulation out-perform the other methods in terms of small c.o.v. and small deviation from the reference solution. Asymptotic and Enhanced sampling show a similar and average performance. Latin Hipercube Sampling improves the results for most methods, especially for Subset Simulation.