Abstract
In recent years, new, intelligent and efficient sampling techniques for Monte Carlo simulation have been developed. However, when such new techniques are introduced, they are compared to one or two existing techniques, and their performance is evaluated over two or three problems. A literature survey shows that benchmark studies, comparing the performance of several techniques over several problems, are rarely found. This article presents a benchmark study, comparing Simple or Crude Monte Carlo with four modern sampling techniques: Importance Sampling Monte Carlo, Asymptotic Sampling, Enhanced Sampling and Subset Simulation; which are studied over six problems. Moreover, these techniques are combined with three schemes for generating the underlying samples: Simple Sampling, Latin Hypercube Sampling and Antithetic Variates Sampling. Hence, a total of fifteen sampling strategy combinations are explored herein. Due to space constrains, results are presented for only three of the six problems studied; conclusions, however, cover all problems studied. Results show that Importance Sampling using design points is extremely efficient for evaluating small failure probabilities; however, finding the design point can be an issue for some problems. Subset Simulation presented very good performance for all problems studied herein. Although similar, Enhanced Sampling performed better than Asymptotic Sampling for the problems considered: this is explained by the fact that in Enhanced Sampling the same set of samples is used for all support points; hence a larger number of support points can be employed without increasing the computational cost. Finally, the performance of all the above techniques was improved when combined with Latin Hypercube Sampling, in comparison to Simple or Antithetic Variates sampling.
Structural reliability; Monte Carlo simulation; intelligent sampling techniques; benchmark study
1 INTRODUCTION
Since the early beginnings in the sixties and seventies, structural reliability analysis has reached a mature stage encompassing solid theoretical developments and increasing practical applications. Structural reliability methods have permeated the engineering profession, finding applications in code calibration, structural optimization, life extension of existing structures, life-cycle management of infrastructure risks and costs, and so on. During the past 30 years, significant advances were obtained in terms of transformation methods (FORM, SORM), as well as in terms of simulation techniques. Transformation methods were found to be efficient in the solution of problems of moderate dimensions and moderate non-linearity. Simulation techniques (Metropolis and Ulam, 1949Metropolis, N., Ulam, S., (1949). The Monte Carlo method. J Am Statist Assoc 44(247): 335-341.; Metropolis et al., 1953Metropolis, N. et al., (1953). Equation of state calculation by fast computing machines. J Chem Phys 21(6): 1087-1092.; Robert and Casella, 2011Robert, C., Casella, G., (2011). A short history of Markov Chain Monte Carlo: Subjective recollections from incomplete data. Statist sci 26(1): 102-115.) have always allowed the solution of highly non-linear high-dimensional problems, although computational cost used to be a serious limitation. This is especially true when failure probabilities are small and limit state functions are given numerically (e.g., finite element models) (Beck and Rosa, 2006Beck, A.T., Rosa, E., (2006). Structural Reliability Analysis Using Deterministic Finite Element Programs. Latin American Journal of Solids and Structures 3: 197-222.). With the recent and exponential advance of computational processing power, Monte Carlo simulation using intelligent sampling techniques is becoming increasingly more viable.
Several intelligent sampling techniques for Monte Carlo simulation have been proposed in recent years (Au and Beck, 2001Au, S.K., Beck, J.L., (2001). Estimation of small failure probabilities in high dimensions by subset simulation. Prob. Eng. Mech. 16(4): 263-277.; Au, 2005Au, S.K., (2005). Reliability-based design sensitivity by efficient simulation. Comput Struct 83: 1048-1061.; Au et al., 2007Au, S.K., Ching, J., Beck, J.L., (2007). Application of subset simulation methods to reliability benchmark problems. Struct Safety 29: 183-193.; Bucher, 2009Bucher, C., (2009). Asymptotic sampling for high-dimensional reliability analysis. Prob. Eng. Mech. 24: 504-510.; Sichani et al., 2011aSichani, M.T., Nielsen, S.R.K., Bucher, C., (2011a). Applications of asymptotic sampling on high dimensional structural dynamic problems. Struct safety 33: 305-316.; Sichani et al., 2011bSichani, M.T., Nielsen, S.R.K., Bucher, C., (2011b). Efficient estimation of first passage probability of high-dimensional nonlinear systems. Prob. Eng. Mech. 26: 539-549.; Sichani et al., 2014Sichani, M.T., Nielsen, S.R.K., Bucher, C., (2014). Closure to "Applications of asymptotic sampling on high dimensional structural dynamic problems". Struct Safety 46: 11-12.; Naess et al., 2009Naess, A., Leira, B.J., Batsevych, O., (2009). System reliability analysis by enhanced Monte Carlo simulation. Struct Safety 31: 349-355; Naess et al., 2012Naess, A., Leira, B.J., Batsevych, O., (2012). Reliability analysis of large structural systems. Prob. Eng. Mechanics 28: 164-168.). However, when such techniques are introduced, they are generally compared with one or two existing techniques, and their performance is evaluated over two or three problems. It is difficult to find in the published literature benchmark studies where several sampling techniques are compared for a larger number of problems (Au et al., 2007Au, S.K., Ching, J., Beck, J.L., (2007). Application of subset simulation methods to reliability benchmark problems. Struct Safety 29: 183-193.; Engelund and Rackwitz, 1993Engelund, S., Rackwitz, R., (1993). A benchmark study on importance sampling techniques in structural reliability. Structural Safety 12: 255-276.; Schuëller and Prandlwarter, 2007Schuëller, G.I., Prandlwarter, H.J., (2007). Benchmark study on reliability estimation in higher dimensions of structural systems - An overview. Struct Safety 29: 167-182.). This article presents a benchmark study, comparing Simple or Crude Monte Carlo with four modern sampling techniques: Importance Sampling Monte Carlo, Asymptotic Sampling, Enhanced Sampling and Subset Simulation over six problems. Moreover, these techniques are combined with three schemes for generating the underlying samples: Simple Sampling, Latin Hypercube Sampling and Antithetic Variates Sampling. Hence, a total of fifteen sampling strategy combinations are explored herein. Due to space constrains, results are presented for only three of the six problems studied. The conclusions, however, cover the six problems studied.
The remainder of the article is organized as follows. The structural reliability problem is formulated in Section 1. The basic techniques for generating the underlying samples are presented in Section 2. The intelligent sampling techniques for failure probability evaluation are presented in Section 3. Problems are studied in Section 4, and Concluding Remarks are presented in Section 5.
2 FORMULATION
2.1 Reliability problem
Let X = {X 1, X 2, ..., Xm } be a random variable vector describing uncertainties in loads, material strengths, geometry, and models affecting the behavior of a given structure. A limit state equation g(X) is written such as to divide the failure and survival domains (Madsen et al., 1986Madsen, H.O., Krenk, S., Lind, N.C., (1986). Methods of structural safety. Prentice Hall, Englewood Cliffs.; Melchers, 1999Melchers, R.E., (1999). Structural Reliability Analysis and Prediction. John Wiley & Sons, Chichester.):
The failure probability is given by:
where f x(x) is the probability density function of random vector X. The biggest challenge in solving the simple multi-dimensional integral in equation (2) is that the integration domain is generally not known in closed form, but it is given as the solution of a numerical (e.g., finite element) model. Monte Carlo simulation solves the problem stated in equation (2) by generating samples of random variable vector X, according to distribution function f x(x), and evaluating weather each sample belongs to the failure or survival domains.
2.2 Crude Monte Carlo Simulation
One straightforward way of performing the integration in equation (2) is by introducing an indicator function I[x], such that I[x] = 1 if x ∈ Ωf and I[x] = 0 if x ∈ Ωs. Hence, the integration can be performed over the whole sample space:
In equation (3), one recognizes that the right-hand term is the expected value (E[.]) of the indicator function. This expected value can be estimated from a sample of size nby:
where nf is the number of samples which belong to the failure domain and n is the total number of samples. The variance of  is given by:
is given by:
In Crude Monte Carlo simulation, sample vector xj can be generated using the Simple Sampling, Antithetic Variates Sampling or Latin Hypercube Sampling, as detailed in the sequence.
3 BASIC SAMPLING TECHNIQUES
In this paper three basic sampling techniques are investigated: Simple Sampling, Latin Hypercube Sampling and Antithetic Variates Sampling. These basic sampling schemes are not specific for the solution of structural reliability problems: they can be employed in the numerical solution of integrals (like equation (2)), in the spatial distribution of points in a given domain (for surrogate modeling, for instance), and so on. These techniques are further combined with specific techniques for solving structural reliability problem via Monte Carlo simulation, as described in Section 3.
3.1 Simple Sampling
The use of Monte Carlo simulation in solving general problems involving random variables (and/or stochastic processes) requires the generation of samples from random variable vector X. The most straightforward way of generating samples of a vector of random variables is by an inversion of their cumulative distribution function F X(x):
-
I. Generate a random vector of components v(l×m) = {vj }, j = 1, ..., m, uniformly distributed between 0 and 1;
-
II. Use the inverse of the cumulative distribution function, such that {xj } = {
 (vj )}, j = 1, ..., m.
(vj )}, j = 1, ..., m.
When components of vector X are correlated, the correlation structure can be imposed by pre-multiplication by the Cholesky-decomposition of the correlation matrix. Details are given in Madsen et al. (1986)Madsen, H.O., Krenk, S., Lind, N.C., (1986). Methods of structural safety. Prentice Hall, Englewood Cliffs. and Melchers (1999)Melchers, R.E., (1999). Structural Reliability Analysis and Prediction. John Wiley & Sons, Chichester..
3.2 Antithetic Variate Sampling
In Simple Sampling, a set of random numbers u(n×1) = {u1j, u2j , ..., unj }t is employed to obtain n samples of random variable Xj. In Antithetic Variate sampling, the idea is to divide the total number of samples by two, and to obtain two vectors u = {u 1, u 2, ..., un/2 }t and  = {1 - u 1, 1 - u 2, ..., 1 - un/2 }t. Now consider that any random quantity P (including the failure probability, Pj ) can be obtained by combining two unbiased estimators
= {1 - u 1, 1 - u 2, ..., 1 - un/2 }t. Now consider that any random quantity P (including the failure probability, Pj ) can be obtained by combining two unbiased estimators  and
and  , such that:
, such that:
The variance of this estimator is:
Thus, by making  = f(u) and
= f(u) and  = f(
= f( ), a negative correlation is imposed, Cov[
), a negative correlation is imposed, Cov[ ,
,  ] becomes negative, hence the variance of
] becomes negative, hence the variance of  is reduced in comparison to the variances of
is reduced in comparison to the variances of  or
or  . The Antithetic Variates technique, when applied by itself, may not lead to significant improvement; when applied in combination with other techniques, more significant improvements can be achieved.
. The Antithetic Variates technique, when applied by itself, may not lead to significant improvement; when applied in combination with other techniques, more significant improvements can be achieved.
3.3 Latin Hypercube Sampling
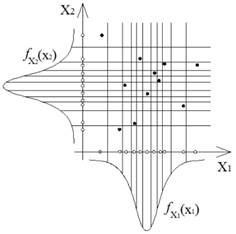
The Latin Hypercube Sampling (LHS) was introduced by McKay et al. (1979)McKay, M.D., Beckman, R.J., Conover, W.J., (1979). A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 21(2): 239-124.. The idea of Latin Hypercube Sampling is to divide the random variable domain in stripes, where each stripe is sampled only once (McKay et al., 1979McKay, M.D., Beckman, R.J., Conover, W.J., (1979). A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 21(2): 239-124.; Olsson et al., 2003Olsson, A., Sandeberg, G., Dahlblom, O., (2003). On latin hypercube sampling for structural reliability analysis. Struct Safety 25: 47-68.), such as in Figure 1. This procedure guarantees a sparse but homogeneous cover of the sampling space.
To obtain the Latin Hypercube, let m be the number of random variables and n the number of samples. A matrix P(n×m) is created, where each column is a random permutation of 1, ..., n. A matrix R(n×m) is created, whose elements are uniform random numbers between 0 and 1. Then, matrix S is obtained as (Olsson et al., 2003Olsson, A., Sandeberg, G., Dahlblom, O., (2003). On latin hypercube sampling for structural reliability analysis. Struct Safety 25: 47-68.):
The samples are obtained from S such that:
where  is the inverse cumulative distribution function of random variable Xj .
is the inverse cumulative distribution function of random variable Xj .
In order to reduce memory consumption, equation (8) can be "solved" is scalar fashion. The following algorithm is adopted:
-
1. Start the loop for random variable j:
-
2. Generate the first column of matrix P, as a random permutation n of 1, ..., n;
-
3. Start the loop for the number of simulations i;
-
4. Generate a single uniform random number between 0 and 1; thus, it is not necessary to create matrix R;
-
5. Compute a number s, and use equation (9) to compute the element xij . Thus, matrix S also does not need to be computed;
-
6. Repeat step 4 until i = n;
-
7. Repeat step 2 until j = m.
For illustration purposes, Figure 2 shows histograms obtained by Simple Sampling (Figure 2a), Antithetic Variates Sampling (Figure 2b) and Latin Hypercube Sampling (Figure 2c), for a random variable X with normal distribution, with mean equal to 0.0 and standard deviation equal to 0.15. Three thousand samples were used to compute these histograms. One observes the smoother distributions obtained by means of Latin Hypercube Sampling.
4 INTELLIGENT SAMPLING TECHNIQUES
4.1 Importance Sampling Monte Carlo
Importance Sampling Monte Carlo centered on design points is a powerful technique to reduce the variance in problems involving small and very small failure probabilities. The drawback is that it needs prior location the design points. Design points can be located using well-known techniques of the First Order Reliability Method, or FORM (Madsen et al., 1986Madsen, H.O., Krenk, S., Lind, N.C., (1986). Methods of structural safety. Prentice Hall, Englewood Cliffs.; Melchers, 1999Melchers, R.E., (1999). Structural Reliability Analysis and Prediction. John Wiley & Sons, Chichester.). However, finding the design point can be a challenge for highly non-linear problems.
Recall the fundamental Monte Carlo simulation equation (equation 3). If numerator and denominator of this expression are multiplied by a conveniently chosen sampling function h x(x), the result is unaltered:
The expected value, in the right-hand side of equation (10), can be estimated by sampling using:
By properly choosing the sampling function h x(x), one can increase the number of "successes", or the number of sampled points falling in the failure domain. This is normally accomplished by centering the sampling function h x(x) in the design point. In other words, the sampling function is usually the joint probability density function f x(x), but with the mean replaced by the design point coordinates (x*). However, observe that in comparison to equation (4), each sampled point falling in the failure domain (I[xi] = 1) is associated to a sampling weight f x(xi)/h x(xi) << 1.
For structures or components with multiple failure modes associated as a series system, the sampling function can be constructed by a weighted sum of functions hix (x), centered at the ithdesign point, such that:
where nls is the number of limit states and pi is the weight related to the limit state i. For a series system, where failure in any mode characterizes system failure, pi is obtained as:
For parallel system, similar expressions are given in (Melchers, 1999Melchers, R.E., (1999). Structural Reliability Analysis and Prediction. John Wiley & Sons, Chichester.).
The application of Importance Sampling Monte Carlo in combination with Simple Sampling or Antitethic Variates Sampling is straightforward. When applying Importance Sampling in combination with Latin Hypercube Sampling, there is a possibility that most samples be generated on one side of the limit state. This can be avoided by adopting a transformation proposed by Olsson et al. (2003)Olsson, A., Sandeberg, G., Dahlblom, O., (2003). On latin hypercube sampling for structural reliability analysis. Struct Safety 25: 47-68.. This transformation rotates the Latin Hypercube, on the standard normal space, according the orientation of the design point. This procedure is presented in Figure 3. Further details are given in Olsson et al. (2003)Olsson, A., Sandeberg, G., Dahlblom, O., (2003). On latin hypercube sampling for structural reliability analysis. Struct Safety 25: 47-68..
Original and rotated Latin Hypercube, adapted from Olsson et al. (2003)Olsson, A., Sandeberg, G., Dahlblom, O., (2003). On latin hypercube sampling for structural reliability analysis. Struct Safety 25: 47-68..
4.2 Asymptotic Sampling
The Asymptotic Sampling technique (Bucher, 2009Bucher, C., (2009). Asymptotic sampling for high-dimensional reliability analysis. Prob. Eng. Mech. 24: 504-510.; Sichani et al., 2011aSichani, M.T., Nielsen, S.R.K., Bucher, C., (2011a). Applications of asymptotic sampling on high dimensional structural dynamic problems. Struct safety 33: 305-316.; Sichani et al., 2011bSichani, M.T., Nielsen, S.R.K., Bucher, C., (2011b). Efficient estimation of first passage probability of high-dimensional nonlinear systems. Prob. Eng. Mech. 26: 539-549.; Sichani et al., 2014Sichani, M.T., Nielsen, S.R.K., Bucher, C., (2014). Closure to "Applications of asymptotic sampling on high dimensional structural dynamic problems". Struct Safety 46: 11-12.) was developed based on the asymptotic behavior of failure probabilities as the standard deviation of the random variables tends to zero. One advantage over Importance Sampling is that it does not require previous knowledge of the design point.
Asymptotic Sampling is based on choosing factors f < 1, related to the standard deviations of the random variables as:
where σi is the standard deviation of random variable i and  is the modified standard deviation for the same random variable. For small values of f < 1, larger standard deviations, hence also larger failure probabilities are obtained. For each pre-selected value of f a Monte Carlo Simulation is performed, in order to obtain the reliability index β(f). Following Bucher (2009)Bucher, C., (2009). Asymptotic sampling for high-dimensional reliability analysis. Prob. Eng. Mech. 24: 504-510., the asymptotic behavior of β with respect to f can be described by a curve:
is the modified standard deviation for the same random variable. For small values of f < 1, larger standard deviations, hence also larger failure probabilities are obtained. For each pre-selected value of f a Monte Carlo Simulation is performed, in order to obtain the reliability index β(f). Following Bucher (2009)Bucher, C., (2009). Asymptotic sampling for high-dimensional reliability analysis. Prob. Eng. Mech. 24: 504-510., the asymptotic behavior of β with respect to f can be described by a curve:
Where A, B and C are constants to be determined by nonlinear regression (e.g. least squares method), using (f, β/f) as support points. After finding the regression coefficients, the reliability index for the original problem is estimated by making f = 1 in equation (13), such that β = A + B. Finally, the probability of failure is obtained as Pf = Φ (-β), where Φ (.) is the standard normal cumulative distribution function. The Monte Carlo simulations for different values of β (support points) can be obtained by Simple Sampling, Latin Hypercube Sampling or Antithetic Variates Sampling.
The parameters influencing the performance of Asymptotic Sampling are the number of support points and the range of f values considered. In this paper, these parameters are not studied: they are fixed at values providing satisfactory responses: 5 support points are employed with f varying from 0.4 to 0.7 or from 0.5 to 0.8, depending on the problem.
4.3 Enhanced Sampling
The Enhanced Sampling technique was proposed by (Naess et al. 2009Naess, A., Leira, B.J., Batsevych, O., (2009). System reliability analysis by enhanced Monte Carlo simulation. Struct Safety 31: 349-355, 2012Naess, A., Leira, B.J., Batsevych, O., (2012). Reliability analysis of large structural systems. Prob. Eng. Mechanics 28: 164-168.) and is based on exploring the regularity of the tails of the PDF's. It aims at estimating small or very small failure probabilities for systems. The original limit state function M = g(x 1, x 2, ..., xm ) is used to construct a set of parametric functions M(λ), with 0 ≤ λ ≤ 1, such that:
where μM is the mean value of M. Thus, it is assumed that the behavior of failure probabilities with respect to λ can be represented as:
Using a set of support points [λ, Pf (λ)], the parameters in equation 15 can be found by nonlinear regression. The probability of failure for the original problem is estimated for λ = 1. One large advantage over Asymptotic Sampling is that, from one single Monte Carlo simulation run, the whole range of parametric functions M(λ) can be evaluated. Hence, a large number of support points can be used, with no penalty in terms of computational cost.
For systems, each limit state or component Mj = gj(x 1, x 2, ..., xm ), with j = 1, ..., nls, must be evaluated. Thus, a parametric set of equations is obtained, such as:
Therefore, for a series system the probability of failure is obtained as:
For a parallel system, the probability of failure is obtained as:
and for a series system with parallel subsystems, the probability of failure is given by:
where Cj is a subset of 1, ..., nls, for j = 1, ..., l.
The parameters of Enhanced Sampling are the number of support points [λ, Pf (λ)] and the values of λ for which failure probabilities are evaluated. Within this paper, these values are kept fixed: 100 support points are used, with λ varying from 0.4 to 0.9.
4.4 Subset Simulation
The Subset Simulation technique was proposed by Au and Beck (2001)Au, S.K., Beck, J.L., (2001). Estimation of small failure probabilities in high dimensions by subset simulation. Prob. Eng. Mech. 16(4): 263-277.aiming to estimate small and very small probabilities of failure in structural reliability. The basic idea of this technique is to decompose the failure event, with very small probability, into a sequence of conditionals events with larger probabilities of occurrence. For the later, small sample Monte Carlo simulation should be sufficient. Since Simple Sampling is not a good option to generate conditional samples, the Markov Chain Monte Carlo and the modified Metropolis-Hastings algorithms are used.
The estimation of conditional probabilities in Subset Simulation depends on the choice of the intermediates events. Consider the failure event E. The probability of failure associated to it is given by:
Considering a decreasing sequence of events Ei , such as E 1 ⊃ E 2 ⊃ ... ⊃ Em = E, thus:
Hence, the probability of failure is evaluated as:
In equation (22), P[E 1] can be evaluated by means of Crude Monte Carlo, using Simple Sampling, Latin Hypercube Sampling or Antithetic Variates Sampling. On the other hand, the conditional probabilities P[Ei |Ei-1 ] are estimated by means of Markov Chains using the Modified Metropolis-Hastings algorithm (Au and Beck, 2001Au, S.K., Beck, J.L., (2001). Estimation of small failure probabilities in high dimensions by subset simulation. Prob. Eng. Mech. 16(4): 263-277.; Au, 2005Au, S.K., (2005). Reliability-based design sensitivity by efficient simulation. Comput Struct 83: 1048-1061.; Au et al., 2007Au, S.K., Ching, J., Beck, J.L., (2007). Application of subset simulation methods to reliability benchmark problems. Struct Safety 29: 183-193.).
In Subset Simulation the intermediate events Ei are chosen in an adaptative way. In structural reliability the probability of failure is estimated by:
As the failure event is defined by:
The intermediate failure events are defined by:
with i = 1, ..., m. Hence, the sequence of intermediate events Ei is defined by the set of intermediate limit states.
For convenience, the conditional probabilities are established previously, such that P[Ei|Ei-1 ] = P0. Also, the number of samples nss (e.g. nss = 500) at each subset is previously established. Hence, sets of samples X0,k , with k = 1, ..., nss are obtained. The limit state functions are evaluated for X0,k , resulting in vector Y0,k = g(X0,k ). Components of vector Y0,k are arranged in increasing order, resulting in vector  . The intermediate limit of failure b1 is established as the sample
. The intermediate limit of failure b1 is established as the sample  for which k = P 0 nss , such that P[{
for which k = P 0 nss , such that P[{ ≤ b 1}] = P 0. Thus, there are P 0 nss samples on the "failure" domain defined by intermediate limit b 1. From each of these samples, by means of Markov Chain simulation, (1 - P 0)nss conditional samples X(1|0),k are generated, with distribution P(.|E 1). The limit state function is evaluated for these samples resulting in vector Y(1|0),k = g(X(1|0),k ) and in ordered vector
≤ b 1}] = P 0. Thus, there are P 0 nss samples on the "failure" domain defined by intermediate limit b 1. From each of these samples, by means of Markov Chain simulation, (1 - P 0)nss conditional samples X(1|0),k are generated, with distribution P(.|E 1). The limit state function is evaluated for these samples resulting in vector Y(1|0),k = g(X(1|0),k ) and in ordered vector  , both related to intermediate limit of failure b2, where k = P0nss. Therefore, P[{
, both related to intermediate limit of failure b2, where k = P0nss. Therefore, P[{ ≤ b 2}] = P 0. Thus, the next intermediate event E 2 = {Y ≤ b 2} is defined. One can notice that P[E 2|E 1] = P[Y ≤ b 2|Y ≤ b 1] = P 0. The P 0 nss conditional samples will be the seeds of the conditional samples for the following level. Repeating the process, one generates conditional samples until the final limit bm is reached, such that bm = 0. This process is illustrated in Figure 4.
≤ b 2}] = P 0. Thus, the next intermediate event E 2 = {Y ≤ b 2} is defined. One can notice that P[E 2|E 1] = P[Y ≤ b 2|Y ≤ b 1] = P 0. The P 0 nss conditional samples will be the seeds of the conditional samples for the following level. Repeating the process, one generates conditional samples until the final limit bm is reached, such that bm = 0. This process is illustrated in Figure 4.
The random walk is defined by its probability distribution (e.g. uniform) and by the standard deviation  , which is considered as the product of a value α by the standard deviation of the problem, such that
, which is considered as the product of a value α by the standard deviation of the problem, such that  = α . σi. Parameters of this algorithm are α, the number of samples for each subset (nss ) and the conditional probability P 0. Different values are used for these parameters for different problems, as detailed in the next Section. In all cases, the random walk is modeled by a uniform probability distribution function.
= α . σi. Parameters of this algorithm are α, the number of samples for each subset (nss ) and the conditional probability P 0. Different values are used for these parameters for different problems, as detailed in the next Section. In all cases, the random walk is modeled by a uniform probability distribution function.
5 COMPARATIVE PERFORMANCE OF SIMULATION STRATEGIES
In this study, three basic sampling techniques are combined with Crude Monte Carlo and with four modern sampling techniques: Importance Sampling Monte Carlo, Asymptotic Sampling, Enhanced Sampling and Subset Simulation. Hence, fifteen sampling schemes are investigated with respect to their performance in solving six structural reliability problems. Due to space limitations, only results for the three most relevant problems are presented herein. Conclusions reflect the six problems studied.
The following analysis procedure consists in two steps. The first step is a study of the convergence of the probability of failure and its coefficient of variation for increasing numbers of samples. Since the required number of samples for Subset Simulation is much lower than for the other techniques, the convergence study is not performed for Subset Simulation. The second step is a comparison of the results for all techniques, including Subset Simulation, considering a small number of samples.
For Examples 1 and 2, the limit state functions are analytic; hence processing time is not a relevant issue. Example 3 involves a Finite Element model with physical and geometrical nonlinearities; hence processing time is more relevant.
5.1 Example 1: non-linear limit state function
The first example has a nonlinear limit state function, where the random variables are modeled by non-Gaussian probability distribution functions. The limit state function is (Melchers and Ahamed, 2004Melchers, R.E., Ahamed, M.A., (2004). Fast approximate method for parameter sensitivity estimation in Monte Carlo structural reliability. Comput Struct 82: 55-61.):
where Xi , with i = 1, ..., 6, are the random variables. The parameters of the probability distributions are given in Table 1.
Random variables of Example 1 (Melchers and Ahamed, 2004Melchers, R.E., Ahamed, M.A., (2004). Fast approximate method for parameter sensitivity estimation in Monte Carlo structural reliability. Comput Struct 82: 55-61.).
The reference probability of failure is obtained using Crude Monte Carlo simulation with Simple Sampling and 2×109 samples. The reference probability of failure is 2.777×10-5 (β = 4.031). This example aims to evaluate the performance of the intelligent sampling techniques in a problem with nonlinear limit state function involving non-Gaussian distribution functions.
Figures 5, 6 and 7 show convergence plots for the mean and coefficient of variation (c.o.v) of the Pf , for Simple Sampling, LHS and Asymptotic Sampling, respectively. Convergence results were evaluated for number of samples varying from 1×103 to 1×106. Results are shown for Crude, Importance, Asymptotic and Enhanced Sampling. For Asymptotic Sampling, the parameter f varies from 0.4 to 0.7, with 5 support points in this range. Subset simulation is not included, because computations are truly expensive for large numbers of samples. On the other hand, only a few samples are required to achieve similar results with Subset simulation, as observed in Table 2.
Two striking results can be observed in Figures 5 to 7. For all basic sampling techniques, the c.o.v. for Importance Sampling converges very fast to near zero. This is a very positive result. On the other hand, it is observed that the failure probability also converges very fast, but with a bias w.r.t. the reference result. This bias, although small and acceptable, is of some concern, and is introduced by the sampling function. It is also observed, in Figures 5 to 7, that for Asymptotic Sampling the c.o.v. convergence is quite unstable, with results oscillating significantly, and convergence for Pf also shows some bias. Both results are especially true for Simple and Anthytetic Variates Sampling, and less so for LHS. In fact, is observed that LHS improves the results for all sampling techniques illustrated in Figures 5 to 7.
A quantitative comparison of the performance of all sampling techniques, in solution of Problem 1, is presented in Table 2. These results are computed for a much smaller number of samples: 2,300. In Subset Simulation the following parameters are adopted: nss = 500, α = 1.5, and P 0 = 0.1.
One observes in Table 2 that Crude Monte Carlo and Asymptotic Sampling do not lead to any results for such a small number of samples. Importance Sampling leads to the smallest c.o.v.s, but with deviations of around 18 to 30% from the reference result. Enhanced Sampling works, but deviations and c.o.v.s are rather large. For such a small number of samples, Subset Simulation provides the best results, with acceptable c.o.v.s and deviations varying from around 5 to 60%. These deviations could be further reduced by a marginal increase in the number of samples.
5.2 Example 2: Hiper-estatic structural system (truss)
In order to investigate the performance of the intelligent sampling techniques in a structural system problem, an hiper-estatic truss is studied. Service failure is characterized by failure of any component (bar) of the truss, which can be due to buckling (compressed bars) or to yielding (tensile bars). System failure, characterized by failure of a second bar (any), given failure of the hiper-estatic bar (any), is not considered in this study (Verzenhassi, 2008Verzenhassi, C.C., (2008). Otimização de risco estrutural baseada em confiabilidade. Masters Dissertation, São Carlos School of Engineering, University of São Paulo.). The truss and its dimensions are shown in Figure 8. The geometrical properties of truss bars are shown in Table 3. Table 4 shows the random variables considered.
Geometrical properties of the truss bars of Example 2 (Verzenhassi, 2008Verzenhassi, C.C., (2008). Otimização de risco estrutural baseada em confiabilidade. Masters Dissertation, São Carlos School of Engineering, University of São Paulo.).
Six limit state functions are employed to solve the problem: four functions related to elastic buckling of bars 1, 2, 3 and 6:
and two functions related to the yielding of bars 4 and 5:
where Ei is the Young's modulus, Ii is the moment of inertia of the U-shaped steel section, Li is bar length, Ai is the transversal section area,  is the steel yielding stress, V is the vertical load, H is the horizontal load, ai is the fraction of the vertical load acting at each bar, bi is the fraction of the horizontal load acting at each bar. The random variables are described in Table 4. A correlation of 0.1 between V and H is considered.
is the steel yielding stress, V is the vertical load, H is the horizontal load, ai is the fraction of the vertical load acting at each bar, bi is the fraction of the horizontal load acting at each bar. The random variables are described in Table 4. A correlation of 0.1 between V and H is considered.
The reference probability of failure is obtained from a Crude Monte Carlo simulation with 2×109 samples using Simple Sampling: Pf = 1.139×10-4 (β = 3.686).
Figures 9, 10 and 11 show the convergence plots for the mean and coefficient of variation (c.o.v) of the Pf , for Simple Sampling, LHS and Asymptotic Sampling, respectively. Convergence results were evaluated for number of samples varying from 1×103 to 1×105. Results are shown for Crude, Asymptotic and Enhanced Sampling. For Asymptotic Sampling, the parameter fvaries from 0.5 to 0.8, with 5 support points. Importance Sampling is not included because the sampling function is composed following equation (12). Hence, the convergence plot could not be obtained. Results for Importance Sampling and for Subset simulation are shown in Table 5, for a fixed (and smaller) number of samples.
One can notice in Figures 9, 10 and 11 that Enhanced Sampling performs very well, comparing to Crude Monte Carlo and to Asymptotic Sampling, w.r.t. convergence of the Pf and of its coefficient of variation. The use of LHS (Figure 10) is advantageous for the studied techniques, since faster and smoother convergence is observed.
The comparison of all intelligent sampling techniques is presented in Table 5, computed for a smaller number of samples: 3,700. For Subset Simulation, the following parameters are adopted: nss = 1,000; α = 1.5; and P 0 = 0.1.
In Table 5, one observes that Crude Monte Carlo does not lead to any results for such a small number of samples. Importance Sampling presents a very good performance in comparison with the other techniques, with very small c.o.v.s and small and acceptable deviations from the reference Pf . Subset Simulation also presents an acceptable performance, with small c.o.v.s and larger, but still acceptable deviations from the reference result. The use of Latin Hypercube Sampling is beneficial for all techniques, for this problem.
5.3 Example 3: non-linear steel frame tower
An optimized plane steel frame transmission line tower (Figure 12) is analyzed by finite elements. The problem is based on Gomes and Beck (2013)Gomes, W.J.S., Beck, A.T., (2013). Global structural optimization considering expected consequences of failure and using ANN surrogates. Comput Struct 126: 56-68., where structural optimization considering expected consequences of failure was addressed. The mechanical problem is modeled by beam elements with three nodes, with three degrees of freedom per node. The frame is composed by L-shaped steel beams. The Finite Element Method with positional formulation (Coda and Greco, 2004Coda, H.B., Greco, M.A., (2004). Simple FEM formulation for large deflection 2D frame analysis based on position description. Comput Method Appl Mech Eng 193: 3541-3557.; Greco et al., 2006Greco, M., Gesualdo, F.A.R., Venturini, W.S., Coda, H.B., (2006). Nonlinear positional formulation for space truss analysis. Finite Elem Anal Des 42: 1079-1086.) is adopted to solve the geometrical non-linear problem. Moreover, the material is assumed elastic perfectly plastic.
The limit state function is defined based on the load-displacement curve (Figure 13) for top nodes 11 and 12. Because several configurations had to be tested in the optimization analysis performed in Gomes and Beck (2013)Gomes, W.J.S., Beck, A.T., (2013). Global structural optimization considering expected consequences of failure and using ANN surrogates. Comput Struct 126: 56-68., a robust limit state function was implemented. The same limit state function is employed herein: g(x,d) = 75º - tan-1(Δδ/ΔL) , where Δδ is the increment in mean displacement in centimeters, for nodes 11 and 12; ΔLis the increment in the non-dimensional load factor; and 75o is the critical angle considered.
5.3.1 Loading
The gravity load from aligned cables is considered. The design wind load on cables and structure is calculated based on Brazilian code ABNT NBR 6123ABNT NBR6123 (1998). Wind loads in buildings. ABNT - Brazilian Association of Technical Codes, Rio de Janeiro (in Portuguese).: Wind loads in buildings. The design wind is taken as v 0 = 45m/s. Thus, the characteristic wind load is calculated as vk = S 1 S 2 S 3 v 0, where S 1, S 2 and S 3 are the topographical (S 1 = 1), the rugosity (S 2 = 1.06) and statistical (S 3 = 1) factors, yielding vk = 47.7 m/s. This characteristic wind is taken at a height of 10 meters. The variation of wind velocity with height follows a parabolic shape, such that v(z) =  , where z is height. To model uncertainty in the wind load, an non-dimensional random variable V is introduced, such that V(z) = v(z) . V. Thus, the wind pressure is evaluated from wind velocities as q(z, V) = 0,613 . (v(z) . V)2, where pressure is given in N/m2, for normal atmospheric conditions (1 atm) and temperature (15 °C). The wind load acts at each element on the tower. The drag coefficient is Ca = 2.1, which is the maximum value for prismatic beams with L-shaped sections. Cables of 2.52 cm diameter were adopted, with an influence area of 300 m and drag coefficient of Ca = 1.2. For these values, one obtains the random force Fa(V) acting in the horizontal direction on nodes 11 and 12, such that Fa(V)
, where z is height. To model uncertainty in the wind load, an non-dimensional random variable V is introduced, such that V(z) = v(z) . V. Thus, the wind pressure is evaluated from wind velocities as q(z, V) = 0,613 . (v(z) . V)2, where pressure is given in N/m2, for normal atmospheric conditions (1 atm) and temperature (15 °C). The wind load acts at each element on the tower. The drag coefficient is Ca = 2.1, which is the maximum value for prismatic beams with L-shaped sections. Cables of 2.52 cm diameter were adopted, with an influence area of 300 m and drag coefficient of Ca = 1.2. For these values, one obtains the random force Fa(V) acting in the horizontal direction on nodes 11 and 12, such that Fa(V)  19,279.65 . V 2.
19,279.65 . V 2.
Random variables considered in this problem are the Young's modulus (E) and the non-dimensional wind variable (V). The random variables are described in Table 6.
Random variables of Example 3 (Gomes and Beck, 2013Gomes, W.J.S., Beck, A.T., (2013). Global structural optimization considering expected consequences of failure and using ANN surrogates. Comput Struct 126: 56-68.).
5.3.2 Results
In Gomes and Beck (2013)Gomes, W.J.S., Beck, A.T., (2013). Global structural optimization considering expected consequences of failure and using ANN surrogates. Comput Struct 126: 56-68., probability of failure is evaluated by FORM, and values Pf,FORM = 1.088×10-4 (β = 3.6976) are obtained for the tower configuration in Figure 12. In this paper, several Monte Carlo Simulation techniques are adopted for evaluating this failure probability. FORM is very efficient, and efficiency is fundamental for solving the structural optimization problem. However, FORM provides only approximate results for problems with non-linear limit state functions.
The reference probability of failure is evaluated by Crude and by Importance Sampling Monte Carlo simulation, using Simple Sampling, Latin Hypercube Sampling and Antithetic Variates Sampling. 1×105 samples are employed for each solution. Results are given in Table 7, where one observes that Crude Monte Carlo with LHS and Importance Sampling Monte Carlo present probabilities of failure very close to the result obtained by FORM. This shows that, in spite of the non-linearity of the limit state function, FORM provides accurate results. For the remainder of the analysis, the average value of Pf = 1.096×10-4 is used as a reference.
Figures 14, 15 and 16 show the convergence plots for the mean and coefficient of variation (c.o.v) of the Pf, for Simple Sampling, LHS and Asymptotic Sampling, respectively. Convergence results were evaluated for number of samples varying from 1×103 to 1×105. Results are shown for Crude, Importance, Asymptotic and Enhanced Sampling. In Asymptotic Sampling, parameter f varies from 0.5 to 0.8, with 5 support points.
In Figs. 14 to 16, one observes that convergence of Importance Sampling, for this problem, is very fast and accurate, for all basic sampling techniques. Also, it can be clearly seen that LHS improves the results for all sampling techniques, reducing oscillations during convergence. The convergence behavior of Asymptotic Sampling is very unstable, both for the c.o.v. and the Pf ; hence this technique does not perform very well for this problem. Enhanced Sampling works much better, providing results similar to Crude sampling for this number of samples.
A quantitative comparison of the performance of all sampling techniques, in solution of Problem 3, is presented in Table 8. These results are computed for 14,800 samples. In Subset Simulation the following parameters are adopted: nss = 4000, α = 1.5, P 0 = 0.1.
One observes in Table 8 that Importance Sampling and Subset simulation out-perform the other methods in terms of small c.o.v. and small deviation from the reference solution. Asymptotic and Enhanced sampling show a similar and average performance. Latin Hipercube Sampling improves the results for most methods, especially for Subset Simulation.
5.3.3 Processing Time
The processing time to compute the results in Table 8 (14,800 samples) are given in Table 9. One observes that processing times are similar for all techniques, except for Importance Sampling: this technique takes a little longer to compute the weights for each sample, following equation (11). Processing times are very similar for the basic sampling techniques. By comparing results of Table 9 with results of Table 7, one observes the massive gain in processing time that is obtained using the intelligent sampling techniques addressed herein. Computing times are much smaller, but the quality of the solutions (small deviation and c.o.v.) are similar.
5.3.4 Processing Time
In order to further evaluate the performance of Subset Simulation using smaller numbers of samples, the following parameters are adopted: nss = 2,000; α = 2; and P 0 = 0.1. Results are presented in Table 10.
Results presented in Table 10 show that Subset Simulation is an effective tool for estimating small probabilities of failure in problems involving numerical evaluation of limit state functions. The original solution via Crude Monte Carlo took approximately 11 hours to compute a probability of failure with coefficient of variation of 0.27 and relative deviations of: 28.68% (Simple Sampling), 1.1% (Latin Hypercube Sampling) and 37.87% (Antithetic Variates Sampling). In comparison, Subset Simulation took approximately 45 minutes to estimate the same probability of failure with coefficient of variation of 0.25 and deviations around 3.7%.
5 CONCLUDING REMARKS
This paper presented a benchmark study on intelligent and efficient sampling techniques in Monte Carlo Simulation. Crude Monte Carlo simulation was compared to Importance Sampling, Asymptotic Sampling, Enhanced Sampling and to Subset Simulation. These five sampling schemes were combined with Simple Sampling, Latin Hypercube Sampling and Antithetic Variates Sampling, resulting in fifteen sampling strategy combinations. The performance of these strategies was investigated for six problems, but results for only three were presented herein. The conclusions below reflect the six problems studied.
It was observed that use of Latin Hypercube Sampling had a significant and positive influence for all sampling techniques with which it was combined. LHS has led to smoother convergence curves and more accurate results for most cases studied. Antithetic Variates also produced better results than Simple Sampling.
Importance Sampling using design points was found to be one of the most efficient techniques for solving problems with small and very small failure probabilities. Convergence is extremely fast, and with a couple of samples one obtains accurate failure probabilities with small sampling error (c.o.v.). However, for one of the problems studied, it was observed that the sampling function introduced some bias in the results, making failure probabilities converge to an inexact yet acceptable value. Also, it is known that use of Importance Sampling can be a problem for highly non-linear problems for which the design point(s) cannot be found.
Results obtained with Asymptotic Sampling were inaccurate for a number of problems, perhaps because a small number of support points were used. The drawback with this scheme is that a new set of samples has to be computed for each additional support point; hence there is a string compromise between the number of support points and the accuracy with which failure probabilities can be estimated for each support point.
Although similar to Asymptotic Sampling, the Enhanced Sampling technique presented consistent results for all problems studied. Enhanced sampling has a large advantage over Asymptotic Sampling, because the same set of samples is used for all support points. Hence, there is no computational penalty for using many support points, and the accuracy of the regression is improved.
Subset Simulation performed extremely well for all problems studied, resulting in accurate estimates of failure probabilities, with very small sampling errors. This explains why Subset Simulation has become so popular among structural reliability researchers, and is being applied extensively in the solution of both time invariant and time variant reliability problems.
Finally, it can be said that Subset Simulation, Enhanced Sampling and Importance Sampling, aided by Latin Hypercube sampling, are efficient ways of solving reliability problems, with a much smaller number of samples than required in Crude Monte Carlo Simulation.
Acknowledgments
The authors wish to thank the National Council for Research and Development (CNPq) for the support to this research.
References
- ABNT NBR6123 (1998). Wind loads in buildings. ABNT - Brazilian Association of Technical Codes, Rio de Janeiro (in Portuguese).
- Au, S.K., (2005). Reliability-based design sensitivity by efficient simulation. Comput Struct 83: 1048-1061.
- Au, S.K., Beck, J.L., (2001). Estimation of small failure probabilities in high dimensions by subset simulation. Prob. Eng. Mech. 16(4): 263-277.
- Au, S.K., Ching, J., Beck, J.L., (2007). Application of subset simulation methods to reliability benchmark problems. Struct Safety 29: 183-193.
- Beck, A.T., Rosa, E., (2006). Structural Reliability Analysis Using Deterministic Finite Element Programs. Latin American Journal of Solids and Structures 3: 197-222.
- Bucher, C., (2009). Asymptotic sampling for high-dimensional reliability analysis. Prob. Eng. Mech. 24: 504-510.
- Coda, H.B., Greco, M.A., (2004). Simple FEM formulation for large deflection 2D frame analysis based on position description. Comput Method Appl Mech Eng 193: 3541-3557.
- Engelund, S., Rackwitz, R., (1993). A benchmark study on importance sampling techniques in structural reliability. Structural Safety 12: 255-276.
- Gomes, W.J.S., Beck, A.T., (2013). Global structural optimization considering expected consequences of failure and using ANN surrogates. Comput Struct 126: 56-68.
- Greco, M., Gesualdo, F.A.R., Venturini, W.S., Coda, H.B., (2006). Nonlinear positional formulation for space truss analysis. Finite Elem Anal Des 42: 1079-1086.
- Madsen, H.O., Krenk, S., Lind, N.C., (1986). Methods of structural safety. Prentice Hall, Englewood Cliffs.
- McKay, M.D., Beckman, R.J., Conover, W.J., (1979). A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 21(2): 239-124.
- Melchers, R.E., (1999). Structural Reliability Analysis and Prediction. John Wiley & Sons, Chichester.
- Melchers, R.E., Ahamed, M.A., (2004). Fast approximate method for parameter sensitivity estimation in Monte Carlo structural reliability. Comput Struct 82: 55-61.
- Metropolis, N. et al., (1953). Equation of state calculation by fast computing machines. J Chem Phys 21(6): 1087-1092.
- Metropolis, N., Ulam, S., (1949). The Monte Carlo method. J Am Statist Assoc 44(247): 335-341.
- Naess, A., Leira, B.J., Batsevych, O., (2009). System reliability analysis by enhanced Monte Carlo simulation. Struct Safety 31: 349-355
- Naess, A., Leira, B.J., Batsevych, O., (2012). Reliability analysis of large structural systems. Prob. Eng. Mechanics 28: 164-168.
- Olsson, A., Sandeberg, G., Dahlblom, O., (2003). On latin hypercube sampling for structural reliability analysis. Struct Safety 25: 47-68.
- Robert, C., Casella, G., (2011). A short history of Markov Chain Monte Carlo: Subjective recollections from incomplete data. Statist sci 26(1): 102-115.
- Schuëller, G.I., Prandlwarter, H.J., (2007). Benchmark study on reliability estimation in higher dimensions of structural systems - An overview. Struct Safety 29: 167-182.
- Sichani, M.T., Nielsen, S.R.K., Bucher, C., (2011a). Applications of asymptotic sampling on high dimensional structural dynamic problems. Struct safety 33: 305-316.
- Sichani, M.T., Nielsen, S.R.K., Bucher, C., (2011b). Efficient estimation of first passage probability of high-dimensional nonlinear systems. Prob. Eng. Mech. 26: 539-549.
- Sichani, M.T., Nielsen, S.R.K., Bucher, C., (2014). Closure to "Applications of asymptotic sampling on high dimensional structural dynamic problems". Struct Safety 46: 11-12.
- Verzenhassi, C.C., (2008). Otimização de risco estrutural baseada em confiabilidade. Masters Dissertation, São Carlos School of Engineering, University of São Paulo.
Publication Dates
-
Publication in this collection
Aug 2015
History
-
Received
19 Mar 2014 -
Accepted
21 Oct 2014
















































 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail