Abstract
A cultural algorithm was utilized in this study to solve optimal design of truss structures problem achieving minimum weight objective under stress and deflection constraints. The algorithm is inspired by principles of human social evolution. It simulates the social interaction between the peoples and their beliefs in a belief space. Cultural Algorithm (CA) utilizes the belief space and population space which affects each other based on acceptance and influence functions. The belief space of CA consists of different knowledge components. In this paper, only situational and normative knowledge components are used within the belief space. The performance of the method is demonstrated through four benchmark design examples. Comparison of the obtained results with those of some previous studies demonstrates the efficiency of this algorithm.
Keywords:
Cultural algorithm; Truss structure design; Size optimization
1 INTRODUCTION
In recent decades, various optimization techniques have been applied to optimal design of truss structure with stress and deflection constraints. The optimum design of truss structures are usually categorized into three different optimization problems: size, layout and topology optimizations. In the first category, only the cross sectional areas of the members are considered to minimize the weight of the structure, while the nodal coordinates of the truss are also taken as design variables in the layout optimization of truss structures. In the third category, the number of members of the structure and the connectivity of them are optimized. This paper focuses on the first category of truss optimum design problem, in which only sizing variables are considered as design variables.
Over the last years, the studies on meta-heuristic search methods such as Particle Swarm Optimization (PSO) (Eberhart and Kennedy, 1995Eberhart, RC., Kennedy, J. (1995). A new optimizer using particle swarm theory. In: Proceedings of the sixth international symposium on micro machine and human science, Nagoya, Japan.), Ant Colony Optimization (ACO) (Dorigo, 1992Dorigo, M. (1992). Optimization, learning and natural algorithms (in Italian), PhD Thesis. Dipartimento di Elettronica, Politecnico di Milano, IT.), Harmony Search (HS) (Geem et al., 2001Geem, ZW., Kim, JH., Loganathan, GV. (2001). A new heuristic optimization algorithm: harmony search. Simulation 76:60-68.), Simulated Annealing (SA) (Kirkpatrick et al., 1983Kirkpatrick, S., Gelatt, CD., Vecchi, MP. (1983). Optimization by simulated annealing. Science 220:671-680.) and Big Bang-Big Crunch (BB-BC) (Erol and Eksin, 2006Erol OK., Eksin, I. (2006). New optimization method: big bang-big crunch. Advances in Engineering Software;37:106-111.) have shown that these methods can be efficiently used to solve engineering optimization problems characterized by non-convexity, discontinuity and non-differentiability. Most of these stochastic search methods are simulation of the specific phenomenon in the nature such as social behavior of bird flocking or fish schooling, evolution theories of the universe and annealing processes in materials.
Researchers have been applied various meta-heuristic optimization algorithms to the optimal design of truss structures. For example, (Camp, 2007Camp, CV. (2007). Design of space trusses using big bang-big crunch optimization. Journal of Structural Engineering;133:999-1008.) employed original BB-BC to size optimization of truss structures with continues and discrete design variables. (Lamberti, 2008Lamberti, L. (2008). An efficient simulated annealing algorithm for design optimization truss structures. Computers and Structures 86:1936-53.) suggested a heuristic algorithm based on SA. (Hasancebi et al., 2009Hasancebi, O., Carbas, S., Dogan, E., Erdal, F., Saka, MP. (2009). Performance evaluation of metaheuristic search techniques in the optimum design of real size pin jointed structures. Computers and Structures 87:284-302.) evaluated the performance of different algorithms in optimal design of pin jointed structures.
As extensions of meta-heuristic algorithms, hybrid algorithms have been developed to improve the performance of original meta-heuristic algorithms. The main aim of developing hybrid algorithms is to provide an adequate balance between the exploration and exploitation mechanisms. The exploration mechanism is related to the ability of algorithm to the performing efficient search in solution space of the optimization problem, while the exploitation mechanism is related to the ability of finding better solutions in the vicinity of the current solutions. Such hybrids have been successfully applied to optimal design of truss structures. For instance, (Li et al., 2007Li LJ., Huang ZB., Liu F., Wu QH. (2007). A heuristic particle swarm optimizer for optimization of pin connected structures. Computers and Structures 85:340-349.) introduced a heuristic particle swarm optimizer (HPSO) for size optimization of truss structures. (Kaveh and Talatahari, 2009aKaveh, A., Talatahari, S. (2009a). Particle swarm optimizer, ant colony strategy and harmony search scheme hybridized for optimization of truss structures. Computers and Structures 87:276-283.) proposed particle swarm optimizer, ant colony strategy and harmony search scheme. This method is based on the particle swarm optimizer with passive congregation (PSOPC), ant colony optimization and harmony search scheme. (Degertekin, 2012Degertekin, S.O. (2012). An improved harmony search algorithms for sizing optimization of truss structures. Computers and Structures 92-93:229-241.) presented an efficient harmony search algorithm (EHS) and self-adaptive harmony search algorithm (SAHS) for sizing optimization of truss structures. In another work, (Degertekin and Hayalioglu, 2013Degertekin, S.O., Hayalioglu, M.S. (2013). Sizing truss structures using teaching-learning-based optimization. Computers and Structures 119:177-188.) used teaching-learning-based optimization (TLBO) method for sizing truss structures which is a new meta-heuristic search method. TLBO simulates the social interaction between the learners and teacher. (Kaveh and Talatahari, 2009bKaveh, A., Talatahari, S. (2009b). Size optimization of space trusses using Big Bang-Big Crunch algorithm. Computers and Structures 87:1129-1140.,2010aKaveh, A., Talatahari, S. (2010a). Optimal design of Schwedler and ribbed domes via hybrid big bang-big crunch algorithm. Journal of Constructional Steel Research 66:412-419.) proposed a hybrid big bang-big crunch (HBB-BC) by combining BB-BC algorithm and with Sub Optimization Mechanism (SOM) for size optimization of space trusses and ribbed domes. In this method, SOM is an auxiliary tool which works as a search-space updating mechanism.
In some cases, researchers utilized novel optimization algorithms. For example, (Kaveh and Talatahari, 2010bKaveh, A., Talatahari, S. (2010b). Charged system search for optimum grillage system design using the LRFD-AISCcode. Journal of Constructional Steel Research 66:767-771. cKaveh, A., Talatahari, S. (2010c). Optimal design of skeletal structures via the charged system search algorithm. Structural and Multidisciplinary Optimization 41:893-911. dKaveh, A., Talatahari, S. (2010d). Optimum design of skeletal structures using imperialist competitive algorithm. Computers and Structures 88:1220-1229.,2012Kaveh, A., Talatahari, S. (2012). Charged system search for optimal design of frame structures. Applied Soft Computing 12:382-393.) utilized Charged System Search (CSS) to optimal design of frame, grillage and skeletal structures and Imperialist Competitive Algorithm (ICA)) for size optimization of skeletal structures. And recently, (Kaveh and Khayatazad, 2013Kaveh, A., Khayatazad, M. (2013). Ray optimization for size and shape optimization of truss structures. Computers and Structures 117:82-94.) employed Ray Optimizer (RO) to size and shape optimization of truss structures. (Sonmez, 2011Sonmez, M. (2011). Artificial bee colony algorithm for optimization of truss optimization. Applied Soft Computing;11:2406-2418.) used Artificial Bee Colony (ABC) algorithm to sizing of truss structures.
In this study, a specific version of Cultural Algorithms (CAs) is utilized to size optimization of truss structures. CA is a population based random search method which simulates the social evolution process. Compared with other meta-heuristic methods, CA uses a belief space beside the population space. The belief space is divided into distinct categories. In this paper, only two categories, called Normative knowledge, and Situational knowledge are used within the belief space. The algorithm is an iterative process in which new populations are obtained using influence function based on knowledge components of belief space. Four truss design examples are utilized with stress and deflection constraints and results are compared with different methods in order to show the efficacy of present approach.
The remainder of this paper is organized as: mathematical description of the optimum design problem is first reviewed in Section 2. Then, Section 3 presents a brief review of the CA. In Section 4, the effectiveness of CA is verified by four design examples. Finally, conclusions are presented in Section 5.
2 OPTIMUM DESIGN PROBLEM
The main aim of optimal design of a truss structure is to minimize the weight of the structure while satisfying some constraints on stresses and deflections. In this class of optimization problems, cross sectional areas are taken as design variables. The optimal design of a truss structure can be formulated as:
Where A is the vector containing the design variables; m is the number of members making up the structure; W(.) is the weight of the structure; γi is the material density of member i; Ai is the cross-sectional area of the member i which is between Amin and Amax; Li is the length of the member i; nd is the number of design variables; n is the number of nodes; and
and are the allowable tension and compressive stresses for member i, respectively; δi is the displacement of node i and δmin and δmax are corresponding lower and upper limits.
are the allowable tension and compressive stresses for member i, respectively; δi is the displacement of node i and δmin and δmax are corresponding lower and upper limits.
Optimal design of truss structure should satisfy the above mentioned constraints. In this study, the constraints are handled by using a simple penalty function method. Thus, a fitness function must be given to evaluate the quality of a solution candidate. For each solution candidates, following cost function is defined:
Where fpenalty, is the penalty function represented by solution A, q is the number of constraints and φ is the penalty factor which is related to the violation of constraints. In order to obtain the values of φi, the stresses and nodal displacements of the structure are compared to the corresponding upper or lower bounds as follow.
As it can be seen from Eq. (4), if the constraints are not violated, the value of the penalty function will be zero. In Eq. (3), the values of parameters ε1 and ε2 are selected considering the exploration and the exploitation rate of the search space. In this study ε1 is taken as unity, and ε2 starts from 2 and gradually increases. The value of ε2 for tth iteration is calculated as follow:
3 CULTURAL ALGORITHM
CA is a stochastic optimization technique originally developed by (Reynolds, 1991Reynolds, R.G. (1991). Version Space Controlled Genetic Algorithms. In Proceedings of the Second Annual Conference on Artificial Intelligence Simulation and Planning in High Autonomy Systems, pages 6-14.,1999Reynolds, R.G. (1999). Cultural Algorithms: Theory and Application. In D. Corne, M. Dorigo, and F. Glover, editors, New Ideas in Optimization, pages 367-378. McGraw-Hill.) inspired by theories of cultural evolution in sociology and archaeology. In fact, each society has a population and the individuals are the members of this population. The individuals of a society have cultural experiences that acquired by the previous generations. Culture can be seen as a set of ideological phenomena shared by a population (Peter et al., 2004Peter J., Richerson R., Boyd. (2004). Not By Genes Alone: How Culture Transformed Human Evolution, University Of Chicago Press.), which consists of the beliefs, art and other things that acquired and transformed to the current generation by the previous generations. Sociologists believe that that the most of those forms of culture might be symbolically encoded and shared among the individuals of the society as a inheritance mechanism, and this mechanism may enhance the adaptability of the societies as well as accelerate the evolution speed of the society by making use of the domain knowledge obtained from generation to generation and spreading those useful information among all the individuals of the society (Youlin et al., 2011Youlin Lu., Jianzhong Zhou., Hui Qin., Ying Wang., Yongchuan Zhang. (2011). A hybrid multi-objective cultural algorithm for short-term environmental/economic hydrothermal scheduling. Energy Conversion and Management; 52:2121-2134.). Based on the described mechanism, the CA simulates the social interactions between the individuals of the population to develop a new optimization method. This algorithm uses the domain knowledge extracted during the optimization in order to bias the search process. As illustrated inFigure 1, CA utilizes two population and belief spaces which influence each other based on influence and acceptance functions. The population space consists of possible solution candidates to the optimization problem and the belief space records the cultural information about the behaviors and experiences of elites in the population space.
3.1 Belief Space
As mentioned before, the belief space consists of different knowledge components. The types of knowledge components depend mainly on the optimization problem being solved. Generally, the belief space consists of the following two knowledge components (Reynolds and Chung, 1997Reynolds, R.G., Chung, C. (1997). Knowledge-based Self-Adaptation in Evolutionary Programming using Cultural Algorithms. In Proceedings of the IEEE Congress on Evolutionary Computation, pages 71-76.):
-
1
. A Situational knowledge component, which is includes the best experience or solution gained by whole individuals in population space. This knowledge component is like global best in particle swarm optimization.
-
2
. A Normative knowledge component, which is record the behaviors and experiences of accepted individuals from the population space and provide a set of intervals, one for each dimension of the problem. These intervals specify the ranges of search space which is good to search, and eliminate undesirable parts.
In addition, another three knowledge components can be added, such as domain knowledge, historical knowledge and topographical knowledge components (Reynolds and Saleem, 2000Reynolds, R.G., Saleem, S. (2000). Cultural Algorithms in Dynamic Environments. In Proceedings of the IEEE Congress on Evolutionary Computation, volume 2, pages 1513-1520.;Peng et al., 2003Peng, B., Reynolds, R.G, Brewster, J. (2003). Cultural Swarms. In Proceedings of the IEEE Congress on Evolutionary Computation, volume 3, pages 1965-1971, 2003.). But in this paper, only two knowledge components (Situational and Normative) are used in the belief space. Thus, the belief space expressed as the tuple:
Where S(t) and N(t) is the Situational and Normative knowledge components, respectively, and can be expressed as:
For each dimension following information is stored:
Where, {A*(t)} is the vector of Situational design variables and nd is the number of design variables. Ij(t) denotes the interval { ,
, } for design variable j, which is assigned
} for design variable j, which is assigned = +∞ and
= +∞ and = -∞ for all design variables at the beginning time t=0. Lj (t) and Uj (t) represents the scores for the lower and upper bounds of design variable j. Lj (t) and Uj (t) initialized to +∞.
= -∞ for all design variables at the beginning time t=0. Lj (t) and Uj (t) represents the scores for the lower and upper bounds of design variable j. Lj (t) and Uj (t) initialized to +∞.
3.2 Acceptance Function
The acceptance function determines the number of solution candidates from the population space to adjust knowledge components of belief space. For this purpose there are two static and dynamic methods. In static method, the number of individuals that accepted to shape beliefs is fixed during the time, while in the dynamic methods changes with respect to time. In this paper, static method is employed to accept individuals to shape beliefs. Thus, the top %N of individuals based on fitness values is accepted to adjust the belief space.
3.3 Adjusting the Belief Space
The knowledge components of belief space are adjusted by selected individuals as follows:
3.3.1 Situational Knowledge
Where W(.) is the weight of the structure, {Ak (t)}is the vector of kth accepted individual and na is the number of accepted individuals to adjust the belief space.
3.3.2 Normative Knowledge
Where (t) is the jth variable of the kth accepted individual to adjust belief space.
(t) is the jth variable of the kth accepted individual to adjust belief space.
3.4 Influence Function
The positions of individuals in the population space are updated by influence function. (Reynolds and Chung, 1997Reynolds, R.G., Chung, C. (1997). Knowledge-based Self-Adaptation in Evolutionary Programming using Cultural Algorithms. In Proceedings of the IEEE Congress on Evolutionary Computation, pages 71-76.) proposed four influence function to update positions. In this paper, only following influence function is used:
Where Aij (t + 1) is the new solution at time t for individual i and variable j, N(0,1) is a normally distributed random variable with a mean of 0 and a standard deviation of 1, ni is the number of individuals used in population space, nd is the number of design variables and σij is the strategy parameter for individual i and design variable j which is calculated as follow:
Where β is the user defined parameter. Finally, the optimal design of truss structures with CA can be summarized as following steps:
-
Step 1
: Initialization In this step, the initial population space is randomly generated between the lower and upper bounds for each design variable.
-
Step 2
: Create and initialize the belief space. The initial belief space created and initialized as explained in Section 3.1.
-
Step 3
: Evaluation Evaluation of each individual in population space and selecting the top %N of individuals based on the fitness values for adjust the belief space.
-
Step 4
: Adjust Beliefs In this step, the knowledge components of belief space are adjusted by accepted individuals as described in Section 3.3.
-
Step 5
: Influence population In this step, the positions of individuals are updated by influence function as explained in Section 3.4.
-
Step 6
: Finish or redoing Steps 3, 4 and 5 repeated until a terminating criterion is fulfilled.
4 DESIGN EXAMPLES
In this section, four design examples have been conducted to assess the performance of the CA approach for the optimal design of truss structures with stress and deflection constraints: 10-bar planar truss, 25-bar spatial truss, 72-bar spatial truss and 120-bar dome truss. The performance of present algorithm is compared with some simple and improved algorithms from literature.
In the all design examples, the population sizes of the algorithm are taken as 10, the number of accepted individuals to adjust belief space is 4 and the value of β parameter is chosen as uniformly random number between 0 and 1. Due to stochastic nature of algorithm, the algorithm carries out independently for 10 times for each design example. Each run stops when the maximum structural analyses are reached. The maximum number of the structural analyses for each design example is different and it is depends on the dimension of the optimization problem. Therefore, the maximum structural analyses are set to 24,000 for example 1 and 20,000 for examples 2 and 3. For the last example, 12,000 structural analyses are considered.
The CA algorithm and direct stiffness method for analysis of truss structures have been implemented in MATLAB program and run in Dell Vostro 1520 with Intel CoreDuo2 2.66 GHz processor and 4 GB RAM memory.
4.1 A 10-bar Planar Truss
The 10-bar planar truss shown inFigure 2is the first design example. The Young's modulus and material density of truss members are 104 ksi and 0.1 lb/in3 , respectively. The members are subjected to the stress limits of ±25 ksi. The maximum nodal displacements in X and Y directions are limited to ±2 in for all free nodes. The minimum allowable cross sectional area of each member is taken as 0.1 in2. In this design example, the loading condition is considered as: P1=150 kips and P2=50 kips.
InTable 1, the results obtained by the CA are compared with those reported in the literature like PSO, PSOPC, HPSO, ABC-AP, EHS, SAHS and TLBO. FromTable 1, it can be concluded that CA gives lightest design as compared to the results obtained by PSO, EHS, SAHS and TLBO, but heavier design than PSOPC, HPSO and ABC-AP methods. However, it is clear fromTable 1that the CA required significantly less structural analyses than PSOPC, HPSO and ABC-AP methods. In addition, TLBO obtained 4678.31 lb after 14,875 structural analyses, while CA found the same weight after 10,510 structural analyses.
In addition, the convergence behaviors of the best solution and the average of 10 independent runs are shown inFigure 3.
4.2 A 25-bar Spatial Truss Structure
The second design example deals with the size optimization of a twenty-five-bar spatial truss structure shown inFigure 4. The Young's modulus and material density of truss members are 104ksi and 0.1 lb/in3, respectively. Twenty five members are categorized into eight groups, as follows: (1) A1, (2) A2 - A5, (3) A6 - A9, (4) A10 - A11, (5) A12 - A13, (6) A14 - A17, (7) A18 - A21, and (8) A22 - A25.
The spatial truss structure is subjected to the multiply loading condition as shown inTable 2. The maximum nodal displacements in all directions are limited to ±0.35 in for all free nodes. The allowable tension stresses are the same for the all design groups, but the allowable compressive stresses depend to the length of the members and it is different for each design group as shown inTable 3. The range of cross sectional areas varies from 0.01 in2 to 3.4 in2.
The optimization results obtained by the CA are presented inTable 4and are compared with those of the PSO, PSOPC, HPSO, BB-BC, EHS, SAHS and TLBO approaches. FromTable 4, it is evident that CA yields lighter structural weight than other methods. The best result of the CA approach is 545.05, while it is 545.19, 545.38, 545.15, 545.49, 545.12 and 545.09 lb for the HPSO, BB-BC, EHS, SAHS and TLBO algorithm, respectively. In addition, it is observed that TLBO found minimum weight of 545.09 lb after 15,318 structural analyses while CA obtained the same weight after 7000 structural analyses. Also the convergence behaviors of the best solution and the average of 10 independent runs are presented inFigure 5.
4.3 A 72-bar Spatial Truss Structure
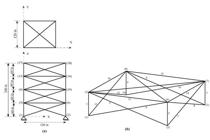
A 72-bar spatial truss shown inFigure 6is the third design example. The Young's modulus and material density of truss members are 0.1 lb/in3 and 104 ksi, respectively. The 72 members of this spatial truss are divided into 16 groups using symmetry, as follows:
(1)A1 - A4, (2) A5 - A12, (3) A13 - A16, (4) A17 - A18, (5) A19 - A22, (6) A20 - A30, (7) A31 - A34, (8) A35 - A36, (9) A37 - A40, (10) A41 - A48, (11) A49 - A52, (12) A53 - A54, (13) A55 - A58, (14) A59 - A62, (15) A63 - A70, (16) A71 - A72.
Scheme of the 72-bar spatial truss: (a) top and side view, (b) element and node numbering pattern for first story.
The spatial truss structure is subjected to the loading conditions given inTable 5. The maximum nodal displacements in all directions are limited to ±0.25 in for all free nodes. The minimum and maximum cross sectional areas for each member are 0.1 in2 and 4 in2, respectively.
The optimization results obtained by the CA are presented inTable 6and are compared with those of the BB-BC, HBB-BC, RO, EHS, SAHS and TLBO approaches. FromTable 6, it can be concluded that CA gives lightest design as compared to the results obtained by BB-BC, RO, EHS, SAHS and TLBO, but slightly heavier design than HBB-BC and TLBO methods. Moreover, the convergence diagrams of the best solution and the average of 10 independent runs are presented inFigure 7.
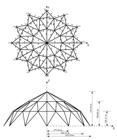
4.4 A 120-bar Dome Truss
The fourth design example is the size optimization of a 120-bar dome truss shown inFigure 8.Table 7presents the nodal coordinates of this structure. The members of the structure are divided into 7 groups using symmetry as shown inFigure 8. The modulus of elasticity is 30,450 ksi, and the material density is 0.288 lb/in3. The yield stress of steel is taken as 58.0 ksi. The dome is subjected to the vertical loading at all free nodes. These loads are taken as −13.49 kips at node 1, −6.744 kips at nodes 2 through 14, and −2.248 kips at the rest of the nodes. The minimum cross sectional area of all members is 0.775 in2 and the maximum cross sectional area is taken as 20.0 in2. The stress and displacement constraints are considered as:
(1) Stress constraint (according to the (AISC ASD, 1989American Institute of Steel Construction (AISC) (1989). Manual of steel construction allowable stress design. 9th ed. Chicago, IL.) code):
Where is calculated according to the slenderness ratio:
is calculated according to the slenderness ratio:
Where E = the modulus of elasticity; Fy = the yield stress of steel; Cc = the slenderness ratio (λi) dividing the elastic and inelastic buckling regions ( ); λi= the slenderness ratio(Yi = kλi/ ri ); k = the effective length factor; λi = the member length; and ri = the radius of gyration. In addition, the radius of gyration (ri ) can be expressed in terms of cross-sectional areas as ri = αA β (Saka, 1990Saka, MP. (1990). Optimum design of pin-jointed steel structures with practical applications. Journal of Structural Engineering 116:2599-2620.), in which α and β are the constants depending on the types of selected sections for the truss members. In this example, similar to the previous works, the pipe section (a=0.4993 and b=0.6777) is selected.
); λi= the slenderness ratio(Yi = kλi/ ri ); k = the effective length factor; λi = the member length; and ri = the radius of gyration. In addition, the radius of gyration (ri ) can be expressed in terms of cross-sectional areas as ri = αA β (Saka, 1990Saka, MP. (1990). Optimum design of pin-jointed steel structures with practical applications. Journal of Structural Engineering 116:2599-2620.), in which α and β are the constants depending on the types of selected sections for the truss members. In this example, similar to the previous works, the pipe section (a=0.4993 and b=0.6777) is selected.
(2) The maximum nodal displacements are limited to 0.1969 in for all free nodes.
In this example, four cases of constraints are considered as follows:
-
Case (1)
: with stress constraints and without any limitations of nodal displacement.
-
Case (2)
: with stress constraints and displacement limitations of ±0.1969 in imposed on all nodes in x- and y-directions.
-
Case (3)
: displacement limitation of ±0.1969 in only in z-direction and without stress constraints.
-
Case (4)
: all constraints explained in cases 1, 2 and 3 are considered together.
The optimal cross sectional areas obtained by the CA and the other optimization methods recently published in literature are reported inTable 8,Table 9,Table 10andTable 11for all cases. In Cases 1, 2 and 3, it is quite evident that CA gives the lightest designs than other techniques in the literature based onTable 8,Table 9andTable 10. For case 4, fromTable 11, it can be concluded that CA gives the lightest design as compared to the results obtained by PSOPC, PSACO, HBB-BC, ICA and RO, but slightly heavier design than CSS method.
For all cases,Figures 9-12compare the existing values (the member's stresses corresponding to the best solution) and allowable values for stress and displacement constraints. Based on these figures, it can be concluded that the stress and displacement constraints of the structure are not violated and the presented optimum designs are completely feasible. In addition, it can be seen that the axial stresses in the most of the members of the structure are very close to the allowable values, which show the optimality of the presented designs.
Finally the convergence characteristics of the CA are shown inFigure 13for all cases.
5 CONCLUSIONS
This work addresses application of Cultural Algorithm (CA) to optimal design of truss structures under stress and deflection constraints. CA is a population based meta-heuristic algorithm which uses the belief space beside the population space. The belief space of the CA has different knowledge components. In this paper, only two normative and situational knowledge components are used in the belief space. In belief space, the behaviors and experiences of elite individuals are recorded and then used to bias the search process of the algorithm. The performance of the CA is evaluated using a set of four well-known truss design examples. The numerical results show the efficiency and capabilities of the CA in finding the optimal designs for truss structures. The comparisons of the results obtained by the CA and other optimization methods show that the CA obtains relatively light structural weights with less structural analyses. Moreover, the same parameters are used for the all design examples and the separate sensitivity analyses of internal parameters are not required for the each design example. Furthermore, the feasibility of the obtained optimum designs are investigated in the last design example and it is shown that the stress and displacement constraints are not violated at the optimum designs. In order to enhance the exploration and exploitation mechanisms and provide more stable results with smaller standard deviations, future works should be focus on presenting of hybrid versions of this algorithm with other optimization techniques to increase the efficiency.
References
- American Institute of Steel Construction (AISC) (1989). Manual of steel construction allowable stress design. 9th ed. Chicago, IL.
- Camp, CV. (2007). Design of space trusses using big bang-big crunch optimization. Journal of Structural Engineering;133:999-1008.
- Dorigo, M. (1992). Optimization, learning and natural algorithms (in Italian), PhD Thesis. Dipartimento di Elettronica, Politecnico di Milano, IT.
- Degertekin, S.O. (2012). An improved harmony search algorithms for sizing optimization of truss structures. Computers and Structures 92-93:229-241.
- Degertekin, S.O., Hayalioglu, M.S. (2013). Sizing truss structures using teaching-learning-based optimization. Computers and Structures 119:177-188.
- Eberhart, RC., Kennedy, J. (1995). A new optimizer using particle swarm theory. In: Proceedings of the sixth international symposium on micro machine and human science, Nagoya, Japan.
- Erol OK., Eksin, I. (2006). New optimization method: big bang-big crunch. Advances in Engineering Software;37:106-111.
- Geem, ZW., Kim, JH., Loganathan, GV. (2001). A new heuristic optimization algorithm: harmony search. Simulation 76:60-68.
- Hasancebi, O., Carbas, S., Dogan, E., Erdal, F., Saka, MP. (2009). Performance evaluation of metaheuristic search techniques in the optimum design of real size pin jointed structures. Computers and Structures 87:284-302.
- Kaveh, A., Talatahari, S. (2009a). Particle swarm optimizer, ant colony strategy and harmony search scheme hybridized for optimization of truss structures. Computers and Structures 87:276-283.
- Kaveh, A., Talatahari, S. (2009b). Size optimization of space trusses using Big Bang-Big Crunch algorithm. Computers and Structures 87:1129-1140.
- Kaveh, A., Talatahari, S. (2010a). Optimal design of Schwedler and ribbed domes via hybrid big bang-big crunch algorithm. Journal of Constructional Steel Research 66:412-419.
- Kaveh, A., Talatahari, S. (2010b). Charged system search for optimum grillage system design using the LRFD-AISCcode. Journal of Constructional Steel Research 66:767-771.
- Kaveh, A., Talatahari, S. (2010c). Optimal design of skeletal structures via the charged system search algorithm. Structural and Multidisciplinary Optimization 41:893-911.
- Kaveh, A., Talatahari, S. (2010d). Optimum design of skeletal structures using imperialist competitive algorithm. Computers and Structures 88:1220-1229.
- Kaveh, A., Talatahari, S. (2012). Charged system search for optimal design of frame structures. Applied Soft Computing 12:382-393.
- Kaveh, A., Khayatazad, M. (2013). Ray optimization for size and shape optimization of truss structures. Computers and Structures 117:82-94.
- Kirkpatrick, S., Gelatt, CD., Vecchi, MP. (1983). Optimization by simulated annealing. Science 220:671-680.
- Lamberti, L. (2008). An efficient simulated annealing algorithm for design optimization truss structures. Computers and Structures 86:1936-53.
- Li LJ., Huang ZB., Liu F., Wu QH. (2007). A heuristic particle swarm optimizer for optimization of pin connected structures. Computers and Structures 85:340-349.
- Peng, B., Reynolds, R.G, Brewster, J. (2003). Cultural Swarms. In Proceedings of the IEEE Congress on Evolutionary Computation, volume 3, pages 1965-1971, 2003.
- Peter J., Richerson R., Boyd. (2004). Not By Genes Alone: How Culture Transformed Human Evolution, University Of Chicago Press.
- Reynolds, R.G. (1991). Version Space Controlled Genetic Algorithms. In Proceedings of the Second Annual Conference on Artificial Intelligence Simulation and Planning in High Autonomy Systems, pages 6-14.
- Reynolds, R.G. (1999). Cultural Algorithms: Theory and Application. In D. Corne, M. Dorigo, and F. Glover, editors, New Ideas in Optimization, pages 367-378. McGraw-Hill.
- Reynolds, R.G., Chung, C. (1997). Knowledge-based Self-Adaptation in Evolutionary Programming using Cultural Algorithms. In Proceedings of the IEEE Congress on Evolutionary Computation, pages 71-76.
- Reynolds, R.G., Saleem, S. (2000). Cultural Algorithms in Dynamic Environments. In Proceedings of the IEEE Congress on Evolutionary Computation, volume 2, pages 1513-1520.
- Shahbazi, M.M., Gholipour, Y., Behnia, A. (2013). An improved version of inverse distance weighting metamodel assisted harmony search algorithm for truss design optimization. 10(2):263-282.
- Sonmez, M. (2011). Artificial bee colony algorithm for optimization of truss optimization. Applied Soft Computing;11:2406-2418.
- Saka, MP. (1990). Optimum design of pin-jointed steel structures with practical applications. Journal of Structural Engineering 116:2599-2620.
- Youlin Lu., Jianzhong Zhou., Hui Qin., Ying Wang., Yongchuan Zhang. (2011). A hybrid multi-objective cultural algorithm for short-term environmental/economic hydrothermal scheduling. Energy Conversion and Management; 52:2121-2134.
Publication Dates
-
Publication in this collection
Sept 2015
History
-
Received
02 Sept 2014 -
Reviewed
28 Oct 2014 -
Accepted
10 Nov 2014































 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail












