Abstract
Composite laminates are made of glass woven roving mats of 610gsm, epoxy resin and nano clay which are subjected to projectile impact. Nano clay dispersion is varied from 1% to 5%. Impact tests are conducted in a gas gun setup with a spherical nose cylindrical projectile of diameter 9.5 mm of mass 7.6 g. The energy absorbed by the laminates when subjected to impact loading is studied, the velocity range is below ballistic limit. The effect of nano clay on energy absorption in vibration, delamination and matrix crack is studied for different weight % of nano clay and for different thickness values of the laminates. The natural frequencies and damping factors are obtained for the laminates during impact and the effect of nano clay is studied. The results show considerable improvement in energy absorption due to the presence of nano clay
Keywords:
Nanocomposite; impact; vibration; energy dissipation
1 INTRODUCTION
Energy absorption due to impact loading has received much attention recently. Application of such materials can be found both in automobile and in military structures. These materials are used increasingly due to their superior strength, light weight and adaptable design. Traditionally, metals have been the most commonly used materials for crashworthy structural applications and impact related problems mainly due to their plastic deformation characteristics that enable them to absorb impact energy in a controlled manner. Unlike metals, polymer composite materials do not typically exhibit plastic deformation, but they are superior to metals for specific energy absorption. (Ganeshbabu et al., 2006Ganeshbabu, M., Velmurugan, R.Gupta, N. K., (2006). Projectile impact on sandwich panels, International Journal of Crashworthiness 11(2): 153-164.) and (2007Ganeshbabu, M., Velmurugan, R., Gupta, N. K., (2007). Heavy mass projectile impact on thin and moderately thick unidirectional fiber/epoxy laminates, Latin American journal of solids and structures 4: 247-256.) studied energy absorption of composite materials subjected to heavy mass projectile. (Lee et al., 2000Lee, D.G., Lim, T.S., Cheon, S.S., (2000). Impact energy absorption characteristics of composite structures, Composite Structures 50: 381-390.) worked on impact energy absorption characteristics of fiber composite materials. (Abrate, 2001Abrate, S. (2001). Modeling of impacts on composite structures, Composite Structures, 51: 129-138.) presented theoretical models for impact studies. The models predict the contact force history and the overall deformation of the plate. Experimental investigation on dynamic behavior was carried out by (Pintado et al., 2001Pintado, P., Pedraza, C., Del, J.M., Castillo, Benitez, F.G. (2001). Experimental investigation of the dynamic response of graphite-epoxy composite laminates under compression, Composite Structures53: 493-497.) for a wide range of impact velocities. (Chandra et al., 1999Chandra. R, Singh, S.P., Gupta, K., (1999). Damping studies in fiber-reinforced composites-a review, Composite Structures 46: 41-51.) reviewed the damping of fiber reinforced composites.
It has been established in recent years that polymer based composites reinforced with small percentage of nano scale fillers can significantly improve mechanical, thermal and barrier properties of pure polymer matrix. (Bourbigot et al., 2003Bourbigot. S, Vanderhart, D.L., Gilman, J.W., Awad, W.H., Davis, R.D., Morgan, A.B., (2003). Investigation of nano dispersion in polystyrene-montmorillonite nanocomposites by solid-state NMR, Journal of Polymer Science Part B: Polymer Physics 41(24): 3188-3213.), (Chen, 2004Chen, B., (2004). Polymer-clay nanocomposites: an overview with emphasis on interaction mechanisms, British Ceramics Transactions 103(6): 241-249.), Gouliang et al.(2008), (Kornmann et al., 2005Kornmann, X., Rees M., Thomann, Y., Necola, A., Barbezat, M., Thomann, R., (2005). Epoxy-layered silicate nano composites as matrix in glass fibre-reinforced composites, Composites Science and Technology 65: 2259-2268.) and (Wu et al., 2002Wu, C.L, Zhang, M.Q., Rong, M.Z., Friedrich, K., (2002). Tensile performance improvement of low nano particles filled-polypropylene composites, Composite Science Technology 62: 1-13.) studied effect of nano particles dispersión in the matrix system to enhance the mechnaical properties of composties. (Wetzela et al., 2003Wetzela, B., Frank, H., Ming, Q.Z., (2003). Epoxy nano composites with high mechanical and tribological performance, Composites Science and Technology 63: 2055-2067.) studied that the addition of nano phase particles in fiber reinforced plastics have also yielded improvement in impact and other mechanical properties of laminates. Moreover these improvements are achieved through conventional processing techniques without any detrimental effect on processing, appearance, density and ageing performance of matrix. Therefore these composites are now considered for different applications in automotive and aerospace industry. When the dimensions of the reinforcement fibers or particles approach the nanometer scale, number of parameters causing the properties of the corresponding composites are different from those of composites reinforced with macro-scale particles. The main factors affecting the properties of nanocomposites include nano filler dispersion, dimensions, weight fraction, the nature of the matrix material, the interfacial characteristics between nano filler and matrix and the manufacturing process. (Mohan et al., 2006Mohan, T.P., Ramesh Kumar, M., Velmurugan, R., (2006). Mechanical and barrier properties of epoxy polymer filled with nanolayered silicate clay particles, Journal of Materials Science 41: 2929-2937.) have observed maximum increase in tensile strength, for 2-3 weight % of nano clay composites when compared to composites without clay. In another study by (Mohan et al., 2006Mohan, T.P., Ramesh Kumar, M., Velmurugan, R., (2006). Thermal, mechanical and vibration characteristics of epoxy-clay nanocomposites, Journal of Materials Science 41(18): 5915-5925.), nano size organo clay (OC) is compared with unmodified clay (UC), for dynamic mechanical analysis (DMA) and thermo gravimetric analysis (TGA). Results show that the addition of OC increases the thermal properties of epoxy/glass fiber more than that of UC filled composites. Chndradass et al. (2007) observed that dispersion of nano clay effectively improves the internal damping of the composites. (Della and Shu, 2007Della, C.N., Shu, D., (2007). Vibration of Delaminated Composite Laminates: A Review, Applied Mechanics Reviews60: 1-20.) reviewed free vibration of composites with delamination. (Avila et al., 2006Avila, A., Duarte H. V., Soares, M. I., (2006). The nano clay influence on impact response of laminated plates Latin American Journal of Solids and Structures 3: 3-20.) studied how nano particles provide better inter phase strength which affects the damping characteristics of composites. In another work, (Avila et al., 2011Avila, A., Neto A. S., H.N. Junior, (2011). Hybrid nanocomposites for mid-range ballistic protection, International Journal of Impact Engineering 38, 669-676.) has proved that the addition of nanoclay and graphene nano sheets to fiberglass/epoxy laminates has not only increased the high velocity impact resistance of these composites, but it also has a major influence on their failure mechanism. Our previous studies, (Velmurugan and Balaganesan, 2013Velmurugan, R., Balaganesan, G., (2013). Energy absorption capability of glass/epoxy nano composite laminates, International Journal of Crashworthiness 18(1): 82-92.) and (2014Velmurugan, R., Balaganesan, G., (2011). Modal analysis of pre and post impacted nano composite laminates, Latin American Journal of Solids and Structures 8: 9-26.), focused on experiments and analytical model on energy absorption of nanocomposites laminates subjected to impact loading above ballistic limits. It is observed that the presence of clay enhances the energy absorbing capacity of the laminates during perforation. There are limited studies on impact energy absorption of nano composites for below ballistic impact loading. When subjected to impact loading which is below ballistic, which may not completely damage the structure, most of the energy is absorbed in vibration in addition to some micro cracks and delamination.
In this work an attempt is made to find the energy absorption of the laminate in vibration mode, delamination and matrix crack, when the structure behaves elastically without much permanent deformations. The effect of nano clay incorporation in the glass/epoxy fiber laminates, with orientation of 0°/90°, is studied for velocities which are below ballistic range. The natural frequencies and damping factors are obtained for the laminates and the effect of nano clay is studied. The effect of nano clay on energy dissipation in vibration, delamination and matrix crack is also studied for laminates of different thickness values and for different impact velocities.
2 EXPERIMENTS
2.1 Preparation of Nanocomposites
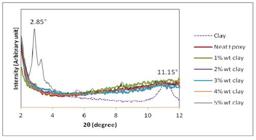
Dispersion of nano inclusions in the matrix is a very important factor in the mechanical behavior of nanocomposites. In this work, the nanocomposite laminates were manufactured in two steps. Clay was dispersed in the resin using shear mixer at 750 RPM for 2hrs and kept in the vacuum oven to remove the air bubbles at room temperature, for better dispersion. Hardener, Tri Ethylene Tetra Amine (TETA) of 10% was mixed with the epoxy-clay mixture, by weight. Fig. 1 shows typical results obtained from XRD tests for nano clay, epoxy and epoxy with 1-5 wt. % of clay.
XRD pattern of clay, epoxy with and without clay, (Velmurugan and Balaganesan, 2011Velmurugan, R., Balaganesan, G., (2011). Modal analysis of pre and post impacted nano composite laminates, Latin American Journal of Solids and Structures 8: 9-26.).
The results obtained are analyzed using Bragg's law to calculate the d-spacing. The reflection peak is the indication for presence of clay in outer gallery of polymer chain. As these clays are dispersed into the resin, the reflection peak typically shifts to a lower angle and reduces intensity. The lower the angle and the intensity peak, the greater is the d-spacing and hence the greater inter gallery spacing of the clay. The improvements in thermal, mechanical and shrinkage properties are dependent on the amount of intercalation and exfoliation structure reached. The increase in gallery spacing is a direct indication of an increase in intercalation or exfoliation structure. In Figure 1, single peak at 11.15° for nano clay and corresponding interlayer distance calculated from Bragg's law is 11.8 Å. It is observed that the basal reflection peak is absent for neat epoxy and epoxy with clay up to 4%. This reveals that the interlayer distance is more than 75 Å which means that Bragg's diffraction condition is not satisfied or exfoliated nano composite structure has formed (Carrado, 2000Carrado, K.A (2000) Synthetic organo- and polymer-clays: preparation, characterization and Materials applications. Applied Clay Sciences 17: 1-23.). Sharp reflection peak is noticed for epoxy with 5% clay at 2.85° and corresponding interlayer distance is 46 Å which indicates that intercalated structure has been formed. The formation of intercalated structure for 5% clay content is due to non-homogenious mixing of clay and uneven curing in the intergallery and extra gallery matrix regions of the nanocomposites.
The laminates of 300 mm square were prepared by hand layup technique and then processed in compression molding machine. The laminates were prepared for the thickness of 2 mm, 3 mm and 5mm respectively and these values were obtained by having 3, 5 and 8 number of layers in the laminates, respectively.
2.2 Impact Test
Experiments were performed using the gas gun test setup, which is shown in Figure 2. Plates of required size were clamped at the edges and were subjected to impact loading by cylindrical projectile. Incident velocity was measured by laser diode. Air pressure in the chamber was varied to get different velocities. Chamber air pressure was maintained by using pressure regulator for getting consistent velocity. Shock accelerometer of capacity 100k g PCB make, model No. 350B21, was used to measure the response through the Data Acquisition (DAQ) Card [NI-PXI 4472] and the response was recorded on the computer. The accelerometer was fixed at a distance of  length of diagonal, from one of its corner. The cylindrical projectile with spherical nose of diameter 9.5 mm of mass 7.6 g was impacted at the centre of the laminates.
length of diagonal, from one of its corner. The cylindrical projectile with spherical nose of diameter 9.5 mm of mass 7.6 g was impacted at the centre of the laminates.
Gas gun setup used for Impact loading, (Velmurugan and Balaganesan, 2011Velmurugan, R., Balaganesan, G., (2011). Modal analysis of pre and post impacted nano composite laminates, Latin American Journal of Solids and Structures 8: 9-26.).
2.3 Impact Response
The vibration waveform is composed of a combination of frequency components of different magnitudes. In order to extract data that can be analyzed, the time-dependent vibration signal has to be subjected to a spectral analysis, which processes it and separates it into frequency components. The data for these tests is analyzed by performing a Fast Fourier Transform (FFT) on the recorded accelerometer signal. FFT is a discrete digital signal processing technique for converting a time-dependent signal into a frequency spectrum. The spectrum graphs are two-dimensional plots of the spectrum with frequency (Hz) on the horizontal axis and the amplitude of each discrete frequency component on the vertical axis. The amplitude is a peak hold, displaying the maximum amplitude for that particular frequency in the processed time frame.
Figure 3 shows the amplitude response and corresponding frequency response plots for 2 mm thickness laminate with 3% clay when subjected to 35 m/s. The peak mode frequency is 655 Hz for which the amplitude ratio is 1. The maximum energy is dissipated in this frequency. From our previous study on modal analysis, (Velmurugan and Balaganesan, 2011Velmurugan, R., Balaganesan, G., (2011). Modal analysis of pre and post impacted nano composite laminates, Latin American Journal of Solids and Structures 8: 9-26.), it is observed that this range of frequency is its fifth mode of vibration. Also it is observed that 2 mm thickness laminates vibrate in various modes up to 2000 Hz and dissipate the energy received from the projectile.
Time response and FFT spectrum for 2 mm thickness laminate with 3% clay subjected to 35 m/s.
The damping factor for each mode of the laminate is obtained by using the half power band width method, (see Figure 2).
The following expression is used to find the damping factor ξ.
Where f2 and f1 are the frequencies and fn is the resonance frequency.
3 ENERGY DISSIPATION
The energy dissipated by the laminates subjected to impact loading, for velocities, below ballistic limit, is in the form of vibration, failure of matrix in the delaminated area and delamination. During impact a localized deformation around the impact region and global deflection away from the point of impact resulting in-plane compression in the front face and tension in the rear face of the laminate, are produced. The deflection of the laminate in the loading direction causes strain in the fibers and matrix. As the velocity of impact is well within ballistic velocity, the strain in the fibers is below the failure strain and within the elastic region. This causes the rebound of the projectile and vibration of the laminate. The stress waves propagate in radial direction. When these stress values exceed the inter laminar shear stress, there is possibility for failure in the matrix and in the lamina interfaces. The first possible failure that occurs in a target is matrix cracking. Matrix cracking leads to decrease in inter laminar strength of the composite, as a result further loading causes delamination. The energy dissipated in vibration, delamination and in matrix crack, is discussed in the following sections.
3.1 Energy Dissipation in Vibration
The energy absorbed by the laminates during vibration is calculated based on its total potential energy when subjected to impact loading.
The total potential energy at the initial of vibration is given by the expression,
Where, k is stiffness of laminates obtained from static penetration test and x is peak amplitude of vibration or deflection at the centre of the laminate which is also the point of impact. The deflection at the centre is obtained from the correlation between the deflection at the location of accelerometer and impact point and the expressions are given in Eqns. (3) to (5).
For 2 mm thickness laminates,
In equation (3), xc2 is the deflection at the centre and xa2 is deflection at the location of accelerometer. Similarly the expressions for 3 mm and 5 mm thickness laminates are given in Eqns. (4) and (5), respectively.
For 3 mm thickness laminates,
For 5 mm thickness laminates,
The maximum deflection at the location of the accelerometer is calculated from the following expression,
In the above equation, Acc is the magnitude of maximum acceleration and w is angular velocity. Both are obtained from the accelerometer signal and the maximum deflection (xa) is obtained from the above equation.
The total energy of the projectile is given by
Where m is mass of the projectile and v is velocity of the projectile.
3.2 Energy Absorbed in Delamination
The area of delamination in the lamínate (Adelam) is measured from the impacted laminates. The energy due to delamination is given by,
Where GIIc is critical strain energy release rate in mode II. The strain energy release rate (GIIc) is calculated from the three point bending test of End Notched Flexural (ENF) specimen (Morrais, 2004Morrais, A.B. de. (2004) Analysis of Mode II inter laminar fracture of multidirectional laminates, Composites Part A 35: 51-57.). The following equation is used to calculate the GIIc values for nanocomposite specimens from the load-deflection results obtained from three point bending test.
Where a is notch length, p is load, c is deflection, b is width of the specimen and L is the half the length between supports.
3.3 Energy Absorbed in Matrix Crack
The area undergoing matrix crack is same as delamination area and hence energy due to matrix crack is given by,
Where,Emt is energy absorbed by matrix cracking per unit volume calculated from load-displacement curves of tensile test results of neat epoxy and clay dispersed epoxy specimens, h is thickness of the laminate and Vm is the volume fraction of the matrix.
4. RESULTS AND DISCUSSION
4.1 Impact response - Natural frequency
Tests were conducted for the velocities ranging between 35 m/s and 82 m/s. The results for laminates of 2 mm, 3 mm and 5mm thickness are discussed. From FFT spectrum, it is understood that the projectile impact induces the laminate to vibrate in different modal frequencies. The natural frequency of the 2 mm thickness laminates is shown in Table 1 for velocities from 35 m/s to 82m/s. The frequency values are given for mode V to mode VIII. It is observed that as the velocity of impact increases the frequency values decrease for all the modes when compared to pre impacted laminate frequency values. The laminate without clay when subjected 82 m/s the decrease in mode V natural frequency is 20% when compared to pre impacted laminate. For the same impact velocity, the decrease in mode V natural frequency of the laminate with 3% clay is 10% when compared that of pre impacted laminate. The laminate with 5% clay has also show 10% less than that of pre impacted laminate. This is due to decrease in damage in the laminates with clay. The same trend is observed in all other modes of 2 mm thickness laminates.
Table 2 shows the frequencies for 3 mm thickness laminates with and without clay when subjected to impact loading. These values are compared with frequency values for the modes IV to VII obtained from impulse hammer technique. The laminates with clay show considerable increase in frequency values up to 3% clay and then marginal increase up to 5% clay. But these values are higher than the values of laminates without clay. The possible reason for measured increase in 5% clay, could be due to the agglomeration of clay particles at higher % level. In mode IV, the frequency of the laminate without clay, when subjected to impact of 35 m/s, is 767 Hz and it is 13.6% less compared to impulse hammer method. For the impact velocities of 50m/s, 65 m/s and 82 m/s, the decrease in frequency values are 17.4%, 20.7% and 22.1% respectively. It is seen that as the impact velocity increases there is decrease in frequency values. This is due to damage of laminates in impact loading. For laminates with 1%, 3% and 5% clay at 35 m/s, the decrease in frequency values in mode IV are 4.4%, 4.2% and 3.4% respectively when compared to pre impact frequency values. At 82 m/s, the laminates with 1%, 3% and 5% clay, the decrease in frequency values in mode IV are 15.6%, 13.8% and 12.8% respectively when compared to pre impact frequency values. The decrease in frequency values are less in nano clay dispersed laminates when compared to laminates without clay. Also the decrease in percentage is less up to 5% clay, this is due to reduction in damage area of the laminates.
Table 3 shows the frequencies for the mode I to IV for 5 mm thickness laminates with and without clay. The mode I frequency of the laminates with 1% and 3% clay and without for 35 m/s, 50m/s and 65 m/s velocity of impact is marginally less than that in pre impact frequency values. But in laminate with 5% clay, the frequency values at 35 m/s and 50 m/s are same as in pre impact values. This is due to negligible damage in the laminates. In mode IV for the laminate without clay, the frequency values at 35 m/s, 50 m/s, 65 m/s and 82 m/s are 7.5%, 7.9%, 8.8% and 12.9% less than the frequency values obtained from impulse hammer technique. The corresponding decrease in percentage values for the laminates with 1% clay are 5.9%, 6.4%, 7.7% and 8.1% respectively. For the laminate with 5% clay, the values are less by 3.2%, 3.3%, 4.1% and 4.4% respectively. The laminate with 5% clay shows less percentage of decrease in frequency values when compared to pre impact values. This is due to dispersion of clay in the 5 mm thickness laminates that controls the damage due to delamination. In general it is understood that the addition of clay in the matrix increases the natural frequency of vibration due to increase in modulus of nanocomposites. In our previous study, (Velmurugan and Balaganesan, 2011Velmurugan, R., Balaganesan, G., (2011). Modal analysis of pre and post impacted nano composite laminates, Latin American Journal of Solids and Structures 8: 9-26.), increase in tensile modulus was observed in nanocomposite specimens when compared to specimens without clay.
4.2 Damping Factor
The damping factors of the impacted specimens are obtained by half power band width technique from FRF plots. The damping factor is obtained for the frequency mode at which maximum energy is dissipated. Figures 3 to 5 correspond to impact damping factor values for laminates of 2 mm, 3 mm and 5 mm thickness values with and without clay, respectively. From these figures, it is clear that as the clay content is increased, there is increase in damping factor which is due to the presence of the additional medium (clay) in the laminate. It is also seen in laminates without clay that as the input velocity increases damping factor increases. This is due to the fact that as the velocity increases the delamination area increases. Laminates of 2mm thickness dissipates maximum energy for the frequency in the range of 600 Hz to 700 Hz for the velocities from 35 m/s to 82 m/s depending upon clay content. From FFT, it is observed that this range of frequency corresponds to its fifth mode of vibration and the damping factor is obtained for this mode. When laminates of 3 mm thickness are subjected to the same range of impact velocities, the peak amplitude is observed in its fourth mode of vibration. This is in the range of 900 Hz to 1000 Hz and the maximum energy is dissipated in this mode. When 5 mm thickness laminates are subjected to impact, the peak amplitude occurs in its third mode of vibration for 35 m/s velocity. For velocities 50 m/s, 65m/s and 82 m/s the peak amplitude occurs in its fourth mode of vibration. Hence it is clear that as the input energy is high the peak amplitude of vibration occurs at higher modes of vibration.
The damping factor values are between 0.02 to 0.08 for all laminates with and without clay and for different modes of vibration. Since most of the energy is dissipated in the peak amplitude, this value is considered for reference and this value is 1 in FFT, the damping factor corresponding to this mode is considered and compared. Figure 4 shows damping factor for the 2 mmthickness laminates subjected to impact loading. At impact velocity 35 m/s the damping factor for laminate without clay is 0.02 and for the laminate with 5% clay the damping factor is 0.07. The damping factor is increased by a factor of 3. When the laminates without clay are subjected to velocities 50 m/s, 65 m/s and 82 m/s the corresponding damping factor values are 0.03, 0.05. and 0.05 respectively. When the lamintes with 5% clay are subjected to the same velocities the improvement in damping factor is about two times. The increase in damping factor is observed in the laminates with clay up to 5%. Rate of increase in damping factor is high in laminates withclay up to 2% dispersion.
Figures 5 and 6 correspond to peak amplitude mode damping factor values for 3 mm and 5 mm thickness laminates, respectively. It is seen that there is improvement in damping factor for laminates when clay is added. When the 3 mm thickness laminate without clay is subjected to 35 m/s, the damping factor is 0.03 and for the laminate with 4% clay the damping factor is 0.04, the improvement in damping factor is 56%. When the laminates without clay are subjected to 50 m/s, 65 m/s and 82 m/s the damping factor values are 0.03, 0.03 and 0.04 respectively. The lamintes with 3% clay are subjected to the same velocities the improvement in the damping factor values are 28%, 26% and 13.5% respectively. The decrease in percentage increase of damping factor at higher velocity of impact is due to higher damage area in laminates without clay. The increase in delamination area makes an increase in damping factor. When 5 mm thickness laminate is subjected to 35 m/s the damping factor for laminate with 3% clay shows an improvement of 75% when compared to laminate without clay. The improvent of damping factor is between 67% to 100% when these laminates with 3% clay are subjected to the velocitiesranging from 35 m/s to 82 m/s.
Among the 2 mm, 3 mm and 5 mm thickness laminates, 2 mm thickness laminates show high improvement in damping factor due to the presence of clay. There is an improvement in damping factor in laminates of thickness values 3 mm and 5 mm as the impact velocity increases. Energy dissipation occurs when interfacial slip of nano scale fillers is activated in host matrix material, which leads to improvement in damping factor. For rigid nano-particles, the high stress area around the particles will lead to initial microcracks and inelastic deformation in the matrix. The interfacial shear strength between nano-filler and matrix is higher than that in conventional composites which is due to the formation of cross-links or shield of the nano-fillers and form thicker interphases. The nano scale filler in the matrix acts as secondary fiber which enhances the energy absorption of the laminates when subjected to impact loading.
4.3 Energy Dissipated in Vibration, Delamination and Matrix Crack
Stiffness of the laminates is calculated from the slope of load displacement plot obtained in static deflection test. The values of stiffness for the laminates of 2 mm, 3 mm and 5 mm thicknesses are given in Table 4. It is observed that there is increase in stiffness values for laminates with clay up to 3%. The improvement for 2 mm thickness laminate with 3% clay is 16.5% when compared to laminate without clay. Corresponding improvements for 3 mm and 5 mm thickness laminates with 3% clay are 20% and 15% respectively. The laminates with 4% and 5% clay show higher stiffness values with respect to laminates without clay, but less than that of the laminates with 3% clay. The strain energy release rate is calculated from Eq. (9). It is observed that the specimens with clay show higher strain energy release rate than the specimen without clay. The values for strain energy release rate and matrix crack energy of epoxy specimens with and without clay are also given in Table 4. The increase in GIIC values is observed for clay up to 5%. The improvement for the specimen with 3% clay and 5% is 25% and 26% respectively when compared to specimen without clay. The matrix crack energy is calculated from the stress-strain curve of specimens made epoxy with and without clay. This energy is used to predict matrix crack energy of laminate during impact loading. The specimen with 3% clay shows highest value compared to other specimens.
Static deflection test stiffness (k), Strain Energy release rate (GIIC) and Matrix crack Energy, Emt of the laminates with and without clay.
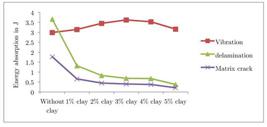
The vibration energy is calculated based on initial deflection and stiffness values of the laminates as given in Eqn. (2).The initial energy varies from 4.65 J to 25.55 J where the impact velocity is varied from of 35 m/s to 82 m/s. The impact tests are performed for velocities, which are below the ballistic limit of the laminates. The rebound of the projectile is observed in all tests and the part of projectile energy is utilised for this. The laminates of 2mm, 3mm and 5 mm are considered for this study. The vibration energy of laminate without clay when subjected to 9.5 J energy of impact is 2.99 J and for the same energy input, the value for the laminate with 3% clay, is 3.62 which is 21% higher than the laminate without clay. The energy absorption in vibration is decreasing when the clay value is above 3% in the matrix. But still the values are higher than the laminates without clay. Figure 7 shows the delamination and matrix crack energies absorbed by the 2 mm thickness laminates with and without clay. When the laminates without clay are subjected impact loading the energy absorption in delamination is higher than the energy absorption in vibration. This value is higher than that in laminates with clay. But in nanocomposites, delamination and matrix crack energies are decreasing up to 5% clay. This is because the dispersion of clay controls delamination area in impact. For the velocity of 50 m/s, the input projectile energy is 9.5 J, and the total energy absorption of glass/epoxy laminate is 8.42 J, in which the vibration energy is 2.99 J, delamination energy is 3.66 J and matrix crack energy is 1.77 J, For the same velocity, nanocomposite laminate with 3% clay absorbs 4.72 J, in which the energy dissipation in vibration, delamination and matrix crack are 3.62 J, 0.69 J and 0.41 J, respectively. Energy dissipation in vibration is higher in nanocomposites which is due to the increase in surface area between matrix and nano filler interface. Also the presence of clay controls the damage of the laminates in impact loading.
Showing the energy absorbed by the 2mm thickness lamínate when subjected to impact velocity 50 m/s.
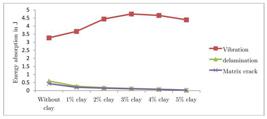
As the velocity of impact increases to 82 m/s, the projectile energy is 25.55 J and the energy absorption in laminate without clay due to vibration is 6.46 J. The increase in energy absorption in vibration is observed in all the cases. The laminate with 3% clay absorbs 9.61 J of energy in vibration which is 50% higher than the laminate without clay. This can be seen in Figure 8. The delamination and matrix crack energies are less than the energy absorbed in vibration for the laminates with and without clay. The energy absorbed by delamination and matrix crack for the nanocomposites is less than that of laminate without clay. The delamination energy of laminate with 3% clay is less by 50% of the laminate without clay. The matrix crack energy for laminate with 3% is about 50% less than that in laminate without clay.
Showing the energy absorbed by the 2 mm thickness laminate when subjected to impact velocity 82 m/s.
Figures 9 and 10 show the energy absorbed by the 3 mm thickness laminates by vibration, delamination and matrix crack for the input projectile energy of 9.5 J and 25.5 J respectively. The vibration energy increases as the % of clay dispersion increases up to 3% and decreases on further increase of clay. This is similar to 2 mm thickness laminates. The maximum energy dissipation in vibration is about 50% higher than the laminate without clay.
Showing the energy absorbed by the 3mm thickness laminate when subjected to impact velocity 50 m/s.
Showing the energy absorbed by the 3mm thickness laminate when subjected to impact velocity 82 m/s.
As the input energy of the laminate increases the energy absorbing capacity of the laminate in vibration also increases. Due to increase in thickness of the laminates, the damage area in delamination is less and, hence the energy absorbed in delamination and matrix crack is less when compared to 2 mm thickness laminates. Figure 10 shows the energy absorbed by the 3 mm thickness laminates for the input projectile energy of 25.5 J. The energy absorbed in delamination and matrix crack is 1 J for the laminates without clay for input energy of 9.5 J and it is about 2 J for input energy of 25.55 J. But in the laminates with clay, the energy due to damage is less by 50% compared to laminate without clay. In nanocomposite laminates, the delamination and matrix crack energies are reduced, further the damage area for 4% and 5% clay dispersion is less. Figure 11 shows the damage area of the laminate when subjected to 50 m/s. It is clear that for the input energy of 9.5 J, there is no damage in the laminate with 5% clay and hence most of the energy is absorbed in vibration mode.
Showing the area of impact of 2mm thickness glass/epoxy laminate with 5% clay when subjected to 50m/s.
Figure 12 shows the energy absorption of the 5 mm thickness laminates when subjected to impact energy of 9.5 J. The energy absorbed in vibration is similar to 2 mm and 3 mm thickness laminates. The matrix crack energy is about 20% higher than the delamination energy in all the cases. The same trend is observed for input energy is 25.55 J which is shown in Figure 13.
Showing the energy absorbed by the 5 mm thickness lamínate when subjected to impact velocity 50 m/s.
Showing the energy absorbed by the 5 mm thickness lamínate when subjected to impact velocity 82 m/s.
As the input energy of the laminate increases the energy absorbing capacity in vibration also increases. The laminates without clay absorb more energy in delamination than the composites with clay showing the same trend as other laminates. Among 2 mm, 3 mm and 5 mm thickness laminates, 2 mm thickness laminates dissipate more energy at lower velocity of impact, 3 mm and 5 mm thickness laminates dissipate more energy at higher velocity. This is due to increase in stiffness of thicker laminates. Thin laminates absorb energy in other failure modes at higher velocity of impact. The delamination and matrix crack energy of 2 mm thickness laminates are higher than 3 mm and 5 mm laminates. The reason is increase in failure area of laminates due to stretching of the layers. Laminates of 5 mm thickness absorbs more energy in delamination and matrix crack than 3 mm thickness laminates. This is because of more damage area which is due to increase in distance between the mid plane and outer layer.
Figure 14 (a) and (b) show the delamination area of laminates of 5 mm thickness, with and without clay respectively. In the laminate without clay the delamination area is 1256 sq. mm and the corresponding value of laminate with 2 % clay is 491 sq. mm. This shows that the presence of clay decreases the area to almost 1/3rd of the delamination area in laminates without clay. Hence it is understood that addition of clay very much controls the delamination area. This is one of the reasons for the increase in vibration energy of the laminates with clay.
(a) Showing the delamination area of 5 mm thickness glass/epoxy lamínate without clay when subjected to 82m/s, (b) Showing the delamination area of 5mm thickness glass/epoxy laminate with 2% clay when subjected to 82m/s.
5. CONCLUSIONS
Laminates of 2 mm, 3 mm and 5 mm thickness were prepared by hand lay-up and compression molding process, and subjected to projectile impact for velocities between 35m/s and 82 m/s in clamped-clamped condition. The frequencies of vibration, damping factor and energy absorbed by the laminates are obtained. The following conclusions are made.
-
•
The increase in frequency of vibration is observed in laminates with clay than laminates without clay.
-
•
Addition of clay improves damping factor in all the laminates irrespective of the velocity of impact.
-
•
Presence of nano clay also improves the energy absorption capacity of laminates in vibration.
-
•
As the velocity increases the energy absorption in vibration mode increases.
-
•
Addition of clay controls the energy absorption of laminates in delamination and matrix crack.
Acknowledgements
The authors gratefully acknowledge the support received from Department of Science and Technology, India through Indo - South African collaboration Research project.
References
- Abrate, S. (2001). Modeling of impacts on composite structures, Composite Structures, 51: 129-138.
- Avila, A., Neto A. S., H.N. Junior, (2011). Hybrid nanocomposites for mid-range ballistic protection, International Journal of Impact Engineering 38, 669-676.
- Avila, A., Duarte H. V., Soares, M. I., (2006). The nano clay influence on impact response of laminated plates Latin American Journal of Solids and Structures 3: 3-20.
- Balaganesan, G., Velmurugan, R., Srinivasan, M., Gupta, N. K., Kanny, K. (2014). Energy absorption and ballistic limit of nanocomposite laminates subjected to impact loading, International Journal of Impact Engineering 74: 57-66.
- Bourbigot. S, Vanderhart, D.L., Gilman, J.W., Awad, W.H., Davis, R.D., Morgan, A.B., (2003). Investigation of nano dispersion in polystyrene-montmorillonite nanocomposites by solid-state NMR, Journal of Polymer Science Part B: Polymer Physics 41(24): 3188-3213.
- Carrado, K.A (2000) Synthetic organo- and polymer-clays: preparation, characterization and Materials applications. Applied Clay Sciences 17: 1-23.
- Chandra. R, Singh, S.P., Gupta, K., (1999). Damping studies in fiber-reinforced composites-a review, Composite Structures 46: 41-51.
- Chandradass. J, Rameshkumar, M., Velmurugan, R., (2007). Effect of Nano clay addition on vibration properties of glass fiber reinforced vinyl ester composites, Materials letter 61: 4385-4388.
- Chen, B., (2004). Polymer-clay nanocomposites: an overview with emphasis on interaction mechanisms, British Ceramics Transactions 103(6): 241-249.
- Della, C.N., Shu, D., (2007). Vibration of Delaminated Composite Laminates: A Review, Applied Mechanics Reviews60: 1-20.
- Ganeshbabu, M., Velmurugan, R.Gupta, N. K., (2006). Projectile impact on sandwich panels, International Journal of Crashworthiness 11(2): 153-164.
- Ganeshbabu, M., Velmurugan, R., Gupta, N. K., (2007). Heavy mass projectile impact on thin and moderately thick unidirectional fiber/epoxy laminates, Latin American journal of solids and structures 4: 247-256.
- Guoliang, P., Guo, Q., Tian, A., Zhiqiang, H., (2008). Mechanical behaviors of Al2O3 nano particles reinforced poly ether ether ketone, Materials Science and Engineering A, 492: 383-391.
- Kornmann, X., Rees M., Thomann, Y., Necola, A., Barbezat, M., Thomann, R., (2005). Epoxy-layered silicate nano composites as matrix in glass fibre-reinforced composites, Composites Science and Technology 65: 2259-2268.
- Lee, D.G., Lim, T.S., Cheon, S.S., (2000). Impact energy absorption characteristics of composite structures, Composite Structures 50: 381-390.
- Mohan, T.P., Ramesh Kumar, M., Velmurugan, R., (2006). Thermal, mechanical and vibration characteristics of epoxy-clay nanocomposites, Journal of Materials Science 41(18): 5915-5925.
- Mohan, T.P., Ramesh Kumar, M., Velmurugan, R., (2006). Mechanical and barrier properties of epoxy polymer filled with nanolayered silicate clay particles, Journal of Materials Science 41: 2929-2937.
- Morrais, A.B. de. (2004) Analysis of Mode II inter laminar fracture of multidirectional laminates, Composites Part A 35: 51-57.
- Pintado, P., Pedraza, C., Del, J.M., Castillo, Benitez, F.G. (2001). Experimental investigation of the dynamic response of graphite-epoxy composite laminates under compression, Composite Structures53: 493-497.
- Velmurugan, R., Balaganesan, G., (2013). Energy absorption capability of glass/epoxy nano composite laminates, International Journal of Crashworthiness 18(1): 82-92.
- Velmurugan, R., Balaganesan, G., (2011). Modal analysis of pre and post impacted nano composite laminates, Latin American Journal of Solids and Structures 8: 9-26.
- Wetzela, B., Frank, H., Ming, Q.Z., (2003). Epoxy nano composites with high mechanical and tribological performance, Composites Science and Technology 63: 2055-2067.
- Wu, C.L, Zhang, M.Q., Rong, M.Z., Friedrich, K., (2002). Tensile performance improvement of low nano particles filled-polypropylene composites, Composite Science Technology 62: 1-13.
Publication Dates
-
Publication in this collection
Dec 2015
History
-
Received
18 Nov 2014 -
Reviewed
24 Feb 2015 -
Accepted
05 May 2015























 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail
 Thumbnail
Thumbnail













