Abstract
This work discusses the experimental results of Acoustic Emission (AE) recordings during repetitive loading/unloading loops of cement mortar beams subjected to three point bending. Six repetitive loading cycles were conducted at a gradually higher load level until the failure of the specimens. The experimental results clearly show the existence and dominance of the Kaiser effect during each loading loop. Regarding the AE data, alternative analysis was conducted using the improved b-value, and the cumulative energy behaviour. Both quantities considered, show qualitative and quantitative characteristics that could be used as pre-failure indicators. In addition, a novel statistical physics analysis involving the AE interevent times was conducted by calculating the cumulative probability function P(>δτ) that follows a q-exponential equation. The entropic index q and the relaxation parameter βq of this equation show systematic changes during the various stages of the failure process. The last cycle led to a q value equal to 1.42, implying the upcoming fracture which is in good agreement with previous results obtained from a wide range of fractured materials.
Keywords:
Acoustic Emissions; Three Point Bending; white cement mortar; Tsallis entropy
1 INTRODUCTION AND GROUND THEORY
One of the basic principles of the restoration of an ancient monument is to respect and (if possible) repeat the ancient method of construction. Unfortunately this is not always possible. A typical example is the case of the classic monuments of the Athenian Acropolis: During the restoration project in progress it has been decided to substitute the molten lead (used by ancient Greeks for filling the grooves in which the iron connectors of structural members were placed) by a suitable cementitious material (mortar). The specific decision was made after exhaustive scientific study of the three-material complex (marble - metallic connector - filling material), on which the construction of these monuments is based. The main arguments for reaching this decision refer to the physico-chemical compatibility (Skoulikidis, 2000Skoulikidis Th. (2000). Corrosion and conservation of building materials of monuments: the Acropolis case, University of Crete Publications, Heraklion, Crete.).
In addition, the mortar used must be compatible with the authentic building material (Pentelic marble) also from a mechanical point of view. The specific aspect is long ago under consideration however a definite decision is not as yet made especially with regards to the damage mechanisms activated in the types of mortar used.
In this context an attempt is here described to gain a better overview of these mechanisms taking into account that both the structural behaviour of white cement mortar and the damage evolution within its volume, under mechanical loading, are of great interest not only for restoration projects but also for the wider range of its applications. Indeed cement is nowadays one of the main construction materials and therefore thorough knowledge of its damage state is sine-qua-non for the evaluation of its remaining life or equivalently of its remaining load-carrying capacity.
This topic seriously concerns the structural-engineering community and as a result the diagnostic methods for the assessment of damage are continuously developed aiming at the estimation of the impending failure. Among the techniques widely used in this direction is the Acoustic Emissions (AE) detection technique. In spite of its wide application the technique is still under further development especially concerning its application for the study of structural health monitoring of cement based materials.
The AE technique is proven one of the most valuable tools for monitoring and understanding the underlying mechanisms of dynamic fracture processes. In addition it is considered as a powerful tool that can give signals related to upcoming failures (Rao and Lakschmi, 2005Rao M.V.M.S., Lakschmi P.K.J. (2005). Analysis of b-value and improved b-value of acoustic emissions accompanying rock fracture, Current Science, 89, pp. 1577-1582.). AE events occur when sequential series of short impulse energy mechanical waves are released due to the activation of internal damage and (micro-) fracture mechanisms caused by externally applied mechanical loads. The released elastic wave travels as a spherical wave within the bulk of the material. The detection of AE events is used for damage localization and damage level assessment in brittle materials such as concrete and rocks (Lockner, 1993Lockner D. (1993). The role of acoustic emission in the study of rock fracture, Int. J. Rock Mech. Min. Sci. Geomech. Abstr., 30, pp. 883-899.; Stanchits et al., 2006Stanchits S., Dresen G., Vinciguerra S. (2006). Ultrasonic velocities, acoustic emission characteristics and crack damage of basalt and granite, Pure Applied Geophys. 163(5-6), pp. 975-994.; Aggelis et al., 2013Aggelis D.G., Mpalaskas A.C., Matikas T.E. (2013). Investigation of different fracture modes in cement-based materials by acoustic emission, Cement and Concrete Research, 48, pp. 1-8.; Stergiopoulos et al., 2013Stergiopoulos C., Stavrakas I., Hloupis G., Triantis D., Vallianatos F. (2013). Electrical and acoustic emissions in cement mortar beams subjected to mechanical loading up to fracture, Engineering Failure Analysis, 35, pp. 454-461.). The AE events, due to crack growth in brittle materials, are usually observed in the high frequency range, typically between 50 kHz and 800 kHz. Their main characteristic and advantage is that they are observed even from the early stages of the damage process. During fracture process in quasi-brittle materials, the micro-cracks formation and growth are manifested by releasing a number of AE events with different amplitudes. The increasing rate in the AE activity, observed as the specimen approaches failure, is strongly correlated with the decay of the mechanical properties of the material (Anzani et al., 2008Anzani A., Binda L., Carpinteri A., Lacidogna G., Manuello A. (2008). Evaluation of the repair on multiple leaf stone masonry by acoustic emission, Materials and Structures, 41(6), pp. 1169-1189.). Specifically, for cement based structures the AE technique is one of the sophisticated methods useful for monitoring crack growth (Rao and Lakschmi, 2005Rao M.V.M.S., Lakschmi P.K.J. (2005). Analysis of b-value and improved b-value of acoustic emissions accompanying rock fracture, Current Science, 89, pp. 1577-1582.).
In the present paper the AE recordings are elaborated through the interevent time analysis, conducted in terms of the normalised cumulative probability function, which obeys a q-exponential equation (Vallianatos et al., 2012aVallianatos F., Triantis D. (2012). Is pressure stimulated current relaxation in amphibolite a case of non-extensivity?, EPL, 99 (1), 18006.). The parameters of this function show systematical changes during the different stages of the failure process. The study is conducted using Non-Extensive Statistical Physics tools. Since disorder and long-range interactions are two of the key components of acoustic emissions originated by microfractures (Vallianatos et al., 2012aVallianatos F., Benson P., Meredith P., Sammonds P. (2012a). Experimental evidence of a non-extensive statistical physics behavior of fracture in triaxially deformed Etna basalt using acoustic emissions, EPL, 97:58002.), a generalization of Boltzmann-Gibbs (BG) statistical physics introduced by Tsallis (Tsallis, 2001Tsallis C. (2001). In Non-extensive statistical mechanics and its applications, Abe S., Okamoto Y. (Eds.), Berlin, Springer, pp. 1-35.; Tsallis, 2009Tsallis C. (2009). Introduction to nonextensive statistical mechanics approaching a complex world, Berlin, Springer.) (referred as non-extensive statistical physics - NESP) is used here to explore the AE organization after the application of mechanical load. The advantage of considering the Tsallis distribution is that, based on the principle of entropy, it can be related to statistical mechanics and reduces to the traditional BG statistical physics as a special case. Fracture related phenomena, as AEs are, exhibit fractality, long range interaction and memory effects (Varotsos et al., 2011Varotsos P., Sarlis N., Skordas E. (2011). Natural time analysis the new view of time, Berlin, Springer.; Vallianatos et al., 2011aVallianatos F., Triantis D., Sammonds P. (2011a). Non-extensivity of the isothermal depolarization relaxation currents in uniaxial compressed rocks, EPL, 94:68008.; Vallianatos et al., 2012aVallianatos F., Benson P., Meredith P., Sammonds P. (2012a). Experimental evidence of a non-extensive statistical physics behavior of fracture in triaxially deformed Etna basalt using acoustic emissions, EPL, 97:58002.). It is exactly phenomena of such nature that constitute the scope of non-extensive statistical mechanics (Tsallis, 2001Tsallis C. (2001). In Non-extensive statistical mechanics and its applications, Abe S., Okamoto Y. (Eds.), Berlin, Springer, pp. 1-35.). Recent applications of NESP to fracture mechanics (Vallianatos et al., 2011aVallianatos F., Triantis D., Sammonds P. (2011a). Non-extensivity of the isothermal depolarization relaxation currents in uniaxial compressed rocks, EPL, 94:68008.) and solid earth physics (in regional or planetary scale) were summarized by (Tsallis, 2009Tsallis C. (2009). Introduction to nonextensive statistical mechanics approaching a complex world, Berlin, Springer.). They are mainly focused in seismology (Abe and Suzuki, 2003Abe S., Suzuki N. (2003). Law for the distance between successive earthquakes, J Geophys Res, 108(B2), pp. 2113-2121.; Abe and Suzuki, 2005Abe S., Suzuki N. (2005). Scale-free statistics of time intervals between successive earthquakes, Physica A, 350, pp. 588-596.; Telesca, 2010aTelesca L. (2010a). Analysis of Italian seismicity by using a nonextensive approach, Tectonophysics, 494, pp. 155-162.; Telesca, 2010bTelesca L. (2010b). A non-extensive approach in investigating the seismicity of L'Aquila area (central Italy), struck by the 6, April 2009 earthquake, Terra Nova, 22, pp. 87-93.; Vallianatos et al., 2012bVallianatos F., Michas G., Papadakis G. , Sammonds P. (2012b). A non-extensive statistical physics view to the spatiotemporal properties of the June 1995, Aigion earthquake (M6.2) aftershock sequence, Acta Geophysica, 60(3), pp. 758-768.), fault lengths distribution (Vallianatos and Sammonds, 2011Vallianatos F. (2011). A non-extensive statistical physics approach to the polarity reversals of the geomagnetic field, Physica A, 390(10), pp. 1773-1778.; Vallianatos et al., 2011bVallianatos F., Kokkinou E., Sammonds P. (2011b). Non-extensive statistical physics approach to fault population distribution a case study from the Southern Hellenic Arc, Acta Geophysica, 59(4), pp. 770-784.) and very recently to natural hazards (Vallianatos, 2009Vallianatos F. (2009). A non-extensive approach to risk assessment, Nat. Hazards Earth Syst Sci, 9, pp. 211-216.), plate tectonics (Vallianatos and Sammonds, 2010Vallianatos F., Sammonds P. (2010). Is plate tectonics a case of non-extensive thermodynamics?, Physica A, 389(21), pp. 4989-4993.) and geomagnetic reversals (Vallianatos, 2011Vallianatos F., Sammonds P. (2011). A non-extensive statistics of the fault-population at the Valles Marineris extensional province Mars, Tectonophysics, 509, pp. 50-54.). Therefore, the applicability of NESP in fracture and in complex geosystems is supported as well. Within the nonextensive thermostatistics formulation, which will be used for the analysis of AE evolution, an entropic index q exists which expresses the degree of non-additivity. In the limit q→1, the standard entropy is recovered and the approach reduces to the well-known Boltzmann-Gibbs (BG) one. The cases with q<1, q=1 and q>1 correspond to super-additivity, additivity and sub-additivity, respectively (Tsallis, 2009Tsallis C. (2009). Introduction to nonextensive statistical mechanics approaching a complex world, Berlin, Springer.).
The question whether AE evolution is properly described by NESP, even at the phenomenological level (i.e. without specifying any underlying model), represents a challenge and this is exactly the problem addressed here. The main motivation of the present work is to investigate the statistical physics of AE in specimens made of cement mortar, which are subjected to mechanical loading, by analyzing the temporal evolution of AEs that occur before the final failure. The aim is not to develop a precise model, but rather to present a simple argument of physical plausibility. In this direction the experimental results of AE recordings, obtained during the repetitive loading/unloading loops of cement mortar beams subjected to three point bending (3PB), are analyzed. Six loading loops were conducted at a gradually higher load level until the fracture of the specimens. The existence of the Kaiser effect is demonstrated through the cumulative counts and the corresponding AE energy during each loading cycle. The AE data are elaborated under the concepts of b-value analysis and NESP aspects. The data analysis clearly shows the existence of pre-failure characteristics that may be used to indicate the upcoming failure of a cement based specimen.
2 EXPERIMENTAL DETAILS
2.1 Specimens
The specimens were made of white cement mortar and subjected to 3PB tests according to the ASTM C-348 standard (see Photo 1). The mortar was prepared using coarse and fine quartz sand mixed with Aalborg white cement according to the procedure adopted by the technicians of the Parthenon worksite of the Athenian Acropolis. The mix proportion was two parts coarse quartz sand, one part fine quartz and one part white cement. In order to calibrate the experimental arrangement and parameters (i.e. limits for the loading frame, loading rate, etc) preliminary 3PB tests were implemented taking special attention to fulfill the Bernoulli - Euler technical bending theory geometrical restrictions. In this context the dimensions of the specimens were 190 mm long (L=190 mm) with square cross-section of 40x40 mm2 (H=B=40mm). The distance between the supporting rollers was equal to 160 mm so that L/B≥4. For obtaining 95% of their total strength the specimens were tested 90 days after their preparation (Kosmatka et al., 2003Kosmatka S., Kerkhoff B., Panarese W. (2003). Design and control of concrete mixtures (14th ed.), Portland Cement Association, Skokie Illinois USA.). These tests provided an average bending strength equal to approximately 15 MPa or equivalently a fracture force (Lf) varying between 3.8 kN and 4.1 kN.
2.2 Loading Protocol
During the 3PB tests sequential loading and unloading (loading cycles) were conducted at gradually higher load levels until the fracture of the specimens. The experiments were carried out under load control. During the first cycle the maximum load was predefined to reach 33% of the 3PB strength of the specimen (as determined from the preliminary tests). During each subsequent cycle, the maximum value of the applied load was 15% higher. Specifically, the maximum loading values during each loading are shown in Table 1. Sequentially to the loading procedure an unloading one was conducted at the same rate (i.e. 34 N/s) leading at a minimum load value of 0.2 kN.
Each experiment was terminated when the specimen was broken independently of the sequence of the loading/unloading cycle. Using the information retrieved from the preliminary tests regarding the expected duration of the experiments, the load frame limits and the mechanical behaviour of the specimens the loading/unloading rate was configured to be 34 N/s.
Based on the authors' experience and taking into account the final target of this work (i.e. to investigate the behaviour of the Tsallis q entropic index and estimate the AE felicity ratio) it was estimated that each specimens should be subjected to six loading cycles. The six load-unload cycles provide a sufficient number of experimental data while on the other hand the maximum load during each loading procedure deviates enough from the previous loading in order to show up the behaviour of the felicity ratio up to the fracture of the specimens. During the 6th loading process the specimens failed at a load value about 8% higher than that of the 5th cycle but before reaching the targeted load value. It is significant to notice that all the specimens tested failed during the 6th loading.
2.3 Experimental Setup
The basic experimental setup for measuring the AE is shown in Figure 1. The cement mortar beam was supported by two rigid metallic cylindrical rods positioned at 80 mm each from the center of the beam (see Photo 2).
An Instron DX-300 electromechanical loading frame (300 kN capacity) was used under load-control mode to apply the loading scheme at a rate of 34 N/s.
The system that was used to detect and record the AE during the whole loading procedure is the 2 channel PCI-2 AE acquisition system (Physical Acoustics Corp). One R15a sensor (manufactured by PAC, resonant frequency at 75 kHz) was used to collect the AE events. The R15a is a narrow band resonant sensor with a high sensitivity. The sensor cavity is machined from a solid stainless steel rod in order to be rugged. It has ceramic face and 30 degree chamfer to cavity in order to electrically isolate the sensor cavity from the structure under test. It must be noted that the small size of the sensor (i.e. 1.9 cm) was suitable for deploying AE measurements in specimens of so small sizes. The AE sensor was placed at the front side of the specimens as shown in Figure 1 and Photo 2 in order to focus at the region where the crack development processes will take place due to the externally applied bending load and reject all the events that originate from the supporting rollers. The sensor was coupled to the test specimen using vacuum grease.
Preamplifier was used along with the sensor with gain set at 40 dB. The signals were bandpass filtered between 20 kHz-400 kHz using the software control of the data acquisition system. To set the threshold value for recording, pencil lead breaks (5 mm, HB leads) were carried out near the area where the crack is expected to appear and the signals recorded were observed. The threshold was set at 40 dB since this value was found to prevent the recording of lower amplitude reflected signals from the pencil lead break tests. For the detected AE data processing the Physical Acoustics Corp. Noesis software was used.
3 RESULTS AND DISCUSSION
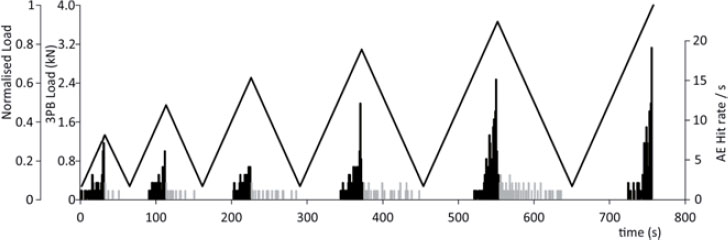
The time variation of the applied mechanical load is shown in Figure 2 (solid line) for a typical test. The applied mechanical load is presented in terms of the 3PB force and the normalised values with respect to the respective maximum value of the specimen. The specific specimen failed at a load level equal to about 4.1 kN during the 6th loading. The corresponding variation of the amplitudes of the AE events is also plotted in Figure 2. Distinguish is made between the AE events recorded during the loading- (square markers) and the unloading-stage (star markers)of the loading cycles. The behaviour of the AE amplitudes reveals that significantly fewer AE events are detected during the unloading branches of the loading cycles. This is expected due to the fact that no further damages but only minor ones appear and micro-movements occur in the body of the specimen during the unloading.
The temporal variation of the 3PB mechanical load (the normalised load values are also shown in secondary left y-axis) and the corresponding amplitude of the AE events during the loading- (square markers) and the unloading-branches (star markers) of a typical test.
In addition it may be observed that during each successive cycle the AE events are detected only when the applied mechanical load reaches and exceeds the corresponding value of the previous loading. This remark makes clear the existence of the Kaiser effect: Consider a brittle material (like cement mortar is) subjected to repetitive loading/unloading loops at a load-level capable to cause internal microdamages. In this case the load applied again during the next loading/unloading loop cannot cause new extensive damages. Thus, during each next application of the same load the number of the AE events are expected to be limited and of lower amplitudes.
Figure 3 shows the AE Hit rate (s-1) temporal variation during the loading and the unloading processes. It is clearly seen that the AE Hit rate gradually increases as approaching the specimen's bending strength. Additionally, it may also be seen that AE activity initiates only when the applied mechanical load becomes higher than each previous loading.
The temporal variation of the 3PB mechanical load (the normalised load values are also shown in secondary left y-axis) and the corresponding AE Hit rate per second during the loading (black lines) - and the unloading-branches (grey lines).
To further support this observation, the number of the cumulative counts of the AE is calculated during each loading process. The results are shown in Figure 4, where the cumulative number of the AE counts is shown with respect to the applied 3PB load (and normalised mechanical load secondary x-axis) during each loading step. Provided that each next loading initiates at a load level near 0.2 kN (i.e. the value that the load attains after unloading) it may be clearly seen that AE counts show significant increase when the applied load reaches approximately the level of the maximum load of the previous loading process. Another observation is that the total number of the counts during the first three loading loops is practically constant. During the last three loading loops the total number of AE counts rapidly increases reaching a maximum value of 9000 AE counts approximately during the last loading step, where the specimen collapsed. This increase indicates the increased rate of non-reversible phenomena (microcracking, etc) within the bulk of the specimen which is directly related to deviation from linearity of the respective load-deflection curve. This is clearly seen in Figure 5 where the load induced is plotted against the deflection of the central section for a typical specimen. Similar behaviour is observed in most rock-like materials, for example Dionysos marble (Exadaktylos et al., 2001Exadaktylos G.E., Vardoulakis I. Kourkoulis S.K. (2001). Influence of nonlinearity and double elasticity on flexure of rock beams - II. Characterization of Dionysos marble International Journal of Solids and Structures, 38(22-23), pp. 4119-4145.), when loaded in bending.
The development of the cumulative counts during each loading cycle with respect to the 3PB load (the normalised load values are also shown in secondary x-axis).
A qualitatively similar behaviour is found regarding the AE released energy. The released cumulative energy of the AE is calculated during each loading process. The results are shown in Figure 6 where the cumulative energy of the AE Hits is plotted with respect to the 3PB load and the normalised mechanical load during each loading. Again, it may be clearly seen that the AE energy shows significant increase when the applied load reaches approximately the level of the maximum load of the previous loading loop. Regarding the behaviour of the totally released AE energy during each loading (see Figure 6) it may be also seen that during the first three loadings the total energy slightly decreases while during the last three ones it increases, reaching a maximum of approximately 107 aJ during the last loading. The observed initial decrease may be attributed to the physical characteristics of the AE events. The fact that during the first three loadings the total number of counts is practically constant but these counts are found of lower energy may be attributed to the fact that the AE events of each next loading loop are of lower duration. This remark may provide the information that the level of the applied mechanical load is still very low and not capable to cause significant and catastrophic internal damages. In conclusion, both Figures 4 and 6 clearly demonstrate the existence of the Kaiser effect.
The development of the cumulative AE Energy during each loading with respect to the 3PB load (the normalised load values are also shown in secondary x-axis).
The Kaiser effect states that a structure will only release significant AE when exposed to applied stresses higher than ones encountered previously. Certain conditions lead to a violation of the Kaiser effect, known as the Felicity effect, quantitatively measured using the Felicity Ratio (FR). Kaiser effect violations demarcate the occurrence of critical micromechanical damage and indicate impending failure. The cumulative number of the AE Hits during each loading process with respect to the applied 3PB load is presented in Figure 7. It becomes clear that significant number of AE activity is shown only when the mechanical load becomes higher than the level of the load previously applied. Thus, and in order to evaluate the level of the Kaiser effect existence and the quality of the AE measurements the FR was calculated according to the following equation:
The cumulative number of the AE events and the felicity ratio with respect to the 3PB load during the whole experimental procedure (the normalised load values are also shown in secondary x-axis).
In Figure 7 the calculated FR is shown with respect to the 3PB load values indicating that its initial value is 0.94 approximately while it reaches gradually lower values during the last three loading loops and specifically reaching its minimum value (i.e. FR=0.8 approximately) during the final loading. Literature reports on similar materials support the observation of the FR reduction (Sagar et al., 2012Sagar R.V., Prasad B.K.R, Kumar S.S. (2012). An experimental study on cracking evolution in concrete and cement mortar by the b-value analysis of acoustic emission technique, Cement and Concrete Research, 42, pp. 1094-1104.; Shah et al., 2014Shah A.A, Naseer A.R., Zhang Ch. (2014). Assessment of Progressive Damages in Concrete with Acoustic Emission Technique, Advances in Applied Acoustics (AIAAS) Volume 3, Doi: 10.14355/aiaas.2014.03.004.
https://doi.org/10.14355/aiaas.2014.03.0...
).
Given that during a loading scheme the amplitude variation of the AE is modified while failure is approached, statistical values (i.e. mean and standard deviation) of a certain number (n) of AE events can be taken into account in order to obtain an "improved b-value" (Ib ). This improved value has been defined as follows (Shiotani et al., 1994Shiotani T., Fujii K., Aoki T., Amou K. (1994). Evaluation of progressive failure using AE sources and improved b-value on slope model tests, Prog. Acoust. Emission, VII, pp. 529-534.; Shiotani et al., 2001Shiotani T., Yuyama S., Li Z.W., Ohtsu M. (2001). Application of the AE improved b-value to qualitative evaluation of fracture process in concrete materials, J. Acoust. Emission, 19, pp.118-132.):
where N is the number of the AE events, μ is the mean amplitude, σ is the standard deviation and α 1 and α 2 are user-defined constants. Usually, α 1=α 2=1. A standard number (n) of successive events can be used for the estimation of the Ib -value which might range between 50 and 100 (Kaphle et al., 2011Kaphle M.R., Tan A., Thambiratnam D., Chan T.H.T. (2011). Damage quantification techniques in acoustic emission monitoring, in WCEAM 2011 Sixth World Congress on Engineering Asset Management.).
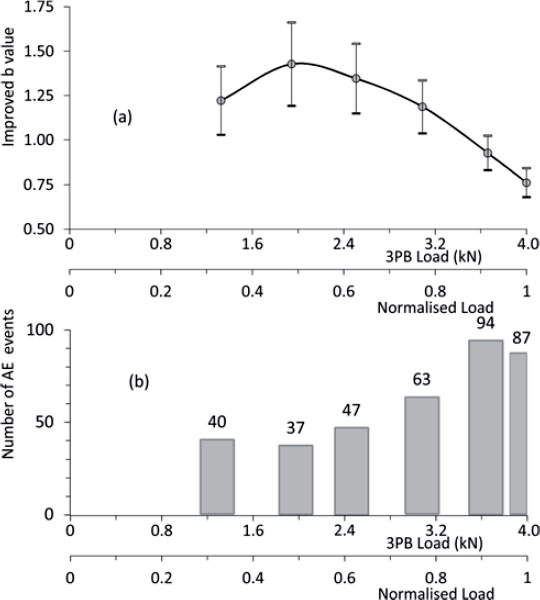
In order to show up the variability of the Ib -value, during the specific test, the set of AE events that occurred during each loading process was used. Consequent Ib -values were calculated corresponding to the maximum 3PB load during each loading loop. Both parameters α 1 and α 2 of Equation 2 were set equal to 1. The results are shown as Ib -values versus the 3PB load in Figure 8a. The error boundaries are calculated following the standard error formula:
where N is the number of the AE events. It is evident that during the first three loading loops the Ib -values exhibit a noticeable increase indicating prevalence of microcracks (Rouchier et al., 2012Rouchier S., Janssen H., Rode C., Woloszyn M., Foray G., Jean-Jacques Roux J.J. (2012). Characterization of fracture patterns and hygric properties for moisture flow modelling in cracked concrete, Constr. Build. Mater., 34, pp. 54-62.). For the three initial loadings high Ib -values (Ib between 1 and 1.1) are obtained due to a large number of low amplitude AE events. This could be attributed to new crack formation and the consequent slow crack growth (Rao and Lakshmi, 2005Rao M.V.M.S., Lakschmi P.K.J. (2005). Analysis of b-value and improved b-value of acoustic emissions accompanying rock fracture, Current Science, 89, pp. 1577-1582.). During the last three loading loops the Ib -values start to decrease intensely exhibiting values lower than 1. Finally slightly before the fracture the Ib -values drop at values around 0.8 approximately. This is indicative of unstable crack growth given that relatively high amplitude AE events are observed in large numbers.
(a) The Improved b-value variation and (b) the total number of the recorded AE events during each loading loop with respect to the 3PB load (the normalised load values are also shown in secondary x-axis).
Figure 8b presents the total number of the recorded AE events during each loading loop. It may be clearly observed that during the first loading a relatively high number of AE events are recorded. Such an activity may be attributed mainly to parasitic effects like loading system frictions and specimen micro-movements or even at specimen's preexisting internal and structural reasons. Beyond that point a clear increase of the AE activity is observed leading to the clear conclusion that the applied mechanical load causes catastrophic damages in the specimen's bulk. At the final loading, during which the specimen failed, a lower number of AE events is recorded but these were of higher amplitudes, higher number of AE counts and higher Energy (see Figures 2, 4 and 6).
NESP modeling, based on implementing the Tsallis entropy, was then applied on the experimental data. The interevent times of the recorded AE were calculated and the cumulative probability function (CPF) was plotted (Figure 9).
The Cumulative Probability Function (CPF) with respect to the interarrival times during each of the six loading cycles. The corresponding fitting line and the estimated values of the q and βq Tsallis parameters.
Sequentially the experimental data were fitted using the following q-exponential equation suggested by (Vallianatos et al., 2012aVallianatos F., Triantis D. (2012). Is pressure stimulated current relaxation in amphibolite a case of non-extensivity?, EPL, 99 (1), 18006.):
where P(>δτ) stands for the probability of observing an interevent time higher than δτ, q and βq are the corresponding Tsallis equation parameters. Studying the experimental data under statistical physics concept, the parameter q suggests a complex picture possibly related with fractures' fractal network that drives the AE events (Vallianatos et al., 2012aVallianatos F., Triantis D. (2012). Is pressure stimulated current relaxation in amphibolite a case of non-extensivity?, EPL, 99 (1), 18006.). Specifically, according to (Landis and Shah, 1995Landis E.N., Shah S.P. (1995). The influence of microcracking on the mechanical behavior of cement based materials, Adv Cement Based Mater, 2, pp.105-118.) and (Landis, 1999Landis E.N. (1999). Micro-macrofracture relationships and acoustic emissions in concrete, Constr Build Mater, 13, pp. 65-72.) where similar materials were tested using the 3PB mechanical testing method the physical processes that dominate are getting closer to a Boltzman-Gibbs statistics when approximating fracture. Equation 4 was used to fit the experimental data as may be seen in Figure 9 in order to estimate the best fitting values for q and βq Tsallis equation parameters.
The fitting results as calculated according to the Tsallis entropy model are shown in Figure 10 providing a full picture of the behaviour of the critical parameters q and βq with respect to the corresponding value of the 3PB load of each loading process. After analyzing the experimental results, the error of the values was calculated using the simplest form of bootstrapping and are estimated to be of the order of 1% regarding the q-exponent and 7% for the βq .
The variation of the Tsallis entropic parameters with respect to the 3PB value of the maximum mechanical load of each loading (the normalised load values are also shown in secondary x-axis).
The initial low value of the q-parameter implies the existence of well-organized processes including mainly reversible grain boundary sliding. During the first three loading loops it is expected to record AE events that are mainly attributed to the interface zones of cement-fine aggregates. Such processes can be characterized as highly deterministic since they are related to the geometry and the composition of the specimen with regard to the water/cement/sand ratio during its preparation. Beyond that point and during the last three loading loops microfracture processes take place involving grain boundary sliding and crack bridging. The values of q while approaching the failure load level reach the critical value of 1.42 (Vallianatos and Sammonds, 2013Vallianatos F., Triantis D. (2013)., A non-extensive view of the Pressure Stimulated Current relaxation during repeated abrupt uniaxial load-unload in rock samples, EPL, 104 (6), 68002.) designating clearly the inevitable upcoming fracture. Since this framework concerns non-extensivity, which is, in turn, related to (multi)fractality (Vallianatos et al., 2015Vallianatos F., Michas G. Papadakis G. (2015). A Description of Seismicity Based on Non-extensive Statistical Physics: A Review, Earthquakes and Their Impact on Society, Springer ed.), it may be said that the behaviour of Tsallis parameters suggests a fractal picture for fractures' network that represents each loading cycle, as has been previously suggested not only in rock physics but in earth sciences too (Vallianatos and Triantis, 2012Vallianatos F., Triantis D. (2012). Is pressure stimulated current relaxation in amphibolite a case of non-extensivity?, EPL, 99 (1), 18006.; Vallianatos and Triantis, 2013Vallianatos F., Sammonds P. (2013). Evidence of non-extensive statistical physics of the lithospheric instability approaching the 2004 Sumatran-Andaman and 2011 Honshu mega-earthquakes, Tectonophysics, 590, pp. 52-58.; Vallianatos and Sammonds, 2014Cartwright-Taylor A., Vallianatos F., Sammonds P. (2014). Superstatistical view of stress-induced electric current fluctuations in rocks Physica A: Statistical Mechanics and its Applications, 414, pp. 368-377.; Michas et al., 2015Michas G., Vallianatos F., Sammonds P. (2015). Statistical mechanics and scaling of fault populations with increasing strain in the Corinth Rift Earth and Planetary Science Letters, 431, pp. 150-163.). Moreover, each loading-unloading cycle contributes to the creation of a rich fractures' network and consequently the collection of AEs is expressed by a q-parameter which gets higher in each repeated loading-unloaded cycle (see Figure 9), approaching approximately 1.5 as the order of the sequential loading-unloading cycle increases, indicating that a q-exponential distribution is approached in the fracture's network as the loading-unloading cycle is repeated indicating a high degree of hierarchical organization similar to that of faults in geodynamic systems fractality (Vallianatos et al., 2015Vallianatos F., Michas G. Papadakis G. (2015). A Description of Seismicity Based on Non-extensive Statistical Physics: A Review, Earthquakes and Their Impact on Society, Springer ed.; Michas et al., 2015Michas G., Vallianatos F., Sammonds P. (2015). Statistical mechanics and scaling of fault populations with increasing strain in the Corinth Rift Earth and Planetary Science Letters, 431, pp. 150-163.).
Further investigation is required in order to use the AE detection technique as a tool to define the development of crack generation and propagation through the q parameter.
4 CONCLUDING REMARKS
An experimental protocol was implemented involving the detection and measurement of AE when three point bending mechanical loading was applied on white cement mortar beams. The Kaiser effect was extremely pronounced; it was clearly seen that during each next loading cycle the AE activity initiates only after exceeding the previously applied load value. From a quantitative point of view a number of about 9000 cumulative AE counts and approximately 107 aJ of cumulative AE energy was recorded during the final loading phase. This observation is further supported by the FR behaviour that is consistent with the existing literature and its initial value of 0.94 gradually drops to a minimum value FR=0.8 during the final loading. Finally, the variation of the Ib -value shows that it drops to the critical values (i.e. lower than 1) only during the last two loadings.
The experimental technique adopted seems to act in a supplementary way for monitoring the damage initiation and propagation processes. Moreover it was clearly shown that adopting the Non-Extensive Statistical Physics description of the data reveals critical hidden features of the damage evolution process.
On the other hand it was indicated that Non-Extensive Statistical Physics can provide indicators that could act as a precursor of upcoming catastrophic fracture. Although further research is required with a wider variety of loading protocols and materials the preliminary results presented here are definitely encouraging. The behaviour of the entropic index q and the relaxation parameter βq of the Tsallis equation show systematic changes during the different stages of the failure process. The last cycle led to a q value equal to 1.42, implying the upcoming fracture which is in good agreement with previous results obtained from a wide range of fractured materials.
Since this work constitutes a preliminary approach, the results at this stage are mainly of qualitative nature. Further experimental evidence is required in order to draw quantitative and statistically evaluated conclusions.
ACKNOWLEDGEMENTS
This research has been co-financed by the European Union (European Social Fund - ESF) and Greek national funds through the Operational Program "Education and Lifelong Learning" of the National Strategic Reference Framework (NSRF) - Research Funding Program: THALES. Investing in knowledge society through the European Social Fund.
REFERENCES
- Abe S., Suzuki N. (2003). Law for the distance between successive earthquakes, J Geophys Res, 108(B2), pp. 2113-2121.
- Abe S., Suzuki N. (2005). Scale-free statistics of time intervals between successive earthquakes, Physica A, 350, pp. 588-596.
- Aggelis D.G., Mpalaskas A.C., Matikas T.E. (2013). Investigation of different fracture modes in cement-based materials by acoustic emission, Cement and Concrete Research, 48, pp. 1-8.
- Anzani A., Binda L., Carpinteri A., Lacidogna G., Manuello A. (2008). Evaluation of the repair on multiple leaf stone masonry by acoustic emission, Materials and Structures, 41(6), pp. 1169-1189.
- Cartwright-Taylor A., Vallianatos F., Sammonds P. (2014). Superstatistical view of stress-induced electric current fluctuations in rocks Physica A: Statistical Mechanics and its Applications, 414, pp. 368-377.
- Exadaktylos G.E., Vardoulakis I. Kourkoulis S.K. (2001). Influence of nonlinearity and double elasticity on flexure of rock beams - II. Characterization of Dionysos marble International Journal of Solids and Structures, 38(22-23), pp. 4119-4145.
- Kaphle M.R., Tan A., Thambiratnam D., Chan T.H.T. (2011). Damage quantification techniques in acoustic emission monitoring, in WCEAM 2011 Sixth World Congress on Engineering Asset Management.
- Kosmatka S., Kerkhoff B., Panarese W. (2003). Design and control of concrete mixtures (14th ed.), Portland Cement Association, Skokie Illinois USA.
- Landis E.N. (1999). Micro-macrofracture relationships and acoustic emissions in concrete, Constr Build Mater, 13, pp. 65-72.
- Landis E.N., Shah S.P. (1995). The influence of microcracking on the mechanical behavior of cement based materials, Adv Cement Based Mater, 2, pp.105-118.
- Lockner D. (1993). The role of acoustic emission in the study of rock fracture, Int. J. Rock Mech. Min. Sci. Geomech. Abstr., 30, pp. 883-899.
- Michas G., Vallianatos F., Sammonds P. (2015). Statistical mechanics and scaling of fault populations with increasing strain in the Corinth Rift Earth and Planetary Science Letters, 431, pp. 150-163.
- Rao M.V.M.S., Lakschmi P.K.J. (2005). Analysis of b-value and improved b-value of acoustic emissions accompanying rock fracture, Current Science, 89, pp. 1577-1582.
- Rouchier S., Janssen H., Rode C., Woloszyn M., Foray G., Jean-Jacques Roux J.J. (2012). Characterization of fracture patterns and hygric properties for moisture flow modelling in cracked concrete, Constr. Build. Mater., 34, pp. 54-62.
- Sagar R.V., Prasad B.K.R, Kumar S.S. (2012). An experimental study on cracking evolution in concrete and cement mortar by the b-value analysis of acoustic emission technique, Cement and Concrete Research, 42, pp. 1094-1104.
- Sagar R.V., Raghu Prasad B.K., Singh R.K. (2014). Kaiser effect observation in reinforced concrete structures and its use for damage assessment, Archives of Civil and Mechanical Engineering, http://dx.doi.org/10.1016/j.acme.2014.05.004
» http://dx.doi.org/10.1016/j.acme.2014.05.004 - Shah A.A, Naseer A.R., Zhang Ch. (2014). Assessment of Progressive Damages in Concrete with Acoustic Emission Technique, Advances in Applied Acoustics (AIAAS) Volume 3, Doi: 10.14355/aiaas.2014.03.004.
» https://doi.org/10.14355/aiaas.2014.03.004 - Shiotani T., Fujii K., Aoki T., Amou K. (1994). Evaluation of progressive failure using AE sources and improved b-value on slope model tests, Prog. Acoust. Emission, VII, pp. 529-534.
- Shiotani T., Yuyama S., Li Z.W., Ohtsu M. (2001). Application of the AE improved b-value to qualitative evaluation of fracture process in concrete materials, J. Acoust. Emission, 19, pp.118-132.
- Skoulikidis Th. (2000). Corrosion and conservation of building materials of monuments: the Acropolis case, University of Crete Publications, Heraklion, Crete.
- Stanchits S., Dresen G., Vinciguerra S. (2006). Ultrasonic velocities, acoustic emission characteristics and crack damage of basalt and granite, Pure Applied Geophys. 163(5-6), pp. 975-994.
- Stergiopoulos C., Stavrakas I., Hloupis G., Triantis D., Vallianatos F. (2013). Electrical and acoustic emissions in cement mortar beams subjected to mechanical loading up to fracture, Engineering Failure Analysis, 35, pp. 454-461.
- Telesca L. (2010a). Analysis of Italian seismicity by using a nonextensive approach, Tectonophysics, 494, pp. 155-162.
- Telesca L. (2010b). A non-extensive approach in investigating the seismicity of L'Aquila area (central Italy), struck by the 6, April 2009 earthquake, Terra Nova, 22, pp. 87-93.
- Tsallis C. (2001). In Non-extensive statistical mechanics and its applications, Abe S., Okamoto Y. (Eds.), Berlin, Springer, pp. 1-35.
- Tsallis C. (2009). Introduction to nonextensive statistical mechanics approaching a complex world, Berlin, Springer.
- Vallianatos F. (2009). A non-extensive approach to risk assessment, Nat. Hazards Earth Syst Sci, 9, pp. 211-216.
- Vallianatos F. (2011). A non-extensive statistical physics approach to the polarity reversals of the geomagnetic field, Physica A, 390(10), pp. 1773-1778.
- Vallianatos F., Benson P., Meredith P., Sammonds P. (2012a). Experimental evidence of a non-extensive statistical physics behavior of fracture in triaxially deformed Etna basalt using acoustic emissions, EPL, 97:58002.
- Vallianatos F., Kokkinou E., Sammonds P. (2011b). Non-extensive statistical physics approach to fault population distribution a case study from the Southern Hellenic Arc, Acta Geophysica, 59(4), pp. 770-784.
- Vallianatos F., Michas G. Papadakis G. (2015). A Description of Seismicity Based on Non-extensive Statistical Physics: A Review, Earthquakes and Their Impact on Society, Springer ed.
- Vallianatos F., Michas G., Papadakis G. , Sammonds P. (2012b). A non-extensive statistical physics view to the spatiotemporal properties of the June 1995, Aigion earthquake (M6.2) aftershock sequence, Acta Geophysica, 60(3), pp. 758-768.
- Vallianatos F., Sammonds P. (2010). Is plate tectonics a case of non-extensive thermodynamics?, Physica A, 389(21), pp. 4989-4993.
- Vallianatos F., Sammonds P. (2011). A non-extensive statistics of the fault-population at the Valles Marineris extensional province Mars, Tectonophysics, 509, pp. 50-54.
- Vallianatos F., Sammonds P. (2013). Evidence of non-extensive statistical physics of the lithospheric instability approaching the 2004 Sumatran-Andaman and 2011 Honshu mega-earthquakes, Tectonophysics, 590, pp. 52-58.
- Vallianatos F., Triantis D. (2012). Is pressure stimulated current relaxation in amphibolite a case of non-extensivity?, EPL, 99 (1), 18006.
- Vallianatos F., Triantis D. (2013)., A non-extensive view of the Pressure Stimulated Current relaxation during repeated abrupt uniaxial load-unload in rock samples, EPL, 104 (6), 68002.
- Vallianatos F., Triantis D., Sammonds P. (2011a). Non-extensivity of the isothermal depolarization relaxation currents in uniaxial compressed rocks, EPL, 94:68008.
- Varotsos P., Sarlis N., Skordas E. (2011). Natural time analysis the new view of time, Berlin, Springer.
Publication Dates
-
Publication in this collection
Dec 2016
History
-
Received
22 Sept 2015 -
Reviewed
25 Apr 2016 -
Accepted
05 May 2016