Abstract
In this paper, the fatigue behavior of the metallic welded U-shape specimens subjected to cyclic loading have been investigated via experimental and numerical analysis. To do so, two sets of the spot welded specimens with different sizes were prepared and fatigue tests were conducted under the various cyclic loads. The crack propagation is numerically examined by using the stress intensity factor values achieved from FE analyses. The modified Paris and Forman-Newman-De Koning models were used to estimate the fatigue crack growth rate. The results indicate that the fatigue life of specimens decreases with any increase in load level.
Keywords:
Crack growth; Fracture mechanics; Finite element; Stress intensity factor; Fatigue life
1 INTRODUCTION
The process of spot welding is widely used to connect the two sheets together particularly in the automotive industries. So far, the fatigue life prediction and modeling of a variety of specimens have been investigated by many researchers (Esmaeili, 2015EsmaeiliF, RahmaniA, BarzegarS, and AfkarA (2015)Prediction of fatigue life for multi-spot welded joints with different arrangements using different multiaxial fatigue criteria. Materials and Design 72: 21-30.; Hassanifard, 2014Hassanifard S., Mohammadpour M, Ahmadi Rashid H (2014)A novel method for improving fatigue life of friction stir spot welded joints using localized plasticity. Materials and Design 53: 962-971.; Mohammadpour, 2014Mohammadpour M, Hassanifard S, Amini A, Reshadi F (2014)An experimental investigation of fatigue behavior and deformation of double spot friction welded joints. Materials and Design 57: 705-711.; Chen, 2014Chen J, Zihui X (2014)A fatigue life prediction method for coke drum base, weld, and HAZ materials from tensile properties. Materials & Design 63: 575-583.; Kang, 2007Kang H, Dong P, Hong JK (2007)Fatigue analysis of spot welds using a mesh-insensitive structural stress approach. International Journal of fatigue 29.8: 1546-1553.). Since the area around the nugget is considered as a natural crack or an initial slot, the spot welding is analyzed and its fatigue life is dealt with in fracture mechanics. Experimental results of the analysis and modeling of the spot welding by the concepts of fracture mechanics play an important role. Because the results of these models must be consistent with the experimental results; otherwise the models are not reliable. One of the studies in which the experiments were performed on all samples of spot weld is the study of Adib et al. (2004Adib H, Gilgert J, Pluvinage G (2004)Fatigue life duration prediction for welded spots by volumetric method. International Journal of Fatigue 26.1: 81-94.) that predicted the fatigue life of spot welds using the volumetric method. Sun et al. (2008Sun X, Stephens EV, Khaleel MA (2008)Effects of fusion zone size and failure mode on peak load and energy absorption of advanced high strength steel spot welds under lap shear loading conditions. Engineering Failure Analysis 15.4: 356-367.) studied the effect of the weld junction size and the decline mode on the maximum load and the energy absorption of high-strength steels. Long et al. (2007Long X, Khanna SK (2007)Fatigue properties and failure characterization of spot welded high strength steel sheet. International journal of fatigue 29.5: 879-886.) investigated the fatigue properties and decline characteristics of high-strength sheets of spot weld. Choi et al. (2007Choi BH, Joo DH, Song SH (2007)Observation and prediction of fatigue behavior of spot welded joints with triple thin steel plates under tensile-shear loading. International journal of fatigue 29.4: 620-627.) studied the fatigue life of steel sheets of ternary spot weld (three sheets on each other). Lin et al. (2006Lin SH, Pan J, Wung P, Chiang J (2006)A fatigue crack growth model for spot welds under cyclic loading conditions. International Journal of Fatigue 28.7: 792-803.) examined the modeling of fatigue crack growth of spot welds under cyclic loading. Pan et al. (2002Pan N, Sheppard S (2002) Spot welds fatigue life prediction with cyclic strain range. International Journal of Fatigue 24.5: 519-528.) investigated the fatigue life prediction of spot welds under cyclic strain range. Kang (2007)Kang HT (2007)Fatigue prediction of spot welded joints using equivalent structural stress. Materials & design 28.3: 837-843. studied the fatigue life prediction of spot welds joints using equivalent structural stress method. Lin et al. (2006)Lin PC, LinSH, Pan J (2006)Modeling of failure near spot welds in lap-shear specimens based on a plane stress rigid inclusion analysis. Engineering fracture mechanics 73.15: 2229-2249. investigated the decline of spot welds with regard to the state of plane stress. Yang et al. (2010Yang X, Xia Y, Zhou Q (2010)A simplified FE model for pull-out failure of spot welds. Engineering Fracture Mechanics 77.8: 1224-1239.) developed a simple model to simulate the pull-out failure behavior of spot welds in vehicles fractures simulation. The model was validated by modeling the tests performed on the spot weld. Hassanifard et al. (2013)Hassanifard S, Ahmadi SR, Mohammad Pour M (2013)Weld arrangement effects on the fatigue behavior of multi friction stir spot welded joints. Materials & Design 44: 291-302. examined the effects of different arrangement of spot welding on fatigue behavior of spot welding joints. Florea et al. (2013Florea RS, Bammann DJ,Yeldell A, Solanki KN, Hammi Y (2013)Welding parameters influence on fatigue life and microstructure in resistance spot welding of 6061-T6 aluminum alloy. Materials & Design 45: 456-465.) studied the welding parameters affecting the fatigue behavior of spot welding for aluminum alloy 6061-T6 experimentally. The results of this study revealed that the welding parameters have a great influence on the microstructure and the fatigue life of spot welding joints and aluminum foil with a thickness of 2 mm.
Nowadays, with developing the analytical and numerical methods in solid mechanics, it is intended to study the different parameters both quantitatively and more accurately instead of qualitative study of their effects. A lot of studies have been conducted using the numerical and analytical methods which have investigated its different aspects. In the literature (Zhang, 1999Zhang S(1999)Approximate stress intensity factors and notch stresses for common spot-welded specimens. WELDING JOURNAL-NEW YORK- 78: 173-s.; Dong, 2001Dong P (2001)A structural stress definition and numerical implementation for fatigue analysis of welded joints. International Journal of Fatigue 23.10: 865-876.;Hadipour, 2011Hadipour M, Alambeigi F, Hosseini R, Masoudinejad R (2011) A study on the vibrational effects of adding an auxiliary chassis to a 6-ton truck. Journal of American Science7(6):1219-26.;MasoudiNejad, 2015MasoudiNejad R, Farhangdoost K, Shariati M (2015)Numerical study on fatigue crack growth in railway wheels under the influence of residual stresses. Engineering Failure Analysis 52: 75-89., 2016MasoudiNejad R, Farhangdoost K, Shariati M (2016) Three-dimensional simulation of rolling contact fatigue crack growth in UIC60 rails. Tribology Transactions (just-accepted): 00-00.; Moghadam, 2016Moghadam DG, Farhangdoost K, MasoudiNejad R (2016) Microstructure and Residual Stress Distributions Under the Influence of Welding Speed in Friction Stir Welded 2024 Aluminum Alloy. Metallurgical and Materials Transactions B 47(3): 2048-2062.), some of these issues are studied using some experimental observation, analytical calculations and FEA calculations within various contexts. Most of the previous studies described above have investigated the fatigue behavior of the metallic welded specimens is a discussion which has not been noticed very much. In this paper, the behavior of the crack growth, the fatigue life of U-shape specimens under different level of loadings and the determination of the sheet thickness on the fatigue life have been investigated by finite element method and experimental tests. A three-dimensional finite element method is employed to provide a prediction of fatigue crack growth in the U-shape specimens. Therefore, the various load levels with constant amplitudes on the fatigue life is assessed by using damage mechanic methods. Also, the fatigue crack growth under dynamic loading is simulated in the three-dimensional model by using Franc3D software (Cornell Fracture Group, 2016Cornell Fracture Group, Cornell University, <www.cfg.cornell.edu>
www.cfg.cornell.edu...
; MasoudiNejad, 2015MasoudiNejad R, Farhangdoost K, Shariati M (2015)Numerical study on fatigue crack growth in railway wheels under the influence of residual stresses. Engineering Failure Analysis 52: 75-89.).
2 EXPERIMENTAL PROCEDURES
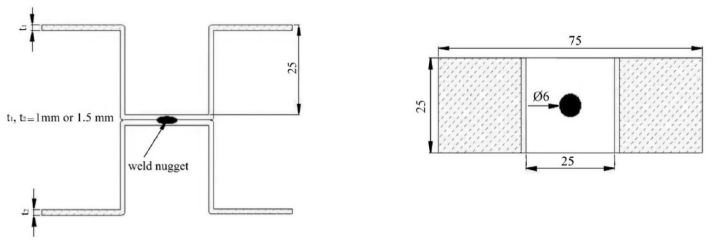
The materials, which have been used in this study, are the two sheets of U-shape specimens with 1 mm and 1.5 mm thickness, manufactured from ST37 steel whose mechanical properties have been summarized in Table 1. The standard tensile tests of tension of metallic materials, E8, are performed to determine the stress-strain diagram according to ASTM standards. The true stress-strain plot of the used material has been illustrated in Figure 1.
Three types of U-shape specimens with different thickness are used in this investigation. The dimensions of test specimens have been illustrated in Figure 2. As shown in the Figure 2 the U-shape specimens with two sheet thickness of 1 by 1mm, 1 by 1.5mm and 1.5 by 1.5mm are weld jointed together. At least 5 specimens of each type under different loading with constant amplitude conditions are used. The specimen's were provided by means of a pedal spot welding apparatus. The condition of welding is as followings:
-
• Current welding : 8 KA
-
• Welding time : 3 seconds
-
• Electrode face diameter : 4-6 mm
-
• Material : mild Steel
As the sheets with two different thicknesses are used the U-shape specimens are divided in two different groups. The specimens are introduced in the form of: UA**-**-*. Where UA and UB refer to the type of specimens with 4mm and 6mm diameter respectively; the first two digit numbers from the left side indicates the thickness size of Sheets. The third number refers to the number of specimen in each series. In this investigation, each series have 5 specimens at least. The experimental tests have been conducted with stress ratio of 0.01 and frequency of 10 Hz using servo-hydraulic INSTRON 8802 machine. In each case, several fatigue tests were performed with different maximum applied longitudinal loads. Figure 3 shows the experimental test setup.
3 FAILURE ANALYSISUNDER FATIGUE TEST
In general, two types of failure are observed in U-shaped samples:
-
1.Nugget Fracture: This type of fracture occurs because of the small nugget diameter or large applied force. This fracture occurs at the interface of between the nugget and the two joined sheets. If the applied force is greater than the spot weld endurance, the decline will occur suddenly without crack growth in joined sheets (Figure 4-a), but if the applied force is lower than the spot welded endurance and strength, first the crack will grow slightly (about 1 to 2 mm) and then will fail.
-
2. Nugget Pull-Out: In this type of fracture, first the crack growths fully in the sheet thickness and then after reaching the sample surface and significant growth in the sample width the nugget will be pulled out and then the failure will occur due to the decrease of sample strength. (Figure 4-b).
Nugget pulled out on applying at extreme loading (a) failure occurs before crack growth (b) failure occurs after a gradual growth.
Figure 5 shows the UB15-15-4 specimen in which the thickness of both sheets is 1.5 mm and is affected by the maximum force of 900 N and endured 202,730 loading cycles. As can be seen, the crack is occurred in both sheets but it grew more only in one of them and the crack passed the sample width largely.
Figure 6 shows the UB10-15-2 specimen when the thickness of one of the sheets is 1 mm and the other one is 1.5 mm and is affected by the maximum force of 650 N and endured 15922 loading cycles. As can be seen before the crack can grow in it, the thinner sheet (left) was torn while the thicker sheet received no damage.
Figure 7 shows the UB10-10-1 specimen in which the thickness of both sheets is 1 mm and is affected by the maximum force of 650 N. As can be seen before the crack can significantly grow in sheets, both sheets were torn due to the thinness.
Figure 8 shows the UB15-15-2 specimen in which the thickness of both sheets is 1.5 mm and is affected by the maximum force of 650 N and endured 342881 loading cycles. It can be seen from Figure 8 that the crack grew significantly in one of the sheets but no crack can be seen in the other sheet. The fatigue life graphs for each of the two types of U-shape specimens with different thickness are shown in Figure 9. The life pertains to all of the three steps of fatigue as initiation, propagation and the fracture of the fatigue for specimen.
The most majority part of the fatigue crack growth at the spot weld and its propagation to the surface of a specimen which cannot to observed. Since the crack growth behavior can be investigated exactly as it clearly appears at the surface, an optical microscope with magnification factor of 100 is used to measure the fatigue crack length at the various loading levels. In order to see the fatigue crack growth obviously the surface of all parts around the nugget were smoothly polished. Also during the loadings, the crack length was measured accurately on the surface of specimens by means of lines that was created by a precision coulisse in 1mm distance from each others.
In Figures 10-11, some images of the crack growth on the surface of U-shape specimens are displayed. Some snapshots for crack growth path relating to UA15-15-1specimen during observation at the surface are shown in figure 10. Also snapshots for crack growth path relating to UA10-10-2specimen during observation at the surface and the final fracture are shown in figure 11. Figure 11-d reveal that complete fracture occurs as quickly as the cracks are observed at the specimen's surface.
Stepwise snapshots for crack growth path of UA15-15-1 specimen during observation at surface after (a) 1,365,000 cycles (b) 1,400,000 cycles.
Stepwise snapshots for crack growth path of UB10-10-2 specimen during observation at surface and complete failure after (a) 230,000 cycles (b) 260,000 cycles (c) 300,000 cycles (d) 325,890 cycles.
4 FINITE ELEMENT SIMULATION
The result of numerical analysis for the U-shape specimens have been done by software named Franc3D (Cornell Fracture Group, 2016Cornell Fracture Group, Cornell University, <www.cfg.cornell.edu>
www.cfg.cornell.edu...
; MasoudiNejad, 2015MasoudiNejad R, Farhangdoost K, Shariati M (2015)Numerical study on fatigue crack growth in railway wheels under the influence of residual stresses. Engineering Failure Analysis 52: 75-89.) which is a software for 3D finite element analysis and especially for studies on crack growth in two dimensional geometries. This software is supplied by the researchers of Cornell University and distributed to the public. This software is able to use the different equations of fatigue crack growth in order to predict the lifetime of the specimen under fatigue loads. Also, at this software the debates which are related to the destruction as a result of the net-section stress of profile at presence of the crack for the lifetime prediction of the section have been discussed.
In figure 12-a the finite element of the U-shape specimen and the existed crack in it have been illustrated which more elements are used to obtain better results around the crack and the place of contact loading imposing. In this study the crack geometry for the crack has been considered semi-elliptical for the crack (figure 12-b). The reason of this form of cracks is the comprehensiveness and field observation in experimental tests. The dimensions of the investigated crack are b=0.4 mm, and a=0.2 mm which are as the initial crack and for the crack illustrated in figure 12-a.
Mesh generation of U-shape specimen for finite elements analysis (a) specimen without any crack (b) specimen with crack.
Linear elastic fracture mechanics (LEFM) is a suitable method for linking data to fatigue crack growth because it describes the stress conditions at the crack tip using only a parameter, i.e. the stress intensity factor. The calculated path is achieved using Maximum Tangential Stress, Maximum Energy Release Rate and Strain Energy Density criterions. Such calculations are carried out in each step of the crack growth. Since proposed path in three criteria have not significant differences, and the use of maximum tangential stress is recommended by FRANC3D software providers, it is used to determine the angle of crack growth (MasoudiNejad, 2013MasoudiNejad R, Salehi SM, Farrahi GH (2013) Simulation of railroad crack growth life under the influence of combination mechanical contact and thermal loads.in 3nd International Conference on Recent Advances in Railway Engineering, Iran., 2014MasoudiNejad R (2014)Using three-dimensional finite element analysis for simulation of residual stresses in railway wheels. Engineering Failure Analysis 45: 449-455.). The crack tip curve can be fit after determining the direction of crack growth. In continue, crack growth can be simulated for another step. After crack growth, Specimen is meshed again and be prepared to solve. This is repeated for each step until the rate of growth is expected. Figure 13 shows crack after 10th stage of growth. Two Fatigue crack growth rate models were used in this study.
4.1 The Modified Paris Model
Modified Paris model is used to calculate crack growth rate and fatigue life. Modified Paris model considers the effects of closure of the crack. The growth rate is defined by the equation as follows (Anderson, 1994Anderson TL (1994) Fracture Mechanics, fundamentals and applications, second edition, CRC press.):
where ∆keff the effective stress intensity factor is defined as the difference between the maximum mode I stress intensity factor (Kmax ) and stress level where the crack first opens(Kop ) and C, n are material constants.
4.2 Forman-Newman-De Koning Model
The FNK fatigue model is expressed as (Newman, 1984Newman Jr JC (1984)A crack opening stress equation for fatigue crack growth. International Journal of Fracture 24.4: R131-R135.):
In the above equation, a and N are the crack length and the number of applied fatigue cycles. C, n, p and q are empirical constant derived by curve fitting the test data R is the load ratio, ∆k is stress intensity factor, Kmax is the maximum applied stress intensity factor range, Kcrit is the critical stress intensity factor range for unstable crack growth, ∆th is threshold stress intensity factor and f is described in order to keep into account the plasticity-induced crack closure:
Here,
where σmax / σF and α are the plain stress/strain constraint factor and the ratio of the maximum applied stress to the flow stress, respectively.
5 OMPaRIsON OF PREDICTED RESULTS AND DISCUSSION
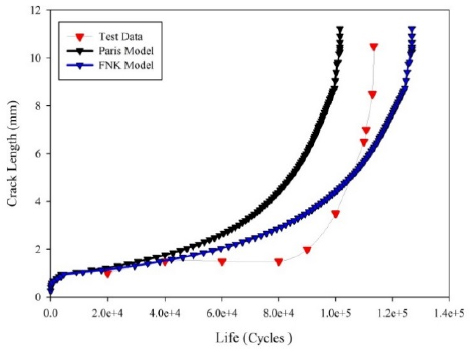
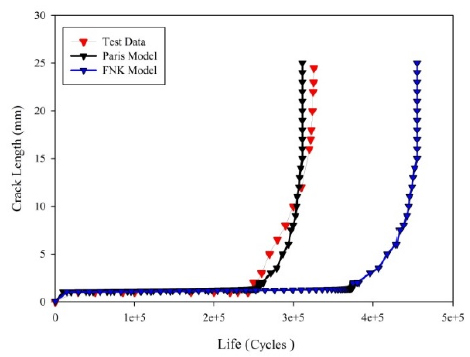
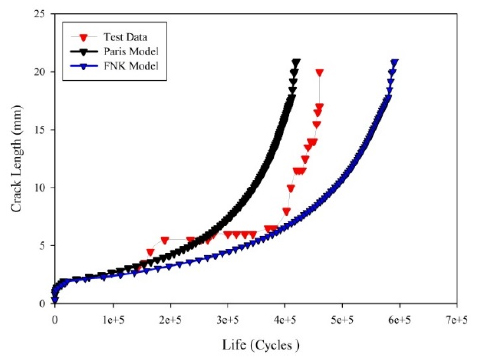
The comparison between the predicted fatigue lives and the experimental lives has been illustrated in Figures 14-18 for welded U-shape specimens. It can be seen from Figure 14 that for UA10-15-2 specimen, the Paris model agrees with the experimental tests results very well. However, estimated fatigue lives by means of FNK model were overestimated.
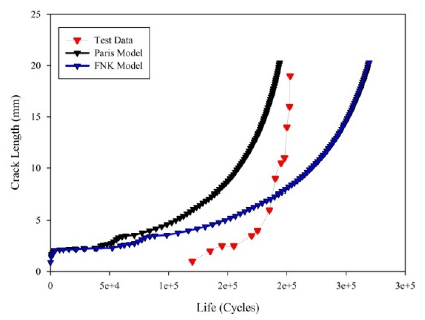
The comparison between the estimated fatigue lives using fatigue models and experimental tests for UA15-15-4 specimen is shown in Figure 15. The FNK model estimates the fatigue life very accurately for this specimen. But, the Paris model does not estimate the fatigue life as accurate as FNK model for this specimen.
The comparison between the estimated fatigue lives using the Paris and Forman-Newman-De Koning models and the experimental lives for UB10-10-2 specimen is illustrated in Figure 16. According to the Figure 16, the Paris model is able to estimate fatigue life with sufficient level of accuracy for this specimen.
The comparison of tested fatigue lives with the predictions by the Paris and Forman-Newman-De Koning models is shown in Figures 17-18. The result shows that the FNK can reasonably predict the fatigue lives of the UB10-15-1 specimen. However, there is a significant deviation between test and predicted fatigue lives for UB10-15-1 specimen and UB15-15-4 specimens.
In accordance with Figs. 14-18, the FNK model covers all three regimes of crack growth rate diagram (from threshold to unstable crack growth) on the basis of stress intensity factor. Besides that, Paris model is acceptable for the two regimes of the mentioned diagram. So it is expected that fatigue life which is predicted using FNK model has a good agreement with experimental results. The comparison between the estimated fatigue lives using the Paris and Forman-Newman-De Koning models and the experimental lives for A-type and B-type specimens are given in Tables 2 and 3, respectively.
According to the experimental results, the crack life can be observed in the stages of initiation and crack growth between the sheet thicknesses (until the visibility of crack at the sample surface that could be observed when its length was about 2 mm). Due to the these results, it is indicated that in specimens with high lifetime (low applied load) the stages of crack initiation and growth include more than half of the final lifetime; while in specimens with low lifetime (high applied load), the stages of crack initiation and growth include about 40 percent of the final lifetime of the specimens.
Cracks reach the external surface suddenly when they are fully grown so that the measurement of micro cracks (less than 2 mm) is not possible using the tool. In general, when cracks appear on the external surface, they have a length about 2.5-4 mm. Also, the location of the crack is in the external surface, around the nugget and the vertical edge.
According to the experimental results, the relationship between the type of failure and the lifetime can be realized. In general, the higher lifetime increases the sudden failure and the spot weld failure. Also, in all displacement curves based on the number of loading cycles, in the low number of course, the slope of the curve is almost constant and close to zero. But after a number of loading cycles (which is different for each sample according to its thickness and loading) the slope of the curve increases. In fact, this spot can be considered almost the same spot that started the crack initiation.
6 CONCLUSIONS
In this paper, the fatigue behavior of the metallic welded U-shape specimens subjected to cyclic loading have been investigated via experimental and numerical analysis. The following results have been obtained from the observations and analysis of the surfaces and the fracture sections:
-
1.The initiation and the fatigue crack growth first occurs in U-shape specimen having small thicknesses in which the crack length is longer.
-
2.In U-shape specimens with the same thicknesses, crack appears in both sheets with an approximately the same length.
-
3. Due to stress concentration at the vicinity of the nugget, crack grows around it as an arc shape and the fracture occurs at the sheet rather than the nugget.
-
4. The majority portion of the fatigue life of spot welds relates to the initiation and the crack growth to the specimen's surface.
-
5. Since in high loading level, the nugget is pulled out after a small crack growth, the fatigue life of specimens decreased with any increase in loading. However, in low loading level, the crack grows significantly.
-
6. The results of three-dimensional finite element analysis have been compared with those achieved from experimental tests. The numerical analysis results obtained show good agreement with those obtained from experimental results.
-
7.Among the applied model, the FNK model has the best accuracy for all types of the specimens.
-
8. The modified Paris model shows rather inaccurate prediction of fatigue life among the employed fatigue model for fatigue strength of spot welded U-shape specimens investigated in this paper.
References
- Adib H, Gilgert J, Pluvinage G (2004)Fatigue life duration prediction for welded spots by volumetric method. International Journal of Fatigue 26.1: 81-94.
- Anderson TL (1994) Fracture Mechanics, fundamentals and applications, second edition, CRC press.
- Chen J, Zihui X (2014)A fatigue life prediction method for coke drum base, weld, and HAZ materials from tensile properties. Materials & Design 63: 575-583.
- Choi BH, Joo DH, Song SH (2007)Observation and prediction of fatigue behavior of spot welded joints with triple thin steel plates under tensile-shear loading. International journal of fatigue 29.4: 620-627.
- Cornell Fracture Group, Cornell University, <www.cfg.cornell.edu>
» www.cfg.cornell.edu - Dong P (2001)A structural stress definition and numerical implementation for fatigue analysis of welded joints. International Journal of Fatigue 23.10: 865-876.
- EsmaeiliF, RahmaniA, BarzegarS, and AfkarA (2015)Prediction of fatigue life for multi-spot welded joints with different arrangements using different multiaxial fatigue criteria. Materials and Design 72: 21-30.
- Florea RS, Bammann DJ,Yeldell A, Solanki KN, Hammi Y (2013)Welding parameters influence on fatigue life and microstructure in resistance spot welding of 6061-T6 aluminum alloy. Materials & Design 45: 456-465.
- Hadipour M, Alambeigi F, Hosseini R, Masoudinejad R (2011) A study on the vibrational effects of adding an auxiliary chassis to a 6-ton truck. Journal of American Science7(6):1219-26.
- Hassanifard S, Ahmadi SR, Mohammad Pour M (2013)Weld arrangement effects on the fatigue behavior of multi friction stir spot welded joints. Materials & Design 44: 291-302.
- Hassanifard S., Mohammadpour M, Ahmadi Rashid H (2014)A novel method for improving fatigue life of friction stir spot welded joints using localized plasticity. Materials and Design 53: 962-971.
- Kang H, Dong P, Hong JK (2007)Fatigue analysis of spot welds using a mesh-insensitive structural stress approach. International Journal of fatigue 29.8: 1546-1553.
- Kang HT (2007)Fatigue prediction of spot welded joints using equivalent structural stress. Materials & design 28.3: 837-843.
- Lin PC, LinSH, Pan J (2006)Modeling of failure near spot welds in lap-shear specimens based on a plane stress rigid inclusion analysis. Engineering fracture mechanics 73.15: 2229-2249.
- Lin SH, Pan J, Wung P, Chiang J (2006)A fatigue crack growth model for spot welds under cyclic loading conditions. International Journal of Fatigue 28.7: 792-803.
- Long X, Khanna SK (2007)Fatigue properties and failure characterization of spot welded high strength steel sheet. International journal of fatigue 29.5: 879-886.
- MasoudiNejad R (2013) Rolling contact fatigue analysis under influence of residual stresses. MS Thesis, School of Mechanical Engineering, Sharif University of Technology, Iran.
- MasoudiNejad R (2014)Using three-dimensional finite element analysis for simulation of residual stresses in railway wheels. Engineering Failure Analysis 45: 449-455.
- MasoudiNejad R, Farhangdoost K, Shariati M (2015)Numerical study on fatigue crack growth in railway wheels under the influence of residual stresses. Engineering Failure Analysis 52: 75-89.
- MasoudiNejad R, Farhangdoost K, Shariati M (2016) Three-dimensional simulation of rolling contact fatigue crack growth in UIC60 rails. Tribology Transactions (just-accepted): 00-00.
- MasoudiNejad R, Farhangdoost K, Shariati M, Moavenian M (2016) Stress intensity factors evaluation for rolling contact fatigue cracks in rails. Tribology Transactions (just-accepted): 1-29.
- MasoudiNejad R, Salehi S M, Farrahi GH, Chamani M (2013) Simulation of crack propagation of fatigue in Iran rail road wheels and Effect of residual stresses. In Proceedings of the 21 st International Conference on Mechanical Engineering, Iran.
- MasoudiNejad R, Salehi SM, Farrahi GH (2013) Simulation of railroad crack growth life under the influence of combination mechanical contact and thermal loads.in 3nd International Conference on Recent Advances in Railway Engineering, Iran.
- MasoudiNejad R, Shariati M, Farhangdoost K (2016) 3D finite element simulation of residual stresses in UIC60 rails during the quenching process. Thermal Science(just-accepted): 13-13.
- MasoudiNejad R, Shariati M, Farhangdoost K (2016) Effect of wear on rolling contact fatigue crack growth in rails. Tribology International 94: 118-125.
- Moghadam DG, Farhangdoost K, MasoudiNejad R (2016) Microstructure and Residual Stress Distributions Under the Influence of Welding Speed in Friction Stir Welded 2024 Aluminum Alloy. Metallurgical and Materials Transactions B 47(3): 2048-2062.
- Mohammadpour M, Hassanifard S, Amini A, Reshadi F (2014)An experimental investigation of fatigue behavior and deformation of double spot friction welded joints. Materials and Design 57: 705-711.
- Newman Jr JC (1984)A crack opening stress equation for fatigue crack growth. International Journal of Fracture 24.4: R131-R135.
- Pan N, Sheppard S (2002) Spot welds fatigue life prediction with cyclic strain range. International Journal of Fatigue 24.5: 519-528.
- Salehi SM, Farrahi GH, Sohrabpoor S,MasoudiNejad R (2014)Life estimation in the Railway Wheels under the Influence of Residual Stress Field. International Journal of Railway Research 1.1: 53-60.
- Sun X, Stephens EV, Khaleel MA (2008)Effects of fusion zone size and failure mode on peak load and energy absorption of advanced high strength steel spot welds under lap shear loading conditions. Engineering Failure Analysis 15.4: 356-367.
- Yang X, Xia Y, Zhou Q (2010)A simplified FE model for pull-out failure of spot welds. Engineering Fracture Mechanics 77.8: 1224-1239.
- Zhang S(1999)Approximate stress intensity factors and notch stresses for common spot-welded specimens. WELDING JOURNAL-NEW YORK- 78: 173-s.
Publication Dates
-
Publication in this collection
Dec 2016
History
-
Received
14 May 2016 -
Accepted
15 Aug 2016