Mathematical Description of a Flexible Connection of Links and its Applications in Modeling the Joints of Spatial Linkage Mechanisms

Abstract

The general mathematical model of a flexible connection of links by means of spring-damping elements is presented in the paper. The formalism of homogeneous transformation matrices is used to derive formulas for the energy of spring deformation and the Rayleigh dissipation function of the spring-damping elements. The formulas have convenient forms to connect them to Lagrange equations of the second order. The replacement models of the spherical and revolute joint are presented as a particular case of the general model and are used for dynamics analysis of a one-DOF RSRRP linkage mechanism. The numerical results obtained here using the replacement models were compared with the results from the cut-joint technique.

Keywords:
modeling; replacement model; spherical joint; revolute joint; statics analysis; dynamics analysis; spatial mechanism; cut-joint technique

Nomenclature
• c  kinematic chain index
• (c,p)  symbol of link (joint) p in chain c
• g  acceleration of gravity
• C_ε,α,b_ε,α|_{α ∈{ x,y,z }}  coefficients of stiffness and damping of the spring-damping element in the α direction, respectively
• l ^{( c,p )}  length of link (c,p)
• m ^{( c,p )}  mass of link (c,p)
• _ñ ^{( cp )} _dof  number of generalized coordinates describing the motion of link (c,p) with respect to link (c, p-1)
• _n ^{( cp )} _dof  number of generalized coordinates describing the motion of link (c,p) with respect to reference system {c, 0}
• n ^{( c )} _l  number of links in chain c
• t ^(1,1) _{dr ,0}  parameter defining the time course of the value of the driving torque (it determines the value of this torque after the starting time)
• t ^(1,1) _st  starting time
• E^tr _p,e,E^rot _p,e  translational and rotational potential energies of spring deformation of the spring-damping element, respectively
• R^tr _e,R^rot _e  translational and rotational Rayleigh dissipation functions of the spring-damping element, respectively
• d ^tr_e , d ^rot _e  vectors of translational and rotational deformation of the spring-damping element, respectively
•  vector of joint force and torque in point A in the local coordinate system, respectively
•  vector of position of point A in the local coordinate system
• r ^(cp) _A  vector of position of point A in the global reference system {0}
• t ^(1,1) _dr  driving torque
• t ^(1,1) _res  resistance torque
• B^tr_e , B^rot_e  matrices of translational and rotational damping of the spring-damping element, respectively
• C^tr_e , C^rot_e  matrices of translational and rotational stiffness of the spring-damping element, respectively
• H ^{( c,p )}  inertial matrix 4 × 4 of link (c,p)
•  rotation matrix 3 × 3 from the local coordinate system of link (c,p) to the system of link (c,p-1)
• R ^{( c,p )}  rotation matrix 3 × 3 from the local coordinate system of link (c,p) to the global reference system {0}
•  transformation matrix 4 × 4 from the local coordinate system of link (c,p) to the system of link (c,p-1)
• T ^{( c,p )}  transformation matrix 4 × 4 from the local coordinate system of link (c,p) to the global reference system {0}
• 
•  parameter defining the time course of the value of the resistance torque
• DOF  degree(s) of freedom
• ODE  ordinary differential equation(s)
• DAE  algebraic differential equation(s)

1 INTRODUCTION

Flexibility of connections between links is a very important feature which should be taken into account when modeling the dynamics of machines. It can be independent of the design, as in the case of cranes or excavators that are placed directly on the ground. It can also be the effect of the assumptions of the design introduced in order to increase the range of the working area (e.g. mobile cranes) or visibility in the case of cranes mounted on platforms or ships (when applied in columns several tens of meters in length).

The case of modeling of multibody systems with a closed-loop kinematic chain requires the cutting of the system (cut-joint technique) in order to obtain a system with open-loop kinematic chains. Then such an approach requires the formulation of constraint equations (Blajer,1998, Farid and Lukasiewicz, 2000, Frączek, 2002, Hanzaki et al., 2009). As a result of this procedure, a system of DAEs is obtained. Solving this system of equations is difficult and requires special calculation methods (Nergut et al., 2006). Another method is to use double differential equations of the constraints (Blajer, 1998) or replacement models of the joints modeled by means of spring-damping elements. In both cases a system of ODEs is obtained. In the first case, sometimes additional stability methods must be used (e.g. Baumgarte's method (Baumgarte, 1972, Frączek, 2002) or extended Lagrange multipliers methods (Frączek, 2002)). A disadvantage of the replacement models is that when large values of stiffness coefficients are used, a system of stiff differential equations is obtained. In order to solve this system, small-step or other integration methods are required.

A particular case of the replacement model, and one that is often used in practice, is the model of a spherical joint. In the literature there are various methods for modeling this joint. The first of these (Fig. 1a) is done by means of one spring-damping element (Schliehlen et al., 2000, Wang et al., 2002). The second approach is to model by using a system of three spring-damping elements (Fig. 1b). In this model the relative displacement of link p with respect to link p - 1 along any axis causes deformations of all spring-damping elements (Ganiev and Kononenko, 1976, Szczotka, 2004, Adamiec-Wojcik et al., 2008, Wittbrodt et al., 2006, Harris and Piersol, 2010, Augustynek, 2010 Urbas, 2011). In the third approach a spherical joint is modeled by means of a system of three one-direction spring-damping elements (Fig. 1c). In this case the relative displacement of link p with respect to link p - 1 along a particular axis causes deformation only of the spring-damping element associated with this axis (Wittbrodt et al., 2006, Urbaś 2011, Urbaś et al., 2011). This way of modeling through the use of directional spring-damping elements causes the imposition of constraints on the appropriate degrees-of-freedom of the body. Therefore, it can be used to model any joint.

Figure 1:
Models of a spherical joint.

The general model of the flexible connection of links by means of the spring-damping elements is presented in the paper. Homogeneous transformations are used to derive the formulas for the energy of spring deformation and the Rayleigh dissipation function of the spring-damping element. As a particular case of the general model, models of the spherical and revolute joint are presented in the statics and dynamics analysis of a one-DOF RSRRP linkage mechanism. The results of calculations using the replacement models were compared with the results obtained using the cut-joint technique. The algorithms for both methods are also presented.

2 GENERAL MODEL OF THE SPRING-DAMPING ELEMENT

Fig. 2 presents two chains connected by means of the spring-damping element (sde e).

Figure 2:
Links (1, n_l ⁽¹⁾) and (2,n_l ⁽²⁾) connected by means of the spring-damping element. n_l ⁽¹⁾). n_l ⁽²⁾). e, respectively - coordinate system connected with link (2, - spring and damping coefficients of sde - coordinate system of sde e connected with link (1, nl(1)) and (2,nl(2)), respectively. - coordinate system connected with link (1,

It is assumed that the axes of the coordinate system coincide with the principal elastic axes of sde e. This means that the axes of the system are selected so that under the influence of the force (moment) directed along the specified axis, displacement (rotation) is only in the direction (around) this axis.

The homogeneous transformation matrices from the local coordinate systems {1, n_l ⁽¹⁾} and {2,n_l ⁽²⁾} to the initial coordinate system {0} can be written in the forms

(1.1)

(1.2)

where n_l ⁽¹⁾} and {2,n_l ⁽²⁾} in {0}, respectively - vectors describing the origins of the coordinate systems {1,

R^{(1, n}_l ⁽¹⁾⁾, R^{(2, n}_l ⁽²⁾⁾ - rotary matrices describing the direction cosines of the axes of the coordinate systems {1, n_l ⁽¹⁾}in {0} and {2,n_l ⁽²⁾}in {0}, respectively.

It is assumed that the position and orientation of systems {1,e} and {2,e} in {1, n_l ⁽¹⁾} and {2,n_l ⁽²⁾} are described by matrices with constant elements.

(2.1)

(2.2)

where e} and {2,e} in {1, n_l ⁽¹⁾} and {2,n_l ⁽²⁾}, respectively, - vectors describing the origin of coordinate systems {1,

e} and {2,e} in {1, n_l ⁽¹⁾}, and {2,n_l ⁽²⁾}, respectively. - rotary matrices describing the orientation of coordinate systems {1,

If sde e is undeformed, then the coordinate systems {1,e} and {2,e} coincide with each other. As a result of the acting of forces and moments on the considered system, there are translations and rotations of coordinate systems {1,e} and {2,e}.

It is assumed that the principal elastic axes of sde e coincide with the axes of system {1,e} connected with link {1, n_l ⁽¹⁾}. This means that the translational and rotational deformations of sde e will be described in the coordinate system {1,e}. The considered situation is presented in Fig. 3.

Figure 3:
The sde connecting with link {1, n_l ⁽¹⁾}.

According to Eqs. (1) and (2), the homogeneous transformation matrices from systems {1,e}and {2,e} to system {0} have the following forms

(3.1)

(3.2)

where

Let us assume that the translational and rotational displacements, being deformations of sde e, have the components

(4.1)

(4.2)

The potential energy of spring deformation and the Rayleigh dissipation function (translational and rotational) of sde e can be presented as follows

(5.1)

(5.2)

(5.3)

(5.4)

where

The coordinates of the origin of system {2,e} can be expressed in the coordinates of system {1,e} by the formula

(6)

and vector d^tr_e as

(7)

Where

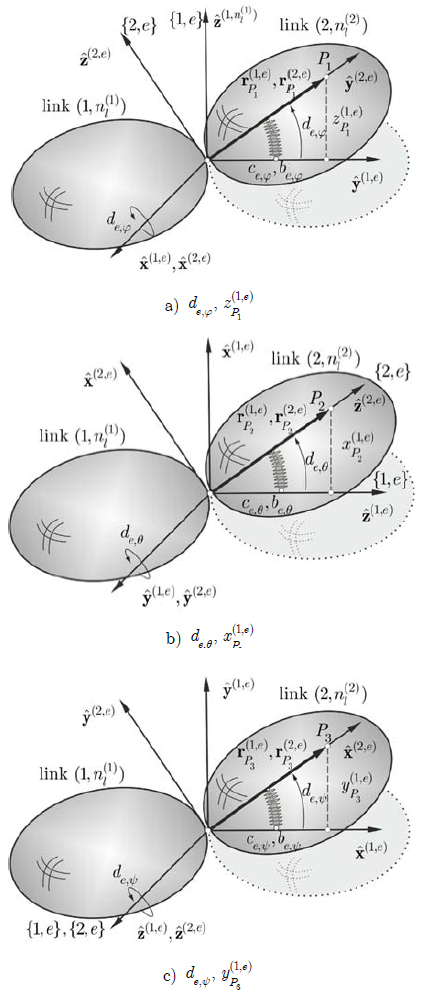
In order to calculate the components of vector d^rot_e , it is assumed that the rotational angles d_e,φ, d_e,θ, d_e,ψ are small. Then it can be written as follows (Fig. 4)

(8.1)

(8.2)

(8.3)

where P ₁ in {1,e}, - coordinate of point ,

P₂ in {1,e}, - coordinate of point ,

P₃ in {1,e}, . - coordinate of point

Figure 4:
Displacements and rotational angles in sde e.

Displacements can be solved from the formulas

(9.1)

(9.2)

(9.3)

Having Eqs. (3) and (8), we obtain

(10)

If we assume that the origins of systems {1,e} and {2,e} coincide with each other, then we take into account that formula (*) in Eq. (10) is equal to zero and can be written as follows

(11.1)

In a similar way we can calculate

(11.2)

and

(11.3)

The components of vectors d^rot_e can be calculated from Eq. (8) as follows

(12.1)

(12.2)

(12.3)

After taking into account Eqs. (7) and (12), the potential energy of spring deformation and the Rayleigh dissipation function of sde e can be written in the following way

(13.1)

(13.2)

where

In order to use these formulas, the derivatives of Eq. (13) for the generalized coordinates describing the motion of links {1, n_l ⁽¹⁾} and {2,n_l ⁽²⁾} in the initial coordinate system {0}can be calculated as follows

(14.1)

(14.2)

where

The formulas presented here can be used to model any joints. Clearances are neglected in these formulas.

The model presented here will be used to derive equations of motion of the one-DOF RSRRP linkage mechanism.

3 DYNAMICS ANALYSIS OF THE SPATIAL LINKAGE MECHANISM

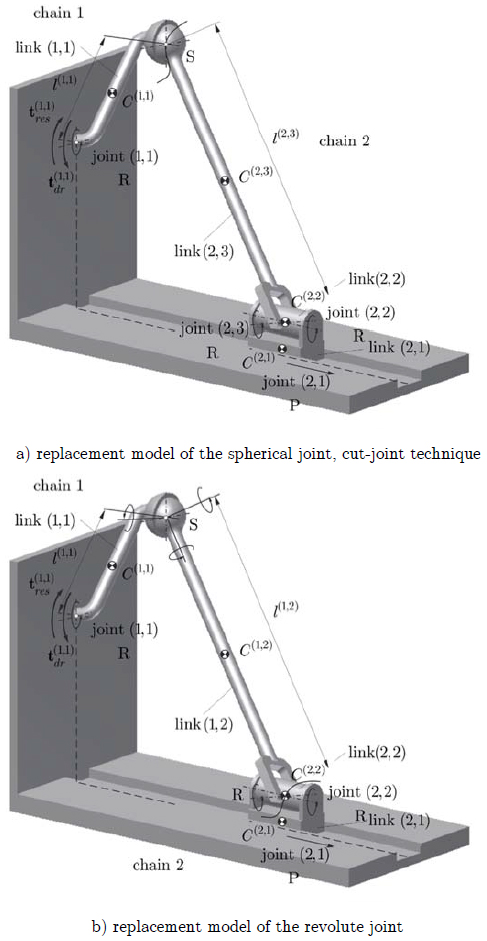
An example of using the replacement models of the spherical and prismatic joint in the one-DOF RSRRP linkage mechanism is shown below (Haug, 1989). The mechanism consists of four rigid links connected to a fixed base - Fig. 5.

Figure 5:
Analyzed spatial mechanism.

The mechanism considered here was divided in the place of spherical joint S for a replacement model of a spherical joint and the cut-joint technique (Fig. 6a). Two open-loop kinematic chains joined with the fixed base were obtained: 1 - is formed by link (1,1), and 2 is formed by links (2,1), (2,2), (2,3). For a replacement model of a revolute joint, the mechanism is cut in the place of revolute joint R (Fig. 6b). This approach also allows to obtain a system with two open-loop kinematic chains but built with: 1 - is formed by links (1,1), (1,2), and 2 is formed by links (2,1), (2,2). In both cases link (1,1) is the driving link loaded by torque t^(1,1) _dr and resistance torque t^(1,1) _res .

Figure 6:
Division of the mechanism into two open-loop kinematic chains.

The local coordinate systems were attached to the particular links according to the Denavit-Hartenberg notation (Denavit and Hartenberg, 1955). The fixed coordinate system {1,0}, related to chain 1, is understood as the global reference system, and system {2,0}, related to chain 2, is the auxiliary reference system. For replacement models, the formed kinematic chains are connected by the spring-damping element. In fact, this element is a system of three stiff springs and three dampers whose invariable action directions are consistent with the versor directions of the global reference system {1,0} (Figs. 7a and b). In the cut-joint technique, joint forces f_S,x , f_S,y , f_S,z and -f_S,x , -f_S,y , -f_S,z , acting on chains 1and 2, respectively, in accordance with the versor directions of the global reference system {1,0} (Fig. 7c), are applied in the place of the mechanism cut.

Figure 7:
Assumed coordinate systems.

The motion of chain c is described by the joint coordinate vectors:

(15)

where:

1) for chain 1:

- replacement model of the spherical joint, cut-joint technique

- replacement model of the revolute joint

2) for chain 2:

- replacement model of the spherical joint and cut-joint technique

- replacement model of the revolute joint

The homogeneous transformation matrices from the local systems attached to the links to the global reference system {1,0} are determined according to the relationship:

(16)

where T^(c,0)= I,

1) for chain 1:

- replacement model of the spherical joint, cut-joint technique

- replacement model of the revolute joint

2) for chain 2:

- replacement model of the spherical joint, cut-joint technique

- replacement model of the revolute joint

The homogeneous transformation matrices from the local systems sde e to the global reference system {1,0} are determined according to the relationship:

(17)

where:

- replacement model of the spherical joint

- replacement model of the revolute joint

4 SYNTHESIS OF THE EQUATIONS OF MOTION AND THE ALGORITHM FOR THEIR SOLUTION

The equations of motion of chains are determined by using the formalism of Lagrange equations on the basis of algorithms given in a monograph by Jurevič (ed.), 1984. The structure of these equations is different depending on the proposed analysis method:

1. Replacement model of the spherical joint

(18.1)

2. Replacement model of the revolute

(18.2)

3. Cut-joint technique

(18.3)

where

The structure and number of equations were different for each of the methods, thus different algorithms were used to solve them.

For the replacement models of a spherical and revolute joint, a system of four and six ODEs of second order was obtained, respectively (Figs. 8a and b). At the beginning of the procedures assumed here the configuration of the mechanism was determined in conditions of static equilibrium of its links. Minimal movements of the links, caused by gravity forces, result from the flexibility of the replacement model. By performing this part of the procedures (i.e. statics analysis), a system of non-linear algebraic equations, obtained on the basis of the differential equation, is solved by the Newton-Raphson method. The positions of the links determined in such a way also determine the initial conditions in the dynamics analysis of the mechanism.

Figure 8:
Algorithms of solving equations of statics and dynamics of the mechanism in question.

The system of seven DAEs which contain, besides the unknown components of the acceleration vectors _S , is obtained for the cut-joint technique (Fig. 8c). All of these unknown values are determined by using the Gauss elimination method. A system of four ODEs of second order is eliminated from the system presented here. Additional calculations using the recursive Newton-Euler algorithm were performed in order to determine the joint forces and torques in the other joint. also unknown components of vector f and

In both cases the components of the acceleration vectors are broken down into a system of ODEs of first order and solved by the Runge-Kutta method of the fourth order with a constant integration step.

5 NUMERICAL CALCULATION RESULTS

The parameters and initial configuration of the mechanism are presented in Fig. 9. It was assumed that at the initial moment of the mechanism's motion the symmetry axes of all its links are in the vertical plane ŷ⁽¹⁰⁾ of the global reference system {1,0}.

Figure 9:
Initial configuration of the mechanism.

The assumed time courses of the value of the driving torque t ^(1,1) _dr and the resistance torque t ^(1,1) _res are presented in Figs. 10a and b, respectively. The following parameters were taken into account in the case considered here,: t ^(1,1) _{dr ,0}= 10Nm, t ^(1,1) _st= 5s,

Figure 10:
Time course of: a) driving torque, b) resistance torque.

It is assumed that the analysis time is 15s. A constant integration step equal to 10^-4s is assumed.

A comparison of the numerical results of the courses of components of joints forces f_S , f_R and torques n_R in both methods are presented in Fig. 11.

Figure 11:
Courses of components of joint forces f_S , f_R and torque n_R .

As can be observed, sufficient compliance results are obtained even at relatively low values of stiffness and damping coefficients and a large value of the integration step size.

Numerical tests carried out with different integration steps did not confirm the necessity of using a stabilization method of constraint equations. The Euclidean norm determined for the integration step equal to 10^-4s has an insignificant value (less than 10^-6m).

6 CONCLUSIONS

The general model of a flexible connection of links is presented in the paper. The connection is done by means of spring-damping elements. It was derived the formulas for the energy of the spring deformation, the Rayleigh dissipation function and their derivatives convenient to introduce them in Lagrange's equations of the second order. The formalism of homogeneous transformations was used to derive these formulas. The general model presented here can be used to formulate the replacement model of any joint.

The models of the spherical and revolute joint are presented as an example of the general model. The results for the replacement models were compared by using the cut-joint technique. Good compatibility can be observed of the results obtained here.

In the author's opinion, the use of replacement models can be efficient when the flexibility and clearances are taken into account.

References

• Adamiec-Wójcik I., Maczyński A., Wojciech S., (2008) Application of homogeneous transformations in modeling of the offshore systems, The Transport and Communication Press, Warsaw (in Polish)
• Augustynek K., (2010) Dynamics analysis of the spatial mechanisms with flexible links, PhD thesis, Radom University, Radom (in Polish)
• Baumgarte, J., (1972) Stabilization of constraints and integrals of motion in dynamical systems, Computer Methods in Applied Mechanics and Engineering, 1, 1-16
• Blajer, W., (1998) The methods for dynamics of the multibody systems, Radom University Press, Radom (in Polish)
• Craig J.J., (1989) Introduction to robotics. Mechanics and control, Addison-Wesley Publishing Company, Inc.
• Denavit J., Hartenberg R.S., (1955) A kinematic notation for lower-pair mechanisms based on matrices, ASME Journal of Applied Mechanics, June
• Farid M., Lukasiewicz S. A., (2000) Dynamic modeling of spatial manipulators with flexible links and joints, Computers and Structures 75, 419-437
• Frączek J., (2002) Modeling of the spatial mechanisms using the methods for multibody system, Warsaw University of Technology Press, No. 196, Warsaw (in Polish)
• Ganiev R.F., Kononenko V.O., (1976) Vibration of rigid bodies, Nauka, Moscow (in Russian)
• Hanzaki R. A., Saha K. S.,·Rao P.V.M., (2009), An improved dynamic modeling of a multibody system with spherical joints, Multibody System Dynamics, 21, 325-345
• Harris C.M., Piersol A.G., (2010) Harries' shock and vibration handbook, 6^th edition, McGraw Hill
• Haug E.J., (1989) Computer aided kinematics and dynamics of mechanical systems, Vol. 1: Basic methods, Allyn and Bacon
• Jurevič E.I., (1984) Dynamics of robots, Nauka, Moscow (in Russian)
• Nergut D., Ottarsson G., Rampalli R., Sajdak A., (2006) On an implementation of the Hilber-Hughes-Taylor method in the context of index 3 differential-algebraic equations of multibody dynamics, DET2005-85096
• Schiehlen W., Rükgauer A., Schirle Th., (2000) Force Coupling versus differential algebraic description of constrained multibody systems, Multibody System Dynamics, 4, 317-340
• Szczotka M., (2004) Modeling of the motion of the vehicles with taking into account different transmission systems, PhD thesis, Bielsko-Biala, (in Polish)
• Urbaś A., (2011) Dynamic analysis and control of the working machines with flexibly supported base, PhD thesis, Bielsko-Biala (in Polish)
• Urbaś A., Szczotka M., Wojciech S., (2011) The influence of flexibility of the support on dynamic behavior of a crane, International Journal of Bifurcation and Chaos, 21(10), 2963-2974
• Wang J., Gosselin C.M., Cheng L., (2002) Modeling and simulation of robotic systems with closed kinematic chains using the virtual spring approach, Multibody System Dynamics, 7, 145-170
• Wittbrodt E., Adamiec-Wójcik I., Wojciech S., (2006) Dynamics of flexible multibody systems. Rigid finite element method, Springer, Berlin

Publication Dates

• Publication in this collection
  Dec 2016

History

• Received
  02 Dec 2015
• Reviewed
  03 Aug 2016
• Accepted
  16 Sept 2016