Vibration Analysis of Rotating Functionally Graded Cylindrical Shells with Orthogonal Stiffeners

Abstract

In this paper, free vibration analysis of rotating functionally graded cylindrical shells with orthogonal stiffeners is presented. Based on Love's first approximation theory and smeared stiffeners technique, the governing equations of motion which take into account the effects of initial hoop tension and also the centrifugal and Coriolis forces due to rotation are derived. The influence of the power law index, the stiffener's height-to-width ratio, the circumferential wave numbers, the shell length-to-radius ratio, and the shell radius-to-thickness ratio on the natural frequencies of the simply supported rotating stiffened functionally graded cylindrical shell are investigated. To validate the present analysis, comparisons are made with those available in the literature for particular cases; very good agreements are achieved.

Keywords:
Natural frequency,rotating; functionally graded material; vibration analysis; cylindrical shell; orthogonal stiffeners

1 INTRODUCTION

Functionally graded materials (FGMs) are a new class of material in which the material properties are varied continuously along a certain dimension of the structure. Typical FGMs are made from a mixture of ceramic and metal. The thermal resistance of the material is increased due to low thermal conductivity of the ceramic and the lack of toughness of ceramics is eliminated by using the metal. Hence, the main applications of FGMs have been in high-temperature environments. Functionally graded cylindrical shells are used in many industrial applications, such as aerospace, mechanical and nuclear engineering.

The vibration of non-rotating functionally graded cylindrical shells has been studied extensively for many years. Loy et al. (1999) used Rayleigh-Ritz methodto analyze free vibration of functionally graded cylindrical shells based on Love's shell theory. They investigated the effects of the constituent volume fractions and the configurations of the constituent materials on the natural frequency. Pradhan et al. (2000) presented the vibration characteristics of functionally graded cylindrical shells with various boundary conditions using Rayleigh method. The effect of boundary conditions and volume fractions on the natural frequency of the functionally graded cylindrical shell was studied. Li et al. (2010) used Flügge's shell theory to study the free vibration of a simply supported three-layer circular cylindrical shell with the inner and the outer layer made of the same homogenous material and the functionally graded middle layer. Vel (2010) presented an exact elasticity solution for the free and forced vibration of functionally graded cylindrical shells.

Structures such as gas turbine engines, electric motors, and rotor systems usually operate under rotation with constant angular velocities. In contrast with non-rotating cylindrical shells, studies on the vibration of rotating cylindrical shells have been sparse. Chen et al. (1993) applied the finite element method for vibration analysis of isotropic high rotating cylindrical shells. The general equations with consideration of Coriolis accelerations and large deformation were established by the method of linear approximation. Based on Sanders's shell theory, Sun et al. (2012) presented free vibration analysis of thin rotating isotropic cylindrical shells with various boundary conditions using the Fourier series expansion method. Lam and Loy (1994) studied the vibrations of thin rotating laminated cylindrical shells based on Love's first approximation theory. The effects of the thickness-to-radius ratio, the length-to-radius ratio and the lamination angle on the fundamental frequency were presented. Lam and Loy (1995) continued their study on the vibration characteristic of rotating laminated cylindrical shells using four common thin shell theories: Donnell's, Flugge's, Love's, and Sanders' shell theories. The free vibration of thick rotating cross-ply laminated composite cylindrical shells was studied by Lam and Qian (1999) based on the first-order shear deformation shell theory. Analytical solutions were presented, and frequency characteristics of thin and thick shells were investigated with respect to the variations of rotating speeds, circumferential wave numbers, and length-to-thicknessratio. The effect of transverse shear deformation was also emphasized. The natural frequency of rotating functionally graded cylindrical shells was calculated by Xiang et al. (2012). Theoretical formulation were established based on Love's first approximation theory; and the effects of the power law index, the wave numbers and the thickness-to-radius ratio on the natural frequency of rotating functionally graded cylindrical shell were carried out. Using Love's shell theory, Loy et al. (1999) analyzed frequency characteristics of the functionally graded cylindrical shell, parametric studies were numerically investigated.

The stiffeners are used to make shells with significantly increasing stiffness. Thus, to study these structures has been a remarkable trend of researchers in recent years. Mustafa and Ali (1989) presented the energy method to determine the natural frequency of orthogonally stiffened isotropic cylindrical shells. Bich et al. (2012) which was based on the classical shell theory and the smeared stiffeners technique, carried out the nonlinear dynamical analysis of eccentrically stiffened functionally graded cylindrical panel. Lee and Kim (1998) studied the vibration of the rotating composite cylindrical shell with orthogonal stiffeners using energy method. The effects of the stiffener's height-to-width ratio, the shell's radius-to-thickness ratio, and shell's length-to-radius ratio on the natural fundamental frequency were examined. Zhao et al. (2002) used Love's shell theory and the energy approach, and carried out the vibration analysis of simply supported rotating cross-ply laminated composite cylindrical shells with stringer and ring stiffeners.

To the best of the authors' knowledge, there is no published research in the literature conducted on the free vibration analysis of the rotating stiffened FG cylindrical shells. Thus, in this paper, based on Love's first approximation theory and smeared stiffeners technique, the vibration analysis of rotating functionally graded cylindrical shell with orthogonal stiffeners is presented. In this study, the governing equations of motion are developed by using smeared stiffeners technique and taking into account the effects of centrifugal and Coriolis forces. The shell is made from functionally graded material and the stiffener from the isotropic material. The presented analysis is verified by comparing the numerical results with those in available literature. The effects of the rotating speed, the power law index, the stiffener's height-to-width ratio, the circumferential wave numbers, the shell length-to-radius ratio, and the shell radius-to-thickness ratio on the natural frequency of the simply supported rotating stiffened cylindrical functionally graded shell are studied.

2 FORMULATION

2.1 Functionally Graded Material

Consider a functionally graded cylindrical shell with orthogonal stiffeners rotating about its horizontal axis at a constant angular velocity Ω as shown Fig. 1, where R, L, and h are the radius, length, and thickness of the shell respectively. The depth of the stringer and ring are denoted by h_s and h_r , respectively, and corresponding widths are denoted by b_s and b_r , respectively. The distances between the stringers, rings are denoted by S_s and S_r . The number of stringers is n_s , andthe number of rings is n_r . Subscripts (s, r) indicate the axial (stringer) and circumferential (ring) stiffeners, respectively. The origin of the coordinate system is located on the edge of the shell, the arbitrary point in the mid-surface is taken by the axial, circumferential and radial axes (x, θ, z). The components of the displacement field in this coordinate system are u in the x, v in the θ and w in the z-direction. Young's modulus, mass density, and Poisson's ratio of stiffeners are E ₀ , ρ ₀ , v ₀. The materials properties are assumed to be graded in the thickness direction and vary according to power law as follow:

(1)

where p is power law index. E ₁ , ρ ₁ , v ₁ are Young's modulus, mass density, and Poisson's ratio of the outer surface of FG shells, respectively. E ₂ , ρ ₂ , v ₂ are Young's modulus, mass density, and Poisson's ratio of the inner surface of FG shells, respectively.

Figure 1:
Coordinate system and geometry of rotating stiffened FGM cylindrical shell.

2.2 Constitutive Relations

According to the Love's shell theory, the strains across the shell thickness at the distance z from the mid-surface are as follows:

(2)

where

where u ₀ , υ ₀ , w ₀ are the displacement components of the point in the mid-surface (z=0).

Stress - strain relation for the shell can be expressed as:

(3a)

and for stiffeners:

(3b)

where E ₀ is Young's modulus of stiffeners (E _{0 =} E ₁ with external stiffeners, E _{0 =} E ₂ with internal stiffeners). This means that material properties change continuously from shell to stringers.

Based on smeared stiffeners technique, by omitting the wrist of stiffeners and using defined formulas from (3a) and (3b) we obtain the expressions for the force and moment resultants of a stiffened cylindrical shell as follows (Bich et al., 2012):

(4)

(5)

where

with

and

Here, the displacements from the mid-surface of the shell to the centroid of the stringer and ring are denoted by z_s and z_r , respectively. A_s and A_r are the area of the cross-sections of the stringer and the ring, respectively.

2.3 Governing Equations

Using Love's first approximation theory and taking to account the effects of initial hoop tension and the centrifugal and Coriolis forces, the equations of motion in terms of the force and moment resultants can be written as follows (Lam and Loy, 1994):

(6)

with

and:

where ρ ₀ and ρ_t are the mass density of the stiffeners and the mass density per unit length of the shell, respectively. Ñ _θ is the initial hoop tension due to the centrifugal force and is defined as Ñ _θ = ρ_t Ω² R ².

Substitution of Eqs. (4) and (5) with expressions from Eq. (2) into Eq. (6) leads to three equations of motion which can be written as:

(7)

where L_ij are the differential operators and are given in the ^Appendix.

3 ANALYTICAL SOLUTION

In this paper, the analytical solution for free vibration of rotating orthogonally stiffened FGM cylindrical shell with simply supported boundary conditions at both axial ends is presented. The mathematical expressions for this boundary condition are given by:

(8)

The displacement fields which satisfy these boundary conditions can be written as follows:

(9)

where A_mn , B_mn , and C_mn are the amplitudes for each directions, m and n are the axial and circumferential wave numbers, respectively and w is the natural angular frequency.

Substituting the displacement field from Eq. (9) into Eq. (7) yields:

(10)

The coefficients k_ij (i, j = 1, 2, 3) are given in detail in ^Appendix.

For non-trivial solutions, one sets the determinant of the characteristic matrix in Eq. (10) to zero. Expanding the characteristic determinant equation, the polynomial for the natural frequencies can be obtained as:

(11)

Equation (11) gives the two smallest eigensolutions for each mode of the vibration. It consists of negative and positive eigenvalues corresponding to the forward and backward traveling waves.

It is noted that the corresponding eigensolution for a non-rotating FG cylindrical shell can also be obtained from Eq. (10) by putting the rotating speed to zero (Ω = 0).

4 RESULTS AND DISCUSSIONS

4.1 Validation of the Present Study

In all of the following examples, the geometrical dimensions and material properties of the shells and stiffeners are given in Table 1.

Table 1:
The geometrical and material properties for the stiffened FG cylindrical shells.

Property				Geometric Data
Type of stiffeners Model	Stringers	Rings	Stringers	Orthogonal rings/stringers	Unstiffened	Orthogonal rings/stringers
	M1	M2	M3	M4	M5	M6
No. of stiffeners	60	19	04	13/20		05/10
Radius (m)	0.242	0.49759	0.1945	0.203	1	0.2
Thickness (m)	6E-4	1.65E-3	4.64E-4	2.04E-3	0.05	0.002
Length (m)	0.6096	0.3945	0.9868	0.813	20	1
Height of stiffeners (m)	0.00702	0.005334	0.0101	0.006/0.006		0.002/0.012
Width of stiffeners (m)	0.002554	0.003175	0.00104	0.004/0.008		0.002/0.012
E0 (N / m2)	6.9E+10	6.9E+10	2.00E+11	2.07E+11		2.00E+11
υ0	0.3	0.3	0.3	0.3		0.3
ρ0 (kg / m3)	2714	2762	7770	7430		5700
E1 (N / m2)					2.07788E+11	2.00E+11
υ1					0.317756	0.3
ρ1 (kg / m3)					8166	5700
E2 (N / m2)					2.05098E+11	7.0E+10
υ2					0.31	0.3
ρ2 (kg / m3)					8900	2702
Stiffening type	External	External	Internal	Internal		External

Firstly, to validate the current analysis, the frequencies are compared with those given in Mustafa and Ali (1989) for stiffened non-rotating isotropic cylindrical shells. The comparison for various stiffened models M1, M2, M3, and M4 is presented in Table 2, which shows the maximum difference in the natural frequency between present results and those of Mustafa and Ali (1989) is 1.98 % for model M3 with (m, n) = (1, 4).

Table 2:
Natural frequencies of vibration of the non-rotating stiffened isotropic cylindrical shells (Hz).

Mode number		Natural frequencies (Hz)
		M1 (stringers)		M2 (rings)		M3 (stringers)		M4 (orth. stiffened)
m	n	Mustafa and Ali (1989)	Present	Mustafa and Ali (1989)	Present	Mustafa and Ali (1989)	Present	Mustafa and Ali (1989)	Present
1	1	1141	1143.1	1204	1225.7	778	778.1	942	936.3
	2	674	672.4	1587	1597.1	317	317.2	439	436.9
	3	427	425.3	4462	4476.4	159	159.3	337	331.0
	4	296	294.5	8559	8593.9	99.6	101.6	482	477.5
	5	225	223.3	13,780	13,874.6	91.5	91.4	740	739.8

The next validation is carried out for un-stiffened non-rotating functionally graded cylindrical shells. The natural frequencies of the simply supported functionally graded cylindrical shells (model M5) with m = 1 and different n, various power law index p are given in Table 3 and are compared with the results of Loy et al. (1999). There is a good agreement between Loy's and the present results (only 0.19 % maximum discrepancy with p = 30).

Table 3:
Natural frequencies of un-stiffened non-rotating FG cylindrical shell (Hz).

Mode number					Natural frequencies (Hz)
		p = 0		p = 1		p = 2		p = 30
m	n	Loy et al.(1999)	Present	Loy et al.(1999)	Present	Loy et al.(1999)	Present	Loy et al.(1999)	Present
1	1	13.572	13.572	13.235	13.235	13.127	13.127	12.937	12.936
	2	33.296	33.296	32.430	32.430	32.170	32.170	31.730	31.670
	3	93.001	93.001	90.553	90.553	89.828	89.828	88.614	88.449
	4	178.06	178.06	173.36	173.36	171.98	171.98	169.66	169.34
	5	287.79	287.79	280.20	280.20	277.95	277.95	274.21	273.70
	6	422.05	422.05	410.91	410.91	407.62	407.62	402.13	401.38
	7	580.78	580.78	565.46	565.46	560.93	560.93	553.37	552.35
	8	763.98	763.98	743.82	743.82	737.86	737.86	727.92	726.57
	9	971.62	971.62	945.98	945.98	938.40	938.40	925.76	924.05
	10	1,203.7	1,203.7	1,171.9	1,171.9	1,162.5	1,162.5	1,146.9	1,144.8

For the final validation, Table 4 presents the non-dimensional frequency parameter Chen et al. (1993) for two rotational velocities Ω = 0.005 and 0.1 rps. Subscripts b and f denote the backward and forward waves, respectively. Equation (45) of Chen et al. (1993) gives w_b , w_f as follows: for a very long rotating isotropic cylindrical shells. Results of the present study are compared with those using equation (45) of

Table 4:
Comparison of frequency parameter h/R=0.002, L/R=200, v = 0.3). for a very long rotating isotropic cylindrical shell (

Ω (rev/s)	Mode number			Natural frequencies (Hz)
			ω'b		ω'f
	m	n	Chen et al.(1993)	Present	Chen et al.(1993)	Present
0.05	1	2	0.00167	0.00167	0.00144	0.00145
		3	0.00447	0.00448	0.00430	0.00431
		4	0.00847	0.00848	0.00834	0.00835
		5	0.01364	0.01366	0.01353	0.01355
0.1	1	2	0.00179	0.00182	0.00135	0.00138
		3	0.00456	0.00461	0.00422	0.00427
		4	0.00854	0.00859	0.00827	0.00833
		5	0.01370	0.01376	0.01348	0.01354

As indicated in the Table 4, the maximum discrepancy between Chen's and the present results is 2.4 % at (m, n) = (1, 2). From the above mentioned validation, it can be confirmed that the present results are in good agreement with those are given by Mustafa and Ali (1989), Loy et al. (1999), and the results using equation (45) of Chen et al. (1993).

4.2 Parametric Study

In the next examples, the rotating stiffened functionally graded cylindrical shells are considered (P-FGM AL/ZrO₂ model M6 in Table 1). The effects of the power law index, the stiffener's height-to-width ratio, the circumferential wave numbers, the shell's length-to-radius ratio, and the shell's radius-to-thickness ratio on the natural frequencies of functionally graded cylindrical shell areinvestigated.

4.2.1 Effects of Rotating Speed on the Fundamental Frequency

Table 5 presents the natural fundamental frequencies of the orthogonally stiffened and unstiffened FG cylindrical shells (power law index p = 20) with various rotating speed. The variation of the natural fundamental frequencies versus rotating speed is illustrated in Fig. 2.It can be seen that the natural fundamental frequencies for the orthogonally stiffened shell are higher than those for the unstiffened shell. As the rotating speed increases, the fundamental frequency for the unstiffened shell increases more rapidly than that for the stiffened shell. For the stiffened shell, the natural fundamental frequencies of the backward waves increase with rotating speed while those of the forward waves decrease with rotating speed. In addition, due to the effect of Coriolis force, the backward and forward wave frequencies are different, and the backward wavesfrequencies are always higher than those of forward waves.

Table 5:
Natural fundamental frequencies (Hz) of stiffened and unstiffened FG cylindrical shell with various rotating speeds.

Type of shell				Ω (rev/s)
		0	10	20	30	50
Stiffened shell	ωb	344.93	353.24	362.11	371.53	391.96
	ωf	344.93	337.16	329.95	323.28	311.55
Unstiffened shell	ωb	193.84	201.55	212.50	226.46	262.07
	ωf	193.84	189.46	188.32	190.19	201.63

Figure 2:
Variation of the natural fundamental frequencies of the orthogonal stiffened and unstiffened FG cylindrical shells with the rotating speed (power law index p = 20).

4.2.2 Effects of the Stiffener Height-to-Width Ratio on the Fundamental Frequency

The natural fundamental frequency of the orthogonally stiffened FG shells with different stiffener height-to-width ratio (h _{( r,s )} / b _{( r, s )}) and various rotating speeds are listed in Table 6 (stiffener width b_{s ( r )} is 2 mm). Fig. 3 depicts the effect of stiffener height-to-width ratio on natural fundamental frequency. It is observed that there is an increasing trend of the natural fundamental frequency with increasing height-to-width ratio. The natural fundamental frequency increase more rapidly for small height-to-width ratiothan for large height-to-width ratio. Higher rotating speed causes a bigger gap between forward and backward wave frequencies.

Table 6:
Natural fundamental frequencies (Hz) of rotating stiffened FG cylindrical shell with the various stiffener height-to-width ratios.

Ω (rev/s)					Stiffener height-to-width ratios (h/b)
		0.5	1	2	3	4	5	7	9
Ω = 10	ωb	201.67	204.38	221.37	255.74	305.20	344.63	364.49	394.09
	ωf	189.58	192.28	209.24	243.56	292.95	328.58	348.37	377.88
Ω = 50	ωb	262.17	264.48	279.06	309.40	354.51	383.46	403.07	432.33
	ωf	201.71	203.96	218.39	248.48	293.26	303.20	322.47	351.31

Figure 3:
Variation of the fundamental frequencies for the orthogonal stiffened FG cylindrical shells with the stiffener height-to-width ratio (power law index p = 20).

4.2.3 Effects of the Power Law Index on the Fundamental Frequency

Table 7 shows the fundamental frequencies with different rotating speeds for the various power law indexes of simply supported FG cylindrical shell. The variation the fundamental frequencies with the rotating speed for the various power law indexes is plotted in Fig. 4.

Table 7:
Natural fundamental frequencies (Hz) of stiffened FGM cylindrical shell with the various power law indexes p.

Power law index						Ω (rev/s)
		0	10	20	30	50	60	70	80	100
p = 0	ωb	369.13	376.11	384.81	395.21	420.86	435.94	448.43	460.07	484.66
	ωf	369.13	363.91	360.41	358.52	346.48	341.18	336.34	331.96	324.52
p = 3	ωb	356.04	364.35	373.18	382.55	402.85	413.76	425.17	437.06	462.22
	ωf	356.04	348.27	341.04	334.33	322.48	317.31	312.64	308.45	301.45
p = 020	ωb	344.93	353.24	362.11	371.53	391.96	402.97	414.48	426.49	451.92
	ωf	344.93	337.16	329.95	323.28	311.55	306.47	301.89	297.81	291.05

Figure 4:
Variation of the fundamental frequencies for the orthogonal stiffened FG cylindrical shells with the rotating speed for the various power law indexes.

As shown in Fig. 4, the backward and the forward waves increase as power law index p decreases. It is basically due to the fact that Young's modulus of ceramic is higher than metal.

4.2.4 Effects of the Circumferential Wave Number on the Natural Frequency

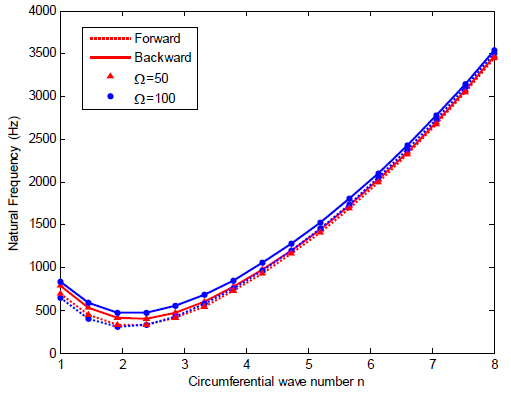
The natural frequencies for the rotating orthogonally stiffened FG cylindrical shell with various rotating speeds and different circumferential wave numbers n are given in Table 8. The variation of the natural frequency with the circumferential wave number n is illustrated in Fig. 5. It is seen that for both rotating speeds, the frequency first decreases to a minimum and then increases with the circumferential wave number n. The backward and forward wave frequencies are almost identical for the large circumferential wave number n.

Table 8:
Natural fundamental frequencies (Hz) of stiffened FG cylindrical shell with various the circumferential wave numbers n.

Ω (rev/s)					n
		1	2	3	4	5	6	7	8
Ω = 50	ωb	794.02	405.84	505.37	855.01	1337.79	1935.81	2645.59	3466.04
	ωf	697.76	326.60	446.62	810.15	1302.46	1907.38	2622.44	3447.11
Ω = 100	ωb	841.22	464.76	583.75	935.80	1417.63	2014.24	2722.61	3541.76
	ωf	648.73	306.27	466.19	846.03	1346.92	1957.35	2676.29	3503.88

Figure 5:
Variation of natural frequencies for the rotating orthogonally stiffened FG cylindrical shell with the circumferential wave number n (power law index p = 20).

4.2.5 Effects of Length-to-Radius Ratio on the Fundamental Frequency

The fundamental frequencies for the rotating orthogonally stiffened FG cylindrical shell with various length-to-radius ratios L / R are listed in Table 9. Variation of the fundamental frequencies for the rotating orthogonally stiffened FG cylindrical shell versus L / R ratio is plotted in Fig. 6. The natural fundamental backward and forward wave frequencies decrease rapidly with L / R ratio at any rotating speed. The effect of the rotating speed on the fundamental frequency for the small L / R ratio is more significant than those for the large L / R ratio.

Table 9:
Natural fundamental frequencies (Hz) of stiffened FG cylindrical shell with various L / R ratios.

Ω (rev/s)					L / R
		2	4	6	12	16	18	20
Ω = 10	ωb	970.641	506.664	284.693	132.437	108.847	95.867	80.265
	ωf	959.431	490.879	268.814	116.486	92.880	76.118	60.476
Ω = 50	ωb	1001.098	542.781	324.830	182.476	156.150	134.928	119.402
	ωf	945.043	463.852	245.427	102.718	57.668	36.185	20.457

Figure 6:
Variation of the fundamental frequencies for the rotating orthogonally stiffened FG cylindrical shell with L / R ratio (power law index p = 20).

4.2.6 Effects of Radius-to-Thickness Ratio on the Fundamental Frequency

Table 10 gives the natural fundamental frequencies for the orthogonally stiffened FG cylindrical shell with various R / h ratios and rotating speeds. Fig. 7 depicts the variation of natural fundamental frequencies with respect to radius-to-thickness ratio R / h. It can be seen that the natural fundamental backward and forward wave frequencies for the orthogonally stiffened rotating cylindrical shell decrease as the R / h ratio increases. The effect of rotating speed for the large R / h ratio is also more significant than those for the small R / h ratio.

Table 10:
Natural fundamental frequencies (Hz) of stiffened FG cylindrical shell with various R / h ratios.

Ω (rev/s)					R / h
		100	150	200	300	400	450	500
Ω = 10	ωb	672.235	351.174	239.728	125.005	87.800	78.195	71.402
	ωf	660.673	339.344	227.794	115.608	78.358	68.741	61.938
Ω = 50	ωb	706.956	396.529	294.480	221.795	195.024	187.476	181.949
	ωf	649.141	337.363	234.782	161.659	134.684	127.061	121.468

Figure 7:
Variation of the fundamental frequencies for the rotating orthogonally stiffened FG cylindrical shell with R / h ratio (power law index p = 20).

5 CONCLUSIONS

Based on the Love's first approximation theory and the smeared stiffeners technique, the analytical solution for the vibrations of the orthogonally stiffened rotating functional graded material cylindrical shell has been presented. The natural frequencies are compared with the existing published results for the non-rotating orthogonally stiffened isotropic cylindrical shell, the non-rotating unstiffened FG cylindrical shells, and the rotating isotropic cylindrical shell. The following points can be outlined from the present study:

The natural fundamental frequency of FG cylindrical shell can beincreased by stiffening with orthogonal stiffeners. The natural fundamental frequencies for the backward and the forward waves increase with the rotating speed, the gap between the backward and the forward waves is greater with higher rotating speed. The backward wave frequencies are higher than the forward frequencies due to the effect of Coriolis force.

The natural fundamental backward and forward wave frequencies for the orthogonally stiffened rotating cylindrical shell decrease with increasing L / R (R / h) ratio. The effect of rotating speed with the large L / R (R / h) ratio is greater than the effect of those with small L / R (R / h) ratio.

Acknowledgements

This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number: 107.02-2015.14.

References

• Bich, Dao Huy, Dao Van Dung, and Vu Hoai Nam(2012).Nonlinear Dynamical Analysis of Eccentrically Stiffened Functionally Graded Cylindrical Panels. Composite Structures 94.8: 2465-2473.
• Chen, Y., Zhao, H. B., Shea, Z. P. (1993). Vibrations of High Speed Rotating Shells With Calculations for Cylindrical Shells. Journal of Sound and Vibration 160: 137-160.
• Lam, K.Y., and Loy,C.T. (1994). On Vibrations of Thin Rotating Laminated Composite Cylindrical Shells. Composites Engineering 4.11: 1153-1167.
• Lam, K.Y., and Loy,C.T. (1995). Analysis of Rotating Laminated Cylindrical Shells by Different Thin Shell Theories. Journal of Sound and Vibration 186.1: 23-35.
• Lam, K.Y., and Wu Qian (1999). Vibrations of thick rotating laminated composite cylindrical shells. Journal of Sound and Vibration 225.3: 483-501.
• Lee, Young-Shin, and Young-Wann Kim(1998). Vibration Analysis of Rotating Composite Cylindrical Shells with Orthogonal Stiffeners. Computers & Structures 69.2: 271-281.
• Li, S. R., Fu, X. H., Batra, R. C. (2010). Free vibration of three-layer circular cylindrical shells with functionally graded middle layer. Mechanics Research Comunications, 37(3), 577-580.
• Loy, C.T., Lam,K.Y., and Reddy,J.N. (1999).Vibration of Functionally Graded Cylindrical Shells. International Journal of Mechanical Sciences 41.3: 309-324.
• Mustafa, B.A.J., and Ali,R. (1989). An Energy Method for Free Vibration Analysis of Stiffened Circular Cylindrical Shells. Computers & Structures 32.2: 355-363.
• Pradhan, S.C. et al(2000). Vibration Characteristics of Functionally Graded Cylindrical Shells under Various Boundary Conditions. Applied Acoustics 61.1: 111-129.
• Sun Shupeng, Shiming Chu, and Dengqing Cao(2012). 'Vibration Characteristics of Thin Rotating Cylindrical Shells With Various Boundary Conditions. Journal of Sound and Vibration 331.18: 4170-4186.
• Vel, S.S. (2010). Exact elasticity solution for the vibration of functionally graded anisotropic cylindrical shells. Composite Structures, 92(8), 2712-2727.
• Xiang, Song et al(2012). Natural Frequencies of Rotating Functionally Graded Cylindrical Shells. Applied Mathematics and Mechanics 33.3: 345-356.
• Zhao, X., Liew, K.M., and Ng,T.Y. (2002). Vibrations of Rotating Cross-Ply Laminated Circular Cylindrical Shells with Stringer and Ring Stiffeners. International Journal of Solids and Structures 39.2: 529-545.

Appendix

The differential operators L_ij in equation (7):

The coefficients k_ij in equation (10):

Publication Dates

• Publication in this collection
  Dec 2016

History

• Received
  23 Mar 2016
• Accepted
  23 Sept 2016