Free Vibration Analysis of Reinforced Composite Functionally Graded Plates with Steady State Thermal Conditions

Abstract

The present paper deals with free vibration of functionally graded fiber reinforced rectangular plates subjected to thermal loads. The rectangular plates are assumed orthotropic. The continuous grading fiber reinforced plates have a smooth variation in matrix volume fraction in the thickness direction. Two different types of volume fraction profiles through the thickness of plate are proposed: classic and symmetric. As the plate is thick, the equations of motion are derived based on three dimensional theory of elasticity. Inevitably, 3D General differential quadrature method is used instead of regular solving methods in order to discretize equations of motion equations as linear set of algebraic equations. The effects of temperature, volume fraction profiles, and boundary conditions are investigated. Some interesting conclusions obtained when the material properties were assumed to be temperature-dependent. It has been observed that temperature and functionality of FG plate have significant effect on the natural frequencies of the plate.

Keywords:
Three dimensional differential quadrature method; Fiber reinforced plates; Thermal vibration; Thermal load; Three dimensional general

1 INTRODUCTION

Functionally Graded Materials (FGMs) was introduced in order to avoid problems associated with material mismatch at the layer interfaces in compare with composite materials. The FGM structures are characterized by variable mechanical properties due to the through-the-thickness variation of the volume fraction distribution of the two constituents and the arbitrary thickness profile. By assigning a continuous gradual variation of the mechanical properties along a specified direction, these composites do not show discontinuities in the material. As a consequence, the residual stresses and the stress concentrations that commonly affect a laminated structure can be reduced by mixing two or more constituents according to a specific graded distribution of the volume fraction [Tornabene et al. (2017)].

Functionally graded fiber reinforced composites materials have been widely used in the aerospace marine, and other engineering industries, recently. These new type of FGMs are often proposed to utilize in high temperature as well as corrosive environments. The effect of environment, temperature distribution and other aspects on the material properties of FGM composites and nonhomogeneous materials were studied by many researchers; some focused on reinforcement by fiber or carbon nanotube (Suresh et al. (1998); Nejati et al. (2016); Nejati et al. (2016); Yas et al. (2016), Yas et al. (2010)). Studies depicted that higher temperature and especially corrosive conditional work decrease the elasticity constants and degrade the strength of composites. Using FGMs have been based on this hypothesis that it can produce a material with good resistance on high temperature and corrosive environment.

Many researchers have concentrated their investigation on plate and beam structure (Jafari et al. (2016); Arani et al. (2011); Shishesaz et al. (2016); Shahrjerdi et al. (2011); Ansari et al. (2016)). They analyzed free vibration of functionally graded fiber reinforced plates via three dimensional elasticity theory.

Some studies have been done focusing on thermal analysis and temperature effects on FGM plates by Yang et al. (2001). Khalili et al. (2012) focused on this effect on free vibration analysis of the FG properties which were assumed temperature dependent.

Within these analyses, some research are based on the classical plate theory i.e. neglecting the effect of transverse shear deformation whereas some others have used elasticity approach to obtain free frequency of laminated and functionally graded composites plates and shells by Matsunaga (2009).

There are limited works about the mechanical stress analysis, free and forced vibration analysis subjected to thermos mechanical loading. A closed-form solution for vibration frequencies of simply supported thick plates was presented by Xiang et al. (1996).

Hosseini-Hashemi et al. (2010) presented analytical solution for free vibration of moderately thick rectangular plates which are composed of particle reinforced FGM and supported on elastic foundation. The analysis was performed based on first-order shear deformation plate theory.

In the recent years, analytical and numerical methods have been applied by the research workers in order to study the plate vibration for different shapes. Moreover, the differences between numerical and analytical methods have been investigated. Finite element method is beneficial but expensive to implement as it is time consuming. Isvandzibaei et al. (2014) study on vibration behavior of functionally graded material cylindrical shell. The FGM shell equations have been established based on strain-displacement relationship using Love-Kirchhoff shell theory. The governing equations of motion were solved by energy functional and applying Ritz method.

On the other hand, meshless approaches have found efficient for FG materials since they require nodal connectivity. Betwixt current numerical approaches, differential quadrature method (DQM) has been considerably attended by researchers since it is straightforward to implement as well as quick to analyze. Moreover, it can overcome the most common programming difficulties, such as complex algorithm and excessive use of memory and calculation time. In DQM, the term quadrature applies to the appropriate evaluation of the integral. This technique could be utilized in a simple and systematic fashion to obtain the computational solution of nonlinear differential-integral equations. The DQ method approximates a derivative at a point as a linear weighted sum of all the functional values on the domain. How to evaluate the weighting coefficients is one of the key points of this technique [Tornabene et al. (2015)]. However, DQM is not always stable increasing the number of collocation points. For this reason Generalized Differential Quadrature (GDQM) [Tornabene et al. (2014)].

The applied boundary condition type directly influences on the solving method. In GDQ, solving method for conditions like SSSS can be one dimensional while for SCSC it can be 2D. But when 3D elasticity theory is used, the only appropriate solving method for FFFF, CCCC and CFCF conditions is to discretize the governing equation by 3D GDQ. Although for these cases, some are some other theories such as shear deformation theory in which 2D or 1D methods are feasible can be implement, the solving method would be more complicated.

There is not proper papers deal with thermo mechanical vibration analysis of fiber reinforced FGMs. There are several efforts in which mechanical and thermo mechanical dynamic response of FGMs have been studied; whereas in the case of vibration analysis of fiber reinforced FGM plate with different boundary condition and effect of temperature via 3D numerical solution, lack of knowledge is perceived.

In the presented work, it is desired to study on the free vibration of fiber reinforced composite plates with functionally graded volume fraction of fiber resting on different types of boundary condition under thermal-mechanical load. Fiber reinforced functionally graded plates are new type of FGMs in which fiber orientation or/and its density varies functionally through desired direction. The material properties of fiber reinforced FG orthotropic plate are estimated through micromechanical model based on simple rule of mixture and are assumed to be function of temperature.

The governing equations are based on three dimensional elasticity theory (Sadd (2009)) and general Von-Karman type strain-displacement equations (Reddy (2004)) which include plate foundation interaction. As various types of boundary conditions were investigated in this paper, 3D general differential quadrature method (GDQ) has been utilized to discretize the governing equation and consequently obtain natural frequencies of FG plate under different types of thermal conditions. Then, the effects of different parameters such as boundary condition, volume fraction as well as temperature are studied.

2 MICROMECHANICS OF ORTHOTROPIC FGM

The micro mechanic of FG fiber reinforced composites is obtained based on a micromechanical model which is able to calculate effective properties when the volume fraction is changed. Fig. 1 demonstrates schematic of FG fiber reinforced rectangular plates.

Figure 1:
Schematic of fiber reinforced FG rectangular plate with fibers` volume fraction variation along thickness.

Here, two functions are considered to present the variations of fibers’ volume fraction through the thickness (Nejati et al. (2015)). The first model is according to Eq. (1) in which V depends on P and z simultaneously. For even power (n), fibers volume fraction variations are symmetric:

(1)

Where z = 0) to 0 in mid-surface, and again reaches to 0.75 in periphery z = h of the plate. The variations incline toward 0 volume fraction of fibers in total thickness of the plate for high even power indices cause the plate to be similar to a homogenous orthotropic plate with 0% volume fraction of fiber and 100% matrix in total thickness. which has values that range from 0 to 1. The exponent n controls the volume fraction profile through the plate’s thickness. According to symmetrical model, changes in fiber`s volume fraction occurs from 0.75 in internal surface (

In the second model distribution of fibers is according to conventional (classic) form according to Eq. (2):

(2)

Based on Classical model, fibers` volume fraction continuously reaches from zero in one surface of the plate to 0.75 in the other one. According to this relation, _^Vi and _^Vo which have values that range from 0 to 1, denote the volume fractions (matrix or fiber) on the inner and outer surfaces, respectively. Fibers volume fraction is zero in z = 0 and 0.75 in z = h.

The alteration inclines toward 0 volume fraction of fiber for high power indices, and the plate looks like a homogenous orthotropic plate with 0% of fibers and 100% of the matrix volume fraction for the total plate thickness in this model.

In the present analysis, it is assumed that fiber angle of the fiber reinforced plate are constant with respect to the x-axis in the x - y surface. The effective mechanical properties of the fiber reinforced plate are obtained based on a micromechanical model as follows (Shen (2009), Vasiliev et al. (2001)):

(3)

Where _^Efii , _^Gfij , _{^{υ f}} and _^ρf are elasticity modulus, shear modulus, Poisson’s ratio and density of the fiber respectively, and _^Emii , _^Gmij , _^υm and _^ρm are corresponding properties for the matrix. _^Vf and _^Vm are the fiber and matrix volume fractions in order and are related by _^Vf +._^Vm = 1.

3 CONSTITUTIVE EQUATIONS

The equations of motion for free vibration analysis of fiber orientation FG rectangular plate can be obtained by using 3D elasticity theory in conjunction with Hamilton principle which is (Reddy (2004)).

(4)

Where KE is the kinetic energy of the rectangular plate and PE is the elastic potential energy of it. The kinetic energy of the plate is obtained as following:

(5)

The elastic potential energy of plate is comprised of strain energy due to vibration and primary stresses resulting from temperature increase respectively which both are obtained as follows:

(6)

(7)

(8)

Where PEP is the strain energy due to vibratory stresses and PET is the strain energy caused by the initial stresses due to temperature rise _^σ0ij (i, j = x, y, z) is pre-stress components due to applied temperature field and _^σij is stress tensor. Υ_^Lij and _^εLij are linear term of shear and normal strain tensor respectively, whereas Υ_^NLij and _^εNLij are nonlinear terms of shear and normal strain tensor respectively.

Strain-displacement relations are considered according to the 3D elasticity theory including nonlinear terms that originally was proposed by Karman and Von (Reddy (2004)). The constitutive relation for orthotropic rectangular plate is according to general form of Hook’s law.

The plate is initially stressed free at temperature to hence pre-stress components should be included by increasing the temperature. The pre-stress components due to temperature rise ΔT are defined by:

(9)

It is assumed that temperature varies uniformly and non-uniformly through the thickness. The elements of Off-axis stiffness matrix [C] are given in (Reddy (2004)).

3.1 The Equations of Motion

By substituting strain-displacement and constitutive relations and Eq. (9) into elastic potential energy, Eqs. (5) and (6) respectively then combining with Hamilton principle the equations of motion with boundary conditions are extracted for fiber reinforced FG plate as follow:

(10)

(11)

(12)

Also, the boundary conditions of the plate are described at the ends z = 0 and h as follow:

(13)

at x=0, a:

(14)

at y=0, b:

(15)

Where, _^Fx , _^Fy and _^Fz are generalized forces along x, y and z directions. For normal mode analysis, the following solution is assumed for the displacement components x, y and z.

(16)

Where coefficients U, V and W, are unknown displacement functions of x, y and z orientations, respectively. Combination of Eqs. (10-15) with Eq. (16) will result the equations of motion as a set of coupled partial differential equations in terms of displacement components. These set of equations have been solved by the general differential quadrature (GDQ) discretization procedure for spatial derivations.

Using the 3D-GDQ method for the spatial derivatives, the discretized form of the equations of motion (Eqs. 10-12) at each domain grid point can be obtained as ^{Appendix A}.

For fully clamped boundary condition on four edges (CCCC_built-in edge), the discretized boundary conditions are obtained as:

(17)

For SCSC type boundary condition, two opposite sides are fully clamped and two others are simply supported, we have:

(18)

In the case of simply supported plate or when all edges are rested on simply supported foundation (SSSS), boundary condition is expressed on the x-constant and y-constant edges as follows:

(19)

Nodes (or grids) distribute along three axes non-uniformly which is defined as Chebyshev- Gauss- Lobatto distribution as follow:

(20)

Fig. 2 shows DQ meshing with uniform distribution of nodes (_^Nx × _^Ny × _^Nz = 13 × 10 × 7)) along three different sections of a three-dimensional domain.

Figure 2:
Non-uniform distribution of GDQ meshes in three directions. (a) X-Y plan, (b) X-Z plan, (c) Y-Z plan.

Using this procedure for all of the governing equations and converting them into set of equation in terms of series form, leads to discretized equations. Then governing equations in the form of differential quadrature relations is produced in terms of series and unknown variables U, V and W. The first and second derivatives of variable U with respect to x, y and z are computed as follows:

(21)

In the above relations, _^Axil , _^Ayjp , _^Azkm and _^Bxil , _^Byjp , _^Bzkm are weighted coefficients of first and second order derivatives along the X, Y and Z directions respectively.

The weighting coefficients for the first-order derivatives in x-direction are thus obtained as (Bert et al. (1996)):

(22)

Where _^Lx is the length of domain along the x-direction.

(23)

According to DQ method, for higher-order derivatives, higher-order weighting coefficient should be employed, i.e. for second order derivatives, weighting coefficient can be expressed as below:

(24)

In a similar way, the weighting coefficients for the y-direction and z-direction can be obtained.

To perform the eigenvalue system of equations, the degree of freedom is separated into the domain and the boundary degree freedom.

In order to carry out the eigenvalue analysis, the domain and boundary degrees of freedom are separated into vector forms. They are denoted as {d}and {b} respectively. Based on this definition, the discretized form of the motion equations and the related boundary conditions take the following forms (Bert et al. (1996)):

Equations of motion (^{Appendix A}. (A1-A3)):

(25)

Boundary conditions (Eqs. (17-19)):

(26)

By eliminating the boundary degrees of freedom in Eq. (25), using Eq. (26), this equation turn into:

(27)

Where [K] = [_^Kdd ] - [_^Kdb ][_^Kbb ]^-1[_^Kbd ]. The above eigenvalue system of equations can be solved to find the natural frequencies and mode shapes of the plates.

4 THERMAL ANALYSIS

Here, the influence of a temperature filed on the behavior of the FGM is investigated. The temperature varies in the thickness direction. Two types of thermal boundary conditions are applied: uniform and non-uniform.

In the case of uniform temperature rise, the temperature difference from the reference temperature _^To for both upper surface ∆_^Ttop and lower surfaces ∆_^Ttop are equal, i.e. ∆_{^{Ttop =}} ∆_{^{Tbottom =}} ∆_^T.

In non-uniform distribution, two different temperatures is imposed on the two surfaces while other sides are isolated. In this case, the temperature distribution along the thickness can be obtained by solving a steady-state heat transfer equation through the thickness of the plate. The equation for the temperature through the thickness is given by:

(28)

Where _^Kz (z) is the thermal conductivity. This equation is solved by imposing boundary condition as following:

(29)

5 RESULTS AND DISCUSSION

To validate the current three dimensional GDQ formulations, the results for an isotropic and homogenous rectangular FGM plate are compared with similar ones obtained by FEM and in the literatures by 2D GDQ.

5.1 Validation

First of all, convergence and validation study of the normalized first six natural frequencies is considered for an isotropic FGM plate in Table 1 to compare with Malekzadeh (2009) and Matsunaga (2008).

Fast rate of convergence of the method is evident for exponent index ‘‘p=1” and it is found that only 11 DQ grid for simply supported FGM plate in the three dimensions can yield accurate results. Good agreement is observed between the results.

In order to evaluate accuracy of 3D GDQ method, non-dimensional natural frequency resulted from this method are compared with 2D GDQ formulations by Malekzadeh (2009) for as well as FEM method in Table 2 for different exponent index (p) for isotropic FGM simply supported plate and 1D GDQ formulation by Yas et al. (2010) in Table 3 in different thickness to width ratio (h/b) for orthotropic FGM simply supported plate while exponent index of 1 (p=1) and length to width ratio of 1 (a/b=1). Good agreement between all the data in Tables 2 and 3 proves the reliability of presented method. It should be noted that 13500 elements of second order 8 nodes with 250 sub-layers were utilized in order to obtain slightly results. Moreover, in this example 13 GDQ grids were used to achieve adequate convergence and concordant results with Malekzadeh (2009).

The comparison shows that the present results agreed well with those in the literature.

Table 1:
Convergence and accuracy of first three frequency parameters of SS-SS FGM plate P = 1,a/b = 1,h/b = 0.1, Ω = ω h).

Nx × Ny × Nz	Ω1	Ω2	Ω3
9×9×9	0.0223	0.0442	0.086
11×11×11	0.0224	0.0443	0.0861
13×13×13	0.0224	0.0443	0.0861
Malekzadeh (2009)	0.02245	0.04426	0.08612
FEM	0.02252	0.04439	0.08616
Matsunaga (2008)	0.02246	0.04427	0.08614

Temperature dependent properties of copper and tungsten are described in Eq. 30 by Gasik (2000).

(30)

Table 2:
Validation of natural frequencies for a FGM plate with SS-SS boundary condition in different volume fractions (a/b = 1,h/b = 0.5, Ω = ω h).

P	Result	Ω1	Ω2	Ω3
0	3-D GDQ	0.94	0.9742	1.3777
	Malekzadeh (2009)	0.94	0.9742	1.3777
	FEM	0.941	0.9746	1.3784
	Matsunaga (2008)	0.94	0.9742	1.3777
0.5	3-D GDQ	0.8225	0.8708	1.2259
	Malekzadeh (2009)	0.8225	0.8708	1.2259
	FEM	0.8218	0.874	1.2363
	Matsunaga (2008)	0.8233	0.8709	1.2259
1	3-D GDQ	0.7475	0.8003	1.1168
	Malekzadeh (2009)	0.7475	0.8003	1.1168
	FEM	0.7398	0.8098	1.1454
	Matsunaga (2008)	0.7477	0.8005	1.1166
10	3-D GDQ	0.5458	0.5663	0.7884
	Malekzadeh (2009)	0.5458	0.5663	0.7884
	FEM	0.5303	0.5753	0.8137
	MatsunagaMatsunaga (2008)	0.546	0.5664	0.7885

Table 3:
Comparison of the first three non-dimensional natural frequencies of a simply supported FGM orthotropic plate with classic model (p=1, a/b = 1). ω b ²/ π ²D _c = _^Ec h ³/12(1-v _c ²)., =

h/b		a(1,1)	(2,2)	(3,3)
0.01	Present	101.8335	203.6654	305.4978
	Yas et al. (2010)	101.833	203.665	305.497
0.1	Present	1.5141	6.9863	14.5332
	Yas et al. (2010)	1.514	6.986	14.533
0.5	Present	1.2983	3.2254	5.1346
	Yas et al. (2010)	1.298	3.225	5.134

• a The number in brackets indicate the vibration mode (m,n)

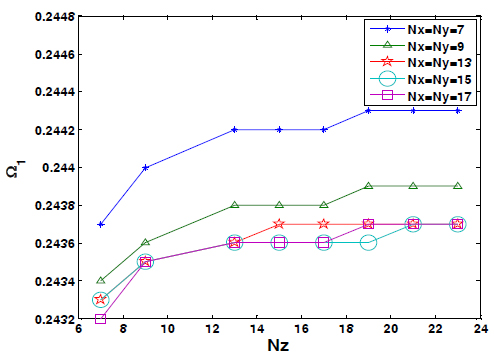
Convergence of current three dimensional GDQ approach is evaluated by obtaining first natural frequency of fiber reinforced orthotropic FGM plate with classic distribution, non-uniform temperature and temperature dependent properties. The plate is on SCSC foundation whose two opposite edges have same boundary conditions. Fig. 3 shows convergence rate of results achieved by different values of Nz when Nx and Ny has specified constant values.

Figure 3:
Convergence of first frequency parameter of fiber orientation with constant value of N_x and N_y (Ω = ωha/b = 1, h/b = 0.2, n = 1,^{_{∆Ttop =}} 800, ^_∆Tbottom = 0).,

Reasonable convergence results and accurate natural frequency is obtained in at least a 13×13×15 or 15×15×21 or 17×17×19 nodes grid.

5.2 Effect of Temperature on the Natural Frequency

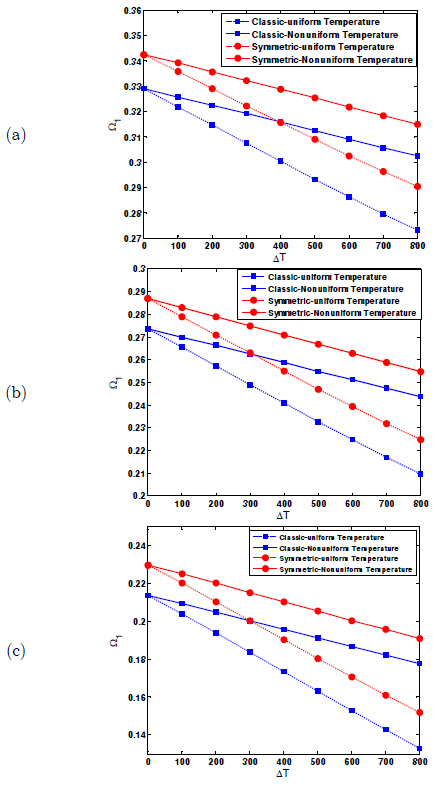
Here natural frequency results, Ω, versus ΔT are evaluated; which ΔT is divergence between maximum temperature of the plate and ambient temperature. According to part 4, maximum temperature of an orthotropic FGM plate in non-uniform temperature distribution occurs in the upper side at z=h while in uniform temperature distribution, whole the plate has a unique temperature which is considered as maximum plate temperature. Fig. 4 demonstrates effect of temperature variation on the first natural frequency in the plate for uniform and non-uniform (see Eq. 28) temperature distributions in presence of three different types of boundary conditions (clamped-clamped, simply supported-simply supported and simply supported-clamped). Besides, effect of considering material property as temperature dependent or independent is evaluated.

Figure 4:
Variation of first natural frequency of an orthotropic FG plate in different conditions of material property and temperature distribution by ΔT in presence of (a) CC-CC, (b) SC-SC, (c) SS-SS (Ω = ωha/b = 1, h/b = 0.2, n = 1, Classic_ profile).,

In this figure, natural frequency would reduce when the temperature rises. Also, including dependency of material property to temperature generally causes the natural frequency to reduce more. Indeed, the results of natural frequency analysis for such these plates which would be considered without effect of temperature dependency in material property should be dealt with more carefully.

In another point of view, regardless boundary condition type and temperature dependency, assuming uniform temperature distribution results in lower natural frequency. Comparing the graphs in Fig. 4 shows CC-CC boundary condition causes that stiffness of the plate increases and natural frequency of SS-SS type boundary condition is the least.

5.3 Effect of Profile of Fiber Volume Fraction on the Natural Frequency

Fig. 5 compares the natural frequencies between classic and symmetric distribution of volume fraction of fiber through the thickness. As the results show, natural frequency of the plate with a symmetric distribution of fiber is considerably higher than one with classic distribution. The other parameters such as distribution of temperature and type of boundary condition affected the plate with symmetric variation of volume fraction just as the classic one.

Figure 5:
Variation of first natural frequency of an orthotropic FG plate in different conditions of volume fraction distribution, material property and temperature distribution by ΔT in presence of a) CC-CC, b) SC-SC, c) SS-SS (Ω = ωha/b = 1, h/b = 0.2).,

Tables 4 and 5 investigate over fiber volume fraction distribution influence on the natural frequencies in another aspect. In these tables, the volume fraction power index of fiber varies for orthotropic FG reinforced plate subjected to different B.C. and in different situation of uniform and non-uniform temperature distributions. The natural frequencies were found for different temperature conditions. The results show that according to equation 2, when its power index increases, the natural frequencies would decrease; a result which is held for the first natural frequencies in all the considered conditions.

Table 4:
First natural frequencies of an orthotropic FG plate in uniform temperature distribution and different B.C. for different volume fraction profiles in different ΔT (Ω = ω ha/b = 1, h/b = 0.2).,

P	B.C.	ΔT(K)
		0	100	200	300	400	500
0	CC-CC	0.3561	0.3506	0.345	0.3395	0.334	0.3285
	SC-SC	0.2954	0.2893	0.2831	0.2769	0.2707	0.2645
	SS-SS	0.2311	0.224	0.2168	0.2095	0.2023	0.1951
1/5	CC-CC	0.344	0.338	0.332	0.326	0.32	0.3141
	SC-SC	0.2851	0.2783	0.2715	0.2646	0.2578	0.251
	SS-SS	0.2245	0.2166	0.2086	0.2005	0.1924	0.1844
1/2	CC-CC	0.3338	0.3273	0.3207	0.3141	0.3076	0.3011
	SC-SC	0.2767	0.2693	0.2617	0.2542	0.2466	0.2392
	SS-SS	0.2162	0.2074	0.1984	0.1892	0.1801	0.1709
1	CC-CC	0.329	0.3219	0.3147	0.3075	0.3004	0.2933
	SC-SC	0.2737	0.2656	0.2574	0.2491	0.2409	0.2327
	SS-SS	0.2136	0.2039	0.1939	0.1837	0.1734	0.1631

Table 5:
First natural frequencies of an orthotropic FG plate in non-uniform temperature distribution and different B.C. for different volume fraction profiles in different temperatures (Ω = ω ha/b = 1, h/b = 0.2).,

P	B.C.	ΔT(K)
		0	100	200	300	400	500
0	CC-CC	0.3561	0.3533	0.3505	0.3477	0.3449	0.3421
	SC-SC	0.2954	0.2924	0.2892	0.2861	0.283	0.2798
	SS-SS	0.2311	0.2276	0.224	0.2203	0.2167	0.2131
1/5	CC-CC	0.344	0.3411	0.3382	0.3353	0.3324	0.3294
	SC-SC	0.2851	0.2819	0.2786	0.2753	0.272	0.2687
	SS-SS	0.2245	0.2207	0.2169	0.2130	0.2091	0.2053
1/2	CC-CC	0.3338	0.3308	0.3277	0.3246	0.3215	0.3184
	SC-SC	0.2767	0.2732	0.2698	0.2662	0.2627	0.2592
	SS-SS	0.2162	0.2121	0.2080	0.2038	0.1996	0.1954
1	CC-CC	0.3290	0.3257	0.3225	0.3192	0.3158	0.3125
	SC-SC	0.2737	0.2700	0.2663	0.2625	0.2587	0.2549
	SS-SS	0.2136	0.2092	0.2048	0.2002	0.1957	0.1911

6 CONCLUSION

In this study, natural frequency of a functionally graded fiber reinforced thick plate was investigated. Response of this plate to variation of some parameters such as volume fraction profile, boundary conditions and mainly temperature distribution was examined. Because the plate is thick, a 3D GDQ method was used to solve the equations. The following conclusions are drawn:

• - The results proved credibility and fast convergence of 3D GDQ method for heat transfer equation and equations of motions for such these plates. Besides, replacing this method by regular solving method such as FEM and combination of high order shear deformation (instead of 3D elasticity) theory and 2D GDQ for thick FG fiber reinforced plates would not only save the time but also relived the solution from unnecessary complexity.

• - Alteration of temperature in FG fiber reinforced plate significantly affects its natural frequency. An increase of temperature leads to a reduction in natural frequency for different types of boundary conditions. As property of the plate transforms in a wide range of temperature, evaluation of the FGFR plate would be complicated when the temperature changes. The results shows including dependency of material property to temperature generally causes the natural frequency to reduce more; in other words, FGFR plates which are more independent from temperature have higher natural frequency in high temperatures.

• - In comparison between uniform and non-uniform temperature distribution in the plate, the uniform one results in lower natural frequency.

• - CC-CC boundary condition causes stiffness of FGFR plate under temperature variation increases that means natural frequencies are the highest among all considered boundary conditions while SS-SS condition graphs demonstrates the lowest one.

• - Volume fraction profile affect the natural frequency of FGFR plates subjected to thermal loads. Natural frequency of the plate with a symmetric distribution of fiber is considerably higher than one with classic distribution and for higher power indexes, the natural frequencies would be lower.

References

• Ansari, R., E. Hasrati, M. Faghih Shojaei, R. Gholami, V. Mohammadi and A. Shahabodini, (2016). Size-Dependent Bending, Buckling and Free Vibration Analyses of Microscale Functionally Graded Mindlin Plates Based on the Strain Gradient Elasticity Theory. Latin American Journal of Solids and Structures,13: 632-664.
• Arani, A. G., S. Maghamikia, M. Mohammadimehr and A. Arefmanesh, (2011). Buckling analysis of laminated composite rectangular plates reinforced by SWCNTs using analytical and finite element methods. Journal of Mechanical Science and Technology,25: 809-820.
• Bert, C. W. and M. Malik, (1996). Differential quadrature method in computational mechanics: a review. Applied Mechanics Reviews,49: 1-28.
• Gasik, S. U., M, (2000). Thermal-elasto-plastic analysis of W-Cu functionally graded materials subjected to a uniform heat flow by micromechanical model. Journal of Thermal Stresses,23: 395-409.
• Hosseini-Hashemi, S., H. R. D. Taher, H. Akhavan and M. Omidi, (2010). Free vibration of functionally graded rectangular plates using first-order shear deformation plate theory. Applied Mathematical Modelling,34: 1276-1291.
• Isvandzibaei, M., H. Jamaluddin and R. R. Hamzah, (2014). Analysis of the vibration behavior of FGM cylindrical shells including internal pressure and ring support effects based on Love-Kirchhoff theory with various boundary conditions. Journal of Mechanical Science and Technology,28: 2759-2768.
• Jafari, S. S., M. M. Rashidi and S. Johnson, (2016). Analytical Approximation of Nonlinear Vibration of Euler-Bernoulli Beams. Latin American Journal of Solids and Structures,13: 1250-1264.
• Khalili, S. and Y. Mohammadi, (2012). Free vibration analysis of sandwich plates with functionally graded face sheets and temperature-dependent material properties: A new approach. European Journal of Mechanics-A/Solids,35: 61-74.
• Malekzadeh, P., (2009). Three-dimensional free vibration analysis of thick functionally graded plates on elastic foundations. Composite Structures,89: 367-373.
• Matsunaga, H., (2008). Free vibration and stability of functionally graded plates according to a 2-D higher-order deformation theory. Composite Structures,82: 499-512.
• Matsunaga, H., (2009). Free vibration and stability of functionally graded circular cylindrical shells according to a 2D higher-order deformation theory. Composite Structures,88: 519-531.
• Nejati, M., A. Eslampanah and M. Najafizadeh, (2016). Buckling and Vibration Analysis of Functionally Graded Carbon Nanotube-Reinforced Beam Under Axial Load. International Journal of Applied Mechanics,8: 1650008.
• Nejati, M. , K. M. Fard and A. Eslampanah, (2015). Effects of fiber orientation and temperature on natural frequencies of a functionally graded beam reinforced with fiber. Journal of Mechanical Science and Technology,29: 3363-3371.
• Nejati, M. , M. H. Yas, A. H. Eslampanah and M. Bagheriasl, (2016). Extended three-dimensional generalized differential quadrature method: The basic equations and thermal vibration analysis of functionally graded fiber orientation rectangular plates. Mechanics of Advanced Materials and Structures0-0.
• Reddy, J. N. (2004). Mechanics of laminated composite plates and shells: theory and analysis, CRC press.
• Sadd, M. H., (2009). Elasticity: Theory, Applications, and Numerics. 2005. Burlington, MA: Elsevier Butterworth-Heinemann.
• Shahrjerdi, A., F. Mustapha, M. Bayat and D. L. A. Majid, (2011). Free vibration analysis of solar functionally graded plates with temperature-dependent material properties using second order shear deformation theory. Journal of Mechanical Science and Technology,25: 2195.
• Shen, H.-S., (2009). A comparison of buckling and postbuckling behavior of FGM plates with piezoelectric fiber reinforced composite actuators. Composite Structures,91: 375-384.
• Shishesaz, M., A. Zakipour and A. Jafarzadeh, (2016). Magneto-Elastic Analysis of an Annular FGM Plate Based on Classical Plate Theory Using GDQ Method. Latin American Journal of Solids and Structures,13: 2736-2762.
• Suresh, S. and A. Mortensen (1998). Fundamentals of functionally graded materials, The Institut of Materials.
• Tornabene, F., N. Fantuzzi and M. Bacciocchi, (2014). The strong formulation finite element method: stability and accuracy. Frattura ed Integrità Strutturale251-265.
• Tornabene, F. , N. Fantuzzi, M. Bacciocchi, E. Viola and J. N. Reddy, (2017). A Numerical Investigation on the Natural Frequencies of FGM Sandwich Shells with Variable Thickness by the Local Generalized Differential Quadrature Method. Applied Sciences,7: 1-39.
• Tornabene, F. , N. Fantuzzi, F. Ubertini and E. Viola, (2015). Strong formulation finite element method based on differential quadrature: a survey. Applied Mechanics Reviews,67: 1-55.
• Vasiliev, V. V. and E. Morozov (2001). Mechanics and analysis of composite materials, Elsevier.
• Xiang, Y., S. Kitipornchai and K. Liew, (1996). Buckling and vibration of thick laminates on Pasternak foundations. Journal of engineering mechanics,122: 54-63.
• Yang, J. and H.-S. Shen, (2001). Dynamic response of initially stressed functionally graded rectangular thin plates. Composite Structures,54: 497-508.
• Yas, M. and B. S. Aragh, (2010). Free vibration analysis of continuous grading fiber reinforced plates on elastic foundation. International Journal of Engineering Science,48: 1881-1895.
• Yas, M. , M. Nejati and A. Asanjarani, (2016). Free Vibration Analysis of Continuously Graded Fiber Reinforced Truncated Conical Shell Via Third-Order Shear Deformation Theory. Journal of Solid Mechanics Vol,8: 212-231.

APPENDIX A

Equations of motion (10-12) based on displacement field by 3D-GDQ method are discretized as:

(A1)

(A2)

(A3)

Publication Dates

• Publication in this collection
  June 2017

History

• Received
  23 Jan 2017
• Reviewed
  24 Mar 2017
• Accepted
  29 Mar 2017