Optimum Design of Effective Parameters for Orthotropic Plates with Polygonal Cut-Out

Abstract

This paper investigates the effect of different parameters on stress analysis of infinite orthotropic plates with central polygonal cutout using gray wolf optimization algorithm. The important features of gray wolf algorithm include flexibility, simplicity, short solution time and ability to avoid local optimums. The effective parameters on stress distribution around cutouts include load angle, curvature radius of the corner of the cutout, cutout orientation and fiber angle for orthotropic materials. The used analytical solution is the expansion of Lekhnitskii’s solution method. The effect of the aforementioned parameters on the stress distribution around triangular, square, pentagonal and hexagonal cutout is examined. The results showed that these parameters have significant effects on stress distribution around the cutouts and the structural load-bearing capacity will increase without changing the type of material if the parameters are correctly chosen.

Keywords:
Orthotropic Plates; Grey Wolf Algorithm; Polygonal Cut-out; Analytical Solution.

1 INTRODUCTION

In engineering structures, different types of cut-out are made to satisfy some service requirements. These cut-out result in the strength degradation of structures and may lead to their failure. It is observed that more failures in aircraft structures have happened in fastened joints having high stress concentrations. In order to predict the behaviour of the structures with such cut-out, it is essential to study the effect of cutout geometry and loading conditions on the stress distribution around the cut-out.In fact, cut-out reduce the weight of structures which is desirable for designers. Cut-out are mostly created in plates to reduce the structural weight or to create points of entry and exit. These changes in the plate geometry lead to severe local stresses that is called stress concentration. Hence, knowing the stress concentration factor is crucial in achieving optimal design. The study of the stress distribution in perforated plates was started by (Muskhelishvili 1962), (Savin 1970) and (Lekhnitskii 1969). They used conformal mappings and complex variable method for stress analysis of isotropic and anisotropic plates containing a central cutout. The complex variable method for solving boundary value problems in two- dimensional elasticity was firstly applied by (Muskhelishvili 1962) for isotropic plates. Shortly after and applying a similar method, (Savin 1970) performed some investigations on infinite isotropic plates with different cut-out and anisotropic plates with only elliptical and circular cut-out. (Lekhnitskii 1969) used an analytical solution to investigate the boundary value problems by complex variable method based on Kolosov-Muskhelishvili formulas for anisotropic plates with circular and elliptical cutout. An accumulation of all previous researches on plates containing cut-out was conducted by (Sternberg 1958), (Neuber 1968) , (Peterson 1974) and (Pilkey 1997). (Theocaris and Petrou 1986) used Schwarz-Christoffel transformation to evaluate the stress concentration factor for an infinite plate with central triangular cut-out. (Daoust and Hoa 1991) analyzed the triangular cut-out in infinite isotropic and anisotropic plate under uniaxial loading. A part from the equilateral triangle, they investigated other triangular cut-out with different aspect ratios. They also studied the effect of the curvature of cutout corner on the stress distribution around the triangular cut-out. (Asmar and Jabbour 2007) also applied the same theory to investigate the stress distribution around the cut-out in an anisotropic plate with a quasi-square cut-out and subjected to uniaxial loading. But this research studied only the effect of bluntness and cut-out orientation for very special cases. (Rezaeepazhand and Jafari 2010) used Lekhnitskii’s theory to study the stress analysis of composite plates with quasi-square cut-out subjected to uniaxial tension. (Batista 2011) investigated stress distribution around polygonal cut-out with rather complex geometries. He used the expansion of Muskhelishvili’s complex variable method and Schwarz-Christoffel mapping function. (Ukadgaonker and Rao 1997) presented solutions for stress distribution around triangular cutout with blunt corners in composite plates. (Wescott et al. 2004)) investigated the stress analysis of near optimal surface notches in 3D plates using two-dimensional (2D) optimal notch shapes. (Sharma 2014) presented a general solution to calculate stress distribution around polygonal cut-out in infinite isotropic plates subjected to biaxial loading. He also studied the effect of cutout geometry and the pattern of loading on the stress analysis of perforated plates. (Kazberuk et al. 2016) studied stress distribution at sharp and rounded V-notches in quasi-orthotropic plane. (Jafari and Ardalani 2016) also studied the stress distribution around several polygonal cut-out in finite isotropic plates. They investigated the effects of cut-out orientation and the bluntness of the polygonal cut-out on the stress concentration.

One of the main concerns of industrial designers is the choice of the optimal values of design variables. The selection of an appropriate method among different methods of optimization depends on the type of problem. Recently, number of researchers attempted to apply them in to different problems in diverse fields such as particle swarm optimization (PSO), ant colony optimization (ACO), genetic algorithm (GA) and etc. to design of composite structures. These algorithms are SI-based algorithms. The successful application of these algorithms in science and industry evidences the merits of SI-based techniques in practice. (Vigdergauz 2001) investigated the effective properties of an elastic perforated plate by using genetic algorithm. (Barbosa et al. 2014) designed a composite lattice structure under torsion and investigated the effects of many materials and geometric parameters on the optimized mechanical behavior of structures. PSO technique was employed in order to maximize the torsion constant of the structures in this work. (Chen et al. 2013) developed a method for optimum designing (based on reliability) of a composite structure based on the combination of PSO and FEA methods. (Muc and Gurba 2001) used a combination of genetic algorithm and finite element analysis in optimization of composite structures. (Kradinov et al. 2007) showed the application of genetic algorithm in the optimal design of bolted composite lap joints. Moreover, (Suresh et al. 2007) investigated the particle swarm optimization approach for multi-objective composite box-beam design. (Kathiravan and Ganguli 2007) showed the application of particle swarm optimization and gradient method in the strength design of composite beams. (Jafari and Moussavian 2016) investigated the optimum design of laminated composite plates containing a quasi-square cut-out. They used swarm intelligence algorithms in this research. (Mirjalili et al. 2014) have recently tested grey wolf optimizer (GWO) on uni-modal, multi- modal, fixed-dimension multimodal, and composite functions. It is efficient in terms of exploration, exploitation, local optimal avoidance, and convergence. It has been shown that the grey wolf optimizer algorithm is able to provide very competitive results compared to other well-known meta-heuristics. The grey wolf optimizer algorithm has been successfully applied to three classical engineering design problems and real optical engineering (Mirjalili et al. 2014). (Song et al. 2014) have successfully applied GWO for solving combined economic emission dispatch problems. (Emary et al. 2015) have used GWO for feature subset selection. (Mirjalili 2015) has investigated the effectiveness of GWO in training multi-layer perceptions (MLP). (Saremi et al. 2015) proposed the use of evolutionary population dynamics (EPD) in the grey wolf optimizer algorithm to further enhance it is performance. (Song et al. 2015) have successfully applied GWO for parameter estimation in surface waves. In this study, relying on Lekhnitskii’s analytical solution and expanding this solution to the polygonal cut-out in orthotropic plates, the comprehensive stress analysis of perforated orthotropic plates is conducted. In this research design variables are load angle, bluntness, cutout orientation and fiber angle. It is tried to introduce the optimum values of the mentioned parameters for uniaxial tensile loading in order to obtain the minimum normalized stress. It is worth mentioning that the normalized stress value around the cutout is considered as cost function (C.F.) for grey wolf optimization algorithm. The main goal of this paper is to obtain the optimal design variables which minimize the maximum stress around polygonal cutout calculated by analytical method based on complex variable method. The optimal values of these parameters are determined using GWO.

2 THEORY ANALYSIS

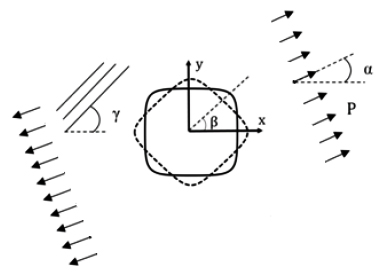
The problem to be investigated in this article is the perforated plate containing polygonal cutout. It is assumed that an infinite orthotropic plate with a centrally cut-out is subjected to a uniformly distributed tensile load at a large distance from the cut-out as shown in Figure 1. The cut-out size is small enough with respect to the plate dimensions. Therefore, its effect will be negligible at a distance of a few diameters from its edge. The load is applied at angle with respect to x-axis (α). The major axis of the cut-out is directed at angle with respect to x-axis (β). As shown in Figure 1, γ is fiber angle for composite plates. The cost function is to obtain the optimal design variables which minimize the maximum stress around different cut-out. As shown in Figure 1, design variables are load angle (α),cut-out orientation (β), fiber angle (γ) and the curvature of cut-out corner (w). The cut-out size is small compared to the size of plate (infinite plate). This investigation is conducted by considering the plane stress state and the absence of body forces. Also, the plate material is in its linear elastic region. Because of the traction-free boundary conditions on the edge of the cut-out, the stresses _^σρ and τ _ρθ at the cutout edge are zero and the circumferential stress σ _θ is only remaining stress.

Figure 1
Infinite plate with quasi-square cut-out under uniaxial load.

Analytical method used in this study is retrieved from the expansion of analytical solution method by (Savin 1961) and (Lekhnitskii 1969). In this method, stress function converts to an analytical expression with undetermined coefficients and displacements and stresses could be calculated by stress function being determined. Equilibrium equation will be satisfied by introducing F(x,y) as stress function according to Eq. (1).

(1)

By replacing stress-strain relations in compatibility relations and rewriting the resultant equation in terms of stress functions and with the assistance of Eq. (1), we will have (Muskhelishvili, 1962):

(2)

Eq. (2) is compatibility equation for anisotropic materials where _^Rij are members of reduced compliance matrix that for plane strain and plane stress states will be according to Eqs. (3) and (4) respectively:

(3)

(4)

where ] is determined in terms of compliance matrix components as follows: are the transformed compliance matrix components of the lamina and [

(5)

where [T₂] and [T₁] are transformation matrix defined as follows:

(6)

We have used m = cosγ and n = sinγ. γ is fiber angle. Compliance matrix in terms of engineering constants will be as below:

(7)

Thus solving 2D planar elasticity problems will lead to presentation and solution of fourth-order differential equation which is expressed by four first-order linear derivative operator as Eq. (8). (Lekhnitskii 1969) proved that this characteristic equation associated with orthotropic material generally has four imaginary roots which are mutually conjugated.

(8)

In curvilinear coordinate systems, the stress components created around the cut-out in two-dimensional region are expressed in terms of the stress functions φ(z ₁) and ψ(z ₂) (Lekhnitskii 1969) showed that the stress components around the cut-out in a plate pulled by uniform tension P applied at a considerable distance from the cut-out edge (in theory, it is infinity), at an angle α; with respect to the x-axis can be calculated as the Eqs. (9) to (11) (Lekhnitskii, 1969):

(9)

(10)

(11)

Where z ₁ = x - μ, y (i = 1,2) and ^_μi are the roots of the characteristic equation of anisotropic materials (Eq. (8)). ψ’(z ₁) and ψ’(z ₂) are the derivatives of the functions ψ’(z ₁) and ψ’(z ₂) with respect to z ₁ and z ₂. These analytic functions can be determined by applying the boundary conditions.

In order to calculate the stress components in the polar coordinates system, the Eqs. (12) and (13) are used. According to Figure 2, in these equations Ω is the angle between the positive x-axis and the ρ.

(12)

(13)

Figure 2
Curvilinear coordinates.

Stress distribution around the circular cutout was investigated by (Savin 1961) using complex variable method. In order to expand their solution to other cut-out, points on boundary of the cut-out with particular shape should be transformed outside the circle with unit radius using a simple mapping function (_^zi = x + _{^{μi y}} ) first, where x and y are obtained from Eqs. (14) and (15):

(14)

(15)

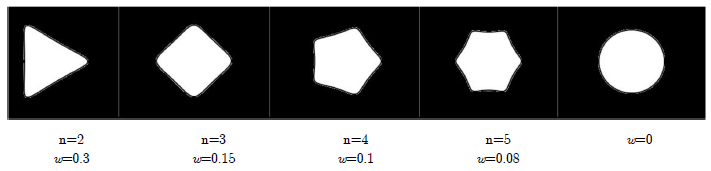
In the above equation, the parameter λ, which is a positive and real number, controls the size of the cutout. Integer n determines the shape of cut-out. Parameter w is the bluntness factor which changes the radius of curvature at the corner of the cut-out. For example, in above trigonometric equation, for quasi-square cut-out with sides of equal length (equilateral) n should be equal to 3. The conditions 0 ≤ w < 1/n ensure that the cut-out shape does not have loops. Effect of the amount of w is shown in Figure 3, according to this figure for a square cut-out when w decreases, corners of the cut-out become smoother until w reaches its minimum value, (becomes zero), in this case, cut-out converts to a circle. Figure 4 shows the effect of w and n on the shape of polygonal cut-out for zero rotation angle of 0° (β = 0).

Figure 3
The influence of w on the cutout geometry.

Figure 4
Effect of w and n on the cutout shape.

3 GREY WOLF OPTIMIZATION (GWO)

Nature is full of social behaviours for performing different tasks. Although the ultimate goal of all individuals and collective behaviours is survival, creatures cooperate and interact in flocks. Wolf packs own one of the most well-organized social interactions for hunting. Grey wolf optimization was proposed by (Mirjalili et al. 2014). Mirjalili creates a bio-inspired optimization algorithm, the so called grey wolf optimization (GWO), which has been inspired from the leadership hierarchy and hunting mechanism of grey wolves in nature. He used twenty nine test functions in order to investigate the performance of the proposed algorithm in terms of exploration, exploitation, local optima avoidance, and convergence. Then, he proved the grey wolf optimizer results were able to provide highly competitive results compared to well-known heuristics such as PSO, GSA, DE, EP, and ES . In addition, the three main steps of hunting, searching for prey, encircling prey, and attacking prey, are implemented (Mirjalili et al. 2014).

3.1 Mathematical Model

The grey wolf optimization is inspired from the hunting behavior and the social hierarchy of grey wolves. The grey wolves are categorized according to societal hierarchy as α’, β’, Λ’ and Ω’. In the grey wolf optimization, the fittest solution is called the α’ while the second and third best solutions are named β’ and Λ’ respectively. The rest of the candidate solutions are assumed to be Ω’. In this paper the hunting mathematical models are provide.

3.1.1 Encircling Prey

A grey wolf can update its position inside the space around the prey in any random location by using Eqs. (16) and (17). The encircling behavior of grey wolves can be represented as : (Mirjalili et al. 2014)

(16)

(17)

Where t is the number of iteration, X is the gray wolf position. The components of ₁ and r₂ are random values in [0,1]. The components of -a,a] as α’, β’, Λ’and Ω’. and are linearly decreased from 2 to 0 over the course of iterations. r is the prey position and are linearly decreased from 2 to 0 over the course of iterations. Moreover, is random values in the interval [, are coefficient vectors,

3.1.2 Hunting

In the GWO algorithm, the hunting (optimization) is guided by α’, β’, and Λ’. The Ω’ wolves follow these three wolves.

(18)

(19)

(20)

α’, β’and Λ’ respectively. The parameters A and C oblige the grey wolves algorithm to explore and exploit the search space. In order to exploration mathematically model from divergence, we utilize C also is changed randomly to resolve local optima stagnation during the course of optimization. Moreover, for mathematical modeling of approaching to the prey, the value of a is linearly decreased. Thus A are in [-1,1] (|Mirjalili et al. 2014) with random values greater than 1 or less than -1 to oblige the search agent to diverge from the prey. This emphasizes exploration and allows the grey wolf optimization algorithm to search globally. The vector contains random values in [0,2]. This component provides random weights for prey in order to stochastically emphasize (C > 1) or de-emphasize (C < 1) the effect of prey in defining the distance. Infact, the parameter | < 1), GWO forces the wolves to attack towards the prey. The parameter a is decreased from 2 to 0 in order to adaptively emphasize exploration and exploitation, respectively. Candidate solutions tend to diverge from the prey when || < 1. Finally, the grey wolf optimization algorithm is terminated by the satisfaction of an end criterion. ( and are position vector of | ≥ 1 and converge towards the prey when | is a random value in the interval [-a, a]. When random values of ,

4 TESTING CONVERGENCE GWO

The constraints contain upper and lower boundaries which can be changed based on shape of the cut-out. Figure 5 shows convergence diagrams for GWO algorithm for Glass/Epoxy plate containing cut-out with various shapes in one of the optimum conditions (w = 0.05, α = 30). The ratio of the maximum stress created around cutout to the applied stress is considered as cost function.

Figure 5
GWO algorithm convergence diagram for Glass /Epoxy material and different cut-out.

In Figure 5, in addition to viewing the convergence for the intended condition, it can be seen that GWO algorithm always tries to search local optimum value that finding the absolute optimum value in a suitable time. Also, the duration of solving the GWO algorithm after several runs, it turned out that GWO algorithm is capable of finding the absolute optimum value in a short time.

5 RESULTS

Many parameters affect the stress distribution around cut-out in orthotropic plates. The correct choice of these parameters is an important role in the design of these plates. In this study, an attempt has been made to obtain the optimal values of different parameters to achieve the lowest stress concentration for various cut-out. Mechanical properties used in this study are presented in Table 1.

Table 1
Materials properties of perforated plate (Rezaeepazhand and Jafari, 2015).

Material	E1(GPa)	E2(GPa)	G12 (GPa)	ν12
Glass/Epoxy (CE 9000)	47.4	16.2	7	0.26
Graphite/Epoxy (T300/5208)	181	10.3	7.17	0.28
Carbon/Epoxy (GY-70/934)	294	6.4	4.9	0.23

5.1 Quasi-triangular cut-out

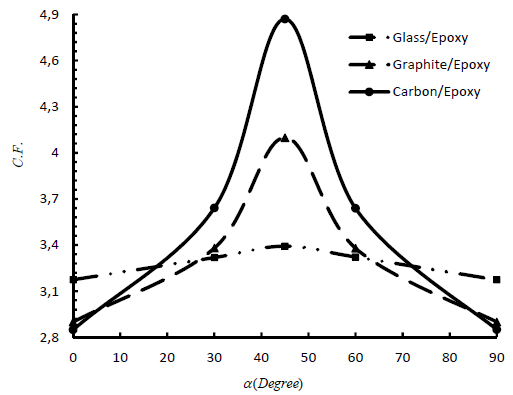
At first for a particular value of w, the optimal values of design variables such as load angle, rotation angle of cut-out and fiber angle are calculated. For this purpose, Figure 6 shows the effects of load angle on the value of the cost function by considering fiber angles and cut-out orientation simultaneously as design variables for the discussed three types of orthotropic materials in quasi-triangular cutout with w = 0.05. Values of fiber angle and cut-out orientation in this case, are optimum values obtained by GWO algorithm. According to the Figure 6, for all three materials, the maximum value of the cost function occurs at loading angle of 45º, and Carbon/Epoxy material has the highest value of stress amongst the three others. For five different load angles, the optimal values of design variables and corresponding cost function in w = 0.05 are shown in Table 2. Moreover, Figure 7 shows the variation of the minimum normalized stress with fiber angle for w = 0.05. In fact in this figure for each fiber angle, the value of minimum normalized stress is obtained for optimum values of load angle and rotation angle.

Figure 6
Variations of the cost function in terms of load angle for quasi- triangular cut-out (w = 0.05).

Table 2
Optimal values of different parameters for triangular cut-out in various load angles (w = 0.05).

Glass/Epoxy				Graphite/Epoxy				Carbon/Epoxy
α	γ	β	C.F.	α	γ	β	C.F.	α	γ	β	C.F.
0	64.8640	180	2.7982	0	90	0	2.4788	0	90	0	2.3747
30	90	153.4997	2.8048	30	90	177	3.1997	30	90	62.1	3.8870
45	90	119.1598	3.1044	45	90	7.577	4.4415	45	0	80.71	5.8798
60	0	176.4992	2.8051	60	0	92.996	3.1993	60	90	148.3	3.8867
90	27.4888	28.7296	2.7980	90	0.134	89.95	2.4788	90	0	150.41	2.3747

Figure 7
Variations of the cost function in terms of fiber angle for quasi- triangular cut-out (w = 0.05).

As shown in this figure, for all materials, maximum cost function occurs when fiber angle is 45 degrees and among the material studied, the highest value function is related to Carbon/Epoxy. For five different fiber angles, the optimal values of design variables and corresponding cost function in w = 0.05 are shown in Table 3. C.F. in this table presents the value of optimum stress. The design variables represented in this table are load angle and rotation angle. Table 4 shows the optimal values of load angle, fiber angle, rotation angle and the corresponding value of the cost function for different values of w.

Table 3
Optimal values of different parameters for triangular cut-out in various fiber angles (w = 0.05).

Glass/Epoxy				Graphite/Epoxy				Carbon/Epoxy
γ	α	β	C.F.	γ	α	β	C.F.	γ	α	β	C.F.
0	61.804	180	2.7992	0	89.96	89.95	2.4788	0	90	29.99	2.3747
30	90	26.50	2.8059	30	90	63.015	3.1991	30	90	58.30	3.8843
45	90	135.83	3.1049	45	0	22.566	4.4421	45	90	4.775	5.8791
60	0	63.518	2.8058	60	0	87	3.1997	60	0	31.722	3.8864
90	28.522	90.52	2.8007	90	0	60.01	2.4788	90	0	180	2.3746

Table 4
Optimal values of different parameters for triangular cut-out for different w.

Glass/Epoxy					Graphite/Epoxy					Carbon/Epoxy
w	γ	β	|γ - α|	C.F.	w	γ	β	|γ - α|	C.F.	w	γ	β	|γ - α|	C.F.
0	23.86	-	60	2.6595	0	0.099	-	90	2.3717	0	0	-	90	2.2614
0.05	87.63	146.46	62	2.7987	0.05	90	0.039	90	2.4788	0.05	90	0	90	2.3746
0.1	0.956	125.84	65	3.1157	0.1	90	180	90	2.7475	0.1	90	180	90	2.65
0.2	70.89	122.126	68	4.2425	0.2	0.531	89.64	90	3.7296	0.2	0	29.828	90	3.69

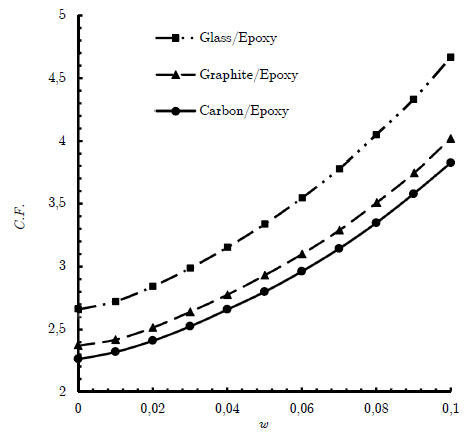
Figure 8 shows the variation of the cost function with respect to w. in this case, the design variables are load angle, fiber angle and rotation angle and the cost function has been calculated in the optimal values of them. As illustrated in this figure, for all used materials, the cost function decreases when the value of bluntness parameters (w) decreases. Therefore, the minimum cost function occurs in w = 0 which is equivalent to a circular cut-out. Finally, the optimal values of all parameters listed in Table 5.

Figure 8
Variations of the cost function in terms of w for quasi-triangular cut-out.

Table 5
Overall optimum results of triangular cut-out.

Material	w	γ	β	|γ - α|	C.F.
Glass/Epoxy	0	18.3	-	60	2.6595
Graphite/Epoxy	0	88.21	-	90	2.3717
Carbon/Epoxy	0	0.001	-	90	2.2614

5.2 Quasi-Square Cut-Out

Figure 9 shows the effects of loading angle on the value of the cost function by considering fiber angle and cut-out orientation simultaneously as design variables for the discussed three types of anisotropic materials with w = 0.05. The values of fiber angle and cut-out orientation in this case, are optimum values obtained by GWO algorithm. According to the Figure 9, for Carbon/Epoxy material, the maximum value of the cost function occurs at loading angle of 45º and it has the highest value of stress amongst the three others materials. Tables 6 show the optimum values of fiber angle, rotation angle and minimum normalized stress corresponding to each loading angle in w = 0.05. Figure 10 shows the changes of the cost function for various fiber angles in plates with square cutout (w = 0.05). Load angle and cutout orientation considered as design variables. As seen in this figure, the maximum of normalized stress occurs at fiber angle of 45 degrees for all used materials. For different fiber angles, Table 7 shows the optimal values of load angle and rotation angle and corresponding normalized stress. Results show that the cost function varies considerably by changing fiber angle. Bluntness parameter (w) is one of the most important parameters that affect the stress distribution around the cut-out. In order to study the influence of this parameter, the optimal values of load angle, rotation angle and fiber angle are presented in Table 8 for different w. According to this table, the minimum value of the normalized stress is strongly dependent on the value of w. Hence, Figure 11 shows the variations of the cost function with the bluntness parameter (w). In this case, design variables are load angle, fiber angle and rotation angle. Unlike the quasi-triangular cut-out, the optimal value of w is not zero. This means that by selecting the appropriate values of design variables stress concentration factor of square cut-out is less than those of circular cutout.

Figure 9
Variations of the cost function in terms of load angle for quasi- square cut-out (w = 0.05).

Table 6:
Optimal values of different parameters for square cut-out in various load angles (w = 0.05).

Glass/Epoxy				Graphite/Epoxy				Carbon/Epoxy
α	γ	β	C.F.	α	γ	β	C.F.	α	γ	β	C.F.
0	69.4123	44.7	2.3956	0	90	44.9973	2.2192	0	90	45	2.214
30	90	79.113	2.4650	30	90	9.20499	2.5542	30	90	19.2805	2.7423
45	90	12.456	2.5786	45	0	63.6778	3.2691	45	0	59.9335	4.1613
60	0	77.531	2.4651	60	0	80.7989	2.542	60	0	70.01	2.744
90	0	45.375	2.3956	90	0	44.9671	2.2191	90	0	44.5932	2.214

Figure 10
Variations of the cost function in terms of fiber angle for quasi-square cut-out (w = 0.05).

Table 7
Optimal values of different parameters for square cut-out in various fiber angles (w = 0.05).

Glass/Epoxy				Graphite/Epoxy				Carbon/Epoxy
γ	α	β	C.F.	γ	α	β	C.F.	γ	α	β	C.F.
0	73.8445	29.39	2.3958	0	89.78	44.66	2.2193	0	90	44.99	2.2141
30	90	40.64	2.4651	30	90	20.801	2.554	30	90	10.70	2.7427
45	0.6380	58.16	2.5589	45	90	18.51	3.2690	45	90	14.687	4.1615
60	0	49.34	2.4651	60	0	69.19	2.5539	60	0	79.29	2.7428
90	16.1255	60.58	2.3956	90	0.663	46.02	2.2196	90	0	45	2.2141

Table 8
Optimal values of different parameters for square cut-out for different w.

Glass/Epoxy					Graphite/Epoxy					Carbon/Epoxy
w	γ	β	|γ - α|	C.F.	w	γ	β	|γ - α|	C.F.	w	γ	β	|γ - α|	C.F.
0	85.2	-	60	2.6595	0	0	-	90	2.3717	0	0	-	90	2.2614
0.05	16.2	44.73	73	2.3956	0.05	90	44.99	90	2.2191	0.05	0	44.96	90	2.2141
0.1	90	45.10	90	2.7037	0.1	90	44.99	90	2.6887	0.1	90	0.706	68	2.9664
0.2	90	46.13	90	4.8959	0.2	90	63.34	90	5.3587	0.2	26.17	18.73	64	5.3198

Figure 11
Variations of the cost function in terms of w for quasi-square cut-out.

Table 9 shows overall optimum results for the anisotropic material. This results optimization process take place for all parameters such as; fiber angle (Y), load angle (α), rotation angle (β) and cutout curvature (w).

Table 9
Overall optimum results of square cut-out.

Material	w	γ	β	|γ - α|	C.F.
Glass/Epoxy	0.0323241	0	90	45	2.3918
Graphite/Epoxy	0.0323241	90	0	45	2.1691
Carbon/Epoxy	0.0260045	0	90	45	2.1081

5.3 Pentagonal Cut-Out

Figure 12 shows the effects of loading angle on the values of the cost function by considering fiber angle and cutout orientation simultaneously as design variables for the discussed three types of orthotropic materials in pentagonal cut-out with w = 0.05. As shown in this figure, for all used materials, the maximum normalized stress occurs at load angle of 45 degrees and Carbon/Epoxy material has the highest value of stress amongst the three others. Moreover, minimum cost function happens at 0 or 90 degrees. For five different load angles, the optimal values of design variables and corresponding cost function in w = 0.05 are shown in Table 10.

Figure 12
Variations of the cost function in terms of load angle for pentagonal cut-out (w = 0.05).

Table 10
Optimal values of different parameters for pentagonal cut-out in various load angles (w = 0.05).

Glass/Epoxy				Graphite/Epoxy				Carbon/Epoxy
α	γ	β	C.F.	α	γ	β	C.F.	α	γ	β	C.F.
0	64.80	144.42	3.3389	0	90	180	2.9251	0	90	36	2.796
30	90	35.494	3.3697	30	90	133.324	3.9122	30	90	102.267	4.778
45	90	25.531	3.7153	45	90	34.7828	5.373	45	90	1.666	7.175
60	0	90.622	3.3699	60	0.23	136.721	3.912	60	0	59.7031	4.779
90	25.38	17.463	3.3387	90	1.15	125.403	2.925	90	0.07	125.912	2.796

For pentagonal cut-out with w = 0.05, the cost function changes with fiber angle is shown in Figure 13. In this case design variables are load angle and rotation angle of the cutout. Similar to what happened for theload angle, the maximum and minimum value of the cost function occurs at fiber angle of 45 degrees and 0 or 90 degrees, respectively. Table 11 represents the optimal values of the design variables for all used materials for different fiber angles. For different values of bluntness parameter (w), the optimal values of the effective parameters are listed in Table 12. As shown in this table, the lowest value of the cost function occurs in w=0 which is equivalent to circular cut-out. Figure 14 shows the variation of the cost function with respect to w for all design variables. As shown in this figure, by reducing the value of w, the cost function decreases. Finally, Table 13 shows overall optimum results for the anisotropic material. This results optimization process take place for all parameters such as; fiber angle, load angle, rotation angle and cutout curvature.

Figure 13
Variations of the cost function in terms of fiber angle for pentagonal cut-out (w = 0.05).

Table 11
Optimal values of different parameters for pentagonal cut-out in various fiber angles (w = 0.05).

Glass/Epoxy				Graphite/Epoxy				Carbon/Epoxy
γ	α	β	C.F.	γ	α	β	C.F.	γ	α	β	C.F.
0	64.581	100.09	3.3404	0	90	53.99	2.9246	0	90	53.98	2.7966
30	90	156.49	3.3698	30	90	130.63	3.9139	30	90	89.81	4.7837
45	90	73.325	3.7168	45	90	64.37	5.355	45	90	61.65	7.1067
60	0	41.434	3.3695	60	0	103.33	3.9118	60	0	72.24	4.7797
90	25.309	25.815	3.3394	90	0.001	0	2.9251	90	0	180	2.797

Table 12
Optimal values of different parameters for pentagonal cut-out for different w.

Glass/Epoxy					Graphite/Epoxy					Carbon/Epoxy
w	γ	β	|γ - α|	C.F.	w	γ	β	|γ - α|	C.F.	w	γ	β	|γ - α|	C.F.
0	78.519	-	60	2.6595	0	0	-	90	2.3717	0	90	-	90	2.2614
0.05	8.251	0.99	66	3.3392	0.05	0.611	125.62	90	2.9251	0.05	1.278	88.71	90	2.796
0.1	90	130.9	66	4.6647	0.1	0.082	53.84	90	4.0161	0.1	0.114	125.77	90	3.8251
0.15	69.69	74.61	66	7.3227	0.15	0.033	18.06	90	6.2186	0.15	2.305	13.66	90	6.1308

Figure 14
Variations of the cost function in terms of w for pentagonal cut-out.

Table 13
Overall optimum results of pentagonal cu-tout.

Material	w	γ	β	|γ - α|	C.F.
Glass/Epoxy	0	59.483	-	60	2.6595
Graphite/Epoxy	0	90	-	90	2.3717
Carbon/Epoxy	0	0	-	90	2.2614

5.4 Hexagonal Cut-Out

For hexagonal cut-out with w = 0.05, the cost function changes with load angle is shown in Figure 15. As shown in this figure, for all used materials, the maximum and minimum values of the cost function occur at load angle of 45 degrees and 0 or 90 degrees, respectively. Table 14 shows the optimum values of fiber angle, rotation angle and minimum normalized stress corresponding to each loading angle in w = 0.05. Moreover, Figure 16 shows the changes of the cost function for various fiber angles in plates with hexagonal cut-out (w = 0.05). Load angle and cut-out orientation considered as design variables. As seen in this figure, the maximum of the normalized stress occurs at fiber angle of 45 degrees. Between all used materials and for fiber angle in the range of 20-70 degrees, the highest normalized stress takes place for Carbon/Epoxy material. For different fiber angles, Table 15 shows the optimal values of load angle and rotation angle and corresponding normalized stress. Also, the optimal values of design variables such as rotation angle, load angle and fiber angle in different values of w are shown in Table 16. Figure 17 shows the changes of the cost function with respect to w. In this case, design variables are load angle, fiber angle and rotation angle. According to this figure, the optimal value of w is not zero. Finally, the optimal values of all effective parameters are present in Table 17.

Figure 15
Variations of the cost function in terms of load angle for pentagonal cut-out (w = 0.05).

Table 14
Optimal values of different parameters for hexagonal cut-out in various load angles (w = 0.05).

Glass/Epoxy				Graphite/Epoxy				Carbon/Epoxy
α	γ	β	C.F.	α	γ	β	C.F.	α	γ	β	C.F.
0	90	0	3.1743	0	90	0.017	2.8995	0	90	60.01	2.8495
30	90	36.05	3.3184	30	90	57.88	3.3799	30	90	4.598	3.6408
45	0	31.01	3.3926	45	0	79.28	4.098	45	90	75.08	4.87
60	0.273	53.75	3.3221	60	0	32.16	3.3788	60	0.037	25.47	3.6386
90	0.089	90	3.1739	90	0.023	90	2.8995	90	0.001	90	2.8495

Figure 16
Variations of the cost function in terms of fiber angle for hexagonal cut-out (w = 0.05).

Table 15
Optimal values of different parameters for hexagonal cut-out in various fiber angles (w = 0.05).

Glass/Epoxy				Graphite/Epoxy				Carbon/Epoxy
γ	α	β	C.F.	γ	α	β	C.F.	γ	α	β	C.F.
0	79.2944	19.99	3.1739	0	89.99	90	2.8996	0	90	90	2.8495
30	90	23.94	3.3177	30	90	62.16	3.3788	30	90	55.47	3.6359
45	0	13.96	3.3925	45	0	25.64	4.09	45	0	30.09	4.8699
60	0.0036	6.063	3.3184	60	0.085	27.98	3.3829	60	0.04	34.66	3.6447
90	0.0086	0	3.1739	90	0.247	0.441	2.8996	90	0	59.98	2.8495

Table 16
Optimal values of different parameters for hexagonal cu-tout for different w.

Glass/Epoxy					Graphite/Epoxy					Carbon/Epoxy
w	γ	β	|γ - α|	C.F.	w	γ	β	|γ - α|	C.F.	w	α	γ	|γ - α|	C.F.
0	76.043	-	60	2.6595	0	0	-	90	2.3717	0	90	-	90	2.2614
0.05	90	0.01	90	3.1739	0.05	90	0.025	90	2.8995	0.05	90	0.072	90	2.8495
0.1	0.06	78.99	79	5.0534	0.1	90	0.06	90	4.5897	0.1	0	29.85	90	4.6234
0.15	85.626	66.42	79	10.6522	0.15	90	51.63	90	10.0553	0.15	90	27.86	90	9.7817

Figure 17
Variations of the cost function in terms of w for hexagonal cut-out.

Table 17
Overall optimum results of hexagonal cut-out.

Material	w	γ	β	|γ - α|	C.F.
Glass/Epoxy	0.0096	25.2487	89.3265	60	2.5606
Graphite/Epoxy	0.00817	0	29.6097	90	2.2855
Carbon/Epoxy	0.006302	0	90	90	2.1983

With the increasing number of cutout sides, the obtained results will be close to results of a circular cut-out. The results of the previous sections suggest that the optimal values of the cost function for all cut-out with odd number of sides are always more than the corresponding value of a circular cut-out while all cut-out with an even number of sides are more efficient than a circular cut-out.

6 CONCLUSIONS

In this study, using gray wolf optimization algorithm (GWO), optimum parameters affecting normalize stress around polygonal cutout in orthotropic plates were determined. Design variables in this study are loading angle, cut-out orientation, fiber angle and bluntness. The grey wolf optimization algorithm is another form of metaheuristic algorithms based on swarm intelligence (SI) that draws inspiration from the social leadership hierarchy and hunting behavior of grey wolves in nature. Results demonstrated that GWO creates a good balance between exploration and exploitation that results in high local optimal avoidance and a suitable convergence. Moreover, the cost function considered in this paper was obtained based on Lekhnitskii’s solution technique which was just for circular and elliptical cut-out and was generalized to polygonal cut-out using conformal mapping and complex variable method. The results also showed that the cut-out bluntness is not the only parameter affecting the reduction of stress concentration, but also the cut-out orientation, and suitable load angle and fiber angle play a major role in the reduction of stress that with choosing the optimum values of these parameters in a specific curvature, stress concentration can be reduced significantly. The optimal values of normalized stress for all cut-out with an odd number of sides were always more than the corresponding value of a circular cut-out while, all cut-out with an even number of sides were more efficient than circular cut-out. Among of all cut-out shapes, quasi-square cut-out has the lowest possible normalized stress.

References

• Asmar G. H., Jabbour T. G. (2007). Stress analysis of anisotropic plates containing rectangular holes. International Journal of Mechanics and Solids 2(1):59-84.
• Barbosa, I. C. J., Loja, M. A. R. (2014). Design of a laminated composite multi-cell structure subjected to torsion. 29th Congress of the International Council of Aeronautical Sciences ICAS 2014: 1-8.
• Batista, M. (2011). On the stress concentration around a cutout in an infinite plate subject to a uniform load at infinity. International Journal of Mechanical Sciences 53(4): 254-261.
• Chen, J., Tang, Y., Ge, R., An, Q., Guo, X. (2013). Reliability design optimization of composite structures based on PSO together with FEA. Chinese Journal of Aeronautics 26(2): 343-349.
• Daoust, J., Hoa, S. V. (1991). An analytical solution for anisotropic plates containing triangular cut-out. Composite Structures 19(2):107-130.
• Emary, E., Zawbaa, H.M., Grosan, C., Hassenian, A.E. (2015). Feature subset selection approach by Gray Wolf Optimizer. Advances in Intelligent Systems and Computing 334: 1-13.
• Jafari, M., Ardalani, E. (2016). Stress concentration in finite metallic plates with regular cut-out. International Journal of Mechanical Sciences 106: 220-230.
• Kathiravan, R., Ganguli, R. (2007). Strength design of composite beam using gradient and particle swarm optimization. Composite Structures 81:471-479.
• Kazberuk, A., Savruk, M. P., Chornenkyi, A. B. (2016). Stress distribution at sharp and rounded V-notches in quasi-orthotropic plane. International Journal of Solids and Structures 85-86: 134-143.
• Kradinov, V., Madenci, E., Ambur, D. R. (2007). Application of genetic algorithm for optimum design of bolted composite lap joints. Composite Structures 77(2): 148-159.
• Lekhnitskiy, S. G. (1969). Anisotropic Plates, Gordon and Breach Science, New York.
• Mirjalili, S. (2015). How effective is the Grey Wolf Optimizer in training multi-layer perceptrons. Applied Intelligence 43:150-161.
• Mirjalili, S., Mirjalili, S.M. Lewis, A. (2014). Grey Wolf Optimizer. Advances in Engineering Software, 69: 46-61.
• Moussavian, H., Jafari, M. (2016) Optimum design of laminated composite plates containing a quasi-square cutout. Structural and Multidisciplinary Optimization. doi:10.1007/s00158-016-1481-7.
  » https://doi.org/10.1007/s00158-016-1481-7
• Muc, A., Gurba, W. (2001). Genetic algorithm and finite element analysis in optimization of composite structures. Composite Structures 54:275-281.
• Muskhelishvili, N. I. (1953). Some basic problems of mathematical theory of elasticity, Netherlands: Oordhooff, Groningen, Holland 56-104.
• Neuber, H. (1968). On the effect of stress concentration in cosserat continua, Springer, verlag Berlin Heidelberg.
• Peterson, R.E. (1974). Stress concentration factors, John Wiley and Sons Inc, New York.
• Pilkey, W. D. (1997). Peterson’s stress concentration factors, John Wiley and Sons Inc, Second Edition, New York.
• Rezaeepazhand, J., Jafari, M. (2010). Stress analysis of composite plates with Quasi-square cut out subjected to uniaxial tension. Journal of Reinforced Plastics and Composites 29:2015-2026.
• Saremi, S., Mirjalili, S.Z., Mirjalili, S.M. (2015). Evolutionary population dynamics and grey wolf optimizer. Neural Computing and Applications 26:1257-1263.
• Savin, G. N. (1961). Stress concentration around cut-out, Pergamon Press, New York.
• Sharma, D. S. (2014). Moment distribution around polygonal cut-out in infinite plate. International Journal of Mechanical Sciences 78(1):177-182.
• Song, H.M., Sulaiman, M.H. Mohamed, M.R. (2014). Anapplication of grey wolf optimizer for solving combined economic emission dispatch problems. International Review on Modelling and Simulations, 2: 838-844.
• Song, X., Tang, L., Zhao, S., Zhang, X., Li, L., Huang, J., Cai, W. (2015). Grey Wolf Optimizer for parameter estimation in surface waves. Soil Dynamics and Earthquake Engineering 75: 147-157.
• Sternberg, E. (1958). Couple-stresses and singular stress concentrations in elastic solids, Springer, verlag Berlin.
• Suresh, S., Sujit, P. B., Rao, A. K. (2007). Particle swarm optimization approach for multi-objective composite box-beam design. Composite Structures 81(4):598-605.
• Theocaris, P. S., Petrou, L. (1986). Stress distributions and intensities at corners of equilateral triangular cut-out. International Journal of Fracture 31(4): 271-289.
• Ukadgaonker, V. G., Rao, D. K. N. (1999). Stress distribution around triangular cut-out in anisotropic plates. Composite Structures 45(3): 171-183.
• Vigdergauz, S. (2001). The effective properties of a perforated elastic plate Numerical optimization by genetic algorithm. International Journal of Solids and Structures 38:8593-8616.
• Wescott, R., Semple, B., Heller, M. (2004). Stress analysis of near optimal surface notches in 3D plates. Journal of Mechanical Design 127(6):1173-1183.

Publication Dates

• Publication in this collection
  June 2017

History

• Received
  15 Oct 2016
• Reviewed
  02 Apr 2017
• Accepted
  03 Apr 2017