Abstract
The thermo-hydro-mechanical problems associated with a poroelastic half-space soil medium with variable properties under generalized thermoelasticity theory were investigated in this study. By remaining faithful to Biot’s theory of dynamic poroelasticity, we idealized the foundation material as a uniform, fully saturated, poroelastic half-space medium. We first subjected this medium to time harmonic loads consisting of normal or thermal loads, then investigated the differences between the coupled thermohydro-mechanical dynamic models and the thermo-elastic dynamic models. We used normal mode analysis to solve the resulting non-dimensional coupled equations, then investigated the effects that non-dimensional vertical displacement, excess pore water pressure, vertical stress, and temperature distribution exerted on the poroelastic half-space medium and represented them graphically.
Keywords:
Coupled thermo-hydro-mechanical dynamic; Generalized thermoelasticity; Thermo-elastic dynamic; Poroelastic; Normal mode analysis
1 INTRODUCTION
The effects of temperature on the behavior of soil is an important engineering concern. Temperature can impact the disposal of high-level radioactive waste, the extraction of oil or geothermal energy, the storage of hot fluids, road subgrades, and furnace foundations. The theory of thermoelasticity was developed in order to analyze these problems associated with thermodynamics.
The classical coupled thermoelasticity proposed by (Biot 1956Biot, M.A. (1956). Thermoelasticity and irreversible thermodynamics, Journal of Applied Physics, 27: 240-253.) predicts an infinite speed for heat propagating in elastic media, which is physically impossible. To eliminate this inherent paradox, subsequent generalized thermoelastic theories have been developed by Lord and Shulman (L-S 1967Lord, H.W. and Shulman, Y. (1967). A generalized dynamical theory of thermoelasticity, Journal of the Mechanics and Physics of Solids, 15: 299-309.), Green and Lindsay (G-L 1972Green, A.E. and Lindsay, K.A. (1972). Thermoelasticity, Journal of Elasticity, 2: 1-7.), and Green and Naghdi (G-N 1991Green, A.E. and Naghdi, P.M. (1991). A reexamination of the basic results of themomechanics, Proceedings of the Royal Society of London A, 432: 171-194., 1992Green, A.E. and Naghdi, P.M. (1992). On undamped heat waves in an elastic solid, Journal of Thermal Stresses, 15: 252-264., 1993Green, A.E. and Naghdi, P.M. (1993). Thermoelasticity without energy dissipation, Journal of Elasticity, 31: 189-208.). An extensive theory of thermoelasticity was formulated by Lord and Shulman that introduced a heat flow rate term together with a thermal relaxation time into Fourier’s law of heat conduction. By modifying both the energy equation and Duhamel-Neumann’s law, Green and Lindsay introduced the concept of allowing two relaxation times. A form of thermoelastic theory that allowed for no energy dissipation was proposed by Green and Naghdi. Other generalized thermoelastic theories include the two-temperature generalized thermoelasticity formulated by (Youssef 2006Youssef, H.M. (2006). Theory of two-temperature-generalized thermoelasticity, IMA Journal of Applied Mathematics, 71: 383-390.) and the dual-phase-lag thermoelasticity introduced by (Tzou 1995Tzou, D.Y. (1995). A unified field approach for heat conduction from macro to micro scales, ASME Journal of Heat Transfer, 117: 8-16.). (Hetnarski and Ignaczak 1999Hetnarski, R.B. and Ignaczak, J. (1999). Generalized thermoelasticity, Journal of Thermal Stresses, 22: 451-476.) examined five concerning theories of the coupled theory of thermoelasticity.
A great deal of research attention has been focused on the wave propagation problem in context of generalized thermoelasticity. (Singh 2007Singh, B. (2007). Wave propagation in a generalized thermoelastic material with voids, Applied Mathematics and Computation, 189: 698-709.) solved a two-dimensional homogeneous, isotropic generalized thermoelastic half-space problem in the context of Lord and Shulman theory of generalized thermoelasticity. The propagation of waves in a transversely isotropic micropolar medium possessing thermoelastic properties under three different theories are discussed by (Kumar and Gupta 2010Kumar, R. and Gupta, R.R. (2010). Propagation of waves in transversely isotropic micropolar generalized thermoelastic half space, International Communications in Heat and Mass Transfer, 27: 1452-1458.). (Bijarnia and Singh 2012Bijarnia, R. and Singh, B. (2012). Propagation of plane waves in an anisotropic generalized thermoelastic solid with diffusion, Journal of Engineering Physics and Thermophysics, 85: 478-486.) investigated the propagation of four different plane waves in a solid half-space with diffusion in the context of the Lord and Shulman theory of generalized thermoelasticity. (Lotfy 2014Lotfy, K.H. and Hassan, W. (2014). Normal mode method for two-temperature generalized thermoelasticity under thermal shock problem, Journal of Thermal Stresses, 37: 545-560.) investigated a two-temperature problem for an isotropic homogeneous elastic half-space under three thermoelastic theories. (Lotfy and Hassan 2014Lotfy, K.H. (2014). Two temperature generalized magneto-thermoelastic interactions in an elastic medium under three theories, Applied Mathematics and Computation, 227: 871-888.) solved a thermoelastic wave propagation problem for a half-space media subject to thermal shock based on the two-temperature theory of thermoelasticity. (Abo-Dahab et al. 2015Abo-Dahab, S.M., Lotfy, K.H., and Gohaly A. (2015) Rotation and magnetic field effect on surface waves propagation in an elastic layer lying over a generalized thermoelastic diffusive half-space with imperfect boundary, Mathematical Problems in Engineering, 2015: 671783.) studied the effects of magnetic field, relaxation times, and rotation on the propagation of surface waves in the context of Green-Lindsay theory. (Singh 2016Singh, B. (2016). Wave propagation in a rotating rransversely isotropic two-temperature generalized thermoelastic medium without dissipation, International Journal of Thermophysics, doi: 10.1007/s10765-015-2015-z.
https://doi.org/10.1007/s10765-015-2015-...
) explored plane wave propagation in a solid half-space which is rotating, transversely isotropic, two-temperature thermoelastic without energy dissipation. (Lotfy 2016Lotfy, K.H. (2016). The elastic wave motions for a photothermal medium of a dual-phase-lag model with an internal heat source and gravitational field, Canadian Journal of Physics, 94: 400-409.) introduced the dual-phase-lag (DPL) heat transfer model to solve the problem for a isotropic generalized thermoelastic medium with an internal heat source.
Wave propagation in a thermoelastic porous media is useful in various engineering fields such as petroleum engineering, chemical engineering, pavement engineering, and nuclear waste management, making it a popular research subject as well. (Kumar and Devi 2008Kumar, R. and Devi, S. (2008). Thermomechanical intereactions in porous generalized thermoelastic material permeated with heat sources, Multidiscipline Modeling in Materials and Structures, 4: 237-254.) investigated a porous, generalized thermoelastic medium subjected to thermomechanical boundary conditions permeated with various heat sources. (Sherief and Hussein 2012Sherief, H.H. and Hussein, E.M. (2012). A mathematical model for short-time filtration in poroelastic media with thermal relaxation and two temperatures, Transport in Porous Media, 91: 199-223.) developed a set of governing equations that effectually create a mathematical model of generalized thermoelasticity in poroelastic materials, then, they used this model to solve a thermal shock problem regarding the use of half-space. (Abbas and Youssef 2015Abbas, I.A. and Youssef, H.M. (2015). Two-dimensional fractional order generalized thermoelastic porous material, Latin American Journal of Solids and Structures, 12: 1415-1431.) solved a two-dimensional problem of a porous material in the context of the fractional order generalized thermoelasticity theory with one relaxation time. (Wei et al. 2016Wei, W., Zheng, R.Y., Liu, G.B., and Tao, H.B. (2016). Reflection and refraction of P wave at the interface between thermoelastic and porous thermoelastic medium, Transport in Porous Media, 113: 1-27.) studied the reflection and refraction phenomenon that occurs in an oblique incidence longitudinal wave at a plane interface between an isotropic, homogeneous, thermoelastic medium and a porous thermoelastic medium. (Schanz 2009Schanz, M. (2009). Poroelastodynamics: linear models, analytical solutions, and numerical methods, Applied Mechanics Reviews, 62: doi: 10.1115/1.3090831.
https://doi.org/10.1115/1.3090831...
) provided an overview of several poroelastodynamic models and analytical solutions, and also discussed two different numerical methodologies including the finite element method and the boundary element method.
The role that fluid flow plays in thermoelasticity was neglected in the above studies. With this in mind, we conducted the present study because we believe that a thorough knowledge of hydrothermal, hydromechanical, and thermal-mechanical processes, as well as knowledge of the interdependence of these processes, is necessary to accurately model the coupled behavior of fluid-saturated media. The thermo-hydro-mechanical (THM) coupled behavior of unsaturated soil is a very common physical phenomenon in nature and very worthy of further research.
Several previous studies of fluid-saturated media informed our current study. The theoretical developments have matured from a simple isotropic poroelastic theory proposed by Biot into a general approach to managing coupling and material anisotropy (Abousleiman and Ekbote, 2005Abousleiman, Y. and Ekbote, S. (2005). Solutions for the inclined borehole in a porothermoelastic transversely isotropic medium, Transactions of the ASME. E: Journal of Applied Mechanics, 72: 102-114.). (Booker and Savvidou 1984Booker, J.R. and Savvidou, C. (1984). Consolidation around a spherical heat source, International Journal of Solids and Structures, 20: 1079-1090.) developed an analytic solution for the consolidation of soil around an impermeable rigid, spherical, heat source and a point source. (Biot 1977Biot, M.A. (1977). Variational Lagrangian-thermodynamics of non-isothermal finite strain mechanics of porous solids and thermomolecular diffusion, International Journal of Solids and Structures, 13: 579-597.) also formulated a new thermodynamics theory for elastic saturated porous solids. (Bai 2006aBai, B. (2006c). Response of saturated porous media subjected to local thermal loading on the surface of semi-infinite space, Acta Mechanica Sinica, 22: 54-61.) solved a double-layered porous space subjected to exponential decaying thermal loading, and derived the thermal consolidation of layered, saturated porous half-space to various thermal loads with time. (Bai 2006bBai, B. (2006b). Fluctuation responses of saturated porous media subjected to cyclic thermal loading, Computers and Geotechnics, 33: 396-403.) established coupled governing equations for one-dimensional thermal consolidation problems regarding saturated porous media subjected to cyclical thermal loading. Based on the thermodynamics of irreversible processes; (Bai and Li 2009Bai, B. and Li, T. (2009). Solutions for cylindrical cavity in saturated thermoporoelastic medium, Acta Mechanica Solida Sinica, 22: 85-94.) investigated a saturated medium with a long cylindrical cavity subjected to variable thermal loading and variable hydrostatic pressure. (Lu et al. 2010Lu, Z., Yao, H.L., and Liu, G.B. (2010). Thermomechanical response of a poroelastic half-space soil medium subjected to time harmonic loads, Computers and Geotechnics, 37: 343-350.) investigated a porous elastic medium subjected to a normal force and a thermal source in the context of generalized thermoelastic theory with one relaxation time. (Liu et al. 2009Liu, G.B., Xie, K.H., and Zheng, R.Y. (2009). Model of nonlinear coupled thermo-hydro-elastodynamics response for a saturated poroelastic medium, Science in China. Series E: Technological Sciences, 52: 2373-2383.; 2010aLiu, G.B., Xie, K.H., and Zheng, R.Y. (2010a). Thermo-elastodynamic response of a spherical cavity in saturated poroelastic medium, Applied Mathematical Modelling, 34: 2203-2222.) developed a method to overcome one-dimensional problems for an isotropic saturated poroelastic medium including a cylindrical cavity and spherical cavity subjected to a time-dependent thermal/mechanical shock in the context of thermodynamics theory. That same year, (Liu et al. 2010bLiu, G.B., Xie, K.H., and Zheng, R.Y. (2010b). Mode of a spherical cavity’s thermo-elastodynamic response in a saturated porous medium for non-torsional loads, Computers and Geotechnics, 37: 381-390.) solved a thermo-hydro-elastodynamic problem in a two-phase porous thermoelastic medium. (Bai and Li 2013Bai, B. and Li, T. (2009). Solutions for cylindrical cavity in saturated thermoporoelastic medium, Acta Mechanica Solida Sinica, 22: 85-94.) developed a spherical space with a spherical cavity based on the irreversible governing equations of saturated porous thermoelastic media and subjected it to variable mechanical and thermal loads. (Kumar et al. 2014Kumar, R., Kaur, M. and Rajvanshi, S.C. (2014). Propagation of waves in micropolar generalized thermoelastic materials with two temperatures bordered with layers or half-spaces of inviscid liquid, Latin American Journal of Solids and Structures, 11: 1091-1113.) investigated the propagation of Lamb waves in solids with layers or half-spaces of inviscid liquid subjected to stress-free boundary conditions in the context of the Green and Lindsay theory of generalized thermoelasticity. (Ailawalia and Singla 2016Ailawalia, P. and Singla, A. (2016). Internal heat source in a thermoelastic hydrostatically initially stressed plate immersed in a liquid, Journal of Engineering Physics and Thermophysics, 89: 1255-1264.) solved an infinite homogeneous isotropic generalized thermoelastic problem under the Lord and Shulman theory of generalized thermoelasticity.
To date, there have been very few works devoted to investigating thermo-hydro-mechanical problems involving normal or thermal loads via normal mode analysis. In this study, we investigated these thermo-hydro-mechanical problems and the characteristic variable properties in a poroelastic half-space soil medium in the context of generalized thermoelastic theory. We subjected this poroelastic half-space to time harmonic loads comprised of normal or thermal loads. The foundation material, under Biot’s dynamic poroelastic theory, was idealized as a uniform, fully saturated poroelastic half-space. The distributions of non-dimensional vertical displacement, excess pore water pressure, vertical stress, and temperature distribution were obtained by means of normal mode analysis. The numerical results were obtained by performing numerical inversion of the transform integrals. These results were then used to analyze the differences between the two methods of coupled thermo-hydro-mechanical dynamic model (THMD) and thermoelastic dynamic model (TMD).
2 BASIC EQUATIONS
We consider the problem of a saturated, homogenous, isotropic porous elastic half-space. Based on theory of three-dimensional consolidation which proposed by (Biot 1941Biot, M.A. (1941). General theory of three-dimensional consolidation, Journal of Applied Physics, 12:155-164.), we assume that solid grains are incompressible because the Biot’s effective stress coefficient α = 1. The dynamic equation for the motion of thermo-hydromechanical coupling in the absence of body forces can be written by Smith and Booker, Bai and Abousleiman, and Bai as follows (1993Smith, D.W. and Booker, J.R. (1993). Green’s functions for a fully coupled thermoporoelastic material, International Journal for Numerical and Analytical Methods in Geomechanics, 17: 139-163., 1997Bai, M. and Abousleiman, Y. (1997). Thermoporoelastic coupling with application to consolidation, International Journal for Numerical and Analytical Methods in Geomechanics, 21: 121-132., 2006cBai, B. (2006c). Response of saturated porous media subjected to local thermal loading on the surface of semi-infinite space, Acta Mechanica Sinica, 22: 54-61.):
where β 1 = (3λ + 2G)αs.
The equation associated with heat conduction for poroelastic soil can be written by Sherief and Saleh, and Ram et al. as follows (2005Sherief, H.H. and Saleh, H.A. (2005). A half-space problem in the theory of generalized thermoelastic diffusion, International Journal of Solids and Structures, 42: 4484-4493., 2008Ram, P., Sharma, N. and Kumar, R. (2008). Thermomechanical response of generalized thermoelastic diffusion with one relaxation time due to time harmonic sources, International Journal of Thermal Sciences, 47: 315-323.):
where m = n 0 ρwcw + (1 - n0 )ρscs .
Based on Darcy’s law, the equation of mass conservation of water is:
where b = ρwg / κd
In the absence of a body force or inner heat source, the constitutive governing equation of thermo-hydromechanical can be written by Smith and Booker as follows (1993Smith, D.W. and Booker, J.R. (1993). Green’s functions for a fully coupled thermoporoelastic material, International Journal for Numerical and Analytical Methods in Geomechanics, 17: 139-163.):
The strain-displacement relation equation is:
3 FORMULATION OF THE PROBLEM
We consider the problem of a saturated, homogenous, isotropic porous elastic half-space soil medium subjected to both normal force and thermal loading. The governing equations are written in the context of the Lord and Shulman model, where the body is under no anybody force. The Cartesian coordinate system (x, y, z) and displacement components ui = (u, 0, w) are introduced below.
These displacement components have the following forms:
Based on Eqs. (5) and (6), the strain components have the following forms:
where e is the cubical dilatation, which is expressed as follows:
Based on Eqs. (1), (4), and (5):
where ∇2 = ∂2/ ∂x 2 + ∂2 / ∂z 2 is a two-dimensional Laplace operator.
In order to facilitate the equation, the following non-dimensional quantities are also introduced:
where η + m/K V = .
.
In terms of the non-dimensional quantities in Eq. (14), we can transform Eqs. (2), (3), (9), and (10) into the following forms (dropping primes for convenience):
Accordingly, the constitutive non-dimensional equations are:
where
Differentiating Eq. (15) with respect to x, and Eq. (16) with respect to z, then adding them together, we arrive at follows:
4 NORMAL MODE ANALYSIS
The solutions for the variables that we considered can be decomposed in terms of normal modes in the following form:
where ω is frequency and a is the wave number in the x-direction.
Using Eq. (23), we obtained the following equations based on Eqs. (17), (18), and (22), respectively:
where D = d / dx.
Eliminating θ* (z) and P* (z) from Eqs. (24), (25), and (26) yields the following fourth-order partial differential equation satisfied by e* (z):
Similarly:
where
A = 2a 2 + b 1
B = a 4 + b 1 a 2 + b 2
b1 = ω + τω 2 + ω 2 - ∅ 1 ω + ∅ 3 ω 2+∅ 0 ω+∅ 0 τω 2
b2 = ω 3- τω 4 + ∅ 1 ω 2 + ∅ 1 ω 3+ ∅ 3 ω 3+∅ 3 τω 4-∅ 0 ∅ 2 ω 2 - ∅ 0 ∅ 2 τω 3
Equation (27) can be factorized as follows:
where k 2 i (i = 1, 2) are the roots of the characteristic equation.
The roots ±k 1 and ±k 2 in Eq. (31) satisfy the following relations:
The solution to Eq. (27) can be expressed as follows:
where e * i (z) is the solution to the following:
The solution of Eq. (30), which is bounded as z → ∞, is provided by:
where Ri (a, ω) are parameters depending on a and ω. Thus, e * i (z) takes the form:
Similarly:
where θ* (z) and P* (z) are also parameters depending on a and ω similar to e * i (z).
By integrating Eqs. (37)-(39) into Eqs. (24)-(26), the relations take the following forms:
Accordingly, Eqs. (38) and (39) can rewritten in the following forms:
The following relations can be used to obtain the displacement w in terms of Eqs. (23) and (16):
Where n 2 = a 2 + β 2 ω 2.
The solution of Eq. (45), which is bounded as z→∞, is given by:
where F = F (a, ω) is a parameter dependent on a and ω.
In terms of Eqs. (8) and (23):
Substituting Eqs. (37) and (46) into Eq. (47) yields the following:
Based on Eq. (23), substituting Eqs. (37), (42), (43), (46), and (48) into Eqs. (19)-(21), respectively, yields the following:
The normal mode analysis is, in fact, to look for the solution in the Fourier transformed domain. Assuming that all the relations are sufficiently smooth on the real line such that the normal mode analysis of these functions exist.
The boundary conditions at z = 0 are necessary to determine the parameters Ri (i = 1, 2) and F. The boundary conditions are as follows:
(1) Surface stress conditions:
(2) Thermal boundary condition, where the half-space surface is subjected to a thermal load:
(3) Excess pore water pressure boundary condition:
By substituting the expressions of the considered variables into the above boundary conditions, we arrive at:
where ψ(x, t) denotes the load and thermal source distribution function along the x - axis. By applying Eq. (23), ψ(x, t) is expressed as follows:
5 NUMERICAL RESULTS AND DISCUSSION
It is necessary to know the material constants to secure accurate calculation results. Most of the mechanical, thermal, and hydraulic parameters used in this paper are the same as those used by (Bai 2006bBai, B. (2006c). Response of saturated porous media subjected to local thermal loading on the surface of semi-infinite space, Acta Mechanica Sinica, 22: 54-61.):
E = 6.0 × 105Pa µ = 0.3 G = E / [2(1 + µ)] λ = Eµ / [(1+ µ)(1-2µ)]
αs = 1.5 × 10-5 / °C αw = 2.0 × 10-4 / °C cs = 800J/ (kg °C) cw = 4000J/(kg°C)
ρs = 2.6 × 103kg/m3 ρw = 1.0 × 103 kg/m3 n 0 = 0.4 K = 0.5W/(m°C)
kd = 1.0 × 10-8 m/s τ = 0.02 T 0 = 273K
where ω = ω
0 + iζ, and i is the imaginary unit, eωt =ζt + i sin ζt). Over small increments of time, we let ω = ω
0. (cos
(cos
The other constants of the problem are taken as
a + 1.2 ψ* = 1
To calculate and verify both the THMD and TMD cases, the density of pore water ρw and porosity n 0 are assumed to be zero; thus, the solution of the THMD model reduces to the TMD situation. The equivalent density of the model ρ = 1.96 × 103 kg/m3 and the equivalent heat capacity c = 2080J/(kg°C). Other material parameters were kept the same as those given above to obtain the corresponding TMD solution.
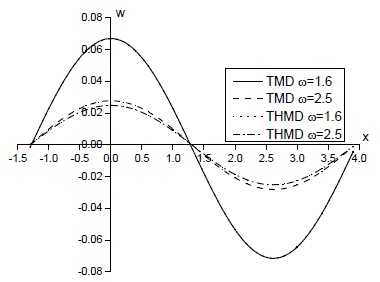
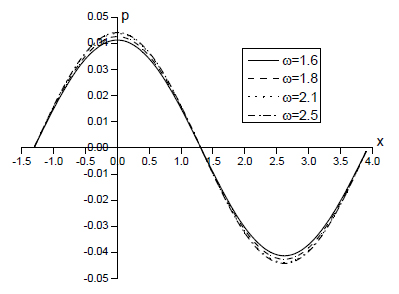
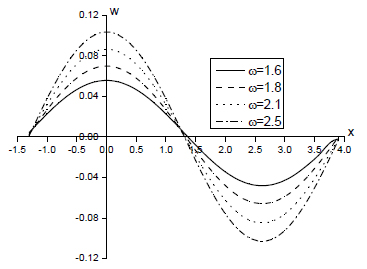
We divided all 12 figures into three cases. In Case 1, based on THMD and TMD methods, we investigated the non-dimensional vertical displacement, excess pore water pressure, vertical stress, and temperature distribution with two different frequencies ω = 1.6 and ω = 2.5, respectively as shown in Figs. 1-4. In Case 2, we considered four different frequencies ω = 1.6, ω = 1.8, ω = 2.1, and ω = 2.5 using the THMD method (Figs. 5-8). The results of both cases indicate variations of non-dimensional vertical displacement w’ = w/q, non-dimensional excess pore water pressurep’ = p/q, non-dimensional vertical stress σ’ = σ/q, and non-dimensional temperature distribution θ’ = θ/q on the surface of the half-space with a distance of x under a uniformly distributed normal force. (For convenience, we dropped the punctuation marks in the figures.) In Case 3 we investigated how the considered variables varied according to the four different frequencies ω = 1.6, ω = 1.8, ω = 2.1, and ω = 2.5 (Figs. 9-12) in terms of the THMD method. With a uniformly distributed thermal source, the variations of non-dimensional vertical displacement w” = w/Q, non-dimensional excess pore water pressure p” = p/Q, non-dimensional vertical stress σ” = σ/Q, and non-dimensional temperature distribution θ” = θ/Q on the surface of the half-space are shown below for Case 3, (again without the punctuation marks.) These computations were carried out at non-dimensional depth z = 1.0 and time t = 0.5.
In the figures above (Case 1), the solid line, dashed line, dotted line, and dashed-dotted line refer to TMD, ω = 1.6; TMD, ω = 2.5; THMD, ω = 1.6; and THMD, ω = 2.5, respectively. Figure 1 shows where the two methods yield identical results when frequency is ω = 1.6. When frequency is high, the difference between the two methods are significant. Because our research medium is saturated porous soil, the difference between the two methods is that the THMD method considers the effects of the fluid. When the normal load is constant, low frequency gives the water more time to drain from the saturated porous soil and the difference between the two methods are not significant. When the frequency is high, there is insufficient time for water to drain from the soil and the difference between the two methods are significant. It is important to take into account non-dimensional excess pore water pressure of the soil because it has a considerable effect on ground response. Accordingly, we investigated the variations in excess pore water pressure with x distance under uniformly distributed normal force, as shown in Fig. 2. The TMD values remained at zero because we did not consider the effects of the fluid in this case. This means that by only using the TMD method, we were unable to assess excess pore water pressure. In actuality, many practical engineering applications are dependent on soil or saturated porous soil such as waste landfill engineering and nuclear waste management. Therefore, non-dimensional excess pore water pressure is an important physical variable in many real life applications. Figure 3 is similar to Fig. 1: As frequency increases, the difference between the two methods becomes more significant. As shown in Fig. 4, frequency ω has an increasing effect under both methods.
In the figures above (Case 2), based on the THMD method, the solid line, dashed line, dotted line, and dashed-dotted line refer to ω = 1.6, ω = 1.8, ω = 2.1, and ω = 2.5, respectively. Our research medium is saturated porous soil, where normal load mainly includes non-dimensional excess pore water pressure and non-dimensional vertical stress. As frequency ω increases, less water drains from the medium while the non-dimensional excess pore water pressure increases. When the normal load is constant, non-dimensional vertical stress decreases as the non-dimensional excess pore water pressure increases. Similarly, non-dimensional vertical displacement decreases as frequency ω increases. The frequency ω has an increasing effect upon all the magnitudes of all physical variables.
In the figures above (Case 3), based on the THMD method, the solid line, dashed line, dotted line, and dashed-dotted line refer to ω = 1.6, ω = 1.8, ω = 2.1, and ω = 2.5, respectively. In this case, we assumed that only a uniformly distributed thermal source was applied to the surface of the half-space. As discussed above, our research medium is saturated porous soil, where normal load mainly includes non-dimensional excess pore water pressure and non-dimensional vertical stress. In this case, only a uniformly distributed thermal source is applied and the normal load is zero. Thus, the absolute value of non-dimensional excess pore water pressure and the absolute value of non-dimensional vertical stress are equal. A plus or minus sign only denotes that the medium is under tension or compression. The thermal expansion coefficient of pore water is greater than the thermal expansion coefficient of solid grains. The extent to which water drains from the medium decreases as frequency ω increases, while non-dimensional vertical displacement, excess pore water pressure, vertical stress, and temperature distribution all increase as frequency continues to increase. The frequency ω has an increasing effect to all the magnitudes of all physical variables. In addition, as observed from the figures, the effect of frequency has the same change trend.
6 CONCLUSIONS
In this study, we investigated the thermo-hydro-mechanical problems of a poroelastic half-space soil medium with variable properties under the theory of generalized thermoelasticity. We were able to solve these problems using normal mode analysis. Based on the numerical results, we arrived at the following conclusions:
-
Thermo-hydro-mechanical problems for a porous elastic half-space soil medium with variable properties were solved by normal mode analysis, which has been successfully applied in dealing with such complex multi-field coupling problems. The proposed method ultimately yields the corresponding fourth-order characteristic equation and exact solutions for the desired physical variables.
-
When subjected to a uniformly distributed normal force, the values of non-dimensional excess pore water pressure in the TMD method are consistently zero because the effect of fluid is not considered. This means that the TMD method is not appropriate for determining non-dimensional excess pore water pressure. Non-dimensional excess pore water pressure is an important physical variable in real life engineering. However, fluid presence attenuates the response in terms of non-dimensional vertical displacement and vertical stress, which is especially pronounced at higher frequencies.
-
The frequency of a uniformly distributed thermal load has a pronounced effect on non-dimensional vertical displacement, excess pore water pressure, vertical stress, and temperature distribution. Furthermore, as observed from the figures of Case 3, the effect of frequency has the same change trend.
-
Frequency plays an important role in examining the deformation of the body.
-
As shown in all figures, it can be clearly observed that the figures reveal is consistent with simple harmonic oscillation, which is mainly dominated by the intrinsic nature of the solution obtained when the normal mode analysis method is applied to decouple the equation.
References
- Abbas, I.A. and Youssef, H.M. (2015). Two-dimensional fractional order generalized thermoelastic porous material, Latin American Journal of Solids and Structures, 12: 1415-1431.
- Abo-Dahab, S.M., Lotfy, K.H., and Gohaly A. (2015) Rotation and magnetic field effect on surface waves propagation in an elastic layer lying over a generalized thermoelastic diffusive half-space with imperfect boundary, Mathematical Problems in Engineering, 2015: 671783.
- Abousleiman, Y. and Ekbote, S. (2005). Solutions for the inclined borehole in a porothermoelastic transversely isotropic medium, Transactions of the ASME. E: Journal of Applied Mechanics, 72: 102-114.
- Ailawalia, P. and Singla, A. (2016). Internal heat source in a thermoelastic hydrostatically initially stressed plate immersed in a liquid, Journal of Engineering Physics and Thermophysics, 89: 1255-1264.
- Bai, B. (2006a). Thermal consolidation of layered porous half-space to variable thermal loading, Applied Mathematics and Mechanics, 27: 1531-1539.
- Bai, B. (2006b). Fluctuation responses of saturated porous media subjected to cyclic thermal loading, Computers and Geotechnics, 33: 396-403.
- Bai, B. (2006c). Response of saturated porous media subjected to local thermal loading on the surface of semi-infinite space, Acta Mechanica Sinica, 22: 54-61.
- Bai, B. and Li, T. (2009). Solutions for cylindrical cavity in saturated thermoporoelastic medium, Acta Mechanica Solida Sinica, 22: 85-94.
- Bai, B. and Li, T. (2013) Irreversible consolidation problem of a saturated porothermoelastic spherical body with a spherical cavity, Applied Mathematical Modelling, 37: 1973-1982.
- Bai, M. and Abousleiman, Y. (1997). Thermoporoelastic coupling with application to consolidation, International Journal for Numerical and Analytical Methods in Geomechanics, 21: 121-132.
- Bijarnia, R. and Singh, B. (2012). Propagation of plane waves in an anisotropic generalized thermoelastic solid with diffusion, Journal of Engineering Physics and Thermophysics, 85: 478-486.
- Biot, M.A. (1941). General theory of three-dimensional consolidation, Journal of Applied Physics, 12:155-164.
- Biot, M.A. (1956). Thermoelasticity and irreversible thermodynamics, Journal of Applied Physics, 27: 240-253.
- Biot, M.A. (1977). Variational Lagrangian-thermodynamics of non-isothermal finite strain mechanics of porous solids and thermomolecular diffusion, International Journal of Solids and Structures, 13: 579-597.
- Booker, J.R. and Savvidou, C. (1984). Consolidation around a spherical heat source, International Journal of Solids and Structures, 20: 1079-1090.
- Green, A.E. and Lindsay, K.A. (1972). Thermoelasticity, Journal of Elasticity, 2: 1-7.
- Green, A.E. and Naghdi, P.M. (1991). A reexamination of the basic results of themomechanics, Proceedings of the Royal Society of London A, 432: 171-194.
- Green, A.E. and Naghdi, P.M. (1992). On undamped heat waves in an elastic solid, Journal of Thermal Stresses, 15: 252-264.
- Green, A.E. and Naghdi, P.M. (1993). Thermoelasticity without energy dissipation, Journal of Elasticity, 31: 189-208.
- Hetnarski, R.B. and Ignaczak, J. (1999). Generalized thermoelasticity, Journal of Thermal Stresses, 22: 451-476.
- Kumar, R. and Devi, S. (2008). Thermomechanical intereactions in porous generalized thermoelastic material permeated with heat sources, Multidiscipline Modeling in Materials and Structures, 4: 237-254.
- Kumar, R. and Gupta, R.R. (2010). Propagation of waves in transversely isotropic micropolar generalized thermoelastic half space, International Communications in Heat and Mass Transfer, 27: 1452-1458.
- Kumar, R., Kaur, M. and Rajvanshi, S.C. (2014). Propagation of waves in micropolar generalized thermoelastic materials with two temperatures bordered with layers or half-spaces of inviscid liquid, Latin American Journal of Solids and Structures, 11: 1091-1113.
- Liu, G.B., Xie, K.H., and Zheng, R.Y. (2009). Model of nonlinear coupled thermo-hydro-elastodynamics response for a saturated poroelastic medium, Science in China. Series E: Technological Sciences, 52: 2373-2383.
- Liu, G.B., Xie, K.H., and Zheng, R.Y. (2010a). Thermo-elastodynamic response of a spherical cavity in saturated poroelastic medium, Applied Mathematical Modelling, 34: 2203-2222.
- Liu, G.B., Xie, K.H., and Zheng, R.Y. (2010b). Mode of a spherical cavity’s thermo-elastodynamic response in a saturated porous medium for non-torsional loads, Computers and Geotechnics, 37: 381-390.
- Lord, H.W. and Shulman, Y. (1967). A generalized dynamical theory of thermoelasticity, Journal of the Mechanics and Physics of Solids, 15: 299-309.
- Lotfy, K.H. (2014). Two temperature generalized magneto-thermoelastic interactions in an elastic medium under three theories, Applied Mathematics and Computation, 227: 871-888.
- Lotfy, K.H. (2016). The elastic wave motions for a photothermal medium of a dual-phase-lag model with an internal heat source and gravitational field, Canadian Journal of Physics, 94: 400-409.
- Lotfy, K.H. and Hassan, W. (2014). Normal mode method for two-temperature generalized thermoelasticity under thermal shock problem, Journal of Thermal Stresses, 37: 545-560.
- Lu, Z., Yao, H.L., and Liu, G.B. (2010). Thermomechanical response of a poroelastic half-space soil medium subjected to time harmonic loads, Computers and Geotechnics, 37: 343-350.
- Ram, P., Sharma, N. and Kumar, R. (2008). Thermomechanical response of generalized thermoelastic diffusion with one relaxation time due to time harmonic sources, International Journal of Thermal Sciences, 47: 315-323.
- Schanz, M. (2009). Poroelastodynamics: linear models, analytical solutions, and numerical methods, Applied Mechanics Reviews, 62: doi: 10.1115/1.3090831.
» https://doi.org/10.1115/1.3090831 - Sherief, H.H. and Hussein, E.M. (2012). A mathematical model for short-time filtration in poroelastic media with thermal relaxation and two temperatures, Transport in Porous Media, 91: 199-223.
- Sherief, H.H. and Saleh, H.A. (2005). A half-space problem in the theory of generalized thermoelastic diffusion, International Journal of Solids and Structures, 42: 4484-4493.
- Singh, B. (2007). Wave propagation in a generalized thermoelastic material with voids, Applied Mathematics and Computation, 189: 698-709.
- Singh, B. (2016). Wave propagation in a rotating rransversely isotropic two-temperature generalized thermoelastic medium without dissipation, International Journal of Thermophysics, doi: 10.1007/s10765-015-2015-z.
» https://doi.org/10.1007/s10765-015-2015-z - Smith, D.W. and Booker, J.R. (1993). Green’s functions for a fully coupled thermoporoelastic material, International Journal for Numerical and Analytical Methods in Geomechanics, 17: 139-163.
- Tzou, D.Y. (1995). A unified field approach for heat conduction from macro to micro scales, ASME Journal of Heat Transfer, 117: 8-16.
- Wei, W., Zheng, R.Y., Liu, G.B., and Tao, H.B. (2016). Reflection and refraction of P wave at the interface between thermoelastic and porous thermoelastic medium, Transport in Porous Media, 113: 1-27.
- Youssef, H.M. (2006). Theory of two-temperature-generalized thermoelasticity, IMA Journal of Applied Mathematics, 71: 383-390.
Publication Dates
-
Publication in this collection
June 2017
History
-
Received
13 Dec 2016 -
Reviewed
25 Mar 2017 -
Accepted
03 Apr 2017