Abstract
Thin walled multi-cell columns are highly efficient energy absorbers under axial compressions. Multi-cell features are usually obtained by placing stiffeners or ribs to get the required geometry features in the columns. In this study, the curved stiffeners with varying numbers in different configurations are used to support the circular single and bi-tubular metallic tubes and their shape, position and number effects are numerically investigated under dynamic axial crushing loads. Number of configurations can be classified by the number of tube/tubes and curved stiffened shells. This study can be divided in three parts; single tubes with cross-curved stiffeners with equal number of cells, single tubes with curved stiffened wall supports with ascending number of stiffeners, and bi-tubular tubes with ascending cross-curved stiffeners. The mass in each configuration is maintained as same by adjusting the thicknesses of the stiffeners. Energy absorption for all of the configurations are compared with published experimental literature of standard single tube and single tube with cross-straight stiffeners. Deformation modes and energy absorption characteristics are evaluated and discussed for all of the proposed configurations. Results indicate that the proposed configurations with curvy stiffeners are superior in energy absorption with increased mean crushing force and enhanced energy absorption along with a high value of crush force efficiency in comparison with the refernce configurations. Bi-tubular configurations with curvy stiffeners show a more stabalized response with the lowest peak crushing force in all of the proposed configurations.
Keywords:
Dynamic Axial Crushing; Curved Stiffeners; Energy Absorption; Finite Element Modeling; Metallic Tubes; Bi-Tubular Tubes
1 INTRODUCTION
Advancement in the automotive and aerospace applications demands the improved energy absorption and enhanced crashworthiness parameters in the structures to increase the human and equipment safety during their service life. Circular metallic tubes are one such element which serve the purpose by absorbing the kinetic energy of impact by collapsing under quasi static and dynamic axial loading (Shakeri et al., 2007Shakeri, M., Mirzaeifar, R., and Salehghaffari, S. (2007). “New insights into the collapsing of cylindrical thin-walled tubes under axial impact load. Proc Int Mech Eng, Part C. J Mech Eng Sci 221:1-17.). Energy absorption characteristics of such tubular structures are dependent on material, size, geometry, cross-section and loading conditions. Structural efficiency enhancement leads the researchers to study different material and geometrical aspects of thin wall structures. Several types of energy absorbing components like circular tubes (Aljawi et al., 2000Aljawi, A., and Alghamdi, A. (2000). Inversion of frusta as impact energy absorbers, New York, USA: Pergamon; 511-19.; Karagiozova et al., 2000Karagiozova, D., Alves, M., and Jones, N. (2000). “Inertia effects in axi-symmetrically deformed cylindrical shells under axial impact.” International Journal of Impact Engineering 24:1083-115.), square tubes (Langseth et al., 1996Langseth, M., and Hopperstad, O. S. (1996). “Static and dynamic axial crushing of square thin walled aluminum extrusions.” International Journal of Impact Engineering 18(7-8):949-68.; 1999Lang Seth, M., Hopperstad, O. S., and Bested, T. (1999). “Crashworthiness of aluminum extrusions: validation of numerical simulation, effect of mass ratio and impact velocity.” International Journal of Impact Engineering 22:829-54.), frusta (Aljawi et al., 2000Aljawi, A. (2000). “Finite element and experimental analysis of axially compressed plastic tubes.” Eur J Mech Environ Eng 45(1):3-10.; Alghamdi et al., 2002Alghamdi, A., Aljawi, A., and Abu Mansour, T. M. (2002). “Modes of axial collapse of unconstrained capped frusta.” Int J Mech Sci 44:1145-61.; Hosseini et al., 2006Hosseini, M., Abbas, H., and Gupta, N. K. (2006). Straight fold analysis for axisymmetric crushing of thin walled frusta and tubes.” Latin American Journal of Solids and Structures 3:345-360.), conical (Hui and Xiong, 2016Hui, Z., and Xiong, Z. (2016). “Crashworthiness performance of conical tubes with nonlinear thickness distribution.” Thin-Walled Structures 99: 35-44.), stepped tubes with external stiffeners (Zahran et al., 2016Zahran, M. S., Xue, P., Esa, M. S., Abdelwahab, M., and Lu, G. (2016). “A New Configuration of Circular Stepped Tubes Reinforced with External Stiffeners to Improve Energy Absorption Characteristics Under Axial Impact.” Latin American Journal of Solids and Structures http://dx.doi.org/10.1590/1679-78253231.
http://dx.doi.org/10.1590/1679-78253231...
a) and multi-corner columns (Abramowicz and Weirzbicki, 1989Abramowicz, W., and Wierzbicki, T. (1989). “Axial crushing of multi corner sheet metal columns.” J Appl Mech 56(1):113-20.) have been studied for their behavior under impact and crush loading. Circular tubes have been a consistent choice for energy absorption applications because of high strength and stiffness with low cost and ease of manufacturing. They absorb the energy by deforming themselves in different kind of deformation modes like locally deformed axisymmetric or concertina mode, non-symmetric or diamond mode, mixed mode or globally deformed Euler buckling mode under axial crushing depending on the geometrical, material parameters and boundary conditions (Zahran et al., 2016bZahran, M. S., Xue, P., Esa, M. S., Abdelwahab, M., and Lu, G. (2016). “A New Configuration of Circular Stepped Tubes Reinforced with External Stiffeners to Improve Energy Absorption Characteristics Under Axial Impact.” Latin American Journal of Solids and Structures http://dx.doi.org/10.1590/1679-78253231.
http://dx.doi.org/10.1590/1679-78253231...
; Karagiozova and Alves, 2004Karagiozova, D., and Alves, M. (2004). “Transition from progressive buckling to global bending of circular shells under axial impact-Part I: Experimental and numerical observations.” Int. J. Solids Struct. 41:1565-1580.).
An ideal energy absorber should exhibit long, flat load-displacement curve in which the peak force which is responsible for damage or injury, is kept below a threshold value. To achieve such a response with improved crashworthiness parameters, researchers adopted different method in tubes such as foam fillers (Hanssen et al., 2000Hanssen, A. C., Langseth, M., and Hopperstad, O. S. (2000). “Static and dynamic crushing of circular aluminum extrusions with aluminum foam filler.” International Journal of Impact Engineering 24(5):475-507.), windows (Song et al., 2013Song, J., Chen, Y., and Lu, G. (2013). “Light-weight thin-walled structures with patterned windows under axial crushing.” Int.J.Mech.Sci. 66:239-248.), grooves (Zhang and Huh, 2009Zhang, X., and Huh, H. (2009). “Energy absorption of longitudinally grooved square tubes under axial compression.” Thin Walled Structures 47(12):1469-1477.; Salehghaffari et al., 2010Salehghaffari, S., Tajdari, M., Panahi, M., and Mokhtarnezhad, F. (2010). “Attempts to improve energy absorption characteristics of circular metal tubes subjected to axial loading.” Thin Walled Structures 48(6):379-390.), gradient thickness features (Sun et al., 2016; Hui and Xiong, 2016Hui, Z., and Xiong, Z. (2016). “Crashworthiness performance of conical tubes with nonlinear thickness distribution.” Thin-Walled Structures 99: 35-44.), axial stacking of tubes (Ronchietto et al., 2009Ronchietto, F., Chung, K. Y., and Nurick, G. N. (2009). “Response of axially stacked square tubes to axial impact loads.” Latin American Journal of Solids and Structures 6:413-440.) and multi-cell strategies (Hong et al., 2014Hong, W., Fan, H., Xia, Z., Jin, F., Zhou, Q., and Fang, D. (2014). “Axial crushing behaviors of multi-cell tubes with triangular lattices. “International Journal of Impact Engineering 63: 106-117.; Hou et al., 2008Hou, S., Li, Q., Long, S., Yang, X., and Li, W. (2008). Multi-objective optimization of multi-cell sections for the crashworthiness design.” International Journal of Impact Engineering 35:1355-1367.; Zhang and Zhang, 2013Zhang, X. and Zhang, H. (2013). "Energy absorption of multi-cell stub columns under axial compression." Thin-Walled Structures 68: 156-163., 2014Zhang, X. and Zhang, H. (2014). "Axial crushing of circular multi-cell columns." International Journal of Impact Engineering 65: 110-125.). Thin-walled tubes can dissipate the impact energy under different mechanism such as fracture, splitting, bending, tension, shear and plastic deformation.
Multi-cell tubes have got special attention in recent years because of superior energy absorption due to increasing number of cells and intersection points (Zahran et al., 2016Zahran, M. S., Xue, P., Esa, M. S., Abdelwahab, M., and Lu, G. (2016). “A New Configuration of Circular Stepped Tubes Reinforced with External Stiffeners to Improve Energy Absorption Characteristics Under Axial Impact.” Latin American Journal of Solids and Structures http://dx.doi.org/10.1590/1679-78253231.
http://dx.doi.org/10.1590/1679-78253231...
b), and has a wide applications scope from automotive structures (Kim, 2002Kim, H. S. (2002). “New extruded multi-cell aluminum profile for maximum crash energy absorption and weight efficiency.” Thin-Walled Structures 40: 311-327.) to train buffers (Marsolek et al., 2004Marsolek, J., and Reimerdes, H. G. (2004). “Energy absorption of metallic cylindrical shells with induced non-axisymmetric folding patterns.” International Journal of Impact Engineering 30: 1209-1223.) to helicopters subfloors (Kindervater, 1997Kindervater, C. (1997). “Aircraft and helicopter crashworthiness: Design and simulation, in Crashworthiness of Transportation Systems: Structural Impact and Occupant Protection.” Springer Science C Business Media: 525-577.). In this regard, single, doubled and tripled cells columns were theoretically investigated under axial crushing and tripled cells columns showed the highest specific energy absorption with the conclusion that the tripled and double cell column were more efficient than single cell columns (Chen and Weirzbicki, 2001Chen, W., and Wierzbicki, T. (2001) “Relative merits of single-cell, multi-cell and foam-filled thin-walled structures in energy absorption.” Thin-Walled Structures 39: 287-306.). A novel type of section with various squared cells attached to the corner demonstrated considerably high crashworthiness as compared to conventional design (Kim, 2002Kim, H. S. (2002). “New extruded multi-cell aluminum profile for maximum crash energy absorption and weight efficiency.” Thin-Walled Structures 40: 311-327.). Zhang and Cheng (2006Zhang, X., Cheng, G. D. and Zhang, H. (2006). “Theoretical prediction and numerical simulation of multi-cell square thin-walled structures.” Thin-Walled Structures 44(11):1185-91.) presented a theoretical solution to determine the dissipated energy in the square multi-cell column by dividing the section in three basic elements using simplified Super Folding Element method. It was shown that the energy absorption efficiency increased significantly when inter ribs were introduced to divide the square cell column in to multi-cell column. Zhiliang et al., (2013) with an inspiration that circular tubes are more efficient energy absorbers as compared to square tubes, studied the multi-cell circular tubes along with parametric study of geometric parameters. The results indicated that multi-cell circular tubes are superior to square multi-cell tubes, also revealed that the wall thickness, the number of cells along the radial and circumferential direction has a distinct effect on the energy absorption. Zhang and Zhang (2014Zhang, X. and Zhang, H. (2014). "Axial crushing of circular multi-cell columns." International Journal of Impact Engineering 65: 110-125.) performed the axial compression tests of circular tubes with single, double, triple and quadruple cells to study the deformation and energy absorption behavior and developed a theoretical prediction model. The optimized cross sectional configuration and optimized dimensions are evaluated by using a multi criteria decision-making method, namely complex proportional assessment (COPRAS) and the Kriging modeling technique along with multi objective particle optimization (MOPSO) algorithm respectively for multi-cell hexagonal cross-sectional columns to enhance the crashworthiness characteristics (Qiu et al., 2015Qiu, N., Gao, Y., Fang, J., Feng, Z., Sun, G. and Li, Q. (2015). “Crashworthiness analysis and design of multi-cell hexagonal columns under multiple loading cases.” Finite Elements in Analysis and Design 104:89-101). A new design of multi-cell devices to evaluate the crashworthiness capability of single and multi-cell members made up of two straight columns with the same shape of cross-section connected together by several ribs is proposed by Pirmohammad and Marzdashti (2016Pirmohammad, S. and Marzdashti, E. S. (2016). “Crushing behavior of new designed multi-cell members subjected to axial and oblique quasi-static loads.” Thin-Walled Structures 108:291-304.). A decision making method COPRAS showed the multi-cell members with inner tube and scale number of 0.5, and the column with circular cross-section as the better energy absorbing devices.
Multi-cell bi-tubular tubes are usually investigated for energy absorption by using foam-filled configurations. Numerical and experimental studies of foam filled single and bi-tubular circular tubes has shown that foam filling gave considerable improvement with respect to energy absorption particularly in bi-tubular configurations (Seitzberger et al., 1997Seitzberger, M., Rammerstorfer, F. G., Degischer, H. P., and Gradinger, R. (1997) “Crushing of axially compressed steel tubes filled with aluminum foam.” Acta Mech. 125: 93-105.; 2000Seitzberger, M., Rammerstorfer, F. G., Degischer, H. P., and Gradinger, R., Blaimschein, M., and Walch, C. (2000). “Experimental studies on the quasi-static axial crushing of steel columns filled with aluminum foam,” Int J Solids Struct. 37: 4125-47.). Bi-tubular tubes with straight stiffeners were investigated by Zhiliang et al., (2013) and reported that the double layered cylindrical multi-cell column was excellent in energy absorption and appropriate in peak force. Along with circular, others shapes like square bi-tubular tubes have also been a topic of research. Bi-tubular square tubes studies with different arrangements under quasi-static axial compression loading showed bi-tubular tubes with shorter inner tube can absorb more energy than single outer tube as well as bi-tubular tubes with equal length of inner and outer tubes showed improved values of SAE and load efficiency factor (Kashani et al., 2013Kashani, M. H. H., Alavijeh, S., Akbarshahi, H., and Shakeri, M. (2013). “Bi-tubular square tubes with different arrangements under quasi-static axial compression loading.” Materials and Design 51:1095-1103.). The crashworthiness studies of double section bi-tubular stainless steel thin-walled structures consist of an outer circular cylinder and an inner tube with different polygonal section such as triangle, square or hexagon show that bi-tubular structures with hexagonal inner tube have more energy absorption capability than the other bi-tube combinations and the single cylinder (Vinayagar and Kumar, 2017Vinayagar, K., and Kumar, A. S. (2017). “Crashworthiness analysis of double section bi-tubular thin-walled structures,” Thin-Walled Structures 112: 184-193.). Manmohan Dass Gohel (2015Manmohan, D. G. (2015). “Deformation, energyabsorptionandcrushing behavior of single, double andmulti-wallfoam filled squareandcircular tubes.” Thin-Walled Structures90:1-11.) studied single, bi-tubular and tri-tubular cylindrical and square tubes under axial compression and found that concentric arrangement of tubes increases the energy absorption along with foam filling. Along with straight stiffeners, single and bi-tubular tubes with S-shaped stiffeners have also been a research interest to mitigate shock forces in collision events. A numerical investigation to observe the crashworthiness of single-cell and multi-cell S-shaped members with various cross-sections including triangular, square, hexagonal, decagon and circular under axial dynamic loading revealed the multi-cell S-rail with decagonal cross-section as the best energy absorber, and the S-rail having the same inner and outer tube with decagonal cross-section with desirable crashworthiness performance (Marzdashti et al., 2016Marzdashti, E. S., Pirmohammad, S. and Marzdashti, S. E. (2016). “Crashworthiness analysis of s-shaped structures under axial impact loading.” Latin American Journal of Solids and Structures http://dx.doi.org/10.1590/1679-78253430
http://dx.doi.org/10.1590/1679-78253430...
). Although multiple efforts have already been put by using radial and longitudinal stiffeners, foam filling, making tube conical in shape and using nested tubes to increase the energy absorption characteristics but curve walls effectiveness against buckling can increase these characteristics with much reduced density. No study by using curved wall supports and cross-wall longitudinal stiffeners with different combinations can be found in the literature as per author’s best knowledge. It is curious that whether the curved stiffened tubes with multiple dimensions can enhance the energy absorption capacity and broaden the vision for their applications in automotive and aerospace structures.
In this study, nature of multi-cells is exploited in single and bi-tubular metallic tubes by using curved stiffeners. The proposed configurations can be divided in three kinds; single tube with cross-curved stiffeners, single tube with curved stiffened wall supports by using ascending number of stiffeners, and bi-tubular tubes with ascending cross-curved stiffeners. A series of numerical studies are performed using finite element package ABAQUS® Explicit Dynamics (ABAQUS Version 6.14, 2015ABAQUS, Version 6.15. “Abaqus analysis user’s manuals.” Simulia Dassault Systems, Rising Sun Mills, 166 Valley Street, Providence, RI 02909-2499, USA.) to investigate the energy absorption characteristics of proposed configurations under dynamic axial crushing. The mass in each configuration is maintained constant by adjusting the thicknesses of the stiffeners. The energy absorption characteristics such as Mean Crushing Force (MCF), Energy Absorption (EA) and Crush Force Efficiency (CFE) are determined and compared within a group for each configuration and among different groups. The effectiveness of the proposed configuration is shown by comparing the results with experimental and theoretical results (Zhang and Zhang, 2014Zhang, X., Zhang, H. and Wen, Z. (2014). “Experimental and numerical studies on the crush resistance of aluminum honeycombs with various cell configurations.” International Journal of Impact Engineering 66: 48-59.; Zhiliang et al., 2013) of selected reference configurations; a single tube and a tube with cross-straight stiffeners.
2 PROPOSED STRUCTURAL CONFIGURATIONS
A set of configurations, broadly categorized in three groups named as Group 1, 2 and 3 and a set of reference configurations are shown in Figure 1. Each configuration in all of the described groups consists of a circular metallic tube of diameter D0, length L and thickness t0 while the bi-tubular tube configurations in Group 3 has an internal tube with inner tube diameter Di , length L and thickness ti=t0 as described in Figure 2. Each group has a unique feature as the internal stiffeners shape and placement is concerned. In Group 1, single tube is stiffened with cross-curved stiffeners in such a way that the number of cells in each configuration is same that is 4 cells in each configuration in this group. The curvature of the curves is randomly selected in an attempt to approximate the different possible variants.
Schematic of proposed structural configurations (a) Group 1 (b) Group 2 (c) Group 3 (d) Reference Configurations.
The configurations nomenclature for Group 1 is defined as ST-CCS-n where ST represents single tube, CCS represents cross-curved stiffeners and n is the configuration number where n varies from 1 to 3. In ST-CCS-1 the normal cross-straight stiffeners (Zhiliang et al., 2013) are modified to curved stiffeners providing non-symmetry about axis and changing normal quarter circle unit cell to quarter circle unit cell with curved walls. In ST-CSS-2, two curved stiffeners are connected with a Y-axis central liner straight curve giving a unique kind of symmetry in XY-plane, generally not attempted before. In ST-CCS-3, three curved stiffeners are arranged to form a 120 degrees formation, from the center lines of each curved stiffener, non-symmetric in XY plane. The nomenclature for Group 2 is defined as ST-CSWS-n where CSWS represents cross-stiffened wall supports and n is the configuration number where n varies from 1 to 4. The curved stiffeners are placed around the circular tube wall at inner face. The number of cross-stiffened wall stiffeners varies in an ascending order from 6 to 12 with an increment of 2 in each configuration that is in ST-CSWS-1 to ST-CSWS-4 respectively. All the configurations are symmetric in the XY plane. Bi-tubular configurations are placed in Group 3 in which the nomenclature is defined as DT-CCS-n where DT represents double tube, CCS represents cross-curved stiffeners and n is the configuration number where n varies from 1 to 3. In DT-CCS-1, the curved stiffeners are 3 in number while DT-CCS-2 has 4 curved stiffeners and DT-CCS-3 has 8 curved stiffeners. The configurations are non-symmetric in XY-plane.
All of the tubes are made of AA 6060 T4 material and the mass of each configuration is kept constant by adjusting the thickness of the stiffeners. The aluminum extrusion dies is the best possible way to make complex extruded aluminum tubes when producing at mass level; at low production level gas shield welding process can be opted. The structural information including the thicknesses of inner tubes, outer tubes and stiffeners are summarized in Table 1 below:
3 ENERGY ABSORPTION INDICATORS
Energy absorption parameters for a tube structure to evaluate its performance under axial loading require the definition of some indicators. This section provides such energy absorption indicators to evaluate and compare the energy absorption capabilities for different proposed configurations. Generally, these indicators can be determined from the load-displacement curve as follows:
Energy Absorption (EA):
It is the area under the force-displacement curve during axial crushing and can be calculated as:
Where F is the crushing force and δ is the crushing distance.
Specific Energy Absorption (SEA):
It is the ratio of absorbed energy to the total mass (m) of the structure. It is used to compare the energy absorbers and can be calculated as:
Mean Crush Force (MCF):
It is obtained by dividing the energy absorbed (EA) by crushing distance δ as shown in Equation 3:
where F is the crushing force and δ is the crushing distance.
Crush Force Efficiency (CFE):
It is the ratio of the mean crushing force to the peak crushing force and can be calculated as:
where Fm is the mean crushing force and Fp is the peak crushing force. For an ideal energy absorber, the CFE is 100%.
4 FINITE ELEMENT MODELING
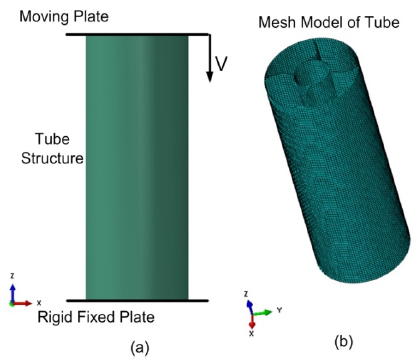
A dynamic analysis is performed for all of the proposed configurations in ABAQUS explicit dynamics (ABAQUS Analysis User Manual) commercial FE package. The boundary conditions for the simulations are shown in Figure 3 (a) in which the proposed tube structure is axially impacted by a moving rigid plate with a constant velocity V=10m/s while the opposite face of the tube is restrained in all degrees of motion with a rigid fixed plate. In the FE model as shown in Figure 3 (b), the shellS4R element is used for tube configurations, which is a 4-node doubly curved thick or thin shell element with reduced integration, hourglass control and finite membrane strains. The top and bottom plate is meshed by using discrete rigid element. The top plate has an impact mass of 50Kgs. After mesh convergence studies, an element size of 2.5mm is found feasible and adopted in this study for all of the configurations. The contact between the top rigid plate and the tube is modeled as general explicit contact with tangential behavior being frictional using frictional coefficient of 0.2 and normal behavior being hard contact. The contact between the lower plate and tube was defined as tie contact and to avoid the inter-penetration while folding of the tube, a self-contact is also defined for all of the elements of the configuration. The boundary conditions for all of the configurations are consistent.
The proposed configurations in this study are all metallic including stiffeners. The material for all of the configurations is aluminum AA 6060-T4 whose properties are tabulated in Table 2 and stress-strain curve is shown in Figure 4 (Tang et al., 2013Tang, Z., Shutian, L., Zhang, Z. (2013). “Analysis of energy absorption characteristics of cylindrical multi-cell columns.” Thin-Walled Structures 62:75-84.).
Stress-strain curve for AA 6060 T4 (Tang et al., 2013Tang, Z., Shutian, L., Zhang, Z. (2013). “Analysis of energy absorption characteristics of cylindrical multi-cell columns.” Thin-Walled Structures 62:75-84.)
5 RESULTS AND DISCUSSION
5.1 Validation of FE Model
A validation study for the adopted finite element model is performed against the published experimental results (Tang et al., 2013Tang, Z., Shutian, L., Zhang, Z. (2013). “Analysis of energy absorption characteristics of cylindrical multi-cell columns.” Thin-Walled Structures 62:75-84.; Zhang and Zhang, 2014Zhang, X., Zhang, H. and Wen, Z. (2014). “Experimental and numerical studies on the crush resistance of aluminum honeycombs with various cell configurations.” International Journal of Impact Engineering 66: 48-59.) for the multi-cell columns by keeping the structural geometry, material properties and the boundary conditions exactly the same as those in the mentioned studies. The comparison of force-displacement curve and deformation modes for Tang et al., and Zhang and Zhang with current numerical modeling is shown in Figures 5 (a, b) and 5(c, d) respectively. The graphs and deformation plots are almost identical in nature with some variations as also observed by the respective authors while comparing numerical and experimental work. Energy absorption parameters for the selected models and present numerical study are compiled in Table 3, where the differences are less than 5% for the Tang et al., model and a maximum difference of 16.6% is observed for MCF in comparison to Zhang and Zhang model. Similar behavior is observed by the Zhang in comparison to experimental work himself. Based on the compared validated results, similar analysis can be performed for all of the proposed configurations in this study.
FE Model validation (a) Force displacement curve. (b) Deformation plots (Zhang and Zhang vs. Current study). (c) Force displacement curve. (d) Deformation plots (Tang et al., vs. Current study).
5.2 Deformation Modes
Deformation modes of thin walled circular stiffened tubes is a complex phenomenon which depends not only on physical parameters like L/D, t/R, number of stiffeners, their geometrical configuration and boundary conditions but also on the material parameters such as strain rate effects. However, strain rate effect of aluminum alloy is almost negligible (Simhachalam et al., 2014Simhachalam, B., Srinivas, K., and Rao, C. L., (2014), “Energy absorption characteristics of aluminum alloyAA7XXX and AA6061 tubes subjected to static and dynamic axial load,” International Journal of Crashworthiness 19:139-152.). Deformation plots for the different structural configuration at different instant of times while impacted by the rigid plate are shown in Figures 6-8 respectively for Groups 1-3. Deformation modes can give an insight to the lobes formation, their type either concertina or diamond and a way to compare the energy evaluation at different instants. The formations of lobes start from the impacted end and gradually increase from the same end. Most of the configurations in Group 1 and 3 observed diamond modes of deformation except ST-CCS-2 and DT-CCS-1 while configuration of Group 2 showed a tendency toward concertina modes. As the wall strengthening and supporting becomes stronger in a configuration, concertina or diamond mode is observed but in ST-CCS-2 and DT-CCS-2 configurations, the wall is supported at relatively larger gaps giving bending its role to play. Formation of lobes in each group is described in Table 4. A concertina, diamond and mixed mode are symbolized as Con, Diam and Mix in the Table 4 to describe the deformation pattern of a specific lobe in each group. The deformation plots for Group 1 configurations are shown in Figure 6. Configuration ST-CCS-1 and ST-CCS-3 are asymmetric about X and Y-axis while ST-CCS-2 is symmetric. It is clear from Figure 6 (a) that a concertina mode in the start is followed by the diamond modes, with similar observation in Figure 6 (c) while ST-CCS-2 in Figure 6 (b) shows a mixed mode scenario.
Deformation plots for Group 1 (a) Deformation Pattern of ST-CCS-1.(b) Deformation Pattern of ST-CCS-2. (c) Deformation Pattern of ST-CCS-3.
Deformation plots for Group 2(a) Deformation Pattern of ST-CSWS-1. (b) Deformation Pattern of ST-CSWS-2. (c)Deformation Pattern of ST-CSWS-3 (d) Deformation Pattern of ST-CSWS-4.
Deformation plots for Group 3 (a) Deformation Pattern of DT-CCS-1.(b) Deformation Pattern of DT-CCS-2. (c)Deformation Pattern of DT-CCS-3.
Group 2 configurations being symmetric in nature showed predominantly concertina modes as shown in Figure 7 (a) to 7(d). After formation of every lobe, energy is released which cause fluctuations in the force-displacement curve. As the formation of lobes proceeds, the wrinkle folding is repeated. ST-CSWS-1 showed 3 concertina folders, ST-CSWS-2,3 showed 5 concertina folders each while ST-CSWS-4 showed 4 concertina modes with varying wavelengths, can be calculated from Table 4. Group 3 configurations are all asymmetric about X and Y-axis and showed diamond or mixed deformation pattern while impacted as shown in Figure 8 (a) to 8(d). Configuration DT-CCS-1 showed lateral deformation which is due to bending phenomenon. The entire Group followed the concertina to diamond mode lobes formation giving a clue for higher energy absorption as observed by Galib and Limam (2004Galib, D., and Limam, A., (2004), “Experimental and numerical investigation of static and dynamic axial crushing of circular aluminum tubes,” Thin-Walled Structures 42:1103-1137.) in his experiments. The diamond mode has multiple corners inducing multiple folding points in a deformation mode though with the drawback of inconsistency. Hence axisymmetric or concertina modes are preferable as they guarantee the progressive collapse despite having less energy absorption. DT-CCS-1 showed 3 mixed deformation modes followed by a concertina mode while DT-CCS-1 and DT-CCS-2 showed 3 diamonds mode each followed by a 2 concertina modes.
5.3 Comparison of Energy Absorption
Force-displacement curves for all of the proposed configurations are shown in Figures 9 to 11. Force-displacement curve can give valuable information about energy absorption indicators such as EA, PCF and MCF whose values can be determined for each of the configuration by using Equations 1 to 4. Different points named as A, B, C to J are marked with different primes representing the lobe formation in a configuration with ascending number of primes showing the ascending lobe numbers. The force-displacement curves for the Group 1 configurations are shown in Figure 9, showing almost a consistent behavior for all of the configurations in the group but in detail, the wavelength of folds and number of lobes and lobes nature is different in each configuration. These configurations have equal number of cells with different arrangements of curved stiffeners. Configuration ST-CCS-2 showed relatively smoother curve with delayed densification while the configuration ST-CCS-3 has larger area under the curve giving an indication of better energy absorption. ST-CCS-1 is having a similar nature to ST-CCS-2; however densification is reached a bit earlier. ST-CCS-1 and ST-CCS-3 showed three and four diamond lobes respectively after the first concertina lobe. ST-CCS-2 showed three mixed modes after the initial concertina lobe. ST-CCS-2 is symmetric while ST-CCS-3 is asymmetric before deformation but after deformation former showed mixed mode zigzag in nature and later showed diamond mode because of less uniform wall supporting and larger unstiffened distance along the circumference of the tube, giving rise to wall bending before the next fold. Once bending initiates a mixed mode, recovery is almost impossible to a stable mode. From Figure 9 and Table 4, it is clear that instead of equal mass and equal number of cells, the number and wavelength of folds is different in each configuration. ST-CCS-1 and ST-CCS-2 showed very similar wavelengths for lobes; however the nature of lobes was different. ST-CCS-3 showed a shorter wavelength of folds after first concertina lobe with an extra lobe in comparison to previous configurations.
The force-displacement curves for the Group 2 configurations are shown in Figure 10. These configurations are symmetric about X and Y-axis with curved wall stiffeners. It is clear from the figure that these configurations have shown higher initial peak jerk along with large fluctuations where each fluctuation corresponds to the formation of a folder. Area under the force-displacement curves is much higher than the configurations in Group 1. Configuration ST-CSWS-2 shows relatively smoother curve comparing with the configuration ST-CSWS-1. Fluctuations are almost in the entire configurations but the amplitude variation is highest in the configuration ST-CSWS-4 with the earliest most densification in the group. It can be said that as the number of curved wall stiffeners increases, the densification starts early. The peak force increases as the number of stiffeners increases. The wavelength of the folders increases from 30mm in ST-CSWS-1 to 35mm, 37.5mm and 42.5mm in ST-CSWS-2, 3 and 4 respectively for first folder wavelength as the number of stiffeners increases, calculated from Table 4. For second folder, the observation remains invalid along with 5 lobes in ST-CSWS-2, 3 configurations each in comparison to 3 lobes in ST-CSWS-1, 4 configurations each. The wavelengths of the second fold observed as 42.5mm, 47.5mm, 27.5mm and 35mm for ST-CSWS-1,4 configurations respectively clearly indicating the folds are not only dependent on stiffeners but also on thicknesses and initial formation.
The force-displacement curves for the Group 3 configurations are shown in Figure 11. These configurations are asymmetric about X and Y-axis with cross-curved stiffeners in a bi-tubular structural arrangement. It is clear from the figure that as the stiffeners number increases; the initial peak force value also increases along with increasing area under the curve. The force variation is there but with lesser cyclic amplitude variation. The configuration DT-CCS-1 has the highest fluctuation with the end dip in the curve before densification because of the sudden collapse of the structure to keep up the progressive buckling. DT-CCS-2 showed the smoothest curve with moderate energy absorption while DT-CCS-3 showing the best performance as the area under the curve is concerned. The folder wavelength increases in DT-CCS-1 from 24 to 34 in first folder while 34 to 64 in second folder with a similar trend in DT-CCS-2 while folder wavelength decreases in DT-CCS-3 from 36 to 28 in first fold calculated from Table 4 on the described points in Figure 11.
It is clear from the Figure 9 to 11 that ST-CCS-2, ST-CSWS-2 and DT-CCS-2 are the best configuration among each group respectively. Figure 12 shows a comparison among these selected configurations from each group to give a comparative relationship among different groups along with the reference configuration called as ST-Reference 1 (Single tube configuration) and ST-CS-Reference 2 (Single tube with straight cross-wall stiffeners) earlier shown in Figure 1 (d). It is worth mentioning that each configuration has same mass category. ST-CCS-2 shows higher force points at the same displacement instant as compare to ST-CS-Reference 2 while at the same time, the curve is much smoother than the ST-Reference 1. Each group configuration has its own merits and demerits as per the specific application.
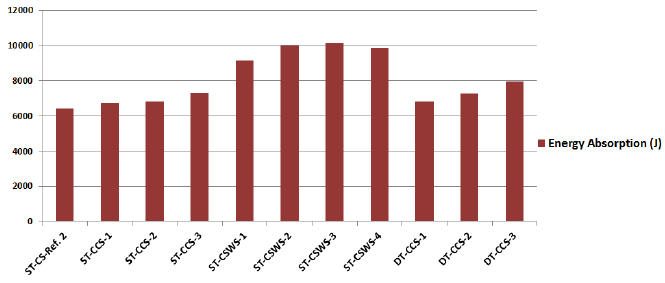
Energy absorption, PCF, MCF, EA and CFE are compared for different configurations in Figures 13 to 15. Energy absorption for the tube configuration with straight cross stiffeners called ST-CS-Reference 2 is chosen as reference to monitor the effectiveness of all other configurations. The energy absorption parameter EA for the said configuration is found to be 6424.82J which is also the lowest as compared to the 6729.37J, 6817.42J, 7287.36J for Group 1 configurations, 9158.32J, 10015.3J, 10148.12J, 9862.26J for Group 2 configurations and 6806J, 7267J, 7945J for Group 3 configurations respectively. The ST-CSWS-3, a configuration of Group 2, showed an increase of 36.7% with the highest energy absorption in entire groups as compared to ST-CS-Reference 2. The configuration ST-CCS-3 in Group 1 showed an increase of 11.8% in energy absorption while the configuration DT-CCS-3 in Group 3 showed an increase of 19.1% in energy absorption value as compared to ST-CS-Reference 2. The lowest increase was observed in the configuration ST-CCS-1 of Group 1 with a value of 4.5%.
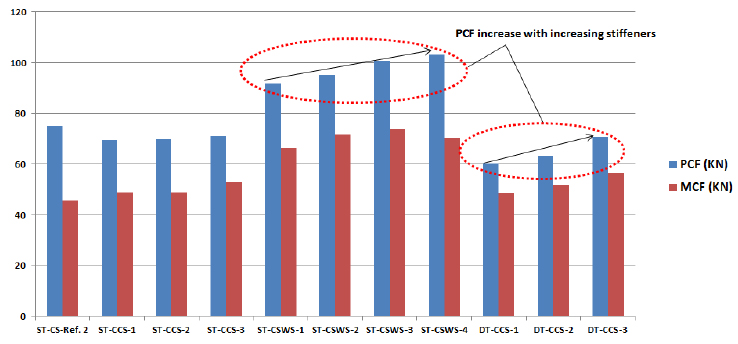
Energy absorption indicators like PCF and MCF are compared in Figure 14 for proposed configurations. It is clear from the plot that the highest peak force is for ST-CSWS-4 configuration with a value of 103.33KN and the lowest PCF is for the configuration DT-CCS-1 with a value of 60.4KN. Introduction of curved cross-stiffeners in the single tube reduced the PCF from 75.24KN in ST-CS-Ref. 2 to 69.59KN and 71.06KN in ST-CCS-1 and ST-CCS-3 respectively. With same circumference, height, and wall thickness, the SEA of a circular tube is higher than that of a square tube (Lu and Yu, 2003Lu, G. and Yu T. (2003). Energy absorption of structures and materials, Elsevier.). The straight walls when replaced with curved walls provide a tube structure that is axially folded and undergoes large plastic deformation when a major portion of the energy dissipation occurs. Thickness is also playing its role as deformation modes hugely depends on D/t ratio. Generally, circular tubes with D/t < 50 deform in the concertina mode, whilst those with D/t > 80 deform in the diamond mode. For the rest, the mixed mode usually takes place (Lu and Yu, 2003Lu, G. and Yu T. (2003). Energy absorption of structures and materials, Elsevier.). The curved walls not only modify the cell shape but curvature induces a relatively varied effective thickness of the walls. Relatively thick tubes failed by material yielding which led to the concertina mode and relatively thin tubes failed elastically in the diamond mode. The formation of stiffeners along the circumference of the tube plays its role in reinforcing the tube walls just like filling tubes with foam or honeycomb. Stable crushing is also dependent on the formation along with minimizing the wave length of folds which is also desirable for better crushing and enhanced energy absorption. Hence, the force-displacement curve becomes smoother and energy absorption increases after the introduction of curvy walls. MCF becomes better with curved stiffeners and an increase of 13.5% in PCF is obtained in ST-CCS-3 as compared to ST-CS-Ref. 2. This also gives an idea to utilize the asymmetry of stiffeners in a way to get the required parameters in configurations. Although same number of cells, same mass is kept in ST-CS-Ref.2 and Group 1 configurations, results got better when curved stiffeners are placed in a wall supporting manner (ST-CCS-3) instead of cross-configurations (ST-CCS-1, ST-CCS-2). Group 2 configurations show high MCF but at the cost of high PCF which is undesirable. The comparison of ST-CSWS-3 and ST-CS-Ref. 2 reveals that 37.9% increase in MCF is obtained at the cost of 25.4% increase in PCF. However, the wall stiffeners shape and radius of curvature can control the high PCF because of better distribution of stress among the stiffeners. Double tube configurations showed the optimal results in terms of PCF and MCF relationship among different groups. The double tube provides a much larger contact area to the impacted plate giving the ability to absorb the initial shock and then allowing delayed lobes formation with a complex diamond mixed modes. The increase of curved stiffeners increases PCF along with MCF in a linear way. PCF in configuration DT-CCS-3 is low with a difference of 4.18KN as compared to ST-CS-Ref.2 while giving an enhanced 19.2% value of MCF.
An ideal energy absorber’s CFE must approach to 100% as it is an indicator of the performance consistency of the structure. Figure 15 shows the CFE for all of the configurations adopted in this study. The highest CFEs are found for Group 3 configurations with very less deviation. All of the configurations adopted in this study showed much improved CFE as compared to ST-CS-Ref. 2 configuration. CFE for DT-CCS-2 is 25.3% higher than the reference configuration which is due to the high mean force and low peak force. As the number of cells increased, the CFE becomes higher; another observation is regarding the arrangement of structure in a way to reduce the PCF value.
6 CONCLUSIONS
The motivation behind this study is to utilize the curved wall enhanced features under buckling loading. In this study, 3 groups of metallic tubes with the basic feature of curved stiffeners; distinct in other features such as equal number of cells in a single tube with stiffeners in Group 1, ascending number of curved stiffened wall supports in a single tube configurations in Group 2 and ascending number of cells in a bi-tubular configurations with curved stiffeners in Group 3 are studied for dynamic axial crushing. The mass and boundary conditions are kept constant in each configuration by adjusting the thickness of the stiffeners. Two configurations which are already theoretically and experimentally verified are chosen as reference with a single metallic tube configuration and a metallic cylindrical tube along with cross-wall straight stiffeners. Each group’s configurations are evaluated for energy absorption characteristics like PCF, MCF and CFE and are compared with the configurations in a particular group and also with optimal configuration of each group. The main findings of the study can be summarized as:
-
The proposed configurations generally showed an improved performance in energy absorption by utilizing the curved stiffeners which are unique in the feature and application, never attempted before in a way as proposed in this study. The energy absorption in each group showed enhanced capabilities with a comparable PCF, increased MCF and CFE. The Group 1 utilized the curved stiffeners by modifying the reference configuration ST-CS-Ref. 2 and showed an improved performance. The geometrical changes in the cross-section further showed the margin of improvement as the ST-CCS 3 showed an increase of 11.8% in the energy absorption, 23% increase in CFE as compared to ST-CS-Ref.2. The adoption of curvy stiffeners reduces the PCF.
-
Cross-walled support stiffeners in Group 2, showed an increasing trend of energy absorption with increasing number of stiffeners. This group shows the highest EA and MCF but the PCF is also high. This group is simple in construction and easy for use as per specific requirement. PCF reduction can be performed using triggers or gradual reduction of thickness of the stiffeners. The highest change with reference configuration is observed as 36.7%, 37.9% increase in EA and MCF, respectively, for ST-CSWS-3 configuration. The CFE for this group remains in the range of 0.7 to 0.75.
-
Bi-tubular configurations are the most stable configurations presented in Group 3. Bi-tubular tube showed enhanced MCF and CFE with less increase in PCF. The reason is the greater contact surface area at the start of contact to distribute dynamic buckling stress. A CFE of 81.7% achieved in this group as compared to reference CFE of 61%.
-
Curved stiffeners can give a higher critical buckling loads and better management of buckling initiation and propagation at the start of impact. An optimal position of curve stiffeners can reduce the waviness of the force-displacement curve with axisymmetric folds and higher energy absorption and with low initial peak force such as in DT-CCS-2 configuration.
The study showed the effectiveness of the curved wall stiffeners and presented a small amount of possible arrangement in a single and bi-tubular metallic tube configuration. It can be concluded that the study has the potential to be effective in multiple applications by standardizing and normalizing the curved stiffeners’ arrangements.
Acknowledgement
The authors gratefully acknowledge the financial supports from National Natural Science Foundation of China under Grants 11472226 and 11672248.
References
- ABAQUS, Version 6.15. “Abaqus analysis user’s manuals.” Simulia Dassault Systems, Rising Sun Mills, 166 Valley Street, Providence, RI 02909-2499, USA.
- Abramowicz, W., and Wierzbicki, T. (1989). “Axial crushing of multi corner sheet metal columns.” J Appl Mech 56(1):113-20.
- Alghamdi, A., Aljawi, A., and Abu Mansour, T. M. (2002). “Modes of axial collapse of unconstrained capped frusta.” Int J Mech Sci 44:1145-61.
- Aljawi, A. (2000). “Finite element and experimental analysis of axially compressed plastic tubes.” Eur J Mech Environ Eng 45(1):3-10.
- Aljawi, A., and Alghamdi, A. (2000). Inversion of frusta as impact energy absorbers, New York, USA: Pergamon; 511-19.
- Chen, W., and Wierzbicki, T. (2001) “Relative merits of single-cell, multi-cell and foam-filled thin-walled structures in energy absorption.” Thin-Walled Structures 39: 287-306.
- Fauzan, D., Shahrum, A., Ahmad, K. A., Nopiahd, Z. M. (2015). “Multi objective optimization of foam-filled circular tubes for quasi-static and dynamic responses, Latin American Journal of Solids and Structures 12:1126-1143.
- Galib, D., and Limam, A., (2004), “Experimental and numerical investigation of static and dynamic axial crushing of circular aluminum tubes,” Thin-Walled Structures 42:1103-1137.
- Guangyong, S., Tong, P., Gang, Z., Jie, S., and Qing, L. (2016). “On energy absorption of functionally graded tubes under transverse loading.” International JournalofMechanicalSciences115:465-480.
- Hanssen, A. C., Langseth, M., and Hopperstad, O. S. (2000). “Static and dynamic crushing of circular aluminum extrusions with aluminum foam filler.” International Journal of Impact Engineering 24(5):475-507.
- Hong, W., Fan, H., Xia, Z., Jin, F., Zhou, Q., and Fang, D. (2014). “Axial crushing behaviors of multi-cell tubes with triangular lattices. “International Journal of Impact Engineering 63: 106-117.
- Hosseini, M., Abbas, H., and Gupta, N. K. (2006). Straight fold analysis for axisymmetric crushing of thin walled frusta and tubes.” Latin American Journal of Solids and Structures 3:345-360.
- Hou, S., Li, Q., Long, S., Yang, X., and Li, W. (2008). Multi-objective optimization of multi-cell sections for the crashworthiness design.” International Journal of Impact Engineering 35:1355-1367.
- Hui, Z., and Xiong, Z. (2016). “Crashworthiness performance of conical tubes with nonlinear thickness distribution.” Thin-Walled Structures 99: 35-44.
- Jones, N. (1989). Structural impact, CambridgeUniversity Press.
- Karagiozova, D., Alves, M., and Jones, N. (2000). “Inertia effects in axi-symmetrically deformed cylindrical shells under axial impact.” International Journal of Impact Engineering 24:1083-115.
- Karagiozova, D., and Alves, M. (2004). “Transition from progressive buckling to global bending of circular shells under axial impact-Part I: Experimental and numerical observations.” Int. J. Solids Struct. 41:1565-1580.
- Kashani, M. H. H., Alavijeh, S., Akbarshahi, H., and Shakeri, M. (2013). “Bi-tubular square tubes with different arrangements under quasi-static axial compression loading.” Materials and Design 51:1095-1103.
- Kim, H. S. (2002). “New extruded multi-cell aluminum profile for maximum crash energy absorption and weight efficiency.” Thin-Walled Structures 40: 311-327.
- Kindervater, C. (1997). “Aircraft and helicopter crashworthiness: Design and simulation, in Crashworthiness of Transportation Systems: Structural Impact and Occupant Protection.” Springer Science C Business Media: 525-577.
- Lang Seth, M., Hopperstad, O. S., and Bested, T. (1999). “Crashworthiness of aluminum extrusions: validation of numerical simulation, effect of mass ratio and impact velocity.” International Journal of Impact Engineering 22:829-54.
- Langseth, M., and Hopperstad, O. S. (1996). “Static and dynamic axial crushing of square thin walled aluminum extrusions.” International Journal of Impact Engineering 18(7-8):949-68.
- Lu, G. and Yu T. (2003). Energy absorption of structures and materials, Elsevier.
- Manmohan, D. G. (2015). “Deformation, energyabsorptionandcrushing behavior of single, double andmulti-wallfoam filled squareandcircular tubes.” Thin-Walled Structures90:1-11.
- Marsolek, J., and Reimerdes, H. G. (2004). “Energy absorption of metallic cylindrical shells with induced non-axisymmetric folding patterns.” International Journal of Impact Engineering 30: 1209-1223.
- Marzdashti, E. S., Pirmohammad, S. and Marzdashti, S. E. (2016). “Crashworthiness analysis of s-shaped structures under axial impact loading.” Latin American Journal of Solids and Structures http://dx.doi.org/10.1590/1679-78253430
» http://dx.doi.org/10.1590/1679-78253430 - Pirmohammad, S. and Marzdashti, E. S. (2016). “Crushing behavior of new designed multi-cell members subjected to axial and oblique quasi-static loads.” Thin-Walled Structures 108:291-304.
- Qiu, N., Gao, Y., Fang, J., Feng, Z., Sun, G. and Li, Q. (2015). “Crashworthiness analysis and design of multi-cell hexagonal columns under multiple loading cases.” Finite Elements in Analysis and Design 104:89-101
- Ronchietto, F., Chung, K. Y., and Nurick, G. N. (2009). “Response of axially stacked square tubes to axial impact loads.” Latin American Journal of Solids and Structures 6:413-440.
- Salehghaffari, S., Tajdari, M., Panahi, M., and Mokhtarnezhad, F. (2010). “Attempts to improve energy absorption characteristics of circular metal tubes subjected to axial loading.” Thin Walled Structures 48(6):379-390.
- Seitzberger, M., Rammerstorfer, F. G., Degischer, H. P., and Gradinger, R. (1997) “Crushing of axially compressed steel tubes filled with aluminum foam.” Acta Mech. 125: 93-105.
- Seitzberger, M., Rammerstorfer, F. G., Degischer, H. P., and Gradinger, R., Blaimschein, M., and Walch, C. (2000). “Experimental studies on the quasi-static axial crushing of steel columns filled with aluminum foam,” Int J Solids Struct. 37: 4125-47.
- Shakeri, M., Mirzaeifar, R., and Salehghaffari, S. (2007). “New insights into the collapsing of cylindrical thin-walled tubes under axial impact load. Proc Int Mech Eng, Part C. J Mech Eng Sci 221:1-17.
- Simhachalam, B., Srinivas, K., and Rao, C. L., (2014), “Energy absorption characteristics of aluminum alloyAA7XXX and AA6061 tubes subjected to static and dynamic axial load,” International Journal of Crashworthiness 19:139-152.
- Song, J., Chen, Y., and Lu, G. (2013). “Light-weight thin-walled structures with patterned windows under axial crushing.” Int.J.Mech.Sci. 66:239-248.
- Tang, Z., Shutian, L., Zhang, Z. (2013). “Analysis of energy absorption characteristics of cylindrical multi-cell columns.” Thin-Walled Structures 62:75-84.
- Vinayagar, K., and Kumar, A. S. (2017). “Crashworthiness analysis of double section bi-tubular thin-walled structures,” Thin-Walled Structures 112: 184-193.
- Zahran, M. S., Xue, P., and Esa, M. S. (2016). “Novel approach for design of 3D-multi-cell thin-walled circular tube to improve the energy absorption characteristics under axial impact loading.” International Journal of Crashworthiness.
- Zahran, M. S., Xue, P., Esa, M. S., Abdelwahab, M., and Lu, G. (2016). “A New Configuration of Circular Stepped Tubes Reinforced with External Stiffeners to Improve Energy Absorption Characteristics Under Axial Impact.” Latin American Journal of Solids and Structures http://dx.doi.org/10.1590/1679-78253231
» http://dx.doi.org/10.1590/1679-78253231 - Zhang, X. and Zhang, H. (2013). "Energy absorption of multi-cell stub columns under axial compression." Thin-Walled Structures 68: 156-163.
- Zhang, X. and Zhang, H. (2014). "Axial crushing of circular multi-cell columns." International Journal of Impact Engineering 65: 110-125.
- Zhang, X., and Huh, H. (2009). “Energy absorption of longitudinally grooved square tubes under axial compression.” Thin Walled Structures 47(12):1469-1477.
- Zhang, X., Cheng, G. D. and Zhang, H. (2006). “Theoretical prediction and numerical simulation of multi-cell square thin-walled structures.” Thin-Walled Structures 44(11):1185-91.
- Zhang, X., Zhang, H. and Wen, Z. (2014). “Experimental and numerical studies on the crush resistance of aluminum honeycombs with various cell configurations.” International Journal of Impact Engineering 66: 48-59.
Publication Dates
-
Publication in this collection
16 Aug 2017
History
-
Received
10 Mar 2017 -
Reviewed
11 May 2017 -
Accepted
14 May 2017