Recent Developments in Damage Identification of Structures Using Data Mining

Abstract

Civil structures are usually prone to damage during their service life and it leads them to loss their serviceability and safety. Thus, damage assessment can guarantee the integrity of structures. As a result, a structural damage detection approach including two main components, a set of accelerometers to record the response data and a data mining (DM) procedure, is widely used to extract the information on the structural health condition. In the last decades, DM has provided numerous solutions to structural health monitoring (SHM) problems as an all-inclusive technique due to its powerful computational ability. This paper presents the first attempt to illustrate the data mining techniques (DMTs) applications in SHM through an intensive review of those articles dealing with the use of DMTs aimed for classification-, prediction- and optimization-based data mining methods. According to this categorization, applications of DMTs with respect to SHM research area are classified and it is concluded that, applications of DMTs in the SHM domain have increasingly been implemented, in the last decade and the most popular techniques in the area were artificial neural network (ANN), principal component analysis (PCA) and genetic algorithm (GA), respectively.

Keywords:
Structural damage detection; data mining technique; artificial neural network; genetic algorithm; principal component analysis

1 INTRODUCTION

Structural systems in civil engineering such as tall buildings, long hydraulic structures, and long span bridges are damage-prone under different loadings such as fatigue, aging, overloading, earthquakes and other natural disasters during their service life (Duan and Zhang 2006; Hakim and Razak 2014a; Khanzaei et al. 2015; Ghaedi et al. 2016, 2017a, b). Existence of damage can disturb functionality and safety of the structure. Therefore, damage detection is one of the most important factors in order to guarantee the integrity and safety of civil structures (Kanwar et al. 2007; Xu et al. 2012; Hakim and Razak 2014b; Hanif et al. 2016).

Many damage identification techniques have been applied to civil structures. For instance, visual inspections are the most common damage detection techniques. However, they have been used in detecting damage of many structures; they are time consuming and costly. These techniques cannot also be used for continuous monitoring of structures (Razak and Choi 2001; He 2008).

With the development of data inverse analysis methods, it is required to combine problem-based internal mechanism analysis and DM technology to facilitate the application of the measured data analyses in complex engineering system modeling (Zhang et al. 2013). Based on this strategy, DMTs have, recently, been employed in SHM area due to their powerful computational ability to detect damage in structural systems, where the main components of any structural damage detection approach consist of a set of accelerometers and a DM procedure. In the monitoring process, the network of accelerometers is utilized to create a database using response data collection. The DM approach is used to extract information on the structural health condition from the database and to obtain the relationship between data in the form of patterns (Edeki 2012; Hou et al. 2013).

In this paper, various DMTs, which are applicable to SHM, have thoroughly reviewed. A brief background and different tasks of DMTs are described in Section 2. Classification, prediction and optimization-based data mining methods and their applications in SHM are presented in Sections 3 and 4. Trend and comparison of DM applications in SHM as well as the most used DMTs with highest application rate are discussed in Section 5. Here, capabilities and limitations of the most applicable data mining-based methods in SHM are presented. Finally, due to the lack of specific straightforward data mining-based SHM as well as requiring more attention to improve the health monitoring of structures, a flow chart based on the DM steps along with prediction and optimization-based algorithms is proposed for SHM assessment. In Section 6, the important conclusions are drawn. To the best of our knowledge, current research is the first attempt to illustrate the DMTs applications in SHM.

2 DATA MINING (DM)

DM is one of the key steps in Knowledge Discovery in Databases (KDD) process. This process is used to identify valid, valuable and understandable forms of data (Buchheit et al. 2000; Miranda et al. 2011). In general, DM can be categorized into two groups: descriptive mining and predictive mining. Each of these groups has its specific tasks (Pang-Ning et al. 2006). For instance, some DM tasks consist of clustering, prediction, classification, exploration and association. The purpose of clustering is to divide the samples into groups with related behavior. The numerical prediction activity determines patterns, rules or models to predict continuous or discrete target values which can also be used for other functions. Classification is used to recognize several rules which can be applied in future work to determine whether a previously unknown item belongs to a known class. Exploration is used to find out dimensionality of an input data and, eventually, the association activity is used to frequently detect occurring related objects. Based on their particular utilizations in consequence of their assumptions and drawbacks, one or combination of some of these tasks can be used to find the hidden information (Obenshain 2004; Liao et al. 2012; Chen and Huang 2013).

3 CLASSIFICATION AND PREDICTION-BASED DATA MINING IN STRUCTURAL DAMAGE DETECTION

Classification and prediction-based DM algorithms can be divided into supervised and unsupervised learning broads. In supervised learning techniques (e.g. ANN, regression, support vector machine, decision tree, Bayesian analysis, etc.), targets are known, nevertheless, in unsupervised learning (e.g. clustering and principal component analysis) target known values do not exist (Liao et al. 2012). Subsequent categorization attempts to summarize the classification and prediction-based DMTs and their applications in SHM. To aid the aim, the applications of DMTs in SHM area are separately presented in a tabular form.

3.1 Artificial Neural Network (ANN)

ANN approach was first proposed in 1980s. It is a self-organizing computational technique and it can solve many functions through pattern recognition (Shahriar and Nehdi 2011; Ahmed et al. 2015). ANN can effectively be used to reconstruct nonlinear relationship learning from training (Ali et al. 2013).

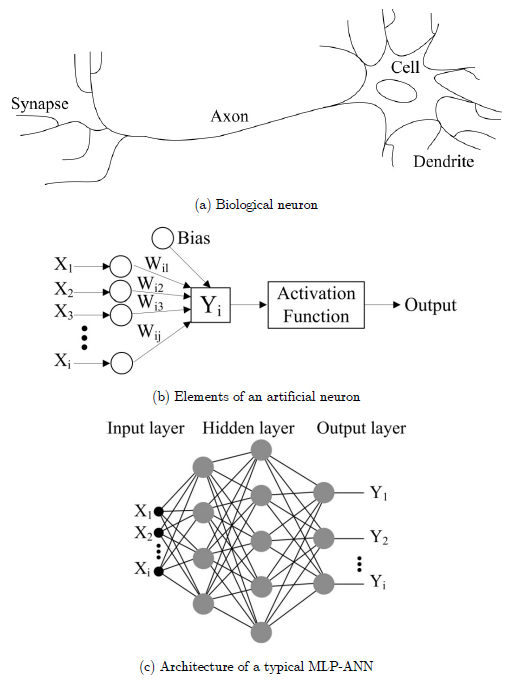
A basic biological neuron, as shown in Figure 1(a), consists of a cell body, axons, dendrites and synapses. Signals (input connections) are carried by the dendrites into the cell body. Axons transfer the signals (output connections) from one neuron to others, whereas synapses are the point contacts between dendrites of one cell and axon of another cell (Karacı and Arıcı 2014). The main elements of an artificial neuron are indicated in Figure 1(b) which includes weights, bias and activation function (Azimzadegan et al. 2012). A typical artificial neural network model has two parts; processing units (neurons) and connections between elements (Ali et al. 2013), in which neurons are located in layers of network. A layered ANN structure, called multilayer perceptron (MLP), is one of the most widespread ANN methods especially in structural identification (He and Yan 2007) (see Figure 1(c)). In general, a conventional ANN has three layers which are input layer, hidden layer and output layer (Mert et al. 2015). ANNs can be categorized by their network topology such as feed forward and feedback or by their learning algorithms such as supervised learning and unsupervised learning (Azimzadegan et al. 2012). Outputs (Yi) of ANN can be defined by following equation:

${\text{Y}}_{\text{i}}={\text{f}}_{\text{i}}({\displaystyle \sum }_{\text{j}=1}^{\text{n}}{\text{w}}_{\text{ij}}{\text{x}}_{\text{i}}+{\text{b}}_{\text{i}})$ (1)

where x_i indicates the input values, w_ij illustrates the connection weight values between input, hidden and output layers, b_i is the bias, and f_i shows the transfer function (Shah and Ghazali 2011; Chu et al. 2014).

Figure 1:
Overview of ANN.

Strain-based emulator neural network (SENN), parametric evaluation neural network (PENN), wavelet neural network (WNN), Bayesian neural network, fuzzy wavelet neural networks (FWNN), neural network-based damage classification, auto-associative neural network (AANN) and displacement-based neural network emulator (DNNE) are some of the important applications of neural networks in SHM. The detailed neural network technique applications are presented in Table 1.

Table 1:
Artificial Neural Networks applications in SHM.

Neural networks applications	References
Damage detection of multi degrees of freedom structures based on ANN	(Wu et al. 2002)
Damage detection using wavelet multi-resolution analysis with ANN	(Taha et al., 2004)
Damage detection using scalable modular neural network	(Goswami and Bhattacharya 2012)
Damage detection using Bayesian neural networks	(Lam and Beck 2006)
Damage detection using displacement-based neural network emulator	(Xu et al. 2012)
Damage detection for framed RCC buildings using ANN	(Kanwar et al. 2007)
Damage detection using ANN for SHM	(Xu and Chen 2007; Aydin and Kisi 2015)
Damage detection in bridge girders using ANN	(Al-rahmani et al. 2013)
Damage detection of a truss structure using ANN	(Osornio-Rios et al., 2012)
Damage detection of steel frame structures using ANN	(Betti et al., 2015; Padil et al., 2017)
Damage detection of Guadiana bridge using ANN	(Santos et al. 2016b)
Damage detection on buildings using wavelet based pattern recognition	(Radhika et al. 2015)
Damage identification based on response-only measurements by ANN	(Dackermann et al. 2014)
Damage identification in a continuous bridge using neural networks	(Bagchi et al. 2010)
Damage identification of a building using wavelet neural network	(Hung et al. 2003)
Damage identification using frequency response functions and ANN	(Samali et al. 2012)
Damage identification of a bridge using Kalman filter-based ANN	(Jin et al. 2016)
Damage identification using Probabilistic Neural Network (PNN)	(Oliveira and Inman 2017)
Seismic damage prediction of R/C buildings using ANN	(Morfidis and Kostinakis 2017)
Vibration-based damage assessment of structures using ANN	(Srinivas et al., 2013)
Prediction of the confinement efficiency of reinforced concrete	(Tang et al. 2003)
Prediction of the confined compressive strength and strain of concrete	(Oreta and Kawashima 2003)
Prediction of structural responses using fuzzy wavelet neural network	(Jiang and Mahadevan 2008a)
Prediction of the cracking pattern of masonry wallet using ANN	(Zhang et al. 2010)
Comparison of the accuracy between RealAdaBoost algorithm and ANN	(Li et al. 2014)
Comparison of the reliability between Fixed Grid Wavelet and ANN	(Hosseinabadi et al., 2014)
Comparison of damage classification in carbon fibre composites	(Mccrory et al. 2015)
Comparison of regression impact identification of an aluminum plate	(Sanchez et al., 2016)
Comparison of ANN and eigensensitivity based model updating	(Prabakaran et al. 2015)
Elimination of temperature effect using auto-associative neural network	(Zhou et al. 2011)
Extraction of environmental factors using auto-associative NN	(Hsu and Loh 2010)
Monitoring of an arch dam using auto-associative neural network	(Loh et al. 2011)
Monitoring of Fei-Tsui arch dam using neural networks	(Li et al. 2011)
Bayesian neural networks for bridge integrity assessment	(Arangio and Beck 2012)
Strain-based emulator neural network (SENN)	(Hung and Kao 2002; Kao and Loh 2013)
Nondestructive evaluation of prestressed concrete beams using ANN	(Jeyasehar and Sumangala 2006)
Neural network-based damage classification of bridge infrastructure	(Kabir et al. 2008)
Geometry optimization of elements using ANN based integrated system	(Golewski et al. 2017)
Fault detection of composite beam using radial basis function NN	(Khan and Parhi 2015)
ANN based damage assessment using incomplete modal data	(Kourehli 2015)
System identification of multistory buildings by ANN	(Khanmirza et al. 2014; Sahoo et al. 2015)
Wavelet damage quantification using ensemble ANN	(Vafaei et al., 2015)
Bridge damage identification using ANN	(Chun et al. 2015; Liu et al. 2015)
On-line early damage detection using neural networks	(Joao P. Santos et al., 2016)
Self organizing maps (SOM) of a bridge	(Marcy et al. 2016)
Pattern recognition of structural behaviors based on neural networks	(Alves et al., 2015a; Cury & Cremona, 2012)

3.2 Fuzzy Logic Technique

Fuzzy logic was proposed by Lotfi Zadeh for the first time in 1965. It has been employed in different applications such as pattern recognition, classification, decision making, etc. (Rutkowski 2004). As Figure 2 indicates, the basic configuration of a fuzzy technique consists of four important components, which are fuzzification, fuzzy rule-base, fuzzy inference and defuzzification. Fuzzification is a mapping from a crisp input to fuzzy membership sets. The fuzzy rule-base has set rules of fuzzy variables described by membership functions. Fuzzy inference is a decision making mechanism of the fuzzy system. The defuzzifier changes the fuzzy consequences from different rules into crisp values (Nyongesa 1998). Fuzzy is a model free technique for structural system identification, where the most important advantages of fuzzy systems are their high parallel implementation, nonlinearity and being capable of adapting (Nerves and Krishnan 1995). Applications of Fuzzy logic in SHM are detailed in Table 2.

Figure 2:
Schematic representation of a fuzzy system (Rafiee et al. 2015).

Table 2:
Fuzzy Logic applications in SHM.

Fuzzy system applications	References
System identification using fuzzy wavelet neural network	(Adeli and Jiang 2006; Jiang et al. 2007)
Pattern recognition using fuzzy similarity prescription	(Altunok et al. 2006)
Fuzzy neural network for damage detection	(Wen et al. 2007; Chakraverty and Sahoo 2017)
Adaptive Takagi-Sugeno fuzzy neural network	(Chiang et al. 2009)
Bridge damage identification using fuzzy logic	(Jiao et al. 2015)
Damage identification of beam-like structures using fuzzy	(Aydin and Kisi 2014)
Damage identification using Simplified Fuzzy ARTMAP	(Oliveira and Inman 2017)
Damage identification of beams using fuzzy adaptive PSO	(Jena et al. 2015)
Minimizing the Euclidean distance in clusters using Fuzzy	(Al-jumaili et al. 2015)

3.3 Classification

Classification, which is based on the machine learning, is used to classify databases into several groups. This technique is employed to indicate not only a form of classification rules but also mathematical formulae from a function of individual classes of data in a database. Therefore, these rules are capable of organizing upcoming data. Consequently, classification method can present a better view of the database contents (Han et al. 2006).Hence, refer to Table 3, key point of this technique is to predict a categorical feature based on other features of known data.

Table 3:
Classification applications in SHM.

Classification applications	References
Classification technique based on wavelet packet transform	(Sun and Chang 2004)
Damage classification of bridge infrastructure	(Kabir et al. 2008)
Damage classification for structural damage detection	(Chen and Hutchinson 2011)
Nearest neighbor classification	(Lautour and Omenzetter 2010)
Statistical pattern classification	(Kesavan and Kiremidjian 2012)
Acoustic emission classification of carbon fibre panel buckling data	(Al-jumaili et al. 2015)

3.4 Support Vector Machine (SVM)

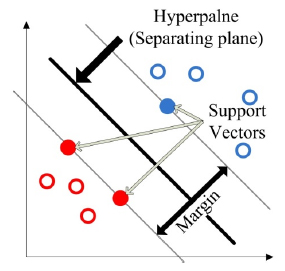
Support vector machine (SVM) was first introduced by Vapnik and his assistants in 1963 (Vapnik 1995; Statnikov et al. 2011). SVM works based on statistical learning theory and because of its high accuracy and good generalization capability, it has the potential to produce high quality predictions in numerous tasks. Therefore, SVM has various applications which can be found in several areas such as machine learning, data classification and pattern recognition (Cristianini and Shawe-Taylor 2000b; Samanta et al. 2003; He and Yan 2007; Tinoco et al. 2014). Basic models of SVM are linear SVM with linear functions and nonlinear SVM with kernel functions (Mita and Hagiwara 2003). Moreover, aim of SVM classifier is to determine a separating hyperplane to divide the given data into two classes (i.e. positive class and negative class) in the optimal form. Therefore, as shown in Figure 3, the optimal separating hyperplane is determined by solving an optimization problem, defined as:

$\begin{array}{l}\text{Minimize to}:\frac{1}{2}{\text{w}}^2\\ \text{Subject to}:{\text{y}}_{\text{i}}\left({\text{w}}^{\text{T}}.{\text{X}}_{\text{i}}+\text{b}\right)\ge \mathrm{1,}\text{i}=\mathrm{1,2,}\dots ,\text{N}\\ {\text{y}}_{\text{i}}\in \left\{\mathrm{1,}-1\right\},{\text{x}}_{\text{i}}\in {\text{R}}^{\text{n}}\end{array}$ (2)

where w, y_i, and x_i are a m-dimensional vector, class label and given data, respectively. N is the number of samples, and b is a scalar (Mita and Hagiwara 2003; Kishore et al. 2014).

Figure 3:
Graphic diagram of SVM.

Wavelet support vector machine (WSVM), nonlinear support vector machines, support vector regression (SVR), multiclass support vector machine and multiclass nonlinear relevance vector machine (MNRVM) are some of the important applications of SVMs in SHM. Table 4 illustrates the different use of SVM applications in detail for SHM area.

Table 4:
Support Vector Machine (SVM) applications in SHM.

SVM applications	References
Wavelet support vector machine (WSVM)	(He and Yan 2007)
Temperature-frequency correlation using PCA and support vector regression	(Hua et al. 2007)
Parameter optimized nonlinear Support Vector Machines	(O’Byrne et al., 2013)
Support vector regression (SVR) for damage detection	(Laory et al., 2013)
Nonlinear multiclass support vector machine-based SHM for smart structures	(Chong et al. 2013)
SVM for damage detection in a steel pipe	(Ying et al. 2013)
Multiclass nonlinear relevance vector machine model in smart structures	(Arsava et al. 2014)
Comparison of the accuracy prediction between RealAdaBoost algorithm and SVM	(Li et al. 2014)
Dams crack monitoring based on support vector regression	(Chen et al. 2017)
Comparison of regression impact identification of plates using least squares SVM	(Sanchez et al. 2016)
Wavelet-based damage identification using SVM	(Radhika et al. 2015)
Damage detection-based SVM using GA, PSO and Grid-search techniques	(Gui et al., 2017)
Damage identification of beam-like structures using SVM	(Satpal et al. 2016)
Pattern recognition of structural behaviors based on SVM	(Alves et al., 2015c; Cury & Cremona, 2012)

3.5 Regression Analysis

Regression analysis is one of the statistical methods that is used for prediction of different functions through different algorithms such as linear regression, nonlinear regression, logistic regression, and stepwise regression. The method is used to find the mathematical relationship between one or more independent and dependent variables (Jeon et al. 2014), as shown in Figure 4. This relationship can be defined as:

${\text{y}}_{\text{i}}=\text{f}\left({\text{x}}_{\text{i}}\right)+\text{e}$ (3)

where x_i indicates the input and y_i illustrates the output; f(x) represents the linear regression function and e shows the independent random error (Liu and Li 2009).

Figure 4:
Schematic illustration of regression analysis.

Support vector regression (SVR), multivariate linear regression (MLR), nonlinear regression and robust regression analysis (RRA) are some of the important applications of regression analysis in SHM. Table 5 shows the applications of regression analysis in SHM, thoroughly.

Table 5:
Regression Analysis applications in SHM.

Regression applications	References
Support vector regression (SVR) for versatile-typed structural identification	(Zhang et al. 2007)
Multivariate linear regression (MLR) in the measurement data from a bridge	(Hua et al. 2007)
Support vector regression (SVR) for structural identification	(Zhang and Sato 2008)
Nonlinear statistical regression analyses for damage quantification	(Sankararaman and Mahadevan 2011)
Support vector regression (SVR) for structural reliability assessment	(Dai et al. 2012)
Regression analysis for damage detection of a bridge	(Ismail et al., 2012)
Nonlinear statistical regression analysis for optimum design of building	(Ganjavi and Hao 2013)
Robust regression analysis (RRA) for damage detection	(Laory et al. 2013)
Linear regression-based techniques for stiffness estimation of a frame	(Yao and Pakzad 2014)
Comparison of RealAdaBoost algorithm and logistic regression	(Li et al. 2014)
Impact identification of an aluminum plate using regression	(Sanchez et al. 2016)
Damage detection of an arch bridge using multiple linear regression	(Comanducci et al., 2016)
Removal of environmental effects using multivariate linear regression	(Ubertini et al., 2016)

3.6 Principal Component Analysis (PCA)

PCA is a well-known method for data analysis, which is used as a dimensional reduction tool (Lautour and Omenzetter 2010; Kwak 2014). PCA also is employed in exploratory data analysis and pattern recognition (Yiqiu et al. 2012). The main concept behind PCA is to transform high-dimensional correlated variables into low-dimensional uncorrelated variables by an orthogonal projection, in which the new low-dimensional uncorrelated variables are known as principal components, as shown in Table 6. Main steps to have the principal components of a database is to (1) construct a matrix from data, (2) construct the normalized matrix, (3) calculate the covariance matrix, and (4) calculate the largest eigenvalue and eigenvector. Architecture of a two-dimensional PCA is shown in Figure 5, where it can principally be defined as:

$\text{Y}={\text{W}}^{\text{T}}\text{X}$ (4)

in which Y shows principal components, W indicates eigenvector and X represents the input data in the new coordinates (Ku and Waszczyszyn 2006; Hua et al. 2007; Hao et al. 2011).

Table 6:
Principal Component Analysis (PCA) applications in SHM.

PCA applications	References
Feature improvement of intact and damaged structures using PCA	(Sohn et al. 2000)
Temperature-frequency correlation using combined PCA and SVR	(Hua et al. 2007)
Identification of temperature and wind effects on modal parameters	(Li et al. 2010)
Damage detection using principal component analysis	(Hsu and Loh 2010)
Damage detection by the multivariate data of the sample coefficients	(Wang and Ong 2010)
Damage detection using moving principal component analysis (MPCA)	(Laory et al. 2013)
Comparison frequency response functions using PCA	(Li et al. 2011)
Wavelet packet transform (WPT) using PCA	(Amiri et al., 2012)
Wavelet‐based damage diagnosis using PCA	(Kesavan and Kiremidjian 2012)
Damage identification using moving principal component analysis(MPCA)	(Laory et al. 2012)
Linear and nonlinear PCA in static deformation data of Fei-Tsui arch dam	(Kao and Loh 2013)
Principled independent component analysis for seismic data compression	(Yang and Nagarajaiah 2014)
Optimal sensor placement using PCA	(Chang and Pakzad 2014)
PCA for dam deformation	(Mata et al. 2014)
Feature extraction from acoustic emission data using PCA	(Al-jumaili et al. 2015)
Seismic usability of unreinforced masonry buildings using PCA	(Zucconi et al. 2017)
Quantification of the earthquake-induce local stress using PCA	(Loh et al. 2016)
PCA-based normalization for early damage detection	(J. P. Santos et al., 2014)
SHM based on kernel principal component analysis	(Langone et al., 2017; Reynders, Wursten, & De Roeck, 2013)
SHM data compression using PCA	(Park et al. 2007; Rao et al. 2015; Pozo et al. 2016)

Figure 5:
PCA transformation.

3.7 Bayesian Analysis

Bayesian analysis is considered as a statistical method, which is applied to pattern recognition (Cristianini and Shawe-Taylor 2000a) and it is a classification method based on Bayes’s theorem. Bayesian method has been used for addressing data uncertainty and modeling errors in structural damage detection (Jiang and Mahadevan 2008b). In recent years, a new type of Bayesian analysis has been derived from neural networks (Arangio and Beck 2012). For instance, a four-phase structural damage identification approach (see Figure 6) can be used by means of Bayesian inference and fuzzy wavelet neural network (WNN) model (Jiang and Mahadevan 2008a). Bayes’s theorem can be defined as follows:

$\text{P}\left(\text{A|B}\right)=\frac{\text{P}\left(\text{B|A}\right).\text{P}\left(\text{A}\right)}{\text{P}\left(\text{B}\right)}$ (5)

where P(A) is prior probability of A with no knowledge of observation B; P(B) is prior probability of B with no knowledge of A; P(A|B) is posterior probability of A after observation B; and P(B|A) is probability of observation B given that A is true (Dawsey et al. 2006; Yuen 2010). Applications of Bayesian analysis are shown in Table 7.

Figure 6:
Damage detection methodology using combination of Bayesian and fuzzy WNN(Jiang and Mahadevan 2008a).

Table 7:
Bayesian Analysis applications in SHM.

Bayesian applications	References
Bayesian wavelet packet denoising for system identification	(Jiang and Mahadevan 2008b)
Bayesian probabilistic inference for nonparametric damage detection	(Jiang and Mahadevan 2008a)
Bayesian neural networks for bridge integrity assessment	(Arangio and Beck 2012)
Bayesian evidence framework (BEF) for dams crack monitoring	(Chen et al. 2017)
Damage detection of bolted connections using Bayesian probabilistic inference	(Yin et al. 2017)
Model updating of structural systems using Bayesian inference	(Sun and Betti 2015)

3.8 Clustering

Clustering is an unsupervised statistical data analysis technique, which is used in pattern recognition, image analysis and bioinformatics (Park et al. 2007). This method is employed to divide datasets into separated similar subsets (clusters) according to typical patterns identified in the clustering analysis (Ghaedi and Ibrahim 2017). Figure 7 indicates the basic concept of clustering. As shown in Figure 7(a), in order to have a successful clustering, maximum intra-cluster similarity as well as minimum inter-cluster similarity is required. Moreover, Figure 7(b) presents a schematic plot of K-means algorithm, which divides the space into three clusters (C1, C2, and C3). The K-means is one of the most descriptive partitioning clustering algorithms with a quite reliable effectiveness at local optimum. However, it can be employed only to numerical datasets. Furthermore, K-means has poor handling for data prone to noise and outliers (Symeonidis and Mitkas 2005). Clustering can also help to decrease the distance between datasets and improve the similarity of datasets in each cluster (Saitta et al. 2008; Yu et al. 2011; Chuang et al. 2011; Chen and Huang 2013; Xiao and Fan 2014). Table 8 illustrates the applications of clustering analysis in SHM system.

Figure 7:
Algorithms of (a) Intra- and inter-cluster similarity, and (b) Schematic plot of K-means clustering (Symeonidis and Mitkas 2005).

Table 8:
Clustering analysis applications in SHM.

Clustering applications	References
Pattern recognition using k-means clustering algorithm	(Park et al. 2007)
Clustering for damage localization problem	(Basseville et al., 2008)
Fuzzy clustering of stability diagrams for vibration-based SHM	(Carden and Brownjohn 2008)
System identification development using clustering	(Saitta et al. 2008)
Discretization of modal parameters using K-means clustering	(Jiang et al. 2011)
Damage detection of Guadiana bridge using K-means clustering	(Santos et al. 2016b)
Comparison of damage classification using Unsupervised Waveform Clustering	(Mccrory et al. 2015)
Cluster analysis of a carbon fibre laminate buckling test	(Al-jumaili et al. 2015)
Structural behavior detection using symbolic data analysis and clustering	(Alves et al. 2015b)
On-line early damage detection using clustering	(Santos et al. 2016c)
SHM based adaptive kernel spectral clustering (AKSC)	(Langone et al. 2017)

3.9 Decision Tree

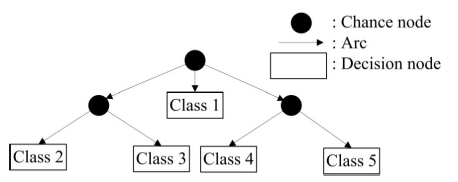
One of the statistical methods in order to solve classification problems is decision tree that can widely be implemented (Gal et al. 2013). Components of a decision tree, as shown in Figure 8, consist of nodes and arcs. The chance nodes indicate features, while decision nodes represent pattern classes and arcs denote feature values. The main advantages of using this approach is easy solution to understand and its higher interpretable capacity compared to other statistical techniques (Wei and Hsu 2008).

Figure 8:
Configuration of a decision tree.

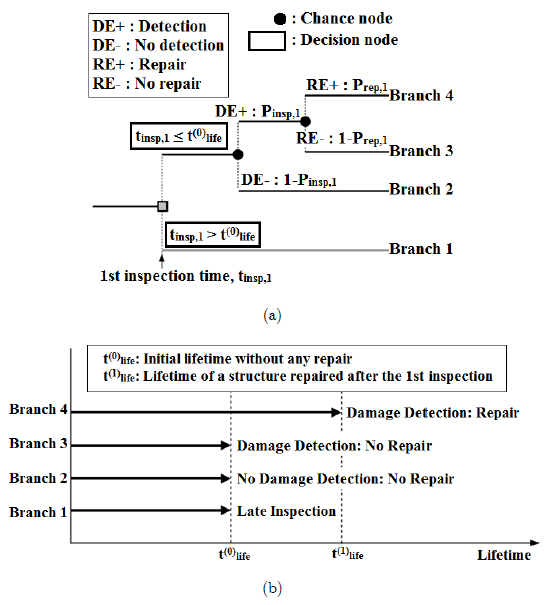
Starting point to design a decision tree model is a decision node creation including several alternatives. For example, Kim et al. (Kim et al. 2011) considered two alternatives (i.e. first inspection time (tinsp,1) after and before initial service life (t(0)life)) and four branches to create a decision tree model for prediction of lifetime of deteriorating structures with one inspection, as shown in Figure 9(a). In Figure 9(b), each branch represents different cases of decision tree including late inspection in first branch, changing node without damage detection in second branch and damage detection in third or fourth branches. The repair process can be conducted by decision maker selection in the third or fourth branch. Applications of decision tree method in SHM are presented in Table 9.

Figure 9:
Application of decision tree for (a) prediction of lifetime with one inspection, (b) extended lifetime of each branch in (a).

Table 9:
Decision Tree applications in SHM.

Decision tree and its applications	References
Damage detection of reinforced concrete structures using decision tree analysis	(Kim et al. 2011)
Comparison the accuracy prediction between RealAdaBoost algorithm and decision tree	(Li et al. 2014)
Pattern recognition of structural behaviors based on Bayesian Decision Trees	(Alves et al., 2015b; Cury & Cremona, 2012)

4 OPTIMIZATION-BASED DATA MINING IN STRUCTURAL DAMAGE DETECTION

4.1 Genetic Algorithms (GA)

Genetic algorithm (GA) was first proposed by John Holland in 1970’s. In GA, a chromosome is used to determine the solution. The chromosome includes a group of genes that optimize parameters. In damage identification problems, damage parameters are determined in real number of genes, which form the chromosome of an individual solution. This algorithm employs a random solution from a current population. Then, next generation will be created using crossover and mutation operators (Kouchmeshky et al. 2008; Aghajanloo and Sabziparvar 2012). Figure 10 illustrates a typical crossover and mutation operator in GA algorithm. Accordingly, the basic steps to form a GA include:

• Select a population of chromosomes;

• Calculate the fitness of each chromosome;

• select parents chromosomes from population, randomly;

• Crossover creates offspring;

• Mutation forms a new generation;

• Calculate the fitness of new chromosomes;

• Repeat the selection of parents chromosomes to find the fittest chromosomes in the next generation (Fu 2000).

Figure 10:
Configuration of Genetic algorithm.

Genetic algorithm is an attractive tool to optimize difficult problems because of its benefits such as parallelism, convergence to global optima, adaptation, and no need for the gradient of the objective function. Considering these benefits, GA has been successfully applied in structural damage identification problems (Sohn et al. 2001; Raich and Liszkai 2003). Applications of GA in SHM are shown in Table 10.

Table 10:
Genetic Algorithm (GA) applications in SHM.

GA applications	References
Damage detection of steel plates using GA	(Betti et al., 2015; Rus et al., 2006)
Damage identification of beam-like structures using GA	(Kuang et al. 2006)
Damage identification based on dead load redistribution using GA	(Shenton Iii and Hu 2007)
Damage identification of multistory shear structure using GA	(Panigrahi et al. 2013)
Optimal sensor placement using GA	(H. G. Chen et al., 2007; Cruz et al., 2009)
GA-based method of search space reduction	(Perry and Koh 2008)
GA-based structural identification	(Kouchmeshky et al. 2008; Trinh and Koh 2012)
Fault detection filter using GA	(Chen and Nagarajaiah 2013)
Vibration-based damage assessment of structures using GA	(Srinivas et al. 2013)
Bridge damage identification using neurogenetic algorithm	(Liu et al. 2015)
Optimization of SVM-based damage detection using GA	(Gui et al. 2017)
Reduction of material uncertainty using GA-based model updating	(Abbasi et al. 2015)
Damage assessment of bridges using GA	(Mosquera et al. 2012; Santos et al. 2016a)

4.2 Particle Swarm Optimization (PSO)

PSO which was first proposed by Kennedy and Eberhart (Kennedy and Eberhart 1995), is one of the population-based artificial intelligence optimization techniques. The approach was simulated by the social behavior of organisms such as bird flocking to be used a suitable tool for global optimization. In PSO, a particle represents a potential solution where each particle has two updatable features; position and velocity. The main steps of this algorithm can be presented as follows:

• Particles initialization with arbitrary position and velocity;

• Objective function evaluation and updating the position and velocity based on the best fitness function;

• Determination of global minimum fitness value;

• Velocity modification and particle movement to new position;

• Process iteration to meet criterion (Talatahari et al. 2013).

Furthermore, PSO is easy to apply and has great computational capacity. In comparison with other optimization approaches, PSO is, however, more efficient and requiring fewer number of function evaluations while gives better or the same quality of results, but it has some weaknesses such as trapping into local optimum in a complex search space and disability to do a good local search around a local optimum (Dimou and Koumousis 2009; Gholizadeh and Fattahi 2014; Gundogdu et al. 2015). Optimization function, as the critical attribute of PSO, is very useful to assess the structural damages; however, as shown in Table 11, PSO implementation in SHM is not as much of GA applications.

Table 11:
Particle Swarm Optimization (PSO) applications in SHM.

PSO applications	References
Comparison of PSO and Big Bang-Big Crunch optimization damage detection method	(Tabrizian et al. 2013)
Damage identification based on improved particle swarm optimization (IPSO)	(Guo and Li 2013)
Maximization of the probability density function utilizing hybrid PSO	(Ng 2014)
Damage parameters identification of tensile specimens using hybrid PSO	(Zhong et al., 2016)
Optimization of SVM-based damage detection using PSO	(Gui et al. 2017)
Damage identification of beams using fuzzy adaptive PSO	(Jena et al. 2015)

4.3 Ant Colony Optimization (ACO)

Ant Colony Optimization (ACO) was introduced by Marco Dorigo in 1992 for combinatorial optimization problems (Yu and Xu 2011; Guerrero et al. 2014; Cottone et al. 2014). ACO is a probabilistic population-based technique inspired by the ants’ foraging activities and their communication system by using pheromone trail, as the most significant role to discover the direction (Amini and Ghaderi 2012; Fidanova et al. 2012; Majumdar et al. 2012). Optimization problems can be solved utilizing ACO by iterating two steps:

• Construct candidate solutions in a probabilistic way by using a probability distribution over the search space;

• Modify the probability distribution by candidate solutions (Yu and Xu 2011).

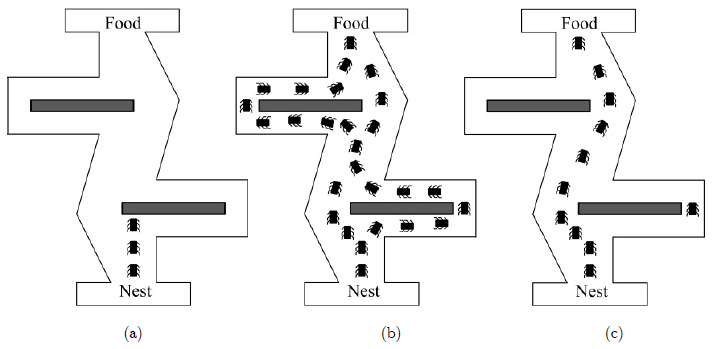
Ant colony based algorithm can be classified into three forms including ant-quantity, ant-density and ant-cycle. The main concept of ACO is the power of finding the shortest way from ant’s nest to food source, as indicated in Figure 11. ACO Applications used by researchers in SHM are shown in Table 12.

Figure 11:
Ant colony algorithm concept. (a) start searching for food, (b) searching all available (short or long) ways, (c) choosing the shortest way (Bachir et al. 2012).

Table 12:
Ant Colony Optimization (ACO) applications in SHM.

Ant colony and its applications	References
ACO based algorithm for optimization problems on structural damage detection	(Yu and Xu 2011)
Damage estimation of truss structures using ACO	(Majumdar et al. 2012)
Damage detection using Lévy ant colony optimization	(Cottone et al. 2014)
Sensor placement using ant colony system	(Shuo and Jingqing 2016)
Damage detection of a damped spring-mass system using ACO	(Braun et al. 2015)

5 RESULTS AND DISCUSSIONS

5.1 Comparison of DMTs Applications in SHM

The DMT applications used in SHM area have been introduced and discussed in sections 3 and 4. As shown in Figure 12, the general development of DM applications in SHM, primarily since 2000, demonstrates that the main three DMTs used in SHM were ANN, PCA and GA, respectively. Overall, outcomes showed that, applications of statistical techniques in the SHM were less than artificial intelligence techniques. The percentage of DMT’s applications in SHM is shown in Figure 13. This figure indicates that ANN and PCA were the highest application rate by conducing 30% and 20% of researches, respectively. Further, GA by 10% application rate stood at the third level. In contrary, decision tree, clustering, Bayesian, PSO, regression and ACO techniques were rarely used in SHM. Other DMTs such as SVM and fuzzy were occasionally used in SHM with 6% to 8% application rate.

Figure 12:
Trend of DM applications in SHM.

Figure 13:
Application percentage of DMTs in SHM.

5.2 Capabilities and limitations

In recent years, there has been a vast increase in the number of reverse analysis in SHM generally based on two methodologies; artificial neural networks and optimization techniques. In optimization-based data mining, meta-heuristic techniques, including (1) biology inspired intelligent global search approaches such as GA and (2) swarm-based techniques such as ACO and PSO, have several applications in SHM. Nevertheless, in general, drawback of optimization approaches is time consuming. On the other hand, these methods have many differences in detail. For instance, PSO has memory and all particles retain the knowledge of good solutions, but in GA, there is no memory and when the population changes, all previous knowledge about the problem will be destroyed. From this viewpoint, ACO is not appropriate for continuous optimization problems. Despite using PCA in several SHM studies as it was able to decrease dimensions of multidimensional datasets, ANN is the most powerful DMT in classification, regression and prediction which has been broadly used in many SHM applications, because of its nonlinear learning abilities. ANN is more flexible and more accurate in comparison to other DMTs. Figure 14 illustrates the discussed DMTs trends for all applicable methods. This is also demonstrated the development of DMTs from 2000 to present.

Figure 14:
Application and developing of DMTs trend used in SHM since 2000.

In the present study, a flow chart based on DM steps along with prediction and optimization-based algorithms is proposed for SHM assessment and indicated in Figure 15. According to proposed flow chart, SHM assessment starts with measuring the damage level. After collecting the data, preprocessing step including cleaning, construction, integration and transformation of data is carried out in order to build the database. In next step (modeling), the suitable DMTs are suggested to be applied for training the data. Since various DMTs such as ANN, Fuzzy, PCA, SVM, GA, PSO, ACO, Bays, etc. exist for the same problem type, therefore, they can be employed for different purposes such as optimization, classification and perdition. Moreover, test design generation, patterns creation and their validation are also detailed in this step to determine the severity and location of damages. After pattern assessment, several rehabilitation activities (e.g. modification and strengthening the structural members, repair or replacement of the existing damaged members, and minor or major maintenance) are suggested to improve the health condition of civil structures. Based on existing problem, one or combination of these activities needs to be done to protect the structural performance.

Figure 15:
Schematic structure of the proposed Data Mining-Based Procedure to be used in SHM.

6 CONCLUSION

DM is just one of the very important steps in the Knowledge Discovery in Databases (KDD) process to extract the models, patterns and rules from raw data in large databases. There are three main approaches, namely statistical techniques, machine learning techniques and artificial intelligence techniques to apply in structural real world problems. In this paper, various DMTs which are applicable to SHM from 2000 were widely reviewed and, consequently, their main concept, methodologies, capabilities and drawbacks were discussed. Based on the presented information, the following conclusions can be drawn.

• ANN, PCA and GA are the most common DMTs in SHM, respectively, in order to structural damage identification of various types of civil structures; buildings, bridges, reinforced concrete beams, dams, truss structures, and steel plates.

• Classification and prediction based DMTs can be categorized into two different methods which are statistical methods and artificial intelligence methods.

• Statistical methods such as decision tree and Bayesian have the lowest application rate in SHM due to lack of capacity, flexibility and complexity. In contrast, artificial intelligence techniques such as ANN and GA have the highest application rate in SHM due to their accuracy, flexibility, autonomy, complexity, and optimization capability.

• In optimization-based DMTs, GA is the best optimal tool to improve the efficiency of difficult problems due to its criteria, which is based on parallelism. GA can utilize a coding set of variable from a population instead of employing the variables directly from a particular solution.

Acknowledgements

The authors would like to express their sincere thanks to University of Malaya (UM) and the Ministry of Education (MOE), Malaysia for the support given through research grants PG144-2016A and UM.C/625/1/HIR/MOHE/ENG/55.

References

• Abbasi F, Mojtahedi A, Ettefagh MM (2015) Fault diagnosis using noise modeling and a new arti fi cial immune system based algorithm. Earthq Eng 14:725-741.
• Adeli H, Jiang X (2006) Dynamic Fuzzy Wavelet Neural Network Model for Structural System Identification. J Struct Eng 132:102-111.
• Aghajanloo M, Sabziparvar A (2012) Artificial neural network - genetic algorithm for estimation of crop evapotranspiration in a semi-arid region of Iran. Neural Comput Appl 23:1387-1393.
• Ahmed R, El Sayed M, Gadsden SA, et al (2015) Artificial neural network training utilizing the smooth variable structure filter estimation strategy.
• Ali A, Amin SE, Ramadan HH, Tolba MF (2013) Enhancement of OMI aerosol optical depth data assimilation using artificial neural network. Neural Comput Appl 23:2267-2279.
• Al-jumaili SK, Holford KM, Eaton MJ, et al (2015) Classification of acoustic emission data from buckling test of carbon fibre panel using unsupervised clustering techniques. Struct Heal Monit 14:241-251. doi: 10.1177/1475921714564640
  » https://doi.org/10.1177/1475921714564640
• Al-rahmani AH, Rasheed HA, Najjar Y (2013) Intelligent Damage Detection in Bridge Girders : Hybrid Approach. J Eng Mech 139:296-304.
• Altunok E, Taha MMR, Epp DS, et al (2006) Damage Pattern Recognition for Structural Health Monitoring Using Fuzzy Similarity Prescription. Comput Civ Infrastruct Eng 21:549-560.
• Alves V, Cury A, Roitman N, et al (2015a) Novelty detection for SHM using raw acceleration measurements. Struct Control Heal Monit 22:1193-1207.
• Alves V, Cremona C, Cury A (2015b) On the use of symbolic vibration data for robust structural health monitoring. Proc Inst Civ Eng Build 169:715-723.
• Alves V, Cury A, Roitman N, et al (2015c) Structural modification assessment using supervised learning methods applied to vibration data. Eng Struct 99:439-448.
• Amini F, Ghaderi P (2012) Optimal locations for MR dampers in civil structures using improved Ant Colony Algorithm. Optim Control Appl Methods 33:232-248.
• Amiri GG, Abdolahi Rad A, Aghajari S, Khanmohamadi Hazaveh N (2012) Generation of Near-Field Artificial Ground Motions Compatible with Median-Predicted Spectra Using PSO-Based Neural Network and Wavelet Analysis. Comput Civ Infrastruct Eng 27:711-730.
• Arangio S, Beck JL (2012) Bayesian neural networks for bridge integrity assessment. Struct Control Heal Monit 19:3-21.
• Arsava SK, Chong JW, Kim Y (2014) A novel health monitoring scheme for smart structures. J Vib Control 1-19.
• Aydin K, Kisi O (2015) Damage diagnosis in beam-like structures by artificial neural networks. J Civ Eng Manag 21:591-604. doi: 10.3846/13923730.2014.890663
  » https://doi.org/10.3846/13923730.2014.890663
• Aydin K, Kisi O (2014) Applicability of a Fuzzy Genetic System for Crack Diagnosis in Timoshenko Beams. J Comput Civ Eng 29:04014073.
• Azimzadegan T, Khoeini M, Etaat M, Khoshakhlagh A (2012) An artificial neural-network model for impact properties in X70 pipeline steels. Neural Comput Appl 23:1473-1480.
• Bachir B, Ali A, Abdellah M (2012) Multiobjective Optimization of an Operational Amplifier by the Ant Colony Optimisation Algorithm. Electr Electron Eng 2:230-235.
• Bagchi A, Humar J, Xu H, Noman AS (2010) Model-Based Damage Identification in a Continuous Bridge Using Vibration Data. J Perform Constr Facil 24:148-159.
• Basseville M, Mevel L, Nasser H, Zhou W (2008) Statistical model-based damage localization : A combined subspace-based and substructuring approach. Struct Control Heal Monit 15:857-875.
• Betti M, Facchini L, Biagini P (2015) Damage detection on a three-storey steel frame using artificial neural networks and genetic algorithms. Meccanica 50:875-886. doi: 10.1007/s11012-014-0085-9
  » https://doi.org/10.1007/s11012-014-0085-9
• Braun CE, Chiwiacowsky LD, Arthur TG (2015) Variations of Ant Colony Optimization for the solution of the structural damage identification problem. Procedia Comput Sci 51:875-884.
• Buchheit RB, Garrett, Jr. JH, Lee SR, Brahme R (2000) A Knowledge Discovery Case Study for the Intelligent Workplace. Comput Civ Build Eng 914-921.
• Carden EP, Brownjohn JMW (2008) Fuzzy Clustering of Stability Diagrams for Vibration-Based Structural Health Monitoring. Comput Civ Infrastruct Eng 23:360-372.
• Chakraverty S, Sahoo DM (2017) Fuzzy neural network-based system identification of multi-storey shear buildings. Neural Comput Appl 28:597-612. doi: 10.1007/s00521-015-2101-y
  » https://doi.org/10.1007/s00521-015-2101-y
• Chang M, Pakzad SN (2014) Optimal Sensor Placement for Modal Identi fi cation of Bridge Systems Considering Number of Sensing Nodes. J Bridg Eng 19:1-10.
• Chen B, Nagarajaiah S (2013) Observer-based structural damage detection using genetic algorithm. Struct Control Heal Monit 20:520-531.
• Chen B, Wu Z, Liang J, Dou Y (2017) Time-Varying Identification Model for Crack Monitoring Data from Concrete Dams Based on Support Vector Regression and the Bayesian Framework.
• Chen HG, Yan YJ, Chen WH, et al (2007) Early Damage Detection in Composite Wingbox Structures using Hilbert-Huang Transform and Genetic Algorithm. Struct Heal Monit 6:281-297.
• Chen TY, Huang JH (2013) Application of data mining in a global optimization algorithm. Adv Eng Softw 66:24-33.
• Chen Z, Hutchinson TC (2011) Structural damage detection using bi-temporal optical satellite images. Int J Remote Sens 32:4973-4997.
• Chiang T, Chiu C, Liu P (2009) Adaptive TS-FNN control for a class of uncertain multi-time-delay systems : The exponentially stable sliding mode-based approach. Int J Adapt Control Signal Process 23:378-399.
• Chong JW, Kim Y, Chon KH (2013) Nonlinear multiclass support vector machine-based health monitoring system for buildings employing magnetorheological dampers. J Intell Mater Syst Struct 25:1456-1468.
• Chu F, Wang F, Wang X, Zhang S (2014) A hybrid artificial neural network-mechanistic model for centrifugal compressor. Neural Comput Appl 24:1259-1268.
• Chuang L-Y, Hsiao C-J, Yang C-H (2011) Chaotic particle swarm optimization for data clustering. Expert Syst Appl 38:14555-14563.
• Chun P, Yamashita H, Furukawa S (2015) Bridge Damage Severity Quantification UsingMultipoint Acceleration Measurement and Artificial Neural Networks.
• Comanducci G, Magalhães F, Ubertini F, Cunha Á (2016) On vibration-based damage detection by multivariate statistical techniques: Application to a long-span arch bridge.
• Cottone G, Fileccia Scimemi G, Pirrotta A (2014) α-stable distributions for better performance of ACO in detecting damage on not well spaced frequency systems. Probabilistic Eng Mech 35:29-36.
• Cristianini N, Shawe-Taylor J (2000a) An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge University Press, UK
• Cristianini N, Shawe-Taylor J (2000b) An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge University Press, UK
• Cruz A, Vélez W, Thomson P (2009) Optimal sensor placement for modal identification of structures using genetic algorithms-a case study: the olympic stadium in Cali, Colombia. Ann Oper Res 181:769-781.
• Cury A, Cremona C (2012) Pattern recognition of structural behaviors based on learning algorithms and symbolic data concepts. Struct Control Heal Monit 19:161-186.
• Dackermann U, Smith WA, Randall RB (2014) Damage identification based on response-only measurements using cepstrum analysis and artificial neural networks. Struct Heal Monit 13:430-444.
• Dai H, Zhang H, Wang W, Xue G (2012) Structural Reliability Assessment by Local Approximation of Limit State Functions Using Adaptive Markov Chain Simulation and Support Vector Regression. Comput Civ Infrastruct Eng 27:676-686.
• Dawsey WJ, Minsker BS, Van Blaricum VL (2006) Bayesian Belief Networks to Integrate Monitoring Evidence of Water Distribution System Contamination. J Water Resour Plan Manag 132:234-241.
• Dimou CK, Koumousis VK (2009) Reliability-Based Optimal Design of Truss Structures Using Particle Swarm Optimization. J Comput Civ Eng 23:100-110.
• Duan Z, Zhang K (2006) Data Mining Technology for Structural Health Monitoring. Pacific Sci Rev 8:27-36.
• Edeki CA (2012) A Comparative Study of Data Mining and Statistical Learning Techniques for Prediction of Canser Survovability. Capella University
• Fidanova S, Marinov P, Alba E (2012) Ant Algorithm for Optimal Sensor Deployment. In: Computational Intelligence, SCI 399. Springer-Verlag Berlin Heidelberg, pp 21-29
• Fu Z (2000) Using Genetic Algorithms to Develop Inteligent Decision Trees. University of Maryland
• Gal G, Skerjanec M, Atanasova N (2013) Fluctuations in water level and the dynamics of zooplankton: a data-driven modelling approach. Freshw Biol 58:800-816.
• Ganjavi B, Hao H (2013) Optimum lateral load pattern for seismic design of elastic shear-buildings incorporating soil - structure interaction effects. Earthq Eng Struct Dyn 42:913-933.
• Ghaedi K, Hejazi F, Ibrahim Z, Khanzaei P (2017a) Flexible foundation effect on seismic analysis of Roller Compacted Concrete (RCC) dams using finite element method. KSCE J Civ Eng 1-13.
• Ghaedi K, Ibrahim Z (2017) Earthquake Prediction. In: Earthquakes - Tectonics, Hazard and Risk Mitigation. InTech,
• Ghaedi K, Ibrahim Z, Adeli H (2017b) Invited Review: Recent developments in vibration control of building and bridge structures.
• Ghaedi K, Jameel M, Ibrahim Z, Khanzaei P (2016) Seismic Analysis of Roller Compacted Concrete ( RCC ) Dams Considering Effect of Sizes and Shapes of Galleries. KSCE J Civ Eng 20:261. doi: 10.1007/s12205-015-0538-2
  » https://doi.org/10.1007/s12205-015-0538-2
• Gholizadeh S, Fattahi F (2014) Design optimization of tall steel buildings by a modi fi ed particle. Struct Des Tall Spec Build 23:285-301.
• Golewski P, Gajewski J, Sadowski T (2017) Optimization of A Thin-Walled Element Geometry Using A System Integrating Neural Networks and Finite Element Method. Arch Metall Mater 62:435-442. doi: 10.1515/amm-2017-0067
  » https://doi.org/10.1515/amm-2017-0067
• Goswami S, Bhattacharya P (2012) A Scalable Neural-Network Modular-Array Architecture for Real-Time Multi-Parameter Damage Detection in Plate Structures Using Single Sensor Output. Int J Comput Intell Appl 11:1-22.
• Guerrero GD, Cecilia JM, Llanes A, et al (2014) Comparative evaluation of platforms for parallel Ant Colony Optimization. J Supercomput 69:318-329.
• Gui G, Pan H, Lin Z, et al (2017) Data-Driven Support Vector Machine with Optimization Techniques for Structural Health Monitoring and Damage Detection. KSCE J Civ Eng 21:523-534. doi: 10.1007/s12205-017-1518-5
  » https://doi.org/10.1007/s12205-017-1518-5
• Gundogdu O, Egrioglu E, Aladag CH, Yolcu U (2015) Multiplicative neuron model artificial neural network based on Gaussian activation function.
• Guo HY, Li ZL (2013) Structural damage identification based on evidence fusion and improved particle swarm optimization. J Vib Control 20:1279-1292.
• Hakim SJS, Razak HA (2014a) Frequency Response Function-based Structural Damage Identification using Artificial Neural Networks-a Review. Res J Appl Sci Eng Technol 7:1750-1764.
• Hakim SJS, Razak HA (2014b) Modal parameters based structural damage detection using artificial neural networks - a review. Smart Struct Syst 14:159-189.
• Han J, Kamber M, Pei J (2006) Data Mining: Concepts and Techniques, 2nd edn. Morgan Kaufmann, San Francisco
• Hanif MU, Ibrahim Z, Jameel M, et al (2016) A new approach to estimate damage in concrete beams using non-linearity. Constr Build Mater 124:1081-1089.
• Hao L, Lewin PL, Hunter J a, et al (2011) Discrimination of multiple PD sources using wavelet decomposition and principal component analysis. Dielectr Electr Insul IEEE Trans 18:1702-1711.
• He H-X, Yan W (2007) Structural damage detection with wavelet support vector machine: introduction and applications. Struct Control Heal Monit 14:162-176.
• He X (2008) Vibration-Based Damage Identification and Health Monitoring of Civil Structures. Doctoral dissertation, University of California
• Hosseinabadi HZ, Nazari B, Amirfattahi R, et al (2014) Wavelet Network Approach for Structural Damage Identification Using Guided Ultrasonic Waves. IEEE Trans Instrum Meas 63:1680-1692.
• Hou Z, Hera A, Noori M (2013) Wavelet-Based Techniques for Structural Health Monitoring. In: Health Assessment of Engineered Structures: Bridges, Buildings and Other Infrastructures. World Scientific, pp 179-202
• Hsu T, Loh C (2010) Damage detection accommodating nonlinear environmental effects by nonlinear principal component analysis. Struct Control Heal Monit 17:338-354.
• Hua XG, Ni YQ, Ko JM, Wong KY (2007) Modeling of Temperature - Frequency Correlation Using Combined Principal Component Analysis and Support Vector Regression Technique. J Comput Civ Eng 21:122-135.
• Hung S, Huang CS, Wen CM, Hsu YC (2003) Nonparametric Identification of a Building Structure from Experimental Data Using Wavelet Neural Network. Comput Civ Infrastruct Eng 18:356-368.
• Hung S-L, Kao CY (2002) Structural damage detection using the optimal weights of the approximating artificial neural networks. Earthq Eng Struct Dyn 31:217-234.
• Ismail Z, Ibrahim Z, Ong AZC, Rahman AGA (2012) Approach to Reduce the Limitations of Modal Identi fi cation in Damage Detection Using Limited Field Data for Nondestructive Structural Health Monitoring of a Cable-Stayed Concrete Bridge. J Bridg Eng 17:867-875.
• Jena PK, Thatoi DN, Parhi DR (2015) Applied Artificial Intelligence : An Dynamically Self-Adaptive Fuzzy PSO Technique for Smart Diagnosis of Transverse Crack. Appl Artif Intell 29:211-232. doi: 10.1080/08839514.2015.1004611
  » https://doi.org/10.1080/08839514.2015.1004611
• Jeon J, Shafieezadeh A, DesRoches R (2014) Statistical models for shear strength of RC beam-column joints using machine-learning techniques. Earthq Eng Struct Dyn 43:2075-2095.
• Jeyasehar CA, Sumangala K (2006) Nondestructive Evaluation of Prestressed Concrete Beams using an Artificial Neural Network (ANN) Approach. Struct Heal Monit 5:313-323.
• Jiang S, Zhang C, Yao J (2011) Eigen-Level Data Fusion Model by Integrating Rough Set and Probabilistic Neural Network for Structural Damage Detection. Adv Struct Eng 14:333-349.
• Jiang X, Mahadevan S (2008a) Bayesian Probabilistic Inference for Nonparametric Damage Detection of Structures. J Eng Mech 134:820-832.
• Jiang X, Mahadevan S (2008b) Bayesian wavelet methodology for structural damage detection. Struct Control Heal Monit 15:974-991.
• Jiang X, Mahadevan S, Adeli H (2007) Bayesian wavelet packet denoising for structural system identification. Struct Control Heal Monit 14:333-356.
• Jiao Y, Liu H, Cheng Y, Gong Y (2015) Damage Identification of Bridge Based on Chebyshev Polynomial Fitting and Fuzzy Logic without Considering Baseline Model Parameters.
• Jin C, Jang S, Sun X, et al (2016) Damage detection of a highway bridge under severe temperature changes using extended Kalman filter trained neural network. J Civ Struct Heal Monit. doi: 10.1007/s13349-016-0173-8
  » https://doi.org/10.1007/s13349-016-0173-8
• Kabir S, Rivard P, Ballivy G (2008) Neural-network-based damage classification of bridge infrastructure using texture analysis. Can J Civ Eng 35:258-267.
• Kanwar V, Kwatra N, Aggarwal P (2007) Damage Detection for Framed RCC Buildings using ANN Modeling. Int J Damage Mech 16:457-472.
• Kao C, Loh C (2013) Monitoring of long-term static deformation data of Fei-Tsui arch dam using artificial neural network-based approaches. Struct Control Heal Monit 20:282-303.
• Karacı A, Arıcı N (2014) Determining students’ level of page viewing in intelligent tutorial systems with artificial neural network. Neural Comput Applic 24:675-684.
• Kennedy J, Eberhart R (1995) Particle swarm optimization. Proc ICNN’95 - Int Conf Neural Networks 4:1942-1948.
• Kesavan KN, Kiremidjian AS (2012) A wavelet-based damage diagnosis algorithm using principal component analysis. Struct Control Heal Monit 19:672-685.
• Khan IA, Parhi DR (2015) Fault detection of composite beam by using the modal parameters and RBFNN technique. J Mech Sci Technol 29:1637-1648. doi: 10.1007/s12206-015-0335-3
  » https://doi.org/10.1007/s12206-015-0335-3
• Khanmirza E, Khaji N, Khanmirza E (2014) Inverse Problems in Science and Engineering Identification of linear and non-linear physical parameters of multistory shear buildings using artificial neural network. Inverse Probl Sci Eng 23:670-687. doi: 10.1080/17415977.2014.933829
  » https://doi.org/10.1080/17415977.2014.933829
• Khanzaei P, Abdulrazeg AA, Samali B, Ghaedi K (2015) Thermal and Structural Response of RCC Dams During Their Service Life. J Therm Stress 38:591-609. doi: 10.1080/01495739.2015.1015862
  » https://doi.org/10.1080/01495739.2015.1015862
• Kim S, Frangopol DM, Zhu B (2011) Probabilistic Optimum Inspection / Repair Planning to Extend Lifetime of Deteriorating Structures. J Perform Constr Facil 25:534-545.
• Kishore B, Satyanarayana MRS, Sujatha K (2014) Efficient fault detection using support vector machine based hybrid expert system.
• Kouchmeshky B, Aquino W, Billek AE (2008) Structural damage identification using co-evolution and frequency response functions. Struct Control Heal Monit 15:162-182.
• Kourehli SS (2015) Damage Assessment in Structures Using Incomplete Modal Data and Artificial Neural Network. Int J Struct Stab Dyn 15:1-17. doi: 10.1142/S0219455414500874
  » https://doi.org/10.1142/S0219455414500874
• Ku K, Waszczyszyn Z (2006) Neural Networks and Principal Component Analysis for Identification of Building Natural Periods. J Comput Civ Eng 20:431-436.
• Kuang KSC, Maalej M, Quek ST (2006) An Application of a Plastic Optical Fiber Sensor and Genetic Algorithm for Structural Health Monitoring. J Intell Mater Syst Struct 17:361-379.
• Kwak N (2014) Principal Component Analysis by L p-Norm Maximization. IEEE Trans Cybern 44:594-609.
• Lam H, Beck JL (2006) Structural Health Monitoring via Measured Ritz Vectors Utilizing Artificial Neural Networks. Comput Civ Infrastruct Eng 21:232-241.
• Langone R, Reynders E, Mehrkanoon S, Suykens JAK (2017) Automated structural health monitoring based on adaptive kernel spectral clustering. Mech Syst Signal Process 90:64-78. doi: 10.1016/j.ymssp.2016.12.002
  » https://doi.org/10.1016/j.ymssp.2016.12.002
• Laory I, Bel N, Ali H, et al (2012) Measurement System Con fi guration for Damage Identi fi cation of Continuously Monitored Structures. J Bridg Eng 17:857-866.
• Laory I, Trinh TN, Posenato D, Smith IFC (2013) Combined Model-Free Data-Interpretation Methodologies for Damage Detection during Continuous Monitoring of Structures. J Comput Civ Eng 27:657-666.
• Lautour OR de, Omenzetter P (2010) Nearest Neighbor and Learning Vector Quantization Classification for Damage Detection using Time Series Analysis. Struct Control Heal Monit 17:614-631.
• Li H, Li S, Ou J, Li H (2010) Modal identification of bridges under varying environmental conditions: Temperature and wind effects. Struct Control Heal Monit 17:495-512.
• Li J, Dackermann U, Xu Y, Samali B (2011) Damage identification in civil engineering structures utilizing PCA-compressed residual frequency response functions and neural network ensembles. Struct Control Heal Monit 18:207-226.
• Li Z, Guo J, Liang W, et al (2014) Structural Health Monitoring Based on RealAdaBoost Algorithm in Wireless Sensor Networks. In: Wirless Algorithms, Systems and Applications. Springer International Publishing Switzerland, pp 236-245
• Liao S-H, Chu P-H, Hsiao P-Y (2012) Data mining techniques and applications - A decade review from 2000 to 2011. Expert Syst Appl 39:11303-11311.
• Liu H, Wang X, Gong Y, Jiao Y (2015) Damage Identification of Urban Overpass Based on Hybrid Neurogenetic Algorithm Using Static and Dynamic Properties.
• Liu Q, Li C (2009) Researches on Support Vector Machine Based Semi-Active Control of Structures. 2009 Int Conf Comput Technol Dev 2:411-415.
• Loh C, Chan C, Chen S, Huang S (2016) Vibration-based damage assessment of steel structure using global and local response measurements. Earthq Eng Struct Dyn 45:699-718. doi: 10.1002/eqe
  » https://doi.org/10.1002/eqe
• Loh C-H, Chen C-H, Hsu T-Y (2011) Application of advanced statistical methods for extracting long-term trends in static monitoring data from an arch dam. Struct Heal Monit 10:587-601.
• Majumdar A, Kumar D, Maity D (2012) Damage assessment of truss structures from changes in natural frequencies using ant colony optimization. Appl Math Comput 218:9759-9772.
• Marcy M, Doz G, Magalhães F, Cunha A (2016) Monitoring of the Infante D. Henrique Bridge with self organizing maps. In: Maintenance, Monitoring, Safety, Risk and Resilience of Bridges and Bridge Networks - Bittencourt, Frangopol & Beck (Eds). Taylor & Francis Group, 6000 Broken Sound Parkway NW, Suite 300, Boca Raton FL 33487-2742 CRC Press, pp 239-239
• Mata J, Castro AT De, Sá J (2014) Constructing statistical models for arch dam deformation. Struct Control Heal Monit 21:423-437.
• Mccrory JP, Al-jumaili SK, Crivelli D, et al (2015) Composites : Part B Damage classification in carbon fibre composites using acoustic emission : A comparison of three techniques. Compos Part B 68:424-430. doi: 10.1016/j.compositesb.2014.08.046
  » https://doi.org/10.1016/j.compositesb.2014.08.046
• Mert İ, Karakuş C, Üneş F (2015) Estimating the energy production of the wind turbine using artificial neural network.
• Miranda T, Correia AG, Santos M, et al (2011) New Models for Strength and Deformability Parameter Calculation in Rock Masses Using Data-Mining Techniques. Int J Geomech 11:44-58.
• Mita BA, Hagiwara H (2003) Quantitative Damage Diagnosis of Shear Structures Using Support Vector Machine. KSCE J Civ Eng 7:683-689.
• Morfidis K, Kostinakis K (2017) Advances in Engineering Software Seismic parameters ’ combinations for the optimum prediction of the damage state of R / C buildings using neural networks. Adv Eng Softw 106:1-16. doi: 10.1016/j.advengsoft.2017.01.001
  » https://doi.org/10.1016/j.advengsoft.2017.01.001
• Mosquera V, Smyth AW, Betti R (2012) Rapid evaluation and damage assessment of instrumented highway bridges. Earthq Eng Struct Dyn 41:755-774.
• Nerves AC, Krishnan R (1995) Active control strategies for tall civil structures. Proc IECON ’95 - 21st Annu Conf IEEE Ind Electron 2:962-967.
• Ng C-T (2014) Bayesian model updating approach for experimental identification of damage in beams using guided waves. Struct Heal Monit 13:359-373.
• Nyongesa HO (1998) Enhancing Neural Control Systems by Fuzzy Logic and Evolutionary Reinforcement. Neural Comput Appl 121-130.
• O’Byrne M, Schoefs F, Ghosh B, Pakrashi V (2013) Texture Analysis Based Damage Detection of Ageing Infrastructural Elements. Comput Civ Infrastruct Eng 28:162-177.
• Obenshain MK (2004) Application of data mining techniques to healthcare data. Infect Control Hosp Epidemiol 25:690-695.
• Oliveira MA De, Inman DJ (2017) Performance analysis of simplified Fuzzy ARTMAP and Probabilistic Neural Networks for identifying structural damage growth. Appl Soft Comput J 52:53-63. doi: 10.1016/j.asoc.2016.12.020
  » https://doi.org/10.1016/j.asoc.2016.12.020
• Oreta AWC, Kawashima K (2003) Neural Network Modeling of Confined Compressive Strength and Strain of Circular Concrete Columns. J Struct Eng 129:554-561.
• Osornio-Rios R a, Amezquita-Sanchez JP, Romero-Troncoso RJ, Garcia-Perez A (2012) MUSIC-ANN Analysis for Locating Structural Damages in a Truss-Type Structure by Means of Vibrations. Comput Civ Infrastruct Eng 27:687-698.
• Padil KH, Bakhary N, Hao H (2017) The use of a non-probabilistic artificial neural network to consider uncertainties in vibration-based-damage detection. Mech Syst Signal Process 83:194-209. doi: 10.1016/j.ymssp.2016.06.007
  » https://doi.org/10.1016/j.ymssp.2016.06.007
• Pang-Ning T, Steinbach M, Kumar V (2006) Introduction to data mining. Pearson Addison-Wesley, Boston
• Panigrahi SK, Chakraverty S, Mishra BK (2013) Damage Identification of Multistory Shear Structure from Sparse Modal Information. J Comput Civ Eng 27:1-9.
• Park S, Lee J-J, Yun C-B, Inman DJ (2007) Electro-Mechanical Impedance-Based Wireless Structural Health Monitoring Using PCA-Data Compression and k-means Clustering Algorithms. J Intell Mater Syst Struct 19:509-520.
• Perry MJ, Koh CG (2008) Output-only structural identification in time domain : Numerical and experimental studies. Earthq Eng Struct Dyn 34.7:517-533.
• Pozo F, Arruga I, Mujica LE, et al (2016) Detection of structural changes through principal component analysis and multivariate statistical inference. Struct Heal Monit 15:127-142. doi: 10.1177/1475921715624504
  » https://doi.org/10.1177/1475921715624504
• Prabakaran K, Kumar A, Thakkar SK (2015) Comparison of eigensensitivity and ANN based methods in model updating of an eight-story building. Earthq Eng Eng Vib 14:453-464.
• Radhika S, Tamura Y, Matsui M (2015) Journal of Wind Engineering Cyclone damage detection on building structures from pre- and post- satellite images using wavelet based pattern recognition. Jnl Wind Eng Ind Aerodyn 136:23-33. doi: 10.1016/j.jweia.2014.10.018
  » https://doi.org/10.1016/j.jweia.2014.10.018
• Rafiee R, Ataei M, KhalooKakaie R (2015) A new cavability index in block caving mines using fuzzy rock engineering system. Int J Rock Mech Min Sci 77:68-76.
• Raich A, Liszkai T (2003) Benefits of Implicit Redundant Genetic Algorithms for Structural Damage Detection in Noisy Environments. In: Genetic and Evolutionary Computation-GECCO 2003. Springer-Verlag Berlin Heidelberg, pp 2418-2419
• Rao ARM, Lakshmi K, Kumar SK (2015) Advances in Engineering Software Detection of delamination in laminated composites with limited measurements combining PCA and dynamic QPSO. Adv Eng Softw 86:85-106. doi: 10.1016/j.advengsoft.2015.04.005
  » https://doi.org/10.1016/j.advengsoft.2015.04.005
• Razak HA, Choi FC (2001) The effect of corrosion on the natural frequency and modal damping of reinforced concrete beams. Eng Struct 23:1126-1133.
• Reynders E, Wursten G, De Roeck G (2013) Output-only structural health monitoring in changing environmental conditions by means of nonlinear system identification. Struct Heal Monit 13:82-93.
• Rus G, Lee SY, Chang SY, Wooh SC (2006) Optimized damage detection of steel plates from noisy impact test. Int J Numer Methods Eng 68:707-727.
• Rutkowski L (2004) Flexible Neuro-Fuzzy Systems: Structures, Learning and Performance Evaluation. Springer Science & Business Media
• Sahoo DM, Das A, Chakraverty S (2015) Interval data-based system identification of multistorey shear buildings by artificial neural network modelling. Archit Sci Rev 58:244-254. doi: 10.1080/00038628.2013.841091
  » https://doi.org/10.1080/00038628.2013.841091
• Saitta S, Kripakaran P, Raphael B, Smith IFC (2008) Improving System Identification Using Clustering. J Comput Civ Eng 22:292-302.
• Samali B, Dackermann U, Li J (2012) Location and Severity Identification of Notch-Type Damage in a Two-Storey Steel Framed Structure Utilising Frequency Response Functions and Artificial Neural Network. Adv Struct Eng 15:743-757.
• Samanta B, Al-Balushi KR, Al-Araimi SA (2003) Artificial neural networks and support vector machines with genetic algorithm for bearing fault detection. Eng Appl Artif Intell 16:657-665.
• Sanchez N, Meruane V, Ortiz-Bernardin A (2016) A novel impact identi fi cation algorithm based on a linear approximation with maximum entropy. Smart Mater Struct 25:095050.
• Sankararaman S, Mahadevan S (2011) Uncertainty quantification in structural damage diagnosis. Struct Control Heal Monit 18:807-824.
• Santos A, Figueiredo E, Silva M, et al (2016a) Genetic-based EM algorithm to improve the robustness of Gaussian mixture models for damage detection in bridges. Struct Control Heal Monit. doi: 10.1002/stc
  » https://doi.org/10.1002/stc
• Santos J, Crémona C, Calado L (2016b) Real-time damage detection based on pattern recognition. Struct Concr 17:338-354.
• Santos JP, Cremona C, Calado L, et al (2016c) On-line unsupervised detection of early damage. Struct Control Heal Monit 23:1047-1069.
• Santos JP, Cremona C, Orcesi AD, Silveira P (2014) Early Damage Detection Based on Pattern Recognition and Data Fusion. J Struct Eng 143:04016162.
• Satpal SB, Guha A, Banerjee S (2016) Damage identi fi cation in aluminum beams using support vector machine: Numerical and experimental studies. Struct Control Heal Monit 446-457. doi: 10.1002/stc
  » https://doi.org/10.1002/stc
• Shah H, Ghazali R (2011) Prediction of earthquake magnitude by an improved ABC-MLP. In: Proceedings - 4th International Conference on Developments in eSystems Engineering, DeSE 2011. IEEE, pp 312-317
• Shahriar A, Nehdi ML (2011) Modeling Rheological Properties of Oil Well Cement Slurries Using Artificial Neural Networks. J Mater Civ Eng 23:1703-1710.
• Shenton Iii HW, Hu X (2007) Damage Identification Based on Dead Load Redistribution : Methodology. J Struct Eng 132:1254-1264.
• Shuo F, Jingqing J (2016) intelligence algorithm 3D sensor placement strategy using the full- range pheromone ant colony system. Smart Mater Struct 25:075003.
• Sohn H, Czarnecki JA, Farrar CR (2000) Structural Health Monitoring using Statistical Process Control. J Struct Eng 126:1356-1363.
• Sohn H, Farrar CR, Hemez F, Czarnecki J (2001) A Review of Structural Health Monitoring Literature 1996 - 2001. LA-UR-02-2095 1-7.
• Srinivas V, Antony Jeyasehar C, Ramanjaneyulu K (2013) Computational Methodologies for Vibration-Based Damage Assessment of Structures. Int J Struct Stab Dyn 13:1-27.
• Statnikov A, Aliferis CF, Hardin DP (2011) Gentle Introduction to Support Vector Machines in Biomedicine: Theory and Methods. World Scientific
• Sun H, Betti R (2015) A Hybrid Optimization Algorithm with Bayesian Inference for Probabilistic Model Updating. Comput Civ Infrastruct Eng 30:602-619. doi: 10.1111/mice.12142
  » https://doi.org/10.1111/mice.12142
• Sun Z, Chang CC (2004) Statistical Wavelet-Based Method for Structural Health Monitoring. J Struct Eng 130:1055-1062.
• Symeonidis A, Mitkas P (2005) DATA MINING AND KNOWLEDGE DISCOVERY : A BRIEF OVERVIEW. In: Agent Intelligence Through Data Mining. pp 11-40
• Tabrizian Z, Afshari E, Ghodrati G, et al (2013) A new damage detection method : Big Bang-Big Crunch ( BB-BC ) algorithm. Shock Vib 20:633-648.
• Taha MMR, Noureldin A, Osman A, El-Sheimy N (2004) Introduction to the use of wavelet multiresolution analysis for intelligent structural health monitoring. Can J Civ Eng 31:719-731.
• Talatahari S, Rahbari NM, Kaveh A (2013) A new hybrid optimization algorithm for recognition of hysteretic non-linear systems. KSCE J Civ Eng 17:1099-1108.
• Tang C, Chen H, Yen T (2003) Modeling Confinement Efficiency of Reinforced Concrete Columns with Rectilinear Transverse Steel Using Artificial Neural Networks. J Struct Eng 129:775-783.
• Tinoco J, Gomes Correia A, Cortez P (2014) Support vector machines applied to uniaxial compressive strength prediction of jet grouting columns. Comput Geotech 55:132-140.
• Trinh TN, Koh CG (2012) An improved substructural identification strategy for large structural systems. Struct Multidiscip Optim 19:686-700.
• Ubertini F, Comanducci G, Cavalagli N (2016) Vibration-based structural health monitoring of a historic bell-tower using output-only measurements and multivariate statistical analysis. Struct Heal Monit 15:438-457.
• Vafaei M, Alih SC, Baharuddin A, et al (2015) A wavelet-based technique for damage quantification via mode shape decomposition. Struct Infrastruct Eng 11:869-883.
• Vapnik V (1995) The nature of statistical learning theory. Springer-Verlag, New York
• Wang Z, Ong KCG (2010) Multivariate Statistical Approach to Structural Damage Detection. J Eng Mech 136:12-22.
• Wei C-C, Hsu N-S (2008) Derived operating rules for a reservoir operation system: Comparison of decision trees, neural decision trees and fuzzy decision trees.
• Wen CM, Hung SL, Huang CS, Jan JC (2007) Unsupervised fuzzy neural networks for damage detection of structures. Struct Control Heal Monit 14:144-161.
• Wu Z, Xu B, Yokoyama K (2002) Decentralized Parametric Damage Detection Based on Neural Networks. Comput Civ Infrastruct Eng 17:175-184.
• Xiao F, Fan C (2014) Data mining in building automation system for improving building operational performance. Energy Build 75:109-118.
• Xu B, Chen G (2007) Parametric Identification for a Truss Structure Using Axial Strain. Comput Civ Infrastruct Eng 22:210-222.
• Xu B, Song G, Masri SF (2012) Damage detection for a frame structure model using vibration displacement measurement. Struct Heal Monit 11:281-292.
• Yang Y, Nagarajaiah S (2014) Data Compression of Structural Seismic Responses via Principled Independent Component Analysis. J Struct Eng 140:1-10.
• Yao R, Pakzad SN (2014) Time and frequency domain regression-based stiffness estimation and damage identification. Struct Control Heal Monit 21:356-380.
• Yin T, Jiang Q, Yuen K (2017) Vibration-based damage detection for structural connections using incomplete modal data by Bayesian approach and model reduction technique. Eng Struct 132:260-277. doi: 10.1016/j.engstruct.2016.11.035
  » https://doi.org/10.1016/j.engstruct.2016.11.035
• Ying Y, Jr JHG, Oppenheim IJ, et al (2013) Toward Data-Driven Structural Health Monitoring: Application of Machine Learning and Signal Processing to Damage Detection. J Comput Civ Eng 27:667-680.
• Yiqiu T, Lei Z, Lun J (2012) Analysis of the Evaluation Indices from TSRST. J Mater Civ Eng 90:1310-1316.
• Yu L, Xu P (2011) Structural health monitoring based on continuous ACO method. Microelectron Reliab 51:270-278.
• Yu Z, Fung BCM, Haghighat F, et al (2011) A systematic procedure to study the influence of occupant behavior on building energy consumption. Energy Build 43:1409-1417.
• Yuen K-V (2010) Basic Concepts and Bayesian Probabilistic Framework. In: Bayesian Methods for Structural Dynamics and Civil Engineering. John Wiley & Sons (Asia) Pte Ltd, pp 11-98
• Zhang J, Sato T (2008) Experimental verification of the support vector regression based structural identification method by using shaking table test data. Struct Control Heal Monit 15:505-517.
• Zhang J, Sato T, Iai S (2007) Non-linear system identification of the versatile-typed structures by a novel signal processing technique. Earthq Eng Struct Dyn 36:909-925.
• Zhang Q, Kang Y, Zheng Z, Wang L (2013) Inverse Analysis and Modeling for Tunneling Thrust on Shield Machine.
• Zhang Y, Zhou GC, Xiong Y, Rafiq MY (2010) Techniques for Predicting Cracking Pattern of Masonry Wallet Using Artificial Neural Networks. J Comput Civ Eng 24:161-172.
• Zhong J, Xu T, Guan K, Zou B (2016) Determination of Ductile Damage Parameters Using Hybrid Particle Swarm Optimization. Exp Mech 56:945-955.
• Zhou HF, Ni YQ, Ko JM (2011) Eliminating Temperature Effect in Vibration-Based Structural Damage Detection. J Eng Mech 137:785-797.
• Zucconi M, Sorrentino L, Ferlito R (2017) Principal component analysis for a seismic usability model of unreinforced masonry buildings. Soil Dyn Earthq Eng 96:64-75. doi: 10.1016/j.soildyn.2017.02.014
  » https://doi.org/10.1016/j.soildyn.2017.02.014

Publication Dates

• Publication in this collection
  Dec 2017

History

• Received
  08 Aug 2017
• Accepted
  28 Aug 2017