Abstract
This paper presents results of the experimental study on the behavior of plain and fiber reinforced cement mortars with different fibers under static and impact compressive load. Glass, polypropylene and carbon fibers were used in equal dosage by mass. The impact test was conducted using an impact tower with drop hammer, which represented the modification of the split-Hopkinson pressure bar system, with strain rates ranging from approximately 35 to 60 s-1. The results of the static test and impact test with two different drop heights were compared and discussed. Among other, it has been concluded that the tested fiber reinforced mortars had no greater static and impact strength compared to the plain mortar. Only their ductility was increased at both static and impact failure. Strengths and ductility of all composite specimens were similar, i.e. without the effect of fiber type. With the increase of strain rate, compressive strength is increased and ductility is decreased for all tested specimens.
Keywords
fiber reinforced mortar; impact test; compressive strength; ductility; strain rate
1 INTRODUCTION
Fiber reinforced cement based composites have wide application all over the world. Different fibers are used in the cement based matrix, such as metallic, glass, polymer, carbon, mineral, organic, etc. In cement based composites, the main role of fibers is to improve the toughness and post-cracking performance of the matrix. The amount of fibers, elasticity modulus ratio of fibers and matrix, strength ratio of fibers and matrix, fiber dimensions and many other factors influence the performance of cement based composites before and especially after cracking.
Many experimental researches on the behavior of fiber reinforced mortar composites under static load have been performed. In general, these researches confirmed the efficiency of fibers in manner of the toughness and ductility at failure, and somewhat of tensile strength. Song et al. (2005) Song, P.S., Hwang, S., Sheu, B.C., (2005). Strength properties of nylon- and polypropylene-fiber-reinforced concretes. Cement and Concrete Research 35:1546-1550. investigated the strength potential of nylon-fiber-reinforced concrete versus that of the polypropylene-fiber-reinforced concrete. Fanella and Naaman (1985) Fanella, D.A., Naaman, A.E., (1985). Stress-strain properties of fiber reinforced mortar in compression. Journal of the American Concrete Institute 82:475-483. performed a comprehensive experimental program to show how the addition of steel, glass, monofilament polypropylene, and twisted polypropylene fibers in various volume fractions affected the compressive stress-strain curves of three mortar matrices. In general, the fibers delayed the crack propagation, thus producing an increase in the peak strain and the post peak ductility. Kim et al. (2008) Kim, D.j., Naaman, A.E., El-Tawil, S., (2008). Comparative flexural behavior of four fiber reinforced cementitious composites. Cement and Concrete Composites 30:917-928. investigated the flexural behavior of fiber reinforced cementitious composites (FRCC) with four different types of fibers and two volume fraction contents within a nominally identical mortar matrix. Chen and Chung (1996) Chen, P.-W., Chung, D.D.L., (1996). A comparative study of concretes reinforced with carbon, polyethylene, and steel fibers and their improvement by latex addition. ACI Materials Journal 93:129-133. compared mortars containing carbon, polyethylene, and stainless steel fibers at the same volume fraction and with similar fiber diameters in terms of tensile, compressive, and flexural properties.
Experimental researches on the behavior of fiber reinforced mortar composites under dynamic and especially impact load have been intensified recently. Herein, the split-Hopkinson pressure bar test (SHPB) has been used mostly. Many researchers confirmed the efficiency of fiber reinforced mortar composites compared to plain mortars in terms of increased ductility and toughness. Mansur and Aziz (1982) Mansur, M.A., Aziz, M.A., (1982). A study of jute fibre reinforced cement composites. International Journal of Cement Composites and Lightweight Concrete 4:75-82. tested cement composite specimens with varying jute fiber contents in direct tension, flexure, axial compression and impact. Naaman and Gopalaratnam (1983) Naaman, A.E., Gopalaratnam, V.S., (1983). Impact properties of steel fibre reinforced concrete in bending. International Journal of Cement Composites and Lightweight Concrete 5:225-233. studied the effects of strain rate of loading including impact on the bending properties of steel fiber reinforced mortar using an instrumented drop-weight impact machine. Zhou et al. (2013) Zhou, X., Ghaffar, S.H., Dong, W., Oladiran, O., Fan, M., (2013). Fracture and impact properties of short discrete jute fibre-reinforced cementitious composites. Materials and Design 49:35-47. conducted research on fracture and impact properties of short discrete jute fiber reinforced cementitious composites (JFRCC) with various matrix for developing low-cost natural fiber reinforced concretes and mortars. Wang et al. (2016) Wang, S., Le, H.T.N., Poh, L.H., Feng, H., Zhang, M.-H., (2016). Resistance of high-performance fiber-reinforced cement composites against high-velocity projectile impact. International Journal of Impact Engineering 95:89-104. performed experimental and numerical studies on the performance of seven high-performance fiber-reinforced cement-based composites against high velocity projectile impact. Zhang et al. (2016) Zhang, H., Liu, Y., Sun, H., Wu, S., (2016). Transient dynamic behaviour of polypropylene fiber reinforced mortar under compressive impact loading. Construction and Building Materials 111:30-42. investigated the dynamic characteristics and the constitutive relationship of polypropylene fiber reinforced mortar (PFRM) materials under compressive impact loading. The impact tests were carried out using an improved SHPB equipment installed with confining pressure device.
This paper presents results of the experimental study on the behavior of a mortar with and without fiber reinforcement under static and impact compressive load. Glass, polypropylene and carbon fibers have been used in the dosage of 1 kg per cubic meter of mortar. Equal fiber dosage in the mortar was adopted in order to compare their efficiency in the performed tests. The impact test was conducted using an impact tower, with a 4 kg drop hammer falling from two different heights. Test equipment and methodology were adopted to approximately simulate the SHPB test. The basic purpose of the conducted research, for the adopted four types of specimens, was to experimentally determine the following: (i) how can the adopted fibers increase static and impact compressive strengths and ductility of the plain mortar; (ii) what is the effect of a strain rate on the increase of strength and decrease of ductility of plain and fiber reinforced mortars; (iii) what is the difference between the considered fibers in terms of their efficiency.
2 TESTED COMPOSITE MORTAR SPECIMENS
Four different types of mortar specimens were tested (see Figure 1 ). The specimens were cast as cylinders with 50 mm diameter and 100 mm height. The specimen M was made of plain mortar. Other specimens were made of the same mortar in combination with different fibers. The specimen M-GF was reinforced with glass fibers, the specimen M-PF with polypropylene fibers and the specimen M-CF with carbon fibers. Herein, the equal fiber content of 1.0 kg per cubic meter of mortar was adopted for all specimens.
The mix design for 1 cubic meter of the fresh mortar is described below. Portland cement CEM I 42.5 N and stone powder (filler) were used as binder material in amount of 310 kg and 50 kg, respectively. A relatively high water cement ratio w/c = 0.5 was adopted, which is often used in practice for better compaction of a mortar. Limestone sand with maximal grain size of 2 mm was used in amount of 1734 kg. Superplasticizer BASF Glenium Sky 629 was used to enhance the flowability of the fresh mortar in dosage of 2 kg.
Adopted fibers are shown in Figure 2 , and their basic properties in Table 1 . The fibers used are the most available fibers in the Croatian market. The efficiency of fibers depends on their geometric and mechanical properties, therefore data in Table 1 will be commented below.
The diameter and length of a fibers influence the efficiency of their anchorage into a mortar under tensile force in them, as well as the workability of mortar. The ratio between diameter (d) of glass, polypropylene and carbon fibers is 1:2.27:0.47, and between their length (l) is 1:2:1. If the fiber has short diameter and greater length, its anchorage in mortar is better. The length/diameter ratio (l/d) for glass, polypropylene and carbon fibers is 400, 353 and 857, respectively. This indicates that the carbon fibers have the most beneficial geometry.
Previous consideration must be associated to tensile stresses in a fiber, i.e. to its tensile strength. Theoretically, the greatest possible tensile force in a fiber (F) is the product of fiber cross-section area and its tensile strength. Using the data in Table 1 , the greatest possible tensile force in glass, polypropylene and carbon fibers is 0.30, 0.45 and 0.16 N, respectively. If the linear distribution of shear stresses (τ) at the fiber-mortar contact is assumed, they should be calculated as τ = 2F/dπl. Taking into account the data for geometry and tensile forces in fibers, shear stresses for glass, polypropylene and carbon fibers should be 2.1, 0.7 and 2.4 MPa, respectively. It is obvious that the polypropylene fibers are the most efficient.
The adhesion between fibers and mortar has a significant effect on the fibers’ efficiency. Namely, the transmission of the shear force on the fiber-mortar contact surface depends on their adhesion. It depends on many factor, such as: fiber shape, surface roughness of fibers, fiber porosity and possibility of propagation of cement crystals into fibers, fresh mortar properties, admixtures, etc. Better adhesion between fibers and mortar is of interest, in order to transmit greater axial force on as much as shorter length of fibers. Metal fibers, which were not used in this research, are usually deformed through their length, or have hooks on their edges for more efficient anchorage into a mortar. Among the fibers used in this research, it is believed that polypropylene fibers have the best adhesion.
One key factor that influences the efficiency of fibers is the elasticity modulus. The elasticity modulus ratio of glass, polypropylene and carbon fibers is 1:0.05:3.3. If the static elasticity modulus is estimated at 15 GPa, the elasticity modulus ratio between fibers and mortar (n) for glass, polypropylene and carbon fibers is 4.8, 0.24 and 16, respectively. By assuming the compatibility of displacements for fibers and surrounding mortar, axial fiber stresses for certain mortar strain are n times greater than mortar stresses. Shear stresses occur at the fiber-mortar contact due to different values of elasticity modulus for the fibers and mortar. It is obvious that the polypropylene fibers are the most efficient due to their lowest elasticity modulus.
Also, another key factor is the break elongation of fibers. The break elongation for glass, polypropylene and carbon fibers is 2.4, 120 and 1.7% (see Table 1 ), respectively, i.e. their ratio is 1:50:0.71. It is obvious that the polypropylene fibers are more ductile than the glass and carbon fibers, i.e. they permit greater elongation of the mortar after cracking.
The bulk density (i.e. weight) of fibers has a certain influence on their distribution in the specimen after compaction (vibration) of the mortar. If fibers are heavier than mortar, they will tend to sink under vibrating. Glass fibers are slightly heavier than the mortar, while polypropylene and carbon fibers are lighter. The lowest density is of polypropylene fibers, which makes them most favorable.
Based on previous analysis of the used fibers, it can be expected that the polypropylene fibers will be more efficient in terms of bearing capacity and ductility than glass and carbon fibers.
The amount of fibers also has a great influence on compaction of the fiber-reinforced mortar, and especially for smaller specimens. By increasing the amount of fibers, the workability of the fiber-reinforced mortar is decreased. The adopted amount of fibers in the conducted study is high, which along with small specimen size made the composite mortars more inert and reduced their workability and compaction.
Mortars were mixed in a mixer for at least 300 seconds. Cement, filler, sand and half of the water were first mixed. Then, the remaining water, superplasticizer and fibers were added slowly to ensure full dispersion. After that, the fresh mortar was cast in 50×100 mm cylindrical and 40×40×160 mm prismatic moulds. The specimens were vibrated on the standard vibrating machine for two minutes. After twenty four hours, specimens were taken off the moulds and immersed in water at a temperature of 20 ± 2°C for 28 days, i.e. until the day of testing.
Volume distribution and orientation of fibers in the composite mortar also have a great effect on its strength and deformability under loading. Several specimens containing fibers were cut horizontally and vertically before static and impact tests in order to perform microscopic analysis. It was noticed that fibers were almost uniformly distributed by volume for all specimens, which confirms that mixtures were nearly homogenous and their casting into moulds was appropriate. It was also noticed that orientation of fibers was more horizontal than vertical, especially for longer polypropylene fibers, which is the result of tendency of fibers to take natural equilibrium position due to gravity. It was noticed that some polypropylene fibers were bended due to their greater length and lower bending stiffness in relation to the remaining adopted fibers. The previous statement was confirmed after inspection of the damaged specimens at the end of static and impact tests.
3 STATIC TESTS
Static tests included non-destructive ultrasonic pulse velocity test, compressive strength test and tensile strength tests by splitting and bending. Each of the tests was conducted on at least three specimens, and the following results are displayed as a mean value. Standard equipment was used for these tests, with common testing methods.
3.1 Ultrasonic pulse velocity test
First, the bulk density (ρ) of specimens was determined according to EN 12390-7 (2009) EN 12390-7:2009 Testing hardened concrete. Density of hardened concrete. European Committee for Standardization , and presented in Table 2 . The densities of fiber reinforced specimens are lower than of plain specimens. This is probably the result of their decreased workability and compaction, i.e. due to presence of greater amount of entrapped air in fresh fiber reinforced mortar specimens during casting.
Then, the ultrasonic pulse velocity test was performed according to EN 12504-4 (2004) EN 12504-4:2004 Testing concrete. Determination of ultrasonic pulse velocity. European Committee for Standardization . Ultrasonic pulse velocities (c) for specimens are given in Table 2 . The velocities are analogous to the bulk densities, i.e. the greatest velocity was for the plain specimen M. The ultrasonic pulse velocity ratio for specimens M, M-GF, M-PF, M-CF is 1:0.95:0.96:0.95. This test also confirms lower compaction of the fiber reinforced specimens than of plain specimen. Dynamic modulus of elasticity is calculated as Ed = c 2ρ, and presented in Figure 3 . The dynamic modulus of elasticity ratio is analogous to the density and pulse velocity ratios. Greater compaction of specimen M-PF compared to specimens M-GF and M-CF is also confirmed.
3.2 Compressive strength
Compressive strength of the specimens was tested according to EN 12390-3 (2004) EN 12390-3:2004 Testing hardened concrete - Part 3: Compressive strength of test specimens. European Committee for Standardization . Obtained results are shown in Table 2 and Figure 4 . The results show that static compressive strength of the plain mortar is greater than compressive strength of fiber reinforced mortars. Most researchers in their works noticed slightly greater strength of fiber-reinforced mortar compared to plain mortar (e.g. Ramli and Thanon Dawood (2011) Ramli, M., Thanon Dawood, E., (2011). High-strength flowable mortar reinforced by steel fiber. Slovak Journal of civil engineering 19:10-16. , Noushini et al. (2014) Noushini, A., Vessalas, K., Samali, B., (2014). Static mechanical properties of polyvinyl alcohol fibre reinforced concrete (PVA-FRC). Magazine of Concrete Research 66:1-19. , Bournas et al. (2007) Bournas, D.A., Lontou, P.V., Papanicolaou, C.G., Triantafillou, T.C., (2007). Textile-reinforced mortar versus fiber-reinforced polymer confinement in reinforced concrete columns. ACI Structural Journal 104:740-748. , Mobasher and Li (1996) Mobasher, B., Li, C.Y., (1996). Mechanical properties of hybrid cement-based composites. ACI Materials Journal 93:284-292. ). However, some researches show similar results as in this study (e.g. Pereira et al. (2015) Pereira, M.V., Fujiyama, R., Darwish, F., Alves, G.T., (2015). On the Strengthening of Cement Mortar by Natural Fibers. Materials Research-Ibero-American Journal of Materials 18:177-183. , Puertas et al. (2003) Puertas, F., Amat, T., Fernández-Jiménez, A., Vázquez, T., (2003). Mechanical and durable behaviour of alkaline cement mortars reinforced with polypropylene fibres. Cement and Concrete Research 33:2031-2036. , Kruszka et al. (2015) Kruszka, L., Mocko, W., Fenu, L., Cadoni, E. (2015). Comparative experimental study of dynamic compressive strength of mortar with glass and basalt fibres. DYMAT 2015 - 11th International Conference on the Mechanical and Physical Behaviour of Materials under Dynamic Loading , Chan and Bindiganavile (2010) Chan, R., Bindiganavile, V., (2010). Toughness of fibre reinforced hydraulic lime mortar. Part-1: Quasi-static response. Materials and Structures/Materiaux et Constructions 43:1435-1444. ). Lower compressive strength of the tested fiber reinforced mortars can be explained by their reduced workability and compaction due to greater amount of fibers and small dimensions of specimens. The compressive strength ratio for specimens M, M-GF, M-PF, M-CF is 1:0.90:0.95:0.91. Obtained slightly greater strength of the specimen M-PF compared to specimens M-GF and M-CF has confirmed the previous expectation that polypropylene fibers will be more efficient than glass and carbon fibers.
Stress-strain relationship of tested specimens under compression is shown in Figure 5 , where it can be noticed that fibers significantly increase ductility of the plain mortar. The strain ratio at failure for specimens M, M-GF, M-PF, M-CF is 1:1.4:1.6:1.3. Also, lower initial stiffness, i.e. lower modulus of elasticity of the fiber-reinforced mortars is noticeable compared to the plain mortar. This confirms that specimens with fiber reinforcement were less compacted than specimens without fibers.
3.3 Tensile splitting strength
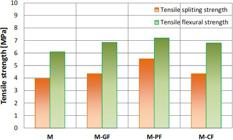
Tensile splitting strength of the cylindrical specimens was tested according to EN 12390-6 (2009) EN 12390-6:2009 Testing hardened concrete. Tensile splitting strength of test specimens. European Committee for Standardization . Obtained results are shown in Table 2 and Figure 6 . The tensile splitting strength ratio for specimens M, M-GF, M-PF, M-CF is 1:1.1:1.4:1.1. It is obvious that fibers increase tensile strength of the mortar, which was previously confirmed by many researchers. The specimen M-PF had the greatest tensile strength, which confirms that the polypropylene fibers were more efficient than the glass and carbon fibers.
3.4 Tensile flexural strength
Tensile flexural strength of the prism specimens was tested according to EN 12390-5 (2009) EN 12390-5:2009 Testing hardened concrete. Flexural strength of test specimens. European Committee for Standardization . Obtained results are shown in Table 2 and Figure 6 . Similar conclusions can be made as for the tensile splitting strength. The tensile flexural strength ratio for specimens M, M-GF, M-PF, M-CF is 1:1.12:1.18:1.11. The greatest tensile strength was for the specimen M-PF, which confirms the efficiency of the polypropylene fibers compared to the glass and carbon fibers.
4 IMPACT TEST
4.1 Impact test equipment
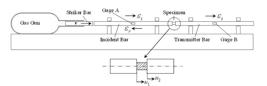
Impact tests with moderate and high strain rates (approximately 101/s – 104/s) were usually performed by the SHPB apparatus (see Figure 7 , taken from http://hrdg.matse.illinois.edu ). It consists of a gas gun, striker bar, incident bar, transmission bar, velocity-measuring device and data acquisition equipment. The striker bar, the incident and transmitted pressure bars are circular high-strength margin steel rods. The specimen was placed between the incident and transmitted bars. The strain gauges were mounted on the middle of the incident and transmission bars.
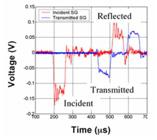
After an impact of the striker bar onto the end of the incident bar, a compression pulse propagates through the incident bar toward the specimen (see Figure 8 , taken from http://www.mecheng.osu.edu ). Once the wave reaches the specimen, it splits into two smaller waves. The transmitted wave travels through the specimen and the transmission bar. The other wave is reflected away from the specimen and returns through the incident bar. The strain gauges on the incident and transmission bars measure the strain duration and amplification in the bars. Data from the strain gauges is routed through amplifiers and an oscilloscope to a computer, where it is stored.
The engineering stress, strain rate and strain in the specimen can be calculated by:
where Ab, As are cross-sectional areas of incident and transmission bars, respectively; Ls is the length of a specimen; Eb is the Young’s modulus of pressure bars; c is the speed of an elastic wave in pressure bars; ε i, εr are the incident and reflected axial strains in the incident bar, respectively; and εt is the transmitted axial strain in the transmission bar (see Graff (1991) Graff, K.F. (1991). Wave Motion in Elastic Solids, New York: Dover Publications. ).
An impact tower was used for impact test in this research, within the Laboratory for static and dynamic testing of materials and structures at Faculty of civil engineering, architecture and geodesy (FGAG), at University of Split (see Figure 9 ). The apparatus used is analogous to the SHPB apparatus, where the impact force on the incident bar is achieved by drop mass (striker), and incident bar, specimen and transmission bar are in vertical position (see Figure 10 ). Soft deformable material (expanded polystyrene) is placed below the transmission bar to reduce the reverse impulse on the upper bars and the specimen as much as possible (to simulate the open loop system as in SHPB). The striker is a bar with 100 mm in length, 80 mm in diameter and with 4 kg of mass. The incident and transmission bars are 1000 mm in length and 60 mm in diameter, made of steel with Young’s modulus of E = 195 GPa. The contact between the specimen and two pressure bars was dry, as in the static test. Three strain gauges were placed at the middle of each pressure bar (HBM, type LY4, length 5 mm). A digital oscilloscope GW Instek GDS 3000 with amplifiers was used to record data from the mounted strain gauges to PC.
Specimens were tested by the drop of the striker from the height h = 4.5 m and h = 9 m, whereas the failure occurred for all specimens. Stress (compressive strength), strain rate and strain of the specimen were calculated according to equations (1) - (3) .
4.2 Impact test results
Only some results of the impact test are shown, with brief description below. Compressive strengths of the specimens, calculated based on the measured strains εi , εr and εt according to equation (1) , are shown in Figure 11 . Along with impact strengths for h = 4.5 m and h = 9 m, static compressive strength of the specimens are also presented. It can be noticed that impact strengths for all tested specimens were almost the same. Herein, the greatest impact strength was for the plain mortar specimen M, which was also established in the static test. For the height h = 4.5 m, the impact/static strength ratio (dynamic factor) for the specimens M, M-GF, M-PF, M-CF was determined as 1.46:1.52:1.48:1.53, respectively. For the height h = 9 m, the impact/static ratio for the specimens M, M-GF, M-PF, M-CF was determined as 1.65:1.72:1.69:1.74, respectively. Therefore, impact compressive strengths are greater than static strengths, where fibers had no practical influence on the compressive strength. The ratio between impact compressive strengths for the fiber-reinforced specimens is almost the same as for the static test.
Calculated strain rates of the specimens under impact according to equation (2) , based on the measured strains εi, εr and ε t, are shown in Figure 12 . The same analogy as for the impact compressive strengths in Figure 11 can be noticed. This is logical since greater strain rates permit greater strength of the material. The greatest achieved strain rates in the performed test for the drop height of 4.5 and 9 m were 44 and 62 s-1, respectively (moderate strain rates).
Calculated limit strains of the specimens under impact according to equation (3) , together with limit strains in the static test, are shown in Figure 13 . It can be noticed that limit strains in the impact test are significantly lower than limit strains in the static test. Herein, the strain in the specimen, i.e. its ductility, is reduced by increasing the drop height (strain rate). Among fiber-reinforced specimens, the specimens with polypropylene fibers M-PF had greatest strains. Similar to static test, fibers increase ductility of a mortar under impact.
The specimens had different failure patterns under impact. A camera record of some specimens before and after the impact is shown in Figure 14 . In tests with the drop height of 9 m, the specimens were more explosively crushed after impact than for tests with the drop height of 4.5 m. This is logical since greater impact force is generated from the greater drop height, and in short time interval. Compared to plain specimens M, fiber-reinforced specimens M-GF, M-PF and M-CF were crushed in smaller number of pieces after the impact. For the drop height of 4.5 m, some specimens with fibers remained almost in one piece. This is also logical since fibers increase tensile strength of the mortar and prevent its further fragmentation after impact.
Impact energy was dominantly absorbed by development of high non-linearities in the tested specimens, most resulting in damage of the specimens. Since absorbed energy under an impact with nonlinear behavior of the specimens is not directly measurable, its general term is often used. Adopted approach in this study, where vertical strains in the specimens are measured directly and stresses and strain rates are indirectly determined, gives more precise and clear response of the specimens’ states than the estimated absorbed energy under an impact. Since all tested specimens were destroyed during the tests, most of the impact energy was absorbed.
Under the compressive impact load, tested composite specimens with randomly oriented fibers M-GF, M-PF and M-CF experienced failure with complicated damage mechanism. It is interaction between different types of damage modes, such as mortar yielding in the direction of compression and cracking in the opposite direction, pulling and breaking of fibers, delamination, local effects, etc. Depending on the strain/load rate under an impact, mechanical properties of mortar and fibers change, which results in certain changes in the interaction of damage modes. Tested plain specimens M had somewhat more simple damage mechanism, which is related only to the cement matrix. Specimens with fibers had more ductile fracture than plain specimens, with significantly smaller pieces at decomposition under an impact (especially specimens with polypropylene fibers – see Fig. 14 ).
5 CONCLUSIONS
Based on the conducted experimental research on the behavior of plain and fiber reinforced mortars with different fibers (glass, polypropylene and carbon), in equal mass dosage, under static and impact compressive load, following conclusions can be brought.
Fiber reinforced mortar specimens were less compacted and showed lower density, ultrasonic pulse velocity and dynamic modulus of elasticity compared to plain mortar specimens. Fibers used have not increased the static compressive strength of the mortar, yet they have decreased it. The causes can be different: increased sluggishness and difficult compaction of the fiber reinforced mortar, small specimen size, fiber dosage, etc. This phenomenon was also noticed by researchers [13-20]. The fibers have significantly increased ductility of the mortar under static compressive failure, as well as both its splitting and flexural tensile strength. All fiber reinforced specimens had almost equal static compressive strength, ductility and tensile strength, whereas polypropylene fiber reinforced specimens showed best properties.
All specimens under impact load had greater compressive strength and lower strain (ductility) than under static load. Herein, the strength and strain ratios between tested specimens under impact were very similar to those under static test. Therefore, the plain mortar specimens had the highest impact strength, while fiber reinforced specimens had similar impact strength. By increasing the strain rate, compressive strength is also increased and compressive strain at failure is decreased.
Under an impact of the hammer of 4 kg mass from the 4.5 m height, the impact/static strength ratio (dynamic factor) was about 1.5 for all tested specimens. Herein, realized strain rates ranged from 35 to 42 s-1. The impact/static compressive strain ratio was about 0.73, which confirms significantly lower ductility of the specimens under impact.
Under an impact of the hammer of 4 kg mass from the 9 m height, the impact/static strength ratio was about 1.7 for all tested specimens. Realized strain rates ranged from 50 s-1 to 60 s-1 for all types of mortar specimens. The impact/static compressive strain ratio was about 0.62. Therefore, by increasing the strain rate of the mortar specimen, its strength is also increased and strain at failure is decreased.
Compared to the plain mortar specimens, fiber reinforced mortar specimens were crushed into small number of pieces under impact failure.
In general, tested fiber reinforced mortar specimens had lower static and impact compressive strengths compared to the plain mortar specimens. Only their ductility was significantly increased at both static and impact failure.
Compared to the plain unreinforced mortar, a composite mortar with fiber reinforcement is more expensive, its manufacturing process is more difficult, its static and impact strengths are not greater, while its both static and impact tensile strengths can be slightly greater. According to the above mentioned, it could be concluded that its practical application is unreasonable. However, the fiber reinforced mortar reaches far larger strains under compressive and tensile failure than the unreinforced mortar, i.e. it can ensure far more ductile behavior of a structure during exploitation and under failure. It ensures more favorable distribution on internal forces in the structure and increases its bearing capacity. The most practical significance of a fiber reinforced mortar than of unrefined mortar are its narrow cracks, which ensures homogeneity and continuity of a structure under failure. Fiber reinforcement is especially desirable since it narrows the width of cracks caused by often unpredictable strains from shrinkage and temperature changes. Therefore, the use of fiber reinforced mortar compared to unreinforced mortar if justified for structures under static, dynamic and impact load.
Further verification of the stated conclusions based on more extensive study with variation of many parameters (type, size, amount and mechanical properties of fibers, size and shape of specimens, mix composition and strength of basic mortar, compaction of the mortar, greater strain rates, etc.) is necessary.
References
- Bournas, D.A., Lontou, P.V., Papanicolaou, C.G., Triantafillou, T.C., (2007). Textile-reinforced mortar versus fiber-reinforced polymer confinement in reinforced concrete columns. ACI Structural Journal 104:740-748.
- Chan, R., Bindiganavile, V., (2010). Toughness of fibre reinforced hydraulic lime mortar. Part-1: Quasi-static response. Materials and Structures/Materiaux et Constructions 43:1435-1444.
- Chen, P.-W., Chung, D.D.L., (1996). A comparative study of concretes reinforced with carbon, polyethylene, and steel fibers and their improvement by latex addition. ACI Materials Journal 93:129-133.
- EN 12390-3:2004 Testing hardened concrete - Part 3: Compressive strength of test specimens. European Committee for Standardization
- EN 12390-5:2009 Testing hardened concrete. Flexural strength of test specimens. European Committee for Standardization
- EN 12390-6:2009 Testing hardened concrete. Tensile splitting strength of test specimens. European Committee for Standardization
- EN 12390-7:2009 Testing hardened concrete. Density of hardened concrete. European Committee for Standardization
- EN 12504-4:2004 Testing concrete. Determination of ultrasonic pulse velocity. European Committee for Standardization
- Fanella, D.A., Naaman, A.E., (1985). Stress-strain properties of fiber reinforced mortar in compression. Journal of the American Concrete Institute 82:475-483.
- Graff, K.F. (1991). Wave Motion in Elastic Solids, New York: Dover Publications.
- http://hrdg.matse.illinois.edu
» http://hrdg.matse.illinois.edu - http://www.mecheng.osu.edu
» http://www.mecheng.osu.edu - Kim, D.j., Naaman, A.E., El-Tawil, S., (2008). Comparative flexural behavior of four fiber reinforced cementitious composites. Cement and Concrete Composites 30:917-928.
- Kruszka, L., Mocko, W., Fenu, L., Cadoni, E. (2015). Comparative experimental study of dynamic compressive strength of mortar with glass and basalt fibres. DYMAT 2015 - 11th International Conference on the Mechanical and Physical Behaviour of Materials under Dynamic Loading
- Mansur, M.A., Aziz, M.A., (1982). A study of jute fibre reinforced cement composites. International Journal of Cement Composites and Lightweight Concrete 4:75-82.
- Mobasher, B., Li, C.Y., (1996). Mechanical properties of hybrid cement-based composites. ACI Materials Journal 93:284-292.
- Naaman, A.E., Gopalaratnam, V.S., (1983). Impact properties of steel fibre reinforced concrete in bending. International Journal of Cement Composites and Lightweight Concrete 5:225-233.
- Noushini, A., Vessalas, K., Samali, B., (2014). Static mechanical properties of polyvinyl alcohol fibre reinforced concrete (PVA-FRC). Magazine of Concrete Research 66:1-19.
- Pereira, M.V., Fujiyama, R., Darwish, F., Alves, G.T., (2015). On the Strengthening of Cement Mortar by Natural Fibers. Materials Research-Ibero-American Journal of Materials 18:177-183.
- Puertas, F., Amat, T., Fernández-Jiménez, A., Vázquez, T., (2003). Mechanical and durable behaviour of alkaline cement mortars reinforced with polypropylene fibres. Cement and Concrete Research 33:2031-2036.
- Ramli, M., Thanon Dawood, E., (2011). High-strength flowable mortar reinforced by steel fiber. Slovak Journal of civil engineering 19:10-16.
- Song, P.S., Hwang, S., Sheu, B.C., (2005). Strength properties of nylon- and polypropylene-fiber-reinforced concretes. Cement and Concrete Research 35:1546-1550.
- Wang, S., Le, H.T.N., Poh, L.H., Feng, H., Zhang, M.-H., (2016). Resistance of high-performance fiber-reinforced cement composites against high-velocity projectile impact. International Journal of Impact Engineering 95:89-104.
- Zhang, H., Liu, Y., Sun, H., Wu, S., (2016). Transient dynamic behaviour of polypropylene fiber reinforced mortar under compressive impact loading. Construction and Building Materials 111:30-42.
- Zhou, X., Ghaffar, S.H., Dong, W., Oladiran, O., Fan, M., (2013). Fracture and impact properties of short discrete jute fibre-reinforced cementitious composites. Materials and Design 49:35-47.
Publication Dates
-
Publication in this collection
2018
History
-
Received
27 June 2017 -
Reviewed
31 Jan 2018 -
Accepted
08 Feb 2018