Abstract
The behavior and response of pipelines subjected to slip fault movement is studied by numerical simulations as well as experimental setup. A finite element modeling is also developed via ABAQUS software. In this study, an artificial accelerogram is applied to the system and matched against the response spectrum according to the standard No. 2800 (Iranian code of practice for seismic resistant design of buildings, 2014). Three different pipe nominal sizes and thicknesses (1 ½”, 2” and 4”) are considered in the experiments on the shaking table. According to the results, plastic hinge as well as the extremum stress and strain is formed in the fixed soil wedge and at locations close to the fault line. Further, as the pipe D/t ratio increases, the plastic hinge forms further away from the fault line. According to the results, the pipe-soil strain ratio (εp/s) has lower values at larger pipe diameters. Also, the axial strains would be greater for the systems with higher (εp/s) ratios.
Keywords:
Dynamic analysis; Experimental; Pipe-soil interaction; Non-linear; Horizontally-bent pipe; Finite element; ABAQUS
1 INTRODUCTION
Earthquakes are a serious threat to infrastructures and facilities, including buried pipelines. Most of the damages in oil and gas pipelines due to earthquakes are caused by permanent ground displacement, because of near-surface fault rupture, landslides, settlements, and liquefaction-induced lateral spreading. It is evident that this could cause a significant environmental and safety disaster.
Vazouras et al. (2015Vazouras, P., Dakoulas, P., and Karamanos, S. A. (2015). Pipe-soil interaction and pipeline performance under strike-slip. Soil Dynamics and Earthquake Engineering, 72:48-75.) investigated the ground-induced actions on the buried pipes crossing strike slide-fault lines and evaluated the corresponding deformational and stress state of the pipeline. In another research, they examined the mechanical response of welded buried steel pipelines crossing active strike-slip seismic faults (Vazouras et al., 2010). The findings show that if the angle between the normal fault planes and the longitude and elongation of the pipeline is close to zero, the pipe will be subjected to buckling. At degrees over zero, the tensile strain would cause damages. In subsequent complementary studies, they assessed the soil interaction with the pipe, and pipeline behavior subjected to slide fault line. They suggested a method to determine the pipe functionality subjected to slide fault line based on longitude pipeline axis via closed-form solution. The results obtained from applying a non-linear force-displacement equation were in line with finite element analysis. In the finite element analysis, the pipe was considered as a beam and the soil as a spring along with it. Applying the closed-form solution indicates that the parameters affecting the magnitude of pipe longitudinal strain during the pipe axial tensile test consist of pipe displacement, pipe connection shear strength, and pipe length. Here, it is observed that the soil stiffness has no significant effect on pipe longitude strain volume.
The pipe boundary conditions were assessed by Vazouras et al. (2012Vazouras, P., Karamanos, S. A., and Kakoulas, P. (2012). Mechanical behavior of buried steel pipes crossing active strike-slip faults. Soil Dynamics and Earthquake Engineering, 41:164-180.), wherein two pipes with limited and unlimited ends were subjected to different tensile loads. The results indicate that the pipes subjected to the above conditions with no angle exhibit local strain in minor displacements. By increasing the fault displacement rate, ovalization phenomena occurs in the local strain spot. For the faults with more than 10 degrees, due to the introduction of tensile force in the pipe, no buckling occurs; which implies a better pipe function and pipe tolerance in resisting more fault displacements. By increasing the fault angle and the tensile force, critical fault movement is reduced along with the pipe through the length.
G. Banushi et al. (2018Banushi, G., Nunziante, S., and Klaus, T. (2018). Innovative analysis of a buried operating pipeline subjected to strike-slip fault movement. Soil Dynamics and Earthquake Engineering, 107:234-239.) studied buried pipelines crossing a strike-slip fault as a parametric analysis. They use the continuum modeling approach, and the contact surfaces of both soil and pipe were meshed with a similar mesh size which will cause better solution convergence. Moreover, they have used higher resolution mesh grids on the limited parts which are vulnerable to local buckling. Therefore, it allows the assessment of the critical fault displacements formed due to the performance limit state, precisely. The numerical model results are compared with the reported data in the literature as well as analytical solutions. It is claimed that the developed model gives a better understanding of the mechanical behavior of soil-pipeline system under strike-slip faulting.
Zhang et al. (2015Zhang, J., Liang, Z., Han, C. J., and Zhang, H. (2015). Numerical simulation of buckling behavior of the buried steel pipeline under reverse fault displacement. Mechanical Sciences, 6(2):203-210.; 2016) investigated buckling behavior of the buried pipeline by finite element method. They showed that fault displacement has a small effect on the maximum strain position of the buried pipeline and the deformation curve of the buried pipeline was smoother as the wall thickness increases.
Shakib and Zia (2004Shakib, H., and Zia, T. R. (2004). Response of steel buried pipelines to three-dimensional fault movement by considering material and geometrical non-linear arities. 13th World Conference on Earthquake Engineering, Vancouver, Canada.) analyzed the results of the buried pipes subjected to fault movement in three-dimensional geometry and non-linear material. They proportioned the pipes into three sections, and each section is considered a beam element. The soil surrounding the pipe is considered a non-linear equivalent spring. The fault is assumed to be in a diagonal form. The results here indicate that the greater the fault displacement rate, the greater the effect along the pipe length, and a reduction in depth increases pipe-soil load bearing tolerance. An increase in the degree of soil internal friction, increases pipe’s soil load bearing tolerance.
A buried gas pipeline behavior, crossing slide fault line was assessed by Ghaznavi and Vatani Oskouei (2017Ghaznavi, O. A., and Vatani Oskouei, A. (2017). The Effect of P-Wave Propagation on the Seismic Behavior of Steel Pipelines. Periodica Polytechnica Civil Engineering, 61(4):889-903.) via the finite element method. In this work, material properties with elastoplastic behavior for pipe and soil, and the soil-pipe interactions were considered. The non-linear static analyses of ground displacement were run on the constructed models and the parametric studies were run on pipe diameter, wall thickness, soil type and fault displacement rate. According to the results, the pipe wall local buckling occurred at compressive strain region. In soft soils, the possibility of pipe deformation was higher, while in the dense soils, the possibility of critical pipe displacement was lower. Therefore, the supports with high resistance against deformation were applied on both sides of the fault line. Due to higher soil rigidity on the buried pipe in all three dimensions, larger displacements would have a stronger effect on pipe response.
Cavaco et al. (2018Cavaco, M.A.M., Viotti, M. R., and Albertazzi, Jr. G.A. (2018). Pipeline stress analysis through stress function fittings. Latin American Journal of Solids and Structures, 15(9), e92:1-11.) performed stress analysis in pipes due to soil-pipe interaction through a hybrid experimental technique. They presented coefficients for stress functions using data fitting. The results show that the model could be used roughly for stress analysis of bended pipes.
The stress and strain of the buried pipes crossing slide-fault lines were investigated by Karamitros et al. (2007Karamitros, D., Bouckovalas, G., and Kouretzis, G. (2007). Stress Analysis of Buried Steel Pipelines at Strike-Slip Fault Crossings. Soil Dynamics & Earthquake Engineering, 27:200-211.) analytically. They applied the equilibrium and displacements adaptation equations to obtain the axial forces inflicted on the pipe. By applying a combination of beam equations on bending subgrade and elastic beam theory, they calculated the inflicted bending momentum. Here, the non-linear matter and non-linear geometry features were indirectly involved in the calculations and by applying the real stress distribution at pipe cross-section, the maximum strain was designed and calculated.
Trifonov and Cherniy (2012Trifonov, O. V., and Cherniy, V. P. (2012). Elastoplastic stress-strain analysis of buried steel pipelines subjected to fault displacements with account for service loads. Soil Dynamics and Earthquake Engineering, 33:54-62.) conducted a study on the modeling of stress-strain of buried steel pipelines exposed to active fault displacements. They also considered the internal pressure and temperature changes. The interactions between pipe and the surrounding soil were included in the modeling in the axial and transverse directions and using bilinear soil springs. The validation and verification of the developed model were carried out by comparing the solutions and the numerical results obtained from beam-type and shell-type models in the finite-element software ANSYS 12.1. According to the results, applying 2D elastoplastic approach in the analytical model of pipeline in active fault crossings are in line with the obtained numerical results from the finite-element model for different conditions and fault intersection angles.
Trifonov (2015Trifonov. O. V. (2015). Numerical stress-strain analysis of buried steel pipelines crossing active strike-slip faults with an emphasis on fault modeling aspects. Journal of Pipeline Systems Engineering and Practice, 6(1):1-10.) in another research, developed an advanced numerical model of pipelines crossing active faults by considering the pipeline as set of shell or solid finite elements. Their advanced model provides a rigorous stress-strain state analysis including the local limit states. In their work, a 3-D numerical model is represented for buried steel pipeline crossing an active tectonic fault focusing on the pipeline-soil interactions and mathematical modeling of the fault. The developed model will predict the values of displacement, strain and contact soil pressure distributions, evolution of the pipe ovalization parameter and bending moment in the critical cross section, and soil deformations in the near-fault zone.
The soil-pipe interaction with regard to the longitude and latitude of pipe orientation was expanded by Kennedy and Chow (2007Kennedy, P. R., and Chow, W. A. (2007). Fault movement effects on buried oil pipeline. ASCE Journal of Transportation Engineering, 103: 617-633.) where the bending stiffness was of concern. They introduced a simple method for obtaining the maximum strain in pipes crossing the fault line where the non-linear features of material and geometry were of concern.
In a laboratory experiment, Rofooei et al. (2012Rofooei, F. R., Attari, K. N., and Alavi, M. (2012). Full-Scale Experimental Testing of Buried Pipelines Subjected to Permanent Ground Displacement Caused by Reverse Faulting, 15th World Conference on Earthquake Engineering, Lisbon, Portugal.) assessed the buried pipe response subjected to normal fault movement. This movement was perpendicular to the pipe, and it changes the direction in the vertical orientation; thus, it causes stress and strain at the pipe wall. The modeling of the soil-pipe system was performed through an accurate implementation of finite elements where large displacements and non-linear material behavior were of concern. They ran the test on clayish-soil in low and high-density states and studied the effect of pipe diameter to wall thickness ratio, pipe internal pressure and the soil type on the pipe response. The obtained results indicate that the damages on the pipe wall were in local strain form. By reducing the pipe diameter to wall thickness ratio, and in the softer soil, the deformation tolerance increases. Also, the pipe will endure larger displacements while the critical strain and buckling will increase as well.
Rofooei et al. (2018Rofooei, F. R., Attari, K. N., and Hojat, J. H. (2018). New method of modeling the behavior of buried steel distribution pipes subjected to reverse faulting. Journal of Pipeline Systems Engineering and Practice, 9(1):1-14.) in another research proposed a new method for modeling of buried steel pipes behavior under reverse faulting. The suggested method was verified using the results of four real-scale experimental tests and finite-element modeling of 4 and 6 inch buried steel gas pipelines. Two soil types (SW and SM) were considered in the modeling. The finite element model takes into consideration the non-linearity effects of geometry and materials as well as soil-pipe interactions. All pipes show a S-shaped deformation pattern with two diamond-shaped buckled sections which represent severe plastic deformation and yielding. The obtained results show that the ovality increases with increasing (D/t) ratio and soil friction angle.
Sayar, M et al. (2016Sayar, M., Ni. P., and Take, W. A. (2016). Response of pipelines of differing flexural stiffness to normal faulting. Journal of Géotechnique, 66(4):275-286.), concentrated their research on the pipeline response against opposing flexural stiffness to normal faulting. Four centrifuge test results were utilized on modeling the pipelines to quantify the flexural response against normal faulting of different pipeline stiffness values.
The response of the pipe subjected to inverse-fault movement with regard to different displacement volumes, different soil conditions, and different inverse fault degrees was assessed in Tarinejad et al. (2012Tarinejad, R., Mahdavi, A., and Jahangir, N. (2012). Buried Pipeline Response Analysis to Reverse-Slip Fault Displacements. 15th World Conference of Earthquake Engineering, Lisbon, Portugal.)’s research. Four types were assigned fora non-coherent state soil. The pipe behavior with regard to inverse fault of different angles (30°, 45°, and 60°) was studied. When the upper wall wedge moves downwards, the fault is normal, and its movement would cause force and stress on the pipe axis. In this research, plastic strain locations along the pipeline, critical fault displacements due to the local buckling or rupture of the pipe wall were obtained by numerical analyses for different cases.
O’Rourke et al. (2009O’Rourke, M. J., Abdoun, T. H., Ha, D., and Symans, M. D. (2009). Factors influencing the behavior of buried pipelines subjected to earthquake faulting. Soil Dynamics and Earthquake Engineering, 29(3):415-427.) and Xie et al. (2011Xie, X., Symans, M. D., O’Rourke, M. J., Abdoun, T. H., O’Rourke, T. D., Palmer, M. C., and Stewart, H. E. (2011). Modelling of Buried HDPE Pipelines Subjected to Strike-Slip Faulting. Journal of Earthquake Engineering, 15(8):1273-1296.) assessed the mechanical behavior of polyethylene pipeline which crosses the slide-fault line in different soil conditions. They analyzed the direct effect of increasing the soil stiffness and increasing the soil-pipe interactions and the stresses in the pipe.
In the study of Yimsiri et al. (2004Yimsiri, S., Soga, K., Yoshiaki, K., Dasari, G. R., and O’Rourke, T. D. (2004). Lateral and Upward Soil-Pipeline Interactions in Sand for Deep Embedment Conditions. Journal of Geotechnical and Geoenvironmental Engineering, 130: 830-841.) on the sandy soil-pipe reactions, Mohr-Coulomb models were applied to the equations to improve the buried pipe modeling. Pipe deformation in a laboratory set up corresponds to the finite element model to an acceptable limit. The analysis is further extended to deeper embedment ratios of as large as 100. The obtained finite element results are used to construct a design chart for deep embedded pipelines.
In this research, the behavior of horizontally-bent buried pipes along fault slip was investigated experimentally and numerically. Different pipe specifications (diameter and wall thickness) as well as soil properties were considered. In addition, the failure mechanisms, deflection of pipes, inflation and deflation of the soil surface, strain and stress changes were studied through the developed model.
2 EXPERIMENTAL MODEL PREPARATION
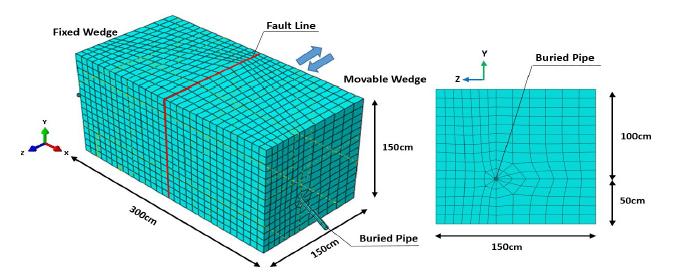
A shaking table which consists of two steel boxes (one fixed and the other movable) equipped with an actuator concerning earthquake acceleration record was utilized in the experiments, Figure 1. The outer sides of both boxes allow pipe layout at specific heights and coordinates.
A 2.0 cm free distance was considered between the fixed and movable boxes to prevent any frictional resistance between the boxes during the tests. For horizontal loading of the system, a rigid steel frame equipped with an appropriate jack for exerting the required force on the movable box was provided, Figure 2.
The dimensions (L, W and H) of both movable and fixed cubical boxes were 150 cm. The pipe entrance and exit sides were of steel plate with 16 × 8” holes, to allow pipe placement, Figure 3.
To measure the strain values, multiple strain gauges were mounted on the pipes. The LVDT devices were provided at the pipe inlet and outlet for recording the displacements. Moreover, a digital ruler was applied for measuring the movable box displacement compared to the fixed one. A load cell with a capacity of 50-ton force was provided on the movable box, Figure 4.
Location of the installed strain-gauges, LVDTs, load cell and digital ruler on the steel pipe.
The outputs of strain gauges, LVDTs, digital ruler and load cell were collected through a data logging system.
The pipe type was of API-5L-X55(2000) with 2.1×106 kg/cm2 module, steel density of 7850 kg/m3 with 0.3 Poison’s ratio. The pipes’ length was 4.0 m with different diameters and thicknesses, Table 1.
To accurately assess the pipe behavior, the steel strain test was ran according to the standard ASTM-D638-14 (2014) and the elastoplastic behavior of pipe was determined in Figure 5.
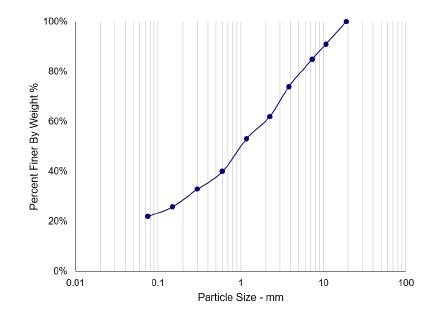
The subject soil was of SC (sandy clay with some gravel) type to provide a semi-elastic bed according to the sieve-analysis, Figure 6.
Considering the tests performed (ASTM-D422-90, 2014), the soil properties were characterized as follows: soil cohesion factor c =0.12 kg/cm2, and the friction angle φ=28°, and density γ=1950 kg/m3.
After the strain gauges have been installed on the pipes, the system was buried at a depth of 1.0 m. The soil was compacted every 30 cm layers to achieve the appropriate soil density either in upper and lower layers around the pipe (up to 95% compaction). The buried pipes were of 137°, Figures 7 and 8.
The final layer of the soil was meshed on the surface at 10 cm intervals to allow better observation and measurement of deformations after it becomes subject to loading, Figure 9.
To apply the input load, an artificial accelerogram was used. This accelerogram (IAR) is matched to the response spectrum via Seismo-Artif (2018) software and in compliance with the standard No. 2800 (Iranian Code of Practice for Seismic Resistant Design of Buildings, 2014), Figure 10.
The displacement, velocity and acceleration behavior corresponding to the accelerogram (IAR) versus time are obtained in Figure 11.
The recording of acceleration, velocity, and displacement corresponding to IAR accelerogram.
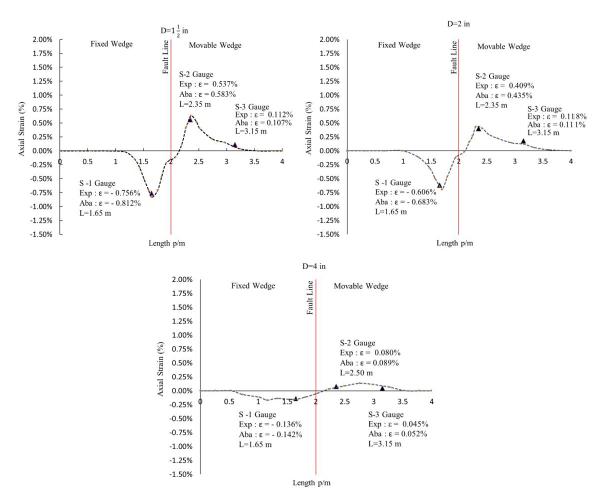
It is performed by the actuator which exerts pressure on the moving box, and the outputs of the displacements and strains are recorded through a data logging system. The strain values through the strain gauges and recorded displacements through LVDTs and digital ruler are obtained for the pipes with diameters of 1½”, 2” and 4”. The maximum strain at location S-1 is shown in Figure 12.
The recorded strain of S-1 about fault displacement for pipes of 1½”, 2” and 4” diameters.
According to the strain-displacement diagrams, the incremental level of strains has a reverse relationship with the pipe diameter. As observed, an increase in pipe diameter and thickness, leads to decrease in strains: for 4” pipe the maximum recorded strain was 0.136%, for 2” pipe the maximum recorded strain was 0.606% and for 1½” pipe the maximum recorded strain was 0.756%. Since the diameter of 1½” and 2” pipes are close, they show slightly similar behavior. The 4” pipe due to more rigidity, has a lower strain value compared to the other two pipes. The strain-force diagrams of the abovementioned tests at interaction points of strain gauge S-1, S-2, and S-3 are represented in Figure 13, 14, and 15 in terms of µε.
Figure 13, 14 and 15 reflects the pipe strain changes (recorded via strain gauges S-1, S-2, and S-3) with force recorded by the load cell. According to the results, the changes in Figure 14 and 15 were similar but different in Figure 13 which indicate the different force-strain response of the pipe in the movable wedge. For all the pipes, the strain-force diagram on strain gauges S-1 and S-2, showed symmetrical and almost same values. It was because of identical distance of strain gauges from the fault line, as well pipe reverse behavior in fixed and movable wedges.
3 NUMERICAL MODELING
Finite element is applied in ABAQUS software for 137° horizontally-bent pipes to obtain numerical results for comparison with the experimental data (ABAQUS, 2017 version). To increase the accuracy and the sensitivity of the analysis, Four-node reduced-integration shell elements (type S4R) were employed for modeling the cylindrical pipeline segment, and eight-node reduced-integration “brick” elements (C3D8R) were used to simulate the surrounding soil. The geometric specifications of the pipes, loading boxes’ diameters, mechanical specifications of the soil properties and pipe types and loading records were the same as the ones applied in the experimental testing. The soil media is meshed in both wedges with a maximum 15 cm mesh length and HEX element shape. Also, the perimeter of the pipe cross-section is divided into 12 nodes with QUAD element shape, Figure 16. The bottom surface of the fixed wedge is restrained, and the movable wedge only can move in the Z-direction.
Furthermore, the mechanical behavior of soil material is described through an elastic-perfectly plastic Mohr-Coulomb constitutive model, characterized by the cohesion c=0.12 kg/cm2, the friction angle φ=28˚, the elastic modulus E=410 kg/cm2, and Poisson’s ratio ν=0.35. The dilation angle ψ is assumed to be zero for all cases considered in this paper.
The interface between the outer surface of the steel pipe and the surrounding soil is simulated with a contact algorithm, which allows separation of the pipe and the surrounding soil, and accounts for interface friction, through an appropriate frictional coefficient µ. In the majority of results reported in the present study, the value of µ is considered equal to 0.32. Moreover, hard-contact behavior model is considered for modeling of soil-pipe interactions.
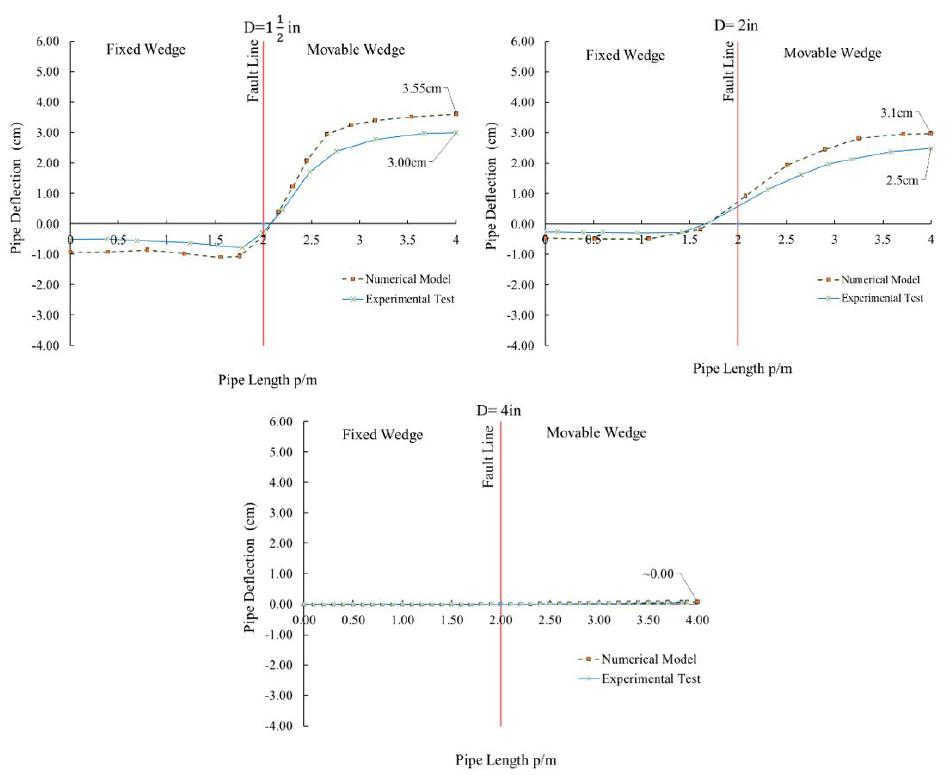
Considering the dynamic inputs, the dynamic explicit analysis method is used in the software modeling. In the modeling, it is assumed that first, the soil gravity load is applied to the pipe and then the dynamic load is exerted to the soil movable wedge as a ground displacement-time history according to Figure 11. The experimental and numerical model results for axial strain in different pipe sizes are shown in Figure 17.
As observed, an acceptable approximation of error (7.8%) in the recorded strain values are in accordance with the numerical model results. The plastic strain and equivalent plastic strain along the pipe length at seismic peak obtained from the numerical model are shown in Figure 18.
The pipes’ plastic strain and equivalent plastic strain at seismic peak for the three subject pipes.
The 1½” pipe had a greater strain value due to the lower rigidity in comparison to the other two pipe diameters. The strain was adjacent to the fault line in the fixed box. Table 2 represents the soil shear strain and axial strain values for different pipe diameters and both soil wedges.
In table 2:
FW: Fixed wedge.
MW: Movable wedge.
εp/s: Pipe-soil strain ratio.
The results show that pipe-soil strain ratio (εp/s) decreases with increase in the pipe D/t ratio in both soil wedges. For the cases with higher pipe-soil strain ratio (εp/s), the pipe resistance against soil displacement was much lower and the pipe-soil system acts as a cohesive system displacement which causes more pipe vulnerability and more severe damages.
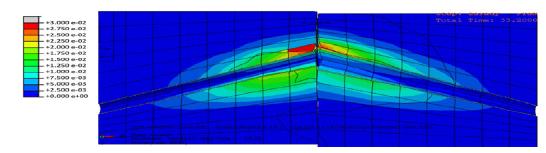
According to the obtained results from the numerical analysis on the subject pipes, the highest level of shear strain in soil was observed at soil-pipe interface close to the fault line, Figure 19. This issue shows that pipe displacement in soil was the most effective factor in soil deformation. The highest level of Von-Mises stress in soil was on 1½” pipe (0.69 MPa), which occurs at the earthquake peak. The maximum stress value corresponds to the pipe axial compressive stress as 4486 kg/cm2 which is close to the pipe ultimate stress. In addition, the maximum axial tensile stress was 4428 kg/cm2. In this model, shear stress was 2288 kg/cm2 which is lower than yield stress. Consequently, the damage mechanism in such pipes was subject to the axial compressive force and local buckling formation.
In this modeling, the maximum Von-Mises stress value of 2” pipes in the soil was 0.55 MPa. For more than 80% of the soil, stress values of less than 0.25 MPa are achieved. The shear strains in soil occur only around the pipes near the fault line, Figure 20.
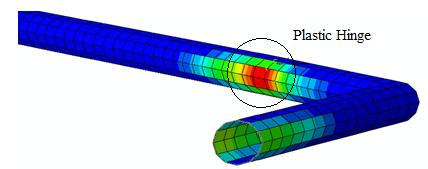
As shown in Figure 21, the pipe at critical point, is where plastic hinge is formed close to the fault line and reached to the yield point. By analyzing the ABAQUS outputs, it was found that the axial tensile stress was 4272 kg/cm2 and the shear stress was 2174 kg/cm2, indicating that the pipe has not reached the yield point. It implies that the shear stress was within the pipe elasticity area. The maximum stress value corresponds to the axial compressive pipe stress as 4318 kg/cm2. Similar to the 1½” pipe, the damage mechanism in such pipes was subject to the axial compressive force and local buckling formation.
According to the 4” pipe model, the maximum Von-Mises stress level of soil was 0.32 MPa. In this model, more than 70% of the soil has a stress less than 0.15 MPa. The soil shear strain occurs only close to the fault line, indicating soil deformation due to soil displacement, Figure 22.
In this model, the axial tensile stress and the axial compressive stress were 3443 and 3487 kg/cm2, respectively; which were observed only in a small segment of the pipe. The shear stress was 1794 kg/cm2 and within the elastic range without yield level. As observed in all the cases, the shear stress values are in the elastic zone.
The shear strain in the soil surrounding the 4” pipes is more extensive compared to 2” and 1½” pipes; because the pipe with higher thickness and diameter is able to make more deformations in soil.
Soil inflation occurred due to pipe buckling which is proportional to the pipe diameter; thus, the larger the pipe diameter, the more inflation in the soil. In larger pipe diameters, more pressure is exerted on the soil and causes an upward displacement. The inflation and deflation of the soil surface were +76 mm and -88 mm at numerical results and +60 mm and -75 mm at experimental tests.
This phenomenon can be attributed to the fact that the soil compaction is assumed as ideally uniform in finite element model, while it is non-uniform in realistic experimental conditions. The numerical results indicate that the pipes with different bend angles can cause the upward displacement in different directions. According to Table 3, inflation and deflation of soil surface in 4” buried pipes decrease with increase in the horizontal bend angle.
According to the 4” pipe model, pipe displacement in any direction inflates soil upwards. Moreover, because of the horizontal bend in the pipe, the head points are not aligned with the soil wedge axes, which causes displacement of other soil sections as well as the middle section. The soil inflation in the experimental model is shown in Figure 23. The deformations in the soil upper layer, were measured after implementing dynamic loads. For 1½” and 2” pipes, the inflation and deflation was insignificant.
Measured deformations of 1½” pipe in experimental test were 30 mm at the pipe (35 mm numerical) and 5 mm at the starting point (10 mm numerical). This deformation for 4”, 2” and 1½” pipes is shown in Figure 24.
According to Figure 21, it is observed that deformations in 2” and 1½” pipes have S-curve behavior and the values are closed. Also, for 4” pipe, the deformation values are much lower and could be neglected.
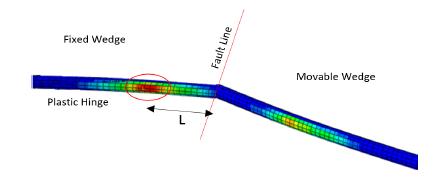
The distance between the location of the plastic hinge formation point and the corresponding fault line is an important parameter to determine the index of the pipe damage mechanism, Figure 25.
To ensure that the pipes comply with API standard with different diameters (API, 2000), the dynamic analysis was subjected to IAR accelerogram, Table 4.
The distance of plastic hinge occurrence point from fault line for pipes of different diameters.
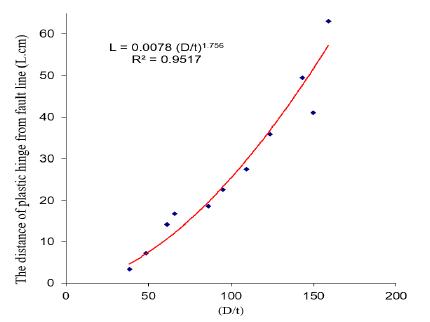
According to the results obtained from numerical modeling as presented in Table 4, the locus of plastic hinge formation could be fitted to the pipe characteristics (D/t) as shown in Figure 26. No plastic hinge formation was observed for the pipes with (D/t) ratios higher than 160 exposed to the dynamic loading.
Diagram of the distance of plastic hinge occurrence point for fault line with regard to pipe D/t.
The result data is fitted to power equation with an acceptable regression error, Equation (1).
It shows with increasing D/t ratio, the plastic hinge would be formed further from the fault line.
4 CONCLUSION
In this research, the behavior of horizontally-bent pipes was studied experimentally based on applying an artificial acceleration record. Also, the behavior of the system was modeled numerically (finite elements method) via ABAQUS software, and failure mechanisms of horizontally-bent buried pipes were determined. The main achievements could be summarized as follows:
Results show good agreement between the test outputs and ABAQUS models in terms of the axial strains, deformation shapes and inflation/deflation of soil surface in pipes with 4”, 2” and 1½” diameters.
The deformation in the models reduces as the D/t ratio increases due to pipe rigidity.
Due to the higher rigidity of the 4” pipe compare to 2” and 1½” pipes, it displaces the soil along the pipe by changing the location of the plastic hinge from the fault line to a point closer to the pipe head within the soil fixed wedge.
According to Equation (1) with increasing D/t ratio, the plastic hinge would be formed further from the fault line.
The soil inflation/deflation for a specific pipe diameter would decrease with increase in the pipe horizontal bend angle.
According to the 4” pipe results, pipe displacement in any direction inflates the soil upwards. Moreover, because of the horizontal bend in the pipe, the head points are not aligned with the soil wedge axes, which causes displacement of other soil sections as well as the middle section.
It is observed that deformations in 2” and 1½” pipes have S-curve behavior and the values are closed. Also, for 4” pipe, the deformation values are much lower and could be neglected.
The pipe-soil strain ratio parameter (εp/s) would be higher in the cases with lower D/t ratio; thus, due to the low resistance of pipe against the soil displacement, the pipe-soil system acts as a cohesive system. Therefore, the soil displacements are transferred to the pipe which make it more vulnerable and causes severe damages.
The shear strain in the soil surrounding the 4” pipes is more extensive compared to 2” and 1½” pipes; because the pipe with higher thickness and diameter is able to make more deformations in soil.
In the pipes with larger diameter, the shear strain values in the pipe-soil interface are lower, because the force is exerted to a larger surface area.
Almost in all the models, the maximum compressive stress is greater than the maximum tensile stress. Hence, the most probable damage mechanisms in these pipes are local and axial buckling.
References
- ABAQUS, C. (2017). Analysis user’s manual, Version 2017.
- API (2000). Specification for Line Pipe, API Specification 5L, Forty-Second Edition, American Petroleum Institute; 1220 L St NW, Washington, DC 20005, USA.
- ASTM- D368-14 (2014). Standard test method for tensile properties of plastics, American Society for Testing and Materials,1850 M Street, NW Suite 1030, Washington, DC 20036, USA.
- ASTM- D422-90 (2014). Standard test method for particle-size analysis of soils, American Society for Testing and Materials, 1850 M Street, NW Suite 1030, Washington, DC 20036, USA.
- Banushi, G., Nunziante, S., and Klaus, T. (2018). Innovative analysis of a buried operating pipeline subjected to strike-slip fault movement. Soil Dynamics and Earthquake Engineering, 107:234-239.
- Cavaco, M.A.M., Viotti, M. R., and Albertazzi, Jr. G.A. (2018). Pipeline stress analysis through stress function fittings. Latin American Journal of Solids and Structures, 15(9), e92:1-11.
- Ghaznavi, O. A., and Vatani Oskouei, A. (2017). The Effect of P-Wave Propagation on the Seismic Behavior of Steel Pipelines. Periodica Polytechnica Civil Engineering, 61(4):889-903.
- Karamitros, D., Bouckovalas, G., and Kouretzis, G. (2007). Stress Analysis of Buried Steel Pipelines at Strike-Slip Fault Crossings. Soil Dynamics & Earthquake Engineering, 27:200-211.
- Kennedy, P. R., and Chow, W. A. (2007). Fault movement effects on buried oil pipeline. ASCE Journal of Transportation Engineering, 103: 617-633.
- O’Rourke, M. J., Abdoun, T. H., Ha, D., and Symans, M. D. (2009). Factors influencing the behavior of buried pipelines subjected to earthquake faulting. Soil Dynamics and Earthquake Engineering, 29(3):415-427.
- Rofooei, F. R., Attari, K. N., and Alavi, M. (2012). Full-Scale Experimental Testing of Buried Pipelines Subjected to Permanent Ground Displacement Caused by Reverse Faulting, 15th World Conference on Earthquake Engineering, Lisbon, Portugal.
- Rofooei, F. R., Attari, K. N., and Hojat, J. H. (2018). New method of modeling the behavior of buried steel distribution pipes subjected to reverse faulting. Journal of Pipeline Systems Engineering and Practice, 9(1):1-14.
- Sayar, M., Ni. P., and Take, W. A. (2016). Response of pipelines of differing flexural stiffness to normal faulting. Journal of Géotechnique, 66(4):275-286.
- Seismo-Artif (2018 version). A program process strong-montion data, http://www.seismosoft.com/seismoartif
» http://www.seismosoft.com/seismoartif - Shakib, H., and Zia, T. R. (2004). Response of steel buried pipelines to three-dimensional fault movement by considering material and geometrical non-linear arities. 13th World Conference on Earthquake Engineering, Vancouver, Canada.
- Standard No.2800 (2014). Iranian Code of Practice for Seismic Resistant Design of Buildings, Standard No.2800. 4th edition, BHRC Publication No. S-253; Tehran, Iran.
- Tarinejad, R., Mahdavi, A., and Jahangir, N. (2012). Buried Pipeline Response Analysis to Reverse-Slip Fault Displacements. 15th World Conference of Earthquake Engineering, Lisbon, Portugal.
- Trifonov, O. V., and Cherniy, V. P. (2012). Elastoplastic stress-strain analysis of buried steel pipelines subjected to fault displacements with account for service loads. Soil Dynamics and Earthquake Engineering, 33:54-62.
- Trifonov. O. V. (2015). Numerical stress-strain analysis of buried steel pipelines crossing active strike-slip faults with an emphasis on fault modeling aspects. Journal of Pipeline Systems Engineering and Practice, 6(1):1-10.
- Vazouras, P., Dakoulas, P., and Karamanos, S. A. (2015). Pipe-soil interaction and pipeline performance under strike-slip. Soil Dynamics and Earthquake Engineering, 72:48-75.
- Vazouras, P., Karamanos, S. A., and Dakoulas, P. (2010). Finite element analysis of buried steel pipelines under strike-slip fault displacement. Soil Dynamics and Earthquake Engineering, 30:1361-1376.
- Vazouras, P., Karamanos, S. A., and Kakoulas, P. (2012). Mechanical behavior of buried steel pipes crossing active strike-slip faults. Soil Dynamics and Earthquake Engineering, 41:164-180.
- Xie, X., Symans, M. D., O’Rourke, M. J., Abdoun, T. H., O’Rourke, T. D., Palmer, M. C., and Stewart, H. E. (2011). Modelling of Buried HDPE Pipelines Subjected to Strike-Slip Faulting. Journal of Earthquake Engineering, 15(8):1273-1296.
- Yimsiri, S., Soga, K., Yoshiaki, K., Dasari, G. R., and O’Rourke, T. D. (2004). Lateral and Upward Soil-Pipeline Interactions in Sand for Deep Embedment Conditions. Journal of Geotechnical and Geoenvironmental Engineering, 130: 830-841.
- Zhang, J., Liang, Z., and Zhang, H. (2016). Response analysis of buried pipeline subjected to reverse fault displacement in rock stratum. Transactions of FAMENA, 40(3):91-100.
- Zhang, J., Liang, Z., Han, C. J., and Zhang, H. (2015). Numerical simulation of buckling behavior of the buried steel pipeline under reverse fault displacement. Mechanical Sciences, 6(2):203-210.
-
Available online: February 25, 2019.
Publication Dates
-
Publication in this collection
08 Apr 2019 -
Date of issue
2019
History
-
Received
01 Jan 2019 -
Reviewed
22 Jan 2019 -
Accepted
21 Feb 2019