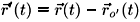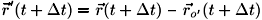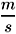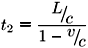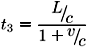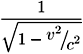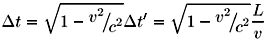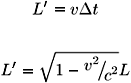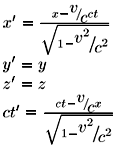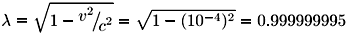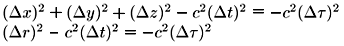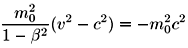Relatividad y el Espacio-Tiempo: Una introduccion para estudiantes de colegio

Relativity and space-time: An introduction to the Special Theory of Relativity for High School Students

Relatividad y el Espacio-Tiempo: Una introduccion para estudiantes de colegio

(Relativity and space-time. An introduction to the Special Theory of Relativity for High School Students)

Alfonso Velarde

Carrera de Física, Universidad Mayor de San Andrés La Paz, Bolivia

[e-mail]

Recebido em 1 abril, 2002. Aceito em 13 de abril, 2002.

Se introducen los conceptos a partir d ejemplos simples y conocidos, procurando profundizar en las ideas de la Relatividad Especial de manera gradual pero siempre sencilla.

Concepts are introduced starting from simple and known examples, going deep into the ideas of the Special Relativity in a gradual but always simple manner.

I Relatividad del movimiento

Hasta aquí, hemos dado por sentado que nuestras mediciones y descripciones del movimiento se dan respecto a un determinado sistema de referencia. Sin embargo, no nos hemos planteado qué pasa cuando tenemos diferentes sistemas de referencia en movimiento relativo unos respecto de otros. Las cosas se presentan de manera muy diferente en uno u otro sistema.

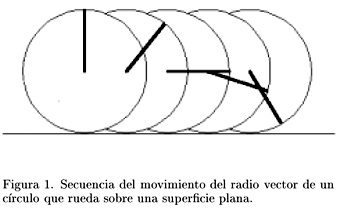
Consideremos, por ejemplo, un disco que rueda sobre una superficie horizontal, de manera que su centro se desplaza con movimiento uniforme rectilíneo. Dibujemos una línea desde el centro del disco a un punto del borde. Desde el sistema fijo a la superficie sobre la cual rueda el disco, ésta se verá girar más o menos como se ilustra en la secuencia de la Fig. 1.

Si tomamos el punto del borde del disco, la trayectoria que describe es la que se muestra en la Fig. 2 y que se conoce como una cicloide.

En cambio, respecto a un sistema de referencia que se desplaza con movimiento uniforme rectilíneo solidariamente al eje del disco, un punto del borde del mismo describe un simple movimiento circular uniforme, como se muestra en la Fig. 3.

Vemos pues que la descripción del movimiento de un cuerpo, es decir su cinemática, es relativa, depende del sistema de referencia según el cual se describe el movimiento.

El movimiento de los planetas tomando al Sol como referencia se reduce a órbitas elípticas simples, en cambio si se toma la Tierra como centro, los planetas describen trayectorias caprichosas describiendo rizos. Pero, no es la simplicidad del movimiento de los planetas respecto al sistema heliocéntrico el argumento para decidir que los planetas giran alrededor del Sol y no alrededor de la Tierra, sino las leyes de la dinámica las que nos permiten dilucidar el problema.

Newton pudo explicar los movimientos de los astros alrededor del Sol aplicando el concepto de fuerza sobre la base de la ley de la gravitación universal. La descripción del movimiento de un cuerpo puede ser diferente según el sistema de referencia desde el que se lo vea, pero no las leyes que determinan el movimiento.

El principio de la relatividad precisamente sostiene que las leyes de la naturaleza deben ser las mismas independientemente de los sistemas de referencia.

En este capítulo analizaremos este postulado fundamental de la física y sus implicaciones.

II Transformación entre sistemas en movimiento relativo.

Consideremos dos sistemas de referencia O y O' en movimiento relativo uno respecto del otro, como se muestra en la Fig. 4.

Ubicándonos en el sistema de referencia O, el sistema de referencia O' está en movimiento. Describimos el movimiento de un cuerpo A y nos interesa establecer las ecuaciones de transformación que nos permitan conocer como se observa el movimiento de A desde el sistema O'.

Si en un instante dado t, la posición del cuerpo A está dada por el vector (t)y la posición del origen del sistema O' por el vector o¢ (t), la posición del cuerpo A respecto al sistema O' será:

En un instante posterior t+Dt, la posición del cuerpo A ha cambiado a la posición

Entonces, el cambio de posición en el intervalo de tiempo Dt es:

La velocidad será:

Que es la ecuación de transformación de velocidades del sistema O al O'.

Un ejemplo: Consideremos dos automóviles que se mueven en una carretera con velocidades, medidas desde el sistema fijo a tierra, v₁ y -v₂, respectivamente como se ilustra e la Fig. 5.

¿Cuál es la velocidad del automóvil 2 respecto al automóvil 1? En este caso el sistema O es el fijo a la carretera y el sistema O' el automóvil 1, entonces:

Esto quiere decir que según el automóvil 1, el automóvil 2 se acerca hacia él (signo negativo) con una velocidad que es la suma de las magnitudes de las velocidades v₁ y v₂.

En forma análoga, de la variación de las velocidades en un intervalo de tiempo Dt, la ecuación de transformación de la aceleración entre sistemas es:

= – _o¢

Ejemplo: Un satélite gira en órbita alrededor de la Tierra. Desde el sistema O, fijo a la Tierra, la aceleración centrípeta que hace que el satélite gire es la aceleración gravitatoria debida a la atracción terrestre. (Debido a la altura del satélite, hacemos notar que en este caso, la aceleración gravitatoria g es menor al popular valor de 9,8m/s²).

Si designamos por O' el satélite:

a_o¢ = g

Cualquier objeto en el satélite, también está sometido a la atracción gravitatoria de la Tierra, entonces:

a = g

Luego, respecto al satélite, la aceleración de los objetos es:

a¢ = g – g = 0

Es decir que, respecto al satélite, las cosas están en estado de ingravidez, no hay aceleración, los objetos flotan libremente en el espacio.

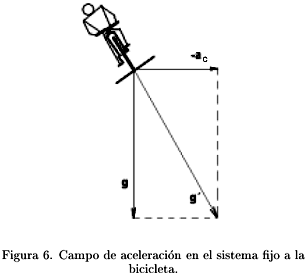
Otro ejemplo: ¿Por qué al dar una curva en bicicleta debemos inclinarnos para mantener el equilibrio?

Desde el punto de vista del sistema "O", fijo a tierra, para girar la bicicleta está sometida una aceleración centrípeta: a_c =

Si nos trasladamos al sistema O', fijo a la bicicleta, tenemos que a_o¢ = a_c . De manera que en el sistema O' los objetos están sometidos a un campo de aceleraciones:

Podemos ver entonces que para mantener el equilibrio debemos inclinar la bicicleta de modo que coincida con la dirección del campo de aceleración en este sistema. Al diseñar una carretera, conocido el radio de una curva, y la velocidad a la que se espera que circulen los vehículos, podemos calcular a_c y determinar el ángulo de inclinación o peralte de la curva.

III Sistemas inerciales y no inerciales.

De la segunda Ley de Newton:

= m

sabemos que si = 0, entonces = 0 que significa que = cste. que es la ley de inercia que nos dice que un cuerpo sobre el que no actúa ninguna fuerza, esto es un cuerpo libre, debe moverse en línea recta uniformemente.

Sin embargo, esta ley sólo es válida si nuestro sistema de referencia no está acelerado. En efecto, sea O un sistema no acelerado y O' un sistema con aceleración

_o¢ . Entonces, un cuerpo que por acción de una fuerza experimenta una aceleración , desde el sistema de referencia acelerado O' tendrá una aceleración:

= – _o¢

Aplicando la segunda Ley de Newton a un cuerpo de masa m sobre el que actúa una fuerza , tendremos:

= – m

_o¢

donde = m viene a ser la fuerza medida desde el sistema acelerado. Aquí aparece una pseudo - fuerza adicional –m

_o¢ que no es resultado de ningún tipo de interacción física sino que es consecuencia de la aceleración del sistema.

Si = 0, es decir, si el cuerpo no está sometido a la acción de ninguna fuerza, en el sistema O', sin embargo, aparecerá una pseudo - fuerza

= –m

_o¢

y una aceleración asociada:

= –o¢ ¹ 0

lo que implica que no se cumple la ley de inercia. El cuerpo es acelerado en sentido contrario a la aceleración del sistema.

Por eso, los sistemas no acelerados se llaman sistemas inerciales. Quiere decir que en ellos se cumple la ley de inercia. En cambio, los sistemas acelerados, en los que no se cumple la ley de inercia, se llaman sistemas no inerciales.

Como se ve, es posible descubrir un sistema no inercial por las pseudo - fuerzas que lo delatan. Cosa que no ocurre entre sistemas inerciales, es decir, entre sistemas no acelerados que se mueven uno respecto al otro con movimiento uniforme rectilíneo (

_o¢ = 0).

Por ejemplo, si viajamos en un vehículo. Desde el punto de vista del sistema fijo a éste, es la carretera y todos los objetos fijos a ella, los postes, los árboles, etc. los que se mueven. Hemos de suponer idealmente que no hay baches y que la carretera es absolutamente recta. Si el vehículo se mueve con velocidad constante, desde el punto de vista de las leyes de la mecánica, no hay ninguna diferencia entre el sistema del vehículo y el sistema fijo a tierra. Las leyes de la mecánica son las mismas en ambos sistemas.

=

Por ejemplo, dos péndulos de la misma longitud, uno montado en tierra y el otro en el vehículo, oscilarán con el mismo periodo.

Ambos sistemas son totalmente equivalentes y ninguno de ellos tiene el derecho de decir yo soy el sistema de referencia privilegiado respecto al cual se define el movimiento del otro.

En cambio, si el vehículo frena; cinemáticamente, desde su sistema los postes y los árboles fijos a tierra también disminuirán su velocidad relativa, sin embargo, sólo dentro del vehículo los objetos experimentarán una pseudo - aceleración que los impulsará hacia delante, cosa que no ocurrirá con los objetos fijos a tierra, de modo que es posible darse cuenta cual de los dos sistemas es el que efectivamente frena, es decir está acelerado.

Igualmente, si el camino es curvo, los ocupantes del vehículo experimentarán una pseudo - aceleración centrífuga que no experimentarán los objetos fijos a tierra aunque cinemáticamente éstos giran respecto al vehículo. Esta es la forma en que la mecánica puede detectar la curvatura del espacio.

En un sistema acelerado, aparece un campo de aceleración ( – _o¢ )que es el mismo para todos los cuerpos, independientemente de su masa inercial y la pseudo - fuerza asociada a ésta es directamente proporcional a ella (= –m

_o¢ ).

Recordemos que esta misma propiedad tiene la fuerza de atracción gravitacional, es decir, el peso de los cuerpos. Más adelante discutiremos sobre las implicaciones de esta propiedad de la atracción gravitatoria.

De hecho no existe un sistema estrictamente inercial. Todos los cuerpos en el espacio están sujetos a fuerzas de interacción mutuas y, en consecuencia, sometidos a aceleraciones. Si tomamos, por ejemplo, como sistema de referencia la Tierra, debido a su rotación y a su traslación alrededor del Sol, no es un sistema inercial. En experimentos terrestres como el de una bola que rueda sobre una mesa, la trayectoria de ésta en libre movimiento, no es realmente recta, sino un poco curvada. Si esto escapa a la medición se debe únicamente a la exigüidad de las dimensiones usadas en el experimento, en comparación con las dimensiones del globo terrestre. De igual modo, un sistema de referencia fijo al Sol es también un sistema acelerado, en consecuencia no inercial, puesto que el Sol gira alrededor del centro de la galaxia. El Sol, sin embargo, se asemeja mejor a un sistema inercial pues su órbita es mucho mayor y en consecuencia su aceleración mucho menor.

Sólo si las aceleraciones del sistema de referencia que utilizamos son despreciables para la precisión de nuestros instrumentos de medida podemos considerar, para fines prácticos, que nuestro sistema es inercial.

Así, las leyes de la mecánica de Newton sólo tiene sentido en referencia a un sistema inercial ideal. Cualquier sistema de referencia empírico establecido por medio de cuerpos materiales, no puede ser fundamento de una ley con el contenido ideal de la ley de inercia. Esta ley es más bien el punto de partida de la postulación del espacio euclidiano cuyo elemento básico es la línea recta y también del transcurrir uniforme del tiempo que se expresa en el movimiento uniforme rectilíneo: espacios iguales recorridos en tiempos iguales. Así llegó Newton a la conclusión de que existe un espacio absoluto en el que los cuerpos materiales se encuentran y se mueven y también un tiempo absoluto. Según sus propias palabras: "El espacio absoluto permanece siempre igual e inmóvil, merced a su naturaleza y sin referencia a un objeto exterior." y: "El tiempo absoluto, verdadero y matemático transcurre en sí y por su naturaleza uniformemente, y sin referencia a ningún objeto exterior."

Así, sólo un sistema fijo al espacio absoluto, es un sistema verdaderamente inercial pero, aquí surge un problema grave: cualquier otro sistema que se mueva con movimiento uniforme rectilíneo respecto al primero es también inercial y completamente equivalente respecto a las leyes de la mecánica. De hecho estamos frente a un principio: el principio de la relatividad de la mecánica clásica, que establece que las leyes de la mecánica son las mismas para todos los sistemas inerciales, lo que implica que el espacio absoluto es indetectable para las leyes de la mecánica. Ningún sistema inercial en él puede decir yo estoy en reposo en el espacio absoluto y los infinitos demás sistemas en movimiento uniforme rectilíneo respecto a mí son los que se mueven.

IV La velocidad de la luz

A fines del siglo XIX, ya se había desarrollado la electrodinámica, o sea el estudio del movimiento de los campos electromagnéticos producidos por las cargas eléctricas en movimiento y se había establecido firmemente que la luz es una onda electromagnética. La luz tiene las mismas propiedades que, por ejemplo, las ondas en el agua o el sonido en el aire. Estas ondas mecánica son el resultado de la propagación de una perturbación en un medio. Esto llevó a suponer que para las ondas electromagnéticas debería existir también un sustrato o medio en el que se propagan estas ondas. A este medio hipotético se lo llamó éter. Todo el espacio estaría lleno de éter y constituiría el sistema de referencia privilegiado respecto al cual podría distinguirse si un cuerpo está en reposo absoluto o movimiento absoluto.

En efecto, si observamos la propagación de las ondas en el agua, es perfectamente posible distinguir entre un sistema fijo al agua y otro que se mueva respecto al ésta con movimiento uniforme rectilíneo. Es decir, entre dos sistemas inerciales. La velocidad de propagación "c" de una onda depende del medio. De manera que si, por ejemplo, un bote está en reposo respecto al agua y produce una onda, observará un frente circular que se aleja con una velocidad constante "c" en todas las direcciones. En cambio, si el bote se está moviendo respecto al agua, observará que las olas que produce se alejan con una velocidad:

= – _o¢

_o¢ es la velocidad del bote respecto al agua.

Más lentamente por delante:

v¢ = c – v_o¢

y, más rápido por detrás:

v¢ = – c – v_o¢ = – (c + v_o¢ )

En la Fig. 7, se ilustran ambas situaciones. Lo que es importante aquí es que se vea que las situaciones son totalmente distinguibles, en este caso diremos que aquel sistema respecto al cual las ondas se propagan con velocidad "c" constante en todas las direcciones es el sistema fijo al medio, caso contrario, el sistema está en movimiento. Así, aunque no viéramos el agua, pero pudiéramos medir la velocidad de propagación de las ondas en todas las direcciones, estaríamos en condiciones de distinguir entre un sistema fijo al agua y otro que no lo esté.

El éter era pues, la solución al problema del espacio absoluto, indetectable por medio de la dinámica newtoniana.

Naturalmente el paso obligado era poder detectar experimentalmente el éter. Siendo, como se sabe, la luz una onda electromagnética, su velocidad de propagación no dependerá de la velocidad de la fuente que la produce sino del medio en que se mueve, en este caso el éter. La velocidad de la luz medida experimentalmente es:

c = 2.9979×10⁸

Si la Tierra se moviera a través del éter sin alterarlo, entonces la velocidad de propagación de la luz con respecto a la Tierra debía ser diferente en diferentes direcciones.

En 1881, los físicos norteamericanos Michelson y Morley idearon un experimento que les permitiera detectar las diferencias en la velocidad de la luz en diferentes direcciones respecto a la Tierra.

En la Fig. 8, se representa esquemáticamente el aparato de Michelson Morley. La fuente luminosa S emite un rayo de luz que al llegar al espejo semitransparente M se divide en dos haces que se propagan por dos caminos perpendiculares entre sí. El haz reflejado va hasta el espejo A y vuelve, en cambio el haz transmitido a través de M va hasta el espejo B donde se refleja y retorna moviéndose en el mismo sentido de la Tierra al ir y en sentido contrario al volver. Ambos haces se encuentran nuevamente en el espejo M y son observados por el interferómetro en O. Un interferómetro es capaz de medir diferencias de tiempo menores a 10^–9s. Para simplificar, suponemos que la distancia L a cada espejo es la misma.

Comencemos por calcular el tiempo que tarda el haz perpendicular en ir y volver. Puesto que la luz se propaga en el éter con velocidad c y la Tierra se mueve respecto al éter con velocidad v (la velocidad de traslación de la Tierra alrededor del Sol es aproximadamente 3×10^{4 m}/_s), tendremos que el recorrido de la luz en el éter viene a ser el que se muestra en la Fig. 9.

Si designamos por t₁ el tiempo que tarda el haz en llegar de M a A:

luego:

El tiempo que tarda en ir y volver a M será el doble, luego:

Calculamos ahora el tiempo que tarda el haz que se mueve paralelamente a la traslación de la Tierra en ir de M a B. De acuerdo a la ley de transformación de velocidades, la velocidad de la luz respecto a la Tierra será:

c¢ = c – v

luego:

L = c¢t₂ = (c – v)t₂

de donde:

La velocidad de la luz respecto al sistema fijo a Tierra, al volver de B a M será:

c¢ = c + v

luego:

L = (c + v)t₃

de modo que:

Luego, el tiempo empleado en ir y volver será:

T₂ = t₂ + t₃ =

Como se ve, los tiempos T₁ y T₂ no son iguales, el tiempo T₂ es mayor en un factor:

que el tiempo T₁. De donde, se espera un retraso del haz que se mueve paralelamente a la traslación de la Tierra respecto al haz que se mueve perpendicularmente.

Con gran sorpresa, el experimento mostró que no tal retraso, lo que significa que la velocidad de la luz es la misma en ambas direcciones y en ambos sentidos, en consecuencia igual que si la Tierra estuviera en reposo respecto al éter, en definitiva la misma para ambos sistemas, destruyendo la teoría del éter.

V La Relatividad Especial de Einstein

Fue Einstein quien en 1905 resolvió la paradoja del experimento de Michelson Morley (aunque, al desarrollar la teoría de la relatividad especial no se proponía resolver este problema). Einstein recupera el principio de la relatividad de la mecánica de Newton.

Él postula lo siguiente: Todas las leyes de la naturaleza son las mismas, es decir son invariantes, para todos los sistemas en movimiento relativo de traslación uniforme rectilíneo.La velocidad de la luz es una constante física invariable para todos los sistemas inerciales de referencia.

En realidad el comportamiento conspirador de la velocidad de la luz contra la relatividad de Newton, no estaba haciendo más que confirmarla sólo que en forma más amplia, en el sentido de que todos los sistemas inerciales son totalmente equivalentes, no sólo para los procesos mecánicos, sino también para los procesos electromagnéticos y ópticos.

VI La dilatación del tiempo. Tiempo propio y tiempo impropio.

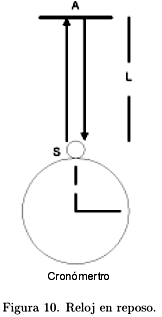
La primera consecuencia es que el tiempo ya no es el mismo en los dos sistemas de referencia. Para demostrarlo construimos dos relojes idénticos de la siguiente manera. Consiste de una fuente luminosa S y un espejo A separados por una distancia L, igual que los brazos del aparato de Michelson Morley. Un destello de luz que parte de S, activa un cronómetro, se refleja en A y vuelve. Junto a la fuente luminosa tenemos un detector de luz que, cuando recibe el retorno del destello registra el intervalo de tiempo y simultáneamente dispara otro destello. Uno de los relojes está en reposo en nuestro laboratorio y el otro se mueve con velocidad constante v, transversal al eje S-A, respecto al laboratorio.

Refiriéndonos a la Fig. 10, en el reloj que está en reposo, el intervalo de tiempo será:

Dt = 2^L/_c

Para este reloj, la salida del destello y su llegada ocurren en un mismo punto del espacio. Llamaremos a este tiempo, tiempo propio del reloj.

Ahora observemos el reloj en movimiento. Refiriéndonos a la Fig. 11 y conforme ya lo hicimos al describir el haz transversal del experimento de Michelson Morley, el intervalo de tiempo transcurrido será:

En este caso la salida del destello y su llegada ocurren en dos lugares diferentes del espacio. Por eso decimos que el tiempo medido con el reloj fijo a nuestro laboratorio es un tiempo impropio.

Tenemos entonces que:

Dtes el tiempo propio medido entre la ocurrencia de dos eventos que se dan en el mismo lugar del espacio. En la Fig. 11, ese tiempo lo mide el reloj en movimiento respecto al laboratorio porque obviamente este está en reposo respecto al sistema S-A. En cambio el reloj fijo a nuestro laboratorio, respecto al cual el otro reloj se mueve registrará el tiempo impropio Dt¢medido entre la ocurrencia de dos eventos que se dan en dos diferentes lugares del espacio.

Como:

v < c Þ < 1 Þ Dt < Dt¢

es decir, el reloj en movimiento relativo se atrasa en un factor , vale decir, el tiempo se dilata. Desde el sistema del laboratorio vemos que todos los procesos en el sistema en movimiento son más lentos. Este fenómeno contradice nuestra experiencia cotidiana. En la vida diaria nadie observa que un reloj en movimiento se retrase respecto a otro en reposo. Un postulado de la mecánica de Newton, precisamente señala que el tiempo transcurre igual y uniformemente independientemente del sistema de referencia. La relatividad especial de Einstein en cambio muestra que el tiempo no es el mismo para todos los sistemas de referencia y que su transcurso depende del estado de movimiento del sistema.

VII Contracción de la longitud

En la Fig. 12 vemos una nave que viaja entre dos planetas separados por una distancia constante L.

En el sistema de referencia de los planetas, la nave viaja con una velocidad v. La nave, en consecuencia, recorre la distancia L en un tiempo Dt¢ = ^L/_v. Este intervalo de tiempo ha sido medido por relojes fijos a los planetas, en consecuencia es un tiempo impropio porque la partida de un planeta y la llegada al otro son dos eventos ocurridos en dos lugares diferentes del espacio. Por otra parte, un reloj fijo a la astronave estará presente en ambos eventos y, por lo tanto, el tiempo Dtregistrado de la duración del viaje por este reloj es el tiempo propio. Como vimos:

En el sistema de la nave, son los planetas los que se mueven, el piloto encontrará que la distancia recorrida entre los dos planetas es igual al producto de su velocidad por el tiempo propio registrado por su reloj, es decir:

Aquí, recordemos, L es la distancia que separa a los dos planetas medida en el sistema en el que ambos planetas están en reposo. En cambio L¢ es la distancia entre los planetas medida desde la nave, respecto a la cual, los planetas están en movimiento.

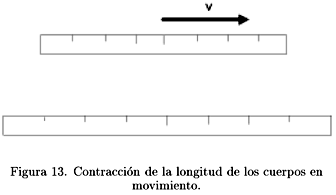
¿Qué significa esto? Que las dimensiones de un cuerpo, cuando está en movimiento, se contraen en la dirección del movimiento relativo uniforme rectilíneo, por un factor . Así, si tenemos dos reglas idénticas que en reposo miden L y una de ellas la ponemos en movimiento uniforme rectilíneo con velocidad v, como se muestra en la Fig. 13, resulta que la regla en movimiento se contrae, es decir, es más corta.

Este es otro sorprendente resultado de la relatividad especial conocido como la contracción de la longitud.

¿Por qué en la experiencia cotidiana no observamos estos efectos? La razón es que las velocidades con que se mueven los cuerpos en nuestro mundo macroscópico son muy pequeñas comparadas con la de la velocidad de la luz de manera que ® 0, entonces ® 1, y en consecuencia: Dt @ Dt¢ y L @ L¢.

VIII El concepto de simultaneidad en la teoría de la relatividad especial

Consideremos un sistema de referencia O, dotado de su cronómetro en reposo respecto a él. Dos eventos son simultáneos si ocurren al mismo tiempo según nuestro reloj. Por ejemplo tenemos una regla de extremos A y B, en reposo. Sea C el punto medio de la regla, equidistante de ambos extremos. En el punto C hay una fuente de luz que emite un destello. Obviamente la luz llegará simultáneamente a ambos extremos.

En la Fig. 14 hemos dibujado un diagrama espacio - tiempo de lo anteriormente descrito. El eje del tiempo lo hemos multiplicado por la velocidad de la luz de manera que también tiene unidades de longitud. Esto equivale a medir el tiempo en unidades de la velocidad de la luz. En efecto:

Las líneas a 45^o son las gráficas del movimiento de dos rayos de luz cuya velocidad en unidades de c es 1. Como se ve alcanza la posición x_A de A, en el mismo instante ct₁ en que alcanza la posición x_B de B.

Analicemos ahora el mismo problema si la regla está en movimiento uniforme rectilíneo respecto al sistema O, con velocidad ^v/_c, en la dirección longitudinal de la regla.

En la Fig. 15 hacemos una gráfica en el espacio - tiempo del movimiento de la regla y de los rayos de luz.

El movimiento de los puntos A, B y C, extremos y centro de la regla respectivamente, está representado por las líneas punteadas, las líneas llenas que parten de C son las gráficas del movimiento de los rayos de luz. Como se ve, ahora el rayo de luz que llega al extremo A, lo hace antes que el rayo de luz que llega al extremo B. Ambos eventos ya no son simultáneos. En cambio, como vimos, según un reloj fijo a la regla si son simultáneos. Estamos frente a un nuevo resultado que violenta nuestra experiencia directa. Estamos acostumbrados a que dos cosas que ocurren al mismo tiempo, son simultáneas para todos los sistemas de referencia independientemente de su estado de movimiento. Nuevamente señalamos que para las velocidades de los cuerpos macroscópicos, insignificantes respecto a la velocidad de la luz, las diferencias son imperceptibles.

En la Fig. 15 hemos representado el sistema O' fijo a la regla. El eje de tiempos: ct' es paralelo a las líneas del movimiento de la regla. Es la línea de movimiento del reloj fijo a la regla. El eje del espacio: X¢ es paralelo a la línea segmentada que une los dos eventos puesto que éstos son simultáneos en este sistema.

De aquí se deriva que el sistema en movimiento O' en el espacio - tiempo: X - ct es representado por un sistema de coordenadas espacio - tiempo: X'- ct' a ángulo agudo, en el cual los dos ejes están inclinados con respecto a los primitivos. El ángulo de inclinación es el de la pendiente del movimiento relativo, es decir, la tangente del ángulo de inclinación es igual a ^v/_c.

El hecho es que la relatividad especial de Einstein muestra que el tiempo es relativo en el mismo sentido en que lo es el espacio. El transcurso del tiempo y las dimensiones del espacio dependen del estado de movimiento del sistema de referencia. El problema de que la simultaneidad sea relativa da cuenta de la inexistencia del tiempo absoluto de Newton del mismo modo que la relatividad del espacio determina que dos cosas que ocurren en el mismo lugar del espacio según un sistema de referencia, ocurren en distintos puntos del espacio respecto a otro sistema en movimiento relativo. Esto último no nos produce ninguna sorpresa, es claro que, si por ejemplo, viajamos en un vagón de tren a velocidad constante y hacemos rebotar una pelota verticalmente contra el suelo, respecto al vagón la pelota cae siempre en el mismo lugar del piso, en cambio respecto a tierra, la pelota avanza con el vagón y cada vez que cae al piso lo hace en un lugar diferente del espacio porque el piso del tren ha cambiado de posición. Una cosa similar ocurre ahora con el tiempo. Lo que ocurre es que estamos acostumbrados a la relatividad del espacio y no a la del tiempo por eso esta última nos parece tan difícil de asimilar.

IX Ecuaciones de transformación

En el espacio - tiempo definimos un suceso como algo que ocurre en un cierto lugar del espacio respecto a un sistema de referencia dado y en cierto instante respecto a un reloj fijo a este sistema de referencia. Si conocemos la posición y el instante en que se ha producido un suceso en un sistema de referencia X - ct dado, ¿cómo podemos saber la posición y el tiempo respecto otro sistema X'- ct' en movimiento relativo uniforme rectilíneo? Las ecuaciones que nos permiten pasar de un sistema a otro son las ecuaciones de transformación.

En la Fig. 16 mostramos dos sistemas de referencia O y O' en movimiento relativo uniforme rectilíneo. Hagamos que los ejes espaciales X y X¢ sean paralelos a la dirección del movimiento relativo. En el instante t = t¢ = 0, X = X'= 0, los orígenes de ambos sistemas coinciden y los relojes de ambos sistemas están sincronizados.

Digamos que nos ubicamos en el sistema O, de manera que el sistema O' se mueve con velocidad v respecto a O. Desde este sistema, el suceso representado por la esfera gris se encuentra en la posición (x,y,z) y ocurre en el instante tsegún el reloj fijo a este sistema. En ese instante, el origen del sistema O' se encuentra en la posición vt y el objeto a una distancia s, en la dirección del eje espacial X, del origen O'.

Entonces:

s = x – vt

La distancia s ha sido medida desde el sistema O y por tanto está contraída con relación a la posición x¢ referida al sistema O'.

s = x¢

Remplazando esta expresión en la anterior obtenemos:

Que es la ecuación de transformación espacial en la dirección del eje paralelo a la dirección del movimiento relativo. En la dirección de los ejes perpendiculares al movimiento relativo, las coordenadas en ambos sistemas son iguales.

y¢ = y z¢ = z

Ahora bien, como ambos sistemas son totalmente equivalentes, desde el sistema O' es el sistema O el que se mueve con velocidad -v, es decir en sentido contrario, y las ecuaciones de transformación espaciales inversas son las mismas excepto por el signo de la velocidad relativa.

Nótese que ahora el tiempo es medido por el reloj fijo al sistema O'.

Eliminando x¢ entre las dos ecuaciones de transformación en la dirección del movimiento relativo, obtenemos la ecuación de transformación del tiempo t¢ en función de x y t.

Multiplicando esta ecuación por la velocidad de la luz c, damos a la componente temporal unidades de longitud y la velocidad se expresa en unidades de la velocidad de la luz. La última expresión entonces, para la coordenada temporal es:

La transformación inversa de la coordenada temporal, es decir de O' a O, por la equivalencia de ambos sistemas, es:

Resumiendo: dado un sistema de referencia O con su reloj, y otro sistema O' con su propio reloj en movimiento relativo uniforme rectilíneo a lo largo del eje X, las ecuaciones de transformación del espacio - tiempo (x,y,z;ct) referido a O, al espacio - tiempo (x',y',z';ct') referido a O' son:

Que se conocen como las ecuaciones de transformación de Lorentz.

La esencia de la teoría especial de la relatividad consiste en la unión inseparable del espacio y el tiempo. El espacio es una unidad espacio - temporal de cuatro dimensiones; su elemento es el "punto" universal: (x,y,z;ct).

En el límite en que ^v/_c ® 0estas ecuaciones se transforman en:

x¢ = x – vt y¢ = y z¢ = z t¢ = t

Que son las ecuaciones de transformación que corresponden a la mecánica no relativista conocidas como ecuaciones de transformación de Galileo.

Como se puede ver, el tiempo es el mismo para ambos sistemas sólo en tanto las velocidades involucradas sean despreciables respecto a la velocidad de la luz.

X La Relatividad General de Einstein

La mecánica clásica distingue, como vimos, entre el movimiento de un cuerpo libre, no sometido a fuerza alguna y el movimiento de un cuerpo bajo la acción de la gravitación, es decir de interacción con otro cuerpo con masa. El primero es un movimiento uniforme rectilíneo en un sistema inercial, el segundo será un movimiento curvilíneo y no uniforme.

La fuerza de atracción gravitatoria es de tal naturaleza que es proporcional a la masa de los cuerpos, la aceleración gravitatoria que produce es la misma para todos los cuerpos, independientemente de su masa.

Por otra parte, vimos cómo la mecánica puede distinguir entre sistemas inerciales y no inerciales por la aceleración que se observa sobre los cuerpos desde un sistema acelerado, que no es resultado de ningún tipo de interacción con otros cuerpos, sino un efecto de la aceleración del sistema. En un sistema no inercial todos los cuerpos, independientemente de su masa inercial, sienten un campo de aceleración que es el mismo para todos. La misma propiedad tiene la interacción gravitacional, la aceleración de la gravedad es la misma para todos los cuerpos. Esta equivalencia entre la fuerza de atracción gravitatoria y la pseudo - fuerza en un sistema no inercial, llevó a Einstein al desarrollo de la teoría general de la relatividad.

Para tratar de explicar las bases de esta teoría, consideremos, por ejemplo, dos cajas cerradas de modo que no haya referencia alguna con el exterior. Una caja esta en reposo sobre la Tierra. En ella hacemos experimentos y vemos que todos los cuerpos están sometidos a una misma aceleración que es la debida a la gravedad terrestre. La otra caja la enviamos en una nave al espacio exterior donde la atracción gravitatoria sea despreciable. La nave es acelerada por sus motores con una aceleración igual a la de la gravedad. Dentro de la caja observaremos que todos los objetos se comportan igual que en la caja en Tierra, experimentan una aceleración que es la misma para todos independientemente de su masa. Ambos sistemas son equivalentes y no hay forma de decidir si la aceleración que se mide en el sistema se debe a la atracción gravitatoria o a que el sistema está acelerado. La acción de la gravedad no se distingue en nada de la acción de la aceleración.

En el ejemplo que dimos de la ingravidez que se produce en una nave en órbita, un objeto al que le damos un impulso se mueve con movimiento uniforme rectilíneo respecto a la nave, sin embargo, basta que nos traslademos al sistema fijo a Tierra respecto al cual la nave gira para que comprobemos que el objeto en cuestión describe una trayectoria curva y está sometido a la aceleración de la atracción terrestre.

Cuando tratamos con sistema no inerciales, Einstein demuestra que, de hecho, la geometría euclidiana es inaplicable. Partamos de un espacio en el cual no existe ningún campo de aceleración, es el caso de nuestra nave en órbita. Consideremos ahora un disco que gira dentro de la nave con velocidad angular constante. En el sistema de referencia fijo al disco domina un campo gravitatorio dirigido hacia fuera y dado por la aceleración centrífuga. Desde el sistema fijo al disco se mide su circunferencia con una cinta métrica, se mide también el radio y se comprueba que el perímetro es dos veces p por R; R es el radio. Desde el sistema fijo a la nave, se observa que el radio del disco es el mismo esto porque el movimiento de giro de cada punto del radio es perpendicular a su dirección, en cambio el perímetro se habrá contraído según la teoría de la relatividad espacial porque la cada elemento del mismo se mueve en la dirección de su longitud. Resultará entonces que el perímetro es menor a dos veces p por R. Es más, mientras consideremos un círculo más alejado del centro, mayor será la contracción de modo que el disco dejará de ser plano para curvarse.

Así, los conceptos de recta y curva son relativizados, las trayectorias curvas están relacionadas a la presencia de campos de aceleración y las rectas a su ausencia. Un observador en un vagón cerrado puede concluir que la riel es curva por la aceleración centrífuga que aparece, e igualmente, la presencia de la aceleración gravitacional puede interpretarse como manifestación de la curvatura del espacio. Podemos pues dar una interpretación geométrica de la gravedad como un fenómeno resultante de que el espacio se curva por la presencia una masa. Si esto es así, se puede esperar que un rayo de luz al pasar cerca de un cuerpo masivo describa una curva porque esa es la forma del espacio o, visto desde el punto de vista gravitacional, que la luz también es atraída gravitatoriamente. En efecto, experimentos realizados durante eclipses solares muestran que la posición de una estrella cuya luz pasa cerca del borde del Sol antes de llegar a la tierra cambia de posición en referencia a donde la veríamos si el Sol no estuviera cerca como se ilustra en la Fig. 17.

Sobre la base del principio de equivalencia entre la atracción gravitacional y la pseudo - fuerza debida a la aceleración del sistema, Einstein pudo ampliar el concepto de la relatividad a todos los sistemas de referencia inerciales o no inerciales. Todas las leyes de la naturaleza son las mismas independientemente del sistema de referencia. En la Relatividad Especial, el espacio - tiempo de cuatro dimensiones es un espacio "plano", o con más propiedad: euclidiano y esto es válido en tanto estemos en un lugar del espacio lejos de otros cuerpos masivos de manera que el campo gravitacional sea despreciable; en cambio, si tomamos en cuenta la interacción gravitacional, el espacio - tiempo es un espacio "curvo" y a la gravedad: la manifestación de la curvatura del espacio.

"Los europeos a principios de siglo solían creer en marcos de referencia privilegiados: que la cultura o la organización política alemana, o la francesa o británica era mejor que la de otros países; que los europeos eran superiores a otros pueblos que habían tenido la fortuna de ser colonizados.... El joven Einstein se rebeló contra el concepto de marcos de referencia privilegiados en física y lo propio hizo en política. En un universo lleno de estrellas que salían proyectadas en todas direcciones no había lugar alguno que estuviera "en reposo", ninguna estructura desde la cual contemplar el universo que fuera superior a otra estructura cualquiera. Este es el significado de la palabra relatividad. La idea es muy sencilla, a pesar de sus adornos mágicos: al observar el universo cualquier lugar es tan bueno como otro cualquiera. Las leyes de la naturaleza han de ser idénticas con independencia de quien las describa."[¹*^]

XI "Relativilandia"

Los efectos relativistas no son perceptibles en el mundo en que vivimos porque las velocidades a las que nos movemos son despreciablemente pequeñas comparadas con la velocidad de la luz. Consideremos, por ejemplo la velocidad de traslación de la Tierra alrededor del Sol; es aproximadamente 3×10^{4 m}/_s, o sea: » 10 ^{– 4}c, una diezmilésima de la velocidad de la luz. El coeficiente de contracción de la longitud o de dilatación del tiempo es, en este caso:

El retraso de un reloj fijo a la Tierra, respecto a otro fijo al Sol sería entonces:

dt = t – t = 5×10 ^{– 9}t

E igualmente, la contracción de la longitud de una regla en la Tierra respecto a una regla en el sistema fijo al Sol:

dL = 5×10 ^{– 9}L

Aquí, t y L son el tiempo y la longitud respectivamente, medidas con el reloj y la regla fijas al sistema del Sol. Representa un retraso de 1.8 cienmilésimas de segundo en una hora o 5 millonésimas de milímetro en un metro.

Lo que queremos mostrar es lo insignificante de los efectos relativistas para las velocidades de los objetos de nuestro mundo.

Para poder observar los efectos relativistas tendríamos que movernos a velocidades comparables con la velocidad de la luz o tener relojes tan precisos para poder medir estas diferencias de tiempo por ejemplo, con satélites en órbita terrestre. De hecho existen relojes atómicos con la suficiente precisión para poder detectar estas pequeñísimas diferencias, pero naturalmente no están a nuestro alcance.

Por ello este experimento es un experimento mental. Imaginemos que vivimos en "Relativilandia", un imaginario lugar donde la velocidad de la luz, en vez de ser de 300.000 Km/s =300.000.000m/s, fuera igual a la velocidad del sonido en el aire » 300^m/_s. En ese caso, un automóvil que desarrolle una velocidad de 100 Km/hr = 27.8 m/s, estaría moviéndose a una velocidad de 0.09c. El factor de contracción de la longitud y de dilatación del tiempo sería entonces:

= 0.9957

¿Cómo sería nuestra experiencia cotidiana?

El señor X vive a 10 Km de su oficina. Su esposa, la señora Y, trabaja en la casa y casi nunca sale. Ambos tienen sus relojes pulsera idénticos y comprobádamente precisos.

Cada día el señor X monta en su auto y a una velocidad promedio de 100 Km/hr va a su oficina.

Desde el sistema de su casa en la que la señora Y permanece, las cosas acontecen del siguiente modo:

La señora Y está familiarizada con los efectos relativistas y sabe que el tiempo transcurrido, medido en su reloj, entre la partida del señor X y su llegada a la oficina es un tiempo impropio porque ocurre en dos lugares diferentes de su espacio, en cambio el tiempo transcurrido en el sistema del señor X: su automóvil, es un tiempo propio porque ambos eventos ocurren en el mismo lugar de su espacio. Por tanto, sabiendo que la distancia es de 10Km y la velocidad de 100 Km/hr sabe que el tiempo transcurrido según su reloj es de 10/100 hr = 0.1 hs = 6 min y puede calcular el tiempo transcurrido según el reloj del señor X.

t¢ = t = 0.9957×6min = 5.97min

El retraso del reloj del señor X es entonces de: (6-5.97) min = 0.03 min = 1.8 s. El tiempo de vuelta es el mismo, la misma distancia, a la misma velocidad aunque en sentido contrario y la partida de la oficina y la llegada a la casa son dos eventos que ocurren en dos puntos diferentes del espacio de la señora Y y en el mismo del señor X, de manera que en total, cuando el señor X regresa a casa, su reloj habrá retrasado 3.6 s. Ahora, no se trata de que sólo el reloj se ha atrasado, en realidad el tiempo para el señor X mientras viajaba de ida y vuelta ha transcurrido más lentamente. El señor X es 3.6 s menos viejo que la señora Y.

Veamos ahora el problema desde el sistema del señor X. Para nosotros que no estamos acostumbrados a los fenómenos relativistas aparentemente aquí habría una paradoja. Según el señor X, o sea desde su automóvil, es la señora Y quien se aleja primero y después vuelve y entonces sería su reloj el que se atrasa, por tanto ella debería ser 3.6 segundo más joven. Sin embargo, el señor X, acostumbrado a la relatividad, no se confunde de esa manera. El distingue perfectamente que en el proceso de ir y volver han habido cuatro eventos: partida de la casa, llegada a la oficina, partida de la oficina, llegada a la casa. Al llegar a la oficina el señor X ha tenido que parar que es como abandonar su sistema de referencia que se mueve con velocidad constante alejándose de su casa y al partir de la oficina ha tenido cambiar de sentido de movimiento que es como subirse a otro sistema que se mueve con la misma velocidad constante pero en sentido contrario. La señora Y, en cambio, siempre ha permanecido en su mismo sistema de referencia. Es decir, que la situación del señor X y la de la señora Y no son equivalentes.

Para el señor X las cosas ocurren de la siguiente manera:

La distancia que recorre está contraída porque la carretera está en movimiento, por tanto la distancia que recorre no es de 10 Km sino:

L¢ = L = 0.9957×10Km = 9.957Km

que a la velocidad de 100 km/hr le demanda un tiempo de:

t¢ = 5.97min

Al regreso ocurre lo mismo, de modo que, según su reloj, el viaje redondo le ha tomado un tiempo de 11.94 min. Ahora, él sabe -la relatividad es algo cotidiano para él- que este tiempo no es un tiempo propio para él porque en realidad ha cambiado de sistema de referencia, en cambio si lo es para la señora Y, ya que la partida del esposo y la vuelta a casa han ocurrido en el mismo lugar de su sistema de referencia. Por tanto el puede calcular el tiempo transcurrido según el reloj de la señora Y:

t =min = 12min

Como vemos, ambos están de acuerdo en que el señor X es 3.6 s menos viejo, no hay ninguna paradoja.

En unos diez años, manteniendo esta rutina, el señor X llegaría a ahorrase más o menos dos horas y media de vida respecto a su sedentaria señora.

Un avión moderno alcanza tranquilamente una velocidad de 864 Km/hr = 240 m/s que, en Relativilandia, significa una velocidad de: 0.8 c. A esta velocidad, el coeficiente de contracción es:

= 0.6

De manera que en Relativilandia, ven pasar el avión notablemente contraído, al 60% de su longitud en reposo y los procesos en el avión notoriamente más lentos.

Mientras mayor sea la velocidad de un objeto, los efectos relativistas son más evidentes. Cuando v ® c,® 0. Entonces, el tiempo en el reloj en movimiento tiende a detenerse y su longitud a hacerse cero. Si pudiéramos viajar a la velocidad de la luz el tiempo se detendría para nosotros y el espacio se contraería hasta desaparecer. La velocidad de la luz es el límite de velocidad que puede alcanzar un objeto. Nada puede moverse más rápido que la luz.

XII Momento lineal y energía relativistas

Como vimos, en el mundo relativista espacio y tiempo constituyen una unidad inseparable. Ambos dependen del estado de movimiento del sistema de referencia. Espacio y tiempo son relativos, pero las leyes de la mecánica son las mismas independientemente del sistema de referencia.

Habíamos visto que las ecuaciones de transformación de las coordenadas del espacio - tiempo entre dos sistemas inerciales O y O' (O' moviéndose con velocidad v en la dirección del eje X), son las siguientes:

Conviene, por comodidad, designar por b = ^v/_c a la velocidad relativa expresada en unidades de la velocidad de la luz. Consideremos además una variación de la posición Dx, Dy, Dz en un intervalo de tiempo Dt . Entonces, las ecuaciones de transformación serán:

Si tomamos los cuadrados de las cuatro coordenadas del espacio - tiempo relativista tenemos:

Y comprobamos que:

Es decir que la suma de los cuadrados de las componentes espaciales menos el cuadrado de la componente temporal es una cantidad invariante.Es la misma en cualquier sistema de referencia. Esta propiedad del espacio - tiempo es equivalente a la propiedad de la validez del teorema de Pitágoras en el espacio físico euclidiano.

Tenemos pues, una cantidad invariante, es decir, independiente del sistema de referencia que llamamos la norma del cuadrivector espacio - tiempo.

Si consideramos una partícula moviéndose con velocidad b respecto al sistema O y tomamos como sistema O' el sistema fijo a la partícula, es decir, el sistema propio de la partícula respecto al cual está en reposo, tendremos que Dx'=Dy'=Dz'=0. Entonces:

donde hemos designado por D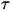 al tiempo propio de la partícula y

(Dr)² = (Dx)² + (Dy)² + (Dz)².

A partir de esta expresión, podemos deducir el momento lineal y la energía relativistas.

Consideremos una partícula moviéndose con velocidad instantánea b respecto a un sistema de referencia O. Sin perder generalidad podemos hacer que en ese instante la partícula pase por el origen de O y que los relojes del sistema O y el sistema propio de la partícula estén sincronizados, es decir que t₀=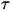0 = 0. Después de un tiempo t muy pequeño, lo suficientemente pequeño como para considerar la velocidad b prácticamente constante:

x² – c²t² = – c²

²

En este caso: Dx=x, Dy=0, Dz=0, Dt=t y D = .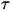

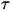Dividiendo nuestra expresión de la invarianza de la norma, entre el tiempo propio , tenemos:

y, recordando la relación entre tiempo propio y tiempo impropio:

tenemos, entonces:

Ahora bien, la partícula tiene una masa m₀ que la podemos pesar en el su sistema propio donde está en reposo. Multipliquemos la última expresión por el cuadrado de la masa a fin de introducir el momento lineal p=mv de la partícula.

Y, aquí vemos que en el sistema O, es decir aquel respecto al cual la partícula esta en movimiento, la masa es:

Entonces:

m²v² – m²c² = – m₀²c² p² – m²c² = – m₀²c²

Como en el caso del cuadrivector espacio - tiempo vemos que hemos encontrado un cuadrivector momento del espacio - tiempo que cumple la misma propiedad de conservación de su norma respecto a cualquier sistema de referencia. Sus componentes espaciales son: = m, es decir el momento lineal y su cuarta componente (componente temporal) es p₄= mc.

Lo importante aquí es que la masa de la partícula es una función de su estado de movimiento. La masa en movimiento es mayor que la masa en reposo.[²*^]

Para encontrar la energía relativista razonamos de la siguiente manera. Nuestra partícula de masa en reposo m₀ está siendo acelerada por la acción de una fuerza. Supongamos que en el instante t₀ = 0, la partícula está en reposo (v₀ = 0) y se encuentra en el origen de nuestro sistema de referencia O, es decir que x₀ = y₀ = z₀ = 0. La fuerza F tiene la dirección del eje x.

En un intervalo de tiempo t muy pequeño, la partícula ha adquirido una velocidad v y por tanto su masa respecto al sistema O será m = . Entonces, en ese instante:

m²v² – m²c² = – m₀²c² m²v² = (m² – m₀² )c²

El trabajo realizado por la fuerza F es igual a la variación de su energía cinética. Inicialmente su energía cinética es cero y después del tiempo t será:

E_K = mv²

Si el intervalo de tiempo t es lo suficientemente pequeño, la velocidad v será pequeña y m @ m₀ , entonces:

m²v² = (m + m₀ )(m - m₀ )c² m²v²@ 2mDmc² mv² = Dmc² DE = D mc²

De donde hemos encontrado que la energía de la partícula es igual a su masa por el cuadrado de la velocidad de la luz, la famosa ecuación de Einstein:

E = mc²

Este es uno de los más importantes descubrimientos de la teoría de la relatividad desarrollada por Einstein. Nos dice que masa y energía pueden transformarse una en la otra. La más dramática comprobación de ello es la bomba atómica. Al dividirse los núcleos (fisión nuclear) la masa de las partes resultantes es menor que la del núcleo original, la diferencia de masas se ha transformado en energía liberada con terribles consecuencias destructivas.

Finalmente diremos que la cuarta componente (componente temporal) del cuadrivector momento lineal es:

p₄ =

En el espacio - tiempo, el momento lineal y la energía forman una unidad: el cuadrivector momento.

Footnotes:

y considerar la masa m₀ como una propiedad invariante de la partícula, es decir, igual en cualquier sistema de referencia.

Fácilmente, de estas ecuaciones, se obtiene la relación entre la energía y momento relativistas:

E² = p²c² +c⁴

Al respecto recomendamos consultar el artículo de Nivaldo A. Lemos, "E=mc²: Origem e Significado", Revista Brasileira de Ensino de Física, vol. 23, no. 1, Marco, 2001.

• [1]Alonso M., Finn E.J., Física, Addison - Wesley Iberoamericana.
• [2]Born Max, La teoría de la relatividad de Einstein y sus fundamentos físicos, Biblioteca de ideas del siglo XX, Ed. CALPE, Madrid - Espańa, 1922.
• [3Dulia A.V., Teoría y problemas resueltos de dinámica, Ed. EDOBOL, La Paz - Bolivia, 1982.
• [4]Dulia A.V., Teoría y problemas resueltos de cinemática, Ed. Papiro, La Paz - Bolivia, 1981.
• [5]Feynman, Leighton, Sands., The Feynman lectures on Physics, Volume 1, Addison - Wesley Publishing Company, 1967.
• [6]Fuchs Walter R., El libro de la física moderna, Ediciones Omega S.A., Barcelona - Espańa, 1969.
• [7]Gamow George, Treinta ańos que conmovieron a la física, Editorial Universitaria de Buenos Aires, 1971.
• [8]Kaufmann William J., Relatividad y Cosmología, HARLA S.A., México, 1977.
• [9]Lemos Nivaldo A., E=mc²: Origem e Significado, Rev. Bras. de Ensino de Física, vol. 23, no. 1, Março, Brasil, 2001.
• [10]Russell Bertrand, ABC da Relatividade, Biblioteca de cultura científica, ZAHAR editores, Rio de Janeiro - Brasil, 1974.
• [11]Sagan Carl, Cosmos, Planeta, México, 1985.
• [12]Smith James H., Introducción a la Relatividad Especial, Editorial Reverté S.A., 1969.
• [13]Velarde Alfonso (A.V. DULIA), Leyes de conservación. Teoría y problemas resueltos., Escuela Profesional Don Bosco, Bolivia, 1984.
• [14]Velarde Alfonso, Curso Teórico Experimental de Física Básica, Carrera de Física, Universidad Mayor de San Andrés, Bolivia, 1999.
• [15]Zaratti Sacchetti Francesco, Física I. Ciclo Medio y Preuniversitario, Editorial Don Bosco, La Paz - Bolivia, 1989.

¹

^[*

^] Carl Sagan, "Viajes a través del espacio y el tiempo", "Cosmos", Ed. Planeta S.A., Barcelona, 1985

²

^[*

^] Esta afirmación es controvesial. No se puede medir directamente la masa de una partícula en movimiento. Sólo podemos medir sus efectos dinámicos, a través de medir su momento lineal y su energía. De donde, si somos estrictos, debemos más bien considerar las expresiones relativistas del momento lineal y de la energía como:

Fechas de Publicación

• Publicación en esta colección
  20 Ene 2003
• Fecha del número
  Set 2002

Histórico

• Acepto
  13 Abr 2002
• Recibido
  01 Abr 2002