Transições de fase sem termodinâmica

Phase transitions without thermodynamics

ARTIGOS GERAIS

Transições de fase sem termodinâmica

Phase transitions without thermodynamics

Adriana G. Dickman^I,1; Ronald Dickman^II,2; Fabrício Almeida Barbosa^I

^IDepartamento de Física e Química, Pontifícia Universidade Católica de Minas Gerais, Belo Horizonte, MG, Brasil

^IIDepartamento de Física, Universidade Federal de Minas Gerais, Belo Horizonte, MG, Brasil

RESUMO

As aplicações de transições de fase vão muito além do contexto da termodinâmica de equilíbrio, de onde surgiu. Nós revisamos um dos principais exemplos de uma transição de fase em um sistema sem termodinâmica, o processo de contato (PC), com ênfase no método de campo médio. Apresentamos um estudo de campo médio aplicado a um modelo para a transmissão da malária em uma população. Discutimos também as novas abordagens da distribuição quase-estacionária e o processo de contato conservativo.

Palavras-chave: transições de fase, processo de contato, aproximação de campo médio, malária.

ABSTRACT

Phase transitions find application well beyond the context of equilibrium thermodynamics, where they arose. We review one of the prime examples of a phase transition in a system lacking thermodynamics, the contact process (PC), emphasizing mean-field theory methods. We also present mean-field results for a model of transmission of malaria in a population, and discuss the new approaches of quasi-stationary distributions, and the conserved contact process.

Keywords: phase transitions, contact process, mean-field approximation, malaria.

1. Introdução

No nosso dia a dia nos deparamos com questões que pensamos serem raramente abordadas por modelos científicos. Será que já foi investigado o porque de ser muito mais comum ficar gripado no inverno do que no verão? Será que fatores como maior agrupamento de pessoas dentro de casa, escritório com janelas fechadas seriam relevantes para esta questão? Será que existe algum modelo matemático que possa ajudar a esclarecer fatos como estes?

O espalhamento de doenças epidêmicas é um dos problemas mais importantes da ciência médica. O número de pessoas contaminadas pela AIDS aumenta a cada dia, e muitas outras doenças como a malária e a influenza ainda fazem um número substancial de vítimas. Em epidemiologia - estudo científico da ocorrência, transmissão e controle da doença, modelos matemáticos são importantes para quantificar padrões de espalhamento da doença e compreender o processo de transmissão.

Neste trabalho procuramos entender um pouco mais sobre o processo de espalhamento de uma epidemia, empregando ferramentas de física teórica. Esta discussão mostra que as idéias de mecânica estatística têm aplicação muito além do contexto termodinâmico, onde nasceu. Para tal utilizamos o processo de contato, introduzido por Harris [1, 2] como um modelo simples para epidemias e um modelo para a transmissão da malária.

Modelos como estes são importantes na área de física estatística, que procura entender os fenômenos relacionados com sistemas de muitas entidades interagentes. Nas décadas passadas, teorias gerais de transições de fases e de fenômenos críticos foram desenvolvidas, unificando a compreensão de transições gás-líquido, transições magnéticas, cristais líquidos e outros sistemas [3, 4, 5]. Esta grande atividade no estudo de transições de fases em sistemas termodinâmicos de equilíbrio, foi acompanhada por desenvolvimentos paralelos em sistemas fora do equilíbrio, e até em sistemas sem termodinâmica (para os quais os conceitos de energia e trabalho não se aplicam). O exemplo proeminente da última categoria é a percolação, o modelo mais simples de uma transição de fase geométrica [6, 7, 8].

A idéia de transições de fases foi umas das mais frutíferas a ser exportada da física para outras áreas; está sendo utilizada na teoria de populações biológicas, em inteligência artificial e em teoria da computação. (Também em áreas mais familiares para os físicos: processos relativos ao funcionamento do laser, processos nucleares, e em hidrodinâmica.) Portanto, seria útil haver uma definição de "transição de fase" que não fosse baseada na termodinâmica. Para a presente discussão, uma definição adequada, não muito formal, seria: uma transição de fase é uma mudança abrupta, singular, das propriedades macroscópicas de um sistema de muitas unidades, como função dos parâmetros de controle. Cabe nesta descrição as transições familiares (a propriedade macroscópica pode ser, por exemplo, a magnetização de um bloco de ferro, enquanto os parâmetros de controle são a temperatura e o campo magnético externo), e também os exemplos de sistemas fora do equilíbrio como os citados acima (percolação, epidemias).

Neste artigo pretendemos apresentar ao leitor uma transição de fase sem termodinâmica, ilustrando alguns dos métodos utilizados para estudá-la: teoria de campo médio e análise de probabilidades. Usamos como exemplos o processo de contato e um modelo matemático para a malária. No processo de contato a interação entre os indivíduos é direta, enquanto que no modelo para a malária há a presença de um vetor na transmissão da doença.

O processo de contato é um sistema de partículas interagentes que pode ser interpretado como um modelo para descrever o espalhamento de uma infecção. Neste contexto, cada sítio de uma rede d-dimensional representa um indivíduo que pode estar infectado ou saudável. O sistema evolui segundo uma dinâmica estocástica, que consiste dos eventos elementares de infecção e recuperação. (Uma definição mais precisa do modelo se encontra na próxima seção.) A infecção se espalha através do contato direto entre indivíduos infectados e saudáveis. O espalhamento da infecção depende de um parâmetro de infecção que chamaremos de l. Indivíduos infectados se recuperam com uma taxa unitária e são suscetíveis a re-infecção. Como um indivíduo deve ter pelo menos um vizinho doente para tornar-se infectado, o estado no qual todos os indivíduos são saudáveis é absorvente: o sistema não pode escapar desta configuração! Neste contexto, o estado absorvente representa o fim da epidemia.

A persistência da epidemia é controlada pelo parâmetro de infecção. Se l é muito pequeno, a extinção da infecção em tempos longos é certa; por outro lado, grandes valores de l asseguram que a infecção pode espalhar indefinidamente. A fronteira entre persistência e extinção é marcada por um ponto crítico, o qual é denotado por l_c. O parâmetro crítico l_c separa os dois estados estacionários que o sistema pode atingir em tempos longos: um estado livre de doenças (absorvente), e um estado "ativo" onde a epidemia sobrevive. l_c marca uma transição de fase contínua entre um estado absorvente e um estado ativo.

O restante deste artigo é organizado do seguinte modo, na seção 2 apresentamos os modelos básicos; na seção 3 discutimos a aproximação de campo médio para o processo de contato; na seção 4 discutimos a distribuição do estado quase-estacionário para o processo de contato; na seção 5 abordamos o processo de contato conservativo e finalmente, na seção 6 apresentamos o modelo para a transmissão da malária e uma análise utilizando as técnicas de campo médio.

2. Modelos básicos

2.1. Processo de contato

Nesta seção definimos as regras do processo de contato (PC), seguida de uma breve discussão da sua relação com a percolação direcionada. Esta relação entre os dois modelos é importante, pois a percolação direcionada define uma classe de universalidade, sendo um modelo bastante estudado e com inúmeras aplicações. Modelos que pertencem à mesma classe de universalidade compartilham o mesmo comportamento singular nas vizinhanças do ponto crítico, em particular, os valores dos chamados expoentes críticos [3, 4, 5].

No PC, cada sítio i de uma rede hiper-cúbica representa um indivíduo que pode estar em um dos dois estados, saudável ou infectado, denotado por s_i = 0 ou 1, respectivamente. O estado s_i de cada indivíduo pode ser alterado de acordo com as seguintes regras: indivíduos infectados podem tornar-se saudáveis (s_i = 1 ® s_i = 0), a uma taxa unitária, independentemente de seus vizinhos; indivíduos saudáveis podem ser infectados a uma taxa nl/2d, onde n é o número de vizinhos infectados e d a dimensão do sistema. Assim, n/2d é a fração dos 2d vizinhos que estão atualmente infectados.

A Fig. 1 mostra as possíveis mudanças de configuração em uma rede unidimensional (d = 1) com condições periódicas de contorno, ou seja, o último sítio da direita é vizinho do primeiro sítio da esquerda, e vice-versa. No diagrama o círculo cheio representa um indivíduo infectado, e o círculo vazio representa um indivíduo saudável. Iniciando com uma configuração do tipo , onde os três indivíduos estão infectados, é possível obter um dos três estados seguintes: , , ou . Em cada um destes estados um dos indivíduos inicialmente infectado se recuperou. Seguindo a linha do estado podemos obter: ou com a recuperação de um dos indivíduos infectados, ou com a reinfecção do único indivíduo saudável. E finalmente, a partir do estado podemos voltar aos estados ou com a reinfecção de um dos indivíduos saudáveis, ou chegar ao estado , do qual o sistema não pode mais sair. Este estado é chamado de estado absorvente. É importante salientar que um indivíduo saudável só será infectado se ele possuir vizinhos infectados.

Para distinguir as duas fases, introduzimos, como é costume na física estatística, um parâmetro de ordem. No PC o parâmetro de ordem r é a densidade estacionária de indivíduos infectados, que se anula no estado absorvente, o qual é caracterizado pela ausência de indivíduos infectados. Quando l aumenta além de l_c o sistema sofre uma transição de fase contínua do estado absorvente para um estado estacionário ativo.

Na transição de fase do PC o parâmetro de ordem (r) cresce continuamente a partir de zero à medida que o parâmetro de infecção aumenta além do valor l_c, como mostrado na Fig. 2. Perto do ponto crítico, o parâmetro de ordem vai para zero segundo uma lei de potência caracterizada por:

r ~ (l – l_c)^b ,

onde b é o expoente crítico associado ao parâmetro de ordem. A independência dos expoentes críticos com os detalhes da maioria dos sistemas é conhecida como universalidade. Modelos com o mesmo conjunto de expoentes críticos formam uma classe de universalidade. Em geral, uma classe de universalidade é determinada por características globais tais como dimensionalidade do espaço, dimensão do parâmetro de ordem, simetria e alcance das interações [9]. Modelos que possuem uma transição contínua para um único estado absorvente geralmente pertencem à mesma classe de universalidade do modelo de percolação direcionada (PD) [10, 11, 12, 13].

2.2. Percolação direcionada

O problema de percolação vem sendo amplamente estudado desde que foi introduzido por Broadbent e Hammersley em 1957 [6, 7, 8] para tentar solucionar o entupimento de máscaras de gás. Percolação de ligação simples é definida sobre uma rede, onde cada sítio está ligado ao sítio vizinho se a ligação entre os dois estiver presente. Cada ligação está presente com uma probabilidade p, independentemente das outras. Se p é pequena, então esperamos apenas regiões conexas bem pequenas (a máscara não serve para respirar). Acima de uma probabilidade crítica p_c, a rede percola, ou seja, existe um agrupamento de sítios infinito conectando bordas opostas da rede. A presença de tal agrupamento pode representar a possibilidade da água percolar através de uma rocha porosa, ou uma condutividade não-nula numa rede diluída de resistores. Apesar do fato de os conceitos de energia e trabalho não se aplicarem, o modelo de percolação apresenta uma transição de fase em p_c. Esta transição foi estudada intensivamente utilizando ferramentas desenvolvidas no estudo de transições ferromagnéticas.

Percolação direcionada (PD) [6] pode ser definida como um problema de percolação de ligação comum, no qual as ligações são distribuídas aleatoriamente sobre a rede com concentração p, com a introdução de uma direção preferencial para o problema, por exemplo, uma rede diluída de diodos (o diodo conduz corrente apenas em uma direção). Para realizar o processo, deve-se girar a rede quadrada usual de 45º, tal que cada sítio tenha dois vizinhos mais próximos na linha acima, e dois na linha abaixo. Cada sítio está ou "molhado" ou "seco" (imaginamos que a linha superior esteja ligada a um reservatório de água que vai percolar a rede se existir um caminho de ligações). Cada elo na rede está presente, independentemente, com uma probabilidade p; a água só pode escoar de cima para baixo. É comum chamar os sítios molhados de "partículas" e os outros de sítios vazios. A Fig. 3 mostra as regras de transição para a percolação de ligação direcionada.

Na Fig. 4 está representada uma configuração típica de percolação de ligação direcionada. A primeira linha representa o estado inicial, o qual é conectado por ligações diagonais às partículas da linha abaixo. Cada uma destas ligações orientadas está presente com uma probabilidade p independente das outras ligações. Um sítio desta rede está conectado à origem se e somente se ele está conectado ao sítio da camada anterior que está por sua vez conectado à origem. Há uma concentração crítica p_c abaixo da qual a probabilidade de formar um agrupamento de percolação infinito é zero. Próximo de p_c o sistema possui os comprimentos característicos x_^ e x_||, perpendicular e paralelo à direção principal, respectivamente, que divergem como:

onde n_^ e n_|| são os expoentes críticos relacionados. x_^ e x_|| representam as dimensões típicas dos agrupamentos para p < p_c. Ambas, percolação isotrópica e percolação direcionada exibem um ponto crítico. Embora não possuam uma interpretação termodinâmica, propriedades de escala associadas com correlações de longo alcance surgem, como em fenômenos críticos de equilíbrio. A diferença de simetria entre os casos isotrópico e dirigido faz com que os expoentes críticos sejam distintos.

Uma interpretação interessante é obtida se considerarmos a direção preferencial como o tempo; as outras dimensões podem representar uma rede espacial. Esta interpretação permite mapear a PD na teoria de campo de Reggeon (RFT) [14], uma teoria de física de partículas de alta energia, que modela a seção de choque de espalhamento de partículas altamente energéticas. Uma análise do RFT mostra que ele apresenta uma transição de fase na mesma classe de universalidade que a PD. A transição do PC também pertence a esta classe de universalidade. Na verdade, o processo de contato d-dimensional corresponde à percolação direcionada em (d + 1) dimensões. Isto pode ser visto considerando um análogo discreto no tempo do PC no qual todos os sítios são atualizados simultaneamente. Uma grande variedade de modelos de catálise também envolve transições de fase com as mesmas características [12, 15].

3. Campo médio para o processo de contato

Como uma primeira aproximação na tentativa de entender o comportamento geral do modelo, utilizamos técnicas de campo médio - aproximação de clusters. Esta é uma técnica bem estabelecida em física estatística, tendo sido aplicada em modelos de spin, e também percolação direcionada e reações de catálise. De modo geral, o método consiste em tratar como independentes, eventos associados com sítios afastados por uma certa distância. Assim, na aproximação de sítios (a mais simples possível), cada sítio é tratado como se fosse independente dos outros. Na aproximação de pares, sítios separados por duas ou mais constantes de rede são considerados como independentes, e assim por diante. Sob a hipótese de independência, a probabilidade conjunta P(s₁,...,s_N) pode ser fatorizada, simplificando a análise radicalmente. Os métodos de campo médio aplicados à energia livre são muito familiares da mecânica estatística de equilíbrio [5, 16]; no contexto de não-equilíbrio trabalhamos com a dinâmica (equação mestra) sendo a distribuição estacionária de probabilidade desconhecida. Os resultados obtidos através desta análise, em geral, dão uma boa descrição qualitativa do modelo, mas são quantitativamente pobres. Ainda assim, a aplicação do método se justifica por ser a técnica mais simples para a abordagem de modelos matemáticos e seus resultados servem de guia para outras investigações. Nesta seção nós mostramos como aplicar este método e obter informações sobre o comportamento do PC no nível de sítios.

Nós consideramos o PC como definido na seção anterior em uma dimensão. s_i = 1 representará o estado do sítio i tendo um indivíduo infectado, e s_i = 0 quando o indivíduo estiver saudável. A probabilidade de que o sítio i esteja infectado no tempo t é representado por P(s_i = 1;t) º r (analogamente, 1 – r representa a probabilidade de que o sítio i não esteja infectado). Na Tabela 1 estão as taxas de mudança para cada evento do PC unidimensional.

No primeiro evento ocorre a infecção do indivíduo localizado no sítio central a uma taxa l; tratando cada sítio independentemente e assumindo homogeneidade espacial, podemos escrever a probabilidade para encontrar o agrupamento nesta configuração como r²(1 – r). Cada contribuição para a equação de evolução é dada pelo produto da taxa de mudança e da mudança no número de partículas, DN. Assim, considerando os quatro eventos possíveis mostrados na Tabela 1, a equação de evolução para r é dada por, após alguma álgebra,

O regime estacionário é caracterizado por dr/dt = 0, não havendo mudanças macroscópicas no sistema. Para l < 1 a única solução estacionária é o vácuo, = 0. Para l > 1 nós encontramos também uma solução estacionária ativa, = 1 – l^–1. Pode-se mostrar que para l > l_c = 1 o estado ativo é estável e o vácuo instável. l_c marca o ponto crítico, no qual a densidade estacionária muda continuamente, porém de uma maneira singular.

A Eq. (1) é a própria equação de Malthus-Verhulst [17], que descreve a evolução temporal do tamanho r de uma população que se reproduz mas cujo crescimento é limitado por fatores ambientais (recursos finitos). É facilmente integrada, dando:

onde µ = l – 1 e r₀> 0 é o tamanho inicial da população. Evidentemente, r(t) se aproxima do valor estacionário (1 – l^–1, se µ > 1, e 0 no caso contrário) para tempos t |µ|^–1. No ponto crítico, µ = 0, a população decai algebricamente:

Voltando à solução estacionária, observamos que é o parâmetro de ordem para esta transição, assumindo um valor não-nulo somente para l > l_c. Perto do ponto crítico o parâmetro de ordem geralmente segue a lei de potência,

onde D º l – l_c. Portanto, na aproximação de campo médio do PC encontramos b = 1, uma vez que = D + (D²) para D > 0. Visto como um sistema dinâmico, podemos afirmar que a Eq. (1) exibe uma bifurcação transcrítica em l = 1 [18], ou seja, nesse ponto há uma troca de estabilidade no sistema. Isso ilustra uma correspondência mais geral, entre uma transição de fase (em um sistema de muitas unidades interagentes) e uma bifurcação na descrição dinâmica de campo médio.

Esta análise simples de campo médio prevê um diagrama de fase qualitativamente correto, enquanto fornece valores muito ruins para o ponto crítico e os expoentes. Por exemplo, l_c @ 3,29 e b @ 0,277 em d = 1. Isto é uma conseqüência direta de se desprezar correlações entre os sítios; de fato eles são altamente correlacionados. É importante observar que os expoentes de campo médio são incorretos para dimensões espaciais d < d_c. d_c é a dimensão crítica, acima da qual os expoentes críticos são do tipo campo médio; d_c = 4 para o PC [10, 11, 16]. Cada sistema possui uma dimensionalidade particular, conhecida como dimensão crítica, acima da qual a teoria de campo médio fornece a descrição correta das propriedades críticas [16].

4. Estado quase-estacionário

Quando simulado em uma rede finita, o processo de contato evolui para, afinal, o estado absorvente. Isso ocorre porque, se o número de configurações é finito, a taxa para entrar no estado absorvente é maior que zero, enquanto a taxa para sair é, por definição, nula. Entretanto, simulações computacionais (sempre de sistemas finitos!) são utilizadas para estudar o estado estacionário do modelo. Como é possível conseguir isto, se o estado estacionário é sempre absorvente, uma rede vazia? Na verdade, para redes razoavelmente grandes e l > l_c, o sistema pode permanecer ativo por um tempo suficientemente longo para que as propriedades (dado que o sistema ainda não tenha atingido o estado absorvente) atinjam valores que independem do tempo. São estas propriedades quase-estacionárias que obtemos em simulações. O estado quase-estacionário converge para o verdadeiro estacionário no limite L ® ¥, onde L é a dimensão linear da rede.

Para uma revisão da teoria e aplicação de distribuições quase-estarionárias veja as referências [19, 20]. Aqui nós ilustramos a idéia com uma conta exata para o PC num anel de três sítios, a partir da equação mestra [21]. O espaço de configurações e as transições neste sistema minúsculo foram representados na Fig. 1 (observe que a configuração não tem nenhuma transição saindo dela, o que a define como absorvente). Apesar de ter oito configurações, a simetria entre as três configurações com apenas uma partícula (e, novamente, entre as três configurações com duas partículas), implica que são necessárias apenas quatro variáveis para escrever a equação mestra do processo:

Aqui, p₁ é a probabilidade de ter qualquer uma das três configurações com uma partícula, analogamente para p₂ com duas partículas, tal que a normalização das probabilidades se escreve: p₀ + 3p₁ + 3p₂ + p₃ = 1. É fácil ver que a probabilidade é conservada pelas equações, e que a única solução estacionária é p₀ = 1. Para encontrar a distribuição quase-estacionária (QE), definimos, para i > 0,

que representa a probabilidade do sistema estar no estado i, dado que o processo tenha sobrevivido até o tempo t. Para tempos longos as p_i,s convergem para a distribuição quase-estacionária. Na Fig. 5 mostramos a densidade , e a razão m = no estado quase-estacionário, em função de l, obtidas por integração numérica das equações. A densidade cresce continuamente, enquanto m (a flutuação relativa da densidade), exibe um máximo. (Observe que para l = 0 ou l ® ¥, a distribuição QE está concentrada ou em 1 ou em 3, e não há flutuações.) É de se esperar que, aumentando o número de sítios, a dependência de r com l se aproxime da curva mostrada na Fig. 5, enquanto o máximo de m fica cada vez mais agudo.

5. Processo de contato conservado

Em mecânica estatística de equilíbrio, podemos estudar o mesmo sistema usando vários ensembles [5]. O que distingue um ensemble do outro são os vínculos. No ensemble microcanônico, por exemplo, a energia do sistema é estritamente fixa, enquanto no ensemble canônico a temperatura é fixa, e a energia flutua. Sabemos que, no limite de tamanho infinito, os vários ensembles fornecem previsões equivalentes para as propriedades macroscópicas. Será que podemos definir ensembles distintos fora do equilíbrio, por exemplo, para o processo de contato?

Uma resposta afirmativa, preliminar, vem do trabalho recente de Tomé e de Oliveira [22], no qual foi investigado o Processo de Contato Conservado (PCC). Neste modelo, N(< L^d) pessoas infectadas são colocadas em uma rede com L^d sítios, que pode ser finita ou infinita. (Como sempre, cada sítio pode ter no máximo uma pessoa.) Cada pessoa saudável pode se tornar infectada com uma taxa n/2d , sendo n o número de vizinhos infectados. Mas agora, quando uma pessoa torna-se infectada, não é por transmissão da infecção, mas sim pela transferência de uma pessoa infectada para tal sítio, escolhida aleatoriamente, entre todas as N pessoas infectadas. Assim, o número N de pessoas infectadas é estritamente conservado.

Para ver a conexão com o processo de contato usual, observe que é possível, por uma simples re-escala da unidade de tempo, dividir todas as taxas de transição no PC por l, tal que um sítio vazio torna-se ocupado com uma taxa n/2d, enquanto o processo reverso ocorre com uma taxa de 1/l. Assim, a taxa do processo no PC é a mesma que no PCC. Para encontrar o valor efetivo de l no PCC, basta encontrar a taxa do processo no PC. Evidentemente a taxa total de tais transições é , onde o numerador representa o número total de pares vizinhos tipo . A taxa para um sítio ocupado tornar-se vazio é então , dando, no estado estacionário,

Fica claro agora que no PCC o parâmetro de ordem, = N/L^d, tem valor fixo, enquanto o parâmetro de controle l flutua (observe que é necessária uma rede infinita para estudar o regime subcrítico, mas isso não causa dificuldades nas simulações, uma vez que N é finito.) Verifica-se em simulações que o valor crítico l_c, e o expoente crítico b, são iguais nos dois ensembles [22]. Logo depois, uma demonstração formal da equivalência foi feita [23]. O PCC também foi usado para localizar o valor crítico com uma precisão inédita em dimensões d = 1 - 5 [24].

Fazemos agora uma análise de campo médio para o PCC unidimensional. Na fase ativa, o tamanho L da rede é finito, e o número esperado de pares tipo é:

onde supomos N 1 e, no espírito da aproximação de campo médio, tratamos o estado de cada sítio como independente. (Assim, (L – N)/L representa a probabilidade de um determinado sítio estar vazio.) Da Eq. (6), encontramos:

exatamente como na teoria de campo médio do PC original. Observe que, para qualquer N (fixo), l ® 1 = l_c, quando L ® ¥. Nas simulações l também aproxima do seu valor crítico, deixando L ® ¥ e o parâmetro de ordem ir a zero. Esta situação lembra a criticalidade auto-organizada [25, 26], em que um sistema com uma transição de fase para um estado absorvente é forçado a permanecer no ponto crítico, na aparente ausência de ajuste de parâmetros [27].

6. Modelo para o espalhamento da malária

Estudamos a transmissão e espalhamento da malária em uma população utilizando as técnicas de campo médio. Para tal, definimos um modelo matemático que descreve os principais mecanismos de transmissão da doença usando como base modelos previamente definidos.

No início do século XX, Ross [28] descobriu que o parasita que causa a malária é transmitido ao ser humano pela fêmea infectada do mosquito Anopheles. O ciclo de vida do parasita se alterna entre hospedeiros humanos e mosquitos, cujas formas evidenciam os diferentes estágios do processo. A seguir damos uma descrição qualitativa do processo, uma vez que detalhes quantitativos irão variar de uma espécie para outra de parasitas, ou de populações humanas diferentes.

A fêmea infectada é caracterizada por possuir glândulas salivares invadidas por formas esporozoitos do parasita. Os esporozoitos são células que infectam novos hospedeiros e constituem a forma infectante para o homem. Uma vez dentro do hospedeiro, os esporozoitos migram para o fígado, onde se multiplicam assexuadamente. Há então uma liberação de formas trofozoitos - estágio ativo no ciclo de vida dos parasitas, na corrente sangüínea. Esses, invadem e permanecem nos glóbulos vermelhos que ao se romperem liberam formas merozoitos - células-filhas dos parasitas resultantes da reprodução assexuada, que invadem novos glóbulos vermelhos, repetindo o ciclo várias vezes. Em um dado momento, os gametócitos, que são formas sexuadas do parasita, surgem de alguns dos merozoitos, assim, o sangue de uma pessoa infectada pode conter diferentes formas do parasita.

As fêmeas do mosquito são infectadas pelos gametócitos ao se alimentarem do sangue de um ser humano infectado. Os gametócitos machos e fêmeas se acasalam no estômago do mosquito formando zigotos, que penetram as paredes estomacais e formam oocistos, que se rompem liberando um grande número de esporozoitos. Alguns desses esporozoitos migram para as glândulas salivares do mosquito e o ciclo completo se repete.

O ciclo de vida do parasita, dentro de hospedeiros sucessivos, é complexo, mas a dinâmica do processo de transmissão pode ser esboçada de uma forma simples. Os seres humanos só podem adquirir malária de mosquitos infectados, e mosquitos só podem adquirir a infecção de seres humanos infectados. Em modelos mais abrangentes, pode-se levar em consideração, por exemplo, mais detalhes do ciclo do parasita, casos de superinfecção, onde cada hospedeiro pode receber uma infecção adicional, e também o impacto da reação imunológica na aquisição de infecção adicional [29, 30, 31].

Em qualquer modelo que descreva a dinâmica da malária, deve-se introduzir a população humana I (tamanho N₁) e a população de mosquito II (tamanho N₂). A dependência recíproca das populações humana e de mosquitos na propagação da malária se assemelha a dois processos de contato entrelaçados. Nos modelos mais simples as populações não mudam de tamanho. Longevidade em I é muito maior do que em II, assim é necessário interpretar a invariabilidade de N₁ e N₂ diferentemente. Em I esta invariabilidade significa que nascimentos, mortes, imigrações ou emigrações são de pouca importância na escala de tempo da epidemia, mas qualquer indivíduo pode ser infectado, então curado, infectado novamente, e assim por diante. Em II, similarmente, não há imigração ou emigração, mas devido ao curto tempo de vida dos mosquitos, podemos supor uma população de tamanho fixo. Para manter o tamanho de uma população constante, simplesmente assumimos que cada morte é compensada por um nascimento.

Definimos o nosso modelo em uma rede quadrada onde cada sítio representa um ser humano que pode estar infectado ou saudável. Cada sítio da rede também pode estar ocupado por um mosquito saudável ou infectado. A evolução do modelo se dá de acordo com as seguintes regras:

• Mosquitos difundem sobre a rede a uma taxa ;

• Mosquitos saudáveis se tornam infectados a uma taxa I ao ocuparem o mesmo sítio que um ser humano infectado;

• Mosquitos infectados se recuperam a uma taxa R₂;

• Seres humanos saudáveis se tornam infectados a uma taxa I ao ocuparem o mesmo sítio que um mosquito infectado;

• Seres humanos infectados se recuperam a uma taxa R₁.

6.1. Campo médio simples

Abordamos o modelo para a malária utilizando a aproximação de sítios (campo médio) como foi explicado na seção 3. Para implementar esta técnica seguimos os passos:

• De acordo com as regras e possíveis arranjos de pessoas e mosquitos na rede, constrói-se uma tabela incluindo todas as taxas de todos os eventos possíveis;

• De posse destas taxas, escreve-se a equação de evolução do número de pessoas infectadas, do número de mosquitos infectados, e assim por diante;

• Deste conjunto de equações extrai-se os valores estacionários para as grandezas de interesse;

• Através da análise dos dados (gráficos, instabilidade) tem-se uma descrição qualitativa do comportamento geral do modelo.

Usaremos a notação mostrada na Tabela 2 para representar os possíveis estados de um sítio.

Na Tabela 3 representamos as possíveis transições entre os estados de sítios diferentes.

Na Tabela 4, listamos as taxas de transição para cada evento possível, de acordo com a Tabela 3.

A partir destas taxas, podemos escrever as equações de evolução para as probabilidades, adicionando os termos que aumentam a probabilidade de um dado estado, e subtraindo os termos que diminuem a probabilidade deste mesmo estado.

Resolvendo estas equações no estado estacionário (onde as derivadas das probabilidades são iguais a zero), e utilizando:

obtemos:

para a densidade de pessoas infectadas, e

para a densidade de mosquitos infectados, onde P_m = A+B+D+E é a probabilidade de se encontrar um mosquito na rede. Na Fig. 6 mostramos os gráficos obtidos para R₁ = 1, R₂ = 2, P_m = 0,6; (a) = 0,1; (b) = 1 e (c) = 100. Da Eq. 10, vemos que a sobrevivência da epidemia depende da condição P_mI²> R₁R₂(R₁ + R₂ + + 2I). Resolvendo para I, encontramos que a sobrevivência exige:

Como podemos observar no gráfico, tanto a densidade de mosquitos infectados como a de seres humanos infectados é maior do que zero a partir de I_c = 68,2 para uma taxa de difusão = 0,1; I_c = 8,3 para = 1 e I_c = 1,9 para = 100. A densidade de pessoas infectadas (representada em linha cheia no gráfico) é descrita por uma curva com uma taxa de crescimento mais acentuada, que atinge a saturação em um valor próximo de 0,6 para = 0,1; 0,75 para = 1,0 e 1,0 para = 100. A densidade de mosquitos infectados (representada em linha fina no gráfico) é descrita por uma curva com uma taxa de crescimento mais suave, atingindo a saturação para I (taxa de infecção) aproximadamente igual ao caso dos humanos. O valor de saturação varia com a taxa de difusão tendendo para os valores r ~ 1 para a densidade de pessoas infectadas, e s ~ 0,6 = P_m para a densidade de mosquitos infectados. Uma alta difusão de mosquitos pela rede, propicia a infecção dos seres humanos, fato que é confirmado pelo maior valor de saturação.

A região acima da curva de linha cheia representa estados do sistema onde as populações de mosquitos e seres humanos não apresentam sinais de infecção. Com o aumento da taxa de difusão de mosquitos esta região diminui e comparando os três gráficos podemos concluir que à medida que a difusão aumenta, esta região torna-se menor. O valor crítico da taxa de infecção I_c também mostra uma dependência com o parâmetro , tornando-se menor à medida que este aumenta. Este valor crítico marca o ponto a partir do qual a infecção sempre estará presente nas populações, portanto, para difusões maiores é natural que isto aconteça em taxas de infecção menores. A difusão atua como um fator que ajuda a aumentar a transmissão da malária.

É natural perguntar se existe alguma correlação entre a presença de um ser humano infectado e um mosquito infectado no mesmo sítio. Para quantificar o grau de correlação calculamos a covariância, ou seja, a probabilidade conjunta de ter ambos infectados no mesmo sítio menos o produto das probabilidades dos dois eventos. Uma covariância nula indica ausência de correlações. A teoria de campo médio fornece:

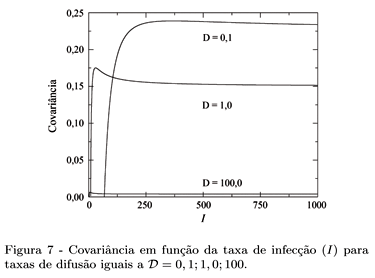
Os gráficos da Fig. 7 mostram a covariância para diferentes valores da taxa de difusão. De acordo com a figura, percebemos que há uma correlação positiva entre s e r, como é de se esperar, pois a presença de uma pessoa infectada aumenta a chance de um mosquito estar infectado no mesmo sítio e vice-versa. É interessante observar que para uma taxa de difusão maior ( = 100), a covariância é praticamente nula. Uma taxa de difusão alta provoca uma mistura dos componentes do sistema, diminuindo as correlações entre as populações.

Uma aproximação mais simples do método, seria considerar as probabilidades de haver um mosquito e um ser humano em um dado estado, ocupando o mesmo sítio, como independentes. Assim, Cov º 0. Na Tabela 4 as taxas seriam simplificadas, por exemplo, a taxa T₁ ficaria:

onde P_m é a probabilidade de haver mosquitos na rede. A mudança nas outras taxas ocorre analogamente, e é deixada como exercício ao leitor interessado. As densidades estacionárias para este caso são:

No ponto crítico os valores estacionários da densidade de mosquitos e seres humanos infectados se anulam, sendo caracterizado por . Os resultados para esta aproximação são mostrados na Fig. 8, para os valores R₁ = 1, R₂ = 2 e P_m = 0,6. Nesta aproximação mais simples a difusão dos mosquitos passa a ser irrelevante para o espalhamento da doença.

7. Conclusões

Apresentamos uma revisão didática do processo de contato, o mais simples modelo que exibe uma transição de fase para um estado absorvente, fenômeno intrinsicamente longe do equilíbrio. O comportamento singular das propriedades macroscópicas como função do parâmetro l, e as evidências de escala na vizinhança do ponto crítico, mostram que um sistema sem uma interpretação termodinâmica é capaz de gerar uma verdadeira transição de fase.

Aplicamos a teoria de campo médio para o modelo para a transmissão da malária e obtemos os diagramas de fases mostrando o comportamento do sistema para diferentes valores da taxa de difusão. O cálculo da covariância reforça a importância das correlações entre os componentes do sistema, principalmente para taxas de difusão baixas.

Discutimos aqui dois métodos muito usados nestes estudos: a teoria de campo médio e a análise probabilista. Cabe mencionar outros métodos muito importantes, cuja discussão deve ficar para uma outra ocasião: simulação Monte Carlo, expansão em série [32] e grupo de renormalização [16, 33].

Atualmente, existe uma grande procura das classes de universalidade de transições para um estado absorvente [34], uma vez que tais transições são associadas aos modelos de catálise, populações, criticalidade auto-organizada, e transição para turbulência. Dadas estas conexões (e outras) com várias áreas da física de sistemas complexos fora do equilíbrio, é de se esperar ainda mais atividade em modelos como o processo de contato e modelos afins no futuro.

8. Agradecimentos

A.G. Dickman e F.A. Barbosa agradecem o apoio financeiro ao projeto de pesquisa Estudo do espalhamento da malária em uma população através de um modelo matemático pelo Fundo Interno de Pesquisa da Pontifícia Universidade Católica de Minas Gerais (FIP-PUCMINAS). R. Dickman agradece ao CNPq pelo apoio financeiro.

Referências

[1] T.E. Harris, Ann. Prob. 2, 969 (1974).

[2] T.M. Liggett, Interacting Particle Systems (Springer-Verlag, New York, 1985).

[3] M. Plischke and B. Bergersen, Equilibrium Statistical Physics (Prentice Hall, Englewood Cliffs, New Jersey, 1989).

[4] J.J. Binney, N.J. Dowrick, A.J. Fisher, and M.E.J. Newman, The Theory of Critical Phenomena (Oxford University Press, Oxford, 1992).

[5] S.R. Salinas, Introdução à Física Estatística (EdUSP, São Paulo, 1999).

[6] S.R. Broadbent and J.M. Hammersley, Proc. Cam. Phil. Soc. 53, 629 (1957).

[7] D. Stauffer and A. Aharony, Introduction to Percolation Theory (Taylor & Francis, London, 1994).

[8] R. Durrett, Lecture Notes on Particle Systems and Percolation (Wadsworth, Pacific Grove, CA, 1998).

[9] J. Marro and R. Dickman, Nonequilibrium Phase Transitions in Lattice Models (Cambridge University Press, Cambridge, 1999).

[10] H.K. Janssen, Z. Physik B 42, 151 (1981).

[11] P. Grassberger, Z. Physik. B 47, 365 (1982).

[12] G. Grinstein, Z.-W. Lai and Dana A. Browne, Phys. Rev. A 40, 4820 (1989).

[13] P. Grassberger, J. Stat. Phys. 79, 13 (1995).

[14] M. Moshe, Phys. Rep. 33C, 255 (1977).

[15] R.M. Ziff, E. Gulari and Y. Barshad, Phys. Rev. Lett. 56, 2553 (1986).

[16] J. Cardy, Scaling and Renormalization in Statistical Physics (Cambridge University Press, Cambridge, 1996).

[17] D. Brown and P. Rothery, Models in Biology: Mathematics, Statistics and Computing (John Wiley & Sons, West Sussex, 1993).

[18] N.F. Ferrara e C.P.C. do Prado, Caos - Uma Introdução (Editora Edgard Blücher Ltda, São Paulo, 1994).

[19] R. Dickman and R. Vidigal, J. Phys. A 35, 1147 (2002).

[20] A.T.F. Atman and R. Dickman, Phys. Rev. E 66, 046135 (2002).

[21] T. Tomé e M.J. de Oliveira, Dinâmica Estocástica e Irreversibilidade (EdUSP, São Paulo, 2001).

[22] T. Tomé and M.J. de Oliveira, Phys. Rev. Lett. 86, 5643 (2001).

[23] H.J. Hilhorst and F. van Wijland, Phys. Rev. E 65, 035103 (2002).

[24] M.M.S. Sabag and M.J. de Oliveira, Phys. Rev. E 66, 036115 (2002).

[25] P. Bak, C. Tang and K. Wiesenfeld, Phys. Rev. Lett. 59, 381 (1987); Phys. Rev. A 38, 364 (1988).

[26] D. Dhar, Physica A 263, 4 (1999).

[27] R. Dickman, M.A. Muñoz, A. Vespignani and S. Zapperi, Braz. J. Phys. 30, 27 (2000).

[28] N.T.J. Bailey, The Mathematical Theory of Infectious Diseases and Its Applications (Hafner Press, New York, 1975).

[29] I. Nåsell, Hybrid Models of Tropical Infections (Springer, Hidelberg, 1985).

[30] I. Nåsell, J. Math Appl. Med. Biol. 3, 211 (1986).

[31] P. Picard, Adv. Appl. Prob. 30, 1027 (1998).

[32] R. Dickman and I. Jensen, Phys. Rev. Lett, 67, 2391 (1991).

[33] F. van Wijland, K. Oerding, and H.J. Hilhorst, Physica A 251, 179 (1998).

[34] H. Hinrichsen, Adv. Phys. 49, 815 (2000); Braz. J. Phys. 30, 69 (2000).

Recebido em 22/8/2005; Aceito em 2/12/2005

Datas de Publicação

• Publicação nesta coleção
  19 Jul 2006
• Data do Fascículo
  2006

Histórico

• Aceito
  02 Dez 2005
• Recebido
  22 Ago 2005