Abstracts
An updated discussion on physical and mathematical aspects of the ergodic hypothesis in classical equilibrium statistical mechanics is presented. Then a practical attitude for the justification of the microcanonical ensemble is indicated. It is also remarked that the difficulty in proving the ergodic hypothesis should be expected.
ergodic hypothesis; statistical mechanics; microcanonical ensemble
Apresenta-se uma discussão atual sobre aspectos físicos e matemáticos da hipótese ergódica em mecânica estatística de equilíbrio. Então indica-se uma eventual postura para se justificar o ensemble microcanônico. Observa-se, também, que a dificuldade em se demonstrar a hipótese ergódica deveria ser esperada.
hipótese ergódica; mecânica estatística; ensemble microcanônico
ARTIGOS GERAIS
Ergodic hypothesis in classical statistical mechanics
Hipótese ergódica em mecânica estatística clássica
César R. de OliveiraI; Thiago WerlangII
IDepartamento de Matemática, Universidade Federal de São Carlos, São Carlos, SP, Brasil
IIDepartamento de Física, Universidade Federal de São Carlos, São Carlos, SP, Brasil
ABSTRACT
An updated discussion on physical and mathematical aspects of the ergodic hypothesis in classical equilibrium statistical mechanics is presented. Then a practical attitude for the justification of the microcanonical ensemble is indicated. It is also remarked that the difficulty in proving the ergodic hypothesis should be expected.
Keywords: ergodic hypothesis, statistical mechanics, microcanonical ensemble.
RESUMO
Apresenta-se uma discussão atual sobre aspectos físicos e matemáticos da hipótese ergódica em mecânica estatística de equilíbrio. Então indica-se uma eventual postura para se justificar o ensemble microcanônico. Observa-se, também, que a dificuldade em se demonstrar a hipótese ergódica deveria ser esperada.
Palavras-chave: hipótese ergódica, mecânica estatística, ensemble microcanônico.
1. Introduction
Important physical theories are built on relations and/or equations obtained through experiments, intuition and analogies. Hypotheses are proposed and experimentally and theoretically tested, then corrections are proposed and sometimes even "revolutions" occur. Outstanding examples are:
1. The Newton equation in classical mechanics F =  , which connects the resultant force to time variation of momentum.
, which connects the resultant force to time variation of momentum.
2. The Schrödinger equation is accepted as the one that dictates nonrelativistic quantum dynamics.
3. General relativity presumes that gravitation is a curvature of spacetime. Its field equation relates the curvature of spacetime to the sources of the gravitational field.
4. The prescription for equilibrium statistical mechanics is a link between microscopic dynamics and macroscopic thermodynamics via an invariant probability distribution.
It is natural to wonder how to justify such kind of physical relations by means of "first principles;" at least to make them plausible. Among the examples cited above, the last one is particularly intriguing, since it involves two descriptions of the same physical system, one of them time reversible (the microscopic dynamics) and the other with irreversible behavior (macroscopic thermodynamics). The justification of such prescription is one of the most fascinating problems of physics, and here the so-called ergodic hypothesis intervenes (and it was the birth of ergodic theory).
In this paper we recall the well-known Boltzmann and Gibbs proposals for the foundation of classical (equilibrium) statistical mechanics, review the usual arguments based on the ergodic hypothesis and discuss the problem, including modern mathematical aspects. At the end, we point out an alternative attitude for the justification of the foundations of classical statistical mechanics. Historical aspects and the "time arrow" will not be our main concerns (Refs. [12,14,18,22,23,38,40,41]). Although most researchers accept the ideas of Boltzmann, there are some opposites, in particular I. Prigogine and his followers (references are easily found).
Most students approaching statistical mechanics have little contact with such questions. Having eyes also for precise statements, we hope this article will be helpful as a first step to fill out this theoretical gap. We can not refrain from recommending the nice article by Prentis [31] on pedagogical experiments illustrating the foundations of statistical mechanics, as well as the article by Mañé [26] on aspects of ergodic theory via examples.
An AppendixAppendix summarizes the first steps of integration theory and presents selected theorems of ergodic theory; it is no more than a quick reference for the readers.
2. Microcanonical ensemble
In this section a discussion based on intuition will be presented. Later on some points will be clarified with mathematical rigor.
2.1. Micro and macrovariables
Establishing a mechanical model for the thermodynamic macroscopic observables is not a simple task. By beginning with the Hamilton equations of motion of classical mechanics
with a general time-independent hamiltonian H = H(q,p) and vectors (the so-called microvariables) of (cartesian) positions q = (q1, ...,qnN) and momenta p = (p1, ...,pnN) coordinates (N denotes the number of identical particles of the system, and n the number of degree of freedom of each particle, so that the dimension of the phase space G is 2nN), one introduces adequate real functions f:G ®  defined on G. A thermodynamic description is characterized by a set of parameters, the so-called thermodynamic observables which constitute the macrovariables or macroscopic observables of the system. Sometimes such identification is rather direct, as in the case of the volume, but usually each thermodynamic quantity is presumably associated with a function f (which must be empirically verifiable). Notable exceptions are the entropy and temperature, which need a probability distribution µ over phase space in order to be properly introduced; for instance, in case of a mechanical system with a well-defined kinetic energy, the temperature is identified with the phase average of the kinetic energy with respect to µ. Such probability distributions are invariant measures, as discussed ahead. Note, however, that in general small portions of phase space have a well-defined temperature, pressure, etc., since their definitions are not clear for situations far from equilibrium (not considered here).
defined on G. A thermodynamic description is characterized by a set of parameters, the so-called thermodynamic observables which constitute the macrovariables or macroscopic observables of the system. Sometimes such identification is rather direct, as in the case of the volume, but usually each thermodynamic quantity is presumably associated with a function f (which must be empirically verifiable). Notable exceptions are the entropy and temperature, which need a probability distribution µ over phase space in order to be properly introduced; for instance, in case of a mechanical system with a well-defined kinetic energy, the temperature is identified with the phase average of the kinetic energy with respect to µ. Such probability distributions are invariant measures, as discussed ahead. Note, however, that in general small portions of phase space have a well-defined temperature, pressure, etc., since their definitions are not clear for situations far from equilibrium (not considered here).
Usually, only macrovariables are subject to experimental observations and some important observables do not depend on all microvariables; for example, the density depends only on the positions of the particles.
Given an initial condition x = (q,p) Î G, also called a microstate, it will be assumed that the Hamiltonian generates a unique solution x(t): = Ttx = (q(t),p(t)) of Eq. (1) for all t Î  (sufficient conditions can be found in texts on differential equations), and the set of points
(sufficient conditions can be found in texts on differential equations), and the set of points  x: = {x(t): t Î
x: = {x(t): t Î  , x(0) = x} is the orbit of x in phase space.
, x(0) = x} is the orbit of x in phase space.
It will be assumed that orbits are restricted to bounded (compact) sets in phase space; this is technically convenient and often a consequence of the presence of constants of motion - as energy, i.e., H(x(t)) is constant as function of time - and also by constraints (as confining walls). Sometimes this fact will be remembered by the expression accessible phase space.
The number f(x(t)) should describe the value of the macroscopic observable represented by f, at the instant of time t, if it is known that at time t = 0 the system was in the microstate x. In principle, different initial conditions will give different values of the macroscopic observable f, without mentioning different times. If the system is in (thermodynamic) equilibrium, in a measurement one should get the same value for each observable, independently of the initial condition and the instant of time the measurement is performed; its justification is at the root of the foundation of statistical mechanics. Note also that the notion of macroscopic equilibrium, from the mechanical (microscopic) point of view, must be defined and properly related to the thermodynamic one.
In the physics literature there are three traditional approaches to deal with the questions discussed in the last paragraph: 1) time averages, 2) density function and 3) equal a priori probability. They are not at all independent, are subject of objections, and will be recalled in the following.
2.2. Three approaches
2.2.1. Time averages
A traditional way of introducing time averages of observables follows. Given a phase space function
f that should correspond to a macroscopic physical quantity, the measurements of the precise values
f(x(
t)) are not possible since the knowing of detailed positions and momenta of the particles of the system would be necessary; it is then supposed that the result of a measurement is the time average of
f.
It is also argued that each measurement of a macroscopic observable at time t0 takes, actually, certain interval of time to be realized; in such interval the microstate x(t) changes and so different values of f(x(t)) are generated, and the time average
may emerge as "constant" (i.e., independent of t0 and t). Next one asserts that the macroscopic interval of time for the measurement is extremely large from the microscopic point of view, so that one may take the limit t ® ¥ in Eq. (2)
This limit does not depend on the initial time t0 (see ahead) and arguing that for such large microscopic intervals of time the system visits all open sets of the phase space G during the measurement process, it sounds reasonable that this limit should coincide with the average value of f over G, defined by
For such integral be meaningful one has to assume that f is an integrable function (see the AppendixAppendix). Summing up, it is expected that
which turns out to be the main version of the ergodic hypothesis (mathematically there are other equivalent formulations; see the end of Section 3 and Theorem in the AppendixAppendix). Note that if this relation holds, then f* does not depend neither on the initial microstate x (excluding a set of measure zero) nor on the initial time, and it describes the equilibrium. Since a measurement for the constant function f1(x) = 1 must result the obvious value 1, one assumes that òG dx = 1; so dx =  dqdp, where
dqdp, where  denotes a normalization factor, dq = dq1...dqnN, dp = dp1...dpnN and so dx is Lebesgue measure. Often the accessible phase space is supposed to be compact so that the Lebesgue measure is normalized and constant functions are integrable.
denotes a normalization factor, dq = dq1...dqnN, dp = dp1...dpnN and so dx is Lebesgue measure. Often the accessible phase space is supposed to be compact so that the Lebesgue measure is normalized and constant functions are integrable.
The assumption that áfñ corresponds to the equilibrium value for each observable f is the so-called microcanonical ensemble or microcanonical measure, as discussed in Section 3. Note the prominent role played by Lebesgue measure in the discussion.
2.2.2. Density function
The initial idea is due to Maxwell and was then developed by Gibbs. Consider a huge collection of identical systems, each with its own initial condition at time t0 (some authors call this collection an "ensemble;" here an ensemble will mean a probability distribution, i.e., a probability measure as defined in the AppendixAppendix); the "typical behavior" of such collection would correspond to equilibrium. This behavior is characterized by an initial positive density function rt0:G ®  +. If rt(x) is the corresponding density function at time t, then òArt(x) dx indicates the average number of microstates that will occupy the set A Ì G at t (i.e., a probability); so òG rt(x) dx = 1 due to the normalization of the total probability. The value of an observable f at time t would be
+. If rt(x) is the corresponding density function at time t, then òArt(x) dx indicates the average number of microstates that will occupy the set A Ì G at t (i.e., a probability); so òG rt(x) dx = 1 due to the normalization of the total probability. The value of an observable f at time t would be
Frequently the condition for equilibrium is written in the form
note that if one makes explicit the time derivative and uses Hamiltonian given by Eq. (1), then it follows that (7) is exactly the famous Liouville equation. This equation has the immediate solution rt = constant, which is equivalent to the invariance of Lebesgue measure dx (see Proposition and Eq. (8)). By taking this solution for granted, that is, by ignoring all other possible solutions, it results in the observable value áfñ above, recovering the microcanonical ensemble as well as the conclusions on equilibrium of the previous subsection. Note again the introduction of averages, which is related to probability, and the latter becomes the main ingredient carrying out the micro-macro connection.
2.2.3. Equal a priori probability
This is the argument for introducing the microcanonical ensemble frequently invoked in textbooks on statistical mechanics. It is a variant of (sometimes complementary to) the previous discussion and, as stated here, the time evolution does not appear explicitly in the argument, and it is as follows.
Since there are no clear reason for certain accessible microstates be more probable than others, one postulates that for an isolated system all microstates are equally probable (maybe under the influence of Laplace's Principle of Insufficient Reason) [,]. In symbols, this is equivalent to taking the density function rt = constant in Eq. (6), that is, exactly the microcanonical ensemble.
In general, textbooks on statistical mechanics do not mention if the models considered are ergodic or not (see Section 3), since the microcanonical ensemble is introduced by means of a postulate instead of a discussion taking into account the dynamics. Due to the fruitfulness of statistical mechanics with respect to applications, some researchers consider that such discussion about ergodicity is not necessary. Another reason this discussion is avoided in textbooks is the high degree of abstraction that ergodic theory has currently reached, with a mathematical apparatus beyond the scope of such textbooks; the consequence is that it is not usually presented to physicists.
The next step here is to discuss some mathematical issues related to the ergodic hypothesis (including its precise definition) and the microcanonical ensemble.
3. A mathematical digression
There is a series of (interesting) questions, discussed in the last section, that an attentive reader could ask for more convincing explanations. For example:
-
a precise mechanical, that is, microscopic, definition of macroscopic equilibrium;
-
the existence of the limit of Eq. (3) defining the time average f*(x);
-
a proof of the validity of Eq. (5);
-
the choice of a constant density function rt(x) = constant, etc.
In principle, suitable answers should be given by ergodic theory, an area of mathematics that was born precisely with such problems in statistical mechanics. Note that it is implicitly assumed the original Boltzmann strategy of taking time averages as the equilibrium values of observables. Some general references on abstract ergodic theory are mentioned in the AppendixAppendix; for works that also discuss the foundations of statistical mechanics see Refs. [8,11,12,14,18,23,24,36,38] and references there in. In this section some useful theorems of ergodic theory will be mentioned and their importance to statistical mechanics discussed; except for some equations, all numbered statements appear in the AppendixAppendix.
Concisely, ergodic theory is the mathematical theory of dynamical systems provided with an invariant measure. The setup of ergodic theory is given by a general map (a dynamical system) tt:W ® W, for each t Î  , which gives the time evolution tt(w) of an initial condition w Î W ; the elements of W are also called microstates of the system. It is usually assumed that the initial time is t = 0 so that t0(w) = w for all w, and also ts+t = tstt (as expected for a time evolution). Note that here we assume the time evolution is reversible, that is, if at time t the microstate of the system is wt = tt(w), then the initial condition is obtained by t-t(wt) = t-t+t(w) = w. In the case of a mechanical system the initial positions can be theoretically obtained by "freezing" the system at time t and then reversing all velocities of the particles; the mechanical system will be back at its initial position at time 2t.
, which gives the time evolution tt(w) of an initial condition w Î W ; the elements of W are also called microstates of the system. It is usually assumed that the initial time is t = 0 so that t0(w) = w for all w, and also ts+t = tstt (as expected for a time evolution). Note that here we assume the time evolution is reversible, that is, if at time t the microstate of the system is wt = tt(w), then the initial condition is obtained by t-t(wt) = t-t+t(w) = w. In the case of a mechanical system the initial positions can be theoretically obtained by "freezing" the system at time t and then reversing all velocities of the particles; the mechanical system will be back at its initial position at time 2t.
Another important ingredient is a measure (also called a probability distribution) µ defined on a suitable s-algebra  of measurable subsets of W, and for A Î
of measurable subsets of W, and for A Î  the positive number µ(A) represents a probability associated to the event A. It will be tacitly assumed that µ(W) = 1, and the integral of an integrable function f with respect to µ will be denoted by òWf(w) dµ(w). Note that in our context of statistical mechanics the s-algebra is the Borel one and we have the following correspondences: W
the positive number µ(A) represents a probability associated to the event A. It will be tacitly assumed that µ(W) = 1, and the integral of an integrable function f with respect to µ will be denoted by òWf(w) dµ(w). Note that in our context of statistical mechanics the s-algebra is the Borel one and we have the following correspondences: W  G, tt« Tt, w
G, tt« Tt, w  x = (q,p), and µ corresponds to the choice of a probability distribution on G, for instance, absolutely continuous measures dµ(x) = r(x) dx (but there are other measures that have no density and so can not be written in this way).
x = (q,p), and µ corresponds to the choice of a probability distribution on G, for instance, absolutely continuous measures dµ(x) = r(x) dx (but there are other measures that have no density and so can not be written in this way).
The connection of the dynamics with equilibrium in ergodic theory is via invariant measures, i.e., µ(tt(A)) = µ(A),"t, for all suitable A (we will refrain to underline that a restriction of A to a s-algebra has to be done; the point is that in many occasions there are sets whose measures are not defined). As an example, suppose the dynamical system tt has an equilibrium point w0, characterized by tt(w0) = w0, "t; if d0 is the probability measure concentrated at w0, that is, for each set A one has
then d0 is an invariant measure for tt. This construction can be carried out similarly to periodic orbits, and to each periodic orbit an invariant probability measure, concentrated on it, is associated. Hence, invariant measures are also understood as suitable generalizations of equilibrium points and periodic orbits of dynamical systems.
If µ is invariant for tt, then it is possible to show that, for integrable functions f: W ® 
for all t; in physical terms it means that the "space" average value of the observable f does not depend on time, which is expected for macroscopic equilibrium. In case of an equilibrium point w0 the average of a continuous function f is
resulting in a constant value, as expected; in case of a periodic orbit the integral results in the average value of f over that orbit (for dissipative systems it is possible that most initial conditions converge to a periodic orbit, and so this orbit describes the long time behavior of the system). Then, by following the original formulation of Boltzmann, we present the definition of macroscopic equilibrium understood here:
Definition The macroscopic equilibria (ensembles) of a dynamical system tt are its invariant measures.
Hence, invariant measures are the objects that can perform the micro-macro connection via time averages given by Eqs. (2) and (8) and von Neumann and Birkhoff theorems presented in the AppendixAppendix. Not all invariant measures are relevant in each situation; e.g., a simple pendulum (with some kind of friction, say) has two equilibrium points, both with null momenta and with the rod at vertical positions (up and down), but one of them (up position) is unstable and is not expected to be found in such system. Thus, an important question is how to select the invariant measure(s) that will describe the observations of the given dynamical system; different invariant measures result in different values of space averages of functions f, and are also associated to different microscopic initial conditionssee the paragraph before Theorem . Note that this question is closely related to the description of (strange) attractors in the theory of dynamical systems.
With respect to statistical mechanics, a major remark is that the Lebesgue measure dx is invariant under Tt, that is, the natural volume measure dx is invariant under the time evolution generated by the Hamiltonian Eqs. (1). This result is known as Liouville theorem and it is also denoted by d(T-1x) = dx. Under the Hamiltonian time evolution a set in phase space can be distorted but its volume keeps the same; this is far from trivial.
Definition Let Tt denotes a Hamiltonian flow. The microcanonical ensemble is the invariant measure dx (see Eq. (5)).
Recall that for a Hamiltonian system the energy is conserved, that is, given an initial condition (q,p) the value of the function H(Tt(q,p)) = E, "t, is constant under time evolution, so that the motion is restricted to the surface (manifold) H(q,p) = E; Liouville theorem then implies that on this restricted dynamics the measure
is invariant (under the assumption ÑH ¹ 0 in this surface); dx|E denotes the Lebesgue measure restricted to the surface of energy E. The norm of the gradient ÑH restricted to the same surface is the right correction to Lebesgue measure that takes into account different particle speeds in different portions of energy surfaces. However, it is simpler to proceed using the measure dx, and the interested reader can consider that dx denotes the above restricted measure, and also that G denotes the surface of constant energy; no difficulty will arise. If there are additional constants of motion, which are often related to symmetries of the system, then all conserved quantities must be fixed, the motion then takes place in the intersection of the corresponding surfaces and the invariant measures must be adapted to each situation [18].
Another major result is the Birkhoff theorem: if a measure µ is invariant under a dynamics tt, then the time averages in Eq. (2) are well defined, except for initial conditions on a set of µ zero measure (i.e., null probability). Combining with Liouville theorem one gets that for Hamiltonian systems the limit defining time averages in Eq. (3) exists a.e. (this means "almost everywhere," a short way of saying "except on a set of zero measure") with respect to Lebesgue measure dx.
If for the initial condition x the time average f*(x) does exist, consider another initial time t1; then
Now
f(Tsx) ds =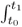 f(Ts+tx) ds and so for reasonable (e.g., bounded) functions f this integral, as well as
f(Ts+tx) ds and so for reasonable (e.g., bounded) functions f this integral, as well as 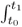 f(Tsx) ds, are bounded; therefore after dividing by t and taking t ® ¥ both vanish. Hence
f(Tsx) ds, are bounded; therefore after dividing by t and taking t ® ¥ both vanish. Hence
and a.e. the time average does not depend on the initial time.
The exclusion of sets of measure zero is not just a mathematical preciosity. For example, for a gas in a box, consider an initial condition so that the motion of all particles are perpendicular to two opposite faces resulting in null pressure on the other faces of the box; another situation is such that all particles are confined in a small portion of the box; such initial conditions are not found in practice and the mathematical formalism is wise enough to include them in a set of Lebesgue measure zero for which the results do not apply.
It is outstanding that the volume measure dx is a macroscopic equilibrium for Hamiltonian mechanics (Liouville theorem), and that merely the existence of this equilibrium has resulted in well-defined time averages and their independence on the initial time in a set of full volume. Although apparently we have answered some of the questions proposed at the beginning of this section, an important point is, however, missing: we are not sure that the microcanonical ensemble dx is the equilibrium to be implemented in statistical mechanics, that is, why is this the invariant measure to be considered? This is the wanted justification of the ergodic hypothesis, a supposition not fully justified yetas discussed ahead.
An invariant measure µ with respect to a general dynamics tt is called ergodic (or the pair (tt,µ) is ergodic) if for every set A Ì W with tt(A) = A, one has either µ(A) = 0 or µ(W\A) = 0, i.e., every invariant set under the dynamics has zero or full measure. Then ergodicity means that the only nontrivial (that is, with nonzero measure) invariant set is just the whole set; in other words, ergodicity is equivalent to the set W be indecomposable under the dynamics (tt,µ). If it is clear what is the invariant measure under consideration, one also says that the system or the dynamics tt is ergodic. This is just one possible way of defining ergodic measures, and a more detailed discussion is presented in the AppendixAppendixcompare with Definition and Theorem 4.
A consequence of the Birkhoff theorem is: if (tt,µ) is ergodic and f is an integrable function, then for µ-a.e. the time averages f*(w) exist, are constant and equal the space average, that is
In the context of Hamiltonian dynamics, if (Tt,dx) is ergodic, then the time averages f*(x) are constant Lebesgue a.e. and Eq. (5) holds, so that for justifying the equality between time and space averages one has to prove that the volume measure dx in phase space is ergodic under the dynamics generated by the Hamiltonian equations: a chief mathematical problem.
Consider now density functions rt (see Eq. (6) and the discussion in Sections 2.2.2 and 2.2.3), that is, the particular class of measures absolutely continuous with respect to Lebesgue of the form
Note first that without Liouville theorem the discussion about density functions in Subsection 2.2.2, including condition given by Eq. (7) for "equilibrium," would be incorrect. Indeed, for the average value áfñ of f over G at time t we have
Liouville theorem was applied in the last equality and the expression rt(x) = r0(T-tx) has been revealed.
As a consequence of another important result of the abstract ergodic theory, which is stated in Theorem 5, one has that if (Tt,dx) is ergodic, then the condition for n in Eq. (12) (i.e., measures defined via density functions) be invariant under Tt implies that the (integrable) function rt(x) = 1, that is, it is necessarily constant. Again we have an important consequence of the (presupposed) ergodicity of dx with respect to the Hamiltonian evolution: the mathematical justification of the equal a priori probability and the use of the mentioned trivial solution of Eq. (7). See also the discussions in Refs. [10,23,25].
As a last consequence of the ergodicity of dx we remark that it implies that a.e. the orbits  x are dense in the accessible phase space G, that is, each orbit intersects every open set of G. This property may not hold for general ergodic measures.
x are dense in the accessible phase space G, that is, each orbit intersects every open set of G. This property may not hold for general ergodic measures.
The time is ripe for a precise statement of the
Ergodic hypothesis in statistical mechanics: The microcanonical ensemble dx is ergodic with respect to the Hamiltonian dynamics.
In the next section we discuss the situation related to this supposition.
4. Discussion on the ergodic hypothesis
From the discussion in the preceding section, if the ergodic hypothesis holds, then we have a precise mechanical definition of macroscopic equilibrium dx, the existence a.e. of time averages of integrable functions f representing macroscopic observables, the equality of such averages with space averages (i.e., relation (5)) and a justification of the adoption of the microcanonical ensemble. In summary, the statistical mechanics prescription would be justified.
In this section many aspects related to the ergodic hypothesis in classical statistical mechanics are discussed. We have tried to cover the main current points, including some numerical indications.
4.1. Success and nonergodicity
Before going on, we present an example of a Hamiltonian system that is not ergodic. Consider two independent harmonic oscillators; since the phase space can be decomposed in two independent parts, one for each oscillator and both of nonzero dx measure, the pair (Tt,dx) is not ergodic. The argument easily generalizes to noninteracting systems with finitely many particles, so that for the ergodicity of (Tt,dx) the interaction among its particles is fundamental.
For the so-called gas of hard spheres whose particles interact only via elastic collisions, it was recently demonstrated by Simányi [35] that elastically colliding N > 2 hard balls, of the same radius and arbitrary masses, on the flat torus of any finite dimension is ergodic (also mixing, see ahead); the energy is fixed and the total momentum is zero. This is a generalization of results by Sinai around 1970 for N = 2. There are some classes of two-particle mechanical systems, i.e., the Hamiltonian is the sum of the kinetic energy K and the potential energy U, on the two-dimensional torus studied by Donnay and Liverani [9], whose potential U is radially symmetric and vanishes outside a disk, for which ergodicity is also proved. These can be considered the most realistic models in statistical mechanics where the ergodic hypothesis has been rigorously established. What is then the attitude when other interactions are present? Unfortunately a satisfactory answer is still missing. Some authors (as in most textbooks) suggest that the postulate of equal a priori probability should be invoked and taking the experimental results as a final confirmation.
Some workers in the area have argued that ergodic theory did not success in explaining the positive results of statistical mechanics. For instance, Earman and Rédei [10] claim that many models for which statistical mechanics works are likely not ergodic and so nonergodic properties must be invoked. As an alternative they have proposed that an ergodic-like behavior, i.e., the validity of Eq. (5) should hold only for a finite set of observables f (see also Eq. [24], where it is proposed to restrict ergodicity and mixing to suitable variables). They assert that for each model the equilibrium statistical mechanics predicts values for only a finite set of observables, and one should investigate whether the ergodic-like behavior holds only for such set, which may differ from system to system.
There are some criticisms on the assumption that the outcome of a measurement can be described by infinite time averages; for example, only results concerning quantities in equilibrium could be obtained in this way (see Refs. [16] p. 84 and [37] p. 176). Note that in this work only equilibrium statistical mechanics is considered. Also that sets of Lebesgue measure zero can be neglected has the opposition of some authors; the interested reader is referred to Ref. [25].
Another suggestive argument employed for the justification of the microcanonical ensemble comes from analogies with the second law of thermodynamics. Separate the phase space G into a finite number of M disjoint cells and associate a probability pj of a representative of the microstate be in the j-th cell; then we have the constrain  pj = 1. Such separation of phase space into cells of nonzero volume is usually called a coarse grain partition and associated to each of them one defines the Gibbs coarse grain entropy
pj = 1. Such separation of phase space into cells of nonzero volume is usually called a coarse grain partition and associated to each of them one defines the Gibbs coarse grain entropy
S(pj) =  pj ln pj.
pj ln pj.
Now impose that the equilibrium is attained for the distribution of pj with maximum entropy under the above constrain; it is left as an exercise to conclude that such maximum is obtained for pj = 1/M, for all j, that is, equal probability. In the formal limit of infinite many cells (with vanishing sizes) one gets an indication for the validity of the equal a priori probability. Note, however, that the microscopic evolution does not enter explicitly in the argument, as should be expected, and that this argument only shift the actual problem to another one.
Since the idea of separating the phase space into finitely many cells was mentioned, it is worth recalling Boltzmann reasoning that led him to the "original formulation of the ergodic hypothesis" [14] in the 1870's. Under time evolution Boltzmann supposed that the cells are cyclically permuted; then it became natural to assume that time averages could be performed by averaging over cells. In the limit of infinite cells one would get Eq. (5).
There is a clear general uncomfortable reaction in the literature with respect to the missing proofs of the ergodic hypothesis for a large class of particle interactions. In our opinion such great difficulty for ergodic proofs should be expected due to the possibility of coexistence of different phases. More precisely, suppose that (Tt,dx) is not ergodic; another mathematical result says that every invariant measure is a convex combination of ergodic ones (see Theorem 5). In case dx = ldµ1 + (1-l)dµ2, with 0 < l< 1 and (Tt,µ1) and (Tt,µ2) ergodic with µ1^ m2, then, given an observable f, there are two disjoint sets A1,A2Ì G with µ1(A1) = 1 = µ2(A2) and µ1(A2) = 0 = µ2(A1), so that by Birkhoff theorem and ergodicity, time averages of f exist for initial conditions x Î Aj and resulting in òG f(x) dµj(x), j = 1,2 (see Eq.(11)). That is, there are two different important equilibrium for the system, one for each ergodic component µ1,µ2, which one can interpret as the coexistence of different phases. The argument generalizes for more than two ergodic measures in the decomposition. From this point of view, the results of Sinai and Simányi [35] can be interpreted as a proof of just one phase for the gas of finitely many hard spheres. This is closely related to a rigorous approach to the description of phase transitions when one works directly with infinite volume systems, in which the corresponding thermodynamic limit is taken on probability measures; the reader is referred to Refs. [19,15] and references there in, and for an introduction to Gibbs states in dynamical systems see Ref. [17].
Without going into a detailed discussion of nonequilibrium, we observe that the usual justification why systems approach to equilibrium under time evolution [20] is via the property of mixing, which was intuitively explored by Gibbs (through the well-known example of stirring a drop of ink in a liquid [23]), but its mathematical definition is due to von Neumann in 1932: (tt,µ) is mixing (µ invariant) if for any A,B Ì W one has
This expression means that as time increases the portion of a given measurable set A that then resides any set B is proportional to the measure of B; thus, according to the probability measure µ, tt(A) becomes uniformly distributed over W. If this condition is satisfied then, necessarily, the system is ergodic; in fact, if tt(A) = A and by taking B = A in (14), it follows that µ(A) = µ(A)2, so that µ(A) = 0 or µ(A) = 1, i.e., (tt,µ) is ergodic. Therefore, the natural condition claimed to assure convergence to equilibrium implies ergodicity. Although this proof sounds simple today, it hides a complex set of developments and such implication was not known by Boltzmann and Gibbs, and was first proved many years after their works on the foundations of statistical mechanics. Certainly, it is usually harder to show that a system is mixing than its ergodicity (in case such properties hold).
Lombardi [24] argued that although some authors take a pragmatic position to the microcanonical ensemble [36,39], in accepting that mixing of dx plays a significant role in the description of the approach to macroscopic equilibrium dx then, according to the preceding paragraph, ergodicity of dx comes up again. Nevertheless, the necessity of mixing for evolution toward equilibrium and irreversibility [22] is not consensus [3].
A system that is ergodic but not mixing is the rotation of the circle S. Let tt:S ® S be defined by tt(x) = x+at, mod 2p, x Î [0,2p], for some irrational number 0 < a < 1 (recall that x mod 2p means that for any integer number n the numbers x and x+n2p are identified and one picks up the representative in the interval [0,2p)). One can show that tt with the Lebesgue measure dx is ergodic, however it is not mixing; in fact, for 0 < a  1 set A = [0,a] and B = [p,p+a], which are two disjoint intervals in S, then tt(A) = [at,a+at] is a rotation, and occurrences of empty and nonempty intersections with B alternate sequentially, so that µ(Tt(A)ÇB) has no limit as t ® ¥. In other words, the rotation does not spread sets (in order to be mixing) although it "spreads sets in average" (the essential difference between ergodicity and mixing is the presence of the time average in the former).
1 set A = [0,a] and B = [p,p+a], which are two disjoint intervals in S, then tt(A) = [at,a+at] is a rotation, and occurrences of empty and nonempty intersections with B alternate sequentially, so that µ(Tt(A)ÇB) has no limit as t ® ¥. In other words, the rotation does not spread sets (in order to be mixing) although it "spreads sets in average" (the essential difference between ergodicity and mixing is the presence of the time average in the former).
4.2. Completely integrable × ergodic systems
Another source of indications of the prevalence of nonergodic Hamiltonian systems (with respect to dx) are the perturbations of the so-called completely integrable Hamiltonian systems. Such systems are those that have as many independent constants of motion (like energy) as degrees of freedom; a combination of results by Liouville and Arnold [1] shows that the solutions of Hamiltonian equations can be explicitly found (up to evaluation of certain integrals and inverse functions) and in case the accessible phase space is compact it can be foliated by invariant tori (whose dimension coincides with the number of degrees of freedom) and each orbit are just rotations in a torus. Hence, in this case the motion is described in a simple way. Think of the harmonic oscillator with one degree of freedom whose phase space can be foliated by its orbits, and these orbits are (continuously deformed) one dimensional tori. Most textbook examples of mechanical systems are completely integrable.
Clearly complete integrable systems with more than one degree of freedom do not satisfy the ergodic hypothesis. For a long time it was conceived that a small nonlinear perturbation of an integrable system would make them ergodic, so that aside from the exceptions of completely integrable cases, Hamiltonian systems were ergodic (at least for "most" compact energy surfaces). However, in one of the first computer simulations in physics performed by Fermi, Pasta and Ulam on anharmonic perturbations of a chain of independent harmonic oscillators (so an integrable system) in 1955, indications were found that the resulting systems were not ergodic. See Ref. [4] for a collection of papers celebrating 50 years of the Fermi-Pasta-Ulam problem and additional references.
A rigorous approach for the lack of ergodicity of perturbations of completely integrable systems is one of the main contents of the KAM theorem [1], named after Kolmogorov, Arnold and Moser. This theorem has shown that weak perturbations of integrable systems just slightly distort most of tori ("most" means of large Lebesgue measure), which are persistent and the resulting systems are not ergodic. For a more precise formulation and Refs. [7,34]. Although the KAM theorem has nothing to say in the complement set of those distorted tori, a huge amount of numerical simulations have revealed "chaotic behavior" and dense trajectories in this remaining region of phase space, and even ergodic behavior for some sufficiently large perturbations.
Markus and Meyer [28] have presented an interesting result on generic Hamiltonian systems; generic means that the set in question is constructed as a countable intersection of open dense sets (and so it is also dense by Baire theorem). For example, in the interval [0,1] the set of irrational numbers is generic, while the set of rational numbers is not. Besides historical remarks on integrability and ergodicity in Hamiltonian systems, they have shown that generic (infinitely) differentiable Hamiltonian systems are neither ergodic nor completely integrable. The proof is actually related to the KAM theorem.
What about most of the systems of interest to statistical physics? And if one restricts the consideration to differentiable Hamiltonians H = K+U, that is, to mechanical systems whose Hamiltonian is the sum of the kinetic energy K and the potential energy U (in suitable phase spaces)? Are the results of Markus-Meyer adaptable, and how? Note, however, that the results of Markus and Mayer are in contrast to the result of Oxtoby and Ulam that a generic set of conservative topological flows is ergodic [30].
Based on numerical simulations some authors suggest that for large perturbations of an integrable Hamiltonian the system can be nonergodic due to a portion of phase space of very small Lebesgue measure, that is, the orbits of a large set of initial conditions would be dense in G\L, and L with small Lebesgue measure, so that for most initial conditions time averages would result in values near the microcanonical average, and relation (5) would hold for practical purposes. This is an attractive argument after Markus-Meyer generic result, but a rigorous approach is still missing. Instead of large perturbations one could think of small perturbations but with large number of particles, which is again related to Fermi-Pasta-Ulam work; even here the resulting picture indicates a difficult problem as illustrated in numerical studies [13].
Another possibility is mentioned by Dobrushin [8]: for a large number of particles it is possible that a lot of ergodic components are present and so intermixed that in each finite subvolume it becomes difficult to distinguish those components.
5. A practical attitude
In this section a possible approach for the justification of the microcanonical ensemble, which does not pass through ergodicity, is discussed. Certainly, Boltzmann and Gibbs have considered it in some way. The canonical and grand canonical ensembles will be freely mentioned.
The idea is simple. Consider all invariant probability distributions in phase space G, i.e., invariant measures, that result in a thermodynamics. Then by taking the limit of infinitely many particles, if one shows that all these thermodynamics are equivalent (see below), then would be no other possibility for the microscopic-macroscopic connection. This argument would justify the usual prescription of equilibrium statistical mechanics. Next this idea will be further detailed.
An invariant measure is said to result in a thermodynamics if Boltzmann heat theorem holds [14]. Given an invariant probability distribution (which usually depends on the number of particles) one defines mechanically the temperature T, pressure p and internal energy U. Let V denotes the volume occupied by the system and pdV the (infinitesimal) work it realizes. Since we are interested in the thermodynamic limit, that is, for V, N ® ¥, it is convenient to consider intensive quantities u = U/N and v = V/N. The thermodynamic limit corresponds to the original question posed by Boltzmann and is necessary for the validity of the heat theorem and then the ensemble equivalence (see ahead).
One says that the heat theorem holds if
 (du + pdv);
(du + pdv);
is an exact differential ds, which allows the introduction of the entropy s as a function of state (u,v), a fundamental ingredient. Note that this is an analytic expression for the second law of thermodynamics. As a matter of fact, the proper way of taking the thermodynamic limit depends on the ensemble considered [14,33], and in some cases different ensembles may correspond to different physical situations; for example, fixed external boundary conditions can generate new ensembles.
Now by restricting to these distributions, and also for the systems one also proves that in the limit V, N ® ¥ the same entropy function s results (as well as the same thermodynamic potentials), then the same thermodynamics is generated without ambiguity. The ergodic question would be avoided, while the number of particles is asked to be very large. Recall that, in principle, the ergodic hypothesis does not require the thermodynamic limit.
We underline that for a large class of particle interactions (including the Lennard-Jones potential, which is often used to describe molecular interactions) the standard microcanonical, canonical and grand canonical distributions generate the same thermodynamics [33]; however, it is worth mentioning that the important cases of Coulomb and gravitational potentials are not included in such proofs.
Maybe, for a given system the choices of distributions that result in a thermodynamics should be restricted on physical grounds, e.g., suitable boundary conditions. Whether only those standard distributions should be considered seems an interesting question. The existence of other possibilities, as coexistence of different thermodynamics for some parameter values of the system and the nonequivalence of ensembles, also opens the door for descriptions of different phases.
Note that this "practical attitude" is the acceptance of the classical approach by Boltzmann and Gibbs, but with one simple additional ingredient: the idea that the equivalence of ensembles could be enough to justify the recipe of statistical mechanics.
6. Conclusions
In statistical mechanics the microscopic information x is not available, and the description of macroscopic states by probability measures is compatible with that. At equilibrium such probability measures should be invariant with respect to the dynamics, and the (invariant) microcanonical ensemble plays a key role in classical statistical mechanics.
Ergodicity seems the plausible argument for the justification of the adoption of microcanonical ensemble for Hamiltonian systems with strong interaction among its particles; the canonical and grand canonical ensembles would be justified by means of equivalence of ensembles [33], that is, by proving they generate the same thermodynamics as the microcanonical one. The lack of proofs of the validity of the ergodic hypothesis for most classes of (mechanical) models in statistical mechanics creates suspicions and debates on its validity, which is reinforced by the rigorous established generic lack of ergodicity for differentiable Hamiltonians. However, besides the arguments at the end of Subsection 4.2, there are two extreme possibilities: first, there are situations one has noninteracting particles, for which nonergodicity is evident, and, second, the particle interaction is so that the nonergodicity indicates a richer behavior as the coexistence of phases.
Due to the discussion in Section 2.2 and the difficulties in proving the ergodic hypothesis, it is hard not taking a pragmatic position and employing the microcanonical ensemble, as has actually been done since the first days of statistical mechanics. This includes the alternative attitude presented in Section 5; note, however, that this approach may be criticized since it does not explain why such ensemble choices work. Surely, more mathematical and physical investigations are necessary.
We mention very interesting related questions we have not dealt with: the problem of irreversibility; the evolution toward equilibrium and the arrow of time; Kinchin approach [18,2] to the ergodic question; ergodicity and phase transitions of systems with an infinite number of degrees of freedom [19,15]. Note that in order to discuss situations far from equilibrium one should go a step further the ideas presented above, in particular for estimating the increase of entropy, and so on.
Finally, we mention a personal view expressed by G. Gallavotti; in his opinion, despite the lack of proper mathematical tools Boltzmann understood many points related to the ergodic hypothesis better than we do now.
Acknowledgments
We thank the anonymous referee for valuable suggestions. C.R. de O. thanks the partial support by CNPq. T.W. thanks a scholarship by FAPESP.
References
[1] V.I. Arnold, Mathematical Methods of Classical Mechanics (Springer-Verlag, Nova Iorque, 1997).
[2] R.W. Batterman, Philosophy of Science 65, 183 (1998).
[3] J. Bricmont, Physicalia Magazine 17, 159 (1995).
[4] Chaos 15, 015101-015121. (2005).
[5] I.P. Cornfeld, S.V. Fomin and Y.G. Sinai, Ergodic Theory (Springer-Verlag, Berlin, 1982).
[6] A.A. de Castro Jr., Curso de Teoria da Medida (Projeto Euclides, IMPA, Rio de Janeiro, 2004).
[7] C.R. de Oliveira, Rev. Bras. Ens. Fís. 21, 22 (1999).
[8] R.L. Dobrushin, Atti Convegni Lincei 131, 227 (1997).
[9] V. Donnay and C. Liverani, Comm. Math. Phys. 135, 267 (1991).
[10] J. Earman and M. Rédei, Brit. J. Phil. Sci. 47, 63 (1996).
[11] P. Ehrenfest and T. Ehrenfest, The Conceptual Foundations of the Statistical Approach in Mechanics (Dover, Nova Iorque, 1990).
[12] I.E. Farquhar, Ergodic Theory in Statistical Mechanics (Interscience, Nova Iorque, 1964).
[13] L. Galgani, A. Giorgili, A. Martinoli and S. Vanzini, Physica D 59, 334 (1992).
[14] G. Gallavotti, Statistical Mechanics. A Short Treatise (Springer-Verlag, Berlin, 1999); J. Statist. Phys. 78, 1571 (1995).
[15] H.-O. Georgii, Th. Rel. Fields 99, 171 (1994).
[16] Y.M. Guttmann, The Concept of Probability in Statistical Physics (Cambridge University Press, Cambridge, 1999).
[17] G. Keller, Equilibrium States in Ergodic Theory (Cambridge University Press, Cambridge, 1998).
[18] A.I. Kinchin, Mathematical Foundations of Statistical Mechanics (Dover, Nova Iorque, 1949).
[19] R. Kotecky, in Highlights of Mathematical Physics, edited by A. Fokas, J. Halliwell, T. Kibble and B. Zegarlinski. (Am. Math. Soc., Providence, 2002), p. 191-207.
[20] N.S. Krylov, Works On the Foundations of Statistical Physics (Princeton University Press, Princeton, 1979).
[21] U. Krengel, Ergodic Theorems (de Gruyter, Berlin, 1985).
[22] J.L. Lebowitz, Physics Today 46, 32 (1993).
[23] J.L. Lebowitz and O. Penrose, Physics Today 26, 23 (1973).
[24] O. Lombardi, Critica: Revista Hispanoamericana de Filosofia 35, 3 (2003).
[25] D.B. Malament and S.L. Zabell, Philosophy of Science 47, 339 (1980).
[26] R. Mañé, Matemática Universitária 4, 64 (1986).
[27] R. Mañé, Ergodic Theory and Differentiable Dynamics (Springer-Verlag, Berlin, 1987).
[28] L. Markus and K.R. Meyer, Generic Hamiltonian Dynamical Systems Are Neither Integrable Nor Ergodic (AMS, Providence, 1974), Mem. Amer. Math. Soc., v. 144.
[29] K. Oliveira, Um Primeiro Curso em Teoria Ergódica (IMPA, Rio de Janeiro, 2005).
[30] J.C. Oxtoby and S.M. Ulam, Ann. Math. 42, 874 (1941).
[31] J.J. Prentis, Am. J. Phys. 68, 1073 (2000).
[32] W. Rudin, Real and Complex Analysis (McGraw-Hill, Nova Iorque, 1987).
[33] D. Ruelle, Statistical Mechanics (Benjamin, Nova Iorque, 1969).
[34] M.B. Sevryuk, Mosc. Math. J. 3, 1113 (2003).
[35] N. Simányi, preprint mp-arc 05-430.
[36] L. Sklar, Philosophy of Science 40, 194 (1973).
[37] L. Sklar, Physics and Chance (Cambridge University Press, Cambridge, 1993).
[38] D. Szász, Studia Sci. Math. Hungar. 31, 299 (1996).
[39] R.C. Tolman, The Principles of Statistical Mechanics (Dover, Nova Iorque, 1979).
[40] J. Uffink, The Stanford Encyclopedia of Philosophy (Winter 2004 Edition), edited by Edward N. Zalta, http://plato.stanford.edu/archives/win2004/entries/statphys-Boltzmann
[41] J. von Plato, Arch. Hist. Ex. Sci. 44, 71 (1992).
[42] P. Walters, An Introduction to Ergodic Theory (Springer-Verlag, Berlin, 1982).
Recebido em 1/6/2006; Aceito em 27/9/2006
1 E-mail: oliveira@dm.ufscar.br
A short discussion on ergodic theory
The (mathematical) ergodic theory can be considered a branch of dynamical systems, particularly of those that preserve a measure. After a discussion of (Lebesgue) integration theory, some abstract results related to ergodicity are presented. It is expected that this collection of results and ideas could clarify many of the statements in the main body of this article. Details of the traditional subject of measure and integration can be found, for instance, in Refs. [6,32], and of ergodic theory in Refs. [5,14,26,27,29,42].
Measure and integration
Measure theory is a generalization of the concept of length, area, etc., as well as of probability and density. For example, in the case of the real line  the natural length of an interval (a,b) is (b-a), its so-called Lebesgue measure, and one tries to extend this notion to all subsets of
the natural length of an interval (a,b) is (b-a), its so-called Lebesgue measure, and one tries to extend this notion to all subsets of  (generalized lengths can also be considered, e.g., (b2-a2), resulting in other measures). However, by using the Axiom of Choice it is possible to construct subsets of
(generalized lengths can also be considered, e.g., (b2-a2), resulting in other measures). However, by using the Axiom of Choice it is possible to construct subsets of  for which their Lebesgue measure depends on the way the set is decomposed. So, clearly such sets can not be considered with a well-defined length, and one says they are not measurable. A consequence of this remark is that each measure must be defined on a specific domain of measurable sets, called a s-algebra; and the theory gets rather involved.
for which their Lebesgue measure depends on the way the set is decomposed. So, clearly such sets can not be considered with a well-defined length, and one says they are not measurable. A consequence of this remark is that each measure must be defined on a specific domain of measurable sets, called a s-algebra; and the theory gets rather involved.
Definition 1A s-algebra in a set W is a collection  of subsets of W (and each element of
of subsets of W (and each element of  is called a measurable set) so that
is called a measurable set) so that
1. W and Æ belong to  .
.
2. If A Î  then W\A Î
then W\A Î .
.
3. If A1,A2,A3,... are elements of , then
, then Aj Î
Aj Î .
.
The Borel s-algebra  in a topological space is the smallest s-algebra that contains all open sets; in this case each measurable set is also called a Borel set.
in a topological space is the smallest s-algebra that contains all open sets; in this case each measurable set is also called a Borel set.
Definition 2A (positive) measure µ on a s-algebra  is a function µ:
is a function µ: ® [0,¥] (in some cases infinity is allowed) so that if A1,A2,A3,... are pairwise disjoint elements of
® [0,¥] (in some cases infinity is allowed) so that if A1,A2,A3,... are pairwise disjoint elements of  , then µ(
, then µ( Aj) =
Aj) =  µ(Aj).
µ(Aj).
From the definitions a series of properties of measures follows. For example: µ(Æ) = 0; if A1,A2 are measurable sets with µ(A1) < ¥ and A2Ì A1, then µ(A1\A2) = µ(A1)-µ(A2).
A measure µ is finite if µ(W) < ¥ and s-finite if W =
Aj with µ(Aj) < ¥, "j. A measure µ is a probability measure if µ(W) = 1. A Borel measure is one defined on the Borel sets. Here all considered measures are Borel and s-finite.In open subsets of
n and differentiable manifolds it is possible to introduce Lebesgue measure on the Borel sets by extending the notion of length, area, and so on, from the respective definitions on intervals, rectangles, etc. (Lebesgue measure is, in fact, a slight generalization of this construction, but this is not important here).Sets of measure zero play a very important role in the theory, particularly in applications. If µ(A) is interpreted as a probability of the occurrence of the events (points) of A, then if µ(A) = 0 with A ¹ Æ there are events that are not expected to occur; it is related to the famous expression "possible but improbable events." A shorthand notation for a property that holds except on a set of µ measure zero is µ-a.e. (almost everywhere). As an illustration, consider a gas with 1023 molecules in a box at certain temperature; a possibility is all molecules moving parallel to each other giving nonzero pressure to just two sides of the box; however, such particular situation is improbable and is not expected to be found in practice, so the whole set of such configurations must have zero measure.
With a measure µ at hand it is possible to integrate certain positive functions f:W ®[0,¥) with respect to µ; for instance if f = cA is the characteristic function of the measurable set A, that is, cA(w) = 1 if w ÎA and zero otherwise, then one defines
Wf dµ =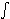 W f(w) dµ(w) := µ(A),
W f(w) dµ(w) := µ(A),
and extends it linearly, that is, for f =  aj cAj Î
aj cAj Î  , Aj measurable, 1 < j < n (the so-called simple functions), then
, Aj measurable, 1 < j < n (the so-called simple functions), then
Functions f that can be approximated by simple functions fn in a pointwise way are called measurable functions, and their integrals are defined by the corresponding limit
For not necessarily positive functions, consider its positive f+(w) = max{0,f(w)} and negative f-(w) = max{0,-f(w)} parts, so that f = f+-f- and define
Wf dµ :=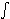 W f+ dµ
W f+ dµ 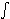 W f dµ.
W f dµ.
If both integrals in this difference is finite one says that f is integrable (or µ-integrable if one wishes to specify the measure) and the space of such functions is denoted by  (W) (sometimes complex-valued functions are allowed).
(W) (sometimes complex-valued functions are allowed).
Fix a set W and a s-algebra  . Given two measures m,n on
. Given two measures m,n on  , then µ is absolutely continuous with respect to n, denoted by µ
, then µ is absolutely continuous with respect to n, denoted by µ  n, if µ(
n, if µ( ) = 0 in case n(
) = 0 in case n( ) = 0. µ and n are equivalent if µ
) = 0. µ and n are equivalent if µ  n and n
n and n  µ. An interesting way of generating a measure µ from another given measure n is by means of densities dµ(w) = r(w) dn(w), that is
µ. An interesting way of generating a measure µ from another given measure n is by means of densities dµ(w) = r(w) dn(w), that is
for some positive n-integrable function (the density) r:W ® [0,¥).
Theorem 1 (Radon-Nikodym)µ  n if, and only if, there exists a density r as above so that dµ(w) = r(w) dn(w).
n if, and only if, there exists a density r as above so that dµ(w) = r(w) dn(w).
Two measures µ and n are mutually singular if there exist a measurable set A so that µ(A) = 0 = n(W\A), which is denoted by m^n. Note that if m^n, then the concepts of µ-a.e. and n-a.e. apply to really different situations!
Basic concepts of ergodic theory
Let W be a compact metric space and tt:W ® W be a flow, that is tt is a continuous and invertible map for each t Î  (identified with time), t0w = w, "w Î W, tt+s = ttts, "t,s Î
(identified with time), t0w = w, "w Î W, tt+s = ttts, "t,s Î  . A Borel measure m is invariant for the flow tt if µ(ttA) = µ(A), "A Î
. A Borel measure m is invariant for the flow tt if µ(ttA) = µ(A), "A Î  and t Î
and t Î  . The existence of invariant measures in this case is assured by Krylov-Bogolioubov theorem.
. The existence of invariant measures in this case is assured by Krylov-Bogolioubov theorem.
Proposition 1 The measure m is invariant under the flow tt if, and only if, for all continuous function f:W ® one has
one has
The presence of an invariant measure implies the existence of time averages
of certain functions f:W ® . This is the main content of theorems usually denominated "ergodic theorems." Here two of such results will be stated, von Neumann Mean Ergodic Theorem and Birkhoff Pointwise Ergodic Theorem, both proved around 1931. The interested reader in a rather complete treatment of ergodic theorems and their variants are referred to Ref. [21].
. This is the main content of theorems usually denominated "ergodic theorems." Here two of such results will be stated, von Neumann Mean Ergodic Theorem and Birkhoff Pointwise Ergodic Theorem, both proved around 1931. The interested reader in a rather complete treatment of ergodic theorems and their variants are referred to Ref. [21].
Theorem 2 (von Neumann) Let f: W ® be a function so that its square |f|2is integrable and m an invariant measure for the flow tt. Then there exists a function
be a function so that its square |f|2is integrable and m an invariant measure for the flow tt. Then there exists a function  :W ®
:W ® so that |
so that | |2is integrable and
|2is integrable and
Theorem 3 (Birkhoff)Let µ be an invariant measure for the flow tt. If f:W ® is integrable, then
is integrable, then
i f*(w): = limt®¥
f(tsw) ds exists µ-a.e. and the function f* is also integrable.ii f*(ttw) = f*(w) µ-a.e., that is, f* is constant over orbits.
ii òWf*(w) dµ(w) = òW f(w) dµ(w).
The proof of Theorem 6 is much simpler than the proof of Birkhoff theorem 6, but the former gives no information on the existence of time averages of individual initial conditions w, since an integral is present before the limit t ® ¥. Item ii in Birkhoff theorem should be expected. Item iii says that "space average" of f coincides with time average of f*, and an important particular case is when the latter is constant.
Definition 3 If for each integrable f the time average f* is constant µ-a.e., then the pair (tt,µ) is called ergodic. Note that this implies that is, the equality of space and time averages.
If the flow tt is fixed, it is also common to say that the invariant measure µ is ergodic. Under the conditions of Krylov-Bogolioubov result mentioned above, it is possible to show that ergodic measures exist. It is worth considering f = cB in case µ is ergodic
that is, ttw visits each set B with frequency equal to the measure of B.
There is a number of characterizations of ergodicity, and we mention some of them ahead. A measurable set A is invariant if tt(A) = A and µ-invariant if µ(ttADA) = 0, "t Î  (recall that ADB = (A\B)È(B\A) is the symmetric difference between the sets A and B), and a measurable function f is invariant if f°tt = f µ-a.e.; for simplicity, in what follows invariant measures are supposed to be probability measures.
(recall that ADB = (A\B)È(B\A) is the symmetric difference between the sets A and B), and a measurable function f is invariant if f°tt = f µ-a.e.; for simplicity, in what follows invariant measures are supposed to be probability measures.
Theorem 4Let µ be an invariant probability measure for tt. The following assertions are equivalent:
i) (tt,µ) is ergodic.
ii) Every invariant measurable function is constant m-a.e.
iii) Every m-invariant set  Î
Î  has µmeasure 0 or 1.
has µmeasure 0 or 1.
iv) Every invariant set  Î
Î  has µ measure 0 or 1.
has µ measure 0 or 1.
The condition in item iv) of Theorem 6 is called indecomposability; sometimes this nomenclature is also used to the condition in item iii). Unfortunately none of the characterizations in this theorem is easy to verify for models in statistical mechanics; however, they have been checked for several dynamical systems in mathematics (see the cited books above).
It is important to realize that consequences of ergodicity depends on the invariant measure under consideration; for example, if µ and n are ergodic (with respect to the same flow), for each function f Birkhoff theorem implies there are sets A,B, with µ(A) = 1 = n(B), so that time averages f*(w) exist for any initial condition w Î A, resulting in òWfdµ, as well as for any w Î B, but now resulting in òW fdn. Since in general òWfdm ¹ òW fdn, different ergodic measures are related to different values of time averages and over different sets of initial conditions.
Theorem 5 Let n  µ. If n is invariant and µ ergodic, then n = µ.
µ. If n is invariant and µ ergodic, then n = µ.
Theorem 6 Let W be a compact metric space, tt a continuous flow on W and µ an invariant probability measure. Then, for each integrable function f:W® one has the following decomposition
one has the following decomposition
with nw denoting ergodic measures (properly) associated to points w Î A Ì W and µ(A) = 1 (note that f Î  (W) for any w Î A).
(W) for any w Î A).
In case f = cB is the characteristic function of the set B one gets
which clarifies that every invariant measure can be written in terms of ergodic measures. In case only two ergodic measures µ1,µ2 are present, this decomposition reduces to convex combinations lm1+(1-l)µ2, with 0 < l< 1. The ergodic measures are the building blocks of invariant measures.
- [1] V.I. Arnold, Mathematical Methods of Classical Mechanics (Springer-Verlag, Nova Iorque, 1997).
- [2] R.W. Batterman, Philosophy of Science 65, 183 (1998).
- [3] J. Bricmont, Physicalia Magazine 17, 159 (1995).
- [4] Chaos 15, 015101-015121. (2005).
- [5] I.P. Cornfeld, S.V. Fomin and Y.G. Sinai, Ergodic Theory (Springer-Verlag, Berlin, 1982).
- [6] A.A. de Castro Jr., Curso de Teoria da Medida (Projeto Euclides, IMPA, Rio de Janeiro, 2004).
- [7] C.R. de Oliveira, Rev. Bras. Ens. Fís. 21, 22 (1999).
- [8] R.L. Dobrushin, Atti Convegni Lincei 131, 227 (1997).
- [9] V. Donnay and C. Liverani, Comm. Math. Phys. 135, 267 (1991).
- [10] J. Earman and M. Rédei, Brit. J. Phil. Sci. 47, 63 (1996).
- [11] P. Ehrenfest and T. Ehrenfest, The Conceptual Foundations of the Statistical Approach in Mechanics (Dover, Nova Iorque, 1990).
- [12] I.E. Farquhar, Ergodic Theory in Statistical Mechanics (Interscience, Nova Iorque, 1964).
- [13] L. Galgani, A. Giorgili, A. Martinoli and S. Vanzini, Physica D 59, 334 (1992).
- [14] G. Gallavotti, Statistical Mechanics. A Short Treatise (Springer-Verlag, Berlin, 1999);
- J. Statist. Phys. 78, 1571 (1995).
- [15] H.-O. Georgii, Th. Rel. Fields 99, 171 (1994).
- [16] Y.M. Guttmann, The Concept of Probability in Statistical Physics (Cambridge University Press, Cambridge, 1999).
- [17] G. Keller, Equilibrium States in Ergodic Theory (Cambridge University Press, Cambridge, 1998).
- [18] A.I. Kinchin, Mathematical Foundations of Statistical Mechanics (Dover, Nova Iorque, 1949).
- [19] R. Kotecky, in Highlights of Mathematical Physics, edited by A. Fokas, J. Halliwell, T. Kibble and B. Zegarlinski. (Am. Math. Soc., Providence, 2002), p. 191-207.
- [20] N.S. Krylov, Works On the Foundations of Statistical Physics (Princeton University Press, Princeton, 1979).
- [21] U. Krengel, Ergodic Theorems (de Gruyter, Berlin, 1985).
- [22] J.L. Lebowitz, Physics Today 46, 32 (1993).
- [23] J.L. Lebowitz and O. Penrose, Physics Today 26, 23 (1973).
- [24] O. Lombardi, Critica: Revista Hispanoamericana de Filosofia 35, 3 (2003).
- [25] D.B. Malament and S.L. Zabell, Philosophy of Science 47, 339 (1980).
- [26] R. Mańé, Matemática Universitária 4, 64 (1986).
- [27] R. Mańé, Ergodic Theory and Differentiable Dynamics (Springer-Verlag, Berlin, 1987).
- [28] L. Markus and K.R. Meyer, Generic Hamiltonian Dynamical Systems Are Neither Integrable Nor Ergodic (AMS, Providence, 1974),
- Mem. Amer. Math. Soc., v. 144.
- [29] K. Oliveira, Um Primeiro Curso em Teoria Ergódica (IMPA, Rio de Janeiro, 2005).
- [30] J.C. Oxtoby and S.M. Ulam, Ann. Math. 42, 874 (1941).
- [31] J.J. Prentis, Am. J. Phys. 68, 1073 (2000).
- [32] W. Rudin, Real and Complex Analysis (McGraw-Hill, Nova Iorque, 1987).
- [33] D. Ruelle, Statistical Mechanics (Benjamin, Nova Iorque, 1969).
- [34] M.B. Sevryuk, Mosc. Math. J. 3, 1113 (2003).
- [35] N. Simányi, preprint mp-arc 05-430.
- [36] L. Sklar, Philosophy of Science 40, 194 (1973).
- [37] L. Sklar, Physics and Chance (Cambridge University Press, Cambridge, 1993).
- [38] D. Szász, Studia Sci. Math. Hungar. 31, 299 (1996).
- [39] R.C. Tolman, The Principles of Statistical Mechanics (Dover, Nova Iorque, 1979).
- [40] J. Uffink, The Stanford Encyclopedia of Philosophy (Winter 2004 Edition), edited by Edward N. Zalta, http://plato.stanford.edu/archives/win2004/entries/statphys-Boltzmann
- [41] J. von Plato, Arch. Hist. Ex. Sci. 44, 71 (1992).
- [42] P. Walters, An Introduction to Ergodic Theory (Springer-Verlag, Berlin, 1982).
Appendix
Publication Dates
-
Publication in this collection
17 Sept 2007 -
Date of issue
2007
History
-
Received
01 June 2006 -
Accepted
27 Sept 2006





























