Abstracts
It is shown, by a first-order perturbation expansion, that the dimensionality of the dynamical equations for the angular variables of two strongly coupled identical overdamped pendulums can be reduced from two to one. The resulting dynamical equation is seen to be similar to the one of a single pendulum with an additional fictitious torque characterized by a second harmonic contribution.
non-linear ordinary differential equations; coupled pendulums
Mostra-se através de uma expansão de perturbação de primeira ordem que a dimensionalidade das equações dinâmicas das variáveis angulares de dois idênticos e fortemente acoplados pêndulos superamortecidos podem ser reduzida para apenas uma. A equação dinâmica resultante é similar àquela de um pêndulo simples com um torque fictício adicional caracterizado por uma contribuição de segundo harmônico.
equações diferenciais não-lineares; pêndulos acoplados
ARTIGOS GERAIS
Strongly coupled overdamped pendulums
Pêndulos superamortecidos fortemente acoplados
R. De Luca1 1 E-mail: rdeluca@unisa.it.
Dipartimento di Matematica e Informatica, Università degli Studi di Salerno, Fisciano, SA, Italy
ABSTRACT
It is shown, by a first-order perturbation expansion, that the dimensionality of the dynamical equations for the angular variables of two strongly coupled identical overdamped pendulums can be reduced from two to one. The resulting dynamical equation is seen to be similar to the one of a single pendulum with an additional fictitious torque characterized by a second harmonic contribution.
Keywords: non-linear ordinary differential equations, coupled pendulums.
RESUMO
Mostra-se através de uma expansão de perturbação de primeira ordem que a dimensionalidade das equações dinâmicas das variáveis angulares de dois idênticos e fortemente acoplados pêndulos superamortecidos podem ser reduzida para apenas uma. A equação dinâmica resultante é similar àquela de um pêndulo simples com um torque fictício adicional caracterizado por uma contribuição de segundo harmônico.
Palavras-chave: equações diferenciais não-lineares; pêndulos acoplados.
1. Introduction
The angular variables φ1 and φ2 of two equal pendulums are shown in Fig. 1. The dynamics of this system is described by two coupled second-order non-linear differential equations in φ1 and φ2. The order of these equations can be reduced to one in the case of overdamped pendulums having small masses and moving in a viscous environment. Therefore, overdamped identical strongly coupled pendulums can be described by a single differential equation for the average angular position  of the two pendulums with respect to a common reference axis.
of the two pendulums with respect to a common reference axis.
Indeed, one can solve for the difference between the two angular positions
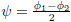 in terms of φ by means of a first order perturbation analysis, so that, upon substitution of this solution in the time evolution equation for φ, one can obtain an effective one-dimensional model for the whole system. Analytic solution of this system provides an approximated solution to the system dynamics.
in terms of φ by means of a first order perturbation analysis, so that, upon substitution of this solution in the time evolution equation for φ, one can obtain an effective one-dimensional model for the whole system. Analytic solution of this system provides an approximated solution to the system dynamics. The paper is organized as follows. In the next section, the equations for the two coupled pendulums are briefly derived and the perturbation solutions are found. In the third section the effective potential energy for the system is found in terms of the average angular position φ and the time average of the angular frequency is found in terms of a constant externally applied torque. Finally, in the last section, conclusions are drawn and a brief discussion on the analogy of this system with a symmetric d. c. SQUID [1] is made.
2. Dynamical equations and perturbative expansion
Consider the mechanical system shown in Fig. 1, consisting of two identical pendulums of mass m and length l, coupled by a massless rod with torsional spring constant kT and freely rotating about the axis a - a. Ifa torque MA is applied on the system, the angular deviations of the pendulums from their vertical equilibrium positions are indicated as φ1 and φ2, respectively. The mechanical system is immersed in a fluid with damping constant b, so that the dynamical equations for the angular variables φ1 and φ2 can be written as follows
where we have assumed that the rigid rods, connecting the point mass of the pendulums and the rotating shaft, are massless. We now introduce the normalized time
In the overdamped case, we may set
Let us now introduce the adimensional parameters  and
and  , and the new variables
, and the new variables  and
and  . By algebraic manipulation we can thus rewrite Eqs. (3a-b) in the following final form
. By algebraic manipulation we can thus rewrite Eqs. (3a-b) in the following final form
The above set of equations is not just rewritten in a different form, where the coupling has now represented by trigonometric functions rather than by linear functions as in Eqs. (3a-b). For small values of β, indeed, we can try to solve Eq. (8) by means of a first-order perturbation analysis with respect to the same parameter β [2]. Assuming β small, we thus set
Substituting Eq. (9) into Eq. (8), we obtain
By having now solved for ψ (τ) in terms of φ (τ) to first order in the parameter β, we substitute the expression
The above equation, together with Eqs. (4) and (9), represents a reduced model for the problem of two coupled overdamped identical pendulums. We notice that the dynamics is similar to that of a single pendulum, to which a fictitious normalized moment  sin 2φ is added. The term
sin 2φ is added. The term  sin 2φ and the cosine term which appears as a factor of sin φ, are reminiscent of the interaction between the two pendulums. Notice also that, once Eq. (11) is solved for φ (τ ), one can recover the time evolution of ψ (τ) from Eqs. (9) and (10).
sin 2φ and the cosine term which appears as a factor of sin φ, are reminiscent of the interaction between the two pendulums. Notice also that, once Eq. (11) is solved for φ (τ ), one can recover the time evolution of ψ (τ) from Eqs. (9) and (10).
3. Effective potential
In the present section we shall derive an expression for the effective potential for the system in normalized units. We start by writing the dynamic equations for the variables φ1 and φ2 (Eqs. (3a-b)) as follows
So that, by Eqs. (3a-b) we obtain the effective potential in terms of the variables φ1 and φ2
In order to obtain the effective potential in terms of the only variable φ, we proceed as follows. We first write the dynamical equations in terms of φ and ψ by means of a change of variables, so that
where the potential is now expressed in terms of the variables φ and ψ, so that
In order to readily obtain the reduced potential Ured (φ), we can either substitute the approximated solution for ψ, taking care of keeping only first order terms in β, or, integrating Eq.(15), taking into account Eq. (11), we can immediately write
which is a washboard-like potential and the constant 2 is arbitrarily chosen. A plot of the reduced potential is given in Fig. 2 for mA = 0 (dotted line), mA = 0.075 (dashed line) and mA = 0.15 (full line). Notice that the constant normalized forcing torque not only tilts the initially periodic potential, which presents infinite degenerate equilibrium states, but also deforms the shape of the curve. In this way, we see that the system, initially in its equilibrium position φ = 0 at mA = 0, suffers an angular shift for nonzero values of the applied torque. Up to a given maximum torque, however, the solution to the problem is static. When this maximum value of the constant externally applied torque is overcome, the solution to Eq. (11) becomes time-dependent. The maximum values of the normalized applied torque can be calculated from Eq. (11), by setting  , realizing that
, realizing that  must be of order β. Therefore, by a first order solution in β of the stationary portion of Eq. (11), we find
must be of order β. Therefore, by a first order solution in β of the stationary portion of Eq. (11), we find  and
and  . Plots of the time evolution of the angular variable φ and its derivative, found by numerically integrating Eq. (11), are shown in Figs. 3a and 3b, respectively, for β = 0.1 and
. Plots of the time evolution of the angular variable φ and its derivative, found by numerically integrating Eq. (11), are shown in Figs. 3a and 3b, respectively, for β = 0.1 and  . Plots of the time evolution of the angular variable ψ and its derivative, found by evaluating Eq. (9), on the other hand, are shown in Figs. 4a and 4b, respectively, for β = 0.1 and
. Plots of the time evolution of the angular variable ψ and its derivative, found by evaluating Eq. (9), on the other hand, are shown in Figs. 4a and 4b, respectively, for β = 0.1 and  .
.
We would now like to calculate the time-averaged value (ω) of the angular frequency  as a function of a constant normalized applied torque mA. We have already noticed that (ω) = 0 for -2β < mA < 2β. For mA >
as a function of a constant normalized applied torque mA. We have already noticed that (ω) = 0 for -2β < mA < 2β. For mA >  , we solve the differential equation (11) and then set
, we solve the differential equation (11) and then set
In this way, we obtain the (ω) vs. mA curves represented in Fig. 5 for three values of the parameter β (β = 0.05, 0.1, 0.2). We notice that the solution  is well detectable in these curves.
is well detectable in these curves.
4. Conclusion
We have shown, by a first order perturbation expansion with respect to the parameter  , that the dimensionality of the dynamical equations for two overdamped identical pendulums of mass m and length l, coupled by a massless rod with torsional spring constant kT , can be reduced from two to one. Owing to this reduction, the resulting dynamical equation is written in terms of the average angular variable
, that the dimensionality of the dynamical equations for two overdamped identical pendulums of mass m and length l, coupled by a massless rod with torsional spring constant kT , can be reduced from two to one. Owing to this reduction, the resulting dynamical equation is written in terms of the average angular variable  and appears to be the same as that of a single pendulum with an additional second harmonic sine term. The reduced potential of this mechanical system is seen to be a washboard-like potential, like the one found for a single Josephson junction [1]. The two systems, the mechanical one and the one containing Josephson junctions, however, differ in what follows. The mechanical system is forced by an externally applied torque, and this forcing quantity appears as the argument of the cosine and of the sine terms, which are the pre-factors of the sin φ and sin 2φ terms in the dynamical equation, respectively. In the Josephson junction case, this role is played by an externally applied normalized magnetic flux Ψex, which appears as a second forcing term besides the bias current iB. In this way, in the case of a d. c. SQUID, where the two Josephson junctions are coupled by an interaction having analogous expression as in the case of the two pendulums studied, the resulting effective dynamical equation is written as follows [3]
and appears to be the same as that of a single pendulum with an additional second harmonic sine term. The reduced potential of this mechanical system is seen to be a washboard-like potential, like the one found for a single Josephson junction [1]. The two systems, the mechanical one and the one containing Josephson junctions, however, differ in what follows. The mechanical system is forced by an externally applied torque, and this forcing quantity appears as the argument of the cosine and of the sine terms, which are the pre-factors of the sin φ and sin 2φ terms in the dynamical equation, respectively. In the Josephson junction case, this role is played by an externally applied normalized magnetic flux Ψex, which appears as a second forcing term besides the bias current iB. In this way, in the case of a d. c. SQUID, where the two Josephson junctions are coupled by an interaction having analogous expression as in the case of the two pendulums studied, the resulting effective dynamical equation is written as follows [3]
Clearly, the role played by the externally applied torque in Eq. (11) is here played, only partially, by the bias current appearing as a forcing quantity in the right hand side of Eq. (20). The magnetic field, on the other hand, plays a complementary role, being the only forcing term present in the left hand side of Eq. (20). A last difference can be noticed in the absence of the perturbation parameter β in the denominator of the right hand side forcing term in Eq. (20), as opposed to the presence of this parameter in the homologous position in Eq. (11).
Acknowledgments
The author would like to thank Dr. Francesco Romeo for having inspired the present work with his constant dedication to finding new ways of approaching solved and unsolved problems.
Recebido em 12/5/2008; Aceito em 4/7/2008; Publicado em 27/2/2009
- [1] A. Barone and G. Paternò, Physics and Applications of the Josephson Effect (Wiley, New York, 1982).
- [2] S.H. Strogatz, Nonlinear Dynamics and Chaos (Perseus Publishing, Cambridge, 2000).
- [3] F. Romeo and R. De Luca, Phys. Lett. A 328, 330 (2004).
Publication Dates
-
Publication in this collection
23 Mar 2009 -
Date of issue
Dec 2008
History
-
Accepted
04 July 2008 -
Received
12 May 2008


 , so the system of equations (1a-b) becomes
, so the system of equations (1a-b) becomes 
 , so that the above set of equations simplify to the following
, so that the above set of equations simplify to the following 



 cos φ into Eq. (7) to get, consistently with the first order approximation in β
cos φ into Eq. (7) to get, consistently with the first order approximation in β















