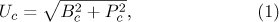Equilíbrio no espaço: experimentação e modelagem matemática

Equilibrium in the space: experimentation and mathematical modelling

ARTIGOS GERAIS

Equilíbrio no espaço: experimentação e modelagem matemática

Equilibrium in the space: experimentation and mathematical modelling

P.A. Pereira Borges, N.A. Toniazzo¹; J.C. da Silva

Departamento de Física, Estatística e Matemática, Universidade Regional do Noroeste do Estado do Rio Grande do Sul, Ijuí, RS, Brasil

RESUMO

A elaboração e realização de experimentos, associadas à interpretação dos resultados, construção e aplicação de conceitos e uso de recursos da informatica, constituem uma opção metodológica desafiadora no ensino de física dos dias atuais, considerando as necessidades de conhecimento, habilidades e criatividade que as novas gerações devem ter para enfrentar os problemas científicos e tecnológicos. Este trabalho tem como objetivos apresentar o problema de cálculo das forças atuantes em cabos e hastes que sustentam massas no espaço, desenvolver um modelo matemático geral, como um estudo de modelagem fortemente integrador dos conteúdos das disciplinas de Mecânica Geral, Algebra Linear e Cálculo Numérico de cursos de engenharia, física ou matemática. O modelo foi testado com verificação experimental para varias situações, sendo três delas descritas no artigo: casos simétrico e assimétrico com forças de tração e um caso assimétrico com força de compressão. Foi realizada a analise de incerteza das medidas de comprimento dos cabos e posicionamento dos apoios. O trabalho evidenciou a riqueza de situações de aprendizagem e aplicação de conceitos, técnicas de tratamento de dados de medida e desafios matemáticos, ao associar ações teóricas e experimentais para a validação do modelo, além de apresentar outras investigações relacionadas com o tema abordado.

Palavras-chave: mecânica, ensino de física, experimentação, tecnologia e ensino.

ABSTRACT

The elaboration and accomplishment of experiments, together with the analysis of the results, construction and application of concepts and the use of computing resources are a challenging methodological option in the physics education when considering the needs of knowledge, abilities and creativity that the new generations must have to face the scientific and technological problems. This work has the objective to present the problem of calculation of acting forces in handles and connecting rods that support masses in the space, to develop a general mathematical model and to argue the nature of the tensions of some specific cases, as a modelling study combining the contents of courses like General Mechanics, Linear Algebra and Numerical Calculus for engineering, physics or mathematics. The model was tested for some situations, being three of them described in this article: symmetrical and anti-symmetrical with traction forces and an anti-symmetrical case with compression force. It is presented the analysis of the uncertainty for the measurements of the handles length and the positioning of the supports. This work shows the variety of learning situations and application of concepts, mathematical techniques of data handling and challenges, when associating theoretical and experimental actions for the validation of the model, besides presenting other related inquiries as extensions of the given subject.

Keywords: mechanics, physics education, experimentation, technology and education.

1. Introdução

A elaboração e execução de experimentos, associadas à interpretação dos resultados, construção e aplicação de conceitos e uso de recursos da informática, constituem uma opção metodológica desafiadora no ensino de física dos dias atuais, considerando as necessidades de conhecimentos, habilidades e criatividade que as novas gerações devem ter para enfrentar os problemas científicos e tecnológicos.

Uma verificação nos livros didáticos de física, tanto do ensino médio [1, 2] como de nível universitário [3, 4], mostra que, na abordagem da primeira condição de equilíbrio dos corpos rígidos, a decomposição das forças é feita somente no plano [5]. Nesse caso, a solução obtida é um sistema linear de segunda ordem. Abordagens teóricas e exercícios desse problema no espaço são propostas, normalmente, nos livros de mecânica geral [6, 7] para os cursos de engenharia.

A sustentação de uma torre metálica mantida na posição vertical com cabos fixos no chão, um candelabro mantido por três correntes em um teto, ou a determinação do modulo das cargas elétricas que geram um campo sobre uma carga de módulo conhecido são alguns exemplos de problemas de decomposição de forças no espaço. Tais problemas são boas aplicações de Sistemas Lineares, normalmente citados como exemplos, nas disciplinas de Álgebra Linear e Cálculo Numérico dos cursos de licenciatura de física e matemática.

A modelagem matemática de problemas físicos é uma alternativa de ensino que articula a teoria e a prática. Alunos e professores são envolvidos na construção de experimentos, interpretação dos resultados, construção e aplicação de conceitos e uso de recursos da informática para a solução dos problemas.

Este trabalho tem como objetivos apresentar o problema de cálculo das forças atuantes em cabos e hastes que sustentam massas no espaço, desenvolver um modelo matemático para um caso geral, bem como discutir os tipos de forças (tração e compreensão) de casos específicos, utilizando procedimentos teóricos e experimentais que se complementam e possibilitam a aplicação de conceitos da física, de técnicas matemáticas e tratamento de dados.

Foi realizada uma revisão conceitual sobre a decomposição de forças no espaço, considerando o caso geral de uma massa sustentada por três cabos/hastes com direções em três retas concorrentes e não co-planares, fixos em três pontos distintos. Foram analisados alguns casos particulares com o objetivo de ilustrar o uso da teoria e verificar a coerência entre os resultados experimentais e teóricos. O primeiro é um caso simétrico útil para verificar o modelo. O segundo é um caso assimétrico onde as forças atuantes são todas de tração. O terceiro também é um caso assimétrico, porém com forças de compressão.

O estudo de forças no espaço pode ser feito como atividade de pesquisa paralela ao programa de Mecânica Geral, Álgebra Linear ou Cálculo Numérico em cursos de engenharia, licenciatura de física ou matemática, pois é um importante caso de aplicação prática e, do ponto de vista teórico, uma extensão do problema bidimensional, que envolve noções de geometria analítica e métodos de solução de sistemas de equações, fundamentais para a formação científica do aluno que vai trabalhar na área de ciências exatas.

2. Experimentos

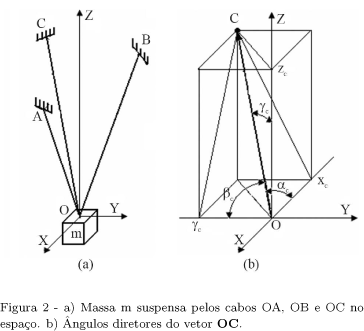
Casos particulares foram montados em laboratório com a construção apresentada na Fig. 1. Três roldanas foram consideradas como pontos de fixação das cordas (A, B e C) que sustentam a massa central (carga) e viabilizam a medição das forças como forças peso. O atrito das roldanas foi desconsiderado, mesmo sabendo que ele pode influenciar significativamente no modulo das forças, na medida em que este é aumentado. O sistema entra em equilíbrio, com a carga assumindo uma determinada posição (vértice, ponto O), sendo essa dependente das massas suspensas em cada roldana, da carga e da posição das roldanas.

A localização dos pontos A, B e C - que são os pontos de tangência das cordas na circunferência da roldana no espaço - foi feita considerando um sistema cartesiano XYZ de referência, com origem no ponto de projeção de A na bancada (plano horizontal, XY) e eixo X na direção da projeção do ponto B. Todas as medidas de distância foram feitas usando uma régua graduada. As distancias AB, BC, CA, AO, BO e CO são as arestas de um tetraedro que, para um caso geral, é irregular. As massas suspensas nos pontos A, B e C foram medidas em uma balança analítica cuja precisão é 0,001 g.

A validação de modelos matemáticos consiste em comparar os resultados experimentais com os simulados, mesmo sabendo que ambos têm erros: os resultados simulados apresentam erros decorrentes dos processos numéricos e os experimentais, os erros de medida. Admitindo que, nos experimentos realizados, as medidas de massa apresentam erros bem menores do que as medidas de comprimento em função do equipamento e das condições de realização das medidas, serão considerados, neste trabalho, somente os erros das medidas de comprimento.

A influencia dos erros, tanto nas medidas em si, como nos erros provocados pela utilização das medidas nas simulações, pode ser avaliada pela análise de incerteza. Essa análise foi realizada [8, 9] considerando a incerteza de precisão (P) (precisão dos instrumentos de medida de comprimento) e a incerteza de processo (B) (avaliação dos erros de repetibilidade). A incerteza total foi obtida pela Eq. (1)

onde U_c é a incerteza nas medidas de comprimento, P_c é a incerteza de precisão e B_c é a incerteza de processo. A incerteza de precisão das medidas de comprimento é a precisão da régua, considerada P_c = 0,001 m.

Para avaliar a incerteza de processo, foi realizada uma série de 10 medidas (Mb) das posições dos pontos A, B e C e das cordas AO, BO e CO, repetindo rigorosamente os mesmos procedimentos utilizados nas medições do experimento. Foi calculada a média de cada medida, o respectivo desvio padrão e o desvio padrão médio (média dos desvios padrões de todas as medidas: σ_m = 0,963). Para usar o desvio padrão no caso específico do problema, é necessário associá-lo ao módulo da medida efetuada, fazendo um percentual em relação à média de uma medida (M), como mostra a Eq. (2)

onde σ_c é o desvio padrão percentual, para cada medida M; e M_b é a medida base usada nos experimentos de incerteza.

O intervalo de variação em torno da média de uma medida, portanto, depende do módulo da grandeza mensurada. Assim, a incerteza de processo da medida de comprimento é dado pela Eq. (3)

onde M é uma medida de comprimento.

Substituindo a Eq. (3) e P_c = 0,001 na Eq. (1), obtém-se a incerteza da medida de comprimento.

As medidas, com as respectivas incertezas, são utilizadas como dados experimentais em uma série de operações matemáticas do algoritmo do cálculo das forças e podem levar a erros significativos.

As combinações das medidas realizadas (posições e cordas) com as incertezas possíveis são infinitas, se consideradas frações da incerteza máxima. Seja M ± aUi uma medida de comprimento acrescida de sua incerteza, onde a é um número real entre 0 e 1. Mesmo para um número finito de combinações, por exemplo, a igual a 0 e 1, só para as medidas de comprimento, tem-se 12 medidas ( coordenadas x, y e z dos 3 pontos, mais as distâncias dos pontos A, B e C ao ponto O, ver Fig. 1) e 3 combinações de incerteza para cada medida: -U_c, 0 e+U_c. A combinação das três incertezas para uma medida tem 3 × 3² possibilidades. Cada uma das 3² possibilidades ocorre para cada uma das 12 medidas, resultando 3 × (3²)¹² = 3²⁵ = 8,4729 × 10¹¹ possibilidades. Obviamente, não é necessário fazer todas essas combinações para avaliar o impacto da incerteza de medida no cálculo das forças, mesmo porque, apesar de grande, esse número é uma parte das combinações possíveis, já que foi determinado usando a hipótese do coeficiente a ter apenas três valores.

Neste trabalho foram adotados os seguintes procedimentos e hipóteses para avaliar o impacto das medidas de comprimento no cálculo das forças:

1. Foi admitido que toda medida de comprimento é uma média de n medidas efetuadas.

2. Foi admitido que ocorrem as seguintes combinações de erros de medida: U₊, U_- e U_o, incerteza máxima a maior, incerteza máxima a menor e incerteza nula, respectivamente.

3. As combinações do item 2 ocorrem diferentemente nas medidas das coordenadas dos pontos A, B e C e no comprimento das cordas.

4. Foram executadas as 27 combinações aplicadas de forma aleatória nas coordenadas dos pontos e no comprimento das cordas. Cada combinação é um vetor (E) composto pelos valores das forças simuladas, nas três cordas.

5. O resultado tomado como base é aquele obtido com a incerteza nula (U_o): vetor R.

6. Um vetor diferença D foi definido como: D = E - R.

7. Foi feita a média das normas dos vetores de diferença D de todas as combinações simuladas.

8. Foi calculado o desvio padrão (σ) da distribuição das normas dos vetores de diferenças D e o desvio padrão percentual, relativo à média.

9. A incerteza de um desvio padrão foi usada em função do módulo da simulação (S), para o cálculo do intervalo da incerteza das medidas no algoritmo do cálculo das forças. Assim, se σ é o desvio padrão percentual médio das normas dos vetores de diferenças, então

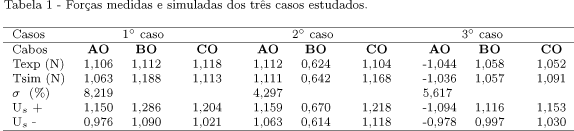
onde S é o valor da simulação e U_s é o reflexo da incerteza das medidas de comprimento quando aplicadas no algoritmo do cálculo das forças. A Tabela 1 apresenta o intervalo das incertezas das medidas de comprimento para três casos simulados, quando tais incertezas são consideradas conforme as hipóteses acima, no cálculo das forças.

3. Decomposição tridimensional de forças

A Fig. 2a ilustra uma situação na qual três cabos OA, OB e OC, fixos em A, B e C, respectivamente, mantém em equilíbrio uma massa m. Colocando a origem do sistema de referência cartesiano XYZ no ponto de fixação dos cabos na massa e entendendo os segmentos de reta OA, OB e OC como vetores com origem em O e extremidade em A, B e C, tem-se

Analogamente ao problema de decomposição de forças no plano, no espaço também é feita a decomposição das projeções das forças atuantes em cada cabo nos eixos coordenados. Isto pode ser feito identificando os ângulos diretores dos vetores e seus respectivos cosenos. A Fig. 2b mostra os ângulos diretores do vetor OC. Para uma melhor visualização desses ângulos, recomenda-se ao leitor que construa a Fig. 2b usando uma caixa de papel aberta nas faces dos planos XZ e YZ e identifique os triângulos retângulos x_cOC, y_cOC e z_cOC. Observe que os ângulos retos estão em x_c, y_c e z_c, Da definição do coseno de um ângulo, o leitor certamente chegará às seguintes razões trigonométricas

O mesmo procedimento deve ser feito para os vetores OA e OB, o que também fica a cargo do leitor.

As forças F₁, F₂ e F₃ atuantes nos cabos OA, OB e OC, respectivamente, podem ser calculadas considerando o sistema em equilíbrio de translação, quando a soma das projeções das forças em cada uma das direções XYZ deve ser nula. Então

onde F₁, F₂ e F₃ são os módulos das forças que atuam nas cordas (N), m é a massa (kg) e g é a aceleração da gravidade (m/s²).

As Eqs. (9) a (11) constituem um sistema de equações lineares. Na forma matricial, podem ser escritos como as Eqs. (12) e (13)

ou

onde A é a matriz dos coeficientes, x é o vetor das incógnitas e b é o vetor dos termos independentes do sistema.

É necessário verificar se o sistema (13) tem solução e se esta é única. Da Algebra Linear, sabe-se que um sistema linear não tem solução, se a matriz A for singular (determinante diferente de zero). Para que isso ocorra é necessário que uma coluna (ou linha) seja proporcional à outra, ou uma combinação linear das outras, ou que uma coluna (ou linha) seja nula. Supondo que os pontos A, B e C sejam três pontos distintos, a matriz A não será singular, pois:

1) Para que uma coluna da matriz A seja proporcional à outra, os co-senos de um vetor devem ser proporcionais aos de outro, o que caracterizaria vetores colineares. Como os pontos A, B e C são distintos, isto não ocorre.

2) Para que uma linha da matriz A seja proporcional à outra, os co-senos dos três vetores em relação a um eixo devem ser proporcionais aos de outro eixo. Isto só pode ocorrer se os vetores forem colineares.

3) Para que uma coluna da matriz A seja nula, todos os co-senos de um dos vetores devem ser nulos. Isto só ocorre para o vetor nulo. E, finalmente, para que uma linha seja nula os co-senos dos três vetores em relação a um eixo coordenado devem ser nulos. Isto também só ocorre se o vetor é nulo.

De acordo com essa análise, o sistema (13), para vetores OA, OB e OC não colineares, sempre terá solução única. Assim, a solução do sistema (13) pode ser obtida por diferentes métodos ensinados no ensino médio (como a Regra de Cramer) ou no ensino superior (como o escalonamento, matriz inversa, pivotação, Gauss-Seidel, e outros).

4. Estudo de casos particulares

Com o objetivo de testar o modelo matemático, foram implementados experimentalmente três casos particulares do problema descrito anteriormente, ilustrados genericamente pela Fig. 2a.

A localização dos pontos A, B e C foi feita conforme descrição no item 2 deste artigo e os co-senos diretores foram calculados de acordo com as Eqs. (8). As forças atuantes nos cabos foram calculadas resolvendo o sistema (13).

Esse conjunto de procedimentos, assim como a resolução do sistema (13) foi implementada computacionalmente e está disponível na Ref. [10].

Foram considerados três casos particulares:

1º ) Caso simétrico: Os pontos A, B e C estão sobre uma circunferência, em um plano paralelo ao plano XY, os cabos têm o mesmo comprimento e as forças nas cordas são as mesmas. A massa m está localizada no ponto O, que é o vértice de um tetraedro de base triangular.

2º) Caso assimétrico com forças de tração: Os cabos estão fixos nos pontos A, B e C e têm comprimentos e forças atuantes diferentes. A massa m está localizada em um ponto O, que é o vértice de um tetraedro irregular, de base triangular, cuja projeção vertical de O no plano dos pontos A, B e C está no interior do triângulo ABC.

3º) Caso assimétrico com forcas de tração e compressão: Os cabos estão fixos nos pontos A, B e C e têm comprimentos e forças atuantes diferentes. A massa m está localizada em um ponto O, que é o vértice de um tetraedro irregular, de base triangular, cuja projeção vertical de O no plano dos pontos A, B e C, está fora do triângulo ABC, caracterizando a presença de uma força de compressão em, ao menos, um dos cabos.

Para aplicar as Eqs. (8) e (13) é necessário encontrar o ponto O (ponto de equilíbrio e fixação da carga m), em função do comprimento dos cabos, em relação ao sistema de referência XYZ usado para localizar os pontos A, B e C. Os comprimentos dos cabos L₁, L₂ e L₃ que são as distâncias AO, BO e CO, respectivamente, colocadas na equação da distância entre dois pontos no espaço [11], resulta em um sistema cujas incógnitas são as coordenadas de O = (x_o, y_o, z_o).

onde x_o, y_o ez_o são as coordenadas do vértice (m) e x_i, y_i, ezi, com i = a, b e c, são as coordenadas dos pontos A, B e C.

O sistema (13) é um sistema não linear, pois as incognitas têm expoente 2, necessitando de um método numérico para sua solução. Foi usado o método de Newton para sistemas não-lineares. Na Ref. [12] o leitor encontrará uma descrição do método de Newton, cuja implementação computacional está disponível na Ref. [10]. O ponto O foi adotado como centro do novo sistema de referência, o que permite a aplicação das Eqs. (8) e (14).

5. Resultados

No primeiro caso, a simetria do problema permite concluir, antecipadamente, que as forças nos três cabos são de tração² (tendem a alongar a corda) e devem ter o mesmo módulo. As dificuldades para implantar condições simétricas no experimento explicam a pequena diferença encontrada, tanto nos dados experimentais (Texp) - as massas suspensas nas roldanas não são exatamente iguais - quanto nos simuladas (Tsim) - os dados inseridos no programa são os dados experimentais -, como mostra a Tabela 1. Porém, observa-se que o módulo das forças nos três cabos é praticamente o mesmo, confirmando o resultado esperado, devido à simetria do problema.

No segundo caso, as forças aplicadas e as medidas dos cabos são diferentes, o que inviabiliza uma estimativa de resultado. A validação fica restrita à comparação dos resultados experimentais e simulados, que como mostram as colunas 5 a 7 da Tabela 1, são bem próximos.

O terceiro caso apresenta uma tensão de compressão no cabo AO, ou seja, esse cabo é uma haste rígida que empurra a carga m. O modelo proposto dá conta deste caso, calculando as forças e apresentando a força em AO com o sinal negativo. Os valores das forças medidas e calculadas são apresentados nas colunas 8 a 10 da Tabela 1 e também são bem próximos entre si.

As ultimas linhas da Tabela 1 mostram os resultados da análise de incerteza. Pode-se observar que todas as forças Texp encontram-se no intervalo [U_s -,U_s+], para os três casos estudados, o que indica que o modelo proposto é coerente com os resultados experimentais.

6. Extrapolando o problema

A teoria do modelo proposto pode ser usada para construir outros modelos, que resolvem problemas diferentes. Como desafio, o leitor fica convidado a elaborar soluções para os seguintes problemas.

Problema 1: Três cargas elétricas q₁, q₂ e q₃ estão posicionadas/estacionadas em P₁,P₂ e P₃ no espaço. Uma carga de prova q está posicionada inicialmente em Po = (x_o, y_o, z_o) e, pela interação do campo elétrico criado pelas cargas q₁, q₂ e q₃, posiciona-se no ponto Pf = (x_f,y_f, z_f). Determine as cargas q₁, q₂ e q₃, considerando conhecido o trabalho realizado pela força elétrica resultante, para deslocar a carga de prova de P_o a P_f.

Problema 2: Uma torre metálica, cujo peso é W e altura H, é mantida na posição vertical com 3 cabos fixos no chão, nos pontos P₁ = (x₁, x₁, x₁), P₂ = (x₂, x₂, x₂) e P₃ = (x₃, x₃, x₃). Que força deve ser aplicada em cada cabo, de modo que seja produzida uma força vertical para baixo, sobre a torre, cujo valor seja maior ou igual ao peso da torre?

7. Considerações finais

A modelagem matemática de problemas de física proporciona atividades teóricas e práticas, porque compreende ações de tradução de fenômenos em linguagem simbólica e requer experimentos para validação dos modelos, além de usar a programação computacional como um meio de resolução de problemas não tão elementares.

Outra característica da modelagem é a proposição de modelos gerais, que resultam em ferramentas para resolver um conjunto de problemas particulares. Desenvolver a capacidade de pensar e implementar soluções gerais é uma tarefa fundamental para a formação dos recursos humanos que atuarão em ciência e tecnologia.

Com relação à validação ao modelo, foram propostas três formas: 1ª) Análise de um caso simétrico: esta análise mostrou que o modelo proposto resolve o problema simétrico, apresentando os resultados esperados em função da simetria; 2ª) Análise de dois casos assimétricos, um só com forças de compressão e outro com uma força de tração: esta análise mostrou que o modelo não só é coerente com os experimentos, mas com o tipo de força atuante nas hastes; e 3ª) Análise de incerteza das medidas: esta análise utilizou um critério para avaliar a incerteza de medida e o reflexo desta no algoritmo do cálculo das forças. De acordo com esse procedimento, os resultados experimentais ficaram sempre dentro do intervalo de incerteza. Outros critérios poderiam ser formulados, por exemplo, com frações de U₊ e U_-, e/ou aumentando o número de combinações possíveis. Tal procedimento certamente mudaria as incertezas encontradas, porém não significativamente, desde que as escolhas das frações contemplem toda a amplitude do intervalo [U_s-, U_s+].

O desenvolvimento de modelos matemáticos em classe, como o modelo proposto neste trabalho, é altamente desafiante, porque implica fazer pesquisas, superar dificuldades com alguns conteúdos, extrapolar os limites formais de estudo (alguns conteúdos que não são ensinados na graduação, como sistemas não lineares, podem ser compreendidos com uma boa bibliografia e acompanhamento do professor), fazer e analisar experimentos e implementar rotinas de cálculo no computador.

Recebido em 30/6/2008

Revisado em 10/3/2009

Aceito em 31/3/2009

Publicado em 30/6/2009

• [1] A. Máximo e B. Alvarenga, Curso de Física (Editora Scipione, São Paulo, 2006).
• [2] A. Gaspar, Física (Editora Atual, São Paulo, 2001).
• [3] H.M. Nussenzveig, Física Básica-Mecanica (Editora Edgar Blücher LTDA, São Paulo, 1981).
• [4] D. Halliday, K.S. Krane e R. Resnick, Física 1 (Livros Técnicos e Científicos Editora S.A., Rio de Janeiro, 2003).
• [5] L.D. Almeida, B.V. Vaniel, Caderno Catarinense de Ensino de Física 2, 134 (1995).
• [6] F. Beer e E.R. Johnston Jr., Mecânica Geral para Engenheiros (Makron Books do Brasil, São Paulo, 1994).
• [7] J.L. Merian e L.G. Kraige, Estática (Livros Técnicos e Científicos Editora S.A., Rio de Janeiro, 1997).
• [8] B.B. Neto, I.S. Scarminio e R.E. Bruns, Como Fazer Experimentos (Editora da Unicamp, Campinas, 2007).
• [9] J. Mandel, The Statistical Analysis of Experimental Data (Interscience, New York, 1964).
• [10] http://www.projetos.unijui.edu.br/matematica/ forcas.zip
  » link
• [11] J.H. Kindle, Geometria Analítica Plana e no Espaço (McGraw-Hill do Brasil, São Paulo, 1977).
• [12] M.A.G. Ruggiero e V.L.R. Lopes, Cálculo Numérico, Aspectos Teóricos e Computacionais (Makron Books do Brasil, São Paulo, 1996).

2

Neste trabalho, foi adotada a convenção de sinal negativo para forcas de compressão e positivo para tração.

Datas de Publicação

• Publicação nesta coleção
  08 Out 2009
• Data do Fascículo
  Jun 2009

Histórico

• Aceito
  31 Mar 2009
• Recebido
  30 Jun 2008
• Revisado
  10 Mar 2009