Resumos
Muitas provérbios surgem através da própria experiência cotidiana. Embora muitas dessas expressões sejam de entendimento direto por parte da população em geral, um olhar mais cuidadoso gera muitas questões e dúvidas a respeito da sua validade. Motivados por uma dessas expressões, no presente artigo, analisamos a transmissão de uma notícia numa rede de contatos eletrônicos (e-mails). Para tanto, são propostos protocolos de transmissão de notícia que reproduzem propriedades de sistemas reais. Esses protocolos são simulados numa rede real de e-mails e na rede aleatória proposta por P. Erdos e A. Rényi. Os resultados sugerem que uma notícia se espalha mais rapidamente na rede aleatória. A presença de vértices concentradores de conexões (hubs) na rede real tende a atrair a notícia, prejudicando os vértices menos conectados.
redes complexas; redes sociais; propagação de notícias
Many proverbs are created through everyday experience. Although many of them are readily understood by ordinary people, a more detailed view generates many questions and doubts related to their credibility. Motivated by one of these proverbs, in the present paper, we analyse propagation of news in a network of electronic contacts (e-mails). More specifically, we propose transmission protocols intended to reproduce properties of real systems. These protocols are simulated in a real e-mail network and in the random network proposed by P. Erdos and A. Rényi. The results suggest that news spreads faster in the random network. The hubs in the real network tend to attract the news, in prejudice to the less connected nodes.
complex networks; social networks; news propagation
ARTIGOS GERAIS
Notícia ruim corre depressa!
Bad news travels fast!
Luis E.C. da Rocha1 1 E-mail: luis.rocha@tp.umu.se.
Department of Theoretical Physics, Umeå University, Sweden
RESUMO
Muitas provérbios surgem através da própria experiência cotidiana. Embora muitas dessas expressões sejam de entendimento direto por parte da população em geral, um olhar mais cuidadoso gera muitas questões e dúvidas a respeito da sua validade. Motivados por uma dessas expressões, no presente artigo, analisamos a transmissão de uma notícia numa rede de contatos eletrônicos (e-mails). Para tanto, são propostos protocolos de transmissão de notícia que reproduzem propriedades de sistemas reais. Esses protocolos são simulados numa rede real de e-mails e na rede aleatória proposta por P. Erdos e A. Rényi. Os resultados sugerem que uma notícia se espalha mais rapidamente na rede aleatória. A presença de vértices concentradores de conexões (hubs) na rede real tende a atrair a notícia, prejudicando os vértices menos conectados.
Palavras-chave: redes complexas, redes sociais, propagação de notícias.
ABSTRACT
Many proverbs are created through everyday experience. Although many of them are readily understood by ordinary people, a more detailed view generates many questions and doubts related to their credibility. Motivated by one of these proverbs, in the present paper, we analyse propagation of news in a network of electronic contacts (e-mails). More specifically, we propose transmission protocols intended to reproduce properties of real systems. These protocols are simulated in a real e-mail network and in the random network proposed by P. Erdos and A. Rényi. The results suggest that news spreads faster in the random network. The hubs in the real network tend to attract the news, in prejudice to the less connected nodes.
Keywords: complex networks, social networks, news propagation.
1. Introdução
O título desse artigo é um provérbio que faz parte de uma gama de ditados e expressões que compõem o dito conhecimento popular. O conhecimento popular é resultante de experiências pelas quais passamos no dia a dia dentro do meio em que vivemos. Uma vez que aprendemos algo, utilizamos esse conhecimento numa situação futura semelhante e eventualmente, repassamos esse conhecimento para outras pessoas através de conselhos, advertências ou até mesmo numa conversa informal. Enquanto do ponto de vista do conhecimento popular essa frase tenha uma interpretação relativamente simples e direta (apesar de subjetiva), aos olhos de um cientista ela gera diversas dúvidas e se mostra bastante instigante. Por exemplo, seria preciso definir o que é uma notícia e também estabelecer uma referência para se classificar essa velocidade como "depressa". Além disso, uma série de perguntas poderiam ser feitas, como por exemplo, qual a influência de uma pessoa e de seu círculo de amizades na velocidade que esta notícia se espalha ou até mesmo, questionar quanto tempo é necessário para que a notícia chegue a um determinado número de pessoas. Mas com todas essas definições, dúvidas e questões, por onde começar então? A resposta é simplificando.
Como cientistas, fundamentalmente criamos um modelo e confrontamos suas propriedades com as observações experimentais do sistema real, se essas observações não condizerem com o modelo, então nós o aperfeiçoamos [1, 2]. Esse modelo deve ser preferencialmente o mais simples possível e deve conter as propriedades mais relevantes do sistema de interesse de forma a reproduzir seu comportamento adequadamente. Desta forma, mesmo sistemas complexos (como a sociedade) podem, a princípio, ser descritos e analisados através de modelos matemáticos relativamente simples. Naturalmente, o grau de "simplicidade" ou "complexidade" varia de acordo com a quantidade de informação que se quer reproduzir.
No presente artigo, propomos um modelo de transmissão de notícias (não necessariamente notícias ruins!) e estudamos algumas de suas propriedades. Em primeiro lugar, vamos considerar a notícia simplesmente como sendo uma partícula, um elemento abstrato sem nenhuma propriedade em particular. As pessoas, que são os responsáveis por transmitir e receber a notícia, são definidas como elementos pontuais no espaço. Cada um desses elementos possui 3 propriedades fundamentais: (i) um canal de comunicação ligando ele a um número fixo de outros elementos pontuais; (ii) a capacidade de agir como remetente e/ou receptor da notícia através desse canal, além de manter a notícia em seu poder pelo tempo que for necessário; (iii) a capacidade de escolher - de acordo com uma regra - o destino da notícia antes de transmití-la.
Escolhidas as propriedades mais significativas do sistema, precisamos traduzi-las para uma notação matemática. Para tanto, utilizamos a teoria das redes complexas. Essa teoria fundamentalmente propõe que representemos um sistema na forma de um grafo (ou uma rede), onde os vértices correspondem aos elementos desse sistema e as arestas à relação entre os vértices. O estudo da estrutura de conexões resultante fornece informações sobre o sistema. Neste trabalho, os vértices representam os indivíduos e as conexões representam os canais de comunição entre eles. O movimento da partícula (notícia) é representado na rede através da ativação ou desativação dos vértices, ou seja, vértices ativados detêm a notícia enquanto os desativados não a possuem. Para não nos limitarmos totalmente à abstração matemática, utilizamos uma rede real de trocas de correspondência eletrônica (e-mail) entre os membros da Universidad Rovira i Virgili (Tarragona - Espanha) [3].
O conceito de redes complexas, assim como sua construção e aplicação em nosso modelo serão mais abordados na próxima seção e o mecanismo de transmissão de informação na seção 3. Em seguida (seção 4), algumas medidas estruturais da rede e a evolução da dinâmica proposta serão analisados e discutidos. Finalmente, na seção de conclusões alguns projetos complementares serão propostos.
2. Redes complexas
Embora a teoria das redes complexas esteja se desenvolvendo rapidamente ao longo da última década, a modelagem matemática de sistemas reais através de grafos tem origem no século XVIII com Leonard Euler [4-6]. Desde sua proposta inicial até a metade do século XX, o estudo dos grafos foi mais restrito a análise de suas propriedades matemáticas. Entretanto, uma série de trabalhos envolvendo a modelagem de sistemas sociais usando grafos surgiu durante a última metade do século XX e acabou resultando na teoria das redes sociais [7]. Neste mesmo período, propriedades dos grafos aleatórios também foram extensivamente investigadas [8].
Algumas definições e medidas de redes complexas serão apresentadas a seguir e então, descreveremos os mecanismos de construção das redes utilizadas: uma real e outra teórica.
2.1. Fundamentos
Uma rede complexa Γ com N elementos pode ser definida como um conjunto V de vértices vi (i = 1,2,..., N) e um conjunto E de arestas (i,j) que conectam os vértices vi e vj de acordo com uma regra determinada (Fig. 1) [2, 4, 5, 9-12]. Um conjunto W de números reais pode ser mapeado nos vértices ou nas arestas para quantificar e representar propriedades específicas dos mesmos.
Uma das formas fundamentais de caracterizar a estrutura de uma rede complexa é através da medida do grau ki do vértice vi, que representa o número de arestas conectadas ao vértice (Fig. 1). Os vértices diretamente conectados a vi são chamados de vizinhos de vi. Outra medida relevante para as discussões subseqüentes é a distância topológica dij entre dois vértices vi e vj, que é definida como o caminho percorrido para chegar a vj a partir de vi. O menor caminho entre dois vértices é chamado de geodésica. O valor da distância é dado em número de arestas (Fig. 1). Considerando a rede como um todo, a maior geodésica (considerando todos os caminhos entre quaisquer pares de vértices) define o diâmetro Drede da rede.
2.2. Rede real
Para analisarmos as propriedades de nosso modelo numa rede real, devemos construir uma rede de amizades ou de contatos. Nessa rede, os vértices representam as pessoas e a conexão entre os vértices é estabelecida no caso das pessoas terem contato com troca de informação através de alguma forma (terem algum grau de relacionamento). Por exemplo, é possível construir uma rede de relacionamento numa escola. A partir de uma lista de alunos, é perguntado para cada aluno quem são as pessoas que cada um tem mais amizade. Se o aluno Fulano vi = 2 responder que tem amizade com o Ciclano vi = 3 e com o Beltrano vi = 5, obteremos as arestas (2,3) e (2,5) (Fig. 1). Embora o conceito de amizade possa variar de pessoa para pessoa 2 2 Ver comentários sobre redes sociais na Ref. [6] , essa é uma forma aproximada de se obter uma rede de contatos entre os alunos da escola.
Dentre alguns métodos para contornar esses problemas de definição (de amizade, por exemplo), é possível estabelecer uma conexão se, e somente se, ambos Fulano e Ciclano disserem que são amigos um do outro. Outra forma é a observação indireta da relação entre os estudantes, por exemplo, observar o tempo que dois alunos ficam juntos durante o intervalo entre as aulas ou se preferem fazer atividades juntos e desta forma, estabelecer uma conexão apenas entre os alunos que interagem assiduamente. Neste ponto, surge uma curiosa questão: Será que uma rede formada por pessoas que permanecem mais tempo juntos é equivalente a rede de amizades formada a partir das perguntas? Bom, vamos deixar essa pergunta e sua resposta como sugestão para um trabalho complementar e voltar para nosso problema inicial.
O método adotado neste trabalho consiste numa outra abordagem bastante utilizada que evita definições pessoais e está diretamente ligada a um meio de comunicação, a www (world wide web ou popularmente, a internet). Para tanto, usaremos uma rede de correio eletrônico (e-mail), ou seja, uma rede onde os vértices representam o remetente i ou o destinatário j e as arestas (i,j) conectam as pessoas que trocaram correspondência eletrônica em algum momento durante o tempo de coleta dos dados. Vamos adotar (i,j) ≡ (j,i), o que indica que a rede não tem direção. Algumas propriedades estruturais dessa rede já foram estudadas [3] e sua estrutura (pares remetente/destinatário) está disponível para domínio público (http://deim.urv.cat/~aarenas/data/welcome.htm).
2.3. Rede teórica
Para confrontar os resultados obtidos com a rede real, vamos compará-los com uma rede aleatória. Existem diversas formas de gerar redes aleatórias com diferentes propriedades para diferentes propósitos. Aqui iremos adotar o modelo mais fundamental conhecido, que foi proposto por Paul Erdos e Alfréd Rényi em 1959 (abrev. ER) [2, 4, 5, 9-12]3 3 Outro método bastante utilizado consiste em manter o número de vizinhos de cada um dos vértices e simplesmente reconectá-los aleatoriamente. . Dado o conjunto de vértices V, dois vértices vi e vj são conectados com uma probabilidade q, que varia de 0 (rede totalmente desconectada) a 1 (rede totalmente conectada). Em termos práticos para nosso modelo, podemos pensar nessa rede como sendo equivalente a andarmos na rua e com uma certa chance, estabelecer contato com os transeuntes.
3. Transmissão da notícia
A mecanismo de escolha do destinatário da notícia (ou partícula) pode ser modelado através de diferentes processos. A seguir, descreveremos alguns processos compostos por regras simples que contêm propriedades motivadas por situações de um sistema real.
3.1. Aleatório
A primeira e mais natural alternativa para simular a escolha do destinatário é simplesmente considerar que todos eles são iguais. A cada instante de tempo t o remetente vi escolhe aleatoriamente com mesma probabilidade (ou probabilidade uniforme)  um dos seus vizinhos vj como destinatário (Eq. (1)). Neste caso, a mensagem é enviada para apenas um destinatário por vez. Esse mecanismo representa a situação onde uma pessoa simplesmente transmite uma informação para outra de forma casual/espontânea. Por exemplo, você passa a notícia espontâneamente para algum conhecido que você encontrou ou escolhe alguém da sua lista de contatos de e-mail. Vamos considerar que o destinatário vj não pode transmitir de volta a notícia para o remetente original vi e que o remetente vi pára de transmitir a notícia após enviá-la para todos os seus vizinhos vj
um dos seus vizinhos vj como destinatário (Eq. (1)). Neste caso, a mensagem é enviada para apenas um destinatário por vez. Esse mecanismo representa a situação onde uma pessoa simplesmente transmite uma informação para outra de forma casual/espontânea. Por exemplo, você passa a notícia espontâneamente para algum conhecido que você encontrou ou escolhe alguém da sua lista de contatos de e-mail. Vamos considerar que o destinatário vj não pode transmitir de volta a notícia para o remetente original vi e que o remetente vi pára de transmitir a notícia após enviá-la para todos os seus vizinhos vj
3.2. Preferencial
O método aleatório assume que o remetente não tem nenhuma informação a respeito de seus possíveis destinatários (exceto o fato de ele ser um destinatário em potencial). Entretanto, muitas vezes quando queremos transmitir uma notícia de forma rápida, escolhemos um destinatário por acreditarmos que ele tem algo em especial que contribuirá para que a notícia chegue ao destino final mais rápido. A escolha do destinatário pode ser baseada em diversos fatores de acordo com o tipo de notícia que se quer transmitir, por exemplo, o tipo de relação com esse contato: amigos, colegas de trabalho ou vizinhos. Em nosso modelo, vamos simplificar novamente e propor que a escolha de um destinatário vj seja proporcional ao seu grau, ou seja, ao número de vizinhos kj do destinatário (Eq. (2))
3.3. Broadcast
O último mecanismo que analisaremos envolve uma situação extrema e que reproduz um fenômeno bastante comum na www, as mensagens em massa (spams em inglês). Neste caso, cada remetente vi envia a mesma mensagem simultâneamente para toda a sua lista de contatos (transmissão simultânea ou broadcast em inglês), sem fazer nenhuma seleção ou ordenação dos vizinhos.
4. Resultados
Antes de investigarmos as dinâmicas propostas nas redes, vamos analisar um pouco a estrutura de conexões da rede de e-mails e da aleatória (ER). Essas informações serão úteis nas análises subseqüentes da dinâmica.
4.1. Estrutura
A rede de e-mails possui 1133 vértices (1133 remetentes ou destinatários) e 5451 arestas (canais de comunicação entre duas pessoas), portanto, cada pessoa possui em média 9,62 parceiros de correspondência. A Fig. 2 mostra a distribuição de graus da rede, ou seja, a porcentagem de vértices P(k) que possuem um número k de conexões na rede de e-mails [13, 14]. A principal informação que obtemos dessa distribuição é que embora a maioria dos vértices possuam grau baixo (k < 10), existem alguns poucos vértices (os concentradores ou hubs, em inglês) que concentram muitas conexões (k > 50). Visivelmente, a distribuição não é simétrica em torno do grau médio. A busca por métodos para encontrar a melhor curva que descreva esse tipo de distribuição é uma área de pesquisa por si só e foge do escopo do presente trabalho. Porém, num trabalho anterior, a partir da análise da distribuição acumulada de graus (usada para diminuir o efeito da baixa amostragem) foi sugerido que essa distribuição é bem descrita pela função exponencial P(k*  k) ∝ exp(-k/9.2) para k
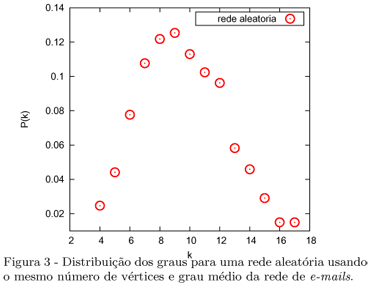
k) ∝ exp(-k/9.2) para k  2 [3]. Em contrapartida, a rede aleatória com mesmo número de vértices e mesmo grau médio possui uma distribuição que é aproximadamente descrita pela distribuição de Poisson P(k) = 〈k〉kexp(-〈k〉)/k! (Fig. 3). Na verdade, essa aproximação se torna mais adequada no limite de N muito grande. Essa propriedade da rede aleatória mostra que ela possui um valor de grau característico (o grau médio), enquanto, a rede de e-mails possui uma maior heterogeneidade de valores de graus.
2 [3]. Em contrapartida, a rede aleatória com mesmo número de vértices e mesmo grau médio possui uma distribuição que é aproximadamente descrita pela distribuição de Poisson P(k) = 〈k〉kexp(-〈k〉)/k! (Fig. 3). Na verdade, essa aproximação se torna mais adequada no limite de N muito grande. Essa propriedade da rede aleatória mostra que ela possui um valor de grau característico (o grau médio), enquanto, a rede de e-mails possui uma maior heterogeneidade de valores de graus.
Como descrito anteriormente, a rede aleatória não beneficia um vértice em especial pois as conexões são estabelecidas com probabilidade uniforme. Por outro lado, numa rede real a existência de diferentes vínculos forçam a rede a crescer com propriedades particulares que são refletidas na sua estrutura de conexões [6].
A medida da distância média entre quaisquer dois vértices na rede mostra que ambas as redes tem valores médios próximos, respectivamente, 3,363 (ER) e 3,606 (e-mail). Entretanto, a diferença na estrutura se torna mais visível através da medida do diâmetro das redes, 6 (ER) e 8 (e-mail), onde o valor é significantemente menor na rede aleatória.
4.2. Dinâmica
Para evoluir os mecanismos de transmissão propostos, inicialmente devemos definir a configuração inicial do sistema. Em todos os casos a seguir, apenas um vértice será inicialmente ativado, ou seja, conterá a notícia. Todos os outros vértices da rede serão desativados. Esse vértice será escolhido aleatória e uniformemente entre os vértices da rede. A seguir, a cada passo de tempo t, o estado de cada vértice é atualizado de acordo com os protocolos propostos. Em processos estocásticos como esse, é importante obter valores médios a partir de diversas realizações com condições iniciais diferentes. Desta forma, evita-se obter resultados particulares que podem levar a conclusões equivocadas. Os resultados apresentados a seguir são obtidos a partir de valores médios sobre 1200 execuções, ou seja, 1200 simulações com configuração inicial diferente. Esse número foi escolhido por permitir que cada vértice possa ser ativado inicialmente pelo menos uma vez.
Considerando a rede de e-mails, a Fig. 4 mostra a evolução do número de pessoas que receberam a notícia com o tempo. De uma forma geral, a notícia se espalha para poucas pessoas no começo e depois se espalha mais rapidamente (a derivada - inclinação - da curva é maior), convergindo para uma saturação no final devido ao tamanho limitado da rede (onde todos os vértices recebem a notícia pois a rede é completamente conectada).
Como era de se esperar, quando uma mensagem é enviada para todos nossos conhecidos ao mesmo tempo, ela se espalha mais rapidamente do que se enviarmos apenas para um destinatário por vez. No caso de broadcast, o tempo máximo para que todos os destinatários recebam a notícia corresponde exatamente ao diâmetro Drede da rede, pois como explicado anteriormente, o diâmetro corresponde ao comprimento da maior geodésica na rede.
No caso de enviarmos apenas para um destinatário por vez, se compararmos o método aleatório com o preferencial, observamos um resultado interessante. Se todas as pessoas que receberem a notícia, retransmitirem-na escolhendo os destinatários aleatoriamente, a curva de crescimento é mais acentuada na região intermediária e menos acentuada no final (demora mais para saturar) em comparação com a mesma curva para o caso preferencial.
Na rede aleatória, os mesmos protocolos geram curvas de crescimento semelhantes. Para quantificar a rapidez do crescimento e analisar os mecanismos de transmissão em relação a estrutura das duas redes é mais apropriado usar o tempo de resposta que não leva em consideração os efeitos da saturação. O tempo de resposta é o tempo necessário para que metade de um valor máximo seja alcançado. No caso da propagação da notícia, o tempo de resposta é dado pelo tempo correspondente a ativação de 50% dos vértices (566 pessoas).
A Fig. 5 apresenta o tempo de resposta para os diferentes mecanismos propostos. O tempo de resposta é menor para a rede aleatória (ER) independentemente do mecanismo de transmissão analisado. A diferença entre as duas redes é mais pronunciada no caso da transmissão preferencial e é mínima no caso do broadcast.
No caso do broadcast, a diferença no tempo de resposta pode ser analisada em termos da diferença na distância média entre quaisquer dois vértices na rede. Como visto na seção anterior, a rede aleatória possui uma distância média levemente menor do que a rede de e-mails. Em média, os vértices estão mais próximos uns dos outros, conseqüentemente, a ativação de metade dos vértices acontece em menos tempo.
Nos outros dois casos (protocolos aleatório e preferencial), a diferença no tempo de resposta reflete uma propriedade mais fundamental das redes usadas, a heterogeneidade da distribuição dos graus. Como visto na seção anterior, a rede aleatória possui um grau característico (o valor médio), ou seja, a maioria dos vértices tem o mesmo grau ou graus próximos ao valor característico. Por outro lado, a rede de e-mails (assim como muitas redes reais [6, 14]) possui uma distribuição diferente onde alguns poucos vértices tem graus altos enquanto a maioria têm valores baixos. Essa assimetria na distribuição faz com que alguns vértices sejam beneficiados em detrimento de outros.
Na transmissão preferencial, todo detentor da notícia a envia preferencialmente para seus vizinhos com maior grau, portanto, os vértices de maior grau são beneficiados e tendem a receber mais vezes a notícia que os vértices com menor grau. Enquanto que na rede aleatória, como os vértices tem graus próximos ao valor característico, esse efeito da escolha preferencial diminui devido a semelhança estrutural entre eles. Conseqüentemente, a notícia circula entre mais vértices diferentes.
Comparando o tempo de resposta da transmissão aleatória com a transmissão preferencial, vemos uma diferença significativa para a rede de e-mail (Fig. 5 - círculos). A transmissão preferencial tende a favorecer alguns indivíduos em detrimento de outros, conseqüemente, se todos os vértices derem preferência para seus vizinhos mais conectados, esses vértices bem conectados tendem a receber um número grande de notícias de diferentes vizinhos concomitantemente. Ao mesmo tempo, os vértices com menos conexões tem uma chance menor e demoram mais para receber a notícia. Importante notar que na rede aleatória, como o grau dos vértices é semelhante, o benefício da transmissão preferencial é pequeno (Fig. 5 - quadrados).
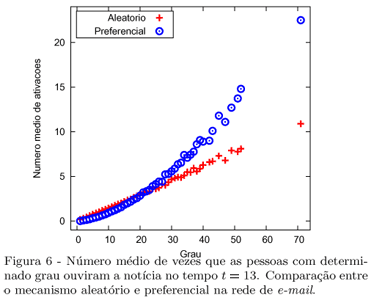
Podemos analisar esse efeito medindo a quantidade média de recebimento de notícias por um vértice em relação ao seu grau para o tempo t = 13 (que foi escolhido por ser um valor próximo ao tempo de resposta para os dois casos - Fig. 6). No caso aleatório, existe uma correlação linear entre o grau do vértice e o número de vezes que este recebeu a notícia. Por outro lado, no caso preferencial a correlação não é linear. Os graus maiores recebem muito mais vezes a notícia através do mecanismo preferencial em comparação com o aleatório.
Apesar de a princípio parecer ser interessante enviar a notícia para alguém que tem vários contatos com a esperança que esta pessoa a retransmita para seus contatos, talvez essa não seja a melhor das estratégias quando se quer espalhar uma notícia o mais rápido possível. Essa sobrecarga de algumas pessoas em especial, pode atrasar a propagação.
Por fim, é importante observar que numa situação real, podem existir alguns outros fatores para se considerar, como por exemplo, a motivação de uma pessoa em transmitir a notícia. Além disso, existe um custo (de tempo ou energia) associado ao envio de cada mensagem e isso pode influenciar o tempo de resposta.
5. Conclusões
O principal objetivo desse trabalho foi sugerir um modelo relativamente simples de um fenômeno cotidiano num sistema complexo, a transmissão de notícias entre pessoas que se comunicam por e-mail. Entre os tópicos diretamente abordados, destacam-se a teoria das redes complexas e processos dinâmicos em redes não regulares.
Através de simulações numéricas foi observado que o tempo de resposta numa transmissão pontual de notícias é menor numa rede aleatória de Erdős e Rényi em comparação com uma rede real de e-mails. Os resultados sugerem que se enviarmos uma notícia para destinatários aleatoriamente, um número maior deles a receberão num menor tempo uma vez que o mecanismo preferencial beneficia os vértices mais conectados em detrimento dos menos conectados.
Embora despretenciosos, os resultados mostraram que através da modelagem relativamente simples podemos obter informações relevantes sobre um sistema complexo. Inclusive, com aplicação dos resultados em nosso cotidiano. Espera-se que a abordagem e resultados apresentados forneçam uma base de conhecimento e motivem os leitores na aplicação de ferramentas matemáticas e conceitos de física em outras áreas, como sociologia, biologia e computação [2, 6, 9, 15, 16].
Sugestões para trabalhos complementares incluem: (a) A construção ou aquisição de redes reais adequadas a um problema específico de interesse (e.g. a rede de amizades sugerida na seção 2); (b) Construção de outras redes teóricas (e.g. a rede de Barabási-Albert [4, 5, 10-12] ou rede "Mundo pequeno" [4, 5, 10-12], comparação de suas propriedades e análise da influência da estrutura na transmissão das notícias (e.g. a contaminação de um vértice depende mais do seu grau ou do grau dos seus vizinhos?); (c) Propor diferentes protocolos para transmissão das notícias (e.g. enviar a notícia para grupos de vértices ao mesmo tempo ou preferencialmente para o vértice menos conectado); (d) Propor protocolos de propagação de opiniões [4, 11, 17] ou transmissão de doenças (e.g. no caso da doença a notícia pode ser vista como uma infecção, onde o vértice se mantém infectado por um período de tempo antes de se curar, durante esse período infectado ele pode contaminar alguns de seus vizinhos); (e) Analisar o processo de transmissão da notícia através de outras medidas (em especial, analisar a importância dos hubs em outros mecanismos de transmissão).
Agradecimentos
O autor agradece a Swedish Foundation for Strategic Research pelo suporte financeiro e a Luana de Freitas Nascimento e Petter Holme por valiosos comentários no texto final.
Recebido em 21/1/2009
Revisado em 19/2/2009
Aceito em 19/3/2009
Publicado em 12/10/2009
- [1] L. da F. Costa, Revista Brasileira de Ensino da Física 25, 164 (2003).
- [2] Luis Enrique Correa da Rocha, Redes Acopladas: Estrutura e Dinâmica Disponível em http://www.teses.usp.br/ (2007).
- [3] R. Guimerà, L. Danon, A. Díaz-Guilera, F. Giralt and A. Arenas, Physical Review E, 68:065103 (2003).
- [4] M.E.J. Newman, SIAM Review 45, 167 (2003).
- [5] S.N. Dorogovtsev and J.F.F. Mendes, Advances in Physics 51, 1079 (2002).
- [6] L. da F. Costa, O.N. Oliveira Jr, G. Travieso, F.A. Rodrigues, P.R. Villas Boas, L. Antiqueira, M.P. Viana e L.E.C. da Rocha, http://arxiv.org/abs/0711.3199/ (2008).
» link - [7] Stanley Wasserman and Katherine Faust, Social Network Analysis - Methods and Applications (Cambridge University Press, New York, 1999).
- [8] Bella Bollobas, Modern Graph Theory (Springer, New York, 2002).
- [9] Matheus Palhares Viana, Metodologia das Redes Complexas para Caracterização do Sistema de Havers, disponível em http://www.teses.usp.br/ (2007).
- [10] R. Albert and A.-L. Barabási, Reviews of Modern Physics 74, 48 (2002).
- [11] S. Boccaletti, V. Latora, Y. Moreno, M. Chaves and D.-U. Hwang, Physics Reports 424, 175 (2006).
- [12] L. da F. Costa, F.A. Rodrigues, G. Travieso and P.R. Villas Boas, Advances in Physics 56, 167 (2007).
- [13] L.C. Cudmani e M.P. Danon, Revista Brasileira de Ensino da Física 12, 78 (1990).
- [14] G. Corso C.R. Fossa e G.B. Oliveira, Revista Brasileira de Ensino da Física 27, 389 (2005).
- [15] I. Gleria, R. Matsushita e S. Da Silva, Revista Brasileira de Ensino da Física 26, 99 (2004).
- [16] H.B. Nascimento Jr., U.L. Fulco, M.L. Lyra, M. Serva e G.M. Viswanathan, Revista Brasileira de Ensino da Física 29, 341 (2007).
- [17] R.A. Zara e E. Koehler, Revista Brasileira de Ensino da Física 26, 53 (2004).
Datas de Publicação
-
Publicação nesta coleção
06 Nov 2009 -
Data do Fascículo
Set 2009
Histórico
-
Aceito
19 Mar 2009 -
Revisado
19 Fev 2009 -
Recebido
21 Jan 2009