Abstracts
There is a situation such that, when a function ƒ(<img src="/img/revistas/rbef/v31n4/a04x.gif" align="absmiddle">) is combined with the Dirac delta function δ(<img src="/img/revistas/rbef/v31n4/a04x.gif" align="absmiddle">), the usual formula <img src="/img/revistas/rbef/v31n4/a04form01.gif" align="absmiddle">does not hold. A similar situation may also be encountered with the derivative of the delta function δ'(<img src="/img/revistas/rbef/v31n4/a04x.gif" align="absmiddle">), regarding the validity of <img src="/img/revistas/rbef/v31n4/a04form02.gif" align="absmiddle">. We present an overview of such unusual situations and elucidate their underlying mechanisms. We discuss implications of the situations regarding the transmission-reflection problem of one-dimensional quantum mechanics.
Dirac delta function; singular functions; quantum mechanics
Existe uma situação tal que quando uma função ƒ(<img src="/img/revistas/rbef/v31n4/a04x.gif" align="absmiddle">) é combinada com a função delta de Dirac, δ(<img src="/img/revistas/rbef/v31n4/a04x.gif" align="absmiddle">), a formula usual <img src="/img/revistas/rbef/v31n4/a04form01.gif" align="absmiddle"> deixa de ser válida. Uma situação similar pode ocorrer com a derivada da função delta, δ'(<img src="/img/revistas/rbef/v31n4/a04x.gif" align="absmiddle">), com relação à formula <img src="/img/revistas/rbef/v31n4/a04form02.gif" align="absmiddle">. Nós apresentamos um apanhado destas situaçãoes não usuais e elucidamos os mecanismos por detrás delas. Nós discutimos as implicações destas situaçãoes em relação ao problema de tranmissão-reflexão em mecânica quântica uni-dimensional.
função delta de Dirac; funções singulares; mecânica quântica
ARTIGOS GERAIS
Unusual situations that arise with the Dirac delta function and its derivative
Situações não usuais originadas da função delta de Dirac e da sua derivada
F.A.B. CoutinhoI,1 1 E-mail: coutinho@dim.fm.usp.br ; Y. NogamiII; F.M. ToyamaIII
IFaculdade de Medicina, Universidade de São Paulo, São Paulo, SP, Brazil
IIDepartment of Physics and Astronomy, McMaster University, Hamilton, Ontario, Canada
IIIDepartment of Computer Science, Kyoto Sangyo University, Kyoto, Japan
ABSTRACT
There is a situation such that, when a function ( ) is combined with the Dirac delta function δ(
) is combined with the Dirac delta function δ( ), the usual formula
), the usual formula  does not hold. A similar situation may also be encountered with the derivative of the delta function δ'(
does not hold. A similar situation may also be encountered with the derivative of the delta function δ'( ), regarding the validity of
), regarding the validity of  . We present an overview of such unusual situations and elucidate their underlying mechanisms. We discuss implications of the situations regarding the transmission-reflection problem of one-dimensional quantum mechanics.
. We present an overview of such unusual situations and elucidate their underlying mechanisms. We discuss implications of the situations regarding the transmission-reflection problem of one-dimensional quantum mechanics.
Keywords: Dirac delta function, singular functions, quantum mechanics.
RESUMO
Existe uma situação tal que quando uma função ( ) é combinada com a função delta de Dirac, δ(
) é combinada com a função delta de Dirac, δ( ), a formula usual
), a formula usual  deixa de ser válida. Uma situação similar pode ocorrer com a derivada da função delta, δ'(
deixa de ser válida. Uma situação similar pode ocorrer com a derivada da função delta, δ'( ), com relação à formula
), com relação à formula  . Nós apresentamos um apanhado destas situaçãoes não usuais e elucidamos os mecanismos por detrás delas. Nós discutimos as implicações destas situaçãoes em relação ao problema de tranmissão-reflexão em mecânica quântica uni-dimensional.
. Nós apresentamos um apanhado destas situaçãoes não usuais e elucidamos os mecanismos por detrás delas. Nós discutimos as implicações destas situaçãoes em relação ao problema de tranmissão-reflexão em mecânica quântica uni-dimensional.
Palavras-chave: função delta de Dirac, funções singulares, mecânica quântica.
1. Introduction
The Dirac delta function δ( ) is a standard subject that appears in textbooks of quantum mechanics. It is such that
) is a standard subject that appears in textbooks of quantum mechanics. It is such that
It can be interpreted as an infinitely high and infinites-imally narrow spike at the origin [1]. As Dirac himself cautioned, however, δ( ) is not a function of x according to the usual mathematical definition of a function, which requires a function to have a definite value for each point in its domain.
) is not a function of x according to the usual mathematical definition of a function, which requires a function to have a definite value for each point in its domain.
If ( ) is an "ordinary" function, which we characterize in due course, we obtain
) is an "ordinary" function, which we characterize in due course, we obtain
where the range of the integration contains the origin. If ( ) is discontinuous at
) is discontinuous at  = 0, we interpret Eq. (2) as
= 0, we interpret Eq. (2) as
where (0+) and (0-) are respectively the limits of ( ) when
) when  approaches 0 from the positive and negative sides. Equation (3) implies that, although δ(
approaches 0 from the positive and negative sides. Equation (3) implies that, although δ( ) itself is not well-defined for
) itself is not well-defined for  = 0, when it occurs as a factor in an integrand, the integral has a well-defined value.
= 0, when it occurs as a factor in an integrand, the integral has a well-defined value.
There is another commonly used formula, i.e.,
where  In this case it is understood that (0+) = (0-) but '(
In this case it is understood that (0+) = (0-) but '( ) may be discontinuous at
) may be discontinuous at  = 0. The range of the integration again contains the origin. In Eq. (4) integration by parts has been done with the understanding that (
= 0. The range of the integration again contains the origin. In Eq. (4) integration by parts has been done with the understanding that ( ) δ (
) δ ( ) vanishes at the limits of the integration.
) vanishes at the limits of the integration.
Although Eqs. (3) and (4) look natural they do not necessarily hold for a certain type of functions. Such situations have been known in the literature that we quote as we proceed. This problem, however, does not seem to have been mentioned in any textbooks of quantum mechanics. Although the situations are rather unusual we believe that we should at least be aware of such possibilities. In this paper we attempt to present a comprehensive overview of the situations and elucidate their underlying mechanisms. Note that we define δ( ) by Eq. (1). If one defines δ(
) by Eq. (1). If one defines δ( ) by Eq. (3) one may be led to self-contradiction unless one chooses an ordinary function for f(
) by Eq. (3) one may be led to self-contradiction unless one chooses an ordinary function for f( ). We examine Eq. (3) in Sec. 2 and Eq. (4) in Sec. 3. We discuss implications of the unusual situations regarding the transmission-reflection problem of one-dimensional quantum mechanics. A summary is given in Sec. 4.
). We examine Eq. (3) in Sec. 2 and Eq. (4) in Sec. 3. We discuss implications of the unusual situations regarding the transmission-reflection problem of one-dimensional quantum mechanics. A summary is given in Sec. 4.
2. The Dirac delta function
Because δ( )= 0 for
)= 0 for 
 0, the validity of Eq. (3) [and also of Eq. (4)] only depends on the behavior of (
0, the validity of Eq. (3) [and also of Eq. (4)] only depends on the behavior of ( ) around the origin. By the "ordinary" function we mean (
) around the origin. By the "ordinary" function we mean ( ) such that it can be expanded around the origin as
) such that it can be expanded around the origin as
where n = 0,1,2,..., θ( ) = 1 (0) if
) = 1 (0) if  > 0 (
> 0 ( < 0) and (n) (0±) = lim
< 0) and (n) (0±) = lim . It is understood that (n) (0±) are all finite. For such a function, Eq. (3) can be justified in the following manner. Define a rectangular function Δ(
. It is understood that (n) (0±) are all finite. For such a function, Eq. (3) can be justified in the following manner. Define a rectangular function Δ( ) by
) by
where  > 0. Note that
> 0. Note that  . We eventually let
. We eventually let 
 0 so that Δ(
0 so that Δ( ) becomes δ(
) becomes δ( ). The integral
). The integral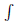 Δ(
Δ( ) (
) ( )d
)d with (
with ( ) expanded as Eq. (5) becomes
) expanded as Eq. (5) becomes
In the limit of
 0, only the n = 0 part remains to contribute to
0, only the n = 0 part remains to contribute to 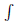 (
( )Δ(
)Δ( ) d
) d and Eq. (3) follow. Although we assumed the specific form of Eq. (6), the details of the form of Δ(
and Eq. (3) follow. Although we assumed the specific form of Eq. (6), the details of the form of Δ( ) are unimportant. For example we can assume a gaussian form and obtain the same result in the narrow width limit.
) are unimportant. For example we can assume a gaussian form and obtain the same result in the narrow width limit.
if ( ) is function that is defined by means of a differencial equation in which δ(
) is function that is defined by means of a differencial equation in which δ( ) is involved, Eq. (3) may turn out to be inconsistent with the definition of (
) is involved, Eq. (3) may turn out to be inconsistent with the definition of ( ) itself. Such an unusual situation was recognized in relation to the Dirac equation in one dimension [2-4]. More recently Griffiths and Walborn (GW) illustrated such a situation by means of a simple mathematical example [5]. We review GW's example and add further clarification. Consider (
) itself. Such an unusual situation was recognized in relation to the Dirac equation in one dimension [2-4]. More recently Griffiths and Walborn (GW) illustrated such a situation by means of a simple mathematical example [5]. We review GW's example and add further clarification. Consider ( ) that is defined by means of the first order differential equation
) that is defined by means of the first order differential equation
where α  0 is a constant. (In GW's example, α = 1.) From Eq. (8) follows
0 is a constant. (In GW's example, α = 1.) From Eq. (8) follows
if Eq. (3) is accepted, Eq. (9) leads to the following boundary condition for ( ) at
) at  = 0 in the limite of
= 0 in the limite of 
 0
0
It turns out, however, that Eq. (10) is inconsistent with Eq. (8) that defines ( ). In order to see this let us start with
). In order to see this let us start with
Before taking the limit of
 0, Δ(
0, Δ( ) is finite and (
) is finite and ( ) is continuous everywhere. Equation (11) can be solved by
) is continuous everywhere. Equation (11) can be solved by
where A is an arbitrary constant. We then obtain  (Constant A can be determined if the value of (
(Constant A can be determined if the value of ( ) at a certain point is specified. This, however, is not essential in the present context.) When
) at a certain point is specified. This, however, is not essential in the present context.) When  is fine, (
is fine, ( ) is continuous everywhere. In the limit of
) is continuous everywhere. In the limit of 
 0, however, (
0, however, ( ) becomes discontinuous at
) becomes discontinuous at  = 0. As
= 0. As  increases through
increases through  = 0, (
= 0, ( ) jump from (-0) =
) jump from (-0) =  to (0) = A and then to (0+) =
to (0) = A and then to (0+) =  . We obtain the boundry condition at
. We obtain the boundry condition at  = 0
= 0
Equations (10) and (13) differ through higher order terms with respect to α
It is crucial that the ordinary function for which Eq.(3) holds is given independently of the limiting process of lim 
 0 Δ(
0 Δ( ) = δ(
) = δ( ). In constrast the (
). In constrast the ( ) defined bRy Eq. (11) depends on
) defined bRy Eq. (11) depends on  . Let us examine the integral
. Let us examine the integral  . We expand as (
. We expand as ( ) as
) as
Note that (n)(0) with n > 0 diverges as 
 0. For the n-th term of the expansion we obtain
0. For the n-th term of the expansion we obtain
Unlike in (7) all the terms with even of the expansion contribute to  . This is the cause of the difference between Eqs. (10) and (13). Although we assumed an explicit form of Δ(
. This is the cause of the difference between Eqs. (10) and (13). Although we assumed an explicit form of Δ( ) of Eq. (6), Eq. (13) obtained above is insensitive to the particular form assumed for Δ(
) of Eq. (6), Eq. (13) obtained above is insensitive to the particular form assumed for Δ( ) [5].
) [5].
There is another closely related problem. If ( ) is an ordinary function, the following substitution is allowed
) is an ordinary function, the following substitution is allowed
When combined with Eq. (16), Eq. (8) becomes
The ( ) defined by Eq. (17), however, turns out to be different from the one defined by Eq. (8). Substitution (16) is not allowed in this sense. Let us examine this problem by starting with the finite width version of Eq.(17), i.e.,
) defined by Eq. (17), however, turns out to be different from the one defined by Eq. (8). Substitution (16) is not allowed in this sense. Let us examine this problem by starting with the finite width version of Eq.(17), i.e.,
Its solution, which is continuous everywhere, can be written as
where A is a constant and
Unlike (14), (n) ( ) = 0 if n > 1. Equation (19) leads to
) = 0 if n > 1. Equation (19) leads to
On the other hand the ( ) of Eq. (19) also yields
) of Eq. (19) also yields
which implies  = A. In the limit of
= A. In the limit of 
 0, Eq. (10) follows from Eq. (21). Substitution (16) in Eq. (8) thus changes the boundary condition of (
0, Eq. (10) follows from Eq. (21). Substitution (16) in Eq. (8) thus changes the boundary condition of ( ) at
) at  = 0 from Eq. (13) to Eq. (10).
= 0 from Eq. (13) to Eq. (10).
In the one-dimensional Dirac equation, which is a first order differential equation for a two-component wave function, if there is a potential of the form of δ( ) Eq. (3) does not hold for the wave function [2-4]. This is essentially for the same reason as the one found in GW's example with Eq. (8). It has also been known that if the potential part of the equation is of the form of
) Eq. (3) does not hold for the wave function [2-4]. This is essentially for the same reason as the one found in GW's example with Eq. (8). It has also been known that if the potential part of the equation is of the form of  where
where  is the Dirac wave function, and if it is replaced by
is the Dirac wave function, and if it is replaced by  then Eq. (3) can be used [2,3,6]. The interaction in this form can be interpreted as a zero-range "separable potential". The mechanism behind this feature is essentially the same as what we pointed out above regarding Eq. (16).
then Eq. (3) can be used [2,3,6]. The interaction in this form can be interpreted as a zero-range "separable potential". The mechanism behind this feature is essentially the same as what we pointed out above regarding Eq. (16).
Next let us turn to the ( ) defined by the second order differential equation
) defined by the second order differential equation
where β is a constant. In this case we find that ( ) is continuous at
) is continuous at  = 0 and that Eq. (3) holds. Equation (23) leads to the boundary condition
= 0 and that Eq. (3) holds. Equation (23) leads to the boundary condition
No complication such as those discussed above arises in this case. In order to confirm the validity of Eq. (3), let us start with
Before taking the limit of
 0, (
0, ( ) and df(
) and df( )/d
)/d can be assumed to be continuous everywhere. Solution (
can be assumed to be continuous everywhere. Solution ( ) for -
) for - <
< <
<  can be written as
can be written as
where A and B are constants. From Eq. (26) follows  . In the limit of
. In the limit of 
 0, we find K
0, we find K 
 0 and hence (
0 and hence ( ) remains continuous, i.e.,
) remains continuous, i.e.,
For  outside the above interval, d2(
outside the above interval, d2( )/d
)/d 2 = 0 and hence (
2 = 0 and hence ( ) is a linear function of
) is a linear function of  . In order to determine the boundary condition for (
. In order to determine the boundary condition for ( ) at x = 0 in the limit of
) at x = 0 in the limit of 
 0, however, we do not need (
0, however, we do not need ( ) for |
) for | | >
| >  . It is sufficient to know (
. It is sufficient to know ( ) for
) for  <
<  <
<  .
.
Let us examine  with (
with ( ) expanded as Eq. (5). The derivative
) expanded as Eq. (5). The derivative 
 diverges as
diverges as 
 0. When it is combined with
0. When it is combined with 1)], however, only the n = 0 term of the expansion contributes to the integral in the limit of
1)], however, only the n = 0 term of the expansion contributes to the integral in the limit of 
 0. As a consequence, we obtain
0. As a consequence, we obtain  which justifies Eq. (3). This is in contrast to the situation found with the (
which justifies Eq. (3). This is in contrast to the situation found with the ( ) of Eq. (12) for which (n)(0) α 1/(2
) of Eq. (12) for which (n)(0) α 1/(2 )n. Let us add that substitution (16) in Eq. (23) can be done without affecting the solution.
)n. Let us add that substitution (16) in Eq. (23) can be done without affecting the solution.
The Schrödinger equation in one dimension for the stationary state of energy E is, where m is the mass of the particle under consideration, V( ) is the potential and
) is the potential and  is the wave function. Equation (23) can be interpreted as the Schrödinger equation with E = 0 and potential
is the wave function. Equation (23) can be interpreted as the Schrödinger equation with E = 0 and potential  . Actually the boundary conditions Eq. (24) and Eq. (27) can be applied to the Schrödinger wave function with any value of E. The effect of the term E
. Actually the boundary conditions Eq. (24) and Eq. (27) can be applied to the Schrödinger wave function with any value of E. The effect of the term E  on the boundary condition is negligible because
on the boundary condition is negligible because  vanishes in the limit of
vanishes in the limit of 
 0. Hence the boundary condition on the wave function at
0. Hence the boundary condition on the wave function at  = 0 is independent of energy E.
= 0 is independent of energy E.
3. The derivative of the delta function
In this section we turn to the validity of Eq. (4). We consider Δ'( )= dΔ(
)= dΔ( )/d
)/d , which in its narrow width limit is reduced to δ'(
, which in its narrow width limit is reduced to δ'( ). The results that we obtained in Sec. 2 are insensitive to the details of the form assumed for Δ(
). The results that we obtained in Sec. 2 are insensitive to the details of the form assumed for Δ( ). In contrast to that, what we are going to obtain regarding δ'(
). In contrast to that, what we are going to obtain regarding δ'( ) in this section depends on what we assume for the form of Δ(
) in this section depends on what we assume for the form of Δ( ) and Δ'(
) and Δ'( ).
).
Let us begin with the Δ( ) of the rectangular form of Eq. (6), which leads to the following dipole form
) of the rectangular form of Eq. (6), which leads to the following dipole form
If ( ) is an ordinary function that is continuous at
) is an ordinary function that is continuous at  = 0, Eq. (4) can be justified by replacing δ'(
= 0, Eq. (4) can be justified by replacing δ'( ) with Δ'(
) with Δ'( ) of Eq. (29) and letting
) of Eq. (29) and letting 
 0 at the end. Equation (4), however, may not hold if (
0 at the end. Equation (4), however, may not hold if ( ) is a function that is defined by means of a differential equation in which δ' (
) is a function that is defined by means of a differential equation in which δ' ( ) is involved. GW mentioned this possibility but did not discuss any details; see the last sentence of note 3 of [5].
) is involved. GW mentioned this possibility but did not discuss any details; see the last sentence of note 3 of [5].
We are interested in the ( ) defined by
) defined by
where  is a constant. If we accept Eq. (4), Eq. (30) leads to the boundary condition [7]
is a constant. If we accept Eq. (4), Eq. (30) leads to the boundary condition [7]
As we show below, however, Eq. (31) is not valid. Let us start with
where Δ'( ) is the one defined by Eq. (29). Before the limit of
) is the one defined by Eq. (29). Before the limit of 
 0 is taken, (
0 is taken, ( ) is continuous everywhere but '(
) is continuous everywhere but '( ) is discontinuous at
) is discontinuous at  = ±
= ± because of the δ(x ±
because of the δ(x ±  ) of Eq. (29). At
) of Eq. (29). At  = ±
= ± , (
, ( ) and '(
) and '( ) are subject to the boundary conditions (24) and (27) with β replaced by
) are subject to the boundary conditions (24) and (27) with β replaced by  . We refer to the three regions,
. We refer to the three regions,  < -
< -  ,-
,-  <
<  <
<  , and
, and  <
<  as I, II and III, respectively. In each of the regions, d2(
as I, II and III, respectively. In each of the regions, d2( )/dx2 = 0 and hence (
)/dx2 = 0 and hence ( ) is a linear function of
) is a linear function of  . Let the (
. Let the ( ) in these regions be i(
) in these regions be i( )=
)=  where i =1, 2, 3 correspond to regions I, II and III, respectively. There are six constants but, if we specify two of them, the others can be determined by using Eqs. (24) and (27) at
where i =1, 2, 3 correspond to regions I, II and III, respectively. There are six constants but, if we specify two of them, the others can be determined by using Eqs. (24) and (27) at  = ±
= ±  . If we assume for example that a2 and b2 are given, we obtain
. If we assume for example that a2 and b2 are given, we obtain
In taking the narrow width limit of Δ( ), let us introduce another parameter η such that η >
), let us introduce another parameter η such that η >  . We let both of E and η approach zero from the positive side. We integrate both sides of Eq. (32) over the interval [-η, η]. From the left hand side we obtain
. We let both of E and η approach zero from the positive side. We integrate both sides of Eq. (32) over the interval [-η, η]. From the left hand side we obtain
where we have used (η)= 3(η) and (-η)= 1(-η) together with Eqs. (33) and (34). The right hand side of Eq. (32) yields
which naturally agrees with Eq. (35). This can also be calculated as
Note that Δ(±η) = 0 and '2( ) = a2.
) = a2.
In the limit of η  0, we obtain '(±η)
0, we obtain '(±η)  (0±), (0+) = a3 and (0-)= a1, and then
(0±), (0+) = a3 and (0-)= a1, and then
Note that Eq. (39) is different from Eqs. (36) and (37). From Eqs. (38) and (39) we see that Eq. (31) is not valid. It is possible to resurrect Eq. (31) by choosing b2 such that b2/ = 0, i.e., either b2 = 0 or b2 scales with
= 0, i.e., either b2 = 0 or b2 scales with  in such a manner. Such a choice of b2, however, is artificial. Here the following remark would be in order. One may erroneously think that [(
in such a manner. Such a choice of b2, however, is artificial. Here the following remark would be in order. One may erroneously think that [( ) - (0)]/
) - (0)]/ â '(0+) and [(0)-(-
â '(0+) and [(0)-(- )]/
)]/
 '(0-). Both of these are equal to a2, which is '2(
'(0-). Both of these are equal to a2, which is '2( ). Note that '(0+) = '3(
). Note that '(0+) = '3( ) and (0-)= í(
) and (0-)= í( ).
).
There is another important aspect of the ( ) that is subject to Eq. (30). In Eqs. (33) and (34) we assumed that 2(
) that is subject to Eq. (30). In Eqs. (33) and (34) we assumed that 2( ) is given first and then determined 1(
) is given first and then determined 1( ) and 3(
) and 3( ). If instead we start with an assumed 1(
). If instead we start with an assumed 1( ) and determine 2(
) and determine 2( ) and 3(
) and 3( ), we obtain
), we obtain
Let us require that 3( ) be finite in the limit of
) be finite in the limit of 
 0. This requirement can be satisfied if we choose b1 = 0. Then we find that b2 = b3 = 0. Alternatively we can assume that b1 is scaled according to b1 = c1
0. This requirement can be satisfied if we choose b1 = 0. Then we find that b2 = b3 = 0. Alternatively we can assume that b1 is scaled according to b1 = c1 . In this case we again obtain b2 = b3 = 0. Thus we arrive at the boundary condition,
. In this case we again obtain b2 = b3 = 0. Thus we arrive at the boundary condition,
Regarding the relation between '(0+) and '(0-), we obtain
where we assumed b1 = c1 . Equation (43) contains c1 that can be chosen arbitrarily. Hence it is not a legitimate boundary condition.
. Equation (43) contains c1 that can be chosen arbitrarily. Hence it is not a legitimate boundary condition.
As we said at the end of the last section, Eq. (30) also can be regarded as the Schrödinger equation with energy E = 0 and potential V ( )=
)= . We pointed out that the energy term E
. We pointed out that the energy term E has no effect on the boundary condition, that is, Eq. (42) can be applied even when E
has no effect on the boundary condition, that is, Eq. (42) can be applied even when E  0. Let us consider the transmission-reflection problem of one-dimensional quantum mechanics with energy E = k2/(2m) where k > 0. Assume that a "plane wave" eikr is incident from the left. The wave function can be written as
0. Let us consider the transmission-reflection problem of one-dimensional quantum mechanics with energy E = k2/(2m) where k > 0. Assume that a "plane wave" eikr is incident from the left. The wave function can be written as
where T (k) and R(k) are the transmission and reflection coefficients, respectively. The probabilities of transmission and reflection are respectively given by |T(k)|2 and |R(k)|2 . Equation (42) requires that
so that there is no transmission at any energies. The incident wave is totally reflected at  = 0. This means that the two half-spaces of
= 0. This means that the two half-spaces of  > 0 and
> 0 and  < 0 become effectively disjoint. This was pointed out by eba a long time ago [8]. In this connection, see Refs. [9,10] also. The T(k) and R(k) for the potential V (
< 0 become effectively disjoint. This was pointed out by eba a long time ago [8]. In this connection, see Refs. [9,10] also. The T(k) and R(k) for the potential V ( )=
)=  with finite
with finite  can be worked out explicitly. When |
can be worked out explicitly. When | k|« 1 we obtain [10]
k|« 1 we obtain [10]
which is reduced to Eq. (45) in the limit of
 0.
0.
On the basis of Eq. (30) Griffths [7] proposed Eq. (31) together with
which also relies on Eq. (4). As we have shown explicitly, Eq. (31) is inconsistent with Eq. (30). In a similar manner it can also be shown that Eq. (47) is inconsis tent with Eq. (30). It is interesting, however, that Eqs. (31) and (47) together represent a legitimate point interaction that can be related to a self-adjoint extension of the kinetic energy operator [10]. Boundary condi tions (31) and (47) can be reinstated if we make the following substitution in Eq. (30) [11, 12],
where δ'p ( ) is defined by
) is defined by
Boundary conditions (31) and (47), however, should be dissociated from δ'( ). Note a similarity between substitutions (16) and (48); they respectively resurrect Eqs. (3) and (4). The substitutions, however, change the physics of the models under consideration.
). Note a similarity between substitutions (16) and (48); they respectively resurrect Eqs. (3) and (4). The substitutions, however, change the physics of the models under consideration.
We have interpreted δ'( ) as the
) as the 
 0 limit of Δ'(
0 limit of Δ'( ) of Eq. (29), which is the derivative of the rectangular function Δ(
) of Eq. (29), which is the derivative of the rectangular function Δ( ) of Eq. (6). A question that arises here is: Does boundary condition (42) depend on the explicit form assumed for Δ'(
) of Eq. (6). A question that arises here is: Does boundary condition (42) depend on the explicit form assumed for Δ'( )? The answer to this question is somewhat surprisingly affirmative. This is in the following sense. Recently Christiansen et al. [13] re-examined the transmission-reflection problem with a potential of the form of δ'(
)? The answer to this question is somewhat surprisingly affirmative. This is in the following sense. Recently Christiansen et al. [13] re-examined the transmission-reflection problem with a potential of the form of δ'( ). They assumed the δ'(
). They assumed the δ'( ) as the narrow width limit of the following rectangular function [see their Eq. (5)]
) as the narrow width limit of the following rectangular function [see their Eq. (5)]
We have replaced their  with 2
with 2 so that the
so that the  of Eq. (51) corresponds to the
of Eq. (51) corresponds to the  of Eq. (29). The Δ'c(
of Eq. (29). The Δ'c( ) is the derivative of a triangular function of a unit area. If (
) is the derivative of a triangular function of a unit area. If ( ) is an ordinary function, Eq. (4) with δ'(
) is an ordinary function, Eq. (4) with δ'( ) = lim
) = lim
 0 Δ'c(
0 Δ'c( ) holds.
) holds.
Christiansen et al. [13] considered the potential
where σ is a dimensionless constant. They solved the Schrödinger equation and then took the limit of
 0. They showed that, if σ satisfies
0. They showed that, if σ satisfies
the potential becomes partially transparent with
This is in contrast to T(k) = 0 of Eq. (45). Equation (53) admits discrete values of σ. They are 3.927, 7.069, 10.210, ...in increasing order. Let us add that there are a variety of other forms of Δ'( ) that lead to non-vanishing but different T(k) [14].
) that lead to non-vanishing but different T(k) [14].
If we assume Eqs. (16) and (47), which are both based on Eq. (4), we obtain
This follows from Eqs. (38) and (49) of [10] with c = σ2 . The σ of Eq. (54) is subject to Eq. (53) but there is no such restriction on the σ of Eq. (55). The T(k)'s of Eqs. (54) and (55) are clearly different. This means that Eq. (4) with the wave function fails when it is used for Vσ( ) with
) with 
 0.
0.
Instead of reviewing it in detail, let us put Christiansen et al.' s analysis in the perspective of the "threshold anomaly"of transmission-reflection problem. With an arbitrarily given potential, the transmission probability usually vanishes at threshold, i.e., |T(k)|2  0 as k
0 as k  0. This is because, no matter how small it is, the potential is insurmountably large as compared with the infinitesimal energy of the incident particle. If there is a bound state at threshold (i.e., with zero energy), however, threshold anomaly can occur such that |T(k)|2 remains finite as k
0. This is because, no matter how small it is, the potential is insurmountably large as compared with the infinitesimal energy of the incident particle. If there is a bound state at threshold (i.e., with zero energy), however, threshold anomaly can occur such that |T(k)|2 remains finite as k  0 [15]. When the strength parameter σ of the potential is chosen to satisfy Eq. (53), indeed there is a bound state at threshold. There are two types of the anomaly, I and II. We obtain |T(0)|2 = 1 in type I whereas |T(0)|2 can take any value between 0 and 1 in type II. Type II can be found only if the potential is asymmetric as a function of
0 [15]. When the strength parameter σ of the potential is chosen to satisfy Eq. (53), indeed there is a bound state at threshold. There are two types of the anomaly, I and II. We obtain |T(0)|2 = 1 in type I whereas |T(0)|2 can take any value between 0 and 1 in type II. Type II can be found only if the potential is asymmetric as a function of  [16]. The partial transparency that was found in [13] is an illustration of the threshold anomaly of type II. Let us add that threshold anomaly does not occur to a potential of the form of Δ'(
[16]. The partial transparency that was found in [13] is an illustration of the threshold anomaly of type II. Let us add that threshold anomaly does not occur to a potential of the form of Δ'( ) of Eq. (29). This can be seen from Eq. (46).
) of Eq. (29). This can be seen from Eq. (46).
The threshold anomaly refers to T(k) with k = 0. The T(k) of Eq. (54) that is due to potential Vσ( ), however, is independent of k. In this sense the threshold anomaly holds for all energies. The reason why T(k) becomes independent of k can be seen as follows. Note that Vσ(
), however, is independent of k. In this sense the threshold anomaly holds for all energies. The reason why T(k) becomes independent of k can be seen as follows. Note that Vσ( )
)  1/
1/ 2 and its spatial range is proportional to
2 and its spatial range is proportional to  . In the Schrödinger equation with Vσ(
. In the Schrödinger equation with Vσ( ), if we introduce dimensionless quantities y =
), if we introduce dimensionless quantities y =  /
/ and η =
and η =  k, we can eliminate
k, we can eliminate  and k in favor of y and η. The transmission coefficient can be expressed in terms of dimensionless parameters σ and η [13]. In the limit of
and k in favor of y and η. The transmission coefficient can be expressed in terms of dimensionless parameters σ and η [13]. In the limit of  â 0 and η â 0, the transmission coeficient is reduced to a function of σ alone, which is independent of k; see Eq. (54). The reason why the T(k) of Eq. (55) is also independent of k can be explained in a similar manner.
â 0 and η â 0, the transmission coeficient is reduced to a function of σ alone, which is independent of k; see Eq. (54). The reason why the T(k) of Eq. (55) is also independent of k can be explained in a similar manner.
4. Summary
Regarding the Dirac delta function δ( ) and its derivative δ'(
) and its derivative δ'( ), Eqs. (3) and (4) appear quite ubiquitously in textbooks of quantum mechanics but we should be aware of some possible danger in using them naively. We presented an overview of unusual situations in which the seemingly natural Eqs. (3) and (4) fail to hold. They can occur when function (
), Eqs. (3) and (4) appear quite ubiquitously in textbooks of quantum mechanics but we should be aware of some possible danger in using them naively. We presented an overview of unusual situations in which the seemingly natural Eqs. (3) and (4) fail to hold. They can occur when function ( ) is not an arbitrarily given function but is specifically defined by a differential equation in which δ(
) is not an arbitrarily given function but is specifically defined by a differential equation in which δ( ) or δ'(
) or δ'( ) appears.
) appears.
We illustrated the mechanism behind the failure of Eq. (3) by starting with function Δ( ) of Eq. (6) that has a finite width 2
) of Eq. (6) that has a finite width 2 and taking its narrow width limit. Equation (3) fails when (
and taking its narrow width limit. Equation (3) fails when ( ) is a function that is defined by a first order differential equation of the form of Eq. (8). In this case (n) (0), given by Eq. (14), diverges as
) is a function that is defined by a first order differential equation of the form of Eq. (8). In this case (n) (0), given by Eq. (14), diverges as 
 0 for all values of n > 0 and this results in the failure of Eq. (3). The commonly used substitution (16) also fails. No such complication arises for (
0 for all values of n > 0 and this results in the failure of Eq. (3). The commonly used substitution (16) also fails. No such complication arises for ( ) that is subject to a second order differential equation such as the Schrödinger equation. The delta function δ(
) that is subject to a second order differential equation such as the Schrödinger equation. The delta function δ( ) that we used is the one defined by Eq. (1). Often Eq. (3) is used in defining δ(
) that we used is the one defined by Eq. (1). Often Eq. (3) is used in defining δ( ). The δ(
). The δ( ) so defined, however, is led to self-contradiction as we illustrated by means of the (
) so defined, however, is led to self-contradiction as we illustrated by means of the ( ) defined through Eq. (8).
) defined through Eq. (8).
The failure of Eq. (4) is associated with the second order differential equation (30) (and also the Schrödinger equation) in which δ'( ) is involved. For Δ'(
) is involved. For Δ'( ), the finite width version of δ'(
), the finite width version of δ'( ), we first consid ered the traditional dipole form of Eq. (29) and explic itly examined how Eq. (4) fails. We also examined the different version (51) that Christiansen et al. [13] re cently considered. Equation (4) again fails in this case. The results obtained in Sec. 2 are insensitive to the details of the form assumed for Δ(
), we first consid ered the traditional dipole form of Eq. (29) and explic itly examined how Eq. (4) fails. We also examined the different version (51) that Christiansen et al. [13] re cently considered. Equation (4) again fails in this case. The results obtained in Sec. 2 are insensitive to the details of the form assumed for Δ( ). In contrast the results obtained in Sec. 3 vary depending on the form of Δ'(
). In contrast the results obtained in Sec. 3 vary depending on the form of Δ'( ). We discussed implications that the unusual situations have regarding one-dimensional quantum mechanics. We related the results of [13] to the threshold anomaly of the transmission-reflection problem.
). We discussed implications that the unusual situations have regarding one-dimensional quantum mechanics. We related the results of [13] to the threshold anomaly of the transmission-reflection problem.
Acknowledgments
We would like to thank Dr. M. Amaku who assisted us in preparing the manuscript. This work was supported by Fundação de Amparo à Pesquisa do Estado de São Paulo, Conselho National de Desenvolvimento Científico e Tecnológico, the Natural Sciences and Engineering Research Council of Canada, the Japan Society for the Promotion of Science and Kyoto Sangyo University.
Recebido em 22/7/2009
Aceito em 26/8/2009
Publicado em 18/2/2010
- [1] P.A.M. Dirac, The Principles of Quantum Mechanics (Clarendon Press, Oxford, 1958), 4. ed., Sec. 15.
- [2] B. Sutherland and D.C. Mattis, Phys. Rev. A 24, 1194 (1981).
- [3] M.G. Calkin, D. Kiang and Y. Nogami, Am. J. Phys. 55, 737 (1987).
- [4] B.H.J. McKellar and G.J.. Stephenson Jr., Phys. Rev. C 35, 2262 (1987).
- [5] D. Griffiths and S. Walborn, Am. J. Phys. 67, 446 (1999).
- [6] M.G. Calkin, D. Kiang and Y. Nogami, Phys. Rev. C 38, 1076 (1988).
- [7] D.J. Griffiths, J. Phys. A: Math. Gen. 26, 2265 (1993).
- [8] P. eba, Rep. Math. Phys. 24, 111 (1986).
- [9] S.H. Patil, Physica Scripta 49, 645 (1994).
- [10] F.A.B. Coutinho, Y. Nogami and J.F. Perez, J. Phys. A: Math. Gen. 30, 3937 (1997).
- [11] T.T. Wu and M.L. Yu, J. Math. Phys. 43, 5949 (2002).
- [12] F.A.B. Coutinho, Y. Nogami, F.M. Toyama and L. Tomio, J. Phys. A: Math. Gen. 37, 10653 (2004).
- [13] P.L. Christiansen, H.C. Arnbak, A.V. Zolotaryuk, V.N. Ermakov and Y.B. Gaidei, J. Phys. A: Math. Gen. 36, 7589 (2003).
- [14] F.M. Toyama and Y. Nogami, J. Phys. A: Math. Theor. 40, F685 (2007).
- [15] P. Senn, Am. J. Phys. 56, 916 (1988).
- [16] Y. Nogami and C.K. Ross, Am. J. Phys. 64, 923 (1996).
Publication Dates
-
Publication in this collection
26 Apr 2010 -
Date of issue
Dec 2009
History
-
Received
22 July 2009 -
Reviewed
26 Aug 2009 -
Accepted
18 Feb 2010



















































