Abstracts
A simple harmonic oscillator model is proposed to describe the mechanical power involved in human locomotion. In this framework, by taking into account the anthropometric parameters of a standard individual, we are able to calculate the speed-power curves in human walking. The proposed model accounts for the well known Margaria's law in which the cost of human running (independent from the speed) is fixed to 1 kcal/(kg km). The model includes the effects of a gentle slope (either positive or negative) and the effect due to the mechanical response of the walking surface. The model results obtained in the presence of a slope are in qualitative agreement with the experimental data obtained by A. Leonardi et al.
movement and locomotion; human walking; race walking; mountain trekking
Propõe-se um modelo simples de oscilador harmônico para descrever a potência mecânica envolvida na locomoção humana. Neste contexto, considerando parâmetros antropométricos de um indivíduo padrão, mostramos como calcular as curvas de velocidade x potência na caminhada de um humano. O modelo proposto explica a conhecida lei de Margaria, segundo a qual o custo de uma corrida (independente da velocidade) é fixo e vale 1 kcal/(kg km). O modelo inclui os efeitos de um aclive (ou declive) pouco acentuado e o efeito devido à resposta mecânica da superfície sobre a qual se caminha. Os resultados obtidos via modelo na presençe um subida/descida concordam qualitativamente com os resultados experimentais obtidos por A. Leonardi et al.
movimento e locomoção; caminhada humana; corrida; trekking em montanha
ARTIGOS GERAIS
A simple model of energy expenditure in human locomotion
Modelo simples de gasto de energia na locomoção humana
F. Romeo1 1 E-mail: fromeo@sa.infn.it.
Dipartimento di Fisica "E. R. Caianiello", Università degli Studi di Salerno, Baronissi, Salerno, Italy
ABSTRACT
A simple harmonic oscillator model is proposed to describe the mechanical power involved in human locomotion. In this framework, by taking into account the anthropometric parameters of a standard individual, we are able to calculate the speed-power curves in human walking. The proposed model accounts for the well known Margaria's law in which the cost of human running (independent from the speed) is fixed to 1 kcal/(kg km). The model includes the effects of a gentle slope (either positive or negative) and the effect due to the mechanical response of the walking surface. The model results obtained in the presence of a slope are in qualitative agreement with the experimental data obtained by A. Leonardi et al.
Keywords: movement and locomotion, human walking, race walking, mountain trekking.
RESUMO
Propõe-se um modelo simples de oscilador harmônico para descrever a potência mecânica envolvida na locomoção humana. Neste contexto, considerando parâmetros antropométricos de um indivíduo padrão, mostramos como calcular as curvas de velocidade x potência na caminhada de um humano. O modelo proposto explica a conhecida lei de Margaria, segundo a qual o custo de uma corrida (independente da velocidade) é fixo e vale 1 kcal/(kg km). O modelo inclui os efeitos de um aclive (ou declive) pouco acentuado e o efeito devido à resposta mecânica da superfície sobre a qual se caminha. Os resultados obtidos via modelo na presençe um subida/descida concordam qualitativamente com os resultados experimentais obtidos por A. Leonardi et al.
Palavras-chave: movimento e locomoção, caminhada humana, corrida, trekking em montanha.
1. Introduction
Several studies have been done to clarify the biomechanical, metabolic and energetic aspects involved in human and bipedal locomotion [1-6]. Due to the tremendous implications in different fields of our life (health, sport, medicine, biology, robotics [7, 8], etc), the research on human motion can be considered as a multidisciplinary domain, where different competences are needed. Due to this, the study of the energetic aspects related to human gait could be considered as a formidable task. Nevertheless, elementary physics can be adopted to obtain several useful indications about energy expenditure in human walking. Following the spring-mass model proposed by Alexander [9-12], the extremely low energetic cost of human walking and running is strongly related to the role of the tendons acting as elastic energy storage elements. Indeed, the elastic energy stored in the right (left) knee bending act, due to the falling of the right (left) foot to the ground, is released at the beginning of a new step. The mentioned mechanism becomes more efficient as the speed of gait increases. In this way, in the range of running velocity 4-6 m/s, the energy expenditure becomes insensitive to the speed and quite surprisingly saturates to a value close to 1 kcal/(kg km), as prescribed by Margaria's law [13, 14].
In this work we shall derive Margaria's law by means of a mechanical model consisting of a forced harmonic oscillator. In this context, we can understand the experimental behaviour of a typical speed-power curve by invoking the presence of a point of inflection, which mimics a saturation of the energy expenditure to 1 kcal/(kg km) for velocities below a threshold value, which is not accessible to human runners. The effect of elastic energy storage of the ground-foot-tendon system is also included in the model by means of a coefficient of restitution α, measuring the ratio between the speed of the impacting foot and its exiting speed from the impact, the latter velocity being evaluated at the beginning of the leg swinging phase. In conclusion, the effects of a moderate positive or negative slope are considered.
2. The model
We describe the gait of an individual characterized by a total mass m whose leg has mass, length and momentum of inertia respectively equal to µ,  and I. The leg is schematized as a single linear homogeneous element. The slope
and I. The leg is schematized as a single linear homogeneous element. The slope  of the ground (both for positive and negative values) is taken into account. The walking model we shall consider consists of three phase (see Fig. 1): 1) rising of the centre of mass; 2) leg swinging of amplitude
of the ground (both for positive and negative values) is taken into account. The walking model we shall consider consists of three phase (see Fig. 1): 1) rising of the centre of mass; 2) leg swinging of amplitude 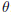 ; 3) lowering of the centre of mass. In the walking action, when displacing the centre of mass in the walking direction of a quantity 2
; 3) lowering of the centre of mass. In the walking action, when displacing the centre of mass in the walking direction of a quantity 2 sin (
sin (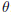 /2), there is at least one foot in contact with the walking surface. In order to fully characterize the dynamics of the system, we need to write the dynamical equation of the swinging leg subjected to an external torque. Therefore, by defining β as the angle formed by the swinging leg with respect to the direction of the gravitational force, one can write (for small β)
/2), there is at least one foot in contact with the walking surface. In order to fully characterize the dynamics of the system, we need to write the dynamical equation of the swinging leg subjected to an external torque. Therefore, by defining β as the angle formed by the swinging leg with respect to the direction of the gravitational force, one can write (for small β)
where Mex is the applied torque required to the muscles to obtain the leg motion. Eq. (1) can be solved by imposing the initial conditions β (0) = -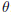 /2 +
/2 +  and β'(0) = ω0. Proceeding as we said, by defining ω =
and β'(0) = ω0. Proceeding as we said, by defining ω =  , we obtain the following expression
, we obtain the following expression
We are now interested in the computation of the value of the external torque Mex we have to apply to obtain a given mean velocity u. Observing that in the time interval  , which elapses in swinging the leg between the angular positions [-
, which elapses in swinging the leg between the angular positions [-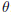 /2 +
/2 +  ,
, 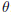 /2+
/2+ ], the system displace its centre of mass of a quantity 2
], the system displace its centre of mass of a quantity 2 sin (
sin (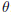 /2), we get
/2), we get 
 Solving now Eq. (2) for Mex imposing β (
Solving now Eq. (2) for Mex imposing β ( )=
)= 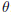 /2+
/2+  , we obtain the following relation
, we obtain the following relation
which is the constant torque we have to apply to the leg in order to complete a step at a mean velocity u. The average mechanical power (ws) involved in swinging the leg can be easily computed by means of the following relation coming from the standard definition
Eq. (4) can be now recast taking into account both Eq. (3) and the explicit value of the momentum of inertia I  as follows
as follows
Apart from the above contribution to the mechanical power involved in human walking, we also need to consider the power involved in the process of rising the centre of mass of the system. This contribution, which in the case of null slope can be calculated as
becomes
for arbitrary but gentle slope. Finally the total mechanical power is obtained as the sum  w
w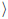 =
= 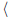 ws
ws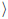 +
+ 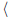 wcm
wcm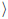 . Nevertheless, the average total power presents an unwanted dependence on the angle
. Nevertheless, the average total power presents an unwanted dependence on the angle 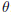 . This problem can be overcome following Bertram and Ruina [15] which find an explanation to the empirical relation linking the amplitude of the step to the mean velocity as the result of the constrained minimization of the O2 consumption. This empirical relation in our notation reads as follows
. This problem can be overcome following Bertram and Ruina [15] which find an explanation to the empirical relation linking the amplitude of the step to the mean velocity as the result of the constrained minimization of the O2 consumption. This empirical relation in our notation reads as follows
where ε =0.58. It is worth to notice that the previous relation is not trivially related to the minimization of the function
w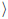 with respect to
with respect to 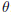 , but is strongly determined by biological conditions. Substituting Eq. (7) in the expression for the mechanical power
, but is strongly determined by biological conditions. Substituting Eq. (7) in the expression for the mechanical power 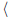 w
w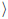 , we can write the energy expenditure W involved in human walking in units kcal/(kg km) as follows
, we can write the energy expenditure W involved in human walking in units kcal/(kg km) as follows
where the numerical values which appears in Eq. (8) are in I.S. units, while the coefficient η represents the muscles efficiency, which is a quantity strongly affected both by climatic parameters (temperature, humidity, etc.) and by metabolic ones.
3. Results
In order to compare our results with the experimental data, we analyse Eq. (8) by fixing g = 9.8 m/s2 and the remaining anthropometric parameters as follows: m = 70 kg; µ = 17.5 kg;  = 0.9. In addition, we fix a coefficient of proportionality, let say A, in Eq. (7) to be
= 0.9. In addition, we fix a coefficient of proportionality, let say A, in Eq. (7) to be
0.17 (m/s)ε s. It is worth to notice that the constant A, which in the real world depends on the individual features, is not arbitrary, but can be theoretically assigned by imposing a condition on the maximum step length obtained at the maximum mean velocity. As a final assumption, we set ω0 =  , where the non-dimensional factor α plays a role which will be clear in the following discussion.
, where the non-dimensional factor α plays a role which will be clear in the following discussion.
In Fig. 2, assuming a null slope, we presents the energy expenditure W as a function of the mean velocity u (m/s) for four different values of the parameter α (from bottom to top α =1.12, α =1.1, α = 1, α =0.9), setting η =0.30. As can be noticed, a saturation behaviour is obtained for α =1.1, according to the well known Margaria's law.
In Fig. 3a we presents the effect of different muscles efficiency ranging from 0.25 to 0.35 leaving the remaining parameters as in Fig. 2. The previous features related to the plateau of the curves are preserved even though the saturation value varies, though remaining close to 1 kcal/(kg km).
The behaviour presented above can be associated to the formation of an inflection point in the W vs. u curves, as shown in Fig. 3b. In fact, in Fig. 3b an extended range of velocities is used in order to emphasize the analytic behaviour responsible for the saturation observed in the experimental data. The condition for the formation of the plateau is related to the parameter α, as shown in Fig. 2. This parameter can be altered in several ways including the nature of the ground [1, 2] (rigid or absorbing ground) or the muscles status. Indeed, under muscular fatigue conditions, a loss of efficiency in the elastic energy storage mechanism of the system muscle-tendon appears and thus an increasing of the energy expenditure involved in the walking is observed. Finally, motivated by recent experimental works by Leonardi [16], in Fig. 4 we plot the energy expenditure as a function of a gentle slope arctan ( ) ≈
) ≈  for different values of α, mimicking different ground responses. As shown in Fig. 4, a linear behaviour is obtained in the slope in agreement with Ref. [16]. The additional energy cost associated with
for different values of α, mimicking different ground responses. As shown in Fig. 4, a linear behaviour is obtained in the slope in agreement with Ref. [16]. The additional energy cost associated with  can be extracted from Eq. (8) by Taylor's expansion to the first order in
can be extracted from Eq. (8) by Taylor's expansion to the first order in  . Following this procedure, we get the following formula
. Following this procedure, we get the following formula
which can be simplified by means of the approximations sin (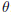 ) ≈
) ≈ 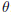 and m ≈ 4µ. In this way, provided that η= 0:30, for a slope of ±0.05 the additional energy cost assumes the numerical value ±0.244 kcal/(kg km), while for a slope ±0.025 the additional cost becomes one half of the previous value.
and m ≈ 4µ. In this way, provided that η= 0:30, for a slope of ±0.05 the additional energy cost assumes the numerical value ±0.244 kcal/(kg km), while for a slope ±0.025 the additional cost becomes one half of the previous value.
4. Conclusions
We presented a model accounting for the energy expenditure in human motion. The well known Margaria's law is recovered and the saturation behaviour observed in the experimental W vs. u curves is explained by imposing the presence of an inflection point, controlled by the parameter α, in those same curves. The supplementary cost due to a slope  is analyzed and the additional effect related to the mechanical properties of the ground is also included. Concerning the effect of the slope, the supplementary cost is roughly found to be equal to
is analyzed and the additional effect related to the mechanical properties of the ground is also included. Concerning the effect of the slope, the supplementary cost is roughly found to be equal to  x 4.88 kcal/(kg km), where the muscles efficiency is set to 0.30,
x 4.88 kcal/(kg km), where the muscles efficiency is set to 0.30,  being expressed in radians. Even though the presented model is rigorously valid only for walking and for race walking, we expect the obtained results to be valid also in the case of running. In addition, the results shown in Fig. 4 are in qualitative agreement with experimental results presented in Ref. [16]. In order to obtain also a quantitative agreement, we should be able to fit the experimental data taking into account the mass and η dependence present in Eq. (9), leaving the parameter α (characterizing the ground mechanical properties) as a free parameter to be determined by means of linear regression. Good quantitative agreement is expected only if the ground properties do not affect too much the walking mechanics. As a final point, we would like to stress that the present model can be considered also as useful pedagogical tool to illustrate the power of elementary physics in the description of every day life.
being expressed in radians. Even though the presented model is rigorously valid only for walking and for race walking, we expect the obtained results to be valid also in the case of running. In addition, the results shown in Fig. 4 are in qualitative agreement with experimental results presented in Ref. [16]. In order to obtain also a quantitative agreement, we should be able to fit the experimental data taking into account the mass and η dependence present in Eq. (9), leaving the parameter α (characterizing the ground mechanical properties) as a free parameter to be determined by means of linear regression. Good quantitative agreement is expected only if the ground properties do not affect too much the walking mechanics. As a final point, we would like to stress that the present model can be considered also as useful pedagogical tool to illustrate the power of elementary physics in the description of every day life.
Acknowledgments
The "Podistica San Giovanni a Piro - Golfo di Policastro" running team is gratefully acknowledged for having stimulated the interest in this research. Furthermore, the author would like to thank Roberto De Luca for several enlightening discussions on the topic of this work.
Recebido em 31/1/2009
Aceito em 30/6/2009
Publicado em 18/2/2010
- [1] P. Zamparo, R. Perini, C. Orizio, M. Sacher and G. Ferretti, Eur. J.Appl. Physiol. 65, 183 (1992).
- [2] T. M. Lejeune, P.A. Willems and N.C. Heglund, Journal of Experimental Biology 201, 2071 (1998).
- [3] T.J. Roberts, R.L. Marsh, P.G. Weyand and C.R. Taylor, Science 275, 1113 (1997).
- [4] B.M. Nigg and M.R. Yeadon, J. Sports Sci. 5, 117 (1987).
- [5] J.P. He, R. Kram and T.A. McMahon, J. Appl. Physiol. 71, 863 (1991).
- [6] G.A. Cavagna, N.C. Heglund and C.R. Taylor, Am. J. Physiol. 233, R243 (1977).
- [7] T. McGeer, Int. J. Robotics Res. 9, 62 (1990).
- [8] M.H. Raibert, Legged Robots that Balance (MIT Press, Cambridge, 1986).
- [9] R. Blickhan, J. Biomech. 22, 1217 (1989).
- [10] P.R. Cavanagh and M.A. Lafortune, J. Biomech. 13, 397 (1980).
- [11] R.M. Alexander, Am. Zool. 24, 85 (1984).
- [12] R.M. Alexander and M.B. Bennett, New Scient. 123, 45 (1989).
- [13] G.A. Cavagna, F.P. Saibene and R. Margaria, J. Appl. Physiol. 18, 1 (1963).
- [14] G.A. Cavagna, F.P. Saibene and R. Margaria, J. Appl. Physiol. 19, 249 (1964).
- [15] J.E.A. Bertram and A. Ruina, J. Theor. Biol. 209, 445 (2001).
- [16] A. Leonardi, F. Schena and A.E. Minetti, in Abstract Book of Young Researcher Seminar, (Innsbruck, 2004).
Publication Dates
-
Publication in this collection
19 Apr 2010 -
Date of issue
Dec 2009
History
-
Reviewed
30 June 2009 -
Received
31 Jan 2009 -
Accepted
18 Feb 2010
















