Abstracts
In this paper we give a rigorous proof of the equivalence of some different forms of Faraday's law of induction clarifying some misconceptions on the subject and emphasizing that many derivations of this law appearing in textbooks and papers are only valid under very special circunstances, thus are not satisfactory under a mathematical point of view. We show also that Faraday's law of induction is a relativistic invariant law in a very precise mathematical sense.
Faraday's law; principle of equivalence; relativistic invariance
Neste trabalho e dada uma prova de equivalência entre diferentes formas de se escrever a lei de induzo de Faraday, elucidando alguns equívocos sobre o tópico e enfatizando que muitas derivações desta lei apresentadas na maioria dos livros e artigos são validas somente sob circunstâncias muito particulares e, portanto, não satisfatórias sob o ponto de vista matemático. Tambem mostramos que a lei de indução de Faraday e relativisticamente invariante em um sentido matematicamente bem preciso.
lei de Faraday; princípio de equivalência; invariancia relativistica
ARTIGOS GERAIS
On equivalent expressions for the Faraday's law of induction
Formulações equivalentes da lei de Faraday
Fabio G. Rodrigues1 1 E-mail: fabior@mpcnet.com.br or ra008618@ime.unicamp.br.
Instituto de Matemática, Estatística e Ciência da Computaçao, Universidade Estadual de Campinas, Campinas, SP, Brasil
ABSTRACT
In this paper we give a rigorous proof of the equivalence of some different forms of Faraday's law of induction clarifying some misconceptions on the subject and emphasizing that many derivations of this law appearing in textbooks and papers are only valid under very special circunstances, thus are not satisfactory under a mathematical point of view. We show also that Faraday's law of induction is a relativistic invariant law in a very precise mathematical sense.
Keywords: Faraday's law, principle of equivalence, relativistic invariance.
RESUMO
Neste trabalho e dada uma prova de equivalência entre diferentes formas de se escrever a lei de induzo de Faraday, elucidando alguns equívocos sobre o tópico e enfatizando que muitas derivações desta lei apresentadas na maioria dos livros e artigos são validas somente sob circunstâncias muito particulares e, portanto, não satisfatórias sob o ponto de vista matemático. Tambem mostramos que a lei de indução de Faraday e relativisticamente invariante em um sentido matematicamente bem preciso.
Palavras-chave: lei de Faraday, princípio de equivalência, invariancia relativistica.
1. Introduction
Let  a smooth closed curve in
a smooth closed curve in  with parametrization x(t,l) which is here supposed to represent a filamentary closed circuit which is moving in an a convex and simply-connected (open) region
with parametrization x(t,l) which is here supposed to represent a filamentary closed circuit which is moving in an a convex and simply-connected (open) region  where at time t as measured in an inertial frame,2
2
For a mathematical defintion of an inertial reference frame in Minkowski spacetime see, e.g., Refs. [1,2].
there are an electric and a magnetic fields
where at time t as measured in an inertial frame,2
2
For a mathematical defintion of an inertial reference frame in Minkowski spacetime see, e.g., Refs. [1,2].
there are an electric and a magnetic fields  , (t, x)
, (t, x) E(t, x) є
E(t, x) є  and
and  , (t, x)
, (t, x)  B(t, x) є
B(t, x) є  . We suppose that when in motion the closed circuit may be eventually deforming. Let
. We suppose that when in motion the closed circuit may be eventually deforming. Let  be a smooth closed curve in
be a smooth closed curve in  with parametrization x(l) representing the filamentary circuit at t = 0. Then, the smooth curve
with parametrization x(l) representing the filamentary circuit at t = 0. Then, the smooth curve  is given by
is given by  where σt (see details below) is the flow of a velocity vector field
where σt (see details below) is the flow of a velocity vector field  , which describes the motion (and deformation) of the closed circuit. It is an empirical fact known as Faraday's law of induction that on the closed loop
, which describes the motion (and deformation) of the closed circuit. It is an empirical fact known as Faraday's law of induction that on the closed loop  acts an induced electromotive force, ε, such that
acts an induced electromotive force, ε, such that
where St is a smooth surface on  such that
such that  is its boundary and n is the normal vector field on St. We write
is its boundary and n is the normal vector field on St. We write  with
with  . Now, on each element of
. Now, on each element of  the force acting on a unit charge which is moving with velocity v(t, x(t, s)) is given by the Lorentz force law. Thus3
3
In this paper we use a system of units such that the numerical value of the speed of light is c =1.
the E is by definition
the force acting on a unit charge which is moving with velocity v(t, x(t, s)) is given by the Lorentz force law. Thus3
3
In this paper we use a system of units such that the numerical value of the speed of light is c =1.
the E is by definition
where  and Faraday's law reads [3-7]
and Faraday's law reads [3-7]
Note that (E + v x B) is the Lorentz force acting on a unity charged carrier in the circuit according to the laboratory observers and it is sometimes called the effective electric field [3]. In the appendix we show how the first term of Eq. (3) is related with measurements done by observers at rest in an inertial reference frame commoving at a given instant t with velocity v relative to the laboratory frame.
We want to prove that Eq. (3) is equivalent to
from where it trivially follows the differential form of Faraday's law, i.e.,
2. Some identities involving the integration of differentiable vector fields
Let  be a convex and simply-connected (open) region,
be a convex and simply-connected (open) region,  , (t, x)
, (t, x)  X(t, x) be a generic differentiable vector field and let
X(t, x) be a generic differentiable vector field and let  be a differentiable velocity vector field of a fluid flow. An integral line4
4
Also called a stream line.
of v passing through a given x ∈ R3 is a smooth curve
be a differentiable velocity vector field of a fluid flow. An integral line4
4
Also called a stream line.
of v passing through a given x ∈ R3 is a smooth curve  which at t = 0 is at x (i.e., σx(0) = x ) and such that its tangent vector at σ(t, x) is
which at t = 0 is at x (i.e., σx(0) = x ) and such that its tangent vector at σ(t, x) is
Let moreover  . We call σt Faraday's law, i.e., at the fluid flow map. Let J = (0,1) Є
. We call σt Faraday's law, i.e., at the fluid flow map. Let J = (0,1) Є  and let
and let  be a closed loop parametrized by
be a closed loop parametrized by  and denote by
and denote by  the loop transported by the flow (see Fig. 1). Then
the loop transported by the flow (see Fig. 1). Then
is clearly a parametrization of  . We have the proposition:
. We have the proposition:
Proposition
where
is the so-called material derivative5 5 Mind that the material derivative is a derivative taken along a path σ t with tangent vector . It is frequently used in fluid mechanics, where it describes the total time rate of change of a given quantity as viewed by a fluid particle moving on σ x. In the present case it appears because in the integral we need the values of X for each t at all points of . and
is the tangent line element6
6
Take notice that dl is not an explicit function of the cartesian coordinates (x, y, z).
of  at σ(t, x(l)).
at σ(t, x(l)).
Proof. We can write
Now, taking into account that for each x(l),  we have
we have
hence, the first term in the right side of Eq. (11) can be written as
Also writing  we see that the last term in Eq. (11) can be written as
we see that the last term in Eq. (11) can be written as
We now recall that for arbitrary differentiable vector fields  it holds
it holds
Setting a = dl and b= v and noting that  it implies that
it implies that
We need also to recall the well known identity
which implies setting a= X, b = dl and c = (∇ x v), that
and also the not so well known identity7 7 See the Appendix for a proof of this identity.
to write that
Finally, using Eq. (13) and Eq. (20) completes the proof of Eq. (8a) and Eq. (8b). Also, from Eq. (8b) it follows if we recall Eq. (15) that
from where the proof of Eq. (8c) follows immediately.
a result that is known in fluid mechanics as Kelvin's circulation theorem (see, e.g., Refs. [8, 9]).
Now,
where, if S is a smooth surface such that  , then
, then  . Also n is the normal vector field to St.
. Also n is the normal vector field to St.
Then using Eq. (8c) we can write
Also, denoting Y: = ∇x X we can write
Despite Eq. (24), for a general differentiable vector field  such that
such that  we have
we have
the so-called Helmholtz identity [10]. Note that the identity is also mentioned in [11]. A proof of Helmholtz identity can be obtained using arguments similar to the ones used in the proof of Eq. (8a). Some textbooks quoting Helmholtz identity are [12-16]. However, we emphasize that the proof of Faraday's law of induction presented in all the textbooks just quoted are always for very particular situations and definitively not satisfactory from a mathematical point of view.
We now want to use the above results to prove Eq. (3) and Eq. (4).
3. Proofs of Eq. (3) and Eq. (4)
We start remembering that in Maxwell theory we have that the E and B fields are derived from potentials, i.e. ,
where  is the scalar potential and
is the scalar potential and  is the (magnetic) vector potential. If Eq. (26) is taken into account we can immediately derive Eq. (3). All we need is to use the results just derived in Section 2 taking X= A. Indeed, the first line of Eq. (23) then becomes
is the (magnetic) vector potential. If Eq. (26) is taken into account we can immediately derive Eq. (3). All we need is to use the results just derived in Section 2 taking X= A. Indeed, the first line of Eq. (23) then becomes
To obtain Eq. (4) we recall that from the second line of Eq. (23) we can write (using Stokes theorem)
Comparing the second member of Eq. (27) and Eq. (28) we get Eq. (4), i.e. ,
from where the differential form of Faraday's law follows.
Remark 2 We end this section by recalling that in the physical world the real circuits are not filamentary and worse, are not described by smooth closed curves. However, if the closed curve representing a 'filamentary circuit' is made of finite number of sections that are smooth, we can yet apply the above formulas with the integrals meaning Lebesgue integrals.
4. Conclusions
Recently a paper [17] titled 'Faraday's law via the magnetic vector potential', has been commented in Ref. [18] and replied in Ref. [19]. Thus, the author of Ref. [17], claims to have presented an "alternative" derivation for Faraday's law for a filamentary circuit which is moving with an arbitrary velocity and which is changing its shape, using directly the vector potential A instead of the magnetic field B and the electric field E (which is the one presented in almost all textbooks).
Now, Ref. [18] correctly identified that the deriva tion in Ref. [17] is wrong, and that author agreed with that in Ref. [19]. Here we want to recall that a presen tation of Faraday's law in terms of the magnetic vector potential A already appeared in Maxwell treatise [20], using big formulas involving the components of the vec tor fields involved. We recall also that a formulation of Faraday's law in terms of A using modern vector calculus has been given by Gamo more than 30 years ago [21]. In Gamo's paper (not quoted in Refs. [17-19]) Eqs. (8c) appear for the special case in which X= A (the vector potential) and B = V x A (the magnetic field), i.e.,
Thus, Eq. (30) also appears in Ref. [17] (it is there Eq. (9)). However, in footnote 3 of [17] it is said that Eq. (30) is equivalent to  where the term
where the term  is missing. This is the error that has been observed by authors [18], which also presented a proof of Eq. (8b), which however is not very satisfactory from a mathematical point of view, that being one of the reasons why we decided to write this note presenting a correct derivation of Faraday's law in terms of A and its relation with Helmholtz formula. Another reason is that there are still people (e.g., Ref. [22]) that do not understand that Eq. (3) and Eq. (4) are equiva lent and think that Eq. (3) implies the form of Maxwell equations as given by Hertz, something that we know since a long time that is wrong [23].
is missing. This is the error that has been observed by authors [18], which also presented a proof of Eq. (8b), which however is not very satisfactory from a mathematical point of view, that being one of the reasons why we decided to write this note presenting a correct derivation of Faraday's law in terms of A and its relation with Helmholtz formula. Another reason is that there are still people (e.g., Ref. [22]) that do not understand that Eq. (3) and Eq. (4) are equiva lent and think that Eq. (3) implies the form of Maxwell equations as given by Hertz, something that we know since a long time that is wrong [23].
We also want to observe that Jackson's proof of Faraday's law using 'Galilean invariance' is valid only for a filamentary circuit moving without deformation with a constant velocity. The proof we presented is general and valid in Special Relativity, since it is based on trustful mathematical identities and in the Lorentz force law applied in the laboratory frame with the motion and deformation of the filamentary circuit mathematically well described.
A Proof of the identity in Eq. (19)
We know from Eq. (16) that
Let {e1, e2, e3} be an orthonormal base of  . We can write, using Einstein convention,
. We can write, using Einstein convention,
where  with
with  are Cartesian coordinates. It follows then
are Cartesian coordinates. It follows then
Using the known identity a x b x c= (a c)b- (a b)c in Eq. (33), we obtain
On the other hand, considering dl = (dl1,dl2,dl3) = dliei, we have
Hence, substituting Eq. (34) and Eq. (35) in Eq. (31), we can rewrite it as
From this last result, it is easy to see that
where
B Phenomenological interpretation of the first member of Eq. (3)
Let S be the inertial laboratory frame and S' the inertial frame that at time t has velocity u= v (t, σ(t, x(l))) (which is the velocity of an element of the circuit  ) .
) .
The electric and magnetic fields observed in S' are [3, 4]
where  is the Lorentz factor and the symbols || and
is the Lorentz factor and the symbols || and  denotes the components parallel and orthogonal to u. Then, taking into account that
denotes the components parallel and orthogonal to u. Then, taking into account that  and
and  and by letting
and by letting  it follows that
it follows that
where  is the flux of B.
is the flux of B.
Using the right-side identity in Eq. (38), we can write
since  is the element of proper time for an observer at rest in the commoving frame S' (with standard coordinates (x'º= t',x'i). The integral
is the element of proper time for an observer at rest in the commoving frame S' (with standard coordinates (x'º= t',x'i). The integral  is interpreted as the difference of potential measured by a voltmeter carried by an observer in S' (this is obviously clear when the field v is constant and the loop Tt is not deforming). So, we see that
is interpreted as the difference of potential measured by a voltmeter carried by an observer in S' (this is obviously clear when the field v is constant and the loop Tt is not deforming). So, we see that  differs by terms of second order in v2 from the differential potential measured by an observer in S'.
differs by terms of second order in v2 from the differential potential measured by an observer in S'.
Finally, we show an important result.8
8
Which may be intelligible for readers with working knowledge of the mathematical methods of modern field theory [1, 2, 24].
Let  a 2-form field, be the so called electromagnetic field [1,24,25], where (xº = t,xi) are standard coordinates in a inertial reference frame in a Minkowski coordinates in a inertial reference frame in a Minkowski spacetime.9
9
Minkowski spacetime [2,24] is a manifold diffeomorphic to
equipped with a metric field η and its Levi-Civita connection. In a standard coordinates of an inertial reference frame
where the matrix with entries η
µv is diag(1,-1,-1,-1).
Then the antisymmetric matrix with entries Fµv is
a 2-form field, be the so called electromagnetic field [1,24,25], where (xº = t,xi) are standard coordinates in a inertial reference frame in a Minkowski coordinates in a inertial reference frame in a Minkowski spacetime.9
9
Minkowski spacetime [2,24] is a manifold diffeomorphic to
equipped with a metric field η and its Levi-Civita connection. In a standard coordinates of an inertial reference frame
where the matrix with entries η
µv is diag(1,-1,-1,-1).
Then the antisymmetric matrix with entries Fµv is
We now show that Φ is an invariant relativistic quantity.
Indeed, it can be written as
To show that, recall that if  is the electromagnetic potential (
is the electromagnetic potential ( being the the scalar potential and A = (A1;A2,A2) the vector potential), then F = dA. Then by Stokes theorem we can write (taking into account that St is, for any t, a 2-dimensional open spacelike surface in Minkowski spacetime and that
being the the scalar potential and A = (A1;A2,A2) the vector potential), then F = dA. Then by Stokes theorem we can write (taking into account that St is, for any t, a 2-dimensional open spacelike surface in Minkowski spacetime and that  is the boundary of St)
is the boundary of St)
This shows that Eq. (3) (and its equivalent Eq. (34)) is a relativistic invariant law.
Recebido em 17/1/2011; Aceito em 20/11/2011; Publicado em 27/2/2012
- [1] W.A. Rodrigues Jr. and E. Capelas de Oliveira, in: Lecture Notes in Physics 722 (Springer, Heidelberg, 2007).
- [2] R.K. Sachs and H. Wu, General Relativity for Mathematicians (Springer-Verlag, New York, 1977).
- [3] N. Rosen and D. Schieber, Am. J. Phys. 50, 974 (1982).
- [4] L.D. Landau and E.M. Lifshitz, Electrodynamics of Continuous Media (Pergamon, New York, 1960), p. 206.
- [5] D.T. Paris and F.K. Hurd, Basic Electromagnetic Theory (McGraw-Hill, New York, 1969), p. 544.
- [6] M. Schwartz, Principles of Electrodynamics (McGraw-Hill, New York, 1972), p. 187.
- [7] A. Shadowitz, The Electromagnetic Field (Dover Publications, Inc., New York, 1988).
- [8] A.J. Chorin and J.E. Mardsen, A Mathematical Introduction to Fluid Mechanics (Springer-Verlag, New York, 1993).
- [9] P.G. Saffman, Vortex Dynamics - Cambridge Monographs on Mechanics and Applied Mathematics (Cambridge Univ. Press, Cambridge, 1992).
- [10] H. Helmholtz, Gesammelt Scriften (Olms-Weidmann, Hildeshein, 2003), v. I (3), p. 597-603 (a reprint of Wissenschaftliche Abhandlungen v. 3 (Johann Ambrosius Barth, Leipzig, 1895).
- [11] H.R. Hertz, Electric Waves (MacMillan, London, 1893), p. 243-247 (also, Dover, New York, 1962).
- [12] M. Abraham and R. Becker, The Classical Theory of Electricity and Magnetism (Blackie, London, 1932).
- [13] J.D. Jackson, Classical Electrodynamics (J. Wiley & Sons, Inc., New York, 1999).
- [14] W.K.H. Panofski and M. Phillips, Classical Electricity and Magnetism (Addison-Wesley Publ. Co., Reading, 1962), p. 160-162.
- [15] A. Sommerfeld, Electrodynamics (Academic Press, New York, 1952), p. 285-287.
- [16] C.R. Paul, K.W. Whites and A.A. Nasar, Introduction to Electromagnetic Fields (McGraw-Hill, Boston, 1998), p. 653-658.
- [17] D.V. Redzic, Eur. J. Phys. 28, N7 (2007).
- [18] A.K. Kholmetskii, O. Missevitch and T. Yarman, Eur. J. Phys. 29, L1 (2008).
- [19] D.V. Redzic, Eur. J. Phys. 29, L5 (2008)
- [20] J.C. Maxwell, A Treatise of Electricity and Magnetism (Dover, New York, 1954), p. 238-243.
- [21] S.A. Gamo, Proc. IEEE 67, 676 (1979).
- [22] T.E. Phipps Jr., Old Physics for New - A Worldview Alternative to Einstein s Relativity Theory (Apeiron, Montreal, 2006).
- [23] A.I. Miller, Albert Einstein's Special Theory of Relativity (Addison-Wesley Publ. Co., Inc., Reading, Ma., 1981), p. 16.
- [24] Y. Choquet-Bruhat, C. DeWitt-Morette and M. Dillard-Bleick, Analysis, Manifolds and Physics (revised edition), (North-Holland Publ. Co., Amsterdam, 1982).
- [25] B. Felsager, Geometry, Particles and Fields (SpringerVerlag, New York, 1998).
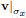 . It is frequently used in fluid mechanics, where it describes the total time rate of change of a given quantity as viewed by a fluid particle moving on σ
. It is frequently used in fluid mechanics, where it describes the total time rate of change of a given quantity as viewed by a fluid particle moving on σ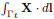 we need the values of
we need the values of 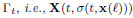 .
.  equipped with a metric field η and its Levi-Civita connection. In a standard coordinates of an inertial reference frame
equipped with a metric field η and its Levi-Civita connection. In a standard coordinates of an inertial reference frame 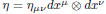 where the matrix with entries η
where the matrix with entries ηPublication Dates
-
Publication in this collection
16 May 2012 -
Date of issue
Mar 2012
History
-
Received
17 Jan 2011 -
Accepted
20 Nov 2011















































