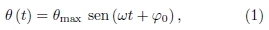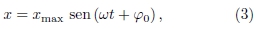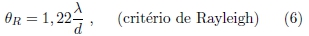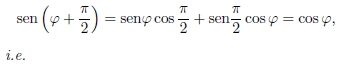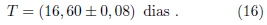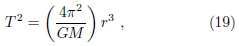As observações galileanas dos planetas mediceanos de Júpiter e a equivalência do MHS e do MCU

The Galilean observations of Jupiter and its medicean stars and the equivalence between SHM and UCM

ARTIGOS GERAIS

As observações galileanas dos planetas mediceanos de Júpiter e a equivalência do MHS e do MCU

The Galilean observations of Jupiter and its medicean stars and the equivalence between SHM and UCM

R.R. Cuzinatto¹; E.M. de Morais; C. Naldoni de Souza

Instituto de Ciência e Tecnologia, Universidade Federal de Alfenas, Cidade Universitária, Pocos de Caldas, MG, Brasil

RESUMO

Este trabalho tem como objetivo usar as características orbitais das quatro Luas Galileanas de Júpiter para mostrar a equivalencia do movimento harmônico simples (MHS) com o movimento circular uniforme (MCU). Em nossos cálculos, empregamos os dados obtidos por Galileu Galilei em suas observações pioneiras com o primeiro telescópio da história, realizadas no começo de 1610, e reportadas na obra fundamental Sidereus Nuncius. Comparamos os desenhos de Galileu do Sidereus Nuncius com as imagens da posição de Jupiter e suas luas segundo o Cartes du Ciel, um programa open-source que funciona como efemérides interativa. Com os dados orbitais extraídos dos gráficos de separação angular dos Planetas Mediceanos até Jupiter, obtemos os raios das órbitas assumindo a terceira lei de Kepler.

Palavras-chave: Luas Galileanas; movimento harmônico simples; movimento circular uniforme.

ABSTRACT

The present work shows the equivalence between the simple harmonic motion and the uniform circular motion using the orbital parameters of the Galilean Moons of Jupiter. We use the data obtained by Galileo Galilei in 1610 with the very first telescope in history, which were published in the monumental book Sidereus Nuncius. We compare the Galilean diagrams featuring in Sidereus Nuncius with the images of Io, Europa, Ganymede and Callisto, obtained with the Cartes du Ciel, an open-source computer program that works as an interactive ephemerides. We obtain the Medicean Planets orbital radii by assuming Kepler's third law and using the orbital data calculated from the plots of the angular separation of the four moons from Jupiter as a function of time.

Keywords: Galilean moons; simple harmonic motion; uniform circular motion.

1. Introdução

Ao sereníssimo Cosme II de Medicis, IV Grão-Duque da Toscana (Galileu Galilei, na dedicatória de sua obra Sidereus Nuncius)

Em 1609, Galilei apontava sua luneta recém-construída para a Lua e Júpiter; e há 404 anos atrás, os resultados das observações do primeiro astrônomo na história da humanidade a usar um telescópio foram publicados no seu Sidereus Nuncius ou (numa tradução livre) O Mensageiro das Estrelas; e a mensagem de Galileu abalou o mundo!

O esquema aristotélico de descrição da natureza baseia-se na associação a formas geométricas harmoniosas. Assim, a Lua era tida como uma esfera perfeita desde a época dos gregos. Galileu observou, com ajuda de seu telescópio, as irregularidades da superfície lunar, suas depressões e elevações. Ele conseguiu até mesmo medir a altura de algumas das montanhas da Lua e verificar que elas possuíam dimensões comparáveis as que conhecemos na Terra. Com isso, Galilei derrubava as consagradas ideias de Aristóteles.

Não bastassem essas críticas (suficientemente desagradáveis até para algumas das pessoas mais esclarecidas da época), outras mais contundentes vieram: as informações das observações de Júpiter fizeram ruir o castelo das idéias geocentristas defendidas pela Igreja.

Com seu "óculo astronômico", Galileu verificou que Júpiter possuía quatro "estrelas companheiras", objetos celestes luminosos móveis, em contraponto com as "estrelas fixas" da abóboda celeste. As "estrelas móveis" identificadas por Galilei são as quatro luas maiores de Júpiter: Io, Europa, Ganimedes e Calisto. Hoje sabemos que elas são do tamanho da Lua ou mesmo de Mercúrio.

Galileu representou as suas descobertas na forma de figuras detalhadas do posicionamento das estrelas errantes - ou "Planetas Mediceanos", como as cunhou - com respeito a Júpiter em dias consecutivos de observações, como exemplificado na Fig. 1.

A posição de Calisto em relação a Júpiter foi medida meticulosamente por Galileu ao longo de muitas noites. Como mostraremos em detalhe na Seção 5, os dados colhidos podem ser colecionados como pontos em um gráfico de distância angular até Júpiter como função do tempo de observação (Fig. 2).

O ajuste de uma função nos pontos do gráfico da Fig. 2 sugere que o ângulo θ (t) de separação entre Calisto e Júpiter é uma função periódica do tipo seno ou cosseno

em que é a amplitude, ou seja, o afastamento máximo de Calisto em relação à Júpiter. é o valor no eixo y correspondente aos picos (ou vales) da função ajustada. A Eq. (1) é uma função típica do movimento harmônico simples, um exemplo de movimento encontrado em sistemas físicos como o conjunto massa-mola em oscilação sobre um plano sem atrito.

Ao ajustar a função seno aos pontos do gráfico, obtém-se a frequência angular e, consequentemente o período de "oscilação" de Calisto em torno de Júpiter,

Veremos que seguindo esse procedimento pode-se calcular: Τ =16, 6 dias.

Mas a grande pergunta é: as Eqs. (1) e (2) implicam, então, que Calisto e Júpiter formam um sistema massa-mola? A resposta é um sonoro NÃO! Seria irracional pensar que uma mola invisível gigante de massa nula estivesse a puxar Calisto de um lado a outro de Júpiter! Como explicar as ob-servações, então?

2. MHS e MCU: vade mecum

Para descartar com propriedade a ideia absurda de que Júpiter e suas Luas Galileanas formam um sistema massa-mola, vamos lembrar rapidamente algumas características do movimento harmônico simples (MHS) e do movimento circular uniforme (MCU).²

O MHS é usualmente estudado em conexão com o sistema massa-mola. A força aplicada pela mola ao bloco de massa m tem a magnitude dada pela lei de Hooke, F = -kx, sendo k a constante elástica da mola e x a deformação por ela sofrida, a qual varia com o tempo t; i.e., x = x (t). Usando a lei de Hooke em conjunto com a segunda lei de Newton, , obtemos uma equação diferencial para a função horária das posições do sistema massa-mola, cuja solução é

onde são constantes e . A Eq. (3) é a equação fundamental do MHS. Observamos desde já que esta é a mesma função que ajusta o conjunto de pontos no gráfico da Fig. 2, o qual representa os tipos de dados obtidos por Galileu em suas observações das quatro maiores luas de Júpiter. De fato, se escrevermos "?" no lugar de "x" na Eq. (3), obtemos exatamente a Eq. (1) da Seção 1. Na Seção 5 entenderemos a razão dessa aparente coincidência estudando o movimento das Luas Galileanas.

O movimento circular uniforme (MCU) é aquele em que uma partícula de massa m move-se em uma trajetória em forma de circunferência com uma velocidade v cuja magnitude é constante no tempo (v = constante). A trajetória tem um centro C e um raio r também constante; por isso, a velocidade angular ω = dφ/dt (φ é o ângulo descrito pela partícula), é uma constante. Integrando essa última equação,

Esta equacão será útil mais tarde, na Seção 4, ao estabelecermos a equivalência entre o MCU e o MHS empregando os dados de Galilei. Definimos o período τ como o tempo de uma volta completa (2π radianos) da massa na trajetória circular. Substituindo , encontramos

Esta é a Eq. (2) que aparece na Introdução.

3. As observações de Galilei de 1610

Como descreve Galileu na quarta parte de seu Si-dereus Nuncius^3, no dia 7 de janeiro de 1610 ele decide observar Júpiter com seu excelente óculo-astronômico e percebe três estrelas pequenas, mas brilhantes, que chamam sua atenção por estarem alinhadas com o planeta. Ele apresenta a ilustração da Fig.3

Com o software Cartes du Ciel ou Skychart⁴ podemos inspecionar o mesmo céu visto por Galileu no começo de 1610. Este programa permite que selecionemos o objeto celeste de interesse, a data e hora na qual queremos observá-lo. É necessário fixar também o local do observatório e, como Galileu era professor da Universidade de Pádua, e publicou seu livro em Veneza, escolhemos o norte da Itália como local de observação, mais especificamente, Pádua. O que se obtém ao buscarmos Júpiter no Skychart na data da primeira observação Galileana e o que consta da Fig. 4.

Galileu afirma que sua observação de 7 de janeiro de 1610 foi feita na primeira hora da noite. Decidimos qual era a hora local lembrando que em janeiro, ápice do inverno no hemisfério norte, a noite cai muito cedo. Usando o software Stellarium⁵ verificamos que às 16h 40min GMT⁶ do referido dia já estava suficientemente escuro em Pádua. Nesse dia, vemos que Galileu representou apenas três das quatro maiores luas de Júpiter; comparando a Fig. 3 com a Fig. 4 percebemos o que provavelmente ocorreu: notamos sem dificuldades que Calisto é a estrela errante mais afastada de Júpiter ao leste, e que Ganimedes é aquela posicionada a oeste dele; porém, Io e Europa estavam tão próximas no momento da observação de Galilei que ele interpretou ambas como um único Planeta Mediceano (aquele mais próximo a leste de Júpiter na Fig. 3).⁷ Em verdade, o telescópio de Galileu possuia características que justificam essa afirmação.

Na p. 4 da Ref. [6], aprendemos que a luneta de Galileu era equipada de uma lente objetiva com uma abertura entre 0, 5 e 1,0 polegada, o que equivale a um diametro d na faixa de 1, 3 a 2, 5 cm. Com essa informação podemos calcular o seu poder de resolução angular , o qual é limitado pelo fenômeno de difração que ocorre em orifícios ou lentes circulares (Ref. [7], capítulo 36). O critério de Rayleigh para resolução angular estabelece que a separação angular entre duas fontes de luz pontuais (duas luas Galileanas, por exemplo) é tal que o máximo central do padrão de difração⁸ de uma das fontes localiza-se sobre o primeiro mínimo do padrão de difração da outra. Com isso é possível empregar a fórmula para a posição angular do primeiro mínimo do padrão de difração de uma abertura circular para calcular como

onde λ e o comprimento de onda da radiação que atravessa a lente (luz refletida pelas luas Galileanas) e é captada pelo detector (olho de Galileu). O pico de sensibilidade do olho humano a luz visível ocorre em torno de λ = 555 nm, que corresponde a sensação que chamamos de amarelo-esverdeado.⁹ Assumindo esse comprimento de onda como aquele percebido por Galilei, podemos estimar a resolução angular de sua luneta como = 7" ao adotarmos o valor intermediário d = 2 cm para o diâmetro da objetiva. Porém, uma resolução dessa ordem só é atingida se não há perturbações ópticas no caminho do raio de luz (como aquelas que ocorrem por influência da atmosfera terrestre), e se as condições de polimento das lentes do telescópio são ideais. Essas condições seguramente não eram satisfeitas nas observações Galileanas. A separação angular entre Io e Europa na observação das 16h 40min do dia 7 de janeiro de 1610 era de 16" de acordo com o Skychart. Considerando a precariedade do intrumento de Galileu, especialmente de suas lentes, torna-se bastante provável que , uma resolução baixa o suficiente para impedir a identificação de Io e Europa como dois objetos distintos.

É apropriado tecermos um comentário um pouco mais detalhado com respeito a determinação da hora das observação Galileanas. Essa não é uma tarefa trivial. Em sua publicação [1], Galileu relata o momento de suas observações em horas, as vezes minutos, depois do pôr-do-sol. Por isso, para sermos absolutamente acurados do ponto de vista histórico, deveríamos calcular o instante do pôr-do-sol em Pádua a cada dia de observação. Esse cálculo pode ser executado de acordo com as instruções de Paul Schlyter constantes na Ref. [8]. Isso foi feito meticulosamente por Ernie Wright na Ref. [9]. Neste trabalho, aproveitamos os resultados de Wright para as horas das observações Galileanas reportadas no Sidereus Nuncius. Insistimos, porém, que o método menos preciso de verificar o momento do pôr-do-Sol em Pádua através do software Stellarium é suficiente para estabelecer gráficos como os da Fig. 2, como ficará evidente mais adiante.

Nos dias 8 e 10 de janeiro de 1610, Galileu confirma que as estrelas alinhadas com Júpiter movem-se ao seu redor - descartando a possibilidade de um movimento de Júpiter com respeito às pequenas estrelas - e decide acompanhá-las cuidadosamente, anotando a distâncias relativas entre elas e Júpiter. No dia 11 do mesmo mês, ele apresenta a primeira das medidas de distância de duas das luas com respeito ao planeta, mas o faz em unidades arbitrárias.

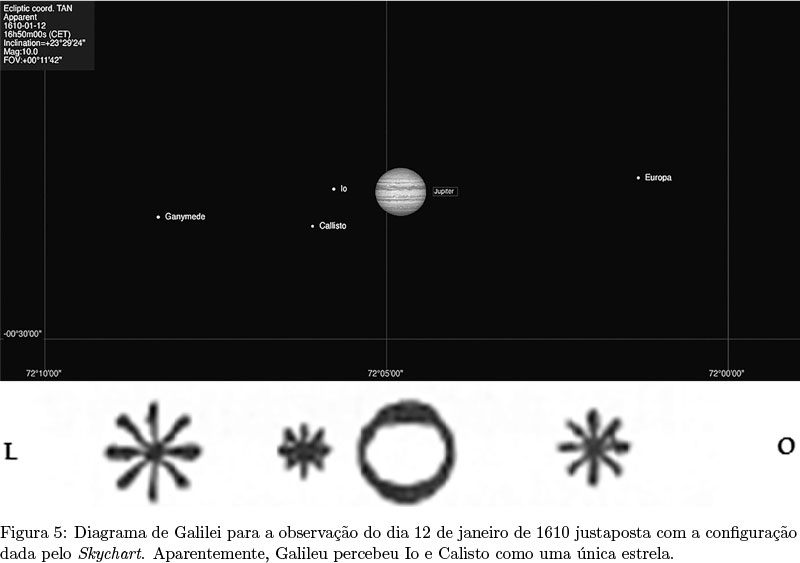
É no dia 12 que Galileu dá os primeiros dados de separação angular em segundos de arco; e, neste mesmo dia, ele vê uma das estrelas móveis aparecer ao lado de Júpiter após duas horas de observação. A Fig. 5 mostra uma composição do diagrama apresentado por Galileu (em branco) com a imagem fornecida pelo Cartes du Ciel. Galileu anota que a separação entre a estrela mais ao leste e Júpiter é de 2', mesma distancia da estrela mais ao oeste ate o planeta. Com o Cartes du Ciel é simples obter os dados de separação angular das luas.¹⁰ No horário das 16h 50min de 12 de janeiro de 1610, obtivemos a separação de 3^'34, 0^'' entre Júpiter e Ganimedes (a lua mais ao leste); a separação entre Júpiter e Europa foi dada como 3^'29, 0^'', que difere do que foi dado por Galilei. Essa diferença (relativamente pequena) pode ser atribuída novamente às limitações do telescópio Galileano, muito mais rudimentar que os recursos contemporâneos. Io, a 58, 9^'' de Júpiter, é a estrela errante que Galileu viu surgir ao lado do planeta. A Fig. 5 também sugere que Galileu tenha visto Io e Calisto (a 1^'23, 1^'' de Júpiter) como uma única lua, já que a separação angular entre ambas é de 24^'', comparável ao poder de resolução de sua luneta.

No dia 13 de janeiro Galilei observa os quatro Planetas Mediceanos pela primeira vez, Fig 6. Ele registra que os três Planetas Mediceanos vistos à direita de Júpiter estão separados entre si e de Júpiter por 1 ^', enquanto que a lua à esquerda de Júpiter estava 2' distante deste. Pelo Skychart percebemos que essa estrela errante à esquerda é Europa, e que sua distância até Júpiter é -1'29, 2'' (onde o sinal negativo é nossa convenção para indicar que a lua está ao lado esquerdo de Júpiter). O mesmo software indica que as distância de Ganimedes, Io e Ca-listo ate Júpiter são +1' 10, 4'', +1'42, 4'' e +2'26, 6'', respectivamente (com o sinal positivo para indicar que essas três luas estão a direita de Júpiter).

No dia 14 de janeiro de 1610 o céu estava enevoado, mas, a partir do dia 15 de janeiro, Galileu passa a tomar os dados de separação das quatro luas até Júpiter em dois horários a cada dia (às vezes três), praticamente todos os dias até 2 de março de 1610. Fizemos o trabalho metódico, extenso e de interesse histórico, de registrar todos os dados de Galileu reportados no Sidereus Nuncius. Esses dados aparecem na Tabela 1 para que fique claro para o leitor quais foram os dados usados para construirmos os gráficos de separação angular θ(') em função do tempo t(dias) que aparecem na Introdução e na Seção 5.

Durante esses dias de observação de Júpiter, de 7 de janeiro a 2 de março de 1610, Galileu faz 64 diagramas¹¹ de Júpiter e suas quatro maiores luas, fornece dados acurados para a posição desses objetos celestes e, apenas uma única vez, em 12 de fevereiro, esboça uma lua que não estava lá. A natureza colossal desse trabalho fica evidente quando lembramos as condições e a época em que foi feito. Aparte a questão técnica, há também as conclusões bombásticas para a astronomia e física: golpe ao ge-ocentrismo e caracterização do movimento circular uniforme, que veremos nas próximas seções.

4. Interpretação dos dados de Galilei: equivalência entre MHS e MCU

Voltemos à pergunta que encerrou a seção intro-dutória: Como explicar as observações que descrevemos na seção anterior? Galilei apontou a resposta: Calisto tinha de orbitar Júpiter em uma trajetória circular a uma distância fixa igual a θ_ΠΆΧ e velocidade angular constante ω = 2π/Τ. Nas palavras de Galilei (Ref. [1], p. 84):

Acima de tudo, uma vez que eles [os Planetas Mediceanos] algumas vezes seguem e outras vezes precedem Júpiter pelos mesmos intervalos, e que eles permanecem dentro de distâncias bastante limitadas seja a leste ou a oeste de Júpiter, acompanhando esse planeta em ambos os seus movimentos direto e retrogrado de forma constante, ninguém pode duvidar que eles completam suas revoluções ao redor de Júpiter e, ao mesmo tempo, efetuam todos juntos um período de doze anos ao redor do centro do uni-verso.¹² Que eles também se movem em círculos desiguais, e deduzido manifestamente do fato que nunca é possível ver dois desses planetas em conjunção à maior elongação de Júpiter, enquanto que, na vizinhança de Júpiter, são encontrados reunidos dois, três e as vezes os quatro deles.

Mas essa é uma declaração muito forte porque estabelece o movimento dos Planetas Mediceanos como o movimento circular uniforme. Daí, segue que o MCU e o MHS são equivalentes, conforme argumentamos abaixo.

De fato, seja φ o ângulo descrito por Calisto (ponto C da Fig. 7) com respeito ao plano de ob-servação (que contém o eixo x e o eixo z saindo perpendicularmente do papel). Como C, de acordo com a hipótese de Galileu, realiza um movimento circular uniforme, então vale a Eq. (4)

(Esta equação é recorrente no estudo de movimentos de rotação.)

A projeção de 0_max no eixo x (ou seja, no plano celeste) é, conforme a Fig. 4

A função cosseno equivale à função seno a menos de uma fase constante φ₀ = π/2. De fato, usando a regra do seno da soma,

Substituindo as Eqs. (7) e (9) na Eq. (8),

que é a equação do movimento harmônico simples, Eq. (1) ou Eq. (3), com a renomeação de x para θ.

Ou seja, partindo da hipótese de movimento circular à velocidade angular constante, chegamos ao movimento harmônico simples por uma projeção ao longo do círculo. A conclusão última é:

O movimento harmônico da lua de Júpiter é sua órbita circular vista de perfil.

Vemos agora porque a descoberta de Galileu é tão revolucionária. Se existem corpos celestes (como Calisto, Ganimedes, Europa e Io) que orbitam outros planetas (como Júpiter), então, talvez a própria Terra orbite outro corpo celeste (o Sol). Isso retira a Terra da posição de centro do universo.

Essa idéia era rejeitada pela Igreja e sua reação foi trancar Galilei em prisão domiciliar perpétua.

5. Os Planetas Mediceanos e seus períodos

O parágrafo de Sidereus Nuncius em que Galileu afirma que o movimento das estrelas errantes tem a forma de circunferências começa assim:¹³

Eis as observações acerca dos quatro planetas Mediceanos recentemente descobertos primeiramente por mim, e, embora os seus períodos ainda não tenham sido reconstruídos de forma numérica por esses dados, é legítimo evidenciar alguns comentários dignos de nota.

Nesta seção, queremos justamente complementar o quadro composto por Galileu e determinar os períodos das Luas Galileanas. Usaremos os dados que ele mesmo coletou com seu óculo-astronômico.

Começaremos arbitrariamente pelo Planeta Me-diceano mais externo, Calisto; estudando, na seqüência, as Luas Galileanas de órbitas com raios progressivamente menores que o da de Calisto: Ga-nimedes, Europa e Io.¹⁴

A Fig. 8 mostra a distribuição dos dados Galile-anos de separação angular θ em função do tempo t para a estrela errante que era vista com maior elongação com respeito a Júpiter: Calisto. O conjunto completo desses dados está disposto na Tabela 1 da Seção 3..

Conforme discutimos na Seção 1, a distribuição tem cristas e vales como uma função seno, que aparece na Eq. (10),

É possível usar um software adequado para a cons-trucão de gráficos de funções, como o Origin, para ajustar uma curva senoidal ao conjunto de pontos. Esses softwares de ajuste funcionam usando valores iniciais dos parâmetros da função a ser ajustada para realizar iterações sucessivas em que novos valores ótimos dos parâmetros são dados. Estes valores ótimos dos parâmetros maximizam a coincidência da função ajustada aos pontos do gráfico, pois minimizam o χ² do ajuste.¹⁵ Os parâmetros da função (10) são a terna

A amplitude é facilmente visualizada do gráfico da Fig. 8 como a distância vertical desde o zero do eixo das ordenadas até o pico superior à esquerda do gráfico, por exemplo. Podemos usar:

De acordo com a Eq. (5),

Logo, encontraremos a estimativa inicial da frequência angular ω da oúrbita de Calisto, se tivermos um "chute instruído" para o valor do período Τ da órbita. Mas isso é obtido diretamente da Fig. 8 como a distância no eixo horizontal entre dois vales consecutivos; essa é a definição de período em uma curva senóide: o intervalo temporal correspondente a separação entre dois picos ou, equivalentemente, entre dois vales. Portanto, o gráfico de Calisto dá: Τ = (35 - 18) dias = 17 dias; o que resulta em ω = 0, 37 (dias)^-1.

O valor estimado para o parâmetro φ_ο deve ser calculado a partir da Eq. (10) e dos valores adotados anteriormente para e . De fato, vamos tomar um valor qualquer de tempo t = t₀ correspondente ao ponto no conjunto de dados de Calisto, e.g. t₀ = 9, 7 dias (primeira hora de ob-servação do dia 16 de Janeiro de 1610) e . Começamos substituindo na Eq. (10)

Agora, invertemos essa equação para isolar o parâmetro φο em termos das outras quantidades

Dessa forma, para um certo ponto da tabela de dados de separação angular de Calisto com o tempo, calculamos φο a partir das estimativas anteriores para e =0,37 (dias)^-1 encontramos: =-2,7 rad.

Alimentando o software de análise gráfica com a terna = obtemos a curva se-noidal ajustada sobreposta aos pontos galileanos da Fig. 8.

Em nosso trabalho, as estimativas preliminares de foram inseridas na opção "Non-Linear Curve Fitting: Fitting Section" do programa Origin. O Origin dá, então, os valores ajustados

que minimizam o χ².

A Tabela 2 exibe os valores dos parâmetros e também as incertezas nesses parâmetros ajustados de acordo com a teoria de erros. Essas incertezas são fornecidas pelo próprio software de ajuste (e estõao de acordo com a te oria da Ref. [4]). Em particular, vemos a incerteza σ_ω = 0,002 (dias)^-1 da frequência angular ω = 0, 379 (dias)^-1. Com este valor ótimo ajustado de ω recalculamos o melhor valor para o período T usando a Eq. (11): T = 16, 60 dias. O erro σ_ω pode ser usado para encontrarmos a incerteza do período orbital T de Calisto. Chamaremos esta incerteza de σ_τ. A regra de propagação de incertezas¹⁶ dá, para

Portanto, obtemos σ_Τ = 0, 08 dias. Logo, o período orbital de Calisto em torno de Júpiter (em dias terrestres) é, de acordo com os dados Galileanos

Caso o ajuste tivesse sido feito sobre os dados para Calisto fornecidos pelo Skychart, teríamos obtido

em total compatibilidade ao resultado encontrado com os dados reportados por Galilei no Sidereus Nuncius. Notoriamente, o resultado (17) apresenta uma incerteza menor que a Eq. (16).¹⁷

O valor tabelado (vide, e.g. a Ref. [5]) é de

que coincide com o resultado (16), que vem dos dados Galileanos, dentro do intervalo de confiança de 95,45% (dois sigmas σ_Τ para mais ou para menos).

A excelente concordância do valor de T obtido de nossos dados pelo ajuste da função senóide com o valor tabelado afirma a natureza circular do movimento orbital de Calisto. De fato, a excentricidade¹⁸ da órbita de Calisto é extremamente baixa [5]: vale 0, 007.

Como exemplo de aplicação para esse nosso cálculo de T, vamos encontrar o raio r da órbita de Calisto em torno de Júpiter. Para isso precisamos usar a Terceira Lei de Kepler:

O quadrado do período orbital de um corpo celeste é proporcional ao cubo do raio de sua órbita.

A versão quantitativa dessa afirmação é a seguinte equação para o período orbital T

sendo G = 6, 673 χ 10^-11 N m²/ kg² a constante universal da gravitação; M é a massa do corpo central e r é o raio da órbita do objeto de interesse.

A Eq. (19) pode ser facilmente encontrada combinando a segunda lei de Newton da dinâmica (F = ma, com o módulo da aceleração centrípeta) [3] e a lei de Newton da gravitação universal , onde m é a massa do corpo menor). Indicamos aqui a leitura da seção 13-7 da Ref. [2].

Se soubermos a massa de Júpiter [5],

podemos usar o valor do período de Calisto, Eq. (16), para calcular o raio r de sua órbita através da Eq. (19). De fato, desta equação temos

dando

onde usamos

que é a expressão para a propagação da incerteza da variável T para a variável dependente r. Note que o raio da órbita de Calisto que obtivemos na Eq. (22) é compatível com aquele fornecido pela literatura [5],

Ou seja, a distância Calisto-Júpiter é maior do que cerca de 5 vezes a distância Terra-Lua (que é 384, 4 χ 10³ km).

Repetiremos o mesmo roteiro de estudo que fizemos para Calisto a seguir, quando analisaremos as caracteróísticas orbitais das outras Luas Galileanas.

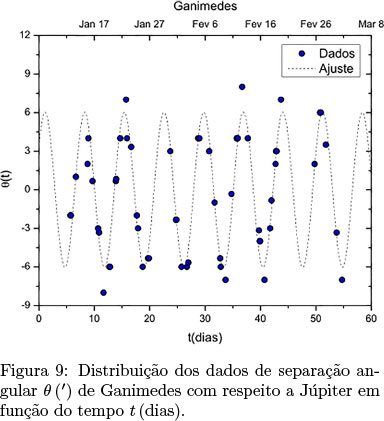
Os dados da Tabela 1 para Ganimedes permitem construir o gráfico de θ por t da Fig. 9.

Podemos ajustar uma curva senoidal ao conjunto dos pontos no gráfico da Fig. 9 estimando (i) a altura do primeiro pico do conjunto de dados de Galileu, = 6'; (ii) o valor do período usando os primeiros vales: (26 - 19) dias = 7 dias, e o valor preliminar de ω = 2π/T que aparece na coluna "Estimativa" da Tabela 3; (iii) o valor de φ₀ a partir do ω preliminar e dos pontos t₀ = 5, 7 dias; θ₀ = -2' da Tabela 1 (correspondente à observação de 12 de janeiro de 1610, às 16 h 50 min). Alimentando o software Origin com os valores estimados da Tabela 3, obtemos a curva tracejada da Fig. 9 e os valores ótimos dos parâmetros da curva senoidal.

Com os dados da coluna "Ajuste" e as Eqs. (11) e (15), obtemos o valor do período orbital de Ganimedes T = (7,16 ± 0, 02) dias da Tabela 3, o qual concorda com o valor Ttab = 7, 155 dias disponível na literatura [5] no intervalo de confiança de σ_τ, o que é bastante satisfatório. Substituindo o valor calculado de T para Ganimedes nas relações (21) para r e (23) para _στ, encontramos o raio de sua órbita com respeito a Jupiter: r = (1071 ± 2) χ 10³ km, ao passo que o valor da literatura [5] para o se-mieixo maior¹⁹ da órbita de Ganimedes é rtab = 1070 χ 10³ km. A excelente concordancia de r e r_tab - que coincidem no intervalo de apenas um σ_τ- pode ser atribuída ao fato da excentricidade da órbita de Ganimedes ser muito pequena 0, 002. Note que a distância Ganimedes-Júpiter é cerca de 3 vezes a distância Terra-Lua.

O gráfico da Fig. 10 mostra os dados coletados por Galileu para Europa durante todo o período de observação reportado no Sidereus Nuncius. A distribuição de pontos não é tão regular como nos casos de Calisto e Ganimedes, nem é tão evidentemente senoidal. O comportamento periódico ficaria claro, entretanto, caso o número de pontos (nesse mesmo intervalo de tempo) fosse maior: então, veríamos o gráfico da Fig. 10 populado de pontos sobre o ajuste senoidal (pontilhado). Isso teria sido obtido caso Galileu tivesse realizado um número maior de observações em uma mesma noite. Convidamos o leitor a usar o software Skychart para simular o conjunto adicional de pontos que se sobrepõe a curva senoidal da função θ ( t) de Europa.

A Tabela 4 mostra os valores da terna estimados para Europa a partir da distribuição dos pontos Galileanos na Fig. 10. A estimativa para foi guiada pelo número de pontos na parte de baixo do gráfico: há mais pontos na região em que θ é da ordem de - 3^'. Para a estimativa do período Τ usamos os dados do dia 17 e 21 de janeiro de 1610 - cf. Tabela 1 e Fig. 10. Alimentando o Origin com os valores estimados, obtivemos os valores ótimos para mostrados na coluna "Ajuste" da Tabela 4.

Realizando os mesmos cálculos descritos em detalhe para os casos de Ganimedes e, sobretudo, Ca-listo, encontramos os parâmetros orbitais de Europa exibidos na parte inferior da Tabela 4. Embora a excentricidade da órbita de Europa - igual a 0, 009 - seja a maior das Luas Galileanas, ela é ainda pequena o suficiente para que o valor de r = (669 ± 1) χ 10³ km por nos encontrado coincida, no intervalo de 2a_r, com o valor do semieixo maior da órbita desta lua, que é: 671 χ 10³ km. Essa distância é cerca de duas vezes a distância Terra-Lua.

O conjunto completo dos dados de Galileu para a separação angular de Io até Júpiter, elencados na Tabela 1, formam a distribuição de pontos exibida na Fig. 11. Aqui a dificuldade de reconhecer um padrão senoidal é ainda maior que no caso de Europa. Todavia, da nossa experiência com as demais Luas Galileanas, sabemos ser coerente tentar um ajuste de uma função periódica aos pontos.²⁰

Os dois primeiros pontos da Fig. 11 permitem as estimativas de e Τ (i.e., ω) que aparecem na Tabela 5. Esses valores estimados levam aos valores ótimos da terna obtidos pelo ajuste senoidal, de acordo com o roteiro estabelecido anteriormente.

A Tabela 5 também mostra os parâmetros orbitais (T, r) que calculamos para Io. O raio orbital de Io obtido a partir de nossos cálculos também é coerente com o da literatura, um fato esperado já que a excentricidade de Io é de apenas 0, 004. A distância Io-Júpiter é aproximadamente a mesma que a distância Terra-Lua.

6. Conclusão

Neste longo trabalho, resumimos as características e equações do movimento harmônico simples (MHS) e do movimento circular uniforme (MCU). Depois vimos como as observações de Galileu das posições angulares das quatro maiores luas de Júpiter poderiam estar relacionadas a esses tipos de movimentos: as estrelas móveis erravam de um lado a outro de Júpiter na abóboda celeste da mesma forma que a massa viaja à esquerda e à direita do ponto de equilíbrio em um sistema massa-mola. Não obstante, Galileu afirmou que os Planetas Medice-anos realizavam um movimento circular uniforme (MCU), descreviam órbitas em formas de círculos (p. 8 da Ref. [1]):

Observa-se também que as revoluções [dos Planetas Mediceanos] são mais rápidas para aqueles planetas que descrevem círculos menores ao redor de Júpiter, uma vez que as estrelas mais próximas de Júpiter são vistas frequen-temente à leste quando no dia anterior eles apareceram ao oeste, e vise-versa, ao passo que o planeta que traça a maior órbita, sob observação acurada de seu ponto de retorno, parece ter um período de meio mês.

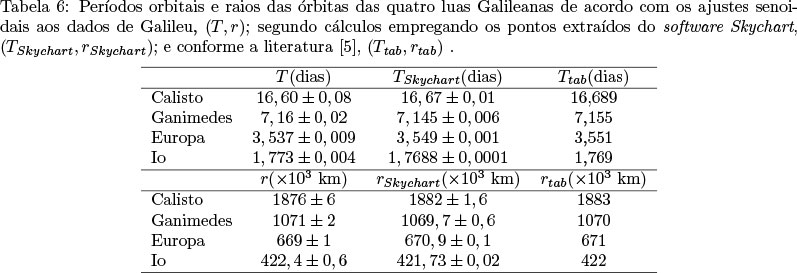
A conclusão é que esses movimentos são equivalentes: o MHS observado na abóboda celeste é a projeção do MCU das estrelas errantes. Note como a frase de Galileu citada acima prevê que tanto maior é o período de uma estrela errante quanto maior for o raio de sua órbita circular. Os cálculos da Seção 5, resumidos na Tabela 6, confirmam justamente essa afirmação.

Os resultados para T e r da Tabela 6 não poderiam ser obtidos sem o ajuste senoidal feito para o conjunto de dados de separação angular θ ( t) de cada Lua Galileana relação a Júpiter. Para obter esses dados, foi necessário construir a Tabela 1, um conjunto completo dos dados vindos das ob-servações de Galileu de 1610 reportadas no seu livro Sidereus Nuncius [1]. Tivemos, portanto, o trabalho de realizar uma leitura meticulosa dessa obra e efetuar o serviço de anotar cada dado de separação angular, para cada uma das luas, no dia e hora especificados por Galileu. Um trabalho todo especial foi dedicado a determinar a hora universal da observação, já que Galileu apenas informa a hora de observação a partir do pôr-do-sol. Tudo isso, dá um caráter histórico ao que fizemos. Além disso, usamos o software Skychart, uma efemérides interativa que nos dá acesso virtual ao céu observado por Galileu em 1610, para fazer a comparação dos diagramas de Galileu em [1] com o que seria observado através de um telescópio moderno - cf. Seção 3. ²¹ Os dados de θ ( t) colhidos pela leitura do "Mensageiro das Estrelas" que aparecem na Tabela 1 mostram os pontos usados na construção das Figs. 8, 9, 10 e 11, talvez as mais importantes deste artigo.

Que conclusão poderia ser melhor para o nosso estudo do que aquela apresentada por Galileu no seu Sidereus Nuncius:²²

Temos aqui um argumento fino e elegante para aplacar as dúvidas daqueles que, embora aceitem com mente tran-quila a revolução dos planetas em torno do Sol no sistema Copernicano, são poderosamente perturbados pela Lua revolver solitária ao redor da Terra e acom-panhá-la na sua rotação anual em torno do Sol. Alguns acreditam que essa estrutura de universo deva ser rejeitada como impossível. Mas, agora, temos não apenas um planeta rodando em torno de outro enquanto ambos percorrem uma grande órbita ao redor do Sol; nossos próprios olhos nos mostram quatro estrelas errantes ao redor de Júpiter, assim como o faz a Lua em torno da Terra, enquanto todos juntos traçam uma enorme revolução em torno do Sol no espaço de doze anos.

Agradecimentos

Agradecemos aos colegas Maira Tomaz de Carvalho, Dr. Artur Justiniano e Dr. Gustavo Rojas pelas discussões produtivas. Estamos em débito com o parecerista anônimo que realizou uma leitura cuidadosa do manuscrito e contribuiu com inúmeras sugestões para melhorar a versão original; dentre esses comentários destacamos àquele sobre o critério de Rayleigh. Este trabalho foi financiado pela FA-PEMIG (processo CEX-APQ-04440-10).

Recebido em 2/10/13

Aceito em 22/3/14

Publicado em 31/7/2014

Novamente indicamos a Ref. [4].

• [1] G. Galilei, Sidereus Nuncius or The Sideral Messenger (University of Chicago Press, Chicago, 1989).
• [2] D. Halliday, R. Resnick e J. Walker, Fundamentos de Física: Gravitação, Ondas e Termodinâmica (LTC, Rio de Janeiro, 2009), 8^a ed.
• [3] H. Moyses Nussenzveig, Curso de Física Basica: Fluidos, Oscilações e Ondas (Edgard Blücher, São Paulo, 1996), 3^a ed.
• [4] J.H. Vuolo, Fundamentos da Teoria de Erros (Ed- gard Bluücher, São Paulo, 1996), 3^a ed.
• [5] H. Karttunen, P. Krüger, H. Oja, M. Poutanen and K.J. Donner, Fundamental Astronomy (Springer, Berlin, 1996), 3^a ed.
• [6] A. van Helden, Galileo's Telescope. Disponível em: http://www.churchmilitant.tv/cia/12Galileo/2.pdf
• [7] D. Halliday, R. Resnick and J. Walker, Fundamentos de Física: Óptica e Física Moderna (LTC, Rio de Janeiro, 2009), 8^a ed.
• [8] P. Schlyter, How to compute rise/set times and altitude above horizon. Disponível em www.stjarnhimlen.se
• [9] E. Wright, Sidereus Nuncius: Galileo's First Jupiter Observations. Disponível em http://home.comcast.net/~erniew/astro/sidnunj.html

2

Essa seção deve ser entendida como um formulário de apoio

(vade mecum). As Refs. [2] e [3] tratam em detalhe dos MHS e MCU.

3

A primeira parte do livro lida com os detalhes da construção da luneta por Galileu; a segunda parte trata das observações da Lua. Na terceira parte, Galileu registra suas observações das estrelas fixas, muito mais abundantes ao telescópio do que a olho nu, e das constelações.

4

O

software Cartes du Ciel, ou

Skychart, é disponibilizado gratuitamente na internet. Vide, por exemplo o sítio

http://www.ap-i.net/skychart/en/download.

5

O

software Stellarium tambem e gratuito para download (

http://www.stellarium.org/).

6

GMT é a sigla para Greenwich Mean time e indica o Tempo Universal, ou o padrão de tempo baseado na rotação da Terra. É ele que estabelece a diferença de fuso horário. A Itália está no fuso +1, o que significa que a hora local de Galileu é uma hora adiantada em relação ao horário de Greenwich: 16h 40min do dia 07/01/1610 em Greenwich corresponderam a 17h 40min para Galileu. Apenas para referência, a parte centro-leste do Brasil está no fuso -3 (três horas mais cedo do que Greenwich).

7

Essa interpretação é consistente com o comentário do tradutor que aparece na Ref. [1], nota de rodapé 78, p. 64.

8

O padrão de difração de uma abertura ou lente circular é um circulo luminoso central cercado de aneis luminosos concentricos cada vez menos intensos. (Vide a Ref. [7], Fig. 36-10.)

9

Vide, por exemplo, a Ref. [7], Fig. 33-2 e comentários na seção 33-2.

10

Ao acessar o programa, estabelece-se o local de observação como Pádua, Itália. Depois, seleciona-se a data e hora de observação. Então, basta encontrar Júpiter com a ferramenta de busca e ancorá-lo (para que não desapareça da tela com a mudança das datas de observação). Por fim, um clique com o botão direito do mouse sob cada uma das luas Galileanas, fornece a separação angular entre elas e Júpiter (dentre outras informações).

11

Na verdade, o número de esboços de Galileu e 65 se contarmos um diagrama do dia 26 de fevereiro de 1610 em que ele repete o resultado da observação da quinta hora depois do pôr-do-sol para adicionar uma estrela fixa observada a 11' a esquerda da estrela mais a leste de Júpiter, e um pouco para o sul.

12

Para Galileu, o centro do universo e o Sol, e não a Terra, como queriam os geocentristas.

13

Vide último parágrafo da p. 83 da Ref. [1].

14

Os cálculos mostrarão os valores dos raios das órbitas das quatro Luas Galileanas. Não é necessário assumir nenhum conhecimento prévio quanto a isso.

15

Indicamos a Ref. [4] para os leitores interessados em aprender sobre o ajuste de funções contínuas a um conjunto de pontos, e estudar sobre os testes de qualidade de ajuste (incluindo o de χ

² e X

²

_red).

16

Suponha que uma grandeza

seja calculada a partir da quantidades

que s~ao medidas diretamente e possuem incertezas

. Então, a incerteza

na quantidade

é encontrada fazendo

17

Isso pode ser explicado pelo fato de o

Skychart fornecer um conjunto muito maior de pontos (melhor estatística para o ajuste). Mais importante que isso, o

Skychart, como efemérides eletrônica, provavelmente usa teoria (equações de mecânica celeste) para fornecer seus dados. Fazer o ajuste da curva senóide ao conjunto de pontos do

Skychart significaria, então, comparar teoria a teoria, e não observações (dados de Galilei) a teoria (ajuste da senóide) - opção esta que é certamente mais significativa.

18

Excentricidade de uma órbita é a medida de o quanto ela se desvia do formato de uma circunferência. Quanto maior a excentricidade, mais pronunciado é o caráter elíptico da trajetória do corpo celeste.

19

O semieixo maior de uma órbita elíptica e a distância desde o centro da elipse, pelo eixo que passa pelos pontos focais, até a sua borda. O semi-eixo maior reduz-se ao raio da órbita quando a elipse degenera em uma circunferência, o que acontece quando a excentricidade tende a zero.

20

Os pontos

t

χ θ formariam um evidente padrão de função senoidal se existissem em maior número, mas os dados Galileanos estão limitados aos da

Tabela 1.

21

Escolhemos o

software Skychart também para demonstrar como ele pode ser empregado como tecnologia de ensino de física e astronomia.

22

Cf. p. 84, Ref. [1].

Datas de Publicação

• Publicação nesta coleção
  18 Set 2014
• Data do Fascículo
  Set 2014

Histórico

• Recebido
  02 Out 2013
• Aceito
  22 Mar 2014