Resumos
Neste artigo, investigamos a sincronização de disparos neuronais em uma rede neuronal com plasticidade sináptica e perturbação externa. Nas simulações, a dinâmica neuronal é descrita pelo modelo de Hodgkin-Huxley, considerando sinapses químicas (excitatórias) entre neurônios. De acordo com a sincronização dos disparos é esperado que uma perturbação cause regimes não sincronizados. No entanto, na literatura existem trabalhos que mostram que a combinação de plasticidade sináptica e perturbação externa podem gerar regime sincronizado. Este artigo descreve o efeito da plasticidade sináptica na sincronização, onde consideramos a perturbação descrita por uma distribuição uniforme. Este estudo é relevante para pesquisas de controle de distúrbios neuronais.
neurônios; plasticidade; sinapses químicas
In this paper, we investigated the neural spikes synchronisation in a neural network with synaptic plasticity and external perturbation. In the simulations the neural dynamics is described by the Hodgkin Huxley model considering chemical synapses (excitatory) among neurons. According to neural spikes synchronisation is expected that a perturbation produce non synchronised regimes. However, in the literature there are works showing that the combination of synaptic plasticity and external perturbation may generate synchronised regime. This article describes the effect of the synaptic plasticity on the synchronisation, where we consider a perturbation with a uniform distribution. This study is relevant to researches of neural disorders control.
neurons; plasticity; chemical synapses
1. Introdução
O crescente número de diagnósticos de perturbações neurológicas é uma preocupação de nível mundial, tanto em termos do bem estar humano como no impacto na economia. Tais perturbações incluem além de traumatismos cerebrais, infecções neurológicas, esclerose múltipla, a doença de Parkinson,1 1 Doença progressiva do movimento devido à disfunção dos neurônios que controlam e ajustam a transmissão dos comandos conscientes vindos do córtex cerebral para os músculos do corpo humano. epilepsias e Mal de Alzheimer. Além de afetarem pessoas de todos os países, independentemente da idade, sexo, nível de educação ou rendimento, tais doenças também afetam o Produto Interno Bruto (PIB) dos países, através da falta de produtividade que decorre do desenvolvimento de uma doença mental, estima-se que essa quebra no PIB seja de 4% ao ano [1[1] World Health Organization, Neurological Disorders: Public Health Challenges (Who Press, Geneva, 2013).].
Segundo relatório publicado pela Organização Mundial de Saúde [1[1] World Health Organization, Neurological Disorders: Public Health Challenges (Who Press, Geneva, 2013).], estima-se que, todos os anos, 6,9 milhões de pessoas morrem devido a perturbações neurológicas. Cerca de 1% da população com mais de 65 anos apresenta a doença de Parkinson, isso corresponde a mais de quatro milhões de pessoas afetadas. E as previsões até 2020 são assustadoras, mais de 85 milhões de pessoas sofrerão com doenças neurológicas, sendo que destas, 50 milhões terão epilepsia2 2 Grupo de transtornos neurológicos de longa duração caracterizados por atividade excessiva e anormal das células nervosas do córtex cerebral. e mais de 35 milhões terão Alzheimer3 3 Doença neurodegenerativa que provoca declínio de funções intelectuais, reduz a capacidade de trabalho, relação social e interfere no comportamento e na personalidade. ou outras demências [1[1] World Health Organization, Neurological Disorders: Public Health Challenges (Who Press, Geneva, 2013).].
Uma das tentativas para solucionar ou pelo menos amenizar essa situação alarmante é o investimento em pesquisas científicas envolvendo diversas áreas e formas de atacar os problemas identificados. Estes que envolvem neurociências funcionam como quebra-cabeças, ou seja, são separados em muitas peças e cada uma é tão necessária quanto a outra, e a física tem colaborado muito para o avanço de modelos que podem auxiliar em tratamentos e desenvolvimento de mecanismos para uma melhor qualidade de vida. Conceitos envolvendo oscilações, circuitos e equações diferenciais permitem a interpretação acurada de fenômenos biológicos, dando cunho para desenvolvimento de pesquisas importantes.
Neste trabalho abordamos a sincronização de neurônios utilizando o modelo de Hodgkin-Huxley (HH) [2[2] A. Hodgkin and, A.F. Huxley, Journal Physiology 117, 500 (1952).], com medidas realizadas a partir dos picos de disparos (do inglês spikes) [3[3] E.M. Izhikevich, Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting (MIT Press, Cambridge, 2007)., 4[4] D. Purves, G.J. Augustine, D. Fitzpatric, W.C. Hall, A. Lamantia, J.O. MacNamara and S.M. Willians, Neuroscience - A Novelty for the Nervous: Neuroscience (MA Sinauer Associates, Sunderland, 1997).] quando submetidos a perturbações externas e plasticidade sináptica. Este estudo é uma aplicação dos conhecimentos em física e tem efeito relevante na descoberta de novas formas de controle de patologias.
A sincronização4 4 Derivação da palavra síncrono e significa ”ocorrência ao mesmo tempo”. está diretamente ligada ao ajuste dos ritmos de osciladores5 5 Corpo que possui uma oscilação. Oscilação é o movimento de um corpo que passa e torna a passar alternativamente pelas mesmas posições. devido à sua interação [5[5] A. Pikovsky, M.G. Rosenblum and J. Kurths, Synchronization: A Universal Concept in Nonlinear Sciences (Cambridge University Press, Cambridge, 2001).]. Pode ocorrer com qualquer tipo de oscilador, seja ele físico, químico e biológico [3[3] E.M. Izhikevich, Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting (MIT Press, Cambridge, 2007).]. O fenômeno de sincronização é foco de estudo em muitas áreas, pois é freqüentemente observado na natureza em sistemas acoplados com comportamento periódico ou caótico [5[5] A. Pikovsky, M.G. Rosenblum and J. Kurths, Synchronization: A Universal Concept in Nonlinear Sciences (Cambridge University Press, Cambridge, 2001).].
Conhecendo os princípios que resultaram na sincronia ou na assincronia de um sistema, é possível responder questões referentes à engenharia, matemática, física e neurociência entre outras. A sincronização de oscilações neuronais, por exemplo, pode ser observada desde os primeiros estágios de muitos sistemas sensoriais de animais, como insetos, sapos e primatas. Alguns estudos realizados com mamíferos demonstraram que as sinapses6 6 No Século 19, Santiago Ramón y Cajal deixou relatado em seus escritos e figuras, a existência de pequenos espaços entre células nervosas. Mais tarde, Charles Sherrington atribuiu nome aos espaços que estavam ligados a passagem de informação: sinapses. entre os neurônios são estabelecidas nos primeiros estágios do desenvolvimento e a sincronização das oscilações neuronais pode ocorrer durante o desenvolvimento e aprendizagem [6[6] I.-H. Lin, R.-K. Wu and C.-M. Chen, Physical Review E 84, 051923 (2011).].
Como o fenômeno de sincronização mostra a correlação da dinâmica de diferentes sistemas quando estes apresentam alguma forma de interação, seu papel na transmissão de informação e estudo de enfermidades é cada vez mais aplicado [7[7] A. Pikovsky and M.G. Rosenblum, Contemporary Physics 44, 401 (2003)., 8[8] R.E. Mirollo and S.H. Strogatz, SIAM Journal on Applied Mathematics 50, 1645 (1990).]. Em pesquisas recentes sobre doença de Alzheimer, análises baseadas na sincronização e dessincronização neuronal são consideradas e auxiliam na conclusão de que a dinâmica de oscilações do tálamo e do córtex são significativamente influenciadas pela perda sináptica cortico-cortical [9[9] K. Abuhassan, D. Coyle and L. Maguire, Frontiers in Computational Neuroscience 8, 65 (2014).].
Em patologias como epilepsia e doença de Parkinson [10[10] J. Modolo, B. Bhattacharya, R. Edwards, J. Campagnaud, A. Legros and A Beuter, Frontiers in Neuroscience: Neuroprosthetics 4, 45 (2010).], fisiologias do funcionamento motor e processamento de informações sensoriais, estudos mostram que é benéfico conhecer a sincronia das oscilações neuronais e como suprimi-las a fim de minimizar as crises [11[11] C. Hammond, H. Bergman and P. Brown, Trends in Neurosciences 30, 357 (2007)., 12[12] P. Uhlaas and W. Singer, Neuron 52, 155 (2006).].
Uma rede pode sofrer perturbações, ou seja, alteração nas condições normais em que se encontra. No caso da rede neuronal, essa perturbação externa pode ser causada como algum dos cinco sentidos (audição, olfato, paladar, tato e visão). Tais perturbações são causadas pela inserção de uma perturbação, que pode variar em termos de intensidade.
A plasticidade sináptica é um fenômeno neuronal, postulado no final da década de 1940, pelo psicólogo Canadense Donald Hebb [13[13] D.O. Hebb, The Organization of Behavior (Wiley, New York, 1949).]. Ele acreditava que se dois neurônios apresentassem uma atividade conjunta, a intensidade das sinapses entre eles deveria ser reforçada. Essa proposta de Hebb foi comprovada experimentalmente por Bliss e colaboradores, realizando medidas com neurônios do hipocampo do cérebro de coelhos [14[14] T.V.P. Bliss and G.L. Collingridge Nature, 361, 31 (1993)., 15[15] T.V.P. Bliss and A.R. Gardner-Medwin, Journal Physiology 232, 357 (1973).].
Entre os diferentes tipos de processos sinápticos descritos na literatura, abordaremos neste artigo a plasticidade sináptica dependente do tempo de disparos de entrada e saída dos neurônios (do inglês spike timing dependent-plasticity: STDP). A inserção deste tipo de regra de plasticidade, nos permitirá ajustar a intensidade das conexões, propiciando um regime de disparos neuronais em tempos próximos, o que contribui para a sincronização dos neurônios [16[16] G.Q. Bi and M.M. Poo, The Journal of Neuroscience 18, 10464 (1998).].
A seguir apresentaremos a metodologia aplicada, o desenvolvimento, os resultados e conclusões referentes à investigação da sincronização dos disparos em uma rede de neurônios com sinapses modificáveis via STDP com e sem a presença de perturbação.
2. Metodologia
Desenvolvemos o presente trabalho utilizando ferramentas computacionais e dados de trabalhos experimentais, obtidos na literatura. Para a elaboração de rotinas computacionais, utilizamos a Linguagem C [17[17] H. Schildt, C: The Complete Reference (McGraw-Hill Osborne Media, California, 2000).].
Na fase de elaboração de rotina, a escolha do modelo neuronal adequado foi um passo importante, que depende do objetivo da análise a ser efetuada. Os principais modelos que encontramos na literatura, foram os do tipo integra-dispara [18[18] L.F. Abbott, Brain Research Bulletin 50, 303 (1999).–20[20] S. Ostojic and N. Brunel, The Journal of Neuroscience 29, 10234 (2009).], Izhikevich [21[21] E.M. Izhikevich, N.S. Desai, E.C. Walcott and F.C. Hoppensteadt, Trends in Neuroscience 26, 161 (2003)., 22[22] E.M. Izhikevich, IEEE Trans. Neural Networks 14, 1569 (2003).], FitzHugh-Nagumo [23[23] R. Fitzhugh, Biophysics Journal 1, 445 (1961).], Hindmarsh-Rose [24[24] J.L. Hindmarsh and R.M. Rose, Nature 296, 162 (1982).], Morris-Lecar [25[25] C. Morris and H. Lecar, Biophysical Journal v. 35, 193 (1981).], Wilson [26[26] H.R. Wilson, Journal Theoretical Biology 200, 375 (1999).] e Hodgkin-Huxley [2[2] A. Hodgkin and, A.F. Huxley, Journal Physiology 117, 500 (1952).]. Comparamos os modelos, e chegamos a conclusão de que o modelo dos pesquisadores Hodgkin e Huxley nos ofereceria as propriedades de disparos, rajadas e uma interpretação biológica significativa.
Após a simulação do primeiro neurônio, e com este respondendo corretamente, passamos a montar a rede com os demais neurônios. Conectamos os neurônios de forma global, pois com esta forma podemos simular sistemas que possuem ligações de longo alcance que ocorrem em física e biologia [27[27] M.Y. Choi, Physical Review Letters 86, 134101–1 (2004).]. No acoplamento global, também conhecido como acoplamento de campo médio [28[28] K. Kaneko, Physica D 54, 5 (1991).], um neurônio pode interagir com todos os outros neurônios da rede.
Após o acoplamento ser inserido e testado na rotina, passamos a inserção de uma perturbação externa e da STDP. A perturbação externa (Iext) é uma das ferramentas que pode ser utilizada para a supressão da sincronização neuronal [29[29] V.O. Popovych, S. Yanchuk and P.A. Tass, Scientific Reports 3, 2926 (2013).]. Nesse trabalho, a perturbação externa foi inserida de maneira aleatória e com uma intensidade suficiente para gerar disparos neuronais. Isto causa uma alteração no tempo de disparos dos neurônios e dependendo da intensidade, propicia um regime não sincronizado.
A STDP é inserida logo em sequência. Entra no modelo modificando o termo no acoplamento e, desta forma, determina a evolução dos pesos sinápticos em função da atividade dos neurônios pré e pós-sináptico, ocasionando uma potenciação ou uma depressão destes [30[30] V.P. Zhigulin, M.I. Rabinovich, R. Huerta and H.D. Abarbanel, Physical Review E 67, 021901 (2003).].
3. O neurônio e seu comportamento
Um modelo neuronal procura simular o mais realisticamente possível, o que ocorre em um neurônio biológico. Quanto a um neurônio biológico, nos referimos a uma célula do sistema nervoso responsável pela condução de impulsos nervosos. Atualmente, acredita-se que no cérebro existam cerca de 86 bilhões de neurônios7 7 Nas Refs. [31–33] é possível conhecer mais a fundo sobre as células neuronais em geral e suas especificidades. [31[31] R. Lent, Cem bilhões de Neurônios? Conceitos Fundamentais de Neurociências (Atheneu, São Paulo, 2010)., 32[32] E. Okuno, I.L. Caldas e C. Chow, Física para Ciências Biológicas e Biomédicas (HARBRA, São Paulo, 1986).], cada um com suas peculiaridades. Na Fig. 1, observamos uma representação esquemática de um neurônio biológico com seus componentes básicos.
O soma é a parte central do neurônio, nele estão presentes as organelas e o núcleo. Os dendritos são numerosos prolongamentos que recebem estímulos nervosos e os transmite para o corpo da célula e o axônio é responsável pela condução dos impulsos elétricos que partem do corpo celular, até outro local mais distante. Os neurônios variam em forma, tamanho e conexões [32[32] E. Okuno, I.L. Caldas e C. Chow, Física para Ciências Biológicas e Biomédicas (HARBRA, São Paulo, 1986).].
Alguns neurônios podem responder a estímulos disparando potenciais de ação a uma frequência constante, outros podem não apresentar uma taxa de disparos constante, então disparam no início do estímulo e, logo na sequência diminuem a taxa de disparos mesmo que o estímulo ainda permaneça.
Na Fig. 2, observamos a atividade neuronal caracterizada por um disparo neuronal com amplitude máxima para uma corrente inicial de 20 mV [33[33] M.F. Bear, B.W. Connors e M.A. Paradiso, Neurociências: Desvendando o Sistema Nervoso (Artmed, Porto Alegre, 2008).]. Este tipo de comportamento é característico da evolução temporal do potencial de ação da membrana de algumas células neuronais [31[31] R. Lent, Cem bilhões de Neurônios? Conceitos Fundamentais de Neurociências (Atheneu, São Paulo, 2010).]. Na ausência de uma corrente (uma perturbação ou estímulo externo), o potencial permanece constante. Entretanto, dependendo do estímulo fornecido à célula, o potencial da membrana começa variar, até que atinge um limiar. A partir desse limiar a subida é rápida até atingir a amplitude máxima.8 8 Esse processo é chamado despolarização da membrana. O retorno ao potencial de repouso9 9 A queda do pico até o limiar é conhecida como repolarização. é mais lento que a ascensão ao pico e, durante o intervalo de quando o potencial retorna ao valor do limiar até alcançar novamente o potencial de repouso,10 10 Período em que o potencial permanece abaixo do potencial de repouso é chamado hiperpolarização. temos um período refratário, onde o neurônio fica quiescente até poder disparar novamente [3[3] E.M. Izhikevich, Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting (MIT Press, Cambridge, 2007).].
Representação da atividade de disparos neuronais, conforme o potencial de membrana sofre alterações, observamos o processo de construção de um pico de potencial de ação neuronal.
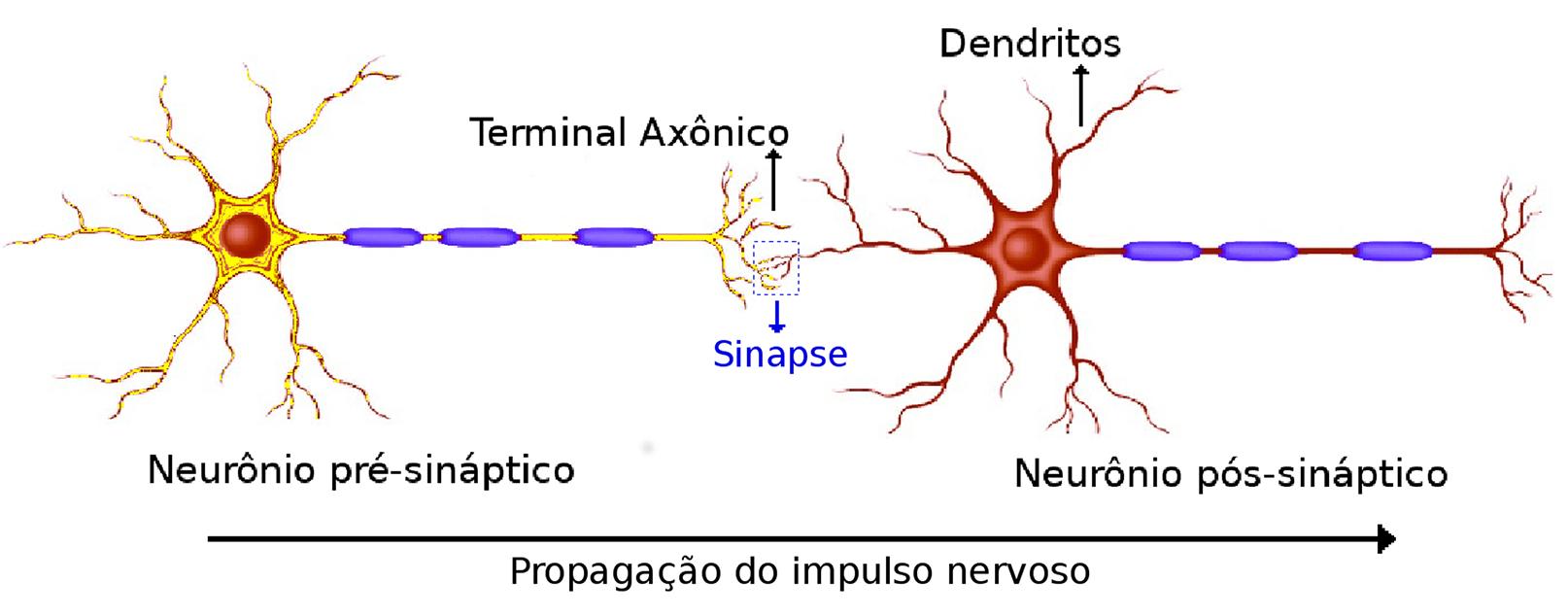
Os valores de potencial sofrem modificações devido às junções (fendas) conhecidas como sinapses. Nas sinapses, um neurônio influencia diretamente outro(s) neurônio(s), através da transmissão de sinais elétricos ou químicos. O neurônio que ocasiona a alteração é chamado pré-sináptico, enquanto o neurônio que sofreu a ação é chamado pós-sináptico, conforme indicado na Fig. 3.
Neurônios pré e pós-sinápticos, demonstrando a região de acoplamento onde ocorre a sinapse. É possível verificar o sentido de propagação do sinal elétrico entre os neurônios pré e pós-sinápticos.
3.1. Sinapses
As sinapses foram observadas na década de 50, mas precisamente em 1959, quando Edward Gray publicou fotomicrografias da fenda sináptica [34[34] E.G. Gray, Nature 6, 1592 (1959).]. Tal comprovação mostra que as sinapses são estruturas microscópicas de contato entre neurônios e/ou outras células, ou seja, são junções especializadas [31[31] R. Lent, Cem bilhões de Neurônios? Conceitos Fundamentais de Neurociências (Atheneu, São Paulo, 2010)., 33[33] M.F. Bear, B.W. Connors e M.A. Paradiso, Neurociências: Desvendando o Sistema Nervoso (Artmed, Porto Alegre, 2008).]. Podem ser elétricas ou químicas. As sinapses elétricas apresentam transmissão rápida de impulsos elétricos, porém, não processam informações. São sincronizadoras de atividade neuronal. Já as sinapses químicas, são moduláveis, podem transmitir e modificar informações e manifestam-se na forma excitatória, resultando em um novo impulso nervoso (como a utilizada neste trabalho) ou na forma inibitória, impedindo a passagem de impulsos [33[33] M.F. Bear, B.W. Connors e M.A. Paradiso, Neurociências: Desvendando o Sistema Nervoso (Artmed, Porto Alegre, 2008)., 35[35] J.H. Byrne, Fundamental Neuroscience (Academic Press, New York, 2008)].
3.2. Plasticidade sináptica dependente do tempo de disparos (do inglês: Spike timing dependent plasticity- STDP)
Donald Hebb formulou uma hipótese em 1949 sobre conexões neuronais sendo reforçadas quando os neurônios apresentam uma atividade conjunta. Baseado nessa hipótese e nas descobertas experimentais posteriores, Wulfram Gerstner11 11 Professor Wulfram Gerstner é diretor do Laboratótio de Neurociência Computacional (LCN) na Escola Politécnica Federal de Lausana na Suíça. mostrou que a comunicação entre os neurônios depende da relação entre os instantes dos disparos dos potenciais de ação [36[36] H. Markram, W. Gerstner and P.J. Sjöström, Frontiers in Synaptic Neuroscience 4, 8 (2012).–38[38] W. Gerstner, Frontiers in Synaptic Neuroscience 2, 50 (2010).]. A proposta de Gerstner foi comprovada experimentalmente em 1997 por Henry Markram [36[36] H. Markram, W. Gerstner and P.J. Sjöström, Frontiers in Synaptic Neuroscience 4, 8 (2012).] e em 1998 por Guo-qiang Bi e Mu-ming Poo [16[16] G.Q. Bi and M.M. Poo, The Journal of Neuroscience 18, 10464 (1998).].
Na Fig. 4 é apresentada uma ilustração do resultado obtido experimentalmente por Bi e Poo [16[16] G.Q. Bi and M.M. Poo, The Journal of Neuroscience 18, 10464 (1998).]. Ocorre fortalecimento (potenciação) na intensidade das conexões entre neurônios se o o neurônio pré-sináptico dispara antes do pós-sináptico (Δt > 0). Caso contrário, (Δt< 0), ocorre o enfraquecimento (depressão) nas conexões. Este processo corrobora o Postulado de Hebb, pois a atividade conjunta dos neurônios leva a modificações na intensidade das sinapses.
A representação apresentada, mostra a plasticidade dependente do tempo dos disparos neuronais (STDP). Podemos observar a variação da intensidade de conexão entre os neurônios da rede (W) e sua dependência com os intervalos de disparos dos neurônios pré e pós-sinápticos.
4. O modelo
Por meio de modelos é possível realizar simulações e estudos comportamentais de neurônios. Os modelos capacitivos representam de forma satisfatória algumas das variáveis de um neurônio. Logicamente, não é um modelo perfeito, porque ainda não se conhece um modelo que seja capaz de simular totalmente as funções de células tão complexas.
O modelo proposto nas simulações é um circuito capacitivo, representando uma membrana neuronal e os canais iônicos que por ela passam. A Fig. 5 é uma representação esquemática do circuito considerado neste artigo, com um capacitor de placas paralelas, com capacitância C. Em paralelo ao capacitor, encontra-se a associação de três ramos, cada um equivalente a um canal iônico. Os canais de Sódio (Na) e de Potássio (K) são representados por potenciômetros que variam de acordo com o potencial V e fontes elétricas (ENa, EK) representando o potencial reverso (dado pela equação de Nernst [32[32] E. Okuno, I.L. Caldas e C. Chow, Física para Ciências Biológicas e Biomédicas (HARBRA, São Paulo, 1986)., 33[33] M.F. Bear, B.W. Connors e M.A. Paradiso, Neurociências: Desvendando o Sistema Nervoso (Artmed, Porto Alegre, 2008).]), enquanto o canal que representa os demais íons é representado por um resistor R conectado em série com uma fonte Vr. O circuito tem uma corrente de entrada I que em um neurônio seriam sinapses, ou outro sinal externo. Este circuito foi proposto por volta de 1952 por Alan Lloyd Hodgkin e Andrew Fielding Huxley, os experimentos eram voltados ao estudo de potenciais de ação, e eram realizados em um axônio de grosso calibre de um molusco (Loligo Pealei) [2[2] A. Hodgkin and, A.F. Huxley, Journal Physiology 117, 500 (1952).]. E pode ser resolvido utilizando as Leis de Kirchhoff.
Circuito elétrico capacitivo, onde a membrana neuronal é representada por um capacitor de placas paralelas, e alguns possíveis canais iônicos são apresentados como ramos do circuito.
O estudo dos pesquisadores Hodgkin e Huxley foi possível graças ao avanço dos mecanismos instrumentais da década de 50. Por meio do conjunto de equações diferenciais não-lineares de 1a ordem, e parâmetros coletados experimentalmente, o modelo descreveu e ainda descreve o comportamento de células neuronais. Na Tabela 1, apresentamos um apanhado geral das medidas experimentais utilizadas para simulações envolvendo o modelo HH [2[2] A. Hodgkin and, A.F. Huxley, Journal Physiology 117, 500 (1952).].
Parâmetros para o modelo de Hodgkin-Huxley considerando o potencial de repouso igual a −65 mV.
O circuito da Fig. 5, ajustado aos parâmetros apresentados na Tabela 1 é descrito pelo sistema de equações diferenciais de 1a ordem
onde CM é a capacitância da membrana neuronal, V é o potencial de membrana do neurônio, VK, VNaeVl, são os potenciais devido aos íons de Potássio, Sódio e demais íons presentes no fluído celular,12 12 É possível verificar mais a fundo a questão dos potenciais nas Refs. [31–33]. respectivamente. As condutâncias específicas máximas para cada um dos canais iônicos são gK, gNa e gl. A corrente constante que desencadeia uma sequência periódica de potenciais de ação13 13 Também chamado de impulso nervoso [32]. neuronais é representada por I. As variáveis me h controlam os estados aonde a membrana conduz ou não a corrente, referente aos íons de Sódio. Enquanto n comanda a fração de canais de Potássio. As funções α e β foram determinadas experimentalmente [39[39] W. Gerstner and W. Kisler, Spiking Neuron Models(Cambridge University Press, New York, 2008).] e são dadas porPodemos investigar o comportamento de uma população de neurônios interligados por sinapses químicas excitatórias. Consideramos a configuração global para a rede neuronal, onde todos os neurônios estão conectados, conforme proposto no trabalho de Popovych e colaboradores [29[29] V.O. Popovych, S. Yanchuk and P.A. Tass, Scientific Reports 3, 2926 (2013).]. Desta forma o sistema de equações diferenciais de 1a ordem não-linear passa a ser
onde Vr = 20 mV é o potencial reverso, N é o número de neurônios, aijfornece a intensidade ou intensidade do acoplamento entre o neurônio pré-sináptico j e o pós-sináptico i. O termo IEXT é a intensidade da perturbação externa aplicada aleatoriamente nos neurônios com uma duração igual a 1 ms. Cada neurônio recebe em média uma perturbação a cada 14 ms. O acoplamento sináptico entre uma população de neurônios é representado por sj(t) que representa a interação via sinapses químicas excitatórias por meio de mecanismo de integração do potencial pós-sináptico dos neurônios (PSP) [3[3] E.M. Izhikevich, Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting (MIT Press, Cambridge, 2007)., 34[34] E.G. Gray, Nature 6, 1592 (1959).]. No caso deste estudo, é a forma de conexão existente entre ou neurônios da rede, resultante de processos de troca iônica, chamado acoplamento excitatório [29[29] V.O. Popovych, S. Yanchuk and P.A. Tass, Scientific Reports 3, 2926 (2013).]. As intensidades das conexões podem ser controladas por processos biológicos, um desses processos é a plasticidade sináptica dependente do tempo (STDP). A STDP é um modelo de plasticidade sináptica que leva em consideração os tempos de disparos entre os neurônios pré e pós-sinápticos.O principal efeito do fenômeno da STDP é o acréscimo (potenciação), ou decréscimo (depressão) na intensidade das sinapses [16[16] G.Q. Bi and M.M. Poo, The Journal of Neuroscience 18, 10464 (1998).], isso ocorre em função da ordem temporal dos disparos, dados por
onde Δtij = ti − tj, com i representando o neurônio pós-sináptico e j o neurônio pré-sináptico. Se o neurônio j dispara alguns instantes antes que o neurônio i, Δtij > 0, e assim, ocorre a potenciação neste sentido, pois este colaborou para o disparo de i. Caso contrário, ocorre a depressão na sinapse entre os neurônios i e j. Os parâmetros do modelo são A1 = 1; A2 = 0,5; τ1 = 1,8 ms e τ2 = 6,0 ms [29[29] V.O. Popovych, S. Yanchuk and P.A. Tass, Scientific Reports 3, 2926 (2013).]. A atualização dos pesos sinápticos é dada por onde a intensidade do acoplamento entre os neurônios pré (j) e pós-sináptico (i) é acrescida do produto de uma taxa de modificação sináptica δ = 0,001 e o peso sinápticoW(apresentado na Eq. (4)).4.1. Sincronização
A história que acompanha o fenômeno de sincronização de sistemas data de meados de 1665, quando Christian Huygens inventou o relógio de pêndulo14 14 O relógio pendular de Christian Huygens está exposto juntamente com uma cópia do livro “Horologium Oscillatorium sive de motu pendulorum” no museu Boerhaave na Holanda. e observou o que dois relógios dispostos na mesma superfície de contato apresentavam um movimento sincronizado (Fig. 6) [40[40] L.H.A. Monteiro, Sistemas Dinâmicos (Editora Livraria da Física, São Paulo, 2006).]. Foi então que realizou testes para verificar se a sincronia persistiria. Perturbou a oscilação dos pêndulos e verificou que após algum tempo, a sincronia voltava a acontecer. Após C. Huygens, diversos pesquisadores investigaram a sincronização em vários sistemas, desde as células cardíacas até o piscar de comunidades de vaga-lumes [41[41] D. di Bernardo, M.G. Signorini and S. Cerutti, International Journal Bifurcation and Chaos 9, 1975 (1998).–44[44] A.K. Engel, P. König, A.K. Kreiter, T.B. Schillen and W. Singer, Trends in Neurosciences 15, 218 (1992).].
Relógios pendulares dispostos na mesma superfície de apoio. São osciladores, onde uma massa é acoplada a um pivô que permite sua movimentação livre.
Em sistemas representados por redes neuronais, é comum observar a sincronização em termos dos picos de disparos ou dos trens de disparos [do inglês burst] neuronais. A condição de sincronia entre os neurônios é observada quando os neurônios começam e terminam os trens de disparos simultaneamente [4[4] D. Purves, G.J. Augustine, D. Fitzpatric, W.C. Hall, A. Lamantia, J.O. MacNamara and S.M. Willians, Neuroscience - A Novelty for the Nervous: Neuroscience (MA Sinauer Associates, Sunderland, 1997).].
A observação do espaço de parâmetros é auxiliada por uma ferramenta de diagnóstico para a sincronização, o parâmetro de ordem de Kuramoto (R). Em 1975, Yoshiki Kuramoto trabalhou com um conjunto de osciladores acoplados todos com a mesma intensidade. Realizando testes com as frequências do sistema, Kuramoto concluiu que os osciladores acoplados ficavam em um círculo unitário no plano complexo [45[45] Y. Kuramoto, International Symposium on Mathematical Problems in Theoretical Physics (Springer-Verlag, New York, 1975)., 46[46] Y. Kuramoto, Chemical Oscillations, Waves, and Turbulence (Springer-Verlag, New York, 1984).] e então propôs a equação que corresponde a média da norma do vetor complexo ao longo do tempo
onde ϕj é a fase do sítio jrepresentada por sendo tj(m) e ϕj o tempo de disparos e fase do neurônio j.O regime de sincronização obedece uma escala numérica onde o valor máximo do parâmetro de ordem de Kuramoto é 1. No caso deste trabalho, à medida que R aproxima-se de 1, permite diagnosticar mais sincronia entre os neurônios, e a sincronização total seria R = 1.
5. Resultados e discussões
A fim de verificarmos o comportamento temporal da intensidade das conexões em uma rede neuronal com STDP, plotamos a Fig. 7. Nesta, verificamos a influência da intensidade da perturbação externa na evolução temporal da intensidade de acoplamento médio entre os neurônios da rede. Os valores iniciais de aij foram distribuídos normalmente com média 0,5 e desvio-padrão 0,02. Estes fornecem a intensidade do acoplamento entre o neurônio pré-sináptico j e o pós-sináptico i, que são mantidos no intervalo [0,0;0,5]. Os neurônios são globalmente conectados e sem auto-conexões, ou seja, com aii = 0.
Evolução temporal da intensidade média de acoplamento (< K >) para uma rede com 100 neurônios submetidos à diferentes valores da perturbação externa μA∕cm2. A linha em preto representa a ausência de perturbação externa (Iext = 0, 0), em azul à influência de Iext = 30, 0; em vermelho Iext = 40, 0 e em verde Iext = 50, 0.
No caso onde consideramos a ausência de perturbação externa (Iext = 0,0), os valores para a intensidade do acoplamento médio entre os neurônios convergem para 0,25. Neste caso a STDP induz um acoplamento unidirecional, onde as sinapses que partem de neurônios de maior frequência para os de menor frequência tendem a 0,5, devido a potenciação e no sentido contrário tendem a zero.
Para o caso onde a inserção de perturbação com intensidades moderadas (5 < Iext < 35), o acoplamento médio assume valores maiores (< K >> 0,4) comparados com o caso onde Iext = 0,0 (Fig. 8). Nesta situação, a perturbação atua de forma construtiva na rede neuronal, alterando os tempos de disparos, principalmente dos neurônios com frequências de disparos menores. Este efeito leva o sistema a uma alternância entre a potenciação e a depressão das conexões entre os neurônios. Como o valor absoluto da potenciação é maior do que a da depressão tem-se um saldo positivo no acoplamento médio para tempos suficientemente grandes. No entanto, nos casos onde a perturbação externa assume valores altos (Iext > 40), o sistema passa a apresentar um regime fracamente acoplado (< K > ∼ 0,0), e assim, este passa a atuar de maneira destrutiva na rede.
Influência da perturbação externa (Iext) na intensidade média de acoplamento (< K >) para uma rede com 100 neurônios.
A sincronização dos neurônios é diretamente influenciada pela perturbação externa. Comprovamos essa afirmação com o auxílio da Fig. 8, onde temos a influência da inserção de perturbação externa no acoplamento médio entre neurônios. Verificamos que conforme a intensidade da perturbação externa sofre acréscimos, os neurônios tendem ao desacoplamento.
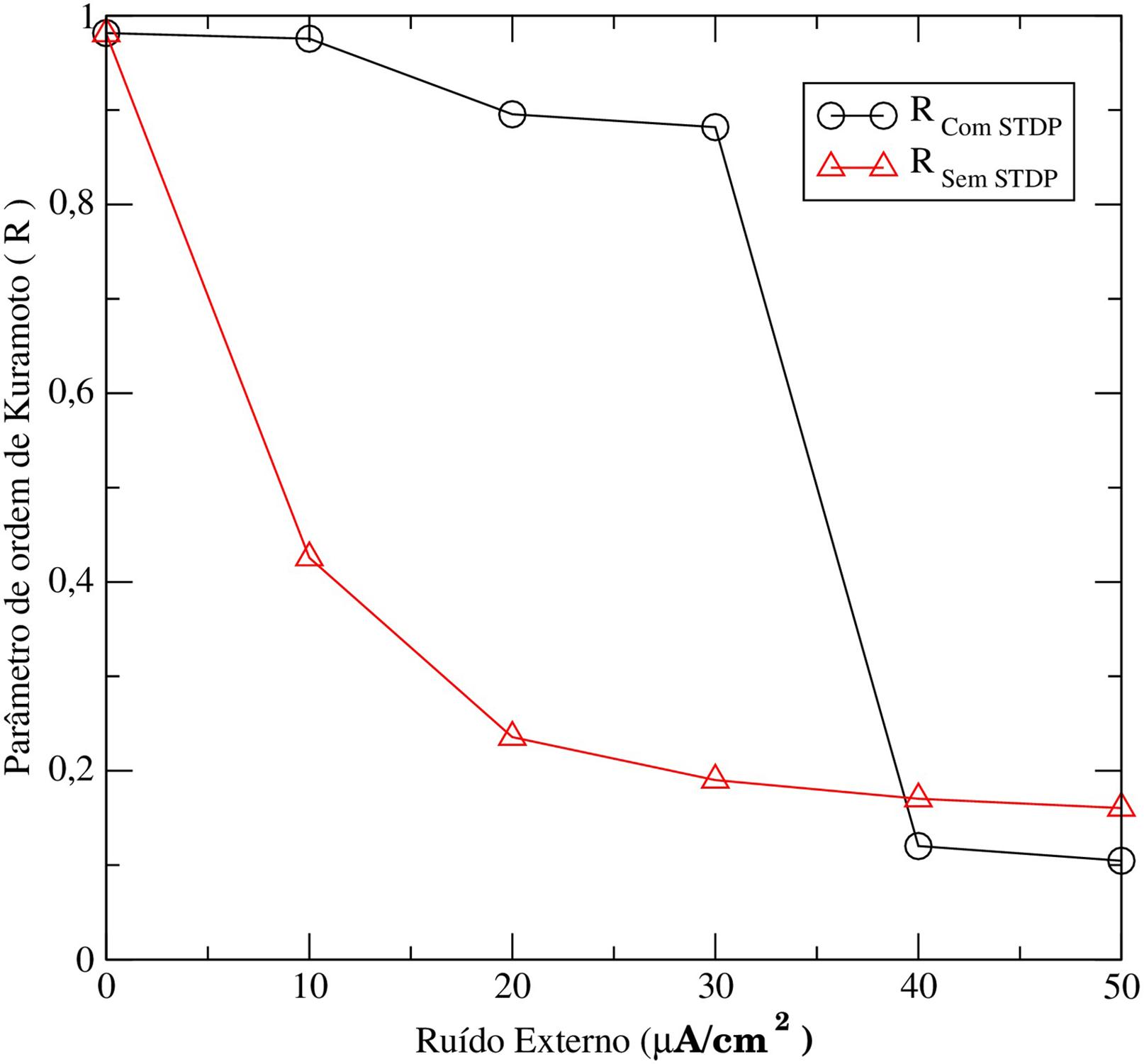
Utilizando o parâmetro de ordem de Kuramoto analisamos o comportamento da sincronização da rede de neurônios acoplados em duas situações: i) sem a inserção do mecanismo da STDP nas equações do modelo e ii) com a inserção da STDP nas equações do modelo. Na Fig. 9 observa-se que para o caso sem STDP (linha preta com círculos), conforme aumentamos a intensidade da perturbação externa a sincronização entre os neurônios cai rapidamente. No entanto, na simulação com STDP (linha vermelha com triângulos), para intensidades moderadas de perturbação, o sistema ainda apresenta um alto valor do parâmetro de ordem. Neste caso, a combinação de plasticidade sináptica e perturbação atuam de forma que sistema permanece sincronizado.
Comportamento de sincronia entre neurônios de uma rede com (linha preta com círculos)/sem (linha vermelha com triângulos) plasticidade sináptica (STDP).
6. Conclusões
Após estruturar didaticamente a apresentação de um modelo de simulação neuronal, baseado em circuitos elétricos, foi possível investigar a sincronização de disparos em redes neuronais com sinapses modificáveis via STDP mesmo com a presença de perturbação. Observamos que a plasticidade sináptica pode agir como um mecanismo contraposto ao efeito de supressão da sincronização devido à perturbação. Para redes com STDP e intensidades de perturbação moderadas foi observado um acréscimo na intensidade de acoplamento médio entre os neurônios na rede, quando comparados ao caso sem STDP. Neste caso, a combinação de plasticidade sináptica e perturbação atuam de forma a reforçar as sinapses pré-existentes. Como consequência a sincronização da rede neuronal torna-se robusta com relação a perturbações externas. No entanto, mesmo com STDP, o sistema evolui para um estado com acoplamento médio fraco, e consequentemente, a um regime não síncrono quando a intensidade da perturbação é suficientemente grande.
Agradecimentos
Ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), à Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), à Fundação Araucária, à Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP, processo 2011/19296-1) e ao Programa Ciência sem Fronteiras processos n° 245377/201 2–3, n° 17656125, n° 99999.010583/2013-00 e n° 5527-13-9.
-
1
Doença progressiva do movimento devido à disfunção dos neurônios que controlam e ajustam a transmissão dos comandos conscientes vindos do córtex cerebral para os músculos do corpo humano.
-
2
Grupo de transtornos neurológicos de longa duração caracterizados por atividade excessiva e anormal das células nervosas do córtex cerebral.
-
3
Doença neurodegenerativa que provoca declínio de funções intelectuais, reduz a capacidade de trabalho, relação social e interfere no comportamento e na personalidade.
-
4
Derivação da palavra síncrono e significa ”ocorrência ao mesmo tempo”.
-
5
Corpo que possui uma oscilação. Oscilação é o movimento de um corpo que passa e torna a passar alternativamente pelas mesmas posições.
-
6
No Século 19, Santiago Ramón y Cajal deixou relatado em seus escritos e figuras, a existência de pequenos espaços entre células nervosas. Mais tarde, Charles Sherrington atribuiu nome aos espaços que estavam ligados a passagem de informação: sinapses.
-
7
Nas Refs. [31[31] R. Lent, Cem bilhões de Neurônios? Conceitos Fundamentais de Neurociências (Atheneu, São Paulo, 2010).–33[33] M.F. Bear, B.W. Connors e M.A. Paradiso, Neurociências: Desvendando o Sistema Nervoso (Artmed, Porto Alegre, 2008).] é possível conhecer mais a fundo sobre as células neuronais em geral e suas especificidades.
-
8
Esse processo é chamado despolarização da membrana.
-
9
A queda do pico até o limiar é conhecida como repolarização.
-
10
Período em que o potencial permanece abaixo do potencial de repouso é chamado hiperpolarização.
-
11
Professor Wulfram Gerstner é diretor do Laboratótio de Neurociência Computacional (LCN) na Escola Politécnica Federal de Lausana na Suíça.
-
12
É possível verificar mais a fundo a questão dos potenciais nas Refs. [31[31] R. Lent, Cem bilhões de Neurônios? Conceitos Fundamentais de Neurociências (Atheneu, São Paulo, 2010).–33[33] M.F. Bear, B.W. Connors e M.A. Paradiso, Neurociências: Desvendando o Sistema Nervoso (Artmed, Porto Alegre, 2008).].
-
13
Também chamado de impulso nervoso [32[32] E. Okuno, I.L. Caldas e C. Chow, Física para Ciências Biológicas e Biomédicas (HARBRA, São Paulo, 1986).].
-
14
O relógio pendular de Christian Huygens está exposto juntamente com uma cópia do livro “Horologium Oscillatorium sive de motu pendulorum” no museu Boerhaave na Holanda.
Referências
-
[1]World Health Organization, Neurological Disorders: Public Health Challenges (Who Press, Geneva, 2013).
-
[2]A. Hodgkin and, A.F. Huxley, Journal Physiology 117, 500 (1952).
-
[3]E.M. Izhikevich, Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting (MIT Press, Cambridge, 2007).
-
[4]D. Purves, G.J. Augustine, D. Fitzpatric, W.C. Hall, A. Lamantia, J.O. MacNamara and S.M. Willians, Neuroscience - A Novelty for the Nervous: Neuroscience (MA Sinauer Associates, Sunderland, 1997).
-
[5]A. Pikovsky, M.G. Rosenblum and J. Kurths, Synchronization: A Universal Concept in Nonlinear Sciences (Cambridge University Press, Cambridge, 2001).
-
[6]I.-H. Lin, R.-K. Wu and C.-M. Chen, Physical Review E 84, 051923 (2011).
-
[7]A. Pikovsky and M.G. Rosenblum, Contemporary Physics 44, 401 (2003).
-
[8]R.E. Mirollo and S.H. Strogatz, SIAM Journal on Applied Mathematics 50, 1645 (1990).
-
[9]K. Abuhassan, D. Coyle and L. Maguire, Frontiers in Computational Neuroscience 8, 65 (2014).
-
[10]J. Modolo, B. Bhattacharya, R. Edwards, J. Campagnaud, A. Legros and A Beuter, Frontiers in Neuroscience: Neuroprosthetics 4, 45 (2010).
-
[11]C. Hammond, H. Bergman and P. Brown, Trends in Neurosciences 30, 357 (2007).
-
[12]P. Uhlaas and W. Singer, Neuron 52, 155 (2006).
-
[13]D.O. Hebb, The Organization of Behavior (Wiley, New York, 1949).
-
[14]T.V.P. Bliss and G.L. Collingridge Nature, 361, 31 (1993).
-
[15]T.V.P. Bliss and A.R. Gardner-Medwin, Journal Physiology 232, 357 (1973).
-
[16]G.Q. Bi and M.M. Poo, The Journal of Neuroscience 18, 10464 (1998).
-
[17]H. Schildt, C: The Complete Reference (McGraw-Hill Osborne Media, California, 2000).
-
[18]L.F. Abbott, Brain Research Bulletin 50, 303 (1999).
-
[19]K. Christof and I. Segev, Methods in Neuronal Modeling (MIT Press, Cambridge, 1998).
-
[20]S. Ostojic and N. Brunel, The Journal of Neuroscience 29, 10234 (2009).
-
[21]E.M. Izhikevich, N.S. Desai, E.C. Walcott and F.C. Hoppensteadt, Trends in Neuroscience 26, 161 (2003).
-
[22]E.M. Izhikevich, IEEE Trans. Neural Networks 14, 1569 (2003).
-
[23]R. Fitzhugh, Biophysics Journal 1, 445 (1961).
-
[24]J.L. Hindmarsh and R.M. Rose, Nature 296, 162 (1982).
-
[25]C. Morris and H. Lecar, Biophysical Journal v. 35, 193 (1981).
-
[26]H.R. Wilson, Journal Theoretical Biology 200, 375 (1999).
-
[27]M.Y. Choi, Physical Review Letters 86, 134101–1 (2004).
-
[28]K. Kaneko, Physica D 54, 5 (1991).
-
[29]V.O. Popovych, S. Yanchuk and P.A. Tass, Scientific Reports 3, 2926 (2013).
-
[30]V.P. Zhigulin, M.I. Rabinovich, R. Huerta and H.D. Abarbanel, Physical Review E 67, 021901 (2003).
-
[31]R. Lent, Cem bilhões de Neurônios? Conceitos Fundamentais de Neurociências (Atheneu, São Paulo, 2010).
-
[32]E. Okuno, I.L. Caldas e C. Chow, Física para Ciências Biológicas e Biomédicas (HARBRA, São Paulo, 1986).
-
[33]M.F. Bear, B.W. Connors e M.A. Paradiso, Neurociências: Desvendando o Sistema Nervoso (Artmed, Porto Alegre, 2008).
-
[34]E.G. Gray, Nature 6, 1592 (1959).
-
[35]J.H. Byrne, Fundamental Neuroscience (Academic Press, New York, 2008)
-
[36]H. Markram, W. Gerstner and P.J. Sjöström, Frontiers in Synaptic Neuroscience 4, 8 (2012).
-
[37]H. Markram, W. Gerstner and P.J. Sjöström, Frontiers in Synaptic Neuroscience 3, 10 (2011).
-
[38]W. Gerstner, Frontiers in Synaptic Neuroscience 2, 50 (2010).
-
[39]W. Gerstner and W. Kisler, Spiking Neuron Models(Cambridge University Press, New York, 2008).
-
[40]L.H.A. Monteiro, Sistemas Dinâmicos (Editora Livraria da Física, São Paulo, 2006).
-
[41]D. di Bernardo, M.G. Signorini and S. Cerutti, International Journal Bifurcation and Chaos 9, 1975 (1998).
-
[42]J. Buck and E. Buck, Scientific American 234, 74 (1976).
-
[43]K.T. Alligood, T.D. Sauer and J.A. Yorke, Chaos: An Introduction to Dynamical Systems(Springer-Verlag, New York, 1996).
-
[44]A.K. Engel, P. König, A.K. Kreiter, T.B. Schillen and W. Singer, Trends in Neurosciences 15, 218 (1992).
-
[45]Y. Kuramoto, International Symposium on Mathematical Problems in Theoretical Physics (Springer-Verlag, New York, 1975).
-
[46]Y. Kuramoto, Chemical Oscillations, Waves, and Turbulence (Springer-Verlag, New York, 1984).
Datas de Publicação
-
Publicação nesta coleção
Jun 2015
Histórico
-
Recebido
09 Jan 2015 -
Aceito
09 Mar 2015