text new page (beta)
Portuguese (pdf)
Article in xml format
Curriculum ScienTI
Automatic translation
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. Introdução
Thomas Young (1773-1829) é comumente celebrado como o iniciador de uma retomada da teoria ondulatória para a luz no início do Século XIX. Seu conceito de luz como ondas e, principalmente, seu princípio de interferência ilustrado pelo famoso experimento da fenda dupla teriam despertado o interesse pela teoria ondulatória adormecido no século anterior, completamente dominado pela concepção corpuscular da luz de Isaac Newton (1642-1727). O resultado foi o completo abandono desta última e o ressurgimento da primeira, alavancado pelo viés matemático dado por Augustin Fresnel (1788-1827).
O objetivo deste trabalho é problematizar esse episódio, a partir da tradução comentada do artigo Teoria Sobre Luz e Cores de Young, lido em 1801 na Royal Society de Londres e publicado em 1802 nas Philosophical Transactions. O artigo apresentou, pela primeira vez, uma exposição detalhada do pensamento de Young sobre luz e cores, além de uma versão inicial de seu princípio de interferência.2 A tradução comentada busca esclarecer questões relevantes para compreendermos a importância do trabalho de Young no contexto da época em que foi escrito, bem como as estratégias adotadas por ele para incentivar a leitura do artigo por seus coetâneos.
Os trabalhos sobre luz representaram apenas uma parcela de toda a atividade de Young na filosofia natural. Formado médico em 1799, ele foi autodidata em várias áreas - como história natural e cálculo - e lia em latim, grego, francês e italiano. Aos 21 anos, foi eleito membro da Royal Society de Londres, o que facilitou sua indicação como conferencista na Royal Institution, por onde teve uma breve passagem entre 1802 e 1803. Nunca ocupou um cargo em uma universidade. De 1810 até sua morte em 1829, ele teve passagens por outras instituições, ou como médico ou como conferencista, e também foi autor anônimo de diversos artigos biográficos e de textos sobre óptica, mecânica e artes mecânicas para revistas da época [2].
O período que concentra os escritos de Young sobre luz e cores compreende os anos de 1800 e 1807 [1,3–9]. O interesse no tema provavelmente foi despertado após seus estudos sobre a voz e a visão humanas, que o levou a repensar na analogia entre luz e som, um dos pilares sempre utilizados pelos defensores de uma teoria vibracional ou ondulatória para a luz [10]. O primeiro artigo em que mencionou a natureza da luz foi lido em janeiro de 1800 na Royal Society de Londres e publicado logo em seguida [3]. O texto tratou essencialmente do som, mas uma parte foi dedicada à analogia entre os fenômenos luminosos e sonoros. Fazendo referência a teóricos favoráveis à concepção vibracional antes dele, tais como Christiaan Huygens (1629-1695) e Leonhard Euler (1707-1783), Young afirmou que algumas considerações poderiam ser feitas no sentido de minimizar as críticas à ideia da luz como vibrações no éter, além de dizer que havia dificuldades na teoria corpuscular proposta por Isaac Newton (1642-1727) que tinham chamado pouca atenção. Os aspectos essenciais desses argumentos foram retomados no artigo de 1802 e, por isso, serão analisados ao longo da tradução comentada.
Por sua vez, alguns pontos mais gerais do artigo de 1800 revelam características importantes do trabalho de Young e da época em que começou a discutir a natureza da luz. Logo no início do texto, ele mencionou a grande influência da teoria corpuscular newtoniana ao longo do Século XVIII:
Desde a publicação dos escritos incomparáveis de Sir Isaac Newton, suas doutrinas de emanação de partículas de luz a partir de substâncias lúcidas e da pré-existência formal de raios coloridos na luz branca têm sido quase universalmente aceitas neste país, e pouco combatida em outros. [11]
A afirmação de Young é verdadeira, mas enviesada pelo próprio contexto em que foi escrita. A concepção corpuscular para a luz, defendida implicitamente por Newton, foi amplamente difundida no Século XVIII, angariando adeptos não somente na Grã-Bretanha, mas em outros países do continente europeu. No entanto, ela também foi alvo de críticas e enfrentou sérios problemas conceituais, principalmente a partir da metade desse século [12–15]. Embora as críticas tenham diminuído sua invencibilidade, ela era aceita pela maioria dos filósofos naturais no início do Século XIX. Young reconheceu que esse era o contexto em que escrevia seu trabalho.
Dois outros pontos de destaque no artigo de 1800 são sua hipótese de que corpos mais densos atraem mais éter e sua explicação para os anéis coloridos visíveis em bolhas de sabão e em filmes finos de ar. Em relação à primeira, ele a manteve no artigo de 1802 e em outros textos da mesma época, mas a rejeitou nos anos seguintes. Em relação à segunda, ele argumentou que o aparecimento sucessivo de cores de acordo com a espessura da película seria semelhante à produção de diferentes sons em tubos de órgão, o que evidenciava a analogia entre luz e som. No artigo de 1802 e nos trabalhos seguintes, Young trocou essa explicação pelo seu princípio de interferência. Denota-se, assim, uma peculiaridade dos escritos de Young sobre a luz neste período inicial: a mudança frequente de ideias e conceitos. De acordo com o historiador da ciência Geoffrey Cantor, vemos neste momento não o nascimento de uma teoria completa ou um renascimento infalível da concepção ondulatória, mas “vislumbres de um cientista em atividade lutando com um número de problemas espinhosos” [16].
O artigo Teoria Sobre Luz e Cores de 1802 representou um significativo avanço se comparado com o texto de 1800. De forma mais completa, Young tratou especificamente da luz, buscando construir uma argumentação que estivesse respaldada no discurso de figuras conhecidas da filosofia natural - novamente citando nomes como Euler e Newton - e ao mesmo tempo amparada em hipóteses plausíveis sobre a natureza da luz e em proposições derivadas delas.
Young sabia que não era o primeiro a advogar favoravelmente a uma concepção ondulatória para a luz. Huygens3 e Euler, por exemplo, já haviam trabalhado nesta hipótese há mais de cem e cinquenta anos, respectivamente. Não foram os únicos, deve-se ressaltar, embora os dois sejam frequentemente mencionados como heróis isolados em meio a dezenas de defensores do sistema corpuscular de Newton.4
A Teoria Sobre Luz e Cores é composta de quatro hipóteses iniciais e nove proposições. Young reconheceu que não proporia opiniões “absolutamente novas”. Da mesma forma, não viu a necessidade de realizar “um único experimento novo”, pois já existiam muitos para serem estudados. Seu trabalho, portanto, constituiu-se mais de uma releitura teórica de fatos, experimentos e ideias que propriamente da discussão de uma prova crucial a favor da teoria ondulatória. Dois elementos principais permeiam e dividem o texto. O primeiro é seu conceito de éter, compondo parte da argumentação em mais de dois terços do artigo. O segundo, discutido no final, é o princípio da interferência. Diferenciar estes dois elementos e compreendê-los como duas facetas independentes do trabalho de Young é importante para redimensionarmos seu papel no resgate da teoria ondulatória da luz [18].
Até a Teoria Sobre Luz e Cores, Young vinha trabalhando com um modelo de éter que presumia ser constituído de partículas que se repeliam, mas que eram atraídas pela matéria dos corpos. Por conseguinte, corpos mais densos possuíam mais éter. No limiar entre dois corpos de densidades diferentes, não haveria, segundo ele, uma mudança abrupta de densidade de éter; pelo contrário, haveria uma transição gradual, ficando o corpo mais denso rodeado de uma atmosfera etérea [19].
O modelo de éter foi aplicado por Young de maneira sutil ao longo do texto, preenchendo o conteúdo das proposições e dos corolários advindos delas. Um indício de sua validade seria o fenômeno da reflexão e refração parciais quando um raio de luz passa por dois meios de densidades diferentes. Young fez uma analogia com o choque de dois corpos: quando um corpo pequeno se choca com um corpo grande, ele é refletido e parte de seu movimento é transmitido para este último; isso explicaria o fenômeno da reflexão e refração parciais quando uma ondulação luminosa passa de um meio mais rarefeito (com menos éter) para um mais denso (com mais éter).
Por sua vez, quando um corpo grande se choca com um corpo pequeno, algo similar ocorre, pois o corpo grande transfere uma parte de seu movimento, mas continua seu caminho; isso explicaria a reflexão e refração parciais quando uma ondulação luminosa passa de um meio mais denso de éter para um mais rarefeito. Neste último caso, a permanência do éter no meio mais denso seria justificada pela atração deste último pelo corpo, que puxaria as partículas etéreas de volta. Não haveria, assim, um deslocamento de éter. Entretanto, Young não deixou claro como o “tamanho” dos corpos no caso do choque mecânico seria análogo à “densidade” do éter no caso dos fenômenos luminosos. Por essa e por outras inconsistências relacionadas ao seu modelo que serão apontadas na tradução, Young acabou por abandoná-lo a partir de 1803 e aceitou que o éter passava livremente pelos corpos, sem sofrer qualquer tipo de atração [20].
O princípio da interferência, enunciado na Proposição VIII do texto, desempenhou um papel distinto. O princípio - que depois se tornaria uma lei para Young - praticamente era um conceito à parte de sua teoria ondulatória. Embora houvesse uma nítida conexão, Young pareceu ver na interferência um conhecimento novo, que explicava adequadamente o comportamento da luz em determinadas situações. Mais que defender a teoria ondulatória, ele aparentemente quis estabelecer a validade de sua lei, independente de qual fosse a concepção para a luz [21, 22].
No artigo de 1800, Young mencionou o princípio da interferência, mas o associou somente aos efeitos sonoros. Apenas em 1802, em suas Notas de Aula [6], ele aplicou a ideia também para os fenômenos da luz. No artigo do mesmo ano, traduzido aqui, ele colocou explicitamente, pela primeira vez, o princípio como um elemento importante de sua teoria sobre luz e cores. No entanto, a formulação inicial do princípio foi alterada significativamente ao longo dos anos. De forma geral, Young frequentemente lidou com problemas para explicar pontos importantes, gerando várias ambiguidades em suas explicações que usavam o princípio [23].
Com o possível intuito de dar credibilidade aos seus argumentos, Young apoiou-se frequentemente nos escritos de Newton, justamente o mais conhecido algoz da teoria ondulatória. Porém, ele foi hábil em utilizar as citações dos textos newtonianos a benefício próprio, valendo-se principalmente das partes do Óptica (1704) que foram ignoradas pelos seus seguidores do Século XVIII. Newton e Young não compartilhavam das mesmas posturas metodológicas em relação aos fenômenos naturais. O primeiro jamais admitiria o uso de hipóteses em sua filosofia natural. O segundo, contudo, não só admitiu as hipóteses, considerando-as elementos essenciais para corroborar seu raciocínio, como colocou as palavras de Newton para compor seus conteúdos. Por trás disso, havia um debate metodológico que envolveu, entre outros aspectos, o uso ou a negação das hipóteses. O debate emergiu entre o final do Século XVIII e início do Século XIX, e não só Young fez parte, como também outros defensores e objetores da teoria ondulatória para a luz [24].
A Teoria Sobre Luz e Cores tornou-se conhecida dos filósofos naturais, o que era de se esperar, uma vez que havia sido publicada em um dos jornais mais importantes da época, as Philosophical Transactions, e, pouco depois, republicada no Nicholson's Journal.5 Não é possível precisar como foi a recepção do trabalho, mas sabe-se que este e outros textos seus foram citados e revisados nas duas décadas seguintes, o que incluiu algumas críticas tanto à estrutura conceitual da teoria de Young quanto ao seu constante emprego de hipóteses. Em relação ao princípio da interferência, este parece ter passado desapercebido por pelo menos dez anos [25]. Nesse sentido, parece-nos mais adequado afirmar que a Teoria Sobre Luz e Cores não foi ignorada completamente, tampouco vangloriada sem restrições.
Entre as críticas recebidas, a mais incisiva certamente foi escrita por Henry Brougham (1778-1868) no Edinburgh Review em 1803 [26].6 Brougham foi um assíduo defensor de Newton e da teoria corpuscular da luz no circuito escocês, pertencendo a uma escola metodológica que combatia o uso de hipóteses na filosofia natural. Há discordância entre os historiadores da ciência a respeito das motivações de Brougham e da relevância de sua crítica para a rejeição das ideias de Young, mas o sentimento geral é que ela deixou claro que o embate entre a teoria corpuscular e a ondulatória foi além do campo das ideias, perpassando igualmente o campo metodológico [29, 30].
Na revisão, Brougham afirmou que o trabalho de Young estava “destituído de toda espécie de mérito”. Criticou a Royal Society por dar espaço a trabalhos que perigosamente afrontavam os “princípios da lógica física” e reprovou as mudanças frequentes de opinião por parte de Young, afirmando que se ele fosse criticado diria: “Minha opinião está mudada, e eu abandonei aquela hipótese; mas aqui está outra para você”. Menosprezou as citações a Newton, alegando que elas provinham quase inteiramente de uma parte especulativa do Óptica e que elas seriam “meras hipóteses”. Por fim, ridicularizou Young por se referir de forma recorrente a trabalhos próprios, alguns não publicados, o que seria “peculiar aos que lidam com hipóteses” [31].
Young escreveu uma resposta às críticas de Brougham meses depois, mais caracterizada como uma defesa pessoal que uma contestação do ponto de vista científico [32]. Ele afirmou que as críticas foram um ataque “não somente a meus escritos e meus propósitos literários, mas praticamente a meu caráter moral”. A resposta, publicada originalmente como um panfleto, parece não ter impressionado, pois de acordo com o editor dos trabalhos completos de Young, George Peacock (1791-1858), o autor disse que “apenas uma cópia foi vendida; consequentemente não produziu efeito em vindicar sua carreira científica” [33]. Os aspectos dessa contenda ilustram que a percepção leiga de que a teoria ondulatória de Young, apesar dos problemas, foi bem recebida e aceita pelos filósofos naturais da época não tem respaldo histórico.
No contexto do ensino de física e de ciências, o estudo da Teoria Sobre Luz e Cores de Young tem importância não somente para ensinar conceitos da teoria ondulatória. Na realidade, não se deve tomar o artigo como uma referência para o ensino de ondas. Embora conceitos essenciais que ainda hoje utilizamos estão presentes no texto de Young, de forma geral, boa parte de seu conteúdo é obsoleta, por exemplo, suas ideias acerca do éter. Nesse caminho, é preciso muito discernimento dos educadores, a fim de usufruir adequadamente do conteúdo relacionado propriamente à física.
Acreditamos no potencial da Teoria Sobre Luz e Cores para trabalhar questões de natureza da ciência [34], especialmente as relacionadas com a construção, aceitação e rejeição do conhecimento científico. A elaboração do conceito de atmosferas etéreas de Young mostra como as ideias científicas podem representar, em um primeiro momento, uma base estável para o desenvolvimento de explicações para os fenômenos, mas, em um segundo, uma estrutura frágil e implausível à medida que elas não sustentam mais a argumentação. O modo como Young trabalhou essa ideia e sua implícita cautela ao abordá-la, afirmando que ele não a considerava fundamental, mas parecia “ser a mais simples e a melhor dentre qualquer uma” que já tivera imaginado, denotam que ele aventou possibilidades e lidou com a dúvida a todo instante.
Por outra perspectiva, seu princípio da interferência ainda estava em fase inicial e seria aprimorado em trabalhos posteriores. A discussão apresentada na Teoria Sobre Luz e Cores revela um Young deparando-se com um conhecimento que havia começado a chamar sua atenção e que posteriormente se tornaria o ponto central de sua defesa à teoria ondulatória da luz. Sendo assim, o princípio da interferência não foi enunciado em sua forma final nos primeiros estudos de Young sobre a natureza da luz. Essa circunstância demonstra que as ideias científicas não se desenvolvem repentinamente, mas são fruto de um processo de amadurecimento e crescimento intelectual dos cientistas, que passo a passo vão aparando as bordas, no intuito de conferir a elas maior fundamentação teórica e experimental.
As críticas que Young recebeu pelo seu trabalho, especialmente aquelas proferidas por Brougham, são um exemplo de como a aceitação de uma teoria envolve não somente o fato de ela ser boa ou ruim. O entendimento de que a Teoria Sobre Luz e Cores, assim como outros trabalhos do autor, representou a vitória da concepção ondulatória sobre a corpuscular é uma visão posterior a Young, difundida após o fim da disputa entre as duas na metade do Século XIX [35]. Torna-se muito conveniente, assim, dizer que Young abriu totalmente as portas para que a óptica de Newton fosse largamente rejeitada, quando sabemos o final da história.7 Trata-se de uma interpretação Whig8 de um evento complexo e repleto de particularidades.
Young enfrentou críticas tanto pelos conceitos quanto pela metodologia adotada na Teoria Sobre Luz e Cores. Como apontamos anteriormente, a mudança frequente de ideias fez parte de seu trabalho nesse período e isso não foi ignorado pelos seus coetâneos. O contexto em que Young escreveu também contribuiu para que suas ideias fossem rejeitadas, a princípio. A conjuntura da Grã-Bretanha do período depunha a favor de Newton e da teoria corpuscular, mesmo com todas as dificuldades e lacunas que possuía. Young não foi o primeiro a defender a teoria ondulatória, nem o primeiro a ser repreendido por isso. Não podemos correr o risco, todavia, de apontar heróis ou vilões. Young ofereceu um primeiro resgate à teoria ondulatória, sobretudo com seu princípio de interferência, mas a sua completa aceitação prolongou-se por mais algumas décadas, ganhando ainda a valiosa contribuição de Fresnel.9 Compreender adequadamente esse episódio envolve aprender que o processo de construção do conhecimento científico é como uma teia, multidirecional e influenciado por um grande número de aspectos, científicos e extracientíficos.
A Teoria Sobre Luz e Cores de Young ajuda a retratar as características de um período importante para a história da óptica e da luz. A tradução comentada que apresentamos neste artigo busca enaltecer as singularidades do trabalho, principalmente no sentido de redimensionar o papel de Young para o desenvolvimento ulterior da teoria ondulatória. O resgate à concepção de luz como ondulações em um meio etéreo trazido por ele foi inicial, mas não menos significativo e relevante para exemplificar a natureza do conhecimento científico sobre a luz.
2. Tradução comentada da Teoria Sobre Luz e Cores de Young
Apresentamos a seguir a tradução integral e comentada do artigo Teoria Sobre Luz e Cores. Buscamos manter a estrutura original do texto, fazendo modificações apenas quando julgamos necessário para facilitar o entendimento do leitor. Da mesma forma, as palavras foram traduzidas de maneira a preservar ao máximo a correspondência com os originais em inglês.
Como mencionamos anteriormente, Young citou vários autores ao longo da “Teoria”. No caso dos trechos de referências que estão disponíveis em português, preferimos não traduzi-los novamente, mas citá-los a partir da versão brasileira. As páginas citadas por Young foram trocadas pelas páginas das edições em português, sendo acompanhadas pelo símbolo (P).
2.1. Tradução
[p. 12]10Conferência Bakeriana.11Sobre a Teoria de Luz e Cores. Por Thomas Young, M.D.12F.R.S.13Professor de Filosofia Natural na Royal Institution14
Lida em 12 de Novembro, 1801
Embora a invenção de hipóteses plausíveis, independentemente de qualquer conexão com observações experimentais, seja de pouco uso para a promoção do conhecimento natural, ainda sim, a descoberta de princípios simples e uniformes, pelos quais um grande número de fenômenos aparentemente heterogêneos são reduzidos a leis universais e coerentes, deve ser sempre admitida como de considerável importância para o aperfeiçoamento do intelecto humano.
O objeto da presente dissertação não é tanto propor quaisquer opiniões que sejam absolutamente novas ou mencionar algumas teorias que já tenham avançado em relação a seus inventores originais, a fim de apoiá-las com evidências adicionais e aplicá-las a um grande número de fatos diversificados, os quais têm permanecido na obscuridade. Tampouco é absolutamente necessário produzir neste instante um único novo experimento, pois de experimentos já temos um amplo estoque, dentre os quais estão os mais excepcionais, uma vez que eles devem ter sido conduzidos com a menor parcialidade para com o sistema pelo qual eles serão explicados. Contudo, alguns fatos ainda não observados serão trazidos à tona, de modo a mostrar a concordância perfeita daquele sistema15 com os variados fenômenos da natureza.16
[p. 13] As observações em óptica de Newton ainda são imbatíveis; e, exceto por algumas imprecisões pontuais, elas só elevam nossa estima, à medida que as comparamos com as últimas tentativas de melhorá-las.17 Uma consideração adicional acerca das cores em filmes finos, do modo como elas são descritas no segundo livro da óptica de Newton,18 transformou aquela pressuposição que eu antes cogitei sobre o sistema ondulatório da luz em uma forte convicção de sua verdade e suficiência. Uma convicção que tem sido desde então confirmada de forma contundente pela análise das cores em substâncias estriadas. Os fenômenos dos filmes finos são, por sua vez, tão singulares, que suas complexidades gerais não são sem grande dificuldade conciliáveis com qualquer teoria que foi então aplicada a eles, por mais complicada [que seja].19 Algumas de suas principais circunstâncias nunca foram explicadas pelos mais infundados argumentos; mas ficará claro que as mínimas particularidades destes fenômenos são não somente perfeitamente consistentes com a teoria que será agora detalhada, mas que elas são todas consequências necessárias desta teoria, sem quaisquer suposições adicionais; e isso [será feito] por inferências tão simples, que elas se tornarão corolários particulares, os quais raramente necessitarão de uma enumeração própria.
Um exame mais extensivo dos vários escritos de Newton tem me mostrado que ele foi de fato o primeiro a sugerir uma teoria tal qual a que eu vou me empenhar a sustentar;20 que suas opiniões diferem menos desta teoria [ao contrário do] que é agora quase universalmente suposto; e que uma variedade de argumentos tem sido elaborada, como se [quisessem] refutá-lo, podendo ser encontrada de maneira quase similar a partir de seus próprios trabalhos; e isto por ninguém menos que um matemático como Leonard Euler, cujo sistema de luz, até onde sei, tanto foi ou pode ter sido, [p. 14] totalmente emprestado de Newton, Hooke, Huygens e Malebranche.
Aqueles que estão atrelados, como eles podem estar, com a maior justiça, a toda doutrina estampada com a aprovação Newtoniana, provavelmente estarão dispostos a conceder muito mais de suas atenções a estas considerações, à medida que elas coincidirem mais proximamente com as opiniões do próprio Newton. Por esta razão, depois de discutir brevemente cada assunto particular da minha teoria, eu citarei, a partir dos vários escritos de Newton, trechos que parecem ser mais favoráveis à sua aceitação. Embora eu deva citar alguns trabalhos que podem ser pensados como tendo sido parcialmente ultrapassados pela publicação de seu Óptica, mesmo assim eu não devo mencionar nada deles que possa ir contra seu julgamento mais maduro.21
2.1.1. Hipótese I
Um Éter luminífero permeia o Universo, altamente rarefeito e elástico
Passagens de Newton22
“A hipótese certamente tem muito mais afinidade com a sua própria hipótese”, isto é, a do Dr. Hooke, “que ele parece estar ciente; as vibrações no éter sendo tão úteis e necessárias nessa [minha hipótese], quanto na dele”. Carta de Newton a Hooke23 [59].
“Mas, passemos à Hipótese; em primeiro lugar, por ela é de supor que existe um meio etéreo, exatamente com a mesma constituição do ar, porém muito mais ralo, mais sutil e mais fortemente elástico. - Mas não se deve supor que esse meio seja uma matéria uniforme, sendo antes composto, em parte, do corpo fleumático principal do éter e, em parte, de outros diversos espíritos etéreos, [p. 15] assim como o ar se compõe do corpo fleumático do ar, misturado com vários vapores e exalações. Os eflúvios elétricos e magnético e o princípio da gravitação parecem defender tal variedade”. A hipótese da luz (P)24 [61].
“Não é o calor do quarto quente transmitido através do vácuo pelas vibrações de um meio muito mais sutil que o ar […]? E não é esse o meio que aquele pelo qual a luz é refratada e refletida e por cujas vibrações a luz comunica calor aos corpos e é colocada em estados de fácil reflexão e fácil transmissão? E não contribuem as vibrações desse meio em corpos quentes para a intensidade e duração de seu calor? E os corpos quentes não comunicam seu calor aos corpos frios contíguos pelas vibrações desse meio propagadas deles para os corpos frios? E não é esse meio extremamente mais rarefeito e sutil do que o ar e extremamente mais elástico e ativo? E não penetra ele prontamente em todos os corpos? E não é ele (por sua força elástica) expandido por todo o firmamento?” Questão 18, Óptica (P) [63].
“Não podem os planetas e os cometas, e todos os grandes corpos, executar seus movimentos […] nesse meio etéreo […]? E não pode a sua resistência ser tão pequena a ponto de ser insignificante? Por exemplo: se esse éter (pois assim lhe chamarei) fosse 700 mil vezes mais elástico do que o nosso ar, e mais de 700 mil vezes mais rarefeito, sua resistência seria mais de 600 milhões de vezes menor do que a da água. E uma resistência tão pequena dificilmente causaria qualquer alteração perceptível nos movimentos dos planetas durante 10 mil anos. Se alguém me perguntasse como pode um meio ser tão rarefeito, eu perguntaria […] como um corpo elétrico pode emitir por fricção uma exalação tão rarefeita e sutil, e, todavia, tão potente […]? E como [p. 16] podem os eflúvios de um imã ser tão rarefeitos e sutis a ponto de atravessar uma lâmina de vidro sem nenhuma resistência […], a ponto de girar uma agulha magnética para além do vidro?” Questão 22, Óptica (P) [64].
2.1.2. Hipótese II
Ondulações são excitadas neste Éter assim que o Corpo torna-se luminoso
Escólio
Eu uso a palavra ondulação, ao invés de vibração, porque vibração é geralmente entendida como implicando um movimento que é alternadamente continuado para trás e para frente, por uma combinação do movimento do corpo com uma força aceleradora, e que é naturalmente mais ou menos permanente. Mas uma ondulação é suposta como consistindo de um movimento vibratório, transmitido sucessivamente através de diferentes partes de um meio, sem qualquer tendência em cada partícula de continuar seu movimento, exceto em consequência da transmissão de ondulações sucessivas partindo de um determinado corpo em vibração; assim como as vibrações de uma corda no ar produzem ondulações que formam o som.25
Passagens de Newton
“Fosse eu presumir uma hipótese, ela seria esta, se proposta em termos mais gerais de modo a não determinar o que é a luz além de [dizer] que ela é uma ou outra coisa capaz de provocar vibrações no éter, pois, desse modo, ela se tornará tão geral e abrangente de outras hipóteses, que deixará pouco espaço para que outras sejam inventadas.”26A hipótese da luz (P) [65].
“Em segundo lugar, é de se supor que o éter seja um meio vibratório como o ar, só que com vibrações muito mais velozes e diminutas; as do ar são feitas pela voz comum de um homem, sucedendo-se umas às outras a uma distância de mais de meio pé ou de um pé [p. 17], enquanto as do éter são feitas a uma distância menor do que a centésima milésima parte de uma polegada. E assim como no ar algumas vibrações são maiores do que outras, mas todas igualmente velozes (pois, num círculo de sinos, o som de cada tom é ouvido a duas ou três milhas de distância, na mesma ordem em que os sinos são tocados), suponho também que as vibrações etéreas difiram em tamanho, mas não em velocidade. Ora, podemos supor que essas vibrações, além de seu uso na reflexão e na refração, sejam os meios principais pelos quais as partes das substâncias em fermentação ou em putrefação, os líquidos fluidos, ou os corpos incandescentes derretidos, ou outros corpos quentes, continuam em movimento […].” A hipótese da luz (P) [67].
“[…] quando um raio de luz incide sobre a superfície de qualquer corpo transparente, e ali é refratado ou refletido, não podem as ondas de vibrações, ou tremores, ser excitadas no meio refrator ou refletor […]? E essas vibrações não se propagam a grandes distâncias a partir do ponto de incidência? E elas não ultrapassam os raios de luz, e, ao ultrapassá-los sucessivamente, não os colocam nos estados de fácil reflexão e fácil transmissão acima descritos?” Questão 17, Óptica (P) [68].27
“[…] a luz se acha em estados de fácil reflexão e fácil transmissão antes de incidir sobre os corpos transparentes. E provavelmente ela assume esses estados na sua primeira emissão dos corpos luminosos e continua neles durante toda sua trajetória.”28Proposição 13, Livro II, Óptica (P) [69]. [p. 18]
2.1.3. Hipótese III
A Sensação de diferentes Cores depende da diferente frequência de Vibrações, excitadas pela Luz na Retina.29
Passagens de Newton
“A hipótese do objetor, assim como a parte fundamental dela, não é contra mim. A suposição fundamental diz que as partes dos corpos, quando vivamente agitadas, excitam vibrações no éter, que são propagadas em linha reta em todas as direções a partir destes corpos e causam a sensação de luz ao baterem e se chocarem contra o fundo do olho, da mesma maneira que as vibrações no ar causam a sensação de som por se chocarem contra os órgãos da audição. Ora, eu considero esta a aplicação mais livre e natural desta hipótese para a solução do fenômeno: que as partes agitadas dos corpos, de acordo com seus diversos tamanhos, formas e movimentos, excitam vibrações de várias grandezas e tamanhos no éter, as quais, sendo propagadas confusamente através daquele meio até nossos olhos, causam em nós a sensação de luz branca. Mas, se por qualquer motivo aquelas [vibrações] de diferentes grandezas sejam separadas uma da outra, a maior gerando uma sensação de cor vermelha e a menor ou mais curta a sensação de violeta intenso, e as [vibrações] intermediárias [gerando a sensação] de cores intermediárias de maneira muito semelhante daquela que os corpos, de acordo com seus vários tamanhos, formas e movimentos, excitam vibrações de diversas grandezas, as quais, de acordo com estas, causam vários tons no som, as maiores vibrações são mais capazes de superar a resistência das superfícies refratoras e então atravessar com a menor refração. Por isso as vibrações [p. 19] de vários tamanhos, isto é, os raios de várias cores que estão misturados na luz, devem ser separados uns dos outros pela refração e então causar o fenômeno dos prismas e de outras substâncias refratoras. E disto também depende da espessura de um filme fino ou bolha, quer uma vibração seja refletida em suas superfícies seguintes ou transmitida; de tal modo que, de acordo com o número de vibrações intercedendo as duas superfícies [do filme ou da bolha], eles [os raios de luz] podem ser refletidos ou transmitidos por muitas espessuras sucessivas. E, uma vez que as vibrações que originam o azul e o violeta são supostas como mais curtas que aquelas que originam o vermelho e o amarelo, elas devem ser refletidas em uma espessura menor do filme, o que é suficiente para explicar todos os fenômenos ordinários daqueles filmes ou bolhas e também dos corpos naturais, cujas partes são parecidas com muitos fragmentos daqueles filmes. Estas parecem ser as condições mais evidentes, genuínas e necessárias desta hipótese. E elas concordam tão precisamente com minha teoria, que se o crítico acha oportuno aplicá-las, ele não precisará divorciar-se dela nesta abordagem. Porém, como ele vai defendê-la de outras dificuldades, eu não sei.”30Carta de Newton a Hooke [73].
“E agora, passemos à explicação das cores; presumo que, assim como os corpos de diversos tamanhos, densidades ou tensões, através da percussão ou de outras ações, provocam sons de tons variáveis e, consequentemente, vibrações de várias grandezas no ar, também quando os raios de luz, ao incidirem sobre as superfícies refratoras duras, provocam vibrações no éter […] de diversas grandezas; os raios maiores, mais fortes ou mais potentes [provocam] as maiores vibrações, e os outros, vibrações mais curtas, conforme seu tamanho, intensidade ou potência. E então, posto que as extremidades dos capillamenta do nervo óptico que pavimentam [p. 20] ou recobrem a retina são superfícies refratoras desse tipo, os raios, ao incidirem sobre elas, devem excitar essas vibrações, as quais (como as do som num tubo ou numa trombeta) percorrem os poros aquosos ou a medula cristalina dos capillamenta através dos nervos ópticos, até chegarem ao sensório31 […], e ali, suponho eu, afetam o sentido com várias cores, conforme sua grandeza e mistura: as maiores com as cores mais fortes, os vermelhos e os amarelos; as menores, com as mais fracas, os azuis e os violetas; as intermediárias, com o verde; e a mistura de todas, com o branco, exatamente da mesma maneira que, no sentido da audição, a natureza utiliza vibrações aéreas de diversas grandezas para gerar sons de diversos tons, pois a analogia da natureza deve ser observada.”32A hipótese da luz (P) [74].
“[…] considerando a duração dos movimentos excitados no fundo dos olhos pela luz, não são eles de natureza vibratória?” Questão 16, Óptica (P) [76].
“[…] não excitam os raios mais refratáveis as vibrações menores […] e os menos refratáveis as maiores […]?” Questão 13, Óptica (P) [77].
“Não podem a harmonia e a discordância das cores resultar das proporções das vibrações propagadas através das fibras dos nervos ópticos para o cérebro, assim como a harmonia e a discordância dos sons resultam das proporções das vibrações do ar?” Questão 14, Óptica (P) [77].
Escólio
Uma vez que, pela razão aqui assinalada por Newton, seja provável que o movimento da retina seja de natureza mais vibratória que ondulatória, a frequência das vibrações deve depender da constituição dessa substância. Ora, como é quase impossível conceber cada ponto sensitivo da retina como contendo um número infinito de partículas, cada uma sendo capaz de vibrar em perfeita harmonia com toda vibração possível, [p. 21] é necessário supor um número limitado, por exemplo, às três cores principais, vermelho, amarelo e azul, às quais as ondulações estão relacionadas tão proximamente quanto os números 8, 7 e 6; e que cada partícula é capaz de ser colocada em movimento mais ou menos forçosamente por ondulações diferindo mais ou menos de uma perfeita unissonância. Por exemplo, as ondulações da luz verde estando próximas da razão
2.1.4. Hipótese IV33
Todos os Corpos materiais têm uma Atração pelo Meio etéreo, através da qual ele é acumulado dentro de suas Substâncias e por uma pequena Distância ao redor deles, em um Estado de maior Densidade, mas não de maior Elasticidade.34
Tem sido mostrado que as três primeiras hipóteses, que podem ser chamadas de essenciais, são literalmente partes do mais complicado sistema Newtoniano. Esta quarta hipótese difere, talvez [p. 22] em certo grau, de qualquer uma que tenha sido proposta por autores anteriores, e é diametricamente oposta àquela de Newton.35 Porém, ambas sendo elas mesmas igualmente prováveis, a oposição é meramente acidental; e só deve ser perguntado qual delas é mais capaz de explicar os fenômenos. Outras suposições podem talvez substituir esta, e, portanto, eu não a considero fundamental, mas ela parece ser a mais simples e a melhor dentre qualquer uma que eu já tenha pensado.
2.1.5. Proposição I
Todos os Impulsos são propagados em um Meio homogêneo elástico com igual Velocidade.36
Cada experimento relativo ao som coincide com as observações já citadas de Newton, as quais [afirmam que] todas as ondulações são propagadas através do ar com igual velocidade; e isto é ademais confirmado por cálculos. Lagrange, Miscellanea Taurinensia, v. 1, p. 91.37 Além disso, [o assunto também pode ser estudado] de forma muito mais concisa em minhas Notas de Aula,38 artigo 289, a serem publicadas em breve [6].
Se o impulso é tão grande de forma a perturbar materialmente a densidade do meio, ele [o meio] não será mais homogêneo. Mas, até onde tange nossos sentidos, a quantidade de movimento pode ser considerada como infinitamente pequena. É surpreendente que Euler, embora atento ao assunto, manteve ainda [a ideia] que as ondulações mais frequentes são mais rapidamente propagadas. Theor. mus. and Conject. phys.39
É possível que a velocidade real das partículas do éter luminífero possa apresentar uma proporção bem menor em relação à velocidade das ondulações que no som. Pois a luz pode ser excitada pelo movimento de um corpo movendo-se a uma taxa de apenas uma milha no tempo que a luz move-se em cem milhões [de milhas].40
[p. 23] Escólio 1
Tem sido demonstrado que, em diferentes meios, a velocidade varia na razão subduplicada da força diretamente41 e da densidade inversamente.42Miscellanea Taurinensia, p. 91. Notas de Aula, artigo 294 [82].
Escólio 2
É evidente, pelos fenômenos dos corpos elásticos e do som, que as ondulações podem se cruzar sem interrupção. Mas, não há necessidade das várias cores da luz branca misturarem suas ondulações. Pois, supondo que as vibrações da retina continuem não obstante cinco centésimos de segundo depois de suas excitações, um milhão de ondulações de cada um milhão de cores deve chegar em sucessão distinta dentro deste intervalo de tempo e produzir o mesmo efeito sensível, como se todas as cores tivessem chegado precisamente no mesmo instante.
2.1.6. Proposição II
Uma Ondulação originada a partir da Vibração de uma única Partícula, deve se expandir através de um Meio homogêneo em uma forma Esférica, mas com quantidades diferentes de Movimento em diferentes Partes.43
Pois, uma vez que todo impulso, considerado como positivo ou negativo, é propagado com uma velocidade constante, cada parte da ondulação deve ter passado através de distâncias iguais em tempos iguais a partir do ponto vibratório. E, supondo que a partícula em vibração, no curso de seu movimento, proceda em direção a uma pequena distância em uma dada direção, a principal força da ondulação estará naturalmente logo antes dela; atrás dela, o movimento será igual, [mas] em direção contrária; e, em ângulos retos à linha de vibração, a ondulação será evanescente.
Agora, para que tal ondulação possa continuar seu progresso a qualquer distância considerável, deve haver em cada parte dela uma tendência a preservar seu próprio movimento em linha reta a partir do [p. 24] centro. Pois, se o excesso de força em qualquer parte fosse comunicado às partículas vizinhas, não há razão pela qual ele não deveria ser logo equalizado ao longo [do caminho], ou, em outras palavras, ser extinto totalmente, visto que os movimentos em direções contrárias naturalmente destruiriam uns aos outros.44 A origem do som a partir da vibração de um acorde é evidentemente dessa natureza; do contrário, em uma onda circular de água, toda parte está ao mesmo instante ou elevada ou deprimida. Pode ser difícil mostrar matematicamente o modo pelo qual esta irregularidade da força é preservada; mas a inferência a partir dos fatos parece ser inevitável. Enquanto a ciência da hidrodinâmica for tão imperfeita a ponto de não podermos sequer resolver o simples problema do tempo requerido para esvaziar um recipiente por uma dada abertura, não poderíamos esperar ser capazes de dar conta perfeitamente de um conjunto tão complicado de fenômenos, como aqueles dos fluidos elásticos. De fato, a teoria de Huygens explica o caso de uma maneira toleravelmente satisfatória: ele supõe que toda partícula do meio propaga uma ondulação distinta em todas as direções;45 e que cada efeito geral somente é perceptível onde uma porção de cada ondulação conspira em um mesmo instante. É fácil mostrar que esta ondulação geral procederia em todos os casos retilineamente, com força proporcional. Mas, acerca dessa suposição, parece seguir que uma maior quantidade de força deve ser perdida pela divergência das ondulações parciais que aquela que parece ser consistente com a propagação do efeito a qualquer distância considerável.46 Contudo, é óbvio que uma parte de tal limitação do movimento deve ser esperada; pois, se supormos que a intensidade do movimento de qualquer parte específica, ao invés de continuar a ser propagada em linha reta, afetasse a vizinhança da ondulação, um [p. 25] impulso deveria então ter viajado de um círculo interno para um externo em uma direção oblíqua, ao mesmo tempo que na direção do raio, e consequentemente com uma maior velocidade, [o que é] contrário à primeira proposição. No caso da água, a velocidade não é de modo algum tão rigorosamente limitada como aquela em um meio elástico. Porém, não é necessário supor e nem é mesmo provável, que não há absolutamente a menor comunicação lateral da força da ondulação, mas que, em meios altamente elásticos, esta comunicação é quase insensível.47 No ar, se um acorde é perfeitamente isolado, de tal maneira a propagar exatamente tais vibrações como as descritas, elas serão na verdade muito menos forçosas que se o acorde for colocado na vizinhança de uma caixa de ressonância, e provavelmente [serão forçosas] em alguma medida por conta dessa comunicação lateral de movimentos de uma tendência oposta. E a diferente intensidade de diferentes partes da mesma ondulação circular pode ser observada segurando um diapasão comum à distância de um braço e afinando-o, de um plano direto ao ouvido para uma posição perpendicular àquele plano.
2.1.7. Proposição III
Uma Porção de Ondulação esférica, passando através de uma Abertura em um Meio em repouso, será propagada retilineamente em Superfícies concêntricas, terminadas lateralmente por Porções fracas e irregulares de novas Ondulações divergentes.48
No instante de admissão, pode-se supor que a circunferência de cada ondulação crie uma ondulação parcial, enchendo o ângulo nascente entre os raios e a superfície que encerra o meio. Mas, nenhum complemento notável será feito [p. 26] à sua força por uma divergência de movimento de quaisquer outras partes da ondulação, pela não coincidência de tempo, como já foi explicado sobre as várias forças de uma ondulação esférica. Se mesmo assim a abertura comportar uma pequena proporção em relação à largura da ondulação, a nova ondulação gerada deve absorver quase a força total da porção admitida; e este foi o caso considerado por Newton nos Principia49 Mas nenhum experimento com a luz pode ser feito nessas circunstâncias, por conta da pequenez de suas ondulações e a interferência da inflexão.50 Além disso, algumas fracas radiações realmente divergem além de quaisquer limites prováveis de inflexão,51 tornando a margem da abertura distintivamente visível em todas as direções; estas são atribuídas por Newton a alguma causa desconhecida, diferente da inflexão (Óptica, Livro III, Observação 5), e elas atendem totalmente à descrição desta proposição.52
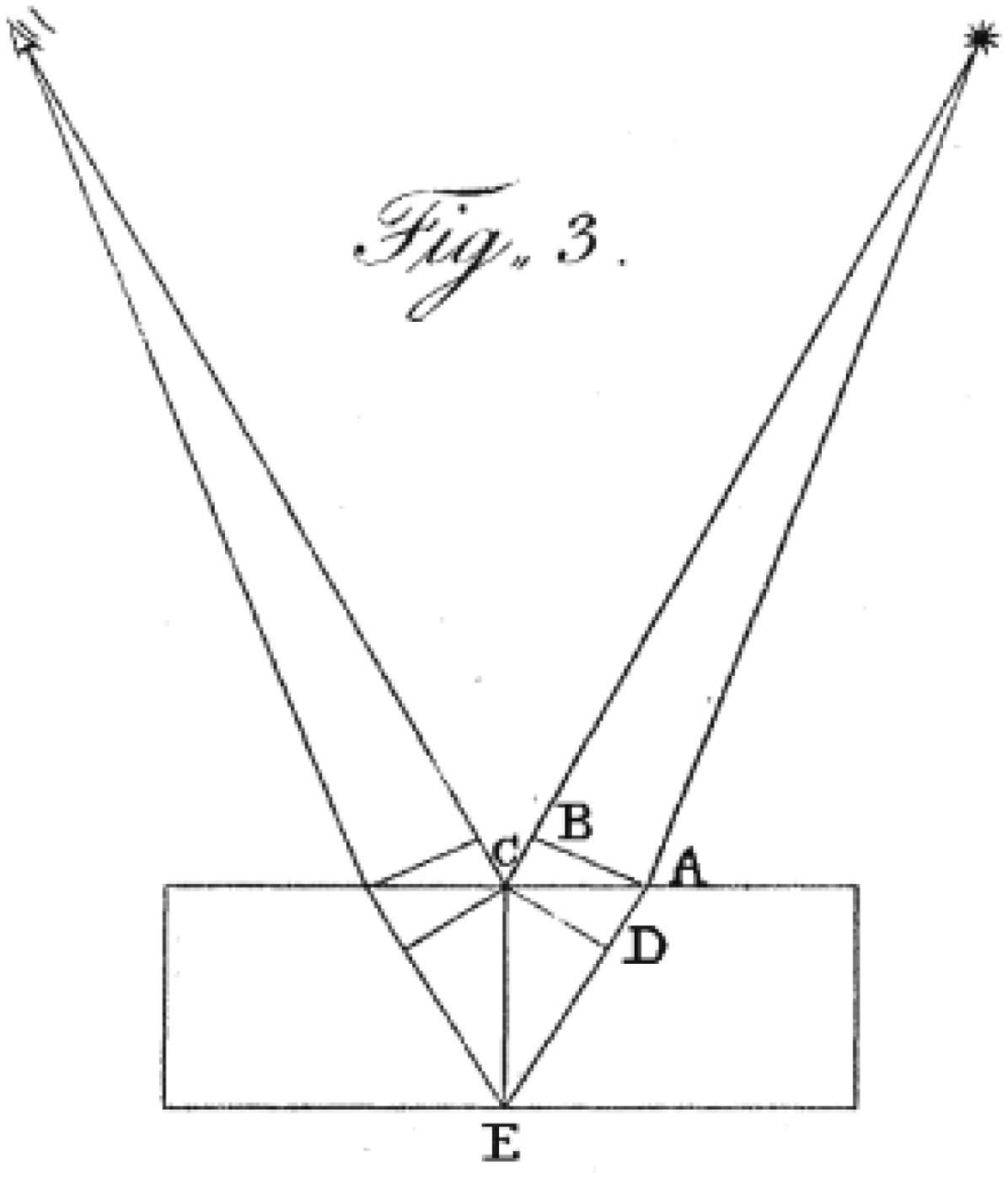
Deixe as linhas concêntricas na Fig. 1 representarem o caso atual das partes similares de um número de ondulações sucessivas divergindo do ponto A. Elas também representarão as situações sucessivas de cada ondulação individual. Deixe a força de cada ondulação ser representada pela largura da linha e deixe o cone de luz ABC ser admitido através da abertura BC. Assim, as ondulações principais procederão em uma direção retilínea em direção a GH, e as radiações fracas de cada lado divergirão a partir de B e C como centros, sem receber qualquer força adicional de qualquer ponto intermediário D da ondulação, por conta da irregularidade das linhas DE e DF. Mas, se permitirmos alguma pouca divergência lateral das extremidades das ondulações, ela deve diminuir suas forças, sem adicionar materialidade àquelas de luz dissipada; e suas [p. 27] terminações assumirão a forma CH, ao invés da linha reta BG; uma vez que a perda de força é mais considerável perto de C que em distâncias maiores. Esta linha corresponde ao limite da sombra da primeira observação de Newton (Fig. 1). É muito mais provável que tal dissipação da luz fosse a causa do aumento da sombra naquela observação que aquela [explicação dizendo que era] devido à ação da atmosfera inflectora, a qual deve ter estendido um trigésimo de polegada em cada caminho de forma a produzi-la; especialmente quando é considerado que a sombra não é diminuída ao cercar o cabelo com um meio mais denso que o ar, o qual possivelmente deve ter enfraquecido e contraído sua atmosfera inflectora. Em outras circunstâncias, a divergência lateral parecerá aumentar a espessura do feixe, ao invés de diminuí-la.
Figura 1 Ilustração de Young para mostrar a propagação das ondulações luminosas após sua passagem por uma pequena abertura
Como o assunto dessa proposição sempre tem sido considerado a parte mais difícil do sistema ondulatório, será propício examinar agora as objeções que Newton colocou sobre ele.
“Pois, para mim, a própria hipótese fundamental [da luz como vibrações no éter] parece impossível; a saber, que as ondas ou vibrações de qualquer fluido possam ser propagadas em linhas retas, como os raios de luz, sem um contínuo e extravagante espalhamento e desvio por todo o caminho pelo meio quiescente, onde elas são terminadas por ele. Engano-me, se não houver tanto um experimento quanto demonstração contrários [ao meu pensamento].” Carta de Newton a Hooke [91].53
“Todo movimento propagado de um fluido diverge de um progresso retilíneo em direção aos espaços imóveis. […] e como [o meio]”, na metade de uma ondulação [p. 28] admitida, “é mais denso lá do que nos espaços em ambos os lados […], ele irá dilatar-se tanto em direção a estes espaços […] quanto em direção aos intervalos rarefeitos entre os pulsos e, portanto […] os pulsos relaxam-se em ambos os lados em direção às partes em repouso do meio […], preenchendo, portanto todo o espaço […]. E também obtemos o mesmo pela experiência com sons […].”Proposição 42, Principia (P) [92].
“Não são errôneas todas as hipóteses segundo as quais a luz consistiria em pressão ou movimento propagados através de um meio fluido? […] E se consistisse em pressão ou movimento propagado ou num instante ou no tempo, ela se curvaria para a sombra. Pois pressão ou movimento não podem ser propagados em um fluido em linhas retas além de um obstáculo que intercepta parte do movimento, mas se curvarão e se espalharão em todas as direções do meio quiescente que está além do obstáculo. […] As ondas sobre a superfície da água estagnada, ao passarem perto dos lados de um objeto largo que intercepta uma parte delas, curvam-se depois e dilatam-se gradualmente para dentro da água estagnada por trás do obstáculo. As ondas, pulsações ou vibrações do ar que constituem o som curvam-se manifestamente, embora não tanto quanto as ondas da água. Pois um sino ou um canhão podem ser ouvidos além de uma colina que intercepta a visão do corpo sonoro, e os sons se propagam tão prontamente através de tubos curvos como através de tubos retos. Mas nunca se soube de a luz seguir passagens curvas nem de se curvar para a sombra. Pois as estrelas fixas deixam de ser vistas devido à interposição de qualquer dos planetas. E assim o fazem as partes do Sol pela interposição da Lua, de Mercúrio ou de Vênus. Os raios que passam muito próximos das bordas de qualquer corpo são um pouco curvados pela ação do corpo […]; mas essa curvatura não se dá em direção à sombra, mas a partir da sombra, [p. 29] e é executada apenas na passagem do raio perto do corpo e a uma distância muito pequena dele. Tão logo o raio tenha passado pelo corpo, segue em linha reta.” Questão 28, Óptica (P) [93].
Agora, a proposição citada dos Principia não contradiz diretamente esta [minha] proposição; pois ela não afirma que tal movimento [das ondas] deve divergir igualmente em todas as direções; tampouco pode sustentar realmente que as partes de um meio elástico comunicando qualquer movimento deve propagar este movimento igualmente em todas as direções. Outlines of Experiments and Inquiries respecting Sound and Light [94].54
Tudo que pode ser inferido pela razão é que as partes marginais da ondulação devem ser de alguma forma enfraquecidas e que deve haver uma fraca divergência em todas as direções. Mas, se qualquer um desses efeitos pode ser de magnitude suficiente para ser sentido, [isso] não pode ser inferido por argumento, se a afirmativa não se fizer provável por experimento.55
Em relação à analogia com outros fluidos, a inferência mais natural disto é a seguinte: “As ondas do ar, das quais consiste o som, curvam-se manifestadamente, embora não tanto quanto as ondas da água”; a água sendo um [meio] inelástico e o ar um meio moderadamente elástico; porém o éter sendo mais altamente elástico, suas ondas curvam-se muito menos que aquelas do ar, e, portanto, quase imperceptivelmente.56 Sons são propagados através de passagens curvas porque seus lados [das passagens] são capazes de refletir som, assim como a luz seria propagada por um tubo curvado, se estivesse perfeitamente polido por dentro.57
A luz de uma estrela é, de longe, muito fraca para produzir, por meio de sua tênue divergência, qualquer iluminação visível da margem de um planeta a eclipsando. A interceptação da luz do sol pela lua é tão estranha para a questão quanto as discussões acerca da inflexão são imprecisas.
Em relação ao argumento colocado por Huygens, [p. 30] em favor da propagação retilínea das ondulações, Newton não respondeu; talvez por conta de sua própria incompreensão acerca da natureza dos movimentos em meios elásticos, como dependentes de uma lei particular de vibração, o que foi corrigido por matemáticos posteriores. Outlines [96].
No geral, presume-se que essa proposição pode ser seguramente admitida como perfeitamente consistente com a analogia e o experimento.58
2.1.8. Proposição IV
Quando uma Ondulação atinge a Superfície que Limita Meios de diferentes Densidades, ocorre uma Reflexão parcial, proporcional à Magnitude da Diferença de Densidades
Isto pode ser ilustrado, se não demonstrado, pela analogia de corpos elásticos de tamanhos diferentes. “Se um corpo elástico pequeno bate contra um grande, é bem sabido que o menor é refletido mais ou menos intensamente de acordo com a diferença de suas magnitudes. Assim, sempre há uma reflexão quando os raios de luz passam de um estrato de éter mais raro para um mais denso; e frequentemente [temos] um eco quando um som bate contra uma nuvem. Um corpo maior batendo em um pequeno o impulsiona, sem perder todo seu movimento. Assim, as partículas do estrato de éter mais denso não transmitem todo seu movimento para o mais rarefeito, porém, em seu esforço para seguir, elas são puxadas pela atração da substância refratora com força equivalente, e assim uma reflexão secundária é sempre produzida quando os raios de luz passam de um estrato mais denso para um mais rarefeito”.59Outlines [99].
Mas não é absolutamente necessário supor uma atração no último caso, uma vez que o esforço para proceder seria propagado de trás para frente sem ela, e a ondulação seria revertida, uma rarefação [p. 31] retornando em lugar de uma condensação; e isto talvez será muito inconsistente com os fenômenos.
2.1.9. Proposição V
Quando uma Ondulação é transmitida através de uma Superfície que limita diferentes Meios, ela procede em uma certa Direção, tal que os Senos dos Ângulos de Incidência e Refração estão na constante Razão da Velocidade de Propagação nestes dois Meios
(Barrow, Lectiones Opticae, Parte II, p. 4;60Huygens, Tratado sobre a Luz, Capítulo 3;61Euler, Conj. Phys.; Outlines [101]; Notas de Aula, artigo 382 [102])
Corolário 2
Pelos experimentos de refração em um ar condensado, parece que a razão da diferença dos senos simplesmente varia como a densidade. Dessa forma, segue, pelo Escólio 1 da Proposição I, que o excesso de densidade do meio etéreo está em uma razão duplicada para a densidade do ar; cada partícula cooperando com suas [partículas] vizinhas para atrair uma maior porção [de éter].
2.1.10. Proposição VI
Quando uma Ondulação atinge a Superfície de um Meio mais rarefeito, tão obliquamente que ela não pode ser refratada normalmente, ela é totalmente refletida, em um Ângulo igual àquele de Incidência
(Outlines [101])
Corolário
Este fenômeno tende a provar o aumento e diminuição graduais de densidade na superfície que limita dois meios, como supostos na Hipótese IV;62 embora Huygens tenha tentados explicá-lo de modo diferente. [p. 32]
2.1.11. Proposição VII
Se Ondulações equidistantes supostamente passam através de um Meio, cujas Partes são suscetíveis a Vibrações permanentes de alguma forma mais lentas que as Ondulações, suas Velocidades serão diminuídas por essa Tendência vibracional; e, no mesmo meio, ainda mais, à medida que as Ondulações tenham mais frequência
Pois, uma vez que o estado de ondulação requer uma mudança no movimento presente da partícula que a transmite, esta mudança será retardada pela propensão da partícula a continuar seu movimento um pouco mais; e este retardamento será mais frequente e mais considerável, à medida que a diferença entre os períodos da ondulação e da vibração natural fique maior.
Corolário
Por um longo tempo, houve uma opinião estabelecida de que o calor consiste em vibrações das partículas dos corpos e é capaz de ser transmitido por ondulações através de um vácuo aparente. Questão 18, Óptica [63].
Essa opinião foi abandonada muito tardiamente. Conde Rumford,63 Professor Pictet,64 e Mr. Davy65 são praticamente os únicos autores que aparentemente são favoráveis a ela. Porém, parece que ela foi rejeitada sem qualquer bom fundamento e terá provavelmente sua popularidade recuperada muito em breve.
Vamos supor que essas vibrações tenham menor frequência que aquelas da luz. Portanto, todos os corpos estão sujeitos a vibrações permanentes mais lentas que aquelas da luz. Na verdade, todos estão praticamente sujeitos às vibrações luminosas, tanto quando [estão] em estado de queima ou quando em circunstâncias de fosforescência solar. Porém estão [sujeitos] muito menos facilmente e em um grau muito menor, em relação àquelas do calor. Seguirá dessas suposições que as ondulações luminosas com frequência maior serão mais retardadas que aquelas com frequência menor, e, [p. 33] consequentemente, que a luz azul será mais refrangível que a vermelha e [terá] o menor calor radiante de todas; uma consequência que coincide exatamente com os experimentos muito interessantes do Dr. Herschel (Philosophical Transactions, p. 284 1800).66
Será também facilmente concebível que a existência real de um estado de vibração mais lento pode tender a retardar ainda mais as ondulações com maior frequência, e que o poder refrator de corpos sólidos pode ser sensivelmente aumentado por uma elevação da temperatura, como de fato parece ter sido nos experimentos de Euler.67 Acad. de Berlin, 1762, p. 328.68
Escólio
Se, contudo, esta proposição parecer não ser demonstrada suficientemente, deve ser considerada pelo menos igualmente explanatória dos fenômenos em relação a qualquer coisa que foi desenvolvida do outro lado, a partir da doutrina de corpúsculos; uma vez que a força aceleradora deve agir em alguma outra proporção que aquela do volume das partículas. Se nós chamarmos isso de atração eletiva, só estaremos disfarçando com um termo químico nossa incapacidade de apontar uma causa mecânica.69 O Sr. Short70, quando encontrou por observação a igualdade da velocidade da luz de todas as cores, percebeu a objeção tão fortemente, que imediatamente elaborou uma inferência a partir disso em favor do sistema ondulatório.71 É assumido na proposição que quando a luz é dispersada por refração, os corpúsculos da substância refratora estão na verdade em estado movimento alternado, e contribuem para sua transmissão. Mas, devemos confessar que não podemos no momento apresentar uma concepção muito decidida e precisa das forças que mantém estas vibrações corpusculares.
2.1.12. [p. 34] Proposição VIII
Quando duas Ondulações, a partir de diferentes origens, coincidem perfeitamente ou quase [coincidem] em Direção, seu efeito conjunto é uma Combinação dos Movimentos pertencentes a cada uma [delas].72
Uma vez que cada partícula do meio é afetada por cada ondulação, sempre que as direções coincidem, a ondulação não pode prosseguir senão pela união de seus movimentos, de modo que a junção do movimento pode ser a soma ou a diferença dos movimentos separados, conforme são coincidentes as partes similares ou diferentes da ondulação.
Em ocasião anterior, insisti de forma geral sobre aplicação deste princípio para harmônicos. Outlines [107]. E ele se mostrará ser, ainda, de utilidade mais abrangente em explicar os fenômenos das cores. As ondulações que estão, agora, para ser comparadas são aquelas de igual frequência. Quando as duas séries coincidem exatamente em um ponto do tempo, é óbvio que a velocidade unida, dos movimentos particulares, deve ser a maior, e, na realidade no mínimo o dobro das velocidades separadas. E, além disso, ela deve ser a menor, e se as ondulações são de igual intensidade, totalmente destruída, quando o período do maior movimento direto pertencente a uma ondulação coincide com aquele do maior movimento retrógrado do outro. No estado intermediário, a ondulação conjunta será de intensidade intermediária. Mas, pelo que as leis deste comprimento intermediário devem variar, não pode ser determinado sem mais dados. É bem conhecido que uma similar causa é produzida no som, aquele efeito que é chamado de batida. Duas séries de ondulações de aproximadamente igual magnitude auxiliando e destruindo umas às outras alternadamente, na medida em que elas coincidam [p. 35] mais ou menos perfeitamente no momento de executar seus respectivos movimentos.
Corolário I. Das Cores das Superfícies estriadas
Boyle73 parece ter sido o primeiro a observar cores de arranhões em superfícies polidas. Newton não as observou. Mazeas74 e o Sr. Brougham75 fizeram alguns experimentos sobre o assunto, ainda sem produzir qualquer conclusão satisfatória. Mas todas as variedades destas cores são muito facilmente deduzidas a partir desta proposição.
Deixe em um determinado plano dois pontos refletores muito próximos um do outro, e deixe o plano situado de modo que a imagem refletida de um objeto luminoso visto nele possa parecer coincidir com os pontos. Então, é óbvio que o comprimento do raio incidente e refletido, tomados em conjunto, é igual em relação a ambos os pontos, considerando-os capazes de refletir em todas as direções. Agora, deixe um dos pontos rebaixado abaixo do plano. Então, todo o caminho da luz refletida a partir dele, será alongado por uma linha que está para a depressão do ponto como duas vezes o cosseno de incidência para o raio [radius] (ver Fig. 2).
Se, então, iguais ondulações de determinadas dimensões são refletidas a partir dos dois pontos, situados próximos o suficiente para parecerem aos olhos como [apenas] um, sempre que esta linha é igual à metade da distância de uma ondulação completa, a reflexão a partir do ponto rebaixado interferirá com a reflexão [originada] a partir do ponto fixo, de forma que o movimento progressivo de uma coincidirá com o movimento retrógrado da outra, e ambas serão destruídas. Mas, quando esta linha é igual à distância completa de uma ondulação, o efeito será dobrado. E, quando [for] um comprimento e meio, [será] novamente destruída. [Sendo que, ocorrerá] deste modo para um número considerável de alternações. E, se as ondulações refletidas forem de diferentes tipos, elas [p. 36] serão afetadas de diferentes modos, de acordo com as suas proporções para os vários comprimentos da linha que é a diferença entre os comprimentos dos seus dois caminhos, e que pode ser denominado [como] o intervalo de retardamento.
A fim de que o efeito possa ser o mais perceptível, um número de pares de pontos deve estar unido em duas linhas paralelas. Se vários desses pares de linhas estão colocados próximos um do outro, eles facilitarão a observação. Se uma das linhas girar em torno da outra como um eixo, a depressão abaixo do plano será como o seno de inclinação. E, enquanto o olho e o objeto luminoso permanecerem fixos, a diferença de comprimento dos caminhos variará conforme este seno.
Os melhores aparelhos para o experimento são os excelentes micrômetros do Sr. Coventry.76 Como estes consistem de linhas paralelas traçadas sobre um vidro, à distância de 1/500 de uma polegada, são os mais apropriados. Cada uma dessas linhas [que] aparece sob um microscópio consiste de duas ou mais linhas muito finas, exatamente paralelas, e à distância de um pouco mais do que um vigésimo daquela das linhas adjacentes. Eu coloco uma destas de forma a refletir a luz do sol em um ângulo de 45°, e fixo-a de tal maneira que enquanto ela gira em torno de uma das linhas como um eixo, eu posso medir seu movimento angular. [Desta forma,] encontrei que a cor vermelha mais brilhante ocorre nas inclinações,
Este experimento permite uma confirmação muito forte da teoria. É impossível deduzir dela qualquer explicação a partir de qualquer hipótese levantada até aqui. Eu acredito que seria [p. 37] difícil inventar qualquer outra que a satisfizesse. Existe uma impressionante analogia entre esta separação das cores e a produção de uma nota musical por sucessivos ecos a partir de estacas de ferro equidistantes; que descobri corresponder de forma muito precisa com a velocidade do som conhecida, e as distâncias das superfícies.
Não é improvável que as cores das cascas de alguns insetos, e de alguns outros corpos naturais, exibindo em diferentes luzes a mais bela versatilidade, podem ser descobertas como sendo desta descrição, e não ser derivada de filmes finos. Em alguns casos, um único arranhão ou sulco pode produzir efeito similar, pela reflexão de suas margens opostas.
Corolário II. Das Cores dos Filmes Finos.
Quando um feixe de luz incide sobre duas superfícies refratoras paralelas, a reflexão parcial coincide perfeitamente em direção. Neste caso, o intervalo de retardamento, tomado entre as superfícies, está para sua distância conforme duas vezes o cosseno do ângulo de refração do raio [radius]. Para o desenho AB e CD perpendicular aos raios [rays], na Fig. 3, o tempo de passagem através de BC e AD será igual, e DE será metade do intervalo de retardamento. Mas, DE está para CE como o seno de DCE para o raio [radius]. Então, [para] que DE possa ser constante, ou que a mesma cor possa ser refletida, a espessura de CE deve variar conforme a cossecante do ângulo de refração CED: o que está exatamente de acordo com os experimentos de Newton;77 já que a correção é perfeitamente não-considerável.
Deixe o meio entre as superfícies ser mais raro do que o meio no entorno. Então, o impulso refletido na segunda superfície, encontrando a subsequente ondulação na primeira, tornará as partículas do meio mais raro capazes de parar completamente [p. 38] o movimento do mais denso, e destruindo a reflexão, (Prop. IV) enquanto elas próprias serão mais fortemente propelidas do que se tivessem estado em repouso; e a luz transmitida será aumentada. De modo que as cores pela reflexão serão destruídas, e aquelas pela transmissão ficarão mais vívidas, quando espessuras duplicadas, ou intervalo de retardamento, for qualquer múltiplo do comprimento inteiro das ondulações. E, na espessura intermediária os efeitos serão reversos. [Estando tudo] de acordo com as observações Newtonianas.78
Se as mesmas proporções encontradas forem verdadeiras em relação aos filmes finos de um meio mais denso, que de fato não é improvável, será necessário adotar a correta demonstração da Prop. IV. Mas, de qualquer forma, se um filme fino for interposto entre um meio mais rarefeito e um mais denso, pode-se esperar que as cores pela reflexão e transmissão mudem de lugar.
A partir das medidas de Newton das [várias] espessuras refletindo diferentes cores, a largura e duração das suas respectivas ondulações podem ser determinados de forma muito precisa. Embora não seja improvável que quando se aproxima muito as lentes, a atmosfera do éter pode produzir alguma pequena irregularidade. O espectro visível inteiro parece estar compreendido dentro da razão de três para cinco, ou uma sexta maior na música. E, as ondulações do vermelho, amarelo e azul, estão relacionadas em magnitude conforme os números 8, 7 e 6. De modo que o intervalo a partir do vermelho para o azul é uma quarta. A frequência absoluta expressa em números é muito grande para ser claramente compreendida, mas ela pode ser melhor imaginada por meio da comparação com o som. Se um acorde tocar o tenor
O comprimento e frequência absolutos de cada vibração são expressos na Tabela 1. Supondo a luz viajar em
Tabela 1 Dados de Young sobre as ondulações luminosas em filmes finos.
| Cores | Comprimento de uma ondulação em partes de uma polegada, no ar | Número de ondulações em uma polegada | Número de ondulações em um segundo |
|---|---|---|---|
| Extremo | .0000266 | 37640 | 463 milhões de milhões |
| Vermelho | .0000256 | 39180 | 482 |
| Intermediário | .0000246 | 40720 | 501 |
| Laranja | .0000240 | 41610 | 512 |
| Intermediário | .0000235 | 42510 | 523 |
| Amarelo | .0000227 | 44000 | 542 |
| Intermediário | .0000219 | 45600 | 561 (=
|
| Verde | .0000211 | 47460 | 584 |
| Intermediário | .0000203 | 49320 | 607 |
| Azul | .0000196 | 51110 | 629 |
| Intermediário | .0000189 | 52910 | 652 |
| Índigo | .0000185 | 54070 | 665 |
| Intermediário | .0000181 | 55240 | 680 |
| Violeta | .0000174 | 57490 | 707 |
| Extremo | .0000167 | 59750 | 735 |
Escólio
Ainda não estava satisfeito em relação a todos estes fenômenos, até que encontrei na Micrographia de Hooke80 uma passagem que poderia ter me levado mais cedo a uma conclusão semelhante. “É mais evidente que a reflexão da face inferior ou mais distante do corpo é a principal causa da produção destas cores. - Deixe o raio [de luz] incidir obliquamente sobre o filme fino, parte então é refletida de volta pela primeira superfície, - parte [é] refratada para a segunda superfície, de onde ele é refletido e refratado novamente. - Deste modo, depois de duas refrações e uma [p. 40] reflexão propaga-se um tipo de raio mais fraco -,” e “em razão do tempo gasto na passagem e repassagem, - este pulso mais fraco vem atrás do” anterior refletido. “De forma que fica (as superfícies estando tão juntas que os olhos não podem discriminá-las a partir de uma [delas]) este pulso confuso ou duplicado, cuja mais forte parte precede, e cuja [parte] mais fraca sucede, produz sobre a retina a sensação de um amarelo. Se, além disso, estas superfícies são distanciadas, o pulso mais fraco pode tornar-se coincidente com a” reflexão do “segundo”, ou com o pulso imediatamente seguinte [refletido] a partir da primeira superfície, “e ficar para trás também, e ser coincidente com o terceiro, quarto, quinto, sexto, sétimo, ou oitavo. - De forma que, se há um corpo fino e transparente, a partir da maior finura [ou seja, o mais fino possível] necessária para produzir cores, faz crescer por graus para a maior espessura [ou seja, o mais grosso possível]. - As cores serão tão [mais] frequentemente repetidas, quanto o pulso mais fraco perder passos com seu primário ou primeiro pulso [ou seja, aquele pulso inicial que o originou], e [com isso tornar-se] coincidente com um” subsequente “pulso. E isso [tudo], coincide ou resulta da primeira hipótese [que] eu tomei das cores, conforme [o] experimento que encontrei em grande quantidade de exemplos [e] que parece prová-lo.” Micrographia [110].81
Isto foi impresso cerca de sete anos antes que quaisquer experimentos de Newton fossem feitos.82 Nós fomos informados por Newton, que Hooke estava disposto a adotar sua “sugestão” da natureza das cores; e apesar disso não parece que Hooke empregou alguma vez aquele aprimoramento para sua explicação destes fenômenos, ou [tenha] investigado a necessária consequência de uma mudança de obliquidade, em sua suposição original, [pois] de outra forma ele não poderia senão ter descoberto uma coincidência impressionante com as medidas registradas por Newton a partir do experimento. Todas as tentativas anteriores para explicar as cores de filmes finos têm também se baseado em suposições [p. 41] que, como [aquela] de Newton, nos levaria a supor as maiores irregularidades na direção dos raios refratados; ou como [aquela] do Sr. Michell,83 [que] exigiria tais efeitos a partir da mudança do ângulo de incidência, [as quais] são contrárias aos efeitos observados. Ou, elas são igualmente deficientes em relação a estas duas circunstâncias, e são inconsistentes com a mais moderada atenção para o principal fenômeno.
Corolário III. Das Cores dos Filmes Espessos
Quando um feixe de luz passa através de uma superfície refratora, especialmente se [for] imperfeitamente polida, uma parte dele é irregularmente dispersada, e faz a superfície visível em todas as direções, mas mais notadamente em direções não muito distantes daquela [direção] da própria luz. E, se uma superfície refletora for colocada paralelamente à superfície refratora, esta luz dispersada, tão bem quanto o feixe principal, será refletida, e também haverá uma nova dissipação de luz, no retorno do feixe de luz através da superfície refratora. Estas duas porções de luz dispersadas coincidirão em direção. E, se as superfícies estiverem [colocadas] de tal forma a juntar os efeitos semelhantes, mostrará anéis de cores. O intervalo de retardamento é, aqui, a diferença entre os caminhos do feixe principal e da luz dispersada entre as duas superfícies. Claro, sempre que a inclinação da luz dispersada é igual àquela do feixe de luz, embora em diferentes planos, o intervalo desaparecerá, e todas as ondulações conspirarão. Em outras inclinações, o intervalo será a diferença das secantes da secante de inclinação ou ângulo de refração do feixe principal. A partir dessas causas, todas as cores de espelhos côncavos observadas por Newton e outros são necessariamente consequências. E, parece que a produção delas, apesar [p. 42] de certa forma semelhante, não é de forma, como Newton imaginou, idêntica à produção daquelas de filmes finos.84
Corolário IV. Da Escuridão
Nos três corolários anteriores, nós consideramos os materiais refratários e refletivos como limitados por uma superfície matemática. Mas, talvez isto nunca seja fisicamente verdadeiro. A atmosfera etérea pode prolongar-se em cada lado da superfície até à distância de uma ou mais ondulações. E, se supormos que elas variam igualmente em densidade em toda a parte, as reflexões parciais de cada um dos infinitos números de superfícies, onde a densidade muda, interferirão umas com as outras e [isso] destruirá uma considerável parte da luz refletida, de forma que o material pode se tornar absolutamente preto. E este efeito pode ocorrer em maior ou menor grau, a medida em que a densidade da atmosfera etérea varia mais ou menos igualmente. [Ainda,] em alguns casos, ondulações específicas sendo mais afetadas do que outras, um matiz de cor pode ser produzido. De acordo [com isso], Sr. Bouguer85 observou uma considerável perda de luz, e em alguns exemplos um matiz de cor, nas reflexões totais na superfície de um meio mais raro.
Corolário V. Das Cores pela Inflexão
Qualquer que possa ser a causa da inflexão da luz passando através de uma pequena abertura, a luz mais próxima de seu centro deve ser a menos desviada, e a [luz] mais próxima de suas bordas a mais [desviada]. Outra parte da luz incidindo muito obliquamente sobre a margem da abertura, será copiosamente refletida em várias direções. Algumas das quais coincidirão perfeitamente, ou quase, em direção com a luz não-refletida e, tendo tomado um [p. 43] caminho não-reto, interferirão com ela provocando uma aparência de cores. O comprimento dos dois caminhos diferirá a menos que a direção da luz refletida tenha sido menos mudada pela sua reflexão, isto é, na luz que passa mais próxima à margem. De modo que os azuis aparecerão na luz mais próxima da sombra. O efeito será aumentado e modificado quando a luz refletida incidir dentro da [região] de influência da borda oposta, de forma a interferir com a luz simplesmente infletida por aquela também.
Mas, a fim de examinar as consequências mais detalhadamente, será conveniente supor a inflexão causada por uma atmosfera etérea, de densidade que varia como um determinado poder da distância a partir do centro, como na oitava proposição da última Conferência Bakeriana [112]. Colocando r = 3 e x = 0.5, eu construí um diagrama (Fig. 4), que mostra, pelos dois pares de curvas, a posição relativa das partes refletida e não-refletida de qualquer ondulação em dois tempos sucessivos. E, também, por linhas escurecidas traçadas através [do diagrama], as partes onde os intervalos de retardamento estão em progressão aritmética, e onde cores semelhantes serão mostradas em diferentes distâncias no material de inflexão. O resultado concorda perfeitamente com as observações do terceiro livro de Newton, e com aquelas dos últimos autores. Mas, eu não considero isto como algo totalmente certo, até que mais experimentos sejam realizados sobre a força de inflexão de diferentes materiais, que a explicação de inflexão do Dr. Hooke, pela tendência da luz divergir, pode não ter algumas pretensões de verdade. Sinto muito por ser obrigado a lembrar aqui a anuência que, à primeira vista, fui induzido a dar para uma suposta melhoria do último autor [113].
Escólio
Na construção do diagrama, fez-se necessário encontrar o tempo gasto por cada raio [ray] em sua passagem. [p. 44] Uma vez que a velocidade era estipulada por
2.1.13. Proposição IX
Luz Radiante consiste em Ondulações de Éter Luminífero
Esta proposição é a conclusão geral de todas as anteriores. E compreende-se que elas conspiram para prová-la de uma forma tão satisfatória quanto pode possivelmente ser esperado da [p. 45] natureza da matéria. É claramente concedido por Newton que existem ondulações, ainda que ele negue que elas constituam luz. Mas, é mostrado nos três primeiros Corolários da última Proposição que todos os casos de aumento ou diminuição da luz são referentes a um aumento ou diminuição de tais ondulações, e que todas as situações as quais as ondulações seriam responsáveis são claramente visíveis nos fenômenos da luz. Então, pode ser logicamente inferido que as ondulações são luz.
Algumas observações destacadas servirão para responder algumas objeções que podem ser levantadas contra esta teoria.
Newton propôs a refração particular do cristal-da-Islândia como um argumento de que as partículas da luz devem ser corpúsculos projetados,86 uma vez que ele pensa [ser] possível que os diferentes lados destas partículas devem ser diferentemente atraídos diferente pelo cristal, e já que Huygens confessou sua inabilidade para explicar de forma satisfatória todos os fenômenos. Mas, contrariamente ao que poderia ter sido esperado da usual precisão e franqueza de Newton, ele estabeleceu uma nova lei para a refração sem dar uma razão para rejeitar aquela de Huygens, a qual Mr. Hauy87 encontrou ser mais precisa do que a de Newton. E, sem tentar deduzir do seu próprio sistema alguma explicação dos efeitos mais gerais e evidentes do cristal duplicador, ele omitiu observar que a teoria mais elegante e engenhosa de Huygens concorda perfeitamente com estes efeitos gerais, em todos os detalhes, e claro, deriva dele argumentos adicionais para a verdade. Isto ele omite, a fim de apontar uma dificuldade, para a qual somente uma solução verbal pode ser encontrada em sua própria teoria, e que provavelmente permanecerá inexplicável por qualquer outro.
-
Sr. Michell fez alguns experimentos que parecem mostrar que os raios de luz têm um real momento, por [p. 46] meio do qual o movimento é produzido quando eles incidem sobre uma placa fina de cobre sensivelmente suspensa. Priestley's Optics.88
Mas, tomando a exata perpendicularidade da placa, e na ausência de qualquer corrente ascendente de ar, [e] ainda posto que em todo o experimento uma maior quantidade de calor deve ser comunicada ao ar na superfície sobre a qual a luz incidirá do que na superfície oposta, o excesso de expansão deve necessariamente produzir um excesso de pressão sobre a primeira superfície, e um recuo muito perceptível da placa na direção da luz. Sr. Bennet repetiu o experimento com instrumentos muito mais sensíveis e, também, na ausência de ar. [Com isso] deduziu corretamente a partir de seu total fracasso, um argumento em favor do sistema ondulatório da luz. Philosophical Transactions, p. 87, 1792.89
Concedendo a máxima sutileza imaginável aos corpúsculos de luz, pode-se esperar que seus efeitos podem naturalmente produzir em alguma proporção os efeitos dos movimentos muito menos rápidos do fluido elétrico, os quais são muito facilmente perceptíveis, mesmo em seus estados mais fracos.
Existem alguns fenômenos da luz de fosforescência solar que à primeira vista podem parecer a favor do sistema corpuscular. Por exemplo, [o fato de] permanecer muitos meses como se [estivessem] em seu estado latente, e sua subsequente re-emissão pela ação do calor. Mas, além dessas considerações, não existe qualquer dificuldade em supor [que] as partículas dos [materiais] fosfóricos foram colocadas a vibrar pela ação da luz, tendo sua ação repentinamente suspensa pela intervenção do frio, como se contraindo o volume do material ou de outra forma. E, novamente, após a retirada da restrição [ele] prossegue em seu movimento, como uma mola faria se fosse segurada rapidamente por um tempo em um estágio intermediário de sua vibração. Nem é impossível que o próprio calor possa, em algumas circunstâncias, tornar-se um modo latente semelhante. Nicholson's Journal, v. II, p. 399.90
[p. 47]. Mas, a ação do calor pode talvez futuramente tornar-se mais inteligível para nós. No momento, parece bastante provável que a luz difere do calor somente na frequência das suas ondulações ou vibrações. Aquelas ondulações que estão dentro de [um] certo limite, em relação à frequência, sendo capaz de afetar o nervo óptico e constituindo luz. E, aquelas que são mais lentas, e provavelmente mais fortes, constituem apenas calor. [A] luz e [o] calor ocorrem para nós cada um em duas situações, o estado vibratório ou permanente e o ondulatório ou transitório. [A] luz vibratória é o pequeno movimento dos corpos inflamados ou da fosforescência solar, e luz ondulatória ou radiante [é] o movimento do meio etéreo excitado por estas vibrações. Calor vibratório é um movimento ao qual todas as substâncias materiais são susceptíveis, e que é mais ou menos permanente. E [o] calor ondulatório [é] aquele movimento do mesmo meio etéreo que tem sido mostrado pelo Sr. King (Morsels of Criticism, p. 99, 1786)91 e [pelo Sr.] M. Pictet (Essais de Physique, 1790) de ser tão capaz de reflexão quanto a luz; e pelo Dr. Herschel [de] ser capaz de ser refratado separadamente. (Philosophical Transactions, p. 284, 1800).92 Quão mais facilmente o calor é comunicado pelos livres acessos das substâncias mais frias, seja por radiação ou por transmissão através de um meio quiescente, foi demonstrado pelos experimentos valiosos do Conde Rumford. É fácil compreender que algumas substâncias, permeáveis à luz, podem ser inadequadas para a transmissão do calor, da mesma maneira que determinadas substâncias podem transmitir alguns tipos de luz, enquanto são opacas em relação a outros.
De forma geral, parece-nos que poucos fenômenos que admitem explicação pelo sistema corpuscular são igualmente consistentes com esta teoria, que muitos outros, que durante muito tempo foram conhecidos mas nunca entendidos, tornam-se por este recurso perfeitamente inteligível; e que muitos novos fatos [p. 48] encontrados ser, assim, apenas redutíveis a uma analogia perfeita com outros fatos e aos simples princípios do sistema ondulatório. Presume-se, que de agora em diante o segundo e terceiro livros do Óptica de Newton serão considerados tão mais completamente compreendidos do que o primeiro foi até o presente momento. Mas, se deve aparecer juízes imparciais, que estão esperando [alguma] evidência adicional para o estabelecimento da teoria, será fácil entrar mais minuciosamente nos detalhes de vários experimentos e mostrar as insuperáveis dificuldades presentes na doutrina newtoniana, que, sem necessidade, seria tedioso e cáustico enumerar [aqui]. Os méritos de seu autor na filosofia natural são grandes, para além de toda a competição ou comparação. Sua descoberta óptica da composição da luz branca, teria sozinha imortalizado seu nome; e os diversos argumentos que tendem a derrubar seu sistema, dão as mais fortes provas da admirável acurácia de seus experimentos.
Suficientes e decisivos como estes argumentos aparecem, não pode ser supérfluo buscar por mais confirmação; que pode com considerável segurança ser esperada, a partir de um experimento muito engenhoso sugerido pelo Professor Robison,93 sobre a refração da luz que retorna para nós da margem oposta do anel de Saturno. Para a teoria corpuscular o anel deve ser consideravelmente alterado quando visto através de um prisma acromático. Uma distorção similar torna-se necessária também de ser observada no disco de Júpiter. Mas, se for encontrado isso um igual desvio é produzido em toda luz refletida a partir desses planetas, dificilmente pode existir qualquer esperança remanescente para explicar as afeições de luz, pela comparação com os movimentos dos projéteis.
